Plan
Comptes Rendus
no. 8

Data selection and estimation of the normal melting temperature of ionic liquids using a method based on homologous cations
José O. Valderrama1, 2  ; Roberto E. Rojas3
1 University of La Serena, Faculty of Engineering, Department of Mechanical Engineering, Casilla 554, La Serena, Chile
2 Center for Technological Information (CIT), c/Monseñor Subercaseaux 667, La Serena, Chile
3 University of La Serena, Faculty of Sciences, Department of Chemistry, Casilla 554, La Serena, Chile
Comptes Rendus. Chimie, Volume 15 (2012) no. 8, pp. 693-699.

Résumé

A simple method based on homologous series for data selection and estimation of the normal melting temperature of ionic liquids is proposed. As known, the values of physicochemical properties of compounds having either homologous cations or anions follow a regular smooth pattern, a characteristic that can help in determining the presence of outliers in a set of experimental data. This characteristic of regular smooth pattern also facilitates the calculation of properties of a given substance by knowing the same property for another substance that has the same cation or anion. A selected database of melting temperature data of ionic liquids available in the literature was constructed and used for determining the melting temperature of those substances for which homology was possible to be applied. The results show that the values determined for the normal melting temperature are accurate enough for engineering calculations and that the melting temperature can be predicted with average uncertainty similar to some experimental data.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2012.04.011
Mots clés : Ionic liquids, Melting temperature, Homologous series, Molecular structure
José O. Valderrama 1, 2 ; Roberto E. Rojas 3

1 University of La Serena, Faculty of Engineering, Department of Mechanical Engineering, Casilla 554, La Serena, Chile
2 Center for Technological Information (CIT), c/Monseñor Subercaseaux 667, La Serena, Chile
3 University of La Serena, Faculty of Sciences, Department of Chemistry, Casilla 554, La Serena, Chile 
@article{CRCHIM_2012__15_8_693_0,
     author = {Jos\'e O. Valderrama and Roberto E. Rojas},
     title = {Data selection and estimation of the normal melting temperature of ionic liquids using a method based on homologous cations},
     journal = {Comptes Rendus. Chimie},
     pages = {693--699},
     publisher = {Elsevier},
     volume = {15},
     number = {8},
     year = {2012},
     doi = {10.1016/j.crci.2012.04.011},
     language = {en},
}
TY  - JOUR
AU  - José O. Valderrama
AU  - Roberto E. Rojas
TI  - Data selection and estimation of the normal melting temperature of ionic liquids using a method based on homologous cations
JO  - Comptes Rendus. Chimie
PY  - 2012
SP  - 693
EP  - 699
VL  - 15
IS  - 8
PB  - Elsevier
DO  - 10.1016/j.crci.2012.04.011
LA  - en
ID  - CRCHIM_2012__15_8_693_0
ER  - 
%0 Journal Article
%A José O. Valderrama
%A Roberto E. Rojas
%T Data selection and estimation of the normal melting temperature of ionic liquids using a method based on homologous cations
%J Comptes Rendus. Chimie
%D 2012
%P 693-699
%V 15
%N 8
%I Elsevier
%R 10.1016/j.crci.2012.04.011
%G en
%F CRCHIM_2012__15_8_693_0
José O. Valderrama; Roberto E. Rojas. Data selection and estimation of the normal melting temperature of ionic liquids using a method based on homologous cations. Comptes Rendus. Chimie, Volume 15 (2012) no. 8, pp. 693-699. doi : 10.1016/j.crci.2012.04.011. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2012.04.011/

Version originale du texte intégral

NotationSymbolsR2

Coefficient of determination

Tm

Melting temperature

%ΔTm

% deviation between correlated and experimental melting temperature

|%ΔTm|

Absolute % deviation between correlated and experimental melting temperature

Tmcal

Calculated melting temperature

Tmexp

Experimental melting temperature

[X][Y]

Ionic liquids having [X] as the cation and [Y] as the anion

AbbreviationsIL, ILs

Ionic liquid and ionic liquids

Tm [X][Y]

Melting temperature of ionic liquid [X][Y]

1 Introduction

The special properties of ionic liquids (ILs), such as very low vapor pressure, large liquidus range, high thermal stability, high ionic conductivity, and large electrochemical window, among others, make these fluids of special interest for several applications. Additionally, since thousand of combinations between cations and anions can be done, ionic liquids can be designed for almost any specific use [1]. Although the first room temperature ionic liquid was discovered more than a century ago, it has been during the last 20 years that these extraordinary fluids have attracted the attention of the scientific community [2].

Current studies on ionic liquids cover a variety of subjects such as electrochemistry, separation science, chemical synthesis, catalysis and pharmaceuticals, The use of ILs as thermal fluids, lubricants, catalysts and solvents, and their application to biomass processing, biphasic chemical processes, photovoltaic cells, fuel cell electrolytes, synthesis of inorganic nanomaterials, extraction of organic compounds, enzymatic reactions, separation of inorganic materials, and many others, are being continuously discussed in the literature and new advances appear every day [3–9]. Classic books such as those of Wypych [10], Wasserscheid and Welton [11] and Koel [12] contain abundant information about properties, uses and applications of ionic liquids. Also of the many recent papers describing the multiple applications of ionic liquids the recent review of Giernoth [13] provides an overview of the wide variety of applications of ILs beyond their use as solvents and discusses the task-specific characteristic of ionic liquids. Also, Aparicio et al. [14] present a good account on thermophysical properties of pure ionic liquids. These authors analyze the type of thermophysical properties data for ionic liquids available in the open literature and the importance of such properties for industrial purposes.

From the industrial point of view, a fundamental understanding of the chemical, physical and thermodynamic properties of ILs should be known before their optimum industrial application. For instance, knowledge of some basic properties is useful in the area of fluid property estimation, thermodynamic property calculations, and phase equilibrium, among others. Several correlations for the density or the heat capacity make use of the critical properties, correlations for the viscosity make use of the density, vapor pressure correlations make use of heat of vaporization, and sublimation pressures make use of melting temperature [15]. This last property, the melting temperature, is of interest in this article.

The melting temperature (Tm) of organic and inorganic substances is a fundamental physical property and has found wide use in chemical identification, purification, and the calculation of other physicochemical properties. In the absence of experimental data, the melting point has to be estimated [16]. Several empirical and semi empirical methods have been used to predict the normal melting point. Among these, group contribution method and neural networks have been employed [16–20]. Although these represent important approaches that should continue being discussed at present there is no general method applicable to any fluid. On the one hand, for neural network applications one needs a reasonable amount of data and a clear picture of the influence of certain properties on that one of interest. In some cases, both requirements are not fulfilled for ionic liquids. On the other hand, group contribution methods were developed for simple substances, mainly hydrocarbons, and its extension to predict properties of ionic liquids is not clear yet. It seems that the way in which molecules are broken into groups is quite different in ionic liquids and most probably the equations that define a property in the group contribution method must be reformulated [21]. Computer simulation and computational chemistry have also been employed and some few applications have been published [22,23].

The concept of homologous series has also been used to correlate melting point data of organic compounds, but still the method is of limiting applicability due to the form in which it has been applied and also due to other inherent limitations as discussed later in this paper [24]. Zhao and Yalkowsky [16] applied a combined approach of group contribution and nonadditive molecular parameters to estimate the melting points of aliphatic compounds. In that study, a similar combined approach is applied to predict the melting points for a database of more complex organic compounds [25].

For ionic liquids, very little progress has been made and very few methods have been used for the estimation of melting points. Katritzky et al. [26] discussed a variety of melting point correlation and prediction methods. In particular they analyzed the capabilities of the CODESSA program (Quantitative Structure/Activity Relationships) for correlating the melting points of imidazolium bromides and benzimidazolium bromides. The descriptors they used for describing these types of ionic liquids were based on the size and electrostatic interactions in the cations. Similar studies have been presented by several other authors [27–30], used a recursive neural network (RNN) to predict the melting points of several pyridinium-based ionic liquids (ILs). According to the authors, the adopted representation of molecular structures captures some significant topological aspects and chemical functionalities of the IL molecules. Huo et al. [31] presented a group contribution method for predicting melting points of imidazolium and benzimidazolium ionic liquids. More recently, Preiss et al. [32] calculated the melting points of crystalline ionic liquids from the ratio of the fusion enthalpy and entropy at the melting point where solid and liquid phases are in equilibrium. The method relies on simple calculations feasible with standard quantum chemical program codes.

2 Melting temperature

Melting happens when the molecules or ions fall out of their crystal structures, and become disordered liquid. This should not be confused with glass transition which is the change that happens from solid state to amorphous solid, but even crystalline solids may have some amorphous portion. This is why the same sample of ILs may have both a glass transition temperature and a melting temperature. Freezing point has the same meaning as melting point but an opposite process [2]. The melting process of ILs is governed by van der Waals forces and electrostatic interaction forces, and the impact of the two forces plays different roles for different kinds of ILs [33].

The liquidus ranges exhibited by ionic liquids can be much greater that those found in common molecular solvents. These ranges go from the melting or glass transition temperature to the decomposition temperature, which is usually before vaporization. Water, for example, at 1 atm. has a liquidus range of 100 °C (0 to 100 °C), refrigerant 134a has 74.8 °C (from −101 to −26.2 °C), and ammonia has only 44.5 °C (from −78 to −33.5 °C). The liquidus range of ionic liquids can be of several hundreds degrees although it is difficult to set an exact range. This because normal boiling temperatures of ionic liquids are unknown (although some estimation methods are available), and the experimental values of normal melting temperature reported in the literature may differ by several degrees. Holbrey and Rogers [2] mention several reasons for the great differences between melting temperatures of ionic liquids reported in the literature:

  • • cooling from the liquid state causes glass formation at low temperatures since solidification kinetics is slow;
  • • on cooling from the liquid, the low-temperature region is not usually bounded by the phase diagram liquidus line;
  • • this region is extended down to a lower temperature limit imposed by the glass transition temperature;
  • • solidification (glass) temperatures recorded on cooling are not true measures and represent kinetic transitions;
  • • formation of metastable glasses is common in molten salts;
  • • in many cases, heating from the glassy state yields an exothermic transition associated with sample crystallization, followed by subsequent melting;
  • • in some cases there is evidence of multiple solid–solid transitions, either crystal-crystal polymorphism or formation of plastic crystal phases.

Besides the inherent differences of the experimental procedure (differential scanning calorimetry, DSC; cold-stage polarizing microscopy, NMR; and X-ray scattering), other factors such as the occurrence of any of the undesirable phenomena indicated above, and probably impurities of the samples before the experiments or contamination during the experiments add more uncertainty to the values reported in the literature.

3 Properties of homologous series

In chemistry, a homologous series is a series of organic compounds with a similar general formula, having similar physicochemical properties due to the presence of the same functional groups. The n-alkanes and the n-alkanols, for instance, form homologous series. The properties of the compounds of a series present in many cases a regular and smooth change as the molecular size, molecular mass or other basic properties, change. Fig. 1 shows this smooth regular change of several properties as the number of carbon increases in the n-alkanes and n-alkanols chains. What is interesting to observe is that of the various properties represented in Fig. 1 (normal boiling temperature, normal melting temperature, normal heat of vaporization, and molecular mass), the melting temperature is the only one that does not follow a smooth monotonous increasing pattern. The melting temperature decreases as the length of the chain increases to then increase again. All the other properties increase with the chain length. This fact is another demonstration of the difficulties found for the estimation of the melting temperature, as discussed above.

Fig. 1

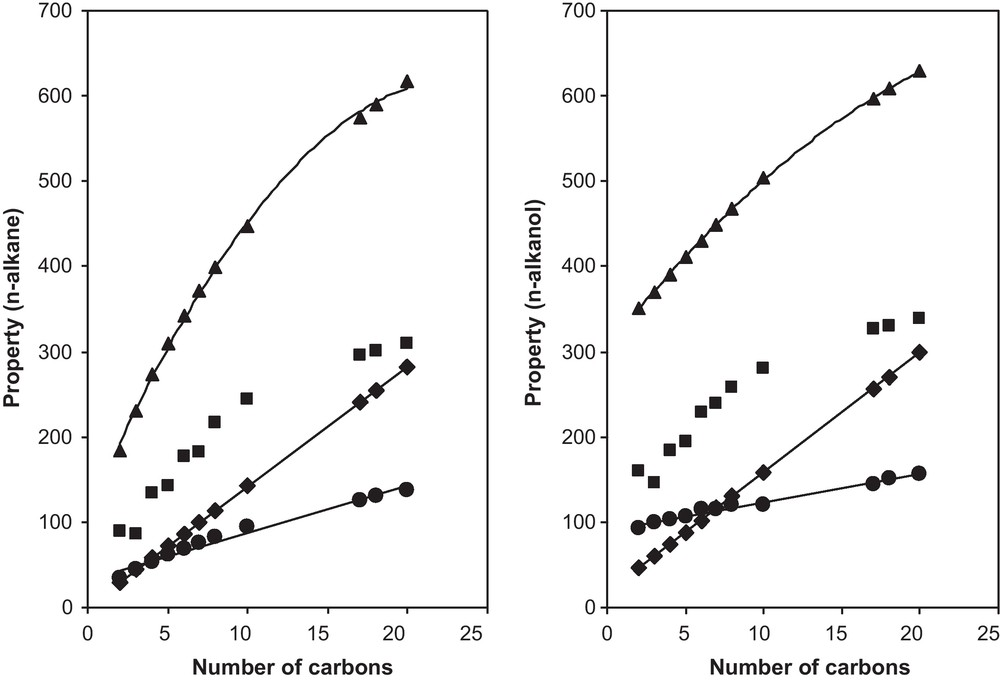
Change of several properties of n-alkanes as a function of the number of carbon in the n-alkane and n-alkanol chain. From bottom to top lines: (♦) molecular weight, (■) melting temperature, (●) heat of vaporization and () normal boiling temperature.

Based on this same concept of homologous series, the concept of homologous compounds seems more interesting in some applications. Karapetyants [34] used this concept in what he called “comparative calculations” to determine several properties of solids and liquids. What the author actually did was relating a given property of compounds that have either the same cation or the same anion. He gave examples for the entropy of formation and the Gibbs free energy of formation. What is interesting about this approach is its extension to estimate the melting temperature of organic compounds and then exploring its application to ionic liquids. Fig. 2 shows the variation of the melting temperature of several homologous inorganic compounds, as suggested by Karapetyants [34]. In Fig. 3, similar plots are presented for organic compounds: Tm of n-alkanes versus Tm of n-alkanols chains and Tm of n-alkanes versus Tm of n-alkenes. As seen in the figure, the comparative calculation described by Karapetyans [34] is well fulfilled in all these cases, with relatively low deviations.

Fig. 2

The melting temperature of homologous inorganic compounds MgX-vs-CaX compound. BaX-vs-PbX compound.

Fig. 3

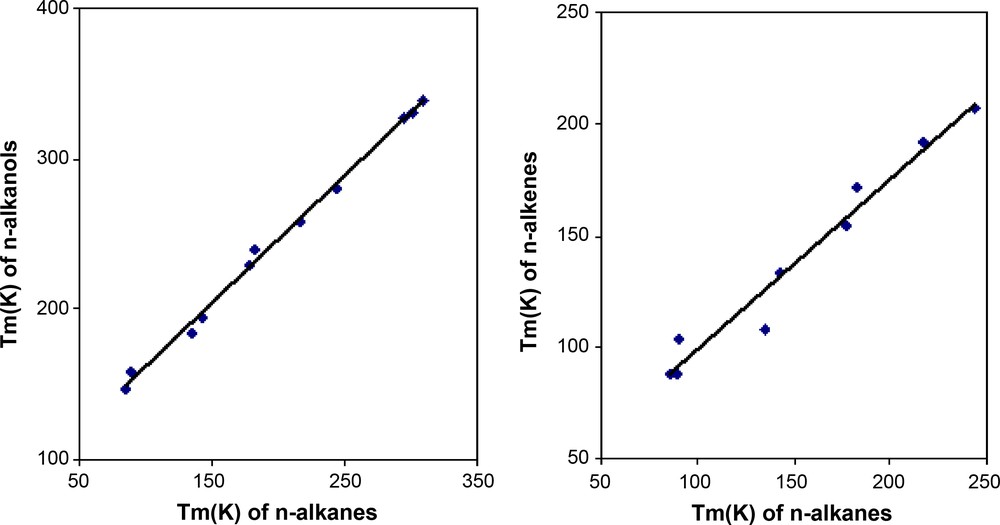
Melting temperature of homologous organic compounds. n-alkanes-vs-alkanols and alkanes-vs-alkenes.

This concept can be extended to predict the melting temperature of ionic liquids for which no accurate methods exist. To do this, melting temperatures for ionic liquids have been collected from the literature and subjected to a first analysis to eliminate doubtful data. This is a necessary step since melting temperature data reported in the literature present great discrepancies and the elimination of doubtful or erroneous data is not a trivial matter in many cases. In fact for some substances several values of melting temperature are found in the literature, sometimes differing for several degrees [35,36].

To visualize the discrepancies in the reported values of Tm, the Fig. 4 shows available melting temperature data for the series [xmim][PF6] and [xmim][BF4]. The great differences in Tm for [C4mim][PF6] and for [C10mim][BF4] (x = 4 and x = 10, respectively) are clearly seen. It should be also noticed that the shape of the curves are similar to that of organic compound presented in Fig. 1, although the decreasing of the melting temperature as the chain length increases is more notorious for ionic liquids. All this makes it necessary to analyze the data as described below. In doing this, the concepts of homologous series and homologous compounds are used.

Fig. 4

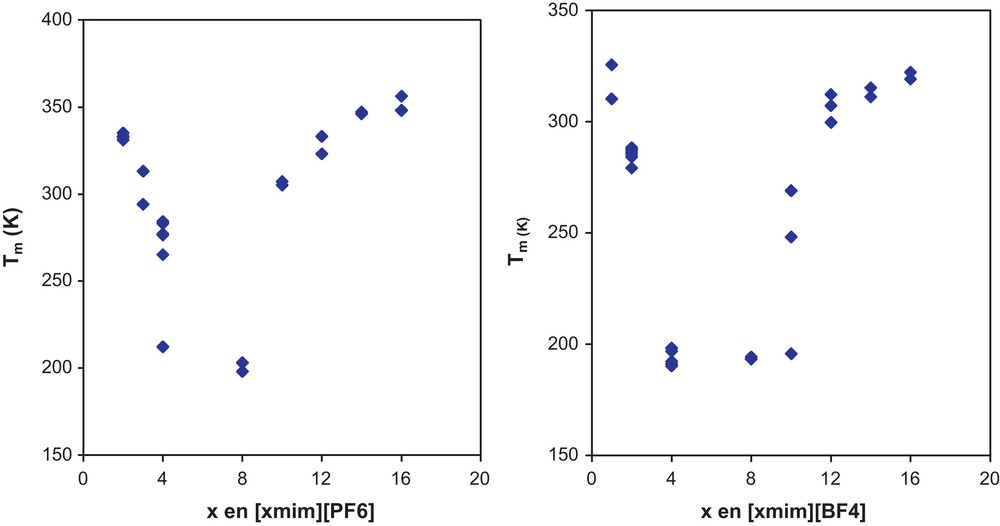
Values of normal melting temperature from different literature sources of [xmim][PF6] and [xmim][BF4] for x = ethyl, propyl, butyl, hexyl, octyl, decyl, dodecyl, tetradecyl, hexadecyl.

4 Data selection

A study of Zhang et al. [36] provides information of literature sources of several properties of ionic liquids available in the open literature. The authors give melting temperature values for 445 ionic liquids while the Dortmund Data Bank [37] provides (as March 2011) melting temperature data for over 400 ILs. The Ionic Liquids Database [38] has melting temperatures for 86 ionic liquids while Merck database has 192 values. The most recent compilation of properties of ionic liquids is that of Zhang et al. [35] who provide melting point data for 975 ionic liquids. All data reported in the literature has been collected to form a database of 1165 values of melting temperature for 953 ionic liquids.

The original set of 1165 data points was reduced and elimination of data was made in the following situations:

  • • data that do not have a clear tendency in an homologous series;
  • • data that according to other sources are liquids at the given melting temperature;
  • • data given as a range instead of a single point;
  • • when only two data are available and they differ for more than 10 K.

These cases are clarified and explained in what follows.

Of the 1165 original values, 18 values corresponded to the higher limit of a range for the solid phase. For instance Tsunashima and Sugiya [39] reported a value for Tm as < 223.15 K for [P2228][Ntf2], meaning that the melting temperature is a value below 223.15 K but no specific value is provided. Similarly, for 86 ILs, ranges of temperature instead of specific values for the melting temperature of ILs are reported. For instance, Pringle et al. [40] reported the range 313.15 to 328.15 K (ΔTm = 15 K) for the melting temperature of N,N-dimethylpyrrolidinium bis(methylsulfonyl)imide. Also, Mikkola et al. [41] reported the range 324.15 to 339.15 K (ΔTm = 15 K) for the melting temperature of N,N,N-trioctyl-N-methylammonium hexafluorophosphate. All these types of uncertain data cannot be used in correlation or prediction models.

Also for 136 ionic liquids some authors report liquid densities at temperatures higher than the reported melting temperature. In these cases, one could trust the density value and assume that the ionic liquid is in the liquid state, or trust the melting temperature and assume that the density is wrong. In this work, values showing this inconsistency were not considered. For instance, for methylimidazolium hexafluorophosphate, Ohno and Yoshizawa [42] reported Tm = 389.15 K while Gu and Brennecke [43] gave a density value of 1.0316 g/cm3 at 298.15 K. For hydrocinnamyl-3-methylimidazolium bis[(trifluoromethyl)sulfonyl]imide, Sergei and Dzyuba [44] reported Tm = 321.15 K while the same authors gave a density value of 1.455 g/cm3 at 298.15 K. Finally, there were 393 repeated values in the original set of 1165 and those not following a clear pattern in homologous families were 98. The several criteria used for selecting data reduced the original 1165 values available in the literature to a consistent database of 671 values of melting temperature, one for each of the 671 ionic liquids of all types. The Table given as supplementary material provides the selected values of melting temperature for these 671 ionic liquids. To the best of the authors’ knowledge, this is the most comprehensive and truthful database of melting temperature data available in the open literature. This does not mean that some values given in the Table could be corrected in the future, when more accurate techniques or a more clear definition of the experimental melting temperature of ionic liquids become available.

Of the selected 671 data, the type of ionic liquid that has more values of melting temperature is that including the anion hexafluorophosphate [PF6]. Therefore this type of ionic liquid is taken as reference to compare the melting temperatures of other ionic liquids using the concept of homologous substances. However, the selection of [X][PF6] as the reference fluid is not compulsory. Any ionic liquid can be taken as reference fluid for homologation. The only requirement is that there are three values of Tm for that reference substance so a reasonable relation between Tm of the reference fluid and that of the ionic liquid of interest can be found.

The Fig. 5 shows the melting temperatures of [X][BF4], [X][Cl], [X][I], [X][Br] in which [X] represent different types of cations, versus the melting temperatures of [X][PF6]. Plots of this type are made for all ionic liquids for which values of melting temperatures for three or more ionic liquids were available and all figures were of similar form. The relatively low dispersion of data around the straight line plotted in Fig. 5 could be ascribed to the inaccuracy of the homologation concept when it is applied to ILs and/or to the inaccuracies of the melting temperature data as discussed in the preceding section.

Fig. 5

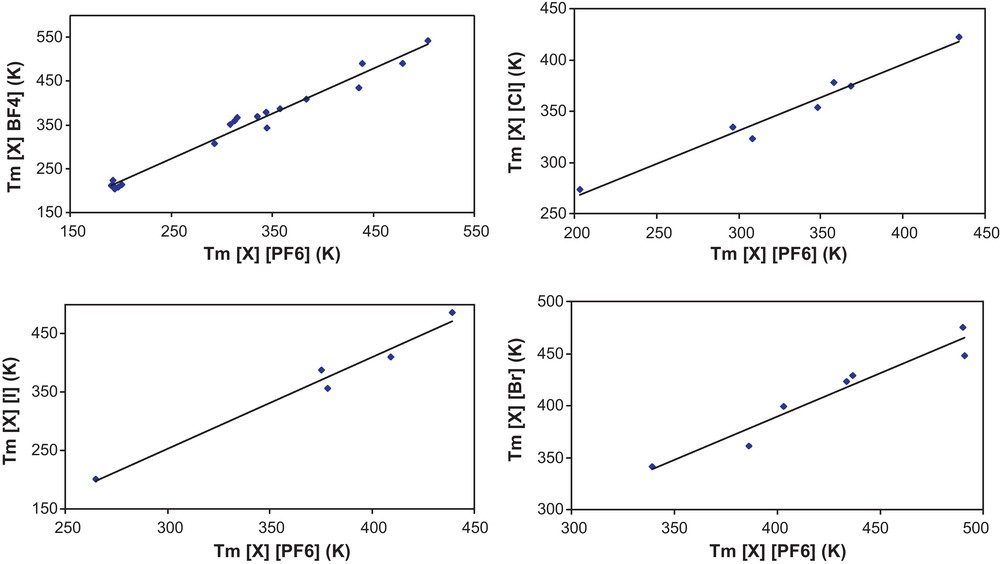
Melting temperatures of selected ionic liquids of common cation [X].

5 Results and discussion

For all cases considered in this study, the linear model seems to be reasonable for a first estimation. Table 1 shows the models for estimating the melting temperature of [X][BF4], [X][Cl], [X][I], [X][TFPB], [X][Br], [X][NO3] and [X][ClO4] by knowing the melting temperature of their homologous [X][PF6].

Table 1

Models for estimating the melting temperature of several ionic liquids of the type [X][Y] by knowing the melting temperature T°m of [X][PF6].

ILType of ILsNModel for Tm for [X][Y]R2%ΔTm|%ΔTm||%ΔTm|max
[X][BF4]Imidazolium
Ammonium
Pyridinium		21Tm [X][BF4] = −6.1963 + 0.9455 × T°m0.9790.313.78.1
[X][Cl]Imidazolium
Ammonium
Pyridinium		9Tm [X][Cl] = 136.75 + 0.648 × T°m0.9690.032.04.1
[X][I]Imidazolium
Ammonium
Thiazolium		5Tm [X][I] = −219.78 + 1.5747 × T°m0.9760.033.65.5
[X][TFPB]Methylimidazolium3Tm [X][TFPB] = 240.49 + 0.5349 × T°m0.996< 0.010.20.3
[X][Br]Imidazolium
Ammonium
Morpholinium
Triazolium		7Tm [X][Br] = 55.935 + 0.8344 × T°m0.9350.072.44.7
[X][NO3]Imidazolium
Imidazolidine
Morpholinium		4Tm [X][NO3] = 132.91 + 0.5654 × T°m0.9840.010.91.5
[X][ClO4]Imidazolium
Ammonium
Morpholinium		3Tm [X][ClO4] = 686.66 − 0.8947 × T°m0.9520.010.71.0

The Table also shows three statistical parameters that according to the authors are the most representative of the accuracy of the method, as discussed by Valderrama and Alvarez [45]. These parameters are: the relative average deviation, the absolute average deviation and the maximum absolute deviation. These are listed in columns 5 to 7 of Table 1 and are defined as:

%ΔTm=100N∑i=1NTmcal−TmexpTmexpi(1)
%ΔTm=100N∑i=1NTmcal−TmexpTmexpi(2)
%ΔTmmax=max   value   of   100×Tmcal−TmexpTmexp(3)

The term R2, the coefficient of determination, is a statistical parameter normally used for linear models and provides a measure of how well the variables under study are likely to be predicted, being 1.0 the best expected value for a linear correlation [46]. As seen in Table 1, the three statistical parameters indicate that the correlations are acceptable for engineering calculations. Relative deviations are below 1%, absolute deviations are below 3.7%, and maximum deviation is 8.1%. The value of R2 is higher than 0.93 for all cases.

6 Conclusions

Literature data on melting temperature of ionic liquids have been analyzed to construct a database of recommended values. The several criteria used for selecting melting temperature data reduced the original 1165 values available in the literature to a consistent database of 671 values. The ionic liquids containing hexaflurophosphate as the anion have been selected as the reference fluid for estimating the melting temperature of various types of ionic liquids. A method based on the homologous substance concept for estimating the melting temperature has been presented and linear models were found for seven families of ILs. The estimation method is considered to give reasonable values of the normal melting temperature for engineering calculations.

Acknowledgements

The authors thank the support of the Direction of Research of the University of La Serena, of the Center for Technological Information of La Serena-Chile, and of the National Council for Scientific and Technological Research (CONICYT), through the research grant FONDECYT 1120162.

Bibliographie

[1] M. Freemantle Chem. Eng. News., 76 (1988), p. 32

[2] J.D. Holbrey, R.D. Rogers, Ionic Liquids in Synthesis, in: P. Wasserscheid, T. Welton (Eds.), Wiley VCH Verlag GmbH and Co. KGaA, 2002.

[3] M. Moniruzzaman; K. Nakashima; N. Kamiya; M. Goto Biochem. Eng. J., 48 (2010), p. 295

[4] D. Han; K.H. Row Molecules, 15 (2010), p. 2405

[5] Z. Ma; J. Yu; S. Dai Adv. Mater., 22 (2010), p. 261

[6] C.F. Poole; S.K. Poole J. Chromatogr. A, 1217 (2010), p. 2268

[7] H. Olivier-Bourbigou; L. Magna; D. Morvan Appl. Catalysis A, 373 (2010), p. 1

[8] S. Van de Vyver; J. Geboers; P.A. Jacobs; B.F. Sels Chem. Cat. Chem., 3 (2011), p. 82

[9] M. Joskowska; I. Kopczynska; B. Debski; D. Holownia-Kedzia; R. Aranowski; J. Hupka Physicochem. Probl. Miner. Process., 48 (2012), p. 129

[10] G. Wypych Handbook of Solvents, Toronto-New York, USA, ChemTec Publishing, 2001

[11] P. Wasserscheid; T. Welton Ionic Liquids in Synthesis, Wiley VCH Verlag GmbH and Co., Weinheim, 2008

[12] M. Koel Ionic Liquids in Chemical Analysis, CRC Press, Taylor and Francis Group, Boca Raton, USA, 2009

[13] R. Giernoth Angewandte Chemie, 49 (2010), p. 2834

[14] S. Aparicio; M. Atilhan; F. Karadas Ind. Eng. Chem. Res, 49 (2010), p. 9580

[15] B.E. Poling; J.M. Prausnitz; J.P. O’Connell The Properties of Gases and Liquids, McGraw-Hill Book Co., New York, 2001

[16] L. Zhao; S.H. Yalkowsky Ind. Eng. Chem. Res., 38 (1999), p. 3581

[17] K.K. Joback; R. Reid Chem. Eng. Comm., 57 (1987), p. 233

[18] P. Simamora; A.H. Miller; S.H. Yalkowsky J. Chem. Inf. Comput. Sci., 33 (1993), p. 437

[19] J.F. Krzyzaniak; P.B. Myrdal; P. Simamora; S.H. Yalkowsky Ind. Eng. Chem. Res., 34 (1995), p. 2530

[20] G.Y. Jain; S.H. Yalkowsky Ind. Eng. Chem. Res., 43 (2004), p. 7618

[21] C.L. Aguirre; L.Z. Cisternas; J.O. Valderrama Int. J. Thermophys., 33 (2011), p. 34

[22] S. Alavi; D.L. Thompson J. Phys. Chem. B, 38 (2005), p. 18127

[23] A.R. Katritzky; A. Lomaka; R. Petrukhin; R. Jain; M. Karelson; A.E. Visser; R.D. Rogers J. Chem. Inf. Comput. Sci, 42 (2002), p. 71

[24] J.S. Chickos; G. Nichols J. Chem. Eng. Data, 46 (2001), p. 562

[25] A. Jain; G. Yang; S.H. Yalkowsky Ind. Eng. Chem. Res., 43 (2004), p. 7618

[26] A.R. Katritzky; R. Jain; A. Lomaka; R. Petrukhin; M. Karelson; A.E. Visser; R.D. Rogers J. Chem. Inf. Comput. Sci., 42 (2002), p. 225

[27] D.M. Eike; J.F. Brennecke; E.J. Maginn Green Chem., 5 (2003), p. 323

[28] S. Trohalaki; R. Pachter; G.W. Drake; T. Hawkins Energy Fuels., 19 (2005), p. 279

[29] N. Sun; X. He; K. Dong; X. Zhang; X. Lu; H. He; S. Zhang Fluid Phase Equilibria, 246 (2006), p. 137

[30] R. Bini; C. Chiappe; C. Duce; A. Micheli; R. Solaro; A. Staritac; M.R. Tinéb Green Chem., 10 (2008), p. 306

[31] Y. Huo; S. Xia; Y. Zhang; P. Ma Ind. Eng. Chem. Res., 48 (2009), p. 2212

[32] U. Preiss; S. Bulut; I. Krossing J. Phys. Chem. B, 114 (2010), p. 11133

[33] J. Pernak; A. Czepukowicz; R. Pozniak Ind. Eng. Chem. Res., 40 (2001), p. 2379

[34] M.K. Karapetyants Chemical Thermodynamics, Mir Pub, Moscow-URSS, 1978

[35] S. Zhang; X. Lu; Q. Zhou; X. Li; X. Zhang; S. Li Ionic Liquids, Physicochemical Properties, Elsevier B.V. Jordan, Oxford, 2009

[36] S. Zhang; N. Sun; X. He; X. Lu; X. Zhang J. Phys. Chem., 35 (2006) no. 4, p. 1475

[37] Dortmund Data Bank, http://www.ddbst.com/en/ddbst/index.php, accessed March. 2011.

[38] National Institute of Standars and Techology (NIST), Ionic Liquids Database-LThermo, http//ilthermo.boulder.nist.gov/IL Thermo/mainmenu.uix, accessed July 2007.

[39] K. Tsunashima; M. Sugiya Electrochem. Commun., 9 (2007), p. 2353

[40] J.M. Pringle; J. Golding; K. Baranyai; C.M. Forsyth; G.B. Deacon; J.L. Scott; D.R. MacFarlane New J. Chem., 27 (2003), p. 1504

[41] J.P. Mikkola; P. Virtanen; R. Sjoholm Green Chem., 8 (2006), p. 250

[42] H. Ohno; M. Yoshizawa Solid State Ionics, 154–155 (2002), p. 303

[43] Z. Gu; J.F. Brennecke J. Chem. Eng. Data., 47 (2002), p. 339

[44] S.V. Sergei; R.A.B. Dzyuba Chem. Phys., 3 (2002), p. 161

[45] J.O. Valderrama; V.H. Alvarez J. Chem. Eng., 83 (2005), p. 1

[46] D.A. Ratkowsky Handbook of Nonlinear Regression Models. 44, Marcel Dekker, New York, USA, 1990

Commentaires - Politique

Ces articles pourraient vous intéresser

Melting properties of molten salts and ionic liquids. Chemical homology, correlation, and prediction

José O. Valderrama; Richard A. Campusano

C. R. Chim (2016)