1 Introduction
During the last decade, heteropolynuclear 3d-4f complexes have attracted the attention of a large number of researchers because they may exhibit interesting magnetic properties [1]. In particular, some 3d/4f metal aggregates behave as single-molecule magnets (SMMs) [2], which are systems exhibiting slow relaxation of the magnetization and magnetic hysteresis below the so-called blocking temperature (TB) without undergoing 3D magnetic ordering. The origin of the SMM behaviour is the existence of an energy barrier (Δ) for the reversal of the molecular magnetization that depends on the large spin multiplicity of the ground state (ST) and the easy-axis (or Ising-type) magnetic anisotropy of the entire molecule (D < 0). Nevertheless, recently, it has been shown that low-coordinate, high spin iron(II) and cobalt(II) complexes with large and positive D values can also exhibit SMM behaviour [3]. These nanomagnets straddle the quantum/classical interface showing quantum effects such as quantum tunnelling of the magnetization and quantum phase interference and are potential candidates for magnetic information storage and quantum computing [4]. In these 3d/4f systems, the magnetic interaction between heavy lanthanide ions, such as TbIII, DyIII, HoIII and ErIII, that provide large magnetic moments and large axial local magnetic anisotropy, and transition metal ions is generally ferromagnetic in nature, and therefore leads to ground states with increased magnetic moments and, depending on the local magnetic moments orientation, to strong easy-axis anisotropy. Recently, it has been shown that (ferromagnetic) 3d/4f metallic aggregates containing isotropic metal ions, a large spin ground state and high spin degeneracy can also exhibit an enormous magneto-caloric effect (MCE) [5]. This is an effect based on the change of magnetic entropy upon application of a magnetic field and can be used for cooling applications via adiabatic demagnetisation; such molecules are referred to as “molecular magnetic coolers” or “molecular refrigerants”. Although a number of 3d-4f heterometallic complexes have been reported so far, those containing CoII are rather limited [6]. Among these systems, three CoII-LnIII-CoII (LnIII = Gd, Tb, and Dy) trinuclear complexes with the tripodal bridging ligand N,N′,N′′-tris(2-hydroxy-3-methoxybenzylidene)-2-aminomethyl-2-methyl-1,3-propanediamine [6a], a CoII-LnIII-CoII trinuclear complex with the tripodal bridging ligand prepared by the condensation of (S)P[N(Me)NH2]3 and o-vanillin [6b], Co2Gd2 and Co2Dy2 tetranuclear complexes containing the o-vanillin [6c] and 2,6-pyridinedimethanol [6d] bridging ligands, respectively, CoIICoIIIDy4 aggregates with the tris(hydroxymethyl)aminomethane ligand [6e], and a dodecanuclear Co2Dy10 wheel complex with the ligand 1,2-bis(2-hydroxy-3-methoxybenzylidene) hydrazine [6f], either exhibit (they show hysteresis loops in magnetization versus field studies) or can exhibit (they show a maximum in the χ′′ ac signal at approximately 2 K) SMM behaviour. In these Co/Ln complexes both the lanthanide and the CoII ions are anisotropic and will contribute to the anisotropy of the whole molecule. However, as suggested by Costes et al. [6c] the introduction of several anisotropic ions does not necessarily lead to an enhanced molecular anisotropy and thus a positive effect on the SMM behaviour. In some cases, to observe the SMM behaviour the presence of a small dc field is needed to fully or partly suppress the fast and efficient zero-field quantum tunneling of magnetization [6b], which can be promoted by strong transverse anisotropy which results from the presence of the anisotropic centres.
Amongst the five examples of CoII-LnIII dinuclear complexes reported so far [6g–k], only three exhibit ferromagnetic interactions between the metal ions [6g–i], and none of them show SMM behaviour. We have designed a new and flexible [non-Schiff base] compartmental ligand with an inner N3O2 coordination pocket and an external O2O2 site that favours the formation of CoIILnIII complexes (Scheme 1).
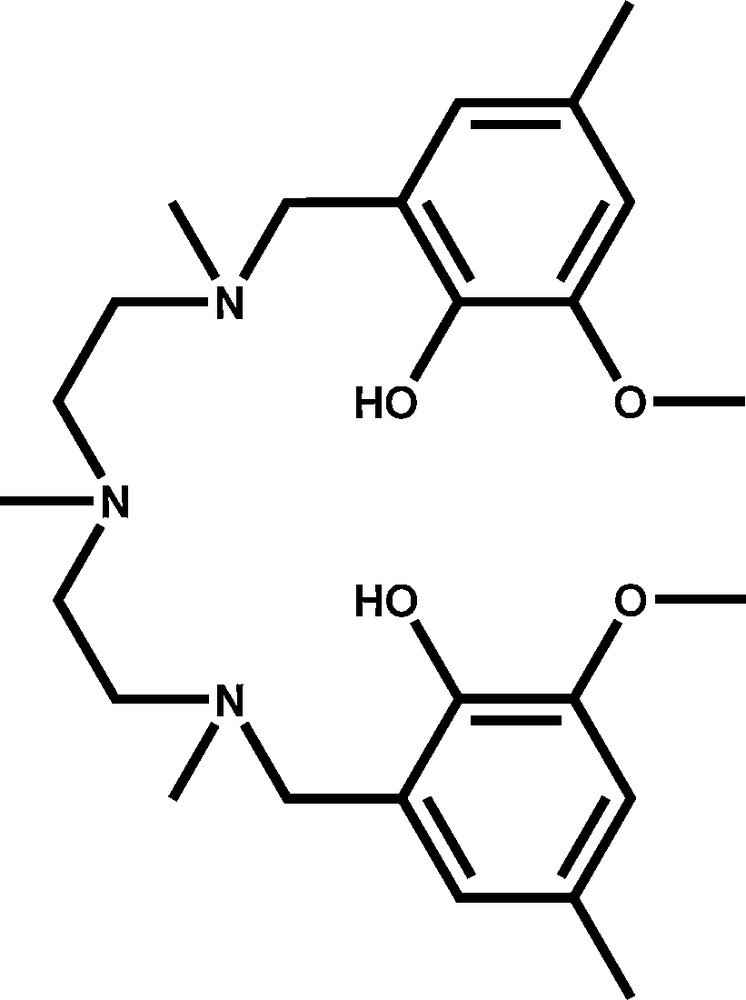
Structure of the ligand H2L.
The CoII ion has a tendency to adopt an octahedral geometry and therefore the pentacoordinating inner site forces this metal ion to saturate its coordination position with an additional donor atom, which can belong to either:
- • a monodentate ligand, leading to doubly-bridged dinuclear CoLn molecules;
- • or a bridging ligand connecting the 3d and 4f metal ions, leading to triply-bridged 3d-4f dinuclear molecules;
- • or a bridging ligand connecting different 3d-4f molecules, affording higher nuclearity CoII/LnIII complexes.
In this article we report the synthesis, structural characterization and magnetic properties of a series of diphenoxo-acetate triply-bridged CoIILnIII (LnIII = Gd, Tb, Dy, Ho and Er) and doubly-bridged CoIILnIII (LnIII = Gd, Tb) dinuclear complexes, as well as a series of tetranuclear rectangular Co2Ln2 (LnIII = Gd, Tb, Dy, Ho and Er) complexes, in which dinuclear CoIILnII dinuclear units are connected by 1,5-dicyanamide bridging ligands. The aim of this work is twofold: to discover whether simple CoIILnIII dinuclear complexes can exhibit SMM behaviour, and if so to analyze if the SMM behaviour is retained when the dinuclear CoIILnIII molecules are connected by bridging (dicyanamide) ligands.
2 Experimental
2.1 General
Unless stated otherwise, all reactions were conducted in oven-dried glassware in aerobic conditions, with the reagents purchased commercially and used without further purification. The ligand H2L was prepared as previously described [7].
2.2 Preparation of complexes
2.2.1 [Co(μ-L)(μ-Ac)Ln(NO3)2] (LnIII = Gd (1), Tb (2), Dy (3), Ho (4), Er (5))
A general procedure was used for the preparation of these complexes: To a solution of H2L (56 mg, 0.125 mmol) in 5 mL MeOH were subsequently added with continuous stirring 31.1 mg (0.125 mmol) of Co(Ac)2·4H2O and 0.125 mmol of Ln(NO3)3·nH2O. The resulting red solution was filtered and allowed to stand at room temperature. After one day, well-formed prismatic pink crystals of compounds 1-5 were obtained with yields in the range 55–65% based on Co.
2.2.2 [Co(H2O)(μ-L)Ln(NO3)3]·S (LnIII = Gd, S = H2O (6), Tb, S = MeOH (7))
These compounds were prepared in 40-50% yield as light pink crystals following the procedure for 1-5, except that Co(NO3)2·6H2O (36 mg, 0.125 mmol) was used instead of Co(Ac)2·4H2O.
2.2.3 [Co(μ-L)(μ-N(CN)2)Ln(NO3)2]2·4MeOH (LnIII = Gd (8), Tb (9), Dy (10), Ho (11), Er (12))
To a solution of H2L (56 mg, 0.125 mmol) in 5 mL MeOH were subsequently added with continuous stirring 36 mg (0.125 mmol) of Co(NO3)2·6H2O and 55 mg (0.125 mmol) of Ln(NO3)3·5H2O. To this solution was added dropwise another solution containing 11 mg of dicyanamide (0.125 mmol). The resulting red solution was filtered, eliminating any amount of insoluble material, and allowed to stand at room temperature for 3–4 days whereupon pink crystals of complexes 8-12 were formed in a yield of 35–45%.
The purity of the complexes was checked by elemental analysis (Table S1).
2.3 Physical measurements
Elemental analyses were carried out at the “Centro de Instrumentación Científica” (University of Granada) on a Fisons-Carlo Erba analyser model EA 1108. The IR spectra on powdered samples were recorded with a ThermoNicolet IR200FTIR by using KBr pellets. Magnetisation and variable temperature (2–300 K) magnetic susceptibility measurements on polycrystalline samples were carried out with a Quantum Design SQUID MPMS XL-5 device operating at different magnetic fields. The experimental susceptibilities were corrected for the diamagnetism of the constituent atoms by using Pascal's tables.
2.4 Single-crystal structure determination
Suitable crystals of 1-12 were mounted on a glass fibre and used for data collection. For compounds 1-3 and 6-7, data were collected with a dual source Oxford Diffraction SuperNova diffractometer equipped with an Atlas CCD detector and an Oxford Cryosystems low temperature device operating at 100 K and using Mo-Kα radiation. Semi-empirical (multi-scan) absorption corrections were applied using Crysalis Pro [8]. For compounds 4 and 5 data were collected with a Bruker AXS APEX CCD area detector equipped with graphite monochromated Mo-Kα radiation (λ = 0.71073 Å) by applying the ω-scan method. Lorentz-polarization and empirical absorption corrections were applied. Crystallographic data for compounds 8-12 were collected with a Nonius-Kappa CCD area-detector diffractometer using graphite monochromatised Mo-Kα radiation (λ = 0.71073 Å). The data were collected by ϕ and ω rotation scans and processed with the DENZO-SMN v0.93.0 software package [9]. Empirical absorption corrections were performed with SADABS [10]. The structures were solved by direct methods by using the program SIR-97 [11] or SHELXS97 [12] and refined with full-matrix least-squares calculations on F2 using SHELXS97 [12]. Figures were drawn with ORTEP-3 for DIAMOND 3.0 [13]. For all compounds the heavy atoms were refined anisotropically. All hydrogen atoms were included at the calculated distances with fixed displacement parameters from their host atoms. Final R(F), wR(F2) and goodness of fit agreement factors, details on the data collection and analysis can be found in Table S2. Selected bond lengths and angles are given in Table S3 for compounds 1-7 and S4 for compounds 8-12. CCDC-866939-866950 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data request.cif.
2.5 Computational details
To consider the neighborhood influence of the DyIII and the CoII cations on the g axis of the CoII and DyIII atoms, respectively, but with the aim to simplify the calculation, two models have been built up. One, where the DyIII atom has been substituted by a closed-shell lanthanide such as LaIII, and the other one, where the CoII atom has been substituted by a closed-shell transition metal such as ZnII.
All calculations have been performed with the MOLCAS 7.2 package [14]. MOLCAS ANO-RCC basis set has been used for all the atoms, with the exception of LaIII and ZnII which have been treated with an embedding model potentials (AIMP) [15]. The following contractions were used: Dy [9s8p6d4f3g2h]; Co [6s5p4d2f]; O [4s3p1d]; N [4s3p1d]; C [3s2p] and H [2s].
To compute the g axis for the DyIII cation a complete active space self-consisting field (CASSCF) calculation has been performed with an (9,7) active space and 21 sextets, 128 quadruplets and 130 doublets have been mixed into the restricted active space state interaction (RASSI-SO) procedure. For the g axis of the CoII cation an (7,5) active space CASSCF calculation has been performed and 10 quadruplets and 35 doublets have been mixed through the RASSI-SO procedure.
Finally, the g axis values were extracted form MOLCAS output (CASSCF/RASSI calculations) by using the SINGLE_ANISO computer code [16].
3 Results and discussion
The reaction of H2L with Co(OAc)2·4H2O and subsequently with Ln(NO3)3·nH2O in MeOH in either 1:1:1 or 2:2:1 molar ratio always affords orange-brown crystals of the triply-bridged compounds [Co(μ-L)(μ-OAc)Ln(NO3)2] (LnIII = Gd (1), Tb (2), Dy(3), Ho (4), Er(5)). Under no circumstances were trinuclear CoIILnIIICoII complexes obtained. The same reaction but using Co(NO3)3·6H2O instead of Co(OAc)2·4H2O and Ln(NO3)3·6H2O (LnIII = Gd, Tb) led to the doubly-bridged complexes [Co(H2O)(μ-L)Ln(NO3)3]·S (S = H2O or MeOH) and (LnIII = Gd (6) and Tb(7)). X-ray quality crystals for the complexes of Dy, Ho, and Er could not be obtained. The tetranuclear complexes [Co(μ-L) (μ-N(CN)2)Ln2(NO3)2]2 (LnIII = Gd (8), Tb (9), Dy (10), Ho (11), Er(12)) could be prepared by reacting a methanolic solution containing H2L, Co(NO3)3·6H2O and Dy(NO3)3·6H2O with NaN(CN)2 in a 1:1:1:1 molar ratio. In the course of the reaction the dinuclear CoIILnIII dinuclear units, formed in situ, are then connected by end-to-end dicyanamide bridging ligands.
The diffuse reflectance electronic spectra of these complexes in the visible region show three absorption bands around 8700, 16,700 (shoulder) and 20,000 cm−1 (the electronic spectra of compound 1 and 8 are given as examples in Fig. S1), which are assigned to the 4T1g→4T2g, 4T1g→4A2g and 4T1g→4T1g (P) transitions, respectively. This is typical of high spin distorted octahedral Co(II) complexes [17]. It can be noticed that the electronic spectra of the dinuclear CoIILnII and tetranuclear CoII2LnIII2 complexes are almost identical, reflecting the similarities between the two electronic environments of the Co(II) ions in both types of complex. It seems that the change from a CoN3O3 coordination environment in the dinuclear CoIILnII complexes to a CoN4O2 coordination environment in the tetranuclear CoII2LnIII2 complex only promotes a minor bathochromic shift of the transitions. This is as expected for the coordination of dicyanamide, which is a weaker field ligand than either acetate or water.
3.1 Crystal structures
Complexes 1 and 4 are isostructural, crystallizing in the triclinic P-1 space group. Their structures are made of two almost identical dinuclear [Co(μ-L)(μ-Ac)Ln(NO3)2] molecules, in which the LnIII and CoII ions are bridged by two phenoxo groups of the L2− ligand and one syn-syn acetate anion. These complexes are isostructural to those previously reported by us for the NiIIDyIII analogue [7]. Complexes 2, 3, and 5 are also isostructural but they crystallize in the monoclinic P21/n space group and their structure is very similar to those of 1 and 4 but having only one crystallographically independent CoIILnIII molecule. The structure of 1 is given as an example in Fig. 1.
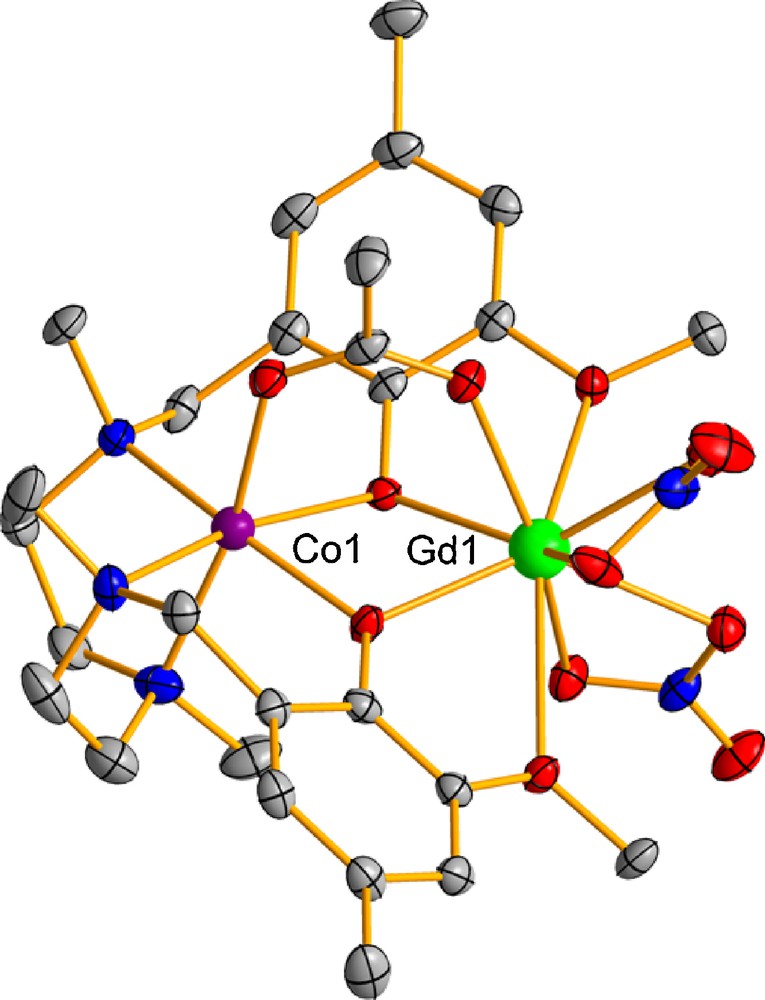
Perspective view of one of the crystallographic independent molecules of complex 1. Color code: N = blue, O = red, Co = violet, Dy = green, C = grey.
Within the dinuclear [Co(μ-L)(μ-Ac)Ln(NO3)2] molecules, the CoII ion exhibits a slightly distorted fac-CoN3O3 octahedral coordination environment. The distortion mainly takes place along the three-fold axis passing through the N3 and O3 faces of the octahedron. In fact, the calculation of the degree of distortion of the CoII coordination polyhedron with respect to an ideal six-vertex polyhedra, by using the continuous shape measure theory and SHAPE software [18], led to shape measures relative to the octahedron (OC-6) and trigonal prism (TPR-6) with values of ∼1.7 and ∼10, respectively, for the isostructural complexes 1 and 4 and with values of ∼2.8 and ∼8.4 for the isostructural complexes 2, 3 and 5. The shape measures relative to other reference polyhedra are significantly larger and therefore the CoN3O3 coordination spheres of complexes 1-5 are found in the OC-6 ↔ TPR-6 deformation pathway close to the octahedral geometry (∼77% for 1 and 4 and ∼70% for 2, 3 and 5). In all these complexes, the corresponding LnIII ion exhibits a rather asymmetric LnO9 coordination sphere, which is comprised of two phenoxo bridging oxygen atoms, two methoxy oxygen atoms, one oxygen atom from the acetate bridging group and four oxygen atoms belonging to two bidentate nitrate anions, with Ln-O bond distances in the range 2.28–2.51 Å.
The average Ln-Ophenoxo bond distances within each series of isostructural compounds 1 and 4, and 2, 3 and 5, respectively, steadily decrease from GdIII to ErIII with a concomitant decrease of the average Co-Ln and Ln-Oacetate bond distances, due to the lanthanide contraction.
The Co(Ophenoxo)2Ln bridging fragment is rather asymmetric as there are two non-equivalent Ln-Ophenoxo and Co-Ophenoxo bond distances, as well as two different Co-O-Ln bridging angles (∼7° of difference). It is interesting to note that in complexes 1-5 the coordination of the syn-syn bridging acetate group induces the folding of the M(μ-O2)Ln bridging fragment, with hinge angles (the dihedral angle between the O-Co-O and O-Ln-O planes) that are close to 22°. In each series of isostructural compounds, the hinge angle increases with decreasing LnIII size, as expected.
The reaction of the H2L ligand with Co(NO3)3·6H2O and subsequently with Ln(NO3)3·6H2O (LnIII = Gd and Tb) led to two isostructural double-phenoxo-bridged dinuclear complexes [Co(H2O)(μ-L)Ln(NO3)3] (Gd (6) and Tb (7)) (Fig. 2).
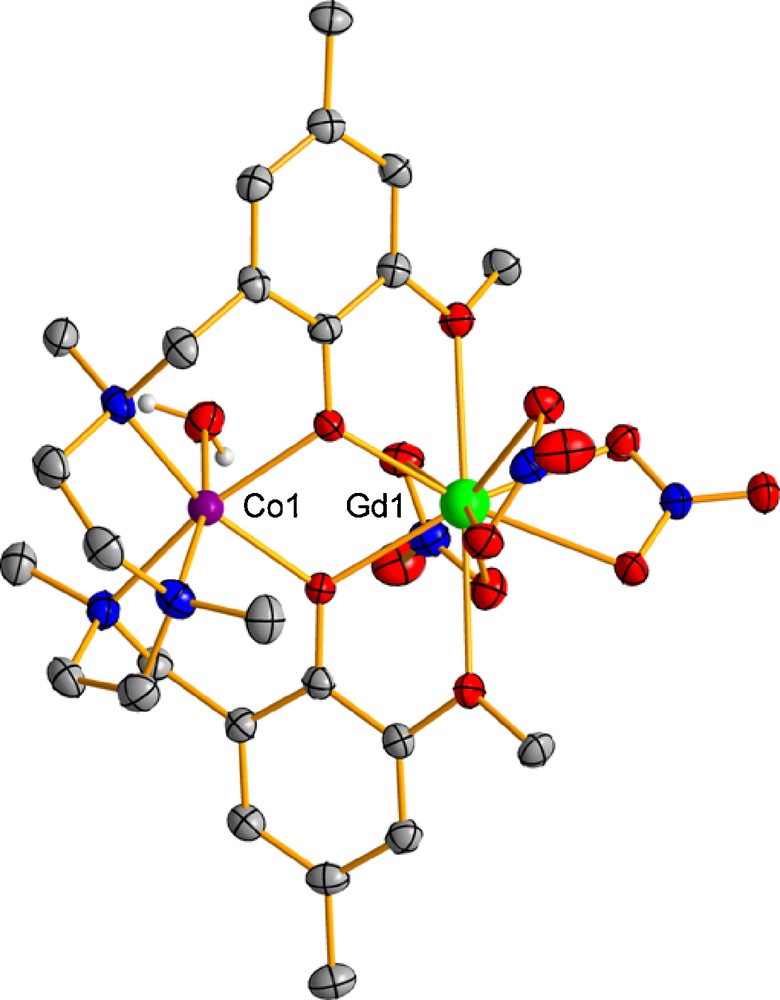
Perspective view of the molecular structure of 6. Color code: N = blue, O = red, Co = violet, Dy = green, C = grey.
Although diphenoxo-nitrate triply-bridged Ni-Ln complexes have been observed for the smaller LnIII ions (from TbIII to ErIII) [19], the TbIII ion is not able to form the triple-bridged complex. It seems that the combined effect of the LnIII and MII sizes plays an important role in the adoption of the triply-bridged structure. Thus when the size of the metal ion increases, the tension of the nitrate bridging ligand becomes larger and, from definite values of the size of the metal ions, the formation of the nitrate bridge is unfavourable. Therefore, subtle changes in the size of the MII ion on going from NiII to CoII may be responsible for the presence of only a double-phenoxo bridge in 7. The absence of the nitrate bridging group in 6 and 7 allows the structure to be more planar (hinge angles of 3.7° and 1.5°, respectively) and the bridging fragment more symmetric (the two Ln-O-Co angles of the bridging fragment are very close to each other with values of ∼109°) than in the case of complexes 1-5. The planarity of the structure gives rise to an increase in the Co-Ln distance with respect to those observed in 1-5. In addition, the Ln coordination sphere, which is rather asymmetric regarding the Ln-O bond distances, expands from LnO9 to LnO10. It should be noted that the sixth position of the CoII is saturated by the coordination of a water molecule, leading to a CoN3O3 octahedral coordination sphere that is more distorted toward trigonal prismatic that those of compounds 1-5. In particular, shape measures relative to the octahedron (OC-6) and trigonal prism (TPR-6) were 2.30 and 9.38 for 6 (73.9% of octahedral geometry) and 2.95 and 11.28, for 7 (81.3% of octahedral geometry).
Complexes 8-12 are isotructural and their structure consists of centrosymmetric tetranuclear molecules [Co(μ-L)(μ-N(CN)2)Ln(NO3)2]2 and four methanol molecules of crystallization. Within each tetranuclear Co2Ln2 molecule, two dinuclear cationic fragments [Co(μ-L)Ln(NO3)2]+ are connected by two 1,5-dicyanamide bridging ligands in a “head to tail” arrangement (Fig. 3).
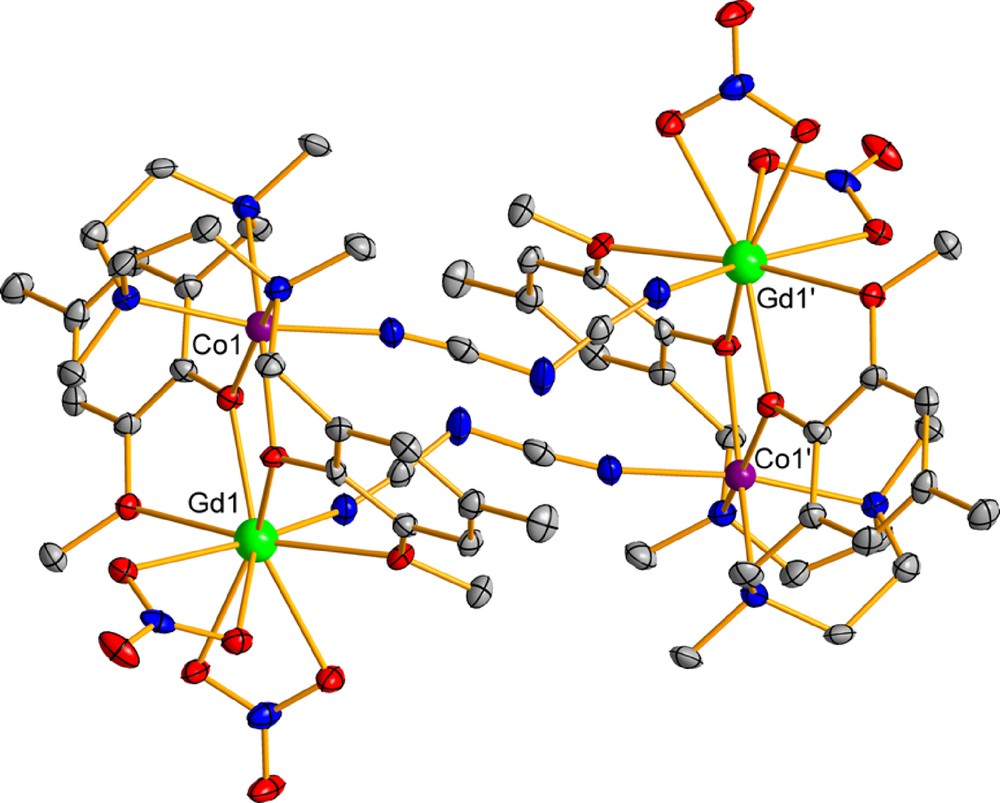
Perspective view of the molecular structure of 8. Color code: N = blue, O = red, Co = violet, Dy = green, C = grey. Symmetry code: (‘) 1-x, -y, 1-z.
The cobalt(II) ions exhibit distorted octahedral CoN4O2 coordination spheres with shape measures relative to the octahedron (OC-6) and trigonal prism (TPR-6) of ∼2.30 and ∼9.8, respectively, and are found in the OC-6 ↔ TPR-6 deformation pathway, close to octahedral geometry (∼75%). The coordination of the dicyanamide bridging ligand to the lanthanide ion leads to a LnO8N coordination sphere, which, as in the dinuclear complexes 1-7, is rather asymmetric regarding the Ln-O bond distances (Table S3). As expected for the lanthanide contraction, the Ln-N, Ln···Co and the average Ln-Ophenoxo bond distances decrease with decreasing LnIII ionic radii on going from GdIII to ErIII. The bridging fragment is asymmetric but the difference between the two Ln-O-Co angles is only ∼3°, whereas the hinge angle is ∼7.5°. When the Ln-O-Co and hinge angles are compared for complexes 1-12, one realizes that the bridging fragment becomes more symmetrical (smaller difference between each couple of Ln-O and Co-O bond distances and Ln-O-Co angles) as its planarity increases (smaller hinge angles).
Complexes 1-5 are devoid of any hydrogen bond interactions. However, compound 6 exhibits both intermolecular and intramolecular hydrogen bond interactions. Neighbouring centrosymmetrically related molecules are held together by two pairs of complementary hydrogen bonds involving either the coordinated water molecules and a coordinated nitrate anion (donor-acceptor distance of 2.878 Å) or the water molecule of crystallization and one coordinated nitrate anion (donor-acceptor distances of 2.692 Å and 2.995 Å). Both types of interactions lead to a chain of hydrogen bonded dinuclear GdIII-CoII molecules that extend along the c axis (Fig. S2). In addition, there exists an intramolecular hydrogen bond involving the coordinated water molecule and a coordinated nitrate anion of the same dinuclear molecule (donor-acceptor distance of 2.898 Å). In complex 7, two centrosymmetrically neighbouring molecules are connected by hydrogen bonds involving the crystallization methanol molecules and one of the coordinated nitrate anions (donor-acceptor distance of 2.988 Å). Besides this, there exists a hydrogen bond involving the coordinated methanol molecule and a coordinated nitrate anion of the same dinuclear molecule (donor-acceptor distance of 2.845 Å). In complexes 8-12, there are hydrogen bond interactions between the crystallization methanol molecules (with O···O distances in the range 2.561–2.705 Å) and between one of these molecules and one of the coordinated nitrate anions of the tetranuclear Co2Ln2 molecules (donor-acceptor distance of 2.810 Å). However, the hydrogen bonds do not connect two different Co2Ln2 tetranuclear molecules (Fig. S2).
3.2 Magnetic properties
The temperature dependence of χMT for complexes 1-7 (χM is the molar magnetic susceptibility per CoLn unit) and 8-12 (χM being the molar magnetic susceptibility per Co2Ln2 unit) were measured in an applied magnetic field of 0.5 T and are displayed in Fig. 4 (complexes 1-3 and 6-7), Fig. 5 (complexes 4 and 5) and Fig. 6 (complexes 8-12).
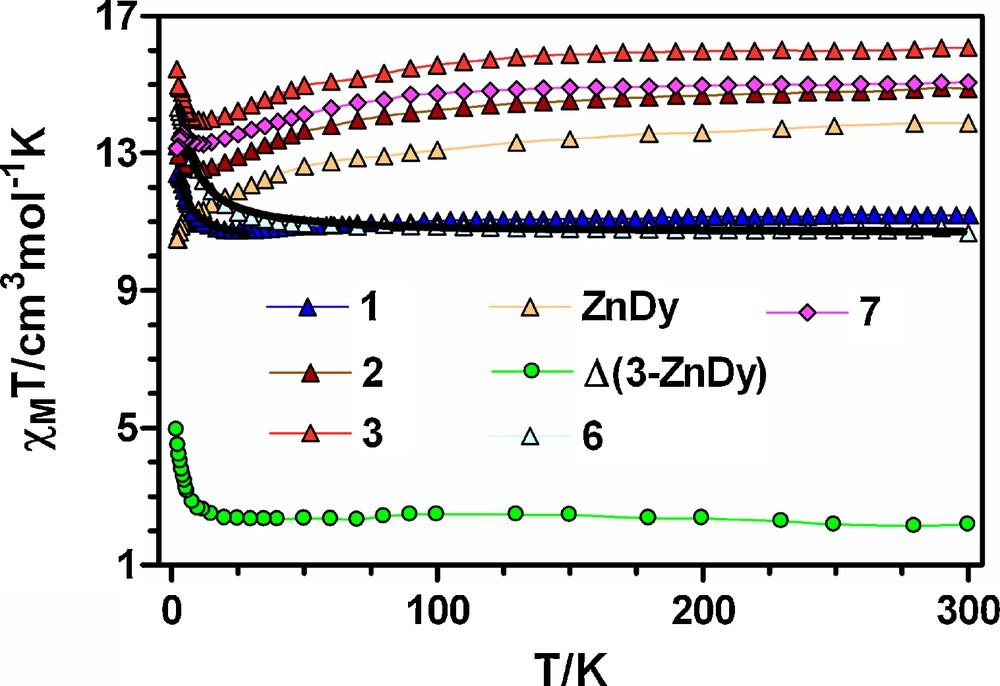
Temperature dependence of the χMT product for 1-3, 6, 7 and the difference ΔχMT(3-ZnDy) = (χMT)CoDy − (χMT)ZnDy = (χMT)Co + JCoDy(T). Black solid lines show the best fits for complexes 1 and 6. The rest of the solid lines are a guide to the eye.

Temperature dependence of the χMT product for 4 and 5 and the differences ΔχMT = (χMT)CoLn − (χMT)ZnLn = (χMT)Co + JCoLn(T). The solid lines are just a guide to the eye.
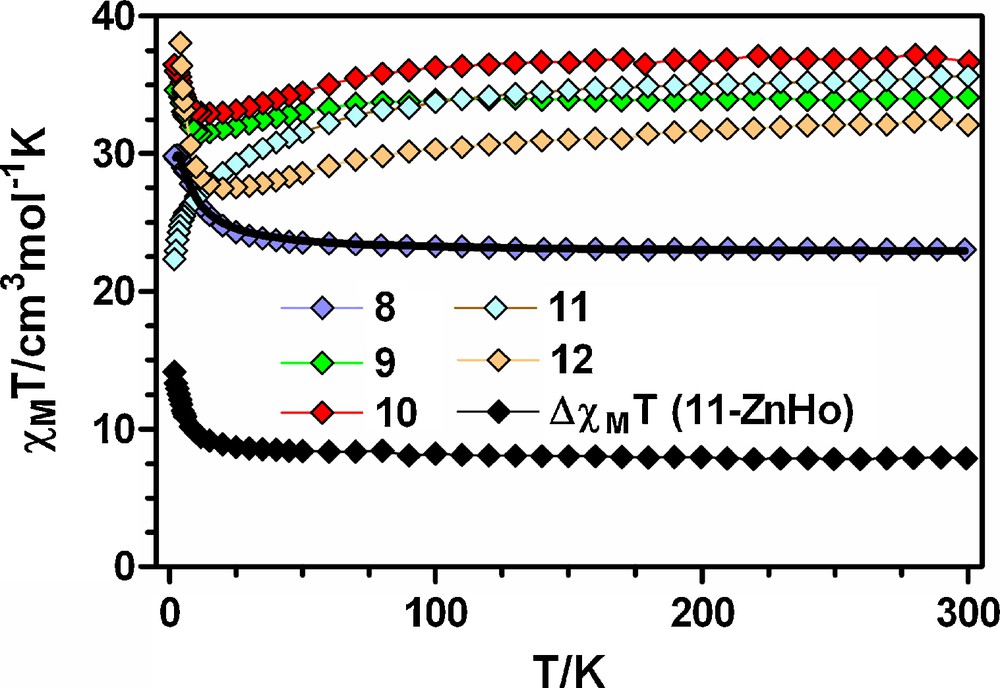
Temperature dependence of the χMT product for 8-12 and the difference ΔχMT(11-ZnHo) = (χMT)Co2Ho2 − 2(χMT)ZnDHo = 2(χMT)Ho + JCoHo(T). The black solid line shows the best fit for complex 8. The rest of the solid lines are just a guide to the eye.
Let us start with the Co-Gd complexes 1, 6 and 8, whose magnetic properties are easier to analyze. At room temperature, the χMT values for 1 and 6 of 11.20 cm3 mol−1 K and 10.68 cm3 mol−1 K are slightly larger than the expected value for non-interacting CoII (S = 3/2) and GdIII (S = 7/2) ions (9.750 cm3 mol−1 K with g = 2), which may be due to both the orbital contribution of the CoII ion with an octahedral geometry and a 4T1g ground term and the ferromagnetic interaction between CoII and GdIII ions (see below). On lowering the temperature, the χMT for 1 first slowly decreases from room temperature to reach a minimum value of 10.75 K cm3 mol−1 K at 26 K and then shows an abrupt increase to12.40 cm3 mol−1 K at 2 K. The observed high temperature decrease is due to the thermal depopulation of the spin-orbit coupling levels arising from the 4T1g ground term, whereas the increase at low temperature indicates a ferromagnetic interaction between CoII and GdIII ions. In the case of 6, the χMT product slightly increases from 300 K to 40 K and then increases sharply to14.34 cm3 mol−1 K at 2 K, thus indicating the existence of a ferromagnetic interaction between the CoII and GdIII ions. The lack of a decrease in χMT in the high temperature region [due to the spin-orbit coupling effect of the CoII ion] suggests that the ferromagnetic coupling in 6 is stronger than in 1. At room temperature, the χMT value for complex 8 of 23.05 cm3 mol−1 K is larger than that expected for two isolated CoII and two isolated GdIII ions with g = 2 (19.5 cm3 mol−1 K), which, as in the cases of 1 and 6, is due to both the spin-orbit coupling effect of the CoII ion and the ferromagnetic interaction between CoII and GdIII ions. This ferromagnetic interaction is, like in 6, responsible for the steady increase of the χMT product from room temperature to 29.82 cm3 mol−1 K at 2 K. It has been previously shown that the cobalt(II) orbital contribution is significantly quenched when its coordination sphere deviates from the ideal octahedral geometry [6c]. In such cases there is no appreciable decrease of the χMT in the high temperature region and the cobalt(II) ions almost follows the Curie law. In agreement with this, compounds 6 and 8, which have coordination spheres that are more distorted from octahedral to trigonal prismatic than compound in 1, show a steady increase in χMT from room temperature. Conversely, complex 1 with a less distorted octahedral geometry clearly exhibits the effect of spin-orbit coupling at high temperature. In view of these considerations the magnetic susceptibility data of compounds 6 and 8 can be analyzed using an isotropic Hamiltonian. Nevertheless, we stress that the magnetic parameters derived from this Hamiltonian can only be viewed as an approximation. The data for compound 1 were analyzed by considering that below 30 K only the lowest Kramer doublet of the CoII ion with an effective spin Seff = 1/2 is thermally populated. This effective spin is related with the real spin by a factor of 5/3 and therefore the Hamiltonian describing the magnetic exchange interaction between GdIII and CoII ions is:
From this Hamiltonian, the molar magnetic susceptibility is calculated to be:
The magnetization isotherm of 1 at 2 K (Fig. S3) reaches a value of 9.28 μB at 5 T, which is close to that expected for a CoII ion with Seff = 1/2 and g = 4.3 and a GdIII ion with S = 7/2 and g = 2.0 of 9.15 μB. The experimental magnetization data fall above the Brillouin curve for a pair of non-interacting CoII (Seff = 1/2) and GdIII ions, thus confirming the existence of a ferromagnetic interaction between these metal ions in the compound.
The magnetic properties of complexes 6 and 8, which present distorted octahedral coordination environments and apparently small orbital contributions, can be analyzed by means of isotropic Hamiltonians. In the case of 6, the isotropic Hamiltonian takes the form:
The best set of parameters obtained from the fitting of the experimental data to the above equation is J = +0.69(1) cm−1, g = 2.090(1) and zJ′ = −0.008(4) cm−1. The magnetic exchange coupling for compound 6 should be stronger than that of 1 as its hinge angle is smaller and the Co-O-Gd bridging angles are bigger than those for 1. However, the magnetic exchange coupling is similar for both compounds. This might be due to the fact that the J values for 6 are underestimated because the effect of the orbital contribution was not taken into account. Other structural factors, such as the deviation of the phenyl carbon atom bonded to the hydroxyl group with respect the Co(O)2Gd bridging plane, or the dihedral angle between the phenyl ring and the bridging Co(O)2Gd bridging plane, may also be responsible. To analyze the magnetic data of 8 the following isotropic Hamiltonian was used:
The field dependences of the magnetization at 2 K for complexes 6 and 8 are given in Figs. S3 and S4, respectively. These plots show a relatively rapid increase in the magnetization at low field, in agreement with a high spin state for these complexes, and a rapid saturation of the magnetization that is almost complete at the maximum applied field of 5 T, reaching values of 9.12 μB and 18.58 μB, close to those expected for the corresponding saturation values of 9.15 μB and 18.30 μB, respectively. In keeping with the ferromagnetic interaction observed for these compounds, the experimental data are well above the Brillouin curve for a pair of non-interacting CoII (Seff = 1/2; g = 4.2 for 6 and 4.3 for 8) and GdIII ions (g = 2.0).
We now discuss the magnetic properties of the Co-Tb compounds 2 and 7. At room temperature, the χMT values for 2 and 7 (14.88 cm3 K mol−1 and 15.08 cm3 K mol−1, respectively) are higher than those calculated [13.69 cm3 K mol−1] for independent CoII (S = 3/2 with gCo = 2.0) and TbIII (4f8, J = 6, S = 3, L = 3, 6F7, gJ = 3/2) ions in the free-ion approximation. This difference is mainly due to the orbital contribution of the CoII ion with an octahedral geometry and a 4T1g ground term. The χMT products for 2 and 7 decrease slowly with decreasing temperature down to minimum values of 12.52 cm3 K mol−1 and 13.25 cm3 K mol−1, respectively, at 12 K. This behaviour is due to both the thermal depopulation the spin-orbit coupling levels arising from the 4T1g ground term of the octahedral CoII ion and the thermal depopulation of the Stark sublevels of the TbIII ion, which arise from the splitting of the 7F6 ground term by the ligand field and whose width is of the order of 100 cm−1 [23]. Below 30 K, the χMT product increases to reach a maximum value of 13.20 cm3 K mol−1 at 2 K for 2 and 13.58 cm3 K mol−1 at 4 K for 7. Below this temperature, compound 7 shows a sharp decrease down to 2 K to a value of 13.14 cm3 K mol−1. The increase in χMT below 30 K is due to a ferromagnetic interaction between CoII and TbIII, whereas the decrease of χMT below 4 K in the case of 7 is likely associated with the presence of antiferromagnetic intermolecular interactions between the dinuclear complexes through the hydrogen bonds.
At room temperature, the χMT products for 4 and 5 are 16.66 cm3 K mol−1 and 13.95 cm3 K mol−1, respectively, which are higher than the calculated values by using the free-ion approximation of 15.94 cm3 K mol−1 and 13.35 cm3 K mol−1, respectively, for independent CoII and LnIII (HoIII, L = 6, S = 2, J = 8, gJ = 5/4, 5I8; ErIII, L = 6, S = 3/2, J = 15/2, gJ = 6/5, 4I15/2) due to the orbital contribution of the CoII ions.
When the temperature is lowered, the χMT product for 4 and 5 decreases, first slightly until ∼60–70 K and then sharply to reach values of 6.57 cm3 K mol−1 at 2 K for 4 and 8.65 cm3 K mol−1 at 4 K for 5. This behaviour is mainly due to the depopulation of the Stark sublevels of the HoIII and ErIII ion, which arise from the splitting of the 5I8 and 4I15/2 ground terms, respectively, by the ligand field, as well as to the thermal depopulation of the levels that arise from spin-orbit coupling in the CoII ion. In the case of 5, the χMT product increases below 5 K which is due to the ferromagnetic interaction between the CoII and ErIII ions. In order to know the nature of the magnetic interaction between CoII and HoIII ions in 4 and to confirm the ferromagnetic interaction between CoII and ErIII ions in 5, the empirical approach developed by Costes et al. was applied [24]. In this approach, the contribution of the crystal-field effects of the LnIII ion is removed by subtracting from the experimental χMT data of 4 and 5 those of the isostructural Zn-Ho and Zn-Er complexes, respectively, whose magnetic behaviour depends only on the LnIII ion. The difference ΔχMT = (χMT)CoLn − (χMT)ZnLn = (χMT)Co + JCoLn is therefore related to the nature of the overall exchange interaction between the CoII and LnIII ions. Thus, positive values are related to ferromagnetic coupling whereas negative values are related to antiferromagnetic interactions. The ΔχMT values first slightly decrease due to the thermal depopulation of the spin-orbit coupling levels of the CoII ion until they reach a minimum at ∼20 K and then increase down to 2 K, thus indicating a ferromagnetic interaction between CoII and LnIII ions. It appears that the magnetic exchange coupling is higher for 5 than for 4 as the former shows an increase in χMT at low temperature and the latter does not. The fact that ΔχMT values for 5 begin to increase at higher temperatures than for 4 is also supporting evidence of the above supposition.
The temperature dependence of compound 3 (Fig. 4) is similar to that observed for compound 2. The value at 300 K (16.08 cm3 K mol−1) is close to that expected (16.04 cm3 K mol−1) for independent CoII (S = 3/2 with gCo = 2.0) and DyIII (4f9, J = 15/2, S = 5/2, L = 5, 6H15/2, gJ = 4/3) ions in the free-ion approximation. The χMT value decreases with decreasing temperature down to a minimum value of 3.96 cm3 K mol−1 at 12 K, then increases at lower temperatures, reaching a maximum value of 15.46 cm3 K mol−1 at 2 K. The decrease between 300 and 12 K is due, as in compounds 2 and 7, to the thermal depopulation of the Stark sublevels of the DyIII ion and to the depopulation of the spin-orbit coupling levels of the CoII ion. It should be noted that, in contrast to that observed for compounds 4 and 5, the difference ΔχMT = (χMT)CoLn–(χMT)ZnLn = (χMT)Co + JCoLn for complex 3 does not decrease on lowering the temperature. This can be due to the fact that the CoO3N3 octahedral coordination environment is rather distorted toward a trigonal prismatic geometry (it exhibits 70% of octahedral geometry), which leads to a partial quenching of the orbital angular momentum and, consequently, to a smaller spin-orbit coupling that is ultimately responsible for the decrease in the ΔχMT vs T plot in the high temperature region. The increase of χMT in the low temperature region supports the existence of a ferromagnetic interaction between CoII and DyIII ions.
The thermal dependence of χMT for compounds 9-12 (Fig. 6) show a similar behaviour to those observed for the analogous acetate-diphenoxo triply-bridged dinuclear Co-Ln complexes 2-5. With the exception of 11, these complexes show an increase of χMT in the low temperature region, which is in agreement with the ferromagnetic interaction expected for these compounds. Conversely, in the case of 11, the χMT product steadily decreases down to 2 K, as for compound 4. To know whether or not the interaction between the HoIII and CoII is ferromagnetic in nature, we have followed the same strategy as for compounds 3-5. We have used the thermal dependence of χMT for the acetate-diphenoxo ZnIIHoIII compound [19] to be subtracted from compound 11, because we have not succeeded in obtaining the analogous dicyanamide-bridged Zn2Ho2 tetranuclear compound. Nevertheless, in view of the results for compounds 8-12, the magnetic behaviour of the ZnHo and Zn2Ho2 compounds must be very similar. As can be observed from Fig. 6, the temperature dependence of the ΔχMT = (χMT)Co2Ho2 − 2(χMT)ZnHo ≈ 2(χMT)Co + JCoHo (where JCoHo is the magnetic interaction through the diphenoxo pathway) clearly shows that the JCoHo is also ferromagnetic. Conversely to that observed for compound 4, the ΔχMT in the high temperature region for compound 11 does not decrease, thus indicating a smaller spin-orbit coupling effect in this compound than in 4, which is in agreement with the larger distortion of the coordination environment observed for 11.
Dynamic ac magnetic susceptibility measurements as a function of the temperature at different frequencies and under zero-external field clearly show that only complex 3 exhibits a frequency dependence of the in-phase (χ′M) and out-of-phase (χ′′M) signals (Fig. S5) but without reaching a maximum in temperature dependence of the χ′′M above 2 K, even at frequencies as high as 1400 Hz. This behaviour indicates that 3 exhibits slow relaxation of the magnetization and possibly SMM behaviour. However, either the energy barrier for the flipping of the magnetization is not high enough to trap the magnetization in one of the equivalent configurations above 2 K or the energy barrier is reduced to an effective value by quantum tunneling of the excited states leading to a flipping rate that is too fast to observe the maximum in the χ′′M above 2 K. When the ac measurements were performed in the presence of a small external dc field of 1000 G to fully or partly suppress the quantum tunneling relaxation of the magnetization, compound 3 shows typical SMM behaviour below 5 K with maxima in the 2.25 K (665 Hz)-2.5 K (1300 Hz) range (Fig. 7).
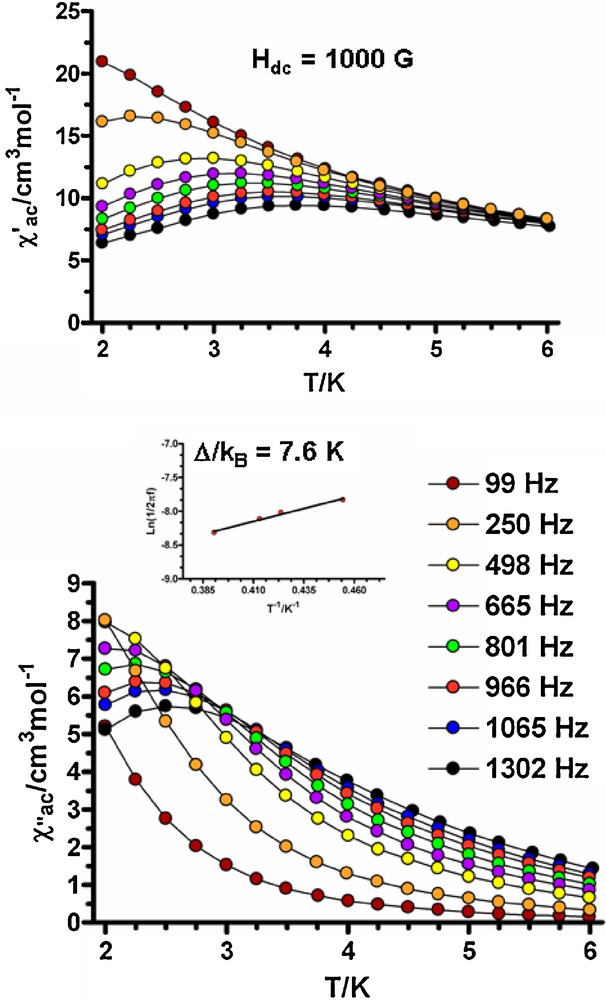
Temperature dependence of in-phase χ′M (top) and out-of-phase χ′′M (bottom) components of the ac susceptibility for complex 3 measured under 1000 Oe applied dc field. Bottom insert: Arrhenius law.
From the temperatures and frequencies of the maxima observed for the χ′′M signals, and by using an Arrhenius plot, τ = τ0 exp(Δ/kBT), the thermally activated energy barrier for the flipping of the magnetization (Δ/kB) was estimated to be 7.6 K and the flipping rate τ0 = 1.3 × 10−5 s. The value of Δ/kB is at the lower end of the experimental range found for similar 3d/4f SMM systems [6,19]. However, the τ0 value is much larger than expected, which suggests that the quantum tunneling of the magnetization is only partly suppressed by the applied field of 1000 G and, therefore, the thermal energy barrier should be higher than 7.6 K.
In order to shed light on the origin of this behaviour, we have performed fragment CASSCF calculations within the MOLCAS 7.2 ab initio package [14]. We have investigated the local magnetic anisotropies of the CoII and DyIII on the hypothetical complexes Co-La and Zn-Dy, respectively, which have the same structural parameters as compound 3. The ground Kramers doublet arising from the ligand field splitting of the 6H15/2 ground atomic term show strong axial anisotropy with gz = 18.9 (gx = 0.06 and gy = 0.09) along the main anisotropy axis, which lies close to the Dy–Co direction (Fig. 8a). The cobalt atom, as expected, is much less anisotropic with gz = 6.71 along the main anisotropy axis (gx = 2.02 and gy = 3.63), which is placed not too far from the normal of the Co-Dy direction (Fig. 8b).

a: main local anisotropic axis for DyIII in 3 (green arrow); b: orientations of the local g tensors for CoII in 3; gz (green), gx (yellow), gy (magenta).
The combination of these magnetic anisotropies could produce a highly uniaxial magnetoanisotropy whose main anisotropy axis would lie close to the Dy anisotropy axis. At low temperature (below ∼30 K), the ground doublet sub-level of DyIII (with Jz = ±15/2) is further split into two levels because of the magnetic exchange interaction with the ground doublet with Seff = 1/2 of the cobalt(II) ion. It has been suggested that the energy gap between these two levels is related to the observed energy barrier [25]. Because the magnetic exchange coupling between DyIII and CoII is expected to be very weak (the JCoLn is ∼+1 cm−1 for the Gd-Co complexes 1, 6 and 8, and it should be lower than this value for heavy LnIII ions because of the lanthanide contraction) a small energy barrier for the reversal of the magnetization is also expected, which is in good agreement with the observed results for compound 3. For the compounds 2, 4, 5 and 7, a weaker uniaxial anisotropy and/or a smaller JCoLn coupling constant promote smaller values of the energy barrier and consequently do not show any out-of-phase signal (χ′′′M) under zero dc applied field. Moreover, the existence of transverse anisotropy could lead to large tunnel splittings and therefore to the observed efficient zero-field quantum tunneling of magnetization.
The fact that tetranuclear Co2Ln2 compounds 9-11 do not exhibit slow relaxation of the magnetization even under an external dc field may be related to the existence of very weak Co-Ln antiferromagnetic interactions between each pair of centrosymmetrically related dinuclear Co-Ln units. These interactions lead to small separations of the low lying split sublevels and consequently to a smaller energy barrier for the flipping of the magnetization.
4 Concluding remarks
We have designed a new and relatively flexible dinucleating compartmental Mannich base ligand, with an N3O2 inner pocket and an O2O2 external site, that allows the formation, in a one pot reaction, of double and triple-bridged CoIILnIII dinuclear complexes (LnIII = Gd, Tb, Dy, Ho and Er). The driving force for the formation of such complexes is the tendency of the CoII ion to adopt octahedral geometry. Thus, the pentacoordinating inner site forces this metal ion to saturate its coordination position with a donor atom, which can belong either to an acetate bridging ligand connecting the CoII and LnIII metal ions, leading to triply-bridged CoIILnIII dinuclear molecules (complexes 1-5) or to a molecule of water leading to doubly-bridged dinuclear CoIILnIII molecules (complexes 6-7). These diphenoxo-bridged CoIILnIII molecules were used as platforms to obtain 1,5-dicyanamide-bridged rectangular tetranuclear Co2IILn2II complexes. The Co(O)2Ln bridging fragment is folded in the diphenoxo-acetate triply-bridged complexes (∼22°), whereas it is close to planar in the remaining complexes (∼3° and ∼7.5°, for complexes 5-6 and 8-12, respectively). In connection with this, the Co-O-Ln bridging angles become larger and more symmetric (smaller difference between each couple of Ln-O and Co-O bond distances Ln-O-Co angles) when its planarity increases. The Ln-N, Ln···Co and the average Ln-Ophenoxo bond distances for the isostructural complexes 8-12 decrease with decreasing LnIII ionic radii on going from GdIII to ErIII, reflecting the lanthanide contraction.
In all these complexes, the magnetic exchange coupling between the CoII and LnIII ions was found to be ferromagnetic in nature and, in the case of the Co-Gd complexes, the JCoGd values were calculated to be between +0.69 cm−1 and +0.75 cm−1. It appears that, for this kind of complex, the structural factors associated with the bridging fragment have less influence than their Ni-Ln analogues. Notice that this work shows for the first time that the CoII-HoIII and CoII-ErIII magnetic interactions are also ferromagnetic. The observed ferromagnetic interactions between CoII and the lanthanide ions from GdIII to ErIII follow the same trend established for related CuLn and NiLn systems.
Slow relaxation of the magnetization, a typical feature of SMM behaviour, is only observed for 3, which indicates that the introduction of two anisotropic ions such as CoII and LnIII does not guarantee a larger uniaxial anisotropy, as the local anisotropies can be combined in a subtractive manner. This possible subtractive effect, together with the very weak JCoLn observed for these compounds (∼ +0.7 cm−1) could promote smaller values of the energy barrier. Moreover, the existence of transverse anisotropy could lead to large tunnel splittings and therefore to efficient zero-field quantum tunneling of magnetization. All these factors would provoke the non observance of SMM behaviour above 2 K for all the compounds with the exception of 3. In the case of this compound, the application of a small dc field is enough to fully or partly suppress the fast and efficient zero-field quantum tunneling of magnetization allowing the observation of SMM behaviour above 2 K. Therefore, the DyIII in 3 seems to have a larger magnetic anisotropy than the other LnIII ions present in complexes 2-5 and 7. From the results of the Co2Ln2 tetranuclear compounds 9-12, it seems to be clear that the weak intermolecular interactions propagated through the dicyanamide bridges between CoLn dinuclear units, leads to small separations of the low lying split sublevels and consequently to a smaller energy barrier for the flipping of the magnetization. In view of this, a good strategy to obtain SMM behaviour in this kind of systems would be that of eliminating the weak MII-LnIII interactions that split the ground sublevels of the LnIII ion. According to this strategy, we are now pursuing the synthesis of a series of dinuclear [Zn(μL)(μ-X)Ln(NO3)2] and mononuclear complexes[(H2L)Ln(NO3)3] complexes which are expected to exhibit SMM behaviour with higher thermal energy barriers.
Acknowledgements
This work was supported by the MEC (Spain) (Project CTQ-2008-02269/BQU and CTQ2011-24478), the Junta de Andalucía (FQM-195 and Project of excellence P08-FQM-03705) and the University of Granada. Financial support from the University of Granada (CEI campus de Excelencia) for the visit of E.C. to the University of Edinburgh is grateful acknowledged. E.K.B. would like to thank the EPSRC and Leverhulme Trust for financial support. We would like to thank the Centro de Supercomputación de la Universidad de Granada for computational resources. Finally, we would like to thank Prof. Liviu Chibotaru for providing us the SINGLE_ANISO program that allows to extract the components of the g tensor.


