Structure sensitivity in heterogeneous catalysis with noncompetitive adsorption of reactants: Selective oxidation of lignan hydroxymatairesinol to oxomatairesinol over gold catalysts

Olga A. Simakova; Elena V. Murzina; Dmitry Yu. Murzin

doi:10.1016/j.crci.2014.01.002

Résumé

Structure sensitivity in heterogeneous catalytic oxidative dehydrogenation of lignan hydroxymatairesinol (HMR) extracted from Norway spruce knots was investigated over a series of alumina-supported gold catalysts. A mathematical model was developed based on the concept of noncompetitive adsorption of reactants. The model, being consistent with kinetic regularities, such as reaction orders in reactants, explains well the dependence of catalytic activity on the gold cluster size.

1 Introduction

A significant amount of experimental data was generated along the years, demonstrating that catalytic activity in transition metal catalysis shows a strong dependence on the cluster size in the nanometer range (e.g., the domain of the cluster sizes between 2 and 20 nm) [1–10].

The catalytic activity as such calculated per total amount of catalytic phase should decline with the increase of cluster size. Since the ratio between surface and volume increases with a decrease in size of nanoclusters and the fraction of surface atoms is increasing, fewer exposed sites are available [1].

Turnover frequency (TOF), defined as the activity per unit of exposed surface, could behave differently with alterations of the cluster size (coined structure sensitivity) [2]. For various systems, it has been shown that TOF not only increases or decreases with the cluster size, but can also pass through a maximum. Several explanations for this phenomenon were put forward in the literature, involving changes in the electronic state, alteration of resistance to deactivation as well as different activities of edges, corners, and terrace atoms. The latter one is based on the fact that the relative ratio between these atoms depends on the cluster size [1]. Therefore the difference in clusters reactivity would be anticipated.

Despite a large number of studies, surprisingly little modeling was done, which explains structure sensitivity from a kinetic viewpoint, incorporating the cluster size in the rate expression.

One of the simplest approaches implementing the cluster size dependence in reaction kinetics would be to view reaction constants as size independent. Therefore, each type of sites (terraces and edges) contributes to the overall rate according to:

v (d) = r_{terraces} f_{terraces} + r_{edges} f_{edges}

(1)

where f_terraces and f_edges are fractions of the cluster terraces and edges respectively; r_terraces and r_edges are the reaction rates over the corresponding surface sites.

This approach was reported before to calculate the turnover frequency [5,11]. In a similar fashion, differences in the reactivity of edges, corners and terraces were considered theoretically for a two-step sequence using as a model fcc cubic and cubo-octahedron clusters [12]. The theoretical concept led to kinetic equations with the rate constants dependence on the cluster size or (?) directly incorporated in the model.

The alternative way is to utilize the thermodynamic approach [13–15] considering variations of the Gibbs energy $Δ G_{r} = - R T \ln K_{r} = f^{'} (r)$ , where variations of the chemical potential of nanoclusters compared to bulk metal are dependent on the cluster size and the presence of adsorbates. A similar description can be obtained based on the explicit difference between the activation energy values for reactions catalyzed by edges and terraces [16,17], leading to different activities of edges and terraces in terms of reaction rates and selectivity.

For the latter approach, which is more chemically sound than the one based on chemical potential variations, mainly a two-step sequence and its special case (Eley–Rideal mechanism) were considered [16,17]. The two-step mechanism described in [18] involves the transformation of one of the most abundant surface intermediates, where two kinetically significant steps are:

\begin{array}{l} 1. {Z+A}_{1} \leftrightarrow {ZI+B}_{1} \\ \underline{2. {ZI+A}_{2} \leftrightarrow {Z+B}_{2}} \\ A_{1} {+A}_{2} \leftrightarrow B_{1} {+B}_{2} \end{array}

(2)

where A₁, A₂ are reactants, B₁, and B₂ are products, Z is the surface site and I is an adsorbed intermediate.

The aim of the current work is to extend this treatment on the cluster size dependence of the reaction rate for a heterogeneous catalytic reaction with noncompetitive adsorption of reactants.

As an example, selective oxidation of lignan hydroxymatairesinol (HMR) via oxidative dehydrogenation over heterogeneous gold catalysts resulting in the formation of oxomatairesinol (oxoMAT) was selected. Valuable lignans presented in the waste from pulping industry demonstrated anticarcinogenic and antioxidative properties [19]. The substrate HMR is found in large amounts in the knots of Norway spruce (Picea abies), while the lignan oxoMAT cannot be extracted in considerable amounts from woody biomass. The selective oxidation of HMR to oxoMAT is in fact selective oxidation of a secondary alcohol into a corresponding ketone. This reaction was previously investigated by our research group using gold catalysts, which demonstrated the 100% selectivity in favor of the desired product [20–24]. The reaction kinetics (Scheme 1) is somewhat complicated by the existence of HMR as a mixture of two diastereomers: (7R,8R,8′R)-(–)-7-allo-hydroxymatairesinol (HMR 1) and (7S,8R,8′R)-(–)-7-allo-hydroxymatairesinol (HMR 2). Recent investigation of the reaction kinetics demonstrated that isomer HMR 2 is much more reactive compared to HMR 1 [24].

Scheme 1
Reaction pathway of lignan hydroxymatairesinol selective oxidation.

Kinetic modeling [24] demonstrated good correspondence between experiments and theoretical predictions. The mathematical treatment included also deactivation, which for the sake of simplicity is omitted in the present work, since only initial activity would be considered.

2 Experimental

The gold catalysts were prepared by applying a direct ion exchange method (DIE), as described elsewhere [25]. Alumina support (UOP, A-201, S_BET = 200 m²/g) was mixed with a HAuCl₄ (HAuCl₄ 99.9% ABCR, Darmstadt) aqueous solution in an amount corresponding to the final metal loading of 2 wt. %. The suspension was kept under vigorous stirring for 1 h at 70 °C, washed with ammonium hydroxide (4 M) during 1 h. The obtained powder was dried over night at 80 °C in the air and after that calcined at 300 °C.

In order to achieve different particle sizes, the initial concentration of the precursor species, the washing procedure and the calcination temperature were varied. Prepared Au/Al₂O₃ catalysts were characterized by TEM, XRD, XPS, ICP–OES. More details are provided in [25].

Hydroximatairesinol was extracted from ground Norway spruce knots according to the procedure described in [19] as a mixture of two diastereomers of HMR: (7R,8R,8′R)-(–)-7-allo-hydroxymatairesinol (HMR 1) and (7R,8R,8′R)-(–)-7-allo-hydroxymatairesinol (HMR 2). The ratio between HMR 2 and HMR 1 in the mixture was 2 mol/mol. The purity of HMR was determined by gas chromatography (GC) to be 95%.

In a typical experiment, the reaction was carried out under atmospheric pressure in a stirred 200-mL glass reactor, equipped with a heating jacket (using silicon oil as the heat-transfer medium), a re-flux condenser (cooling medium set at −20 °C), an oil lock, a pitched-blade turbine, and stirring baffles. Catalysts (2 wt. % Au/Al₂O₃, grain size of 45–63 μm) were pre-activated in situ by heating under a hydrogen (AGA, 99.999%) flow (100 mL/min) until 120 °C; thereafter the reactor was cooled down to the reaction temperature under nitrogen (AGA, 99.999%) flow (100 mL/min). The reactant solution (100 mL) with an HMR dissolved in 2 vol. % propan-2-ol (Sigma-Aldrich, 99.8%) was poured into the reactor. The procedure was described in detail previously [20]. The gas flow was changed for a 20:80 vol.% oxygen:nitrogen mixture (AGA, 99.999%). The reaction mixture was stirred at 1000 rpm to avoid external mass transfer limitations, and the experiments were performed in the kinetic regime. Samples were taken from the reactor at different time intervals and analyzed by GC. The analytical procedure has been reported elsewhere [20].

2.1 Kinetic constant dependence on the cluster size

Considering only terraces and edges as sites with different reactivities, the adsorption Gibbs energy is expressed in the following way:

Δ G_{ads} = Δ G_{ads,terraces} f_{terraces} + Δ G_{ads,edges} f_{edges} = Δ G_{ads,terraces} (1 - f_{edges}) + Δ G_{ads,edges} f_{edges} = Δ G_{ads,terraces} f_{edges} (Δ G_{ads,edges} - Δ G_{ads,terraces})

(3)

In eq. (3), where $Δ G_{ads,terraces}$ and $Δ G_{ads,edges}$ correspond to adsorption on terraces and edges, respectively, $f_{terraces}, f_{edges}$ denote fractions of these surface sites. The sum of these fractional values is equal to unity.

For the cubo-octahedral shape of nanoparticles, the fraction of edges to the total number of atoms on the surface, which includes besides edges also square and triangular faces, is given by [16]:

f_{edges} = \frac{N_{edges}}{N_{edges} + N_{square_faces} + N_{triangular_faces}}

(4)

Applying the relationship between equilibrium constants and Gibbs energy of adsorption, one gets:

K_{ads} = exp [- \frac{Δ G_{ads,terraces} + f_{edges} (Δ G_{ads,edges} - Δ G_{ads,terraces})}{R T}]

(5)

Implementing the linear free energy (or Brønsted–Evans–Polanyi) relationship between reaction constants k and equilibrium constants K in a series of analogous elementary reactions (k = g K^α, where g and Polanyi parameter α are constants), the rate constant of adsorption is expressed as:

k_{ads} = k_{ads}^{'} \exp [\frac{- α f_{edges} (Δ G_{ads,edges} - Δ G_{ads,terraces})}{R T}]

(6)

The fraction of the edges can be expressed in a simplified way as $f_{edges} \approx 1 / d_{cluster}$ , where d is given in nanometers [16], allowing one to describe reaction rates (or turnover frequency) dependencies on cluster size.

2.2 Reaction mechanism

The reaction pathway of the lignan HMR oxidative dehydrogenation considering only one reactive isomer (HMR 2) transforming into the product oxoMAT is described by eq. (7).

\begin{array}{l} 1. HMR 2 +^{*} \leftrightarrow HMR 2^{*} \\ 2. O_{2} +^{*'} \leftrightarrow {O_{2}}^{*'} \\ 3. HMR 2^{*} + {O_{2}}^{*'} \to HMR 2- {O_{2}}^{*} +^{*'} \\ 3^{'} . 2 HMR 2- {O_{2}}^{*} \to 2 {OxoMAT}^{*} + 2 H_{2} O (fast) \\ 3^{''} . {OxoMAT}^{*} \to {OxoMAT+}^{*} (fast) \end{array}

(7)

Eq. (7) displays the reaction steps in HMR selective aerobic oxidation to oxoMAT over Au catalysts.

This mechanism assumes a noncompetitive adsorption of HMR and molecular oxygen on different sites (* and *′) and can be essentially simplified if the coverage of the product is neglected (i.e. desorption is fast), giving:

\begin{array}{l} 1. A+Z = ZA (quasi-equilibrium) \\ 2. B+Z' = Z'B (quasi-equilibrium) \\ \underline{3. ZA+Z'B \to C+Z+Z'} \\ A+B \to C \end{array}

(8)

In eq. (8), the surface reaction between the two adsorbed species (i.e. step 3 in eq. (7) and eq. (8)) is considered to be the rate-determining step. In eq. (8), A stands for the reactant, B for oxygen and Z and Z′ are respectively different surface sites. This mechanism is consistent with kinetic regularities described previously in [24]. It was demonstrated that the reaction order for oxygen (B in eq. (8)) is close to zero, while the one for HMR (A in eq. (8)) is fractional, suggesting that oxygen and HMR adsorb on different sites. Moreover, in anaerobic conditions, the reaction rate is dramatically decreased [20]. The experimental data in a wide range of HMR and oxygen concentrations were successfully fitted into a kinetic model describing mechanism (8), which involves product adsorption and catalyst deactivation. Since in the current work only initial activity was considered for modeling purposes, the influence of the product and the catalyst's deactivation can be neglected.

The reaction rate per exposed site for eq. (8) is expressed by:

v = \frac{k_{3} K_{1} C_{A} K_{2} C_{B}}{(1 + K_{1} C_{A}) (1 + K_{2} C_{B})}

(9)

where k₃ should be corrected for the reactant stoichiometric coefficient.

Following previous considerations [16,17], the rate expression for activity (per gram of catalyst) takes the form:

r a t e = \frac{k_{3}^{'} e^{(α - 1) (χ_{A} + χ_{B}) / d_{cluster}} K_{1} e^{χ_{A} / d_{cluster}} C_{A} K_{2} e^{χ_{B} / d_{cluster}} C_{B}}{(1 + K_{1} e^{χ_{A} / d_{cluster}}) (1 + K_{2} e^{χ_{B} / d_{cluster}} C_{B}) d_{cluster}} = \frac{k_{3}^{'} e^{α (χ_{A+} χ_{B}) / d_{cluster}} K_{1} C_{A} K_{2} C_{B}}{(1 + K_{1} e^{χ_{A} / d_{c l u s t e r}} C_{A}) (1 + K_{2} e^{χ_{B} / d_{cluster}} C_{B}) d_{cluster}}

(10)

where α is the Polanyi parameter for the third step, and parameter χ reflects differences in the Gibbs energy of adsorption on edges and terraces respectively for HMR and oxygen:

χ = \frac{(Δ G_{ads,edges} - Δ G_{ads,terraces})}{R T}

(11)

Eq. (10) can account for zero order for oxygen $(1 < < K_{2} e^{χ_{B} / d_{cluster}} C_{B})$ and a fractional order for HMR leading to a simplified rate expression:

r a t e = \frac{k_{3}^{'} e^{α χ_{A} / d_{cluster}} K_{1} C_{A}}{(1 + K_{1} e^{χ_{A} / d_{cluster}} C_{A}) d_{cluster}}

(12)

r a t e = \frac{p_{1} e^{p_{2} p_{3} / d_{cluster}}}{(1 + p_{4} e^{p_{3} / d_{cluster}}) d_{cluster}}

(13)

with

p_{1} = k_{3}^{'} k_{1} C_{A}, p_{2} = α, p_{3} = χ_{A}, p_{4} = k_{1} C_{A}

(14)

The experimental data for the reaction rate dependence on the cluster size are given in Fig. 1. Comparison between eq. (12) and the experimental data is also presented on Fig. 1.

Fig. 1
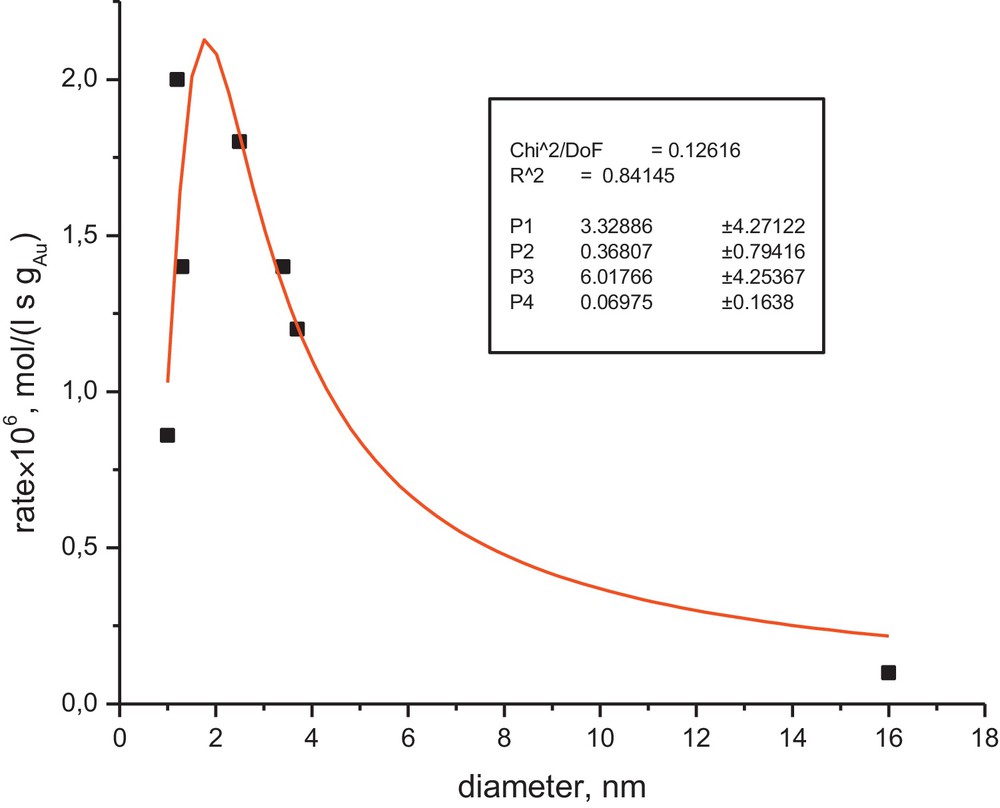
Dependence of the initial rate of the oxidative dehydrogenation of the lignan hydroxymatairesinol on the gold cluster size.

As can be seen from Fig. 1, the model correctly captures the dependence of the reaction rate on the cluster size, which is also consistent with the global kinetic model discussed previously [24]. It should be noted that an alternative rate expression of a Langmuir–Hinshelwood type, which includes adsorption of oxygen and HMR on the same sites, can provide a similar level of description for the cluster size dependence, although not being in line with kinetic regularities, even if the value of the Polanyi parameter is close to 0.5, which is rather typical for heterogeneous catalytic reactions [18].

Moreover, some other alternatives, assuming for example a first-order reaction for HMR and a zero-order one for oxygen, were not able to describe the experimental data shown in Fig. 1. An apparent drawback of the numerical data fitting was a limited set of experimental points, which resulted in very high deviations in the values of parameters, preventing meaningful discussion of these values.

The presented example nicely illustrates a necessity to elucidate quantitatively the cluster size dependence along with a detailed kinetic study.

3 Conclusions

The structure sensitivity of the gold catalyzed aerobic selective oxidation of a naturally occurring lignan hydroxymatairesinol (HMR) was revealed. The model incorporating cluster size dependence and kinetic regularities (zero order with respect to oxygen, fractional towards HMR) was proposed based on the assumption of noncompetitive adsorption of reactants. The advanced model allowed describing quantitatively a maximum in the activity as a function of cluster size.

^☆ Thematic issue dedicated to François Garin.