The Kwak–Mansoori approach to the Peng–Robinson equation for determining the thermodynamic consistency of VLE in ethanol + congener mixtures

Claudio A. Faúndez; María F. Millaldeo; José O. Valderrama

doi:10.1016/j.crci.2015.05.001

The Kwak–Mansoori approach to the Peng–Robinson equation for determining the thermodynamic consistency of VLE in ethanol + congener mixtures

Claudio A. Faúndez ¹ ; María F. Millaldeo ¹ ; José O. Valderrama ^2,³

¹ Universidad de Concepción, Faculdad de Ciencias Físicas y Matemáticas, Casilla 160, Concepción, Chile
² University of La Serena, Faculty of Engineering, Department of Mechanical Engineering, Casilla 554, La Serena, Chile
³ Centro de Información Tecnológica, Mons. Subercaseaux 667, La Serena, Chile

Comptes Rendus. Chimie, Volume 18 (2015) no. 8, pp. 867-874.

Résumé

The modified Peng–Robinson equation of state proposed by Kwak and Mansoori (PR/KM) is used in a thermodynamic consistency test of phase equilibrium data for binary ethanol + congener mixtures found in alcoholic distillation processes. Congener substances are those components in a must that are present at very low concentration, but their presence is necessary to give the distilled liquor their particular aromatic and tasting characteristics. The congener substances considered in this study are: acetic acid, ethyl acetate, furfural, methanol, 2-methyl-1-propanol, 1-pentanol, 1-propanol and methyl acetate. A flexible area test method is applied to analyse 25 isothermal P–x–y data of ethanol + congener mixtures available in the open literature. The consistency method determines the value of three integral expressions derived from the Gibbs–Duhem equation; one integral is calculated using experimental data only and the other two by using values calculated with the PR/KM model. For all cases, the method gives a clear answer about consistency or inconsistency of a set of isothermal P–x–y data.

Métadonnées

Reçu le : 2015-02-06
Accepté le : 2015-05-05
Publié le : 2015-07-14

DOI : 10.1016/j.crci.2015.05.001

Mots clés : Ethanol + congeners, Equation of state, Kwak–Mansoori, Thermodynamic consistency

Affiliations des auteurs :

Claudio A. Faúndez ¹ ; María F. Millaldeo ¹ ; José O. Valderrama ^{2, 3}

@article{CRCHIM_2015__18_8_867_0,
     author = {Claudio A. Fa\'undez and Mar{\'\i}a F. Millaldeo and Jos\'e O. Valderrama},
     title = {The {Kwak{\textendash}Mansoori} approach to the {Peng{\textendash}Robinson} equation for determining the thermodynamic consistency of {VLE} in ethanol + congener mixtures},
     journal = {Comptes Rendus. Chimie},
     pages = {867--874},
     publisher = {Elsevier},
     volume = {18},
     number = {8},
     year = {2015},
     doi = {10.1016/j.crci.2015.05.001},
     language = {en},
}

TY  - JOUR
AU  - Claudio A. Faúndez
AU  - María F. Millaldeo
AU  - José O. Valderrama
TI  - The Kwak–Mansoori approach to the Peng–Robinson equation for determining the thermodynamic consistency of VLE in ethanol + congener mixtures
JO  - Comptes Rendus. Chimie
PY  - 2015
SP  - 867
EP  - 874
VL  - 18
IS  - 8
PB  - Elsevier
DO  - 10.1016/j.crci.2015.05.001
LA  - en
ID  - CRCHIM_2015__18_8_867_0
ER  -

%0 Journal Article
%A Claudio A. Faúndez
%A María F. Millaldeo
%A José O. Valderrama
%T The Kwak–Mansoori approach to the Peng–Robinson equation for determining the thermodynamic consistency of VLE in ethanol + congener mixtures
%J Comptes Rendus. Chimie
%D 2015
%P 867-874
%V 18
%N 8
%I Elsevier
%R 10.1016/j.crci.2015.05.001
%G en
%F CRCHIM_2015__18_8_867_0

Claudio A. Faúndez; María F. Millaldeo; José O. Valderrama. The Kwak–Mansoori approach to the Peng–Robinson equation for determining the thermodynamic consistency of VLE in ethanol + congener mixtures. Comptes Rendus. Chimie, Volume 18 (2015) no. 8, pp. 867-874. doi : 10.1016/j.crci.2015.05.001. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2015.05.001/

Version originale du texte intégral

1 Introduction

Vapour-liquid separation processes such as wine distillation can be done in batch or in a continuous manner and in both processes heat is used as the external separating agent. The concentration of the distilled product is considered as the most important variable in the produced spirit, so its prediction or correlation is of paramount importance in distillation simulation. In these processes, there are several substances that are present at very low concentrations, substances that are called “congeners”. Even though the concentrations of the congener compounds are of the order of part per million, 10⁻⁶ to 10⁻⁴ mg/L [1,2], they must be considered when modelling VLE data. Thermodynamic modelling is more difficult to handle for mixtures in which some components are present at such low concentrations [3]. The treatment of low-pressure vapour–liquid equilibrium data (VLE) in modelling and in consistency tests is commonly done using activity coefficient models, through the so-called Gamma–Phi (γ–ϕ) method. The equation of state method, known as Phi–Phi (ϕ–ϕ) method, has also been used by some authors [4]. In both methods, binary parameters are calculated from experimental isothermal VLE data [5].

Water + congener and ethanol + congener mixtures have been studied and presented in the literature. Also, phase equilibrium data are available in specialized handbooks and databases [6–8]. However, systems of interest in alcoholic distillation have been treated in a more limited manner. During the last years, we have analysed a number of binary and ternary mixtures containing water + congener, ethanol + congener and water + ethanol + congener. The authors have presented some studies on the modelling of these systems and have summarized the results in a general review paper [9,10].

Since accurate VLE data are required for the development and design of different separation processes such as alcoholic distillation, the thermodynamic consistency of phase equilibrium data becomes of especial importance for checking the accuracy of experimental data used in process design and simulation [11,12]. Thermodynamic consistency means that the data fulfil some rigorous thermodynamic equations within defined and acceptable limits of accuracy. Consistency test methods of experimental phase equilibrium data follow two main approaches:

• consistency of binary or multicomponent VLE data using the Gibbs–Duhem equation;
• consistency of binary VLE and heat of mixing data by the Gibbs–Helmholtz equation [13].

Some thermodynamic consistency tests for mixtures containing alcohols have been presented in the literature to validate new experimental data. Table 1 shows a selection of works on the thermodynamic consistency of alcoholic mixture data.

Reference	Systems	Comments
[14]	Alcohol + hydrocarbon	Analysed VLE data for 36 binary systems. The method combined thermodynamic consistency tests, data correlation, comparison with enthalpy of mixing data, and comparison of VLE data for various mixtures
[12]	Alcohol + hydrocarbon	Evaluated data for 46 alcohol + hydrocarbon systems at low-pressures using the PAI test (Point, Area, Infinite dilution test). The PAI test is combined with the NRTL equation
[15]	Methanol + water, ethanol + water	Proposed a thermodynamic consistency test for binary constant temperature VLE data. The binary parameters involved in the activity coefficients equations are numerically optimized to satisfy the Gibbs–Duhem equation
[16]	Methanol + water, ethanol + water, ethanol + (methanol, 1-propanol, 2-propanol)	Investigated an empirical consistency test for binary constant temperature and for constant-pressure VLE data
[17]	Methanol + (methyacetate, ethanol, water), ethanol + water	Reported isobaric VLE data at 101.3 kPa for the binary mixtures. The experimental data were tested for thermodynamic consistency by means of the Wisniak method and were demonstrated to be consistent
[18]	Methyacetate + ethanol	Reported experimental data of the isobaric VLE for the mixture methyl acetate + ethanol at 0.3 and 0.7 MPa. The experimental data passed positively the consistency test of Van Ness

2 Thermodynamic consistency

As described above, the thermodynamic model used in this work is the Peng–Robinson equation of state modified by Kwak and Mansoori, PR/KM [19,20]. This PR/KM model has been previously discussed in the literature and has demonstrated to have the adequate flexibility and accuracy for correlating VLE data and to provide appropriate representation of the experimental data, a requirement of the consistency test [21,22]. The model and the test employed to check the thermodynamic consistency of isothermal P–x–y equilibrium data have been previously described by the authors for other types of mixtures [23–27]. These authors have established certain requirements to define a good consistency criterion for analysing phase equilibrium data, which are summarized in the following section. To the best of the authors’ knowledge, the method has not been used to test P–x–y data of binary congener + ethanol mixtures, as done in this paper.

The different approaches presented in the literature not only use different equilibrium data, but also different thermodynamic functions that are calculated either directly, using experimental data, or indirectly, including different thermodynamic models. As explained in previous papers, the consistency method proposed by the authors is model-dependent; this means that the method requires a thermodynamic model that can accurately fit the experimental data to the consistency test. The equation of state method is used in this work for phase equilibrium correlation and the cubic equation of state proposed by Peng and Robinson [19] is the chosen model.

Kwak and Mansoori [20] presented a different attractive approach for interpreting the mixing and combining rules for cubic equations of state (EoS) of van der Waals type. According to the authors, their proposal is consistent with the statistical-mechanical theory of the van der Waals mixing rules. Also, it is based on statistical-mechanical arguments and on the fact that rules are for constants of an equation of state and not for any thermodynamic state function, such as the α(T) function commonly used in the attractive pressure term of van der Waals EoS. The approach of Kwak and Mansoori considers rewriting the Peng–Robinson expression so that the transformed equation of state contains three temperature-independent parameters (c_m, b_m, and d_m). The three EoS parameters are expressed using the classical van der Waals mixing rules, each one including one adjustable parameter.

The Peng–Robinson model belongs to the so-called van der Waals type equations of state, and can be written as follows [19]:

P = \frac{R T}{V - b} - \frac{a}{V (V + b) + b (V - b)}

(1)

In this equation, a is a function of the reduced temperature (T_R = T/T_c) and b is a parameter determined using the critical properties of the substance of interest:

\begin{array}{l} a = a_{c} α (T_{R}) \\ a_{c} = 0.4572 \frac{R^{2} T_{c}^{2}}{P_{c}} \\ α (T_{R}) = {[1 + F (1 - T_{R}^{0.5})]}^{2} \\ b = 0.0778 \frac{R T_{c}}{P_{c}} \\ F = 0.3746 + 1.5423 ω - 0.2699 ω^{2} \end{array}

(2)

For mixtures, the PR equation is written as follows:

P = \frac{R T}{V - b_{m}} - \frac{a_{m}}{V (V + b_{m}) + b_{m} (V - b_{m})}

(3)

In this equation, a_m and b_m are the equation of state parameters for the mixture, to be calculated using defined mixing rules.

The PR/KM model

The modified EoS proposed by Kwak and Mansoori that has been designated as PR/KM is:

P = \frac{R T}{V - b} - \frac{c + R T d - 2 \sqrt{R T c d}}{V (V + b) + b (V - b)}

(4)

with

\begin{array}{l} c = a_{c} (1 + F^{2}) \\ a_{c} = 0.4572 \frac{R^{2} T_{c}^{2}}{P_{c}} \\ F = 0.3746 + 1.5423 ω - 0.2699 ω^{2} \\ b = 0.0778 \frac{R T_{c}}{P_{c}} \\ d = \frac{a_{c} F^{2}}{R T_{c}} \end{array}

(5)

For mixtures, the modified PR/KM equation is:

P = \frac{R T}{V - b_{m}} - \frac{c_{m} + R T d_{m} - 2 \sqrt{R T c_{m}} d_{m}}{V (V + b_{m}) + b (V - b_{m})}

(6)

and the mixing and combining rules proposed by Kwak and Mansoori are:

\begin{array}{c} c_{m} = \sum_{i} \sum_{j} x_{i} x_{j} c_{i j} & c_{i j} = \sqrt{c_{i} c_{j}} (1 - k_{i j}) & c_{i} = c_{c i} (1 + F_{i}^{2}) \\ b_{m} = \sum_{i} \sum_{j} x_{i} x_{j} b_{i j} & b_{i j} = (\frac{b_{i}^{1 / 3} + b_{j}^{1 / 3}}{2}) (1 - β_{i j}) & b_{i} = 0.0778 \frac{R T_{c i}}{P_{c i}} \\ d_{m} = \sum_{i} \sum_{j} x_{i} x_{j} d_{i j} & d_{i j} = (\frac{d_{i}^{1 / 3} + d_{j}^{1 / 3}}{2}) (1 - δ_{i j}) & d_{i} = \frac{a (T_{c i}) F^{2}}{R T_{c i}} \end{array}

(7)

In these equations, x_i is the mole fraction of component i in the liquid or gas phase. As seen in eq. (7), the PR/KM model contains up to three adjustable parameters (k_ij, β_ij, δ_ij), one for each of the constants, and they are assumed to be the same for both phases, liquid and gas. Usually the parameter that most affect the accuracy of the model is k_ij, the interaction parameter for c in the PR/KM model, and several mixtures can be modelled with β_ij = δ_ij = 0 [4]. Additionally, the model requires the critical properties (T_c and P_c) and the acentric factor (ω) for each of the components in the mixture.

The accuracy of the model for correlating the experimental VLE data is determined by calculating the relative deviation in the correlated pressure (%ΔP), the absolute deviation in the correlated pressure (|%ΔP|), and the relative deviation in the correlated mole fraction of the congener in the gas phase (%Δy₁). These deviations are defined as follows:

{% Δ P = \frac{100}{N} \sum (\frac{P^{cal} - P^{\exp}}{P^{\exp}})}_{i}

(8)

{% Δ y_{i} = \frac{100}{N} \sum (\frac{y_{i}^{cal} - y_{i}^{\exp}}{y_{i}^{\exp}})}_{i}

(9)

|% Δ P| = \frac{100}{N} \sum \frac{{|P^{cal} - P^{\exp}|}_{i}}{P_{i}^{\exp}}

(10)

The thermodynamic consistency test can be applied if these deviations are within pre-established ranges. Once the modelling of the VLE data is accepted, the Gibbs–Duhem equation is applied to check the thermodynamic consistency of the data. The equations that described the consistency test are shown in Table 2. This table summarizes the method explained with details elsewhere by the authors [24]. In eq. (A) of Table 2, x_i is the concentration of component i in the liquid or gas phase. In eq. (B), φ_i is the fugacity coefficient of component i in the corresponding phase, H^R is the residual enthalpy, V^R is the residual volume, T is the absolute temperature, and P is the pressure of the system. The fugacity coefficient for the PR/KM model is given by eq. (D) in Table 2. As seen in the table, the final test is reduced to the calculation of two integral terms designated as A_P and A_φ [eq. (E)].

A	Gibbs–Duhem equation in terms of residual properties: $\sum x_{i} d [\frac{G^{R}}{R T}] = - \frac{H^{R}}{R T^{2}} d T + \frac{V^{R}}{R T^{2}} d P$
B	In terms of fugacity coefficients: $\sum x_{i} d l n φ_{i} = - \frac{H^{R}}{R T^{2}} d T + \frac{V^{R}}{R T} d P$ at constant temperature: $[\frac{(Z - 1)}{P}] d P = x_{1} d (ln φ_{1}) + x_{2} d (ln φ_{2})$
C	Arranging terms: $\int \frac{1}{P} d P = \frac{x_{1}}{(Z - 1) φ_{1}} d φ_{1} + \frac{(1 - x_{1})}{(Z - 1) φ_{2}} d φ_{2} and \int \frac{1}{P x_{1}} d P = \int \frac{1}{(Z - 1) φ_{1}} d φ_{1} + \int \frac{(1 - x_{1})}{x_{1} (Z - 1) φ_{2}} d φ_{2}$
D	Fugacity coefficient for the PR/KM model: $\begin{array}{l} ln ϕ_{i} = \frac{(2 {\bar{B}}_{i} - b_{m}) (Z - 1)}{b_{m}} - ln (Z - B) - \frac{A}{2 \sqrt{2 B}} [\frac{2 {\bar{A}}_{i} + 2 R T {\bar{D}}_{i} - \frac{2 \sqrt{R T (a_{m} {\bar{D}}_{i} + d_{m} {\bar{A}}_{i})}}{\sqrt{a_{m} d_{m}}}}{c} - \frac{(2 {\bar{B}}_{i} - b_{m})}{b_{m}}] \ln [\frac{Z + B (1 + \sqrt{2})}{Z + B (1 - \sqrt{2})}] \\ A = \frac{c P}{R^{2} T^{2}} B = \frac{b_{m} P}{R T} c = a_{m} + d_{m} R T - 2 \sqrt{a_{m} d_{m} R T} \\ {\bar{A}}_{i} = \sum_{j}^{N} x_{j} a_{i j} {\bar{B}}_{i} = \sum_{j}^{N} x_{j} b_{i j} {\bar{D}}_{i} = \sum_{j}^{N} x_{j} d_{i j} \end{array}$
E	Experimental and estimated areas: $\begin{array}{l} A_{P} = \int \frac{1}{P x_{1}} d P \\ A_{φ} = \int \frac{1}{(Z - 1) φ_{1}} d φ_{1} + \int \frac{(1 - x_{1})}{x_{1} (Z - 1) φ_{2}} d φ_{2} \end{array}$
F	Individual per cent area deviation in the range [−20% to + 20%]: $% Δ A_{i} = 100 \frac{{\|A_{ϕ} - A_{P}\|}_{i}}{A_{P}}$ Individual deviation in the system pressure in the range [−10% to + 10%]: $% Δ P_{i} = 100 {\|\frac{P^{cal} - P^{\exp}}{P^{\exp}}\|}_{i}$

Thus, if a set of data is considered to be consistent, A_P should be equal to A_φ within acceptable defined deviations. To set the margins of errors, the individual relative per cent area deviation %ΔA_i and the individual absolute per cent area deviation $|% Δ A_{i}|$ between experimental and calculated values are defined as:

% Δ A_{i} = 100 {(\frac{A_{ϕ} - A_{P}}{A_{P}})}_{i}

(11)

|% Δ A_{i}| = 100 {[\frac{A_{ϕ} - A_{P}}{A_{P}}]}_{i}

(12)

In eq. (E), in Table 2, A_P is determined using the experimental P–x data at fixed temperature, while a thermodynamic model (an equation of state) is employed to evaluate A_φ in eq. (E). If the data are adequately correlated, which means that the deviations in the calculated pressure (%ΔP) are within the established margins of error, and the individual area deviations %ΔA_i in the consistency test are also within defined margins of errors, then the data set is considered to be consistent.

To evaluate the integrals given by eq. (E) in Table 2, the following must be defined:

• an equation of state;
• a set of mixing rules;
• a set of combining rules.

In principle, any appropriate equation of state and any mixing and combining rules can be used to evaluate the pressure. This model is used for determining the fugacity coefficients φ_i and the compressibility factor Z. Once the model is defined and the optimum parameters are determined from the experimental P–T–x data, the area A_φ is calculated. For a set of N experimental data points at a fixed temperature, there are (N–1) values of the area A_P and (N–1) values of the area A_φ must calculated [24].

To define the criteria for consistency and inconsistency, it is first required to check if the model is able to correlate the data within acceptable deviations. The model is accepted if the deviation defined by eq. (8) is within −10% to + 10% for %ΔP. After the model is found appropriate, it is required that the deviations in the individual areas defined by eq. (11) are all within the limits −20% to +20% to declare the data as being thermodynamically consistent. All these criteria that have been used by the authors for several years are summarized in Table 2 [23–26]. However, not only the criteria of deviations are considered for determining consistency or inconsistency, but also the distribution of such deviations. If some few points (up to 25% of the original points) do not pass the area test, but the rest of the data does pass the test, there is no reason to eliminate the whole set of data. So, the original set of data is declared to be not fully consistent (NFC). If more than 25% of the data do not pass the test, then the whole original set is declared to be thermodynamically inconsistent (TI).

3 Experimental data studied

The study considers data of eight binary congener + ethanol mixtures at pressures ranging from 0.039 to 6.20 bar and temperatures ranging from 298 to 393 K. These include 25 isotherms with a total of 267 data points. The congeners included in these mixtures are: acetic acid, ethyl acetate, furfural, methanol, 2-methyl-1-propanol, 1-pentanol, 1-propanol and methyl acetate. Table 3 shows pure component properties for all the substances considered in this study. In this table, M is the molecular weight, T_c is the critical temperature, P_c is the critical pressure, V_c is the critical volume and ω is the acentric factor. The values for these properties were obtained from Daubert et al. [28].

Components	M (kg/kmol)	T_c (K)	P_c (bar)	V_c (m³/kmol)	ω
Ethanol	46.1	513.95	61.37	0.168	0.6436
Acetic acid	60.1	591.95	57.86	0.180	0.4665
Ethyl acetate	88.1	523.35	38.80	0.286	0.3664
Furfural	96.1	670.15	56.60	0.252	0.3678
Methanol	32.0	512.65	80.84	0.117	0.5659
2-Methyl-1-propanol	74.1	547.75	49.95	0.274	0.5857
1-Pentanol	88.2	588.10	38.97	0.326	0.5731
1-Propanol	60.1	536.75	51.69	0.218	0.6204
Methyl acetate	74.1	506.55	47.50	0.228	0.3313

Table 4 gives some details on the experimental data used in the study including the literature source for each data set [6,8]. In this table, T is the temperature (expressed in kelvins), N is the number of experimental data, P is the pressure (expressed in bar), Δx₁ is the liquid mole fraction range of component 1 and Δy₁ is the vapour mole fraction range of component 1.

Systems Ethanol (2) +	Reference	T(K)	N	Range of date
				P (bar)	Δx₁	Δy₁
Acetic acid	[6]	308	13	0.0387–0.1062	0.2380–0.9400	0.0350–0.8860
		318	12	0.0633–0.1765	0.2380–0.9320	0.0380–0.8710

Ethyl acetate	[6]	313	14	0.1821–0.2603	0.0060–0.9600	0.0220–0.9280
		328	14	0.3789–0.4865	0.0055–0.9440	0.0185–0.9020
		333	18	0.4812–0.6465	0.0505–0.9760	0.1100–0.9393
		343	15	0.7312–0.9493	0.0065–0.9750	0.0175–0.9480

Furfural	[6]	323	9	0.0387–0.2932	0.0201–0.9800	0.0046–0.3240
		338	9	0.0746–0.5598	0.0201–0.9800	0.0048–0.3510
		353	9	0.1333–1.0730	0.0201–0.9800	0.0051–0.3603

Methanol	[6]	298	11	0.0856–0.1612	0.0841–0.9165	0.1610–0.9610
		373	10	2.3293–3.4465	0.0620–0.9410	0.0890–0.9610
		393	10	4.2774–6.2037	0.0610–0.9420	0.0820–0.9590

2-Methyl-1-propanol	[6]	323	9	0.1022–0.2783	0.1000–0.9000	0.0310–0.6600
		333	9	0.1711–0.4436	0.1000–0.9000	0.0330–0.6750
		343	9	0.2751–0.6879	0.1000–0.9000	0.0350–0.6870
		353	9	0.4291–1.0253	0.1000–0.9000	0.0370–0.7010

1-Pentanol	[8]	348	19	0.1352–0.8489	0.0500–0.9500	0.0070–0.6610

1-Propanol	[6]	323	9	0.1440–0.2823	0.1000–0.9000	0.0480–0.7580
		333	9	0.2374–0.4508	0.1000–0.9000	0.0510–0.7680
		343	9	0.3819–0.7011	0.1000–0.9000	0.0530–0.7770
		353	9	0.5825–1.0398	0.1000–0.9000	0.0550–0.7820

Methyl acetate	[6]	323	8	0.3212–0.7598	0.0269–0.9217	0.1101–0.9511
		333	8	0.4932–1.0796	0.0269–0.9217	0.1066–0.9480
		343	8	0.7731–1.5088	0.0269–0.9217	0.1052–0.9449
		353	8	1.1463–2.0660	0.0269–0.9217	0.0842–0.9430

4 Results and discussion

Table 5 presents the results of the consistency test for the mixtures considered in this study. As observed in the table, 13 of the 25 data sets were found to be thermodynamically consistent (TC), three sets were found to be not fully consistent (NFC), and nine sets were found to be thermodynamically inconsistent (TI). Of the nine sets found to be thermodynamically inconsistent, seven did not fulfil the area test and two sets were declared to be TI because the model could not fit the data in an accurate manner (%ΔP_max greater than 10%). Since the other isotherms could be modelled by the PR/KM model in an acceptable way (%ΔP_max lower than 10%), the area test is not applied, but the data are declared to be inconsistent. Also, in Table 5, the average absolute deviations for the pressure $|% Δ P|$ , the maximum individual relative deviations for the bubble pressure %ΔP_max, the average absolute deviations for the vapour mole fraction $|% y_{1}|$ , and the average absolute area deviations $|% Δ A_{i}|$ are provided. The average deviations $|% Δ P|$ and $|% Δ A_{i}|$ for a set of N data are defined by eqs. (10) and (12).

Systems Ethanol (2) +	T (K)	k₁₂	β₁₂	δ₁₂	$\|Δ P %\|$	$\|P_{\max} %\|$	$\|Δ y_{1} %\|$	$\|Δ A %\|$	Results
Acetic acid	308	−0.14488	0.25451	−0.76646	4.5	−9.9	10.7	39.3	TI
	318	−0.16897	0.15049	−0.60760	6.2	−9.9	8.8	28.1	TI

Ethyl acetate	313	0.09107	0.12565	0.00316	0.5	2.6	2.0	9.7	TC
	328	0.12728	0.16984	0.04015	0.4	2.6	4.6	10.5	NFC
	333	−0.05943	−0.05628	−0.11753	7.7	17.6	12.1	–	TI*
	343	0.08636	0.14462	−0.02646	0.4	2.6	3.3	14.1	NFC

Furfural	323	0.05978	−0.07166	0.11860	12.7	25.2	12.5	–	TI*
	338	−0.01638	−0.23892	0.14416	6.1	8.9	12.9	13.3	NFC
	353	−0.01385	−0.15270	0.03372	3.3	9.8	10.7	27.1	TI

Methanol	298	0.38225	0.55352	0.20042	1.6	−4.9	2.9	28.4	TI
	373	0.06155	0.02533	0.12259	0.6	1.6	1.9	20.1	TI
	393	−0.10148	−0.17580	−0.03435	1.0	3.0	1.9	19.6	TI

2-Methyl-1-propanol	323	0.11385	0.18477	0.05496	2.5	6.4	13.0	12.2	TC
	333	0.14828	0.04808	0.28130	1.8	5.4	10.0	8.4	TC
	343	0.0974	0.18997	0.00429	1.4	4.2	8.7	7.1	TC
	353	0.08682	0.08641	0.09587	1.2	1.6	6.2	7.4	TC

1-Pentanol	348	−0.02311	−0.02503	−0.04859	1.4	4.4	8.6	5.3	TC

1-Propanol	323	0.06194	0.11260	0.01337	1.9	6.9	7.1	11.0	TC
	333	0.05801	0.10592	0.01209	1.5	5.6	5.7	9.6	TC
	343	0.08325	0.06628	0.10817	1.1	3.6	4.7	7.4	TC
	353	0.03765	0.07136	0.00149	1.2	3.4	4.0	10.0	TC

Methyl acetate	323	0.07887	0.08683	0.06734	0.6	1.8	3.6	7.2	TC
	333	−0.09295	−0.01183	−0.24173	2.2	4.9	3.4	8.6	TC
	343	0.30410	0.26966	0.36825	0.9	2.3	5.2	9.8	TC
	353	0.26088	0.19238	0.35252	2.9	7.6	2.0	64.8	TI

As indicated in Table 5, the PR/KM model reproduces the bubble pressure of these binary mixtures with average absolute deviations below 12.8% for any temperature. In 21 of the 25 isotherms studied, pressure deviations are below 5.0%. With respect to the congener concentration in the vapour phase (y₁), this quantity is predicted in all cases studied with average absolute deviations ranging from 1.9% to 13.0%. It should also be mentioned that the highest deviations are generally found for those cases in which the congener concentration in the vapour phase is very low.

For the 13 isotherms considered to be thermodynamically consistent, for instance the system 2-methyl-1-propanol (1) + ethanol (2) at all temperatures, the modelling is acceptable as seen in Table 5 and deviations in the areas are within the established limits.

Three cases are declared to be not fully consistent (NFC), such as the system furfural (1) + ethanol (2) at T = 338 K. This is so in these cases because there are some few points in the original data set that give high area deviations, but the remaining areas give deviations within the established limits. If those points showing high deviation are not considered in the analysis (one or two points for each one of the systems), the remaining data give area deviations below the established limits (20%). Thus, the remaining set is TC but the original set is declared to be NFC.

For the nine cases considered to be thermodynamically inconsistent (TI), seven did not fulfil the area test. For instance, for the system acetic acid (1) + ethanol (2) at T = 308 and 318 K, the area deviations are very high for more than 25% of the points of the original data set, despite the fact that the modelling is acceptable and within the limits established by the method. Also, two cases were declared to be TI because the modelling is not accurate enough (some deviations in the individual pressures are higher than 10%). For instance, this is the situation for the systems ethyl acetate (1) + ethanol (2) at T = 333 K and furfural (1) + ethanol (2) at T = 323 K.

A graphical description of the results is show on Figs. 1–3. Fig. 1 shows the relative area deviations for the liquid phase %ΔA_i for the system 1-propanol (1) + ethanol (2) at T = 343 K, declared to be thermodynamically consistent (TC). As observed in the figure, all area deviations are below 20%. Fig. 2 shows the relative area deviations for the liquid phase %ΔA_i for the system ethyl acetate (1) + ethanol (2) at T = 328 K, declared to be not fully consistent (NFC). In this case, two points present area deviations higher than 20%. Fig. 3 shows the relative area deviations for the system methanol (1) + ethanol (2) at T = 393 K, declared to be thermodynamically inconsistent (TI). For this case, 44% of the original data give deviations higher than 20%.

Fig. 1
Area deviations for the liquid phase %ΔA_i for the system 1-propanol (1) + ethanol (2) at T = 343 K, declared to be thermodynamically consistent (TC).

Fig. 2
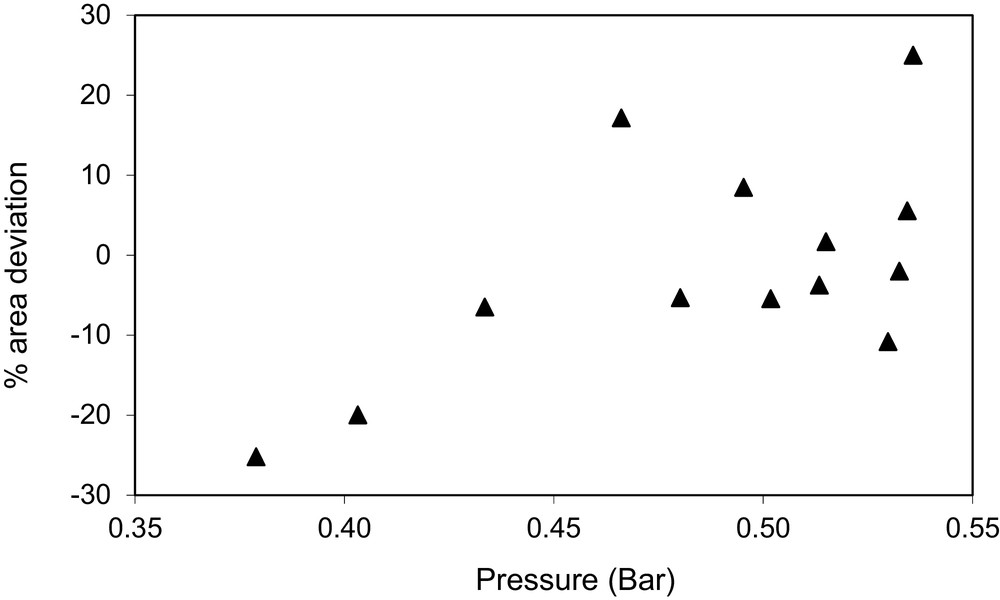
Area deviations for the liquid phase %ΔA_i for the system ethyl acetate (1) + ethanol (2) at T = 328 K, declared to be not fully consistent (NFC).

Fig. 3
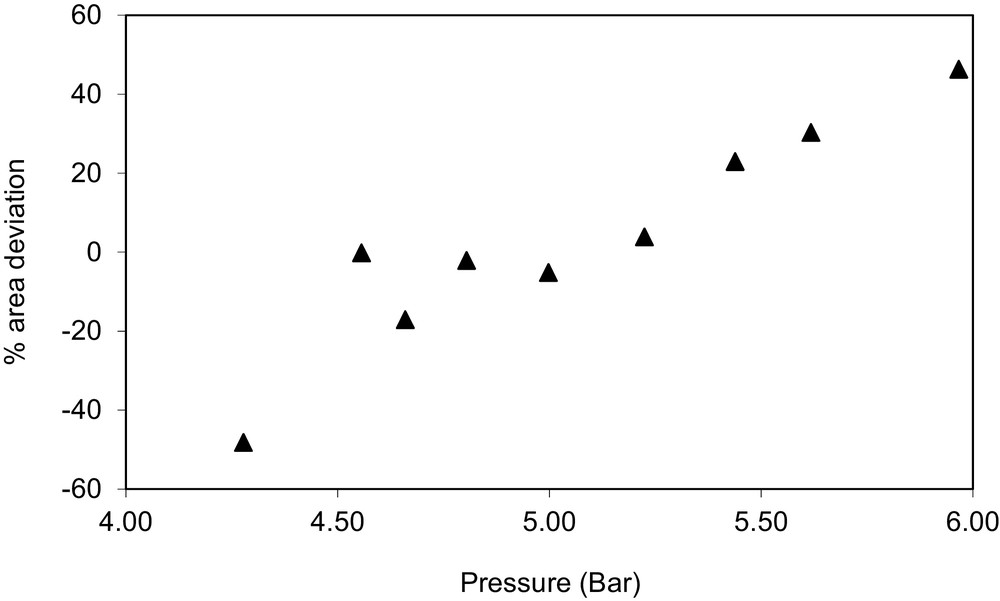
Area deviations for the system methanol (1) + ethanol (2) at T = 393 K, declared to be thermodynamically inconsistent (TI).

5 Conclusions

Based on the results, the following main conclusions can be drawn:

• the equation of state method using appropriate mixing rules such as that of Kwak and Mansoori can be used to model low-pressure VLE data in ethanol + congener mixtures;
• bubble pressures can be correlated with good accuracy with the PR/KM model, giving absolute average deviations below 12.8% for each isothermal data set and the overall absolute average deviations is 2.6%;
• the congener concentration in the vapour phase, y₁, can be obtained with good accuracy, giving absolute average deviations below 13.1% for each isothermal data set and the overall absolute average deviations is 6.6%;
• the proposed consistency test method allows to globally analyse P–T–y data;
• the method gives an adequate answer about the consistency or inconsistency of a set of experimental P–T–y data.

Acknowledgements

The authors thank the support of the National Council for Scientific and Technological Research (CONICYT), through the research grant FONDECYT 1070025. JOV thanks the University of La Serena and the Centre for Technological Information of La Serena-Chile, for permanent support. CAF and MFM thank the Direction of Research of the University of Concepcion for the support through the research grant DIUC 211.011.054-1.0.

Bibliographie

[1] V. Athès; P. Paricaud; M. Ellaite; J. Souchon; W. Fürst Fluid Phase Equilib., 265 (2008), p. 139

[2] J. Lora; M.I. Iborra; R. Pérez; I. Carbonell Rev. Esp. Cien. Tec. Ali., 32 (1992), p. 621

[3] C.A. Faúndez; V. Álvarez; J.O. Valderrama Thermochim. Acta, 450 (2006), p. 110

[4] J.O. Valderrama Ind. Eng. Chem. Res., 42 (2003), p. 1603

[5] S.M. Walas Phase Equilibria in Chemical Engineering, Butterworth Publication, Storeham, USA, 1985

[6] J. Gmehling; U. Onken; W. Arlt Vapour-Liquid Equilibrium Data Collection, Dechema, Germany, 1982

[7] The Dortmund Data Bank (DDB) Thermophysical Properties of Pure Component and Mixtures, 2011 http://www.ddbst.com/en/ddbst/index.php

[8] S. Ohe Vapour–Liquid Equilibrium Data, Physical Sciences Data 37, Kodansha Ltd./Elsevier Science Publishers B. V, Tokyo/Amsterdam, 1989

[9] J.O. Valderrama; C.A. Faúndez; L.A. Toselli Food Bioprod. Process, 90 (2012), p. 819

[10] J.O. Valderrama; C.A. Faúndez; L.A. Toselli Food Bioprod. Process, 90 (2012), p. 832

[11] J.D. Raal; A.I. Mühlbauer Phase Equilibria. Measurement and Computation, Taylor and Francis, UK, 1998

[12] K. Kurihara; Y. Egawa; S. Lino; K. Ochi; K. Kojima Fluid Phase Equilib., 257 (2007), p. 151

[13] D. Miklós; S. Kemény; G. Almásy; K. Kollar-Huneck Fluid Phase Equilib., 110 (1995), p. 89

[14] M. Góral; P. Oracz; A. Skrzecz; A. Bok; A. Maczyski J. Phys. Chem. Ref. Data, 32 (2003), p. 1429

[15] S. Kato Fluid Phase Equilib., 297 (2010), p. 192

[16] S. Kato Fluid Phase Equilib., 302 (2011), p. 202

[17] V.H. Álvarez; S. Mattedi; M. Iglesias; R. Gonzalez-Olmos; J.M. Resa Phys. Chem. Liq., 49 (2011) no. 1, p. 52

[18] P. Susial; R. Rios-Santana; A. Sosa-Rosario Braz. J. Chem. Eng., 28 (2011), p. 325

[19] D.Y. Peng; D.B. Robinson Ind. Eng. Chem. Fundam., 15 (1976), p. 59

[20] T.Y. Kwak; G.A. Mansoori Chem. Eng. Sci., 41 (1986), p. 1303

[21] J.O. Valderrama; V.H. Álvarez AIChE J., 50 (2004), p. 480

[22] J.O. Valderrama; F. Urbina; C.A. Faúndez J. Supercrit. Fluids, 64 (2012), p. 32

[23] J.O. Valderrama; P.A. Robles Fluid Phase Equilib., 242 (2006), p. 93

[24] J.O. Valderrama; C.A. Faúndez Thermochim. Acta, 499 (2010), p. 85

[25] C.A. Faúndez; J.F. Díaz-Valdés; J.O. Valderrama Fluid Phase Equilib., 348 (2013), p. 33

[26] C.A. Faúndez; L.A. Barrientos; J.O. Valderrama Int. J. Refrig., 36 (2013), p. 2242

[27] C.A. Faúndez; J.F. Díaz-Valdés; J.O. Valderrama Fluid Phase Equilib., 375 (2014), p. 152

[28] T.E. Daubert; R.P. Danner; H.M. Sibul; C.C. Stebbins Physical and Thermodynamic Properties of Pure Chemicals. Data compilation, Taylor & Francis, London, UK, 1996

Commentaires - Politique

Ces articles pourraient vous intéresser

Validation of gentamicin congeners using HPLC with electrochemical detection: comparison with fluorimetric detection

Issa T. Somé; Rasmane Semde; Ouedraogo Moustapha; ...

C. R. Chim (2004)

Modeling associating hydrocarbon + alcohol mixtures using the Peng-Robinson equation of state and the Wong-Sandler mixing rules

Claudio A. Faúndez; José O. Valderrama

C. R. Chim (2013)

Extrabuccal infralabial secretion outlets in Dromophis, Mimophis and Psammophis species (Serpentes, Colubridae, Psammophiini). A probable substitute for ‘self-rubbing’ and cloacal scent gland functions, and a cue for a taxonomic account

Cornelius C. de Haan

C. R. Biol (2003)