1 Introduction
Building green power grids is crucial to realize sustainable society. At present, it is difficult to balance uneven power demands and intermittent power from renewable sources. Therefore, advanced batteries need to be developed, which can increase our energy control and efficiency in power grids [1]. Although lithium-ion batteries are currently powering most portable electronics owing to their high energy density (ca. 250 Wh/kg and 600 Wh/L), substantial gaps exist for wide use in power grids, in terms of energy density, power density, cycle life, elemental abundance, and cost [2].
Focusing on the energy density, the positive and negative electrodes of a battery generally work using reversible ion (de)intercalation in host materials (HP and HN, where P and N denote positive and negative electrodes, respectively). The (de)intercalation reaction at the cathode can be described as follows: HP + A+ + e− ↔ A(HP), where A+ is intercalant cation such as Li+ or Na+. The net reaction, HP + A(HN) ↔ A(HP) + HN, of a full cell gives a charge/discharge voltage, E, as
Another important issue is the power density that represents the charge/discharge rate capability of a battery. It is well known that the charge/discharge rate capability is limited by various polarizations: (1) polarization in electrodes, influenced by electronic conduction and ionic diffusion, (2) polarization at interfaces, impacted by overpotential and transport number, and (3) polarization in electrolytes, dependent on ionic conduction and ionic diffusion [4]. In particular, slow ion transport in host materials is considered as a major rate-determining step. Therefore, it is necessary to rationally design porous host materials that can exhibit fast ion transport [5].
Upon considering these requisites for the electrode materials of advanced batteries, coordination compounds are attractive, because they can exhibit (nano)porous and flexible structures, enabling reversible ion (de)intercalation. Importantly, the rational structural/electronic design of coordination networks allows us to control
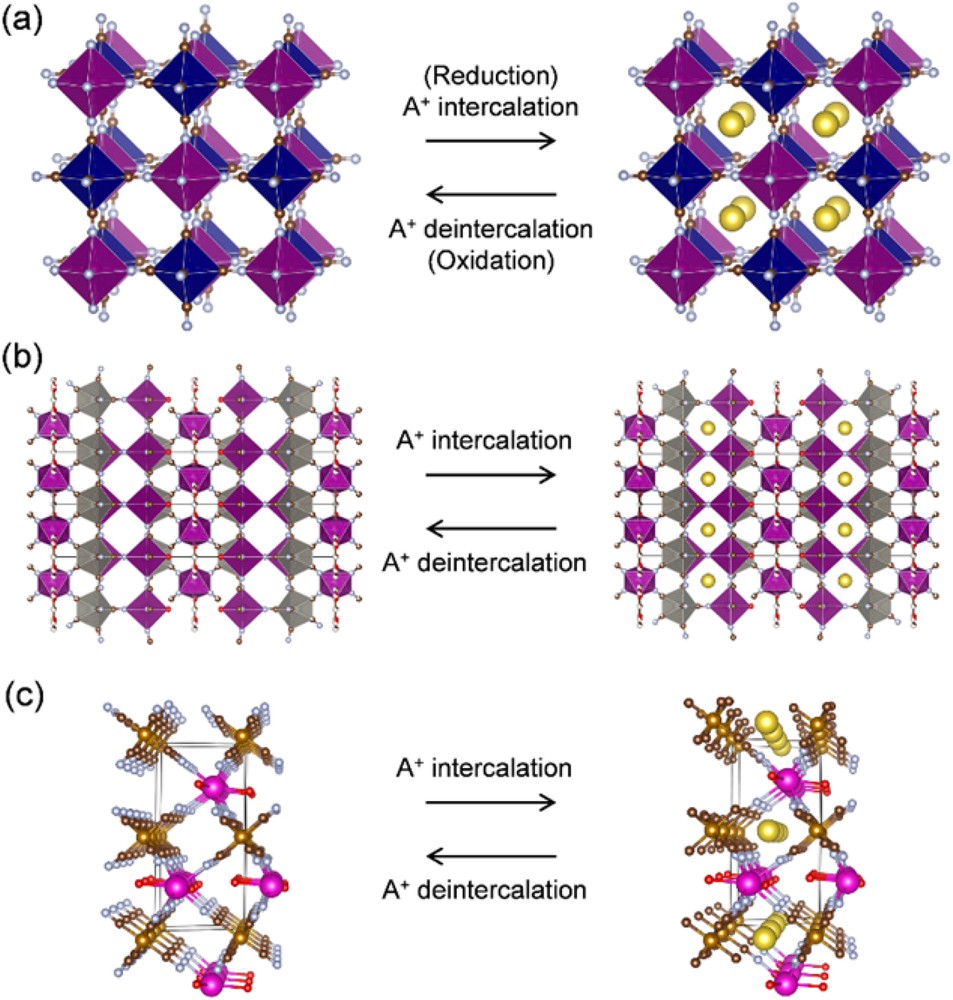
Schematic illustration of ion (de)intercalation in coordination polymers: (a) Prussian blue analogue, (b) [Mn(H2O)][Mn(HCOO)2/3(H2O)]3/4[Mo(CN)8]·H2O, and (c) Eu[Fe(CN)6]·4H2O.
In this review, we summarize the fundamental solid-state electrochemistry of cyanido-bridged coordination compounds.
2 Thermodynamic aspects
High energy density is achieved using positive electrode materials capable of dense ion storage at high voltage. For the electrode reaction of HP + xA+ + xe− ↔ Ax(HP), the electrode potential, E, versus a reference electrode is expressed as
Most frameworks of cyanido-bridged coordination compounds are built from transition-metal or lanthanide cations MAl+ bridged by cyanidometallates [MB(CN)m]n−. For example, hexacyanidometallates [MB(CN)6]n− bridge MAl+ to form Prussian blue analogues (PBAs), having a three-dimensional (3D) face-centered cubic structure [11,12]. PBA is frequently found in a nonstoichiometric form with the general formula A1−xMAII[MBIII(CN)6]1−x/3□x/3 (A = alkali ion, □ = cyanidometallate vacancies). The presence of hexacyanidometallate vacancies ensures the electroneutrality of the coordination framework. Variations of MA and cyanidometallates result in various, sometime lower dimensional, non-PBA-type porous frameworks [13,14]. Hence, using octacyanidometallates [M(CN)8]4−/3− (M = Mo, W) generates various extended networks of different dimensionalities with either transition metals or lanthanide ions [15]. For instance, although the compound [Mn(H2O)][Mn(HCOO)2/3(H2O)]3/4[Mo(CN)8]·H2O is a 3D structure made of interconnected double-deck planes creating 2D open channels [16], the lanthanide-based [Tb(H2O)5][W(CN)8] compound is a 2D coordination network formed by corrugated layers with strong hydrogen bonds between coordinated water molecules that ensure the interlayer's interactions [17,18]. However, regardless of MA and the framework, in most cases, the cyanidometallates [MB(CN)m]n− are the redox center of cyanido-bridged coordination compounds, which primarily determines
To demonstrate the dominant role of cyanidometallates in determining E, Fig. 2a and b show the potential profiles of reversible Li (de)intercalation in two PBAs, K0·1Mn[Fe(CN)6]0.7·□0.3·4.3H2O and K0·25Ni[Fe(CN)6]0.75·□0.25·5H2O (□ indicates a [Fe(CN)6] vacancy), in a nonaqueous Li+ electrolyte [8,19]. Both PBAs exhibit reversible Li+ (de)intercalation associated with the solid-state redox reaction [FeIII(CN)6]3−+ e− ↔ [FeII(CN)6]4−. Regardless of the transition metals, Ni or Mn in the MA site, the average reaction voltage E for both compounds is approximately 3.3 V versus Li/Li+, close to the standard redox potential of [FeIII(CN)6]3−/[FeII(CN)6]4− (0.36 V versus standard hydrogen electrode (SHE), i.e., 3.4 V versus Li/Li+). Fig. 2c and d show the potential profiles of Li+ (de)intercalation for the 3D framework [Mn(H2O)][Mn(HCOO)2/3(H2O)2/3]3/4[Mo(CN)8]·H2O and the bidimensional network [Tb(H2O)5][W(CN)8] in a nonaqueous Li+ electrolyte [16,20]. Their average reaction voltages are approximately 3.5 and 3.4 V versus Li/Li+, respectively, near the standard redox potentials of [MoV(CN)8]3−/[MoIV(CN)8]4− (0.80 V versus SHE, i.e., 3.84 V versus Li/Li+) and [WV(CN)8]3−/[WIV(CN)8]4− (0.46 V versus SHE, i.e., 3.5 V versus Li/Li+). Although the redox potential of cyanidometallates involved in the network should be modulated by the acidity of the MA linked to the N atoms, the standard redox potential of a cyanidometallate in solution primarily governs the reaction voltage of cyanido-bridged coordination compounds. Indeed, among the hexacyanidometallates of first row transition metals Ti, Cr, Mn, Fe, and Co that can occupy the [MB(CN)6]n−-site of the PBA-like networks, the standard redox potential of [FeIII(CN)6]3−/[FeII(CN)6]4− is the most suitable to the positive electrodes of various batteries, and most studies on the solid-state electrochemistry of cyanido-bridged coordination compounds have focused on hexacyanidoferrates [9,21,22].
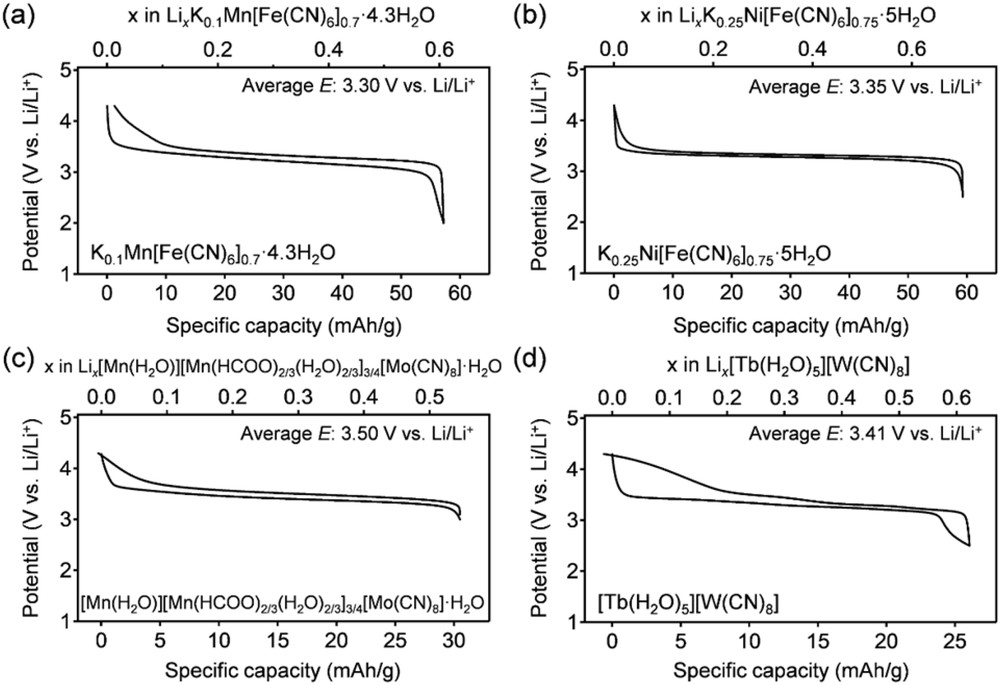
Reversible Li+ (de)intercalation potential profiles of (a) K0·1Mn[Fe(CN)6]0.7·□0.3·4.3H2O [8], (b) K0·25Ni[Fe(CN)6]0.75·□0.25·5H2O [19], (c) [Mn(H2O)][Mn(HCOO)2/3(H2O)]3/4[Mo(CN)8]·H2O [16], and (d) [Tb(H2O)5][W(CN)8] [20] in a 1.0 M LiClO4/PC electrolyte. PC, propylene carbonate.
The electrode potential is also influenced by the chemical potential of the cation,
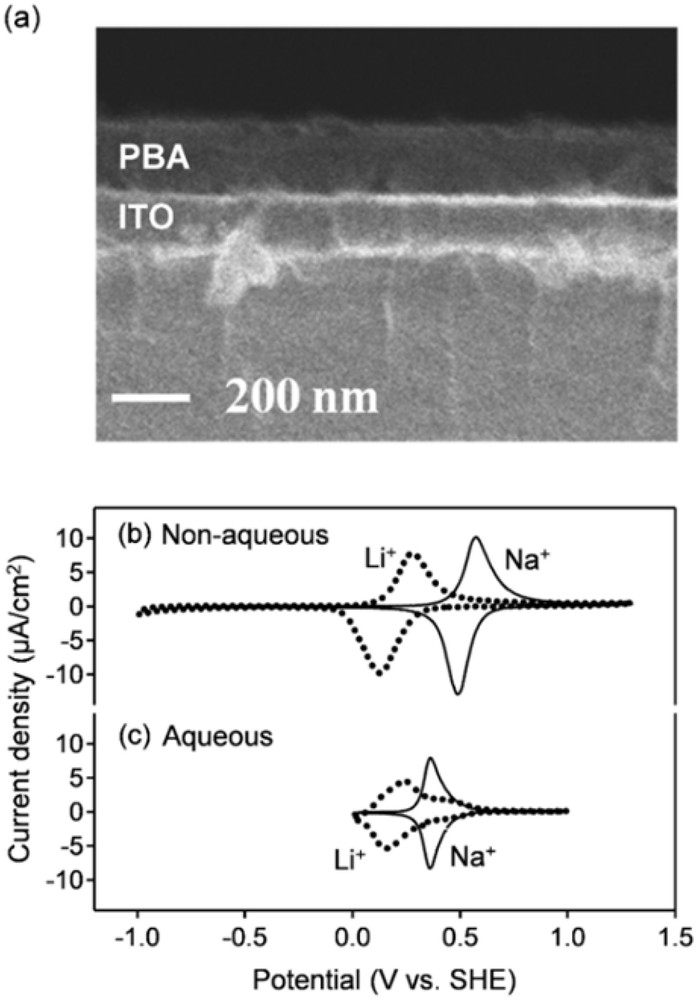
(a) Scanning electron microscope image of the thin film electrode of PBA (MA = Ni, MB = Fe). Cyclic voltammetry (CV) curves at the scan rate of 1.0 mV/s with (b) nonaqueous Li+ and Na+ electrolytes, and (c) aqueous Li+ and Na+ electrolytes [23]. Solid and dotted lines are CV curves with Li+ and Na+ electrolytes, respectively.
Another important aspect of the solid-state electrochemistry is the phase transformation mechanism upon ion (de)intercalation, which is generally classified into either a solid-solution or a two-phase mechanism. For the solid-solution mechanism of HP + xA+ + xe− ↔ Ax(HP), A+ and e− are distributed homogeneously in Hp, where the concentration of A+ changes continuously during charge/discharge. PBAs frequently exhibit a typical solid-solution reaction, which can be evidenced by the smooth shift of X-ray diffraction (XRD) peaks during charge/discharge (Fig. 4a) [19,26,27]. The linear change in lattice parameters as a function of the number of intercalated ions (Vegard's law) indicates that ion (de)intercalation occurs topochemically with preserving the host structure. On the other hand, for the two-phase mechanism of HP + xA+ + xe− ↔ x[A(HP)] + (1 − x)[HP], phase separation between A(HP) and HP occurs, where the volume fraction of each phase changes during charge and discharge. As an example of a two-phase system, the ex situ XRD patterns for Eu[Fe(CN)6]·4H2O show the emergence of new peaks at the expense of initial peaks upon Na+ intercalation (Fig. 4b) [28].
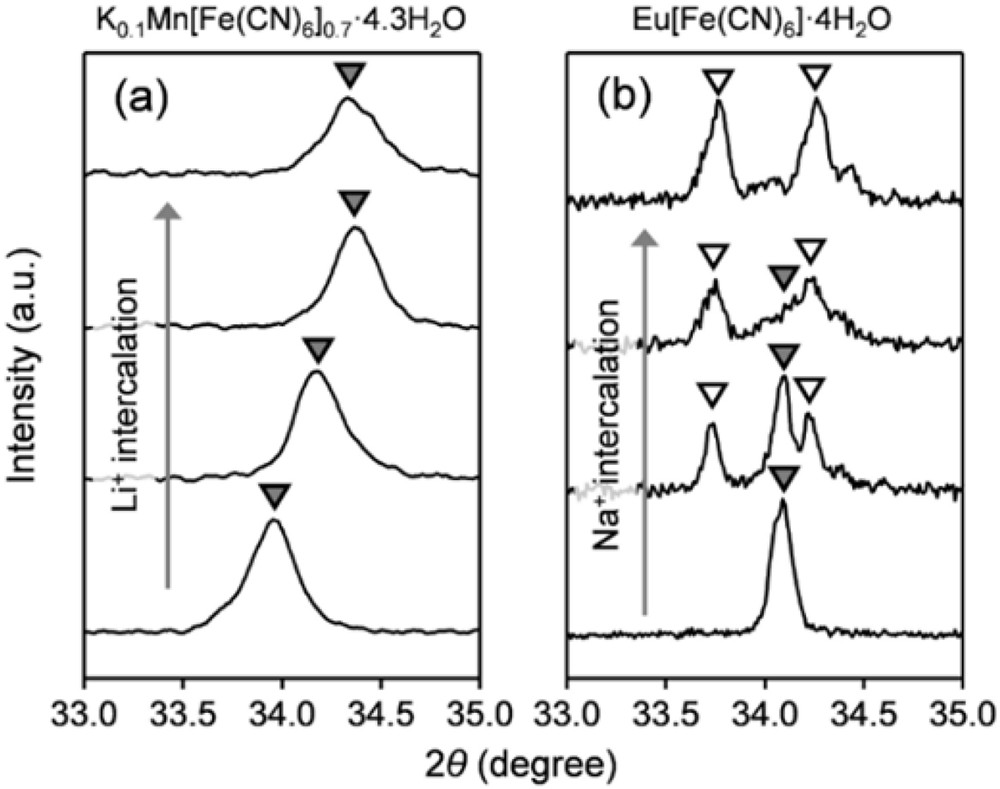
Ex situ XRD patterns of (a) solid-solution system K0·1Mn[Fe(CN)6]0.7·□0.3·4.3H2O upon 0.7 Li+ intercalation [8], and (b) two-phase system Eu[Fe(CN)6]·4H2O upon 1.0 Na+ intercalation [28].
For conventional electrode materials such as oxides and polyanionic compounds, the unit cell volume change by ion intercalation is considered as a descriptor of whether the reaction proceeds through the solid-solution or two-phase state [10]. Elastic repulsion between initial and final states because of the volume change increases mixing enthalpy, leading to the phase separation. However, for cyanido-bridged coordination compounds, their flexible framework can easily accommodate intercalated ions through the rotation of cyanidometallates. Indeed, the volume change of the two-phase system Eu[Fe(CN)6]·4H2O upon Na+ intercalation is only 1.4%, which is much smaller than that for conventional two-phase systems (6.0% for Li1+xMn2O4, 6.6% for Li1−xFePO4, and 8.3% Na3−xV2(PO4)3) [28]. Most likely, cooperative rotation of cyanidometallates induces the phase separation in sodiated Eu[Fe(CN)6]·4H2O. Therefore, to tailor electrochemical properties of cyanido-bridged coordination compounds, a careful structural investigation is needed.
It is also important to note that structural changes within the cyanido-bridged coordination compound electrodes are strongly influenced by the dimensionality of their framework. For example, 3D frameworks such as PBAs or [Mn(H2O)][Mn(HCOO)2/3(H2O)2/3]3/4[Mo(CN)8]·H2O do not lose its crystallinity upon ion (de)intercalation (Fig. 5a) [16]. On the other hand, lithiation induces disorder and/or defects in the crystal networks of [Tb(H2O)5][W(CN)8] layers or [Fe(Tp)(CN)3]2[Ni(H2O)2] chains (Tp = hydrotrispyrazolylborate), resulting in amorphous states (Fig. 5b and c) [20,29]. However, regardless of the dimensionality, the magnetic properties of the framework solids are recovered after ion intercalation and deintercalation and very close to those of an initial state, indicating that the MB-CN-MA links are preserved although the materials become amorphous. Therefore, the cyanido-bridged coordination networks are maintained during ion (de)intercalation even in the amorphous states.
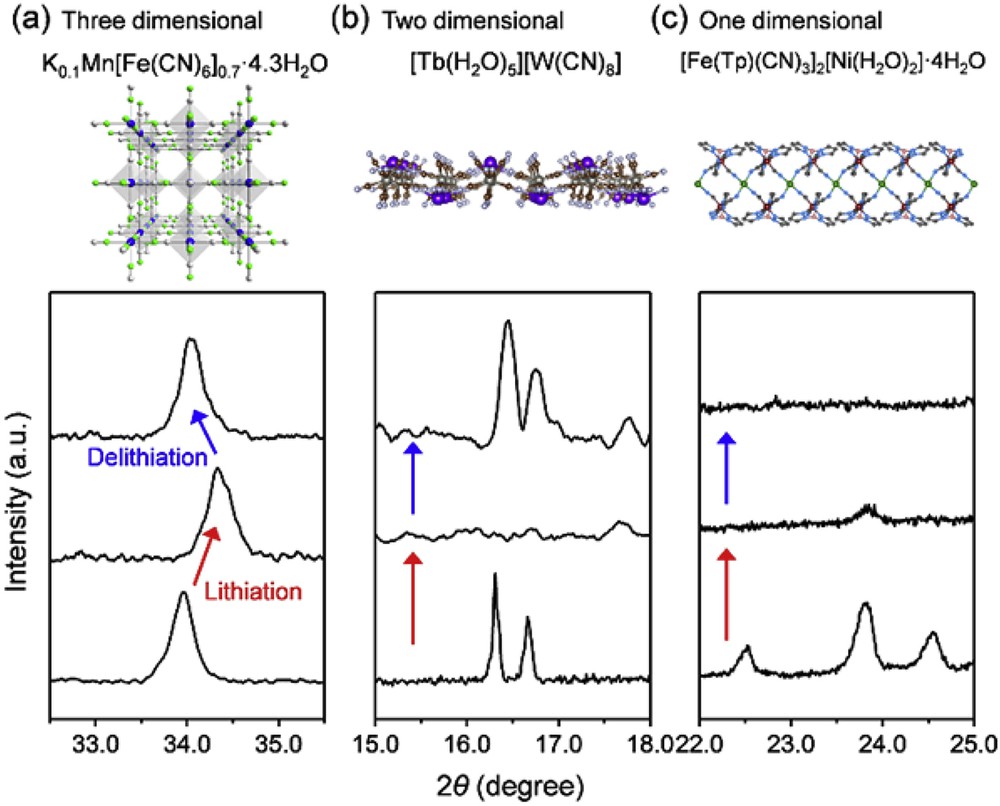
Ex situ XRD patterns for (a) 3D PBA K0·1Mn[Fe(CN)6]0.7·□0.3·4.3H2O during 0.7 Li+ (de)intercalation [8], (b) 2D [Tb(H2O)5][W(CN)8] during 1.0 Li+ (de)intercalation [20], and (c) 1D [Fe(Tp)(CN)3]2[Ni(H2O)2]·4H2O during 2.0 Li+ (de)intercalation [29].
3 Kinetic aspects
As mentioned in Section 1, the charge/discharge rate capability is limited by (1) polarization within electrodes, (2) polarization at interfaces, and (3) polarization in electrolytes. For systems that exhibit solid-solution behavior during charge and discharge, one effective way to reduce these resistances is by reducing particle size [30–32]. Although ion diffusion and electron conduction lengths become short, the large surface area of the small PBA particles reduces the areal current density and surface ion flux. Indeed, a particle size reduction of PBA (MA = Ni, MB = Fe) from 295 to 140 nm effectively suppresses the polarization in charge–discharge potential profiles, providing a larger capacity (Fig. 6) [33]. However, further particle-size reduction can decrease the available capacity, presumably because the number of redox-inactive sites, which may be present at the surface, increases. Therefore, it is necessary to balance the capacity and the rate capability.
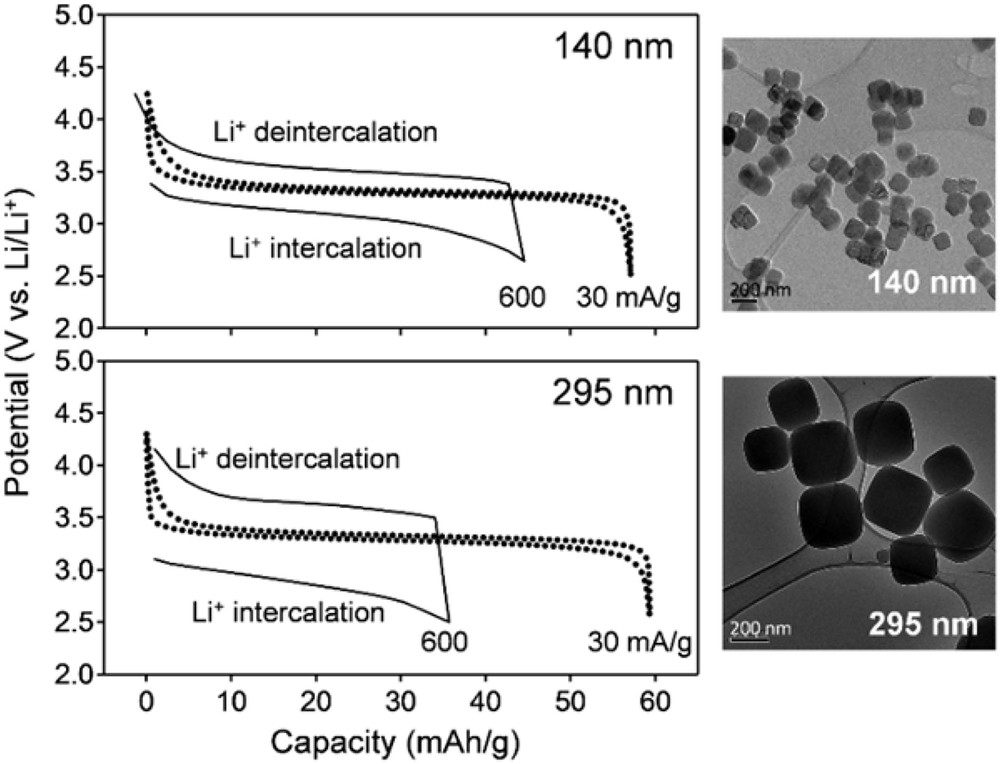
Rate capability of PBA (MA = Ni, MB = Fe) with the average particle sizes of 140 and 295 nm, respectively [33]. Solid and dotted lines are potential profiles at the charge and discharge rates of 600 and 30 mA/g, respectively.
In the case of the two-phase mechanism, as the charge–discharge processes are accompanied by a change in the volume fraction of each phase, the migration of phase boundaries is an important factor that predominantly limits reaction rates [34]. Large energy barriers for the boundary migration were widely reported for two-phase systems such as Li1+xMn2O4 (0.42 eV) and Li1−xFePO4 (0.41 eV) [32,35]. The two-phase reaction of a 3D cyanido-bridged coordination compound NaxEu[Fe(CN)6]·4H2O exhibits 1D boundary migration, the so-called domino cascade, where the Kolmogorov–Johnson–Mehl–Avrami analysis revealed an energy barrier for the boundary migration as 0.11 eV [28]. This specifically small value, which was ascribed to the small volume change between sodiated and desodiated phases, indicates that the boundary migration may not be the rate-determining step in NaxEu[Fe(CN)6]·4H2O. The kinetics of the two-phase reaction of cyanido-bridged coordination compounds is yet to be fully understood, hence further microscopic investigation on the boundary migration is needed.
Reducing interfacial polarization by surface modification also improves the power density. In general, large solvated ions in organic electrolytes can penetrate the host framework only after desolvation, resulting in large energy barriers of approximately 0.5 eV for interfacial charge transfer [36]. For example, inherent surface passivation layers on PBA (MA = Cu, MB = Fe) decelerate interfacial charge transfer to give a poor rate capability (Fig. 7a and c) [26]. However, when the protective shell of another PBA (MA = Ni, MB = Fe) with lower interfacial charge–transfer resistance is deposited on the PBA (MA = Cu, MB = Fe), the core–shell nanoparticles enable efficient ion (de)intercalation even at high charge/discharge rates (Fig. 7b and d) [37–39]. The surface modification of cyanido-bridged coordination compounds using soft chemistry is a clear advantage over conventional electrode materials [12].
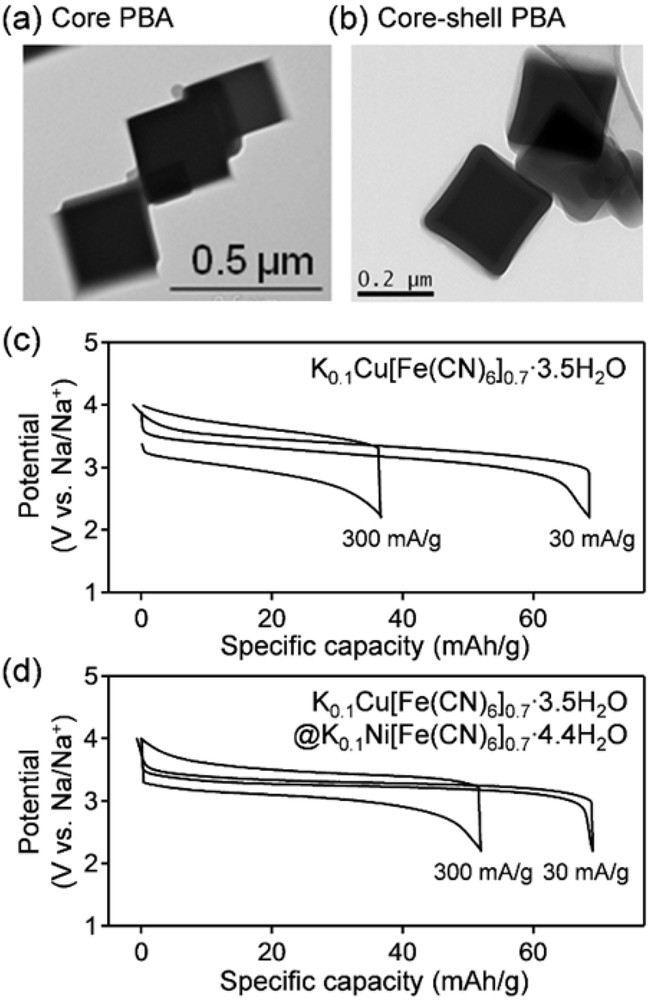
TEM images of (a) core PBA (MA = Cu, MB = Fe) and (b) core–shell PBA (core, MA = Cu, MB = Fe; shell, MA = Ni, MB = Fe). Rate capability of (c) core PBA and (d) core–shell PBA in a nonaqueous Na+ electrolyte [38]. Potential profiles at 300 and 30 mA/g are shown for comparison.
4 Conclusions
We have summarized the fundamental solid-state electrochemistry of cyanido-bridged coordination compounds. Their large electronic and structural tunability offer appealing alternatives to conventional electrode materials. From the thermodynamic point of view, the solid-state redox potential is predominantly determined by the standard redox potential of cyanidometallates in solution, albeit with a slight perturbation from ion chemical potential
Acknowledgments
This work was financially supported by the ANR-JST Strategic International Collaborative Research Program (SICORP), Molecular Technology, Molecular Materials for Magnesium Batteries (MoMa). M.O. and R.L. thank Michel Verdaguer for his kind intermediation to launch MoMa. J.L. thanks the University of Montpellier, CNRS, and PAC of ICGM.


