1 Introduction
Titanium disulfide TiS2 belongs to the layered transition metal dichalcogenide family, which has been widely studied for decades because of the variety of their electronic properties [1,2]. After the discovery of graphene and the advance of new synthetic methods, renewed interest has been focused on two-dimensional (2D) M-doped transition metal dichalcogenides (M = transition metal) for their new potential applications (see Refs. [3–7] and references therein for recent results).
TiS2 [8] and its intercalation compounds have been intensively studied and shown to be promising cathode materials in rechargeable batteries [9] and as potential hydrogen storage materials [10]. The most salient features of the Ti1+xS2 system are its surprising capacity for adopting various structures and their coexistence, the polytypism, nonstoichiometry, and order/disorder phenomena [11,12]. Various morphologies of TiS2, such as nanotubes [13,14] and fullerene-like [15], have been successfully synthesized. This complexity appears to be a specific property of the titanium–sulfur atomic pair with no equivalent in other systems [16].
Polytypism in TiS2 was observed by Legendre et al. [17] and Tronc et al. [18], with different periodicities along the c axis. The structures of these polytypes are all based on close-packing layers of sulfur, very similar to those of Cdl2. The titanium atoms occupy the octahedral holes between the S atoms. Two types of titanium layers alternate along the c axis: filled and partially filled. In fact, in addition to the three basic forms 1T, 4H, and 12R, many structures form 2H, 9R, 8H, 10H, and so forth.
A superstructure in the Ti1+xS2 was first found by Bartram [19] in the 4H–Ti1.33S2 structure [20]. Some kinds of superstructures designated (4H)2, (4H)3, and (2H)2 were also synthesized and analyzed by means of X-ray diffractometry and high-resolution electron microscopy [20–22]. Each superstructure arises from a specific ordering pattern of Ti vacancies in the partially occupied Ti layers.
A preliminary observation of diffuse scattering features on the X-ray diffraction (XRD) and electron diffraction patterns on the Ti1+xS2 was made by Moret et al. [23,24]. These diffuse features were attributed to the incomplete 2D ordering (short range order (SRO) or nanosized domains) of titanium atoms in the partly occupied layers of the structure.
Some metal transitions (M) as Fe, Co, and Ni have been successfully inserted into the gap of TiS2 and show unusual physical properties compared with nondoped/intercalated TiS2 (see Refs. [25–27] and references therein).
In MxTiS2 (M = Fe, Ni, and Co) several types of superstructures were found (see Refs. [28,29] and references therein) by maximum entropy method, XRD, and neutron powder diffraction analyses, and are caused by the ordered/partial ordered atomic arrangement of intercalated M atoms.
Recently, X-ray powder diffraction, electronic, magnetic, and thermal properties of M-doped 1T-TiS2 (M = 3d transition metal) have been reported in many studies. In these studies, it has been shown that crystal structure and physical properties of M-doped 1T-TiS2 strongly depend on the type of guest M atoms, their concentration, and synthesis conditions (see Refs. [29,30] and references therein; [31]). To the best of our knowledge, no germanium intercalated or doped TiS2 has been reported.
In this study, we present our results concerning single-crystal XRD and transmission electron microscopy (TEM), and a study of the metal–metal interactions of the first germanium doped TiS2 polytypes: 1T, (4H)2, 12R, and their corresponding new a√3 × a√3 superstructure.
2 Experimental methods
2.1 Synthesis
Single crystals of the title compound were prepared via the chemical vapor transport method by two different mixtures of starting materials: pure Ge, Ti, and S elements in a ratio 0.5:1:2 and in a mixture of pure Ge and TiS2 previously prepared in a ratio 0.5:1.
TiS2 was prepared by heating the appropriate mixture of elements in silica tubes at 900 °C for 1 week. The tubes were subsequently slowly cooled to room temperature. The mixture was then sealed into an evacuated quartz tube with iodine (<5 mg/cm3) as a transport agent to favor crystallization and heated between 900 and 1000 °C for 15 days, then slowly cooled to room temperature.
Gray thin platelet-like crystals with rough surface of M1+xS2 (M = Ge/Ti) were obtained with typical lengths between 3 and 7 mm and thickness ranging between 0.02 and 0.07 mm. In addition, some blue crystals of TiO2 were also obtained in some preparations.
2.2 Description of the single-crystal structure
Four different polytypes were identified in the single crystals of MxTiS2 (M = Ge/Ti): 1T, (4H)2, 12R, and their corresponding a√3 × a√3 superstructure.
The most frequent obtained polytypes are 1T and 12R, and it seems that a mixture of the starting materials with a ratio of 0.5:1 promotes the synthesis of polytypes with superstructures as (4H)2 and 12R-a√3 × a√3. The single crystals of TiO2 were identified as rutile (tetragonal; a = b = 4.5932(7) Å, c = 2.9656(6) Å; space group P42/mnm). This is probably caused by both prolonged exposure to air during grinding materials and the affinity of Ti to react with the silica tube at high temperature [32,33].
2.3 X-ray diffraction
Single-crystal data were recorded using a SMART-APEX CCD X-ray diffractometer (Bruker AXS) with graphite-monochromated Mo Kα radiation.
The reflection intensities were integrated with the SAINT [34]. An empirical absorption correction was applied [35]. Primary structure solution was given by superflip [36], and the structure refinement was performed by Jana 2006 [37].
In the final cycles of refinement, all the atoms in the different structures were refined anisotropically, and the refined site occupancy factors (SOF), which did not deviate significantly (about 2%), were reset to full or nonoccupancy.
Details concerning the structure refinement and final results are presented in Table 1, and atomic coordinates, anisotropic displacement parameters (ADPs), and selected bond distances are listed in Tables S1, S2, and S3 of the supporting information.
Selected single-crystal data and structure refinement parameters for the 1T-MS2, 12R-M1.111S2, 12R-super M1.206S1.91, (4H)2-M1.244S1.945 (M = Ge/Ti) polytypes.
| M1+xS2 polytype | 1T-M1S2 | 12R-M1.111S2 | 12R-superM1.206S1.91 | (4H)2-M1.244S1.945 |
| Molar mass (g mol−1) | 112.4 | 119.4 | 121.6 | 122.9 |
| Crystal size (mm3) | 0.22 × 0.12 × 0.02 | 0.41 × 0.35 × 0.02 | 0.16 × 0.11 × 0.10 | 0.25 × 0.16 × 0.07 |
| Space group | Cc | |||
| Z | 1 | 6 | 18 | 24 |
| Unit cell dimensions (Å) | a = 3.4014(6) | a = 3.4383(13) | a = 5.9424(5) | a = 5.97(3) |
| c = 5.687(10) | c = 34.590(13) | c = 34.276(3) | b = 10.339(5) | |
| c = 23.0249(10) | ||||
| β= 94.980(9) | ||||
| Volume (Å3) | 56.981(17) | 356.2(2) | 1048.20(15) | 1415 (6) |
| Calculated density (g cm−3) | 3.2737 | 3.339 | 3.467 | 3.4603 |
| Absorption coefficient (mm−1) | 5.277 | 6.054 | 6.627 | 6.055 |
| Angular range T (°) | 6.93–27.26 | 3.51–28.63 | 1.19–40.28 | 1.78–28.67 |
| Index ranges | −4 < h < 3/−4 < k < 3 | −3 < h < 4/−4 < k < 4 | −8 < h < 10/−8 < k < 6 | −7 < h < 5/−13 < k < 13 |
| −7 < l < 7 | −45 < l < 35 | −61 < l <62 | −30 < l <30 | |
| Rint | 0.0353 | 0.0675 | 0.0432 | 0.0337 |
| Total recorded reflections | 381 | 1036 | 39,861 | 6280 |
| Independent reflections | 66 (Rint = 0.0353) | 150 (Rint = 0.0675) | 2467 (Rint = 0.0432) | 2647 (Rint = 0.0432) |
| Reflections with I > 3σ(I) | 66 | 146 | 1800 | 1188 |
| Tmin/Tmax | 0.707/0.902 | 0.4624/0.7833 | 0.2769/0.5148 | 0.3877/0.6547 |
| Data | 10 | 19 | 77 | 204 |
| Goodness-of-fit on F2 | 1.98 | 1.93 | 2.86 | 1.15 |
| (R/Rw)obs (%) | 0.0248/0.0290 | 0.0232/0.0271 | 0.1322/0.0923 | 0.0519/0.1027 |
| (R/Rw)all (%) | 0.0248/0.0290 | 0.0234/0.0271 | 0.1681/0.1042 | 0.1347/0.1174 |
| Δρmax, Δρmin (e−/Å3) | 0.51, −0.74 | 0.35, −0.67 | 5.03, −3.04 | 0.72, −0.61 |
Supplementary crystallographic data have been deposited via the joint CCDC/FIZ Karlsruhe deposition service. CSD-deposition number 1904551–1904554. These data can be obtained free of charge from FIZ Karlsruhe via www.ccdc.cam.ac.uk/structures.
2.4 Transmission electron microscopy
TEM studies were performed using a JEOL JEM 2100 HT microscope equipped with an INCA microanalysis suite. High-resolution transmission electron microscopy (HRTEM) and high angle annular dark field-scanning transmission electron microscopy (HAADF-STEM) images were obtained using a JEOL JEM 3000F microscope fitted with an INCA microanalysis suite. The corresponding single crystals used for XRD data were crushed and ultrasonically dispersed in n-butanol, a few drops of the suspension were deposited on a copper grid covered with a holey carbon film as support of the crystallites.
3 Results and discussion
3.1 1T-M1S2 (M = Ge/Ti) crystal structure
The 1T-Ti1+xS2 is the most stable TiS2 polymorph, which exhibits possible applications in thermoelectric devices. The compound is related to the CdI2 structure type, and consists of edge-sharing TiS6 octahedrons in a triangular geometry forming S–Ti–S layers and linked to each other by strong covalent interaction within the layers, whereas the layers are linked by weak van der Waals forces. In most cases the self (auto)-intercalation of Ti occurs and the TiS2 crystals are nonstoichiometric as a consequence of sulfur volatilization [38,39].
The excess of titanium atoms are located into the van der Waals gap giving the stacking sequence …aBαCaB (B and C refer to the sulfur layers; a to the completely filled titanium layers; and α to the partially filled titanium layers) (Fig. 1). This nonstoichiometry can affect significantly the thermoelectric properties of the doped/intercalated Ti1+xS2 materials (see Ref. [40] and references therein).
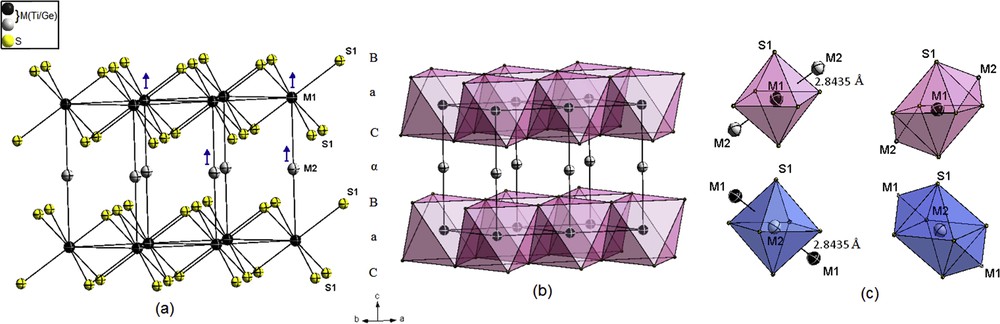
Crystal structure of 1T-MS2 (M = Ge/Ti). (a) Trigonal prismatic packing of sulfur layers. (b) Clinographic view of the edge-sharing MS6 octahedra. (c) Distorted bicapped octahedral coordination around metal atoms, showing the short M–M distance. Color key: Metal atoms (M) in the fully and partially filled layers are drawn as black and gray, respectively, including 95% probability displacement ellipsoids. The blue arrows indicate the dominant thermal vibration direction of M atoms (ADPs). The polyhedrons around metal atoms in the fully and partially filled layers are drawn in pink and blue, respectively.
The structure of 1T-M∼1S2 was refined on the basis of 1T-TiS2 as host structure. During the refinement, difference Fourier synthesis indicated a maximum peak at the 1b (0 0 ½) position, which was attributed to the excess of titanium (Ti2) with a refined site occupancy about 0.017(2) leading to a decrease in the residual electronic density.
During the refinement, the mixed occupation of Ti and Ge atoms was checked and it seems almost to occur in the Ti1 position 1a, with a refined site occupation factor of M (Ge/Ti) = 0.015(6)/0.968(6), that is, with a total occupation of 98.3% and 1.7% vacancy. Ti1 and Ge1 atoms probably occupied the crystallographic positions 1a in a random fashion. M1–S and M2–S distances (2.4239(5) and 2.4250(5) Å) are close, as observed in other X-ray single-crystal structure determinations [28,41–43].
A characteristic feature of this 1T structure is the short M1–M2 distance 2.8435(10) Å comparable to the close-contact distance in Ti metal 2.896 Å, this indicates strong metal–metal bonding.
The M atoms are surrounded by 6S + 2M in distorted bicapped octahedrons (CN = 8) linked via one vertex along the c direction (Fig. 1c).
The ionic radius of Ge atoms in an octahedral coordination 0.53 Å is smaller than that of Ti atoms 0.604 Å [44], as the Ge atoms replace Ti atoms to form the covalent bond, we expect a shrink in the lattice parameters and in the trigonal distortion compared with the host structure. Similar observations were reported in some doped MxTi1−xS2 [M = Co, Cd, Ni with x = 0.02–0.15, < 0.025, 0.06, respectively) ([29,30,45] and references therein).
For all atoms, the amplitude of ADPs U33 in the interlayer is larger than the amplitude in-plane U11, indicating weak bonding along the c axis (Fig. 1a). The refinement reveals a strong correlation between the occupation factor of M2 site and its thermal parameters (Uij). Thus, it is difficult to refine these two parameters simultaneously; the two Ti atomic positions were then restricted to have the same Uij.
The final refinement converged to reliability factor Robs = 2.48% and Rwobs = 2.90%, with the remaining electron densities (Δρmax, Δρmin) about 0.51 e/Å−3 and −0.74/Å−3.
The composition obtained with the structure refinement is almost stoichiometric 1T-Ge0.015Ti0.985□0.017S2, that is, M∼1□0.017S2 (□ denotes the vacancies in the M = Ge/Ti positions).
3.2 12R-M1.111S2 (M = Ge/Ti) crystal structure
The 12R polytype has been previously studied by different groups [11,12,19,46–48]. Its structure was determined by XRD [49,50] before the discovery of polytypism in the Ti–S system.
The structure is based on a close packing of sulfur layers with a stacking sequence …BαCbAγ BcAγBaCβAbCβAcBαCa… (A, B, and C refer to the sulfur layers; a, b, and c to the completely filled titanium layers; and α, β, and γ to the partially filled titanium layers). The structure can be described by layers of the type prism–prism–octahedron–octahedron [SM6] (Fig. 2).
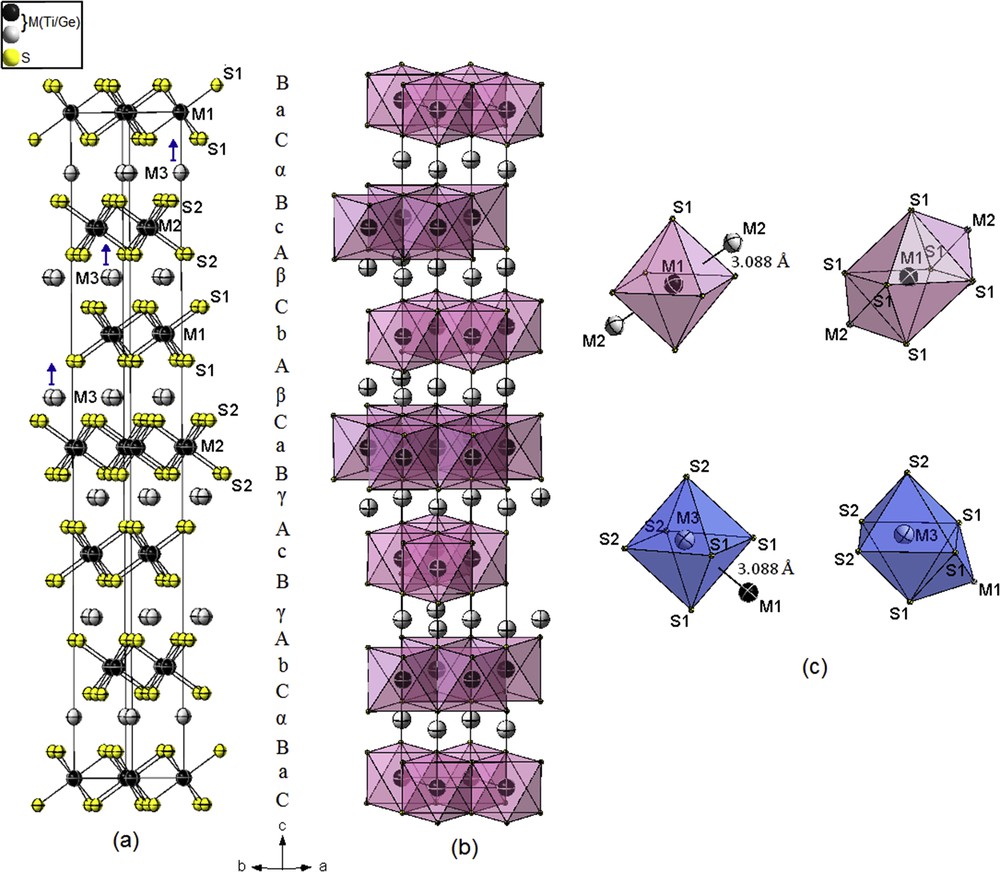
Crystal structure of 12R-M1.111S2 (M = Ge/Ti). (a) Prism–prism–octahedron–octahedron packing of sulfur layers. (b) Clinographic view of the edge-sharing MS6 octahedrons. (c) Distorted bicapped and monocapped octahedral coordination around metal atoms showing the short M–M distances. The color key is same as given in Fig. 1.
If we focus on the coordination of the sulfur atoms, there are two types of titanium polyhedrons surrounding an atom of sulfur: trigonal prism or slightly deformed octahedron, different successions of layers of these two types of polyhedrons correspond to the diverse polytypes observed. In the structure 2H, only the first type is present, within 4H both types alternate along the c direction. Every atom of titanium is practically located at the center of an octahedron of atoms of sulfur.
Unlike to the 1T-doped polytype, the refinement indicates that the mixed occupation of M = Ge/Ti atoms seems to occur in all positions with different occupancy, especially in the partial occupied position, where the occupation factor of Ge ranged between 3.5% and 5.7%. The distribution of Ge atoms observed over the fully occupied and partially filled atom layers is 54.76% and 45.23%, respectively.
The octahedral holes between adjacent prism–prism and adjacent octahedron–octahedron sulfur layers are not fully occupied by M atoms (the position 3b is refined with 4.8% of vacancy), with six equivalent distances: M6–S = 2.4596(3) and 2.4614(3) Å.
The octahedral holes between adjacent prism–octahedron layers are partially occupied by M3 (position 6c). In this case, the refined site occupancy factor is (Ge/Ti) = 0.038/0.109 in a random fashion, with three short M3–S and three long distances 2.3486(16) and 2.5722(19) Å, respectively. The M3S6 octahedrons are slightly more distorted (S–M3–S = 83.88(8)−90.785(11)°) compared with the MS6 octahedrons (S–M–S = 88.604(11–)–91.395(11)°).
In comparison to the results obtained by Tronc et al. [50], all the atoms are refined anisotropically and there is a slight expansion in the distances and in the c parameter. This expansion is probably caused by the intercalation of Ge atoms, as it was observed in some doped (MxTi1−x)1+yS2 [M = Mn (up to 1), Ni (up to 0.06), and Cu (up to 0.6)] ([51] and references therein; [52,53]).
The range in the M–S bond distances is because of the corrugation of the M layers as a consequence of M–M pair interactions. In fact, the short M–M distance is about 3.088(3) Å and deviate from the ideal distance 2.896 Å (in Ti metal) as observed in the 4H-Ti1.225S2 polytype [54]. This fairly short distance larger by only 0.288 Å than the sum of the atomic radii [55] is still strong enough for M–M bonding interactions.
The M atoms are arranged in six-, seven-, and eight-vertex polyhedrons (CN = 6, 7, and 8). The coordination polyhedrons of the M1 atoms with two additional M3 are distorted bicapped octahedrons, whereas the coordination M3 atoms with one additional M1 neighbor are in slightly distorted monocapped octahedrons; theses polyhedrons are linked via common faces with the distorted octahedrons of M2 along the c direction (Fig. 2c). Higher coordination of titanium atoms was also observed in some titanium-rich sulfur Ti8S3 and Ti2S [56,57].
The amplitude ADPs U33 (interlayer) is larger than the amplitude in-plane U11 for most atoms except the fully occupied M positions (M1 and M2), in which the thermal motions are nearly isotropic (Fig. 1c). On the other hand, there is no correlation between the occupation factor of M3 site and its ADPs; these two parameters are then simultaneously refined.
The final refinement converged to reliability factor Robs = 2.32% and Rwobs = 2.71%, with the remaining electron densities (Δρmax, Δρmin) about (0.35 e/Å−3 and −0.67/Å−3).
The composition obtained with the structure refinement is 12R-Ge0.084Ti1.027□0.074S2, that is, M1.111□0.074S2, close to that observed by Tronc et al. [50] 12R-Ti1.17S2.
3.3 M1.206S1.91-12R-a√3 × a√3 × c superstructure (M = Ge/Ti)
The a0√3 ×a0√3 superstructures have been observed by different groups [22,23,58–60]. They are associated with diverse stacking sequences of the defective layers leading to different 3D superstructures. All these superstructures arise from ordering of Ti vacancies in the partially occupied Ti layers, being the metal vacancies confined to every second metal layer.
Each polytype has a tendency to generate the corresponding superstructure [60]. The new 2D superstructure a0√3 × a0√3 of 12R-M1.1□0.074S2 polytype was found in our attempt to dope/intercalate germanium into TiS2 layers. Several single crystals have been tested and the same parameters, a = b = a0√3 = 5.94 Å and c = c0 = 34.27 Å, were obtained (a0 and c0 are the parameters of the reference 12R-type structure).
The superstructure is based on a close packing of sulfur of the type prism–prism–octahedron–octahedron [SM6].
A highly disordered structural model was refined in the space group (subgroup of the 12R polytype: ) on the basis of the 12R polytype, with 10Ti and 8S independent atom sites, obeying to the same stacking sequence aBαCbAγBcAγBaCβAbCβAcBαC (A, B, and C refer to the sulfur layers; a, b, and c to the completely filled titanium layers; and α, β, and γ to the partly filled titanium layers) (Fig. 3).
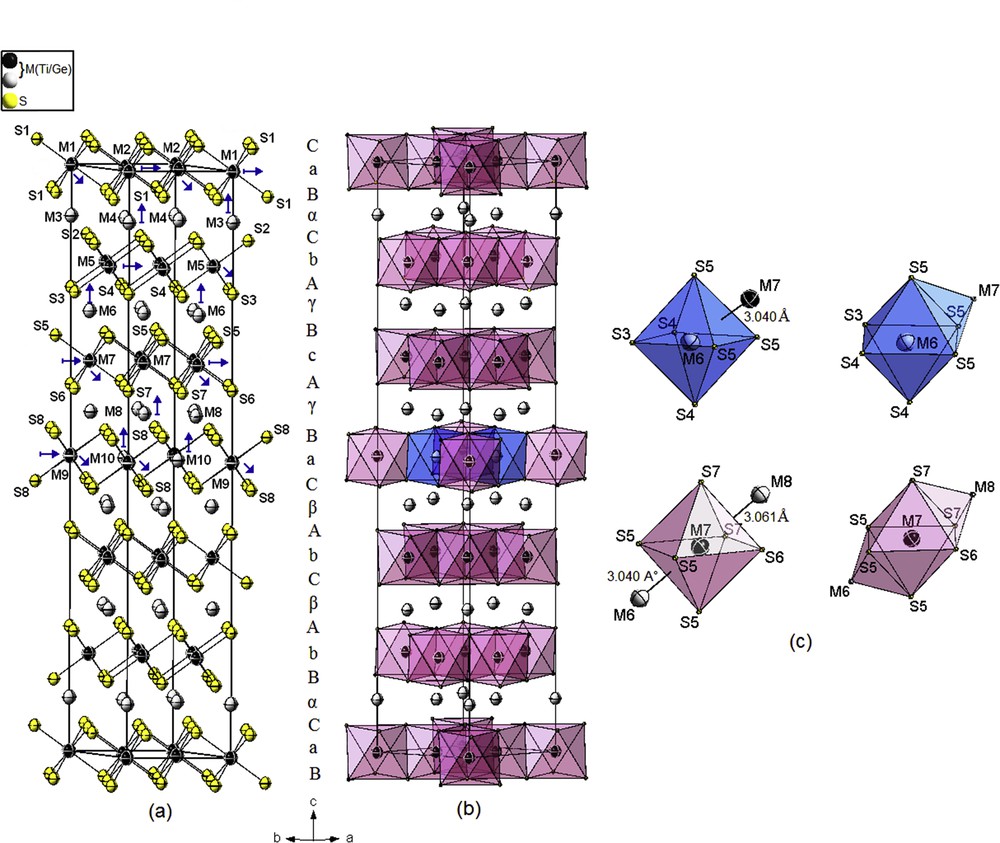
Crystal structure of 12R-super M1.206S1.91 (M = Ge/Ti). (a) Prism–prism–octahedron–octahedron packing of sulfur layers. (b) Clinographic view of the edge-sharing MS6 octahedrons. (c) Distorted bicapped and monocapped octahedral coordination around metal atoms showing the short M–M distances. The color key is same as given in Fig. 1.
As observed in the 12R substructure, the mixed occupation of Ge/Ti atoms seems to occur in all positions with different occupancy, in addition to a small number of vacancies in both fully occupied Ti and S layers, probably due to the presence of structural defects. An equal proportion distribution of Ge occupied observed over the fully (54.03%) and partially filled atom layers (45.96%) is also observed.
The structure refinement, with statistical replacements of Ti sites by some Ge atoms, exhibits a strong correlation between site occupancies and parameters of thermal motion of such atoms.
The ADPs in the (ab) plane U11 = U22 are larger than U33 for most atoms, except for partly M positions because of the weaker bonding along the c axis (Fig. 3a).
The refinement was unstable and results in a large parameter U33 for M10 position (2/3 1/3 1/2) and significantly the ADPs for M9 position (0 0 1/2), with unrealistic U33 value. A stable refinement was obtained by adopting additional disorder in this fully occupied M layer in the form of shifting the 1b M9 atom position to the 2c Wyckoff position (0 0 0.502(3)) and refining the occupancy of the M10 position.
The displacement of M9 atom can be explained by the presence of vacancies at the S2 atom site 6c about 15.6%, which lead to a shift in this atom toward the ideal position.
The refinement converged to rather higher reliability factor Robs = 13.22% with higher electron densities Δρmax about 5.02 e/Å−3 around M10 atom.
A refinement by considering a split-atom model for M9 into two subsites with partial occupancy factors failed because of the closeness of the positions and the high correlation generated between all structural parameters of the Ti9/Ge9 atoms especially in the case of position splitting.
The M–S distances range from 2.441(3) to 2.473(3) Å for full occupation atom positions, and from 2.291(5) to 2.610(5) Å for the distorted M = Ge/Ti atoms in the partial occupation positions.
The M–S distances show more range than those observed in the substructure 12R (2.4596(3)–2.4614(3) and 2.3483(16)–2.5722(19) Å), this range can be explained by the displacement of deficient metallic atomic layers from their ideal positions. These displacements are caused by M = Ge/Ti sublattice distortions and revealed by structural refinement of some polytype [17,50].
The four short M–M distances, which range from 3.040(4) to 3.068(8) Å, are larger by 0.241–0.26 Å, respectively, than the sum of the atomic radii (0.241–0.26 Å) [55], and still correspond to strong enough bonding interactions.
As observed in the substructure 12R, the M atoms are then arranged in six-, seven-, and eight-vertex polyhedrons (CN = 6, 7, and 8). The coordination of the M atoms within the partly filled layers are slightly distorted monocapped octahedrons, whereas the coordination polyhedrons of the M atoms within the fully occupied layers alternate between distorted bicapped octahedrons and distorted octahedrons along the c axis (Fig. 3c).
The composition obtained with the structure refinement is (Ge0.11Ti1.096)□0.115S1.91Δ0.09, that is, M1.206□0.115S1.91Δ0.09 (□ and Δ denote the vacancies in the Ti and S positions, respectively), taking account of the vacancies the composition is M1.321S2, which is close to the ideal one with x = 0.33 for extra atoms.
However, there are very few polytypic crystals of satisfactory quality; the coexistence of several polytypes together with stacking disorder regions is the most frequent situation.
The XRD pattern shows reflections that exhibited a rod-shaped streaking along the c* axis (Supporting information, Fig. 1S). These kinds of diffuse streaks, which have been observed frequently in Ti1+xS2, correspond to a disordered stacking of hexagonal layers and, they hinder conventional structure refinement from XRD data.
Diffuse scattering because of the stacking disorder also contributes to the total diffracted intensity. This could explain the rather higher R factor values (13.22%) obtained.
Nevertheless, the results seem to be very reliable in comparison to what has been found for the parent structures in powder diffraction, if we consider the highly disorder, vacancy, and some defects that characterize this kind of polytypes.
3.4 (4H)2-M1.244S1.945 superstructure (M = Ge/Ti)
The 3D-superstructure of 4H-Ti1.33S2 was first found by Bartram [19]. Two predominant (4H)-based superlattices noted (4H)2-TiS1.46 and (4H)3-TiS1.51 have been observed and analyzed by means of X-ray diffractometry and high-resolution electron microscopy [20–23,58,59].
The 3D-superstructures (4H)2 and (4H)3 are considered to arise from the same type of ordering Ti atoms and vacancies in the partially filled layers, but with different stacking sequences. The stacking sequence lowers the symmetry from P63mc in 4H to Cc (subgroup of the 4H polytype, P63mc) in both (4H)2 and (4H)3.
In comparison to the earlier study by Onoda et al. [20] in powder diffraction, the superstructure of the current determination was described in the same space group Cc with a measured β angle about 95° instead 90°, and using only 9M and 12S independent atoms obeying in the (ac) plane to the stacking sequence …AcDγBdCβAcDγBdCβA… (A, B, and C refer to the sulfur layers; a, b, and c to the completely filled titanium layers; and α, β, and γ to the partly filled titanium layers) (Fig. 4a); there are 3M independent atoms less in the partially filled layers than the model proposed by Onoda et al. [20].
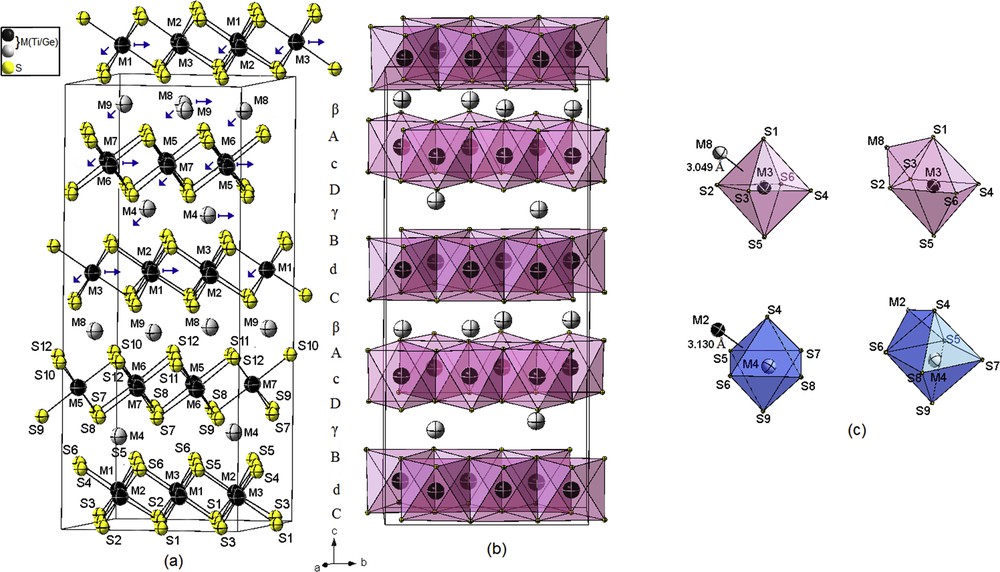
Crystal structure of (4H)2-M1.244S1.945 (M = Ge/Ti) superstructure. (a) Prism–octahedron–prism–octahedron packing of sulfur layers. (b) Clinographic view of the edge-sharing MS6 octahedrons. (c) Distorted monocapped octahedral coordination around metal atoms showing the short M–M distances. The color key is same as given in Fig. 1.
As observed in the 12R polytype and its superstructure, the mixed occupation of Ge/Ti atoms seems to occur in all positions with different occupancy, in addition to some vacancies in the fully occupied M and S layers.
The refinement indicates a mixed occupation of M = Ge/Ti atoms at all positions with different occupancy, especially in the partially occupied position, the occupation factor of Ge ranging between 3.5% and 5.7%. On the other hand, there is no correlation between site occupancies and parameters of thermal motion of such atoms, these two parameters are refined simultaneously.
The proportion of the distribution of Ge atoms over the fully (52.50%) and partially occupied atom layers (47.50%) is comparable to the proportion observed in the two 12R polytypes.
In comparison, with other polytypes, all the M atoms are surrounded by six different sulfur atoms. The M–S distances range from 2.365(16) to 2.540(7) Å for full occupation positions (correspond to M6) and from 2.293(8) to 2.587(18) Å for partial occupation positions (correspond to M8).
The range observed in M–S distances is more significant than observed in other polytypes, and we can expect more distortions of metallic atomic layers from their ideal positions. The three short M–M distances range from 3.034(7) to 3.144(5) Å, are larger by 0.234–0.344 Å, respectively, than the sum of the atomic radii, and still correspond to strong enough M–M bonding interactions.
As observed in the substructure 4H-Ti1.225S2 [53], the M atoms are arranged in six- and seven-vertex polyhedron (CN = 6 and 7). The coordination M atoms within the partly filled layers are slightly distorted monocapped octahedrons, whereas the coordination polyhedrons of the M atoms within the fully filled layers are distorted monocapped octahedrons or distorted octahedrons along the c axis (Fig. 4c).
The ADPs in the (ab) plane U11 and U22 are larger than U33 for most atoms include the partly M positions. This suggests that these atoms are shifted toward their positions, and the M polyhedrons are likely to tilt each other within the (ab) plane. Such ADPs for the M atoms in the partially occupied position are common for some intercalate compounds in TiS2 [28,61], the less amplitude of U33 can be explained by the large SOFs between 0.478 and 0.728, the M atoms are then less disordered compared with the 12R superstructure or other polytypes.
The final refinement converged to reliability factor Robs = 5.20% and Rwobs = 10.29%, with the remaining electron densities (Δρmax, Δρmin) about 0.75 e/Å−3 and −0.60/Å−3.
The composition obtained with the structure refinement is (Ge0.04Ti1.204)□0.044S1.945Δ0.55, that is, M1.244□0.044S1.945Δ0.55 is less by 6.57% of M atoms than the composition obtained by Onoda et al. [20] with M1.37S2.. Taking account of vacancy the composition obtained is about M1.288S2, which is almost close the ideal one with x = 0.33 for extra atoms.
3.5 Metal–metal interactions (M= Ge/Ti)
In the TiS2 system, linkage of octahedra by face sharing gives short metal–metal distance. This M–M pair interaction indicates strong metal–metal bonding, but can also be analyzed in terms of electrostatic repulsion. The current crystal structure refinement of the different polytypes supports the conclusions reported in Refs. [59,62].
The results show that the atoms are shifted away from the center of the octahedron, as a consequence of metal–metal M–M corrugated layers across the sulfur layers (Supporting information, Fig. 2S).
The M–S distances are then altered with short and long distances, especially in the metal partially occupied layers.
The distortion δ (Å) observed in the M–S distances, which expressed the difference between the longest and the shortest distances, is more significant in the superstructures compared with the correspondent basic structure (Fig. 5a). Within the same superstructure polytype, this distortion seems altered or decreases with M–M distances but in a nonlinear way. The larger value of distortion is observed in the 12R superstructure at the M8 atom, and it can be explained by the presence of vacancies at the S atoms (ranging from 8.1% to 15.6%), which lead to a shift in the M atom toward the ideal position (Supporting information, Fig. 3Sa).
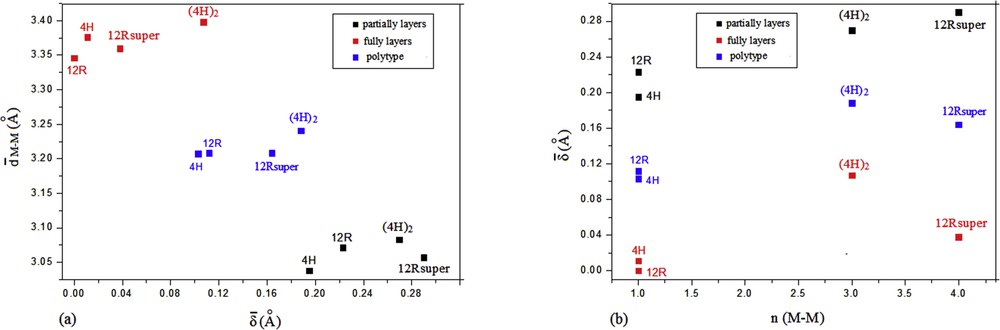
(a) Variation in the mean distortions (Å) with the mean of the short distances (M–M) (Å) in the 4H-M1.225S2 [54], 12R-M1.111S2, 12R-super M1.206S1.91, and the (4H)2-M1.244S1.945 (M = Ge/Ti) polytypes. (b) Variation in the mean distortions (Å) with frequency observation of short distances n (M–M) in the 4H-M1.225S2 [54], 12R-M1.111S2, 12R-super M1.206S1.91, and the (4H)2-M1.244S1.945 (M = Ge/Ti) polytypes.
The fact that the M–M distances deviate from the ideal values is a very common feature of TiS2 polytypes, but the frequency of occurrence of short M–M distances and their deviations from the ideal value are more significantly within long-range ordering of M atoms in 2D (12R) or in 3D (4H)2 superstructures (Fig. 5b).
An increase in M–M distances within the same superstructure polytypes is observed along with the varying increase in the SOF of M atoms in the partially filled layers, probably to minimize the M–M electrostatic repulsions, but this tendency do not exhibit a linear behavior (Supporting information, Fig. 3Sb).
A mixed occupation of Ge/Ti atoms with different occupancy distributed over most of the M sites is obtained during the current refinements. Except in the 1T polytype, an almost equal proportion of the distribution of Ge atoms is observed over the fully and partially occupied layers, with the increase in concentration of the Ge atoms in the polytype. Indeed, a strong replacement of Ti atoms in the partially filled layers by Ge atoms would destabilize the structure by breaking the Ti–Ti interactions across the face-sharing octahedral, the Ge atoms have to occupy some sites in the fully filled layers. A similar phenomenon was observed in some nonstoichiometric chromium titanium selenides [63].
Except the 1T polytype, both the short (s) and the long (l) M–M distances alternate on parallel zigzag chains along the c direction in the sequence s–l–s–l for 4H and s–s–l–l–s–s for 12R, 12R -superstructure and (4H)2 polytypes (Supporting information, Fig. 4S). The shortest M–M distance 2.8435(10) Å is observed in the most stable polytype 1T-M∼1□0.017S2, with a low SOF of M atoms in the partially filled layer; shorter M–M distances should correspond to decreased repulsions and longer distances to increased repulsion. The relaxation probably occurs following a defect model by introducing vacancy in the adjacent M filled layer, the atoms are then displaced toward the created vacancy to minimize the formation of M–M pair interaction [59,64]; this can explain the observation of some vacancy in the filled M layers during the different structures' refinement by XRD.
These 2D and 3D ordering superstructures seem to also affect the ADPs in the (ab) plane, U11 and U22 become larger than U33 for most atoms including the partially M positions as observed in the (4H)2 superstructure.
The bond-valence model was used to calculate the bond valence sum (BVS) of M atoms, using the M–S results obtained for the four polytypes [65] ranging from 3.275 to 3.887 v.u. (Supporting information, Table S4).
The higher BVS values are observed for M atoms in the partially filled layers and are almost close to their formal valence state +4, whereas the BVS for M atoms in the filled layers are lower. This trend can be explained by a valence compensated between the M atoms to keep the number of electrons transferred to the S atoms roughly constant.
In addition, a correlation exists between the calculated valence of M atoms and the M–M distances. M atoms, in which BVS decreases with increase in M–M distances, seem to occur in pairs between adjacent M layers.
This correlation can be correspondingly interpreted as a valence ordering of M atoms, caused by an adjustment of the M–M distances to minimize the electrostatic repulsion.
This kind of complex pattern with changes in M–M distances and valences was also observed in some Magnéli phases [66].
3.6 Electron microscopy
The analysis results by X-ray energy dispersive spectroscopy (XEDS) with the TEM, summarized in Table 2, are the average of three to five measurements on several different crystallites of each polytype sample, which yields to a composition M1+xS2 (M = Ge/Ti) in the range 1.02 < 1 + x < 1.40.
XEDS results obtained from different crystallites of each polytype M1+xS2 (M = Ge/Ti) sample.
| M1+xS2 polytype | Ge (at.%) | Ti (at.%) | S (at.%) | 1 + x = M/S |
| 1T | 0.41–1.79 | 33.92–34.46 | 63.82–65.45 | 1.05–1.10 |
| 12R | 0.14–0.54 | 37.22–40.90 | 58.78–62.39 | 1.21–1.40 |
| 12R-super | 0.9–3.7 | 38.86–37.87 | 62.10–61.09 | 1.22–1.27 |
| (4H)2 | 0.23–7.08 | 33.91–35.97 | 56.52–70.10 | 1.02–1.40 |
The XEDS spectrum in Fig. 6 shows the simultaneous presence of Ge, Ti, and S elements. The Ge energy peaks were clearly identified at 2.1 keV (Lβ1) and 9.8 keV (Kα), respectively. The highest Ge-doping level was observed in the monoclinic sample with 7.08% atomic ratio.
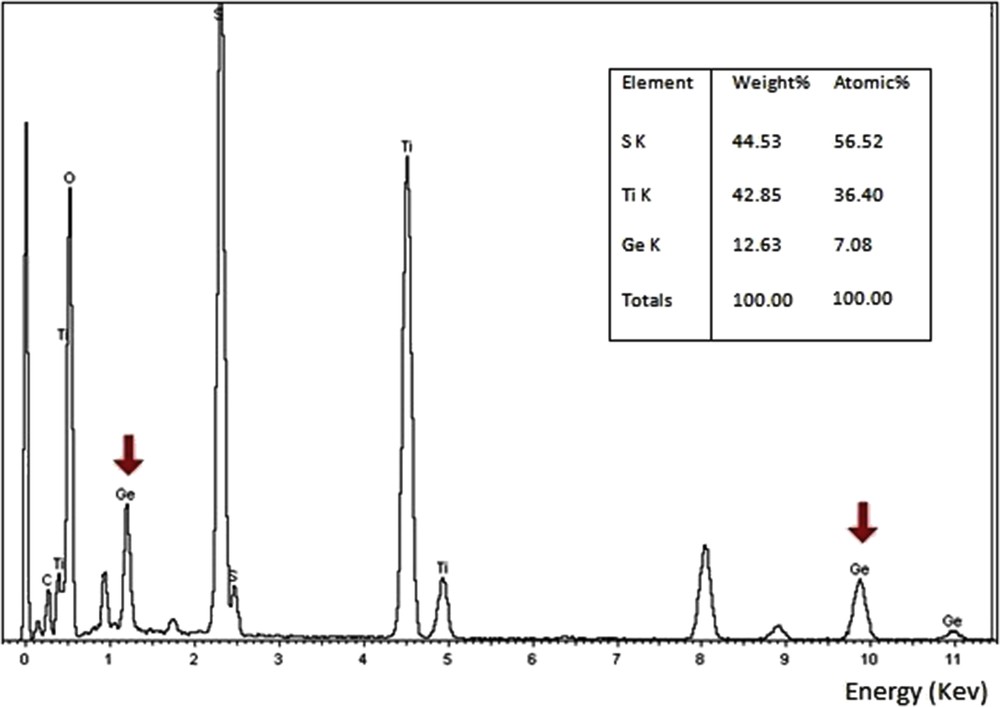
Typical TEM-EDS spectra obtained on single crystals of the monoclinic sample, showing the presence of Ge energy peaks at 2.1 keV (Lβ1) and 9.8 keV (Kα), respectively.
Fig. 7a shows a selected area electron diffraction (SAED) pattern of 1T-M1+xS2 (M = Ge/Ti, x ∼ 0.05) taken along [0001] zone axis, only the basic reflections of 1T-TiS2 are observed.

(a) [0001] Zone axis SAED pattern of 1T-M1+xS2 (M = Ge/Ti), for x ∼ 0.05, only the basic reflections are observed. (b, c) For x ∼ 0.23 and x ∼ 0.25 (M = Ge/Ti), the pattern consists of the basic reflections of 12R-M1+xS2 and a structured diffuse scattering distribution made up of curved segments arranged in triangles sharing vertices, sharp weak spots with periodicities a* × b* (a is the parameter of the basic unit cell) are also observed and marked with arrows. (d) For x ∼ 0.40, the SAED pattern shows an increase in the length and intensity of these diffuse segments.
The SAED patterns shown in Fig. 7b–d correspond to a 12R-TiS2 polytype structure. In addition to the strong basic reflections, a highly structured diffuse scattering surrounding the main spots is observed, which is similar to that observed in Ti1+xS2 [23,24,67,68] and in some of the intercalate compounds AxNbX2 (A = Ge, Fe and X = S, Se) [69,70]. It can be attributed to the short-range ordering of M = Ge/Ti atoms in the partially filled layers. These diffuse segments are arranged in triangles sharing vertices, and they correspond to 2a* × 2a* superstructure. Fig. 7d, with x ∼ 0.40, shows an increase in the length and the intensity of these diffuse segments accompanying the main reflections. In addition to the main reflections and structured diffuse scattering, sharp weak spots are also observed in the position of the forbidden 10-10 type reflections of Fig. 8b–d, they correspond to the intercepts of streaking running along c* (see Fig. 8b). Isolated stacking faults may account for the aforementioned streaking running among main reflections.
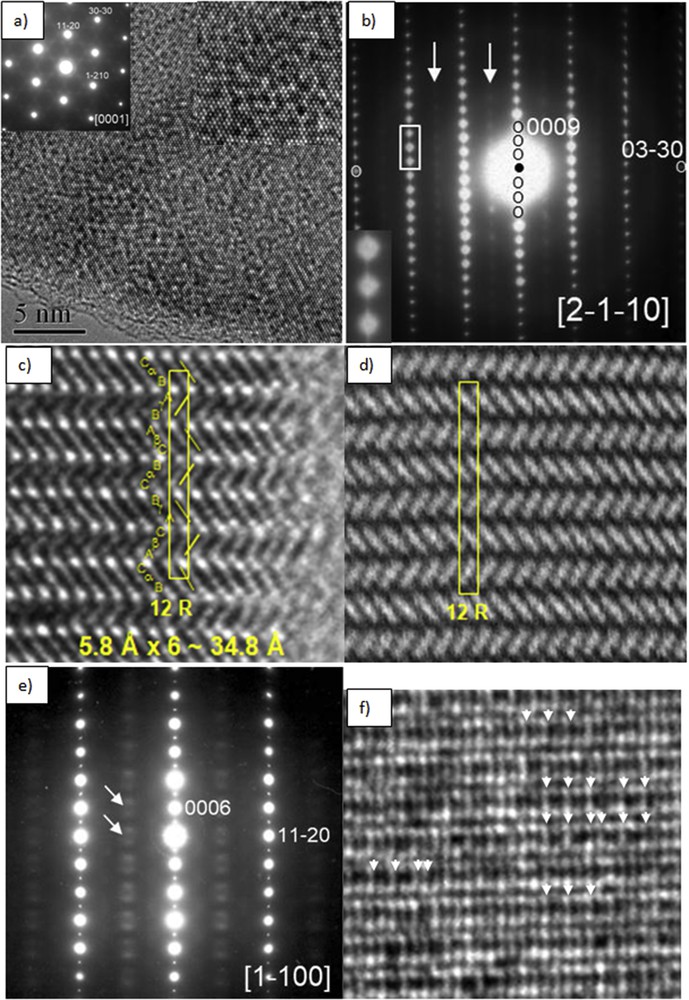
(a) HRTEM image of 12R-M1+xS2 (with x ∼ 0.21, M = Ge/Ti) taken along the [0001] zone axis; the insets show the corresponding SAED pattern and an enlargement of the micrograph. (b) [2-1-10] Zone axis SAED pattern, the inset shows streaking running along c* among the main reflections; the arrows point to diffuse extra reflection rows. (c, d) Corresponding HRTEM and HAADF-STEM images showing the 12R stacking sequence …aBαCbAγBc…. (e) [1–100] Zone axis SAED pattern showing diffuse intensity along c* marked by arrows and assigned to short-range ordering of extra atoms and vacancies. (f) Corresponding HRTEM image, the arrows highlight a few small domains with a double periodicity along [11–20]*.
Fig. 8a shows the HRTEM image with x ∼ 0.21 taken with the incident beam parallel to the stacking direction [0001], note the mottled contrast associated with the SRO.
The SAED patterns shown in Fig. 8b and e, with x ∼ 0.21, are characteristic of the 12R-M1+xS2 polytype; the lattice spacing measured along 00l reflections is 1.16 nm, which did not vary from one pattern to another and it corresponds to one-third of the c axis, as it was observed by Tilley [46] for the composition Ti1.25S2.
The lattice parameters measured in the SAED patterns (Fig. 8b) are a = 0.30 nm and c = 3.45 nm (1.15 × 3 nm), which are in good agreement with the lattice parameter of the host structure measured by XRD (a = 0.34 nm and c = 3.46 nm).
Fig. 8c and d shows the HRTEM and HAADF-STEM images taken along the [2-1-10] zone axis, with a 12R stacking sequence …AγBCαBCβA….
The fact that the 2a* × 2a* superstructure is revealed only by electron diffraction suggests the presence of microdomain with different ordering schemes of extra atoms M, too small to be observed by XRD (see Fig. 8f).
The 12R-a√3 × a√3 superstructure is revealed by both electron diffraction and XRD by the presence of satellite reflections. Fig. 9a is an SAED pattern of a 12R-M1+xS2 crystal flake taken along the [0001] zone axis, the pattern consists of the strong basic reflections of the rhombohedral polytype and additional weaker satellite reflections located at 1/3〈11–20〉*. Fig. 9b and c shows a [2-1-10] zone axis SAED pattern and the corresponding HRTEM image, where a 12R stacking sequence …AγBCαBCβA… is evidenced. Fig. 9d shows a [1–100] zone axis SAED pattern, in addition to the strong basic reflections, rows of diffuse intensity along c* are observed and marked by arrows, these rows intercept at 1/3 and 2/3 of [11–20]*, and they are assigned to the ordering of extra atoms and vacancies. In the corresponding HRTEM image (Fig. 9e) the arrows highlight this threefold order along [11–20]*, that is √3a; notice the disorder along the stacking direction c*, which gives rise to the diffuse intensity rows along c*.

(a) SAED pattern of 12R-M1+xS2 (with x ∼ 0.27, M = Ge/Ti) taken along the [0001] zone axis, notice the sharp satellite reflections running along 〈11–20〉*. (b) [2-1-10] Zone axis SAED pattern. (c) HRTEM image taken along [2-1-10] zone axis. (d) [1–100] Zone axis SAED pattern showing diffuse intensity along c* marked by arrows and assigned to short-range ordering of extra atoms and vacancies. (e) Corresponding HRTEM image, the arrows highlight a threefold order along [11–20]*, that is, √3a; notice the disorder along the stacking direction c*.


