1. Introduction
Carbon dioxide (CO2) is regarded as one of the main factors of the greenhouse gas effect and eventual global warming [1, 2]. Since CO2 production is difficult to be suppressed or diminished, reduction of CO2 emissions at the very emission source has become a major issue to be addressed. Gas capture methods using compounds like amines, whitewash or base-like adsorbents such as alkaline ash, activated carbons, porous silica, zeolites, ions exchange resins and mesoporous silicates, activated alumina, metal oxide and others showed promising prospects [3, 4].
However, such methods unavoidably produce wastes like carbamates and carbonates that need to be removed or regenerated. So-called Temperature Swing Adsorption (TSA) and Pressure Swing Adsorption (PSA) techniques for on-site regeneration via repetitive fluctuations of temperature and pressure without removing the adsorbents showed satisfactory performances in treating industrial flue emissions [5, 6, 7]. However, their energy consumption even partly compensated by the heat evacuated by the very flue emission, the use or organic compounds and production of undesirable by-products still remain major shortcomings.
The reversible capture of CO2 at ambient temperature from low concentrated gas emissions requires a new approach that targets gas retention in CO2-rich atmospheres with subsequent release at nearly ambient conditions in less concentrated media. This concept involves respiratory systems for concentrating CO2 onto a solid surface that can be regenerated by a mere equilibrium contact with CO2-free media or upon forced convection under strong carrier gas stream. This concept has barely been tackled so far. The targeted equilibrium shift that favors CO2 desorption requires not only specific adsorption sites capable of displaying weak and purely physical interactions with CO2 on the adsorbent surface but also optimization of many parameters that govern these interactions.
Successful attempts in this regard have demonstrated that CO2 can reversibly be retained through weak interaction with amphoteric to weakly basic surfaces. Indeed, CO2 was found to adsorb on a wide variety of clay-supported polyalcohols. The OH groups of the incorporated organic moieties were found to act as adsorption sites [8, 9, 10, 11]. The moisture content of such adsorbents showed a significant contribution to CO2 retention [9, 12]. One of these organoclay materials, namely montmorillonite intercalated with H30 Bolton dendrimer has particularly attracted attention. Due to its optimum surface properties, appreciable CO2 retention capacity (CRC) was induced by increased number of available OH groups without intermolecular dendrimer aggregation into dense hydrophobic clusters [11, 12, 13].
The adsorption–desorption cycle on OH-enriched montmorillonites appears to be strongly influenced by a series of parameters such as temperature, total pressure, CO2 partial pressure, contact time and carrier gas throughput [9, 12, 13]. The lack of data dealing with the effects and possible interactions occurring between these parameters has stimulated research in this direction. For this purpose, the reversible capture of CO2 was modeled and optimized using 33 factorial experiment designs. Preliminary experiments showed that, as expected, numerous factors can influence the adsorption desorption of CO2, but only some of them, namely the flow rate, contact time and impregnating CO2 quantity can be regarded as being key parameters that govern the processes efficiency. A judicious choice of the parameters range is an essential requirement for achieving high CRC values. The latter along with the water moisture were modeled as response-functions using Na+ exchanged montmorillonite containing 1 wt% of dendrimer H30 (NaMt-H30). The individual effects and interactions of these parameters were investigated in order to detect and assess a possible synergy on CO2 adsorption.
2. Materials and methods
2.1. Preparation of NaMt-H30 and characterization
Na+ exchanged montmorillonite (NaMt) containing 1 wt% of dendrimer H30 (NaMt-H30) has been prepared and characterized in previous works [9, 11, 12, 13]. As a reminder, NaMt originated from the purification of commercial crude bentonite supplied by Aldrich with a 1.58 silica/alumina weight ratio, as previously described. A bulky polyester-alcohol with the chemical formula 2,2-bis(methylol)propionic acid (bis-MPA) with an idealized structure illustrated in Scheme 1 was employed as organic moiety [14, 15]. This compound is commercially designated as dendrimer H30 (supplied by Boltorn Technology Co. Ltd.) and having an average 3607.6 g⋅mol−1 molecular weight.
Idealized configuration of Boltorn dendrimer H30.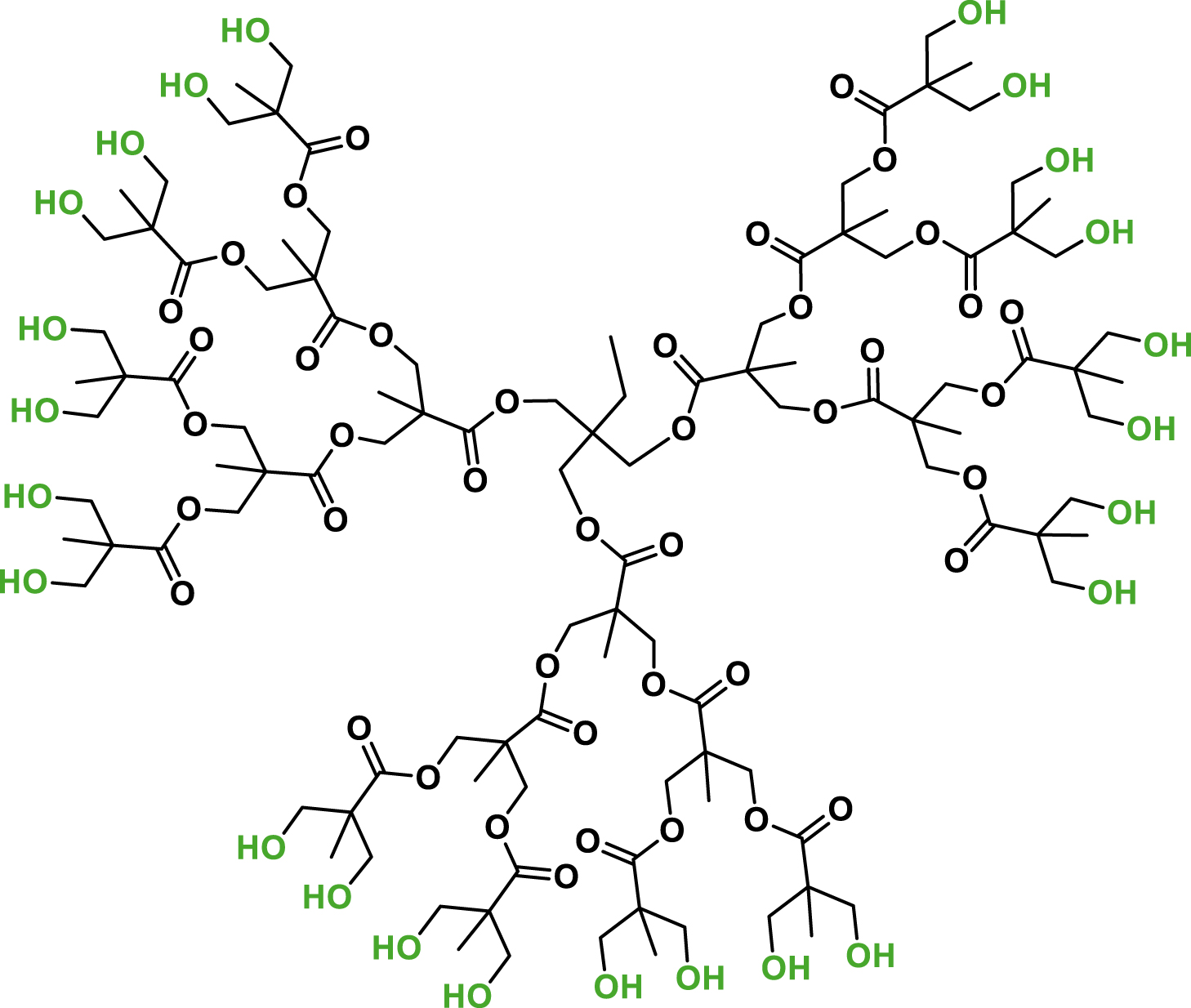
Clay intercalation with H30 was achieved by mere electrostatic self-assembly in aqueous media between a NaMt suspension and the organic polyol species. For this purpose, attempts were performed by impregnating NaMt samples in powder form (500 mg) with a diluted aqueous solution containing 1 wt% polyol H30 (5 mg). The resulting mixture was then stirred overnight at room temperature. The organoclay sample (organo-Mt) was dried overnight at room temperature until total evaporation of the solvent, and then at 120 °C for 6 h before being smoothly crushed for preventing structure alteration.
NaMt and NaMt-H30 were both characterized by X-rays diffraction (Siemens D5000 instrument, Co-Kα at 1.7890 Å), Fourier Transform infrared ATR-mode spectroscopy (using a KBr IR cell and a Model IR 550 Magna Nicolet instrument) and thermal gravimetric analyses (TG/TDA6200 Seiko Instrument Inc., under a 100 mL⋅min−1 nitrogen stream and a 5 °C⋅min−1 heating rate) [9, 11, 12, 13]. The specific surface area and pore size distribution were assessed by BET method calculations. For this purpose, measurements through N2 adsorption isotherms were achieved at 77 K by means of a Quantachrome Instruments equipped with an Autosorb automated gas sorption system control. For the sake of conciseness, the related spectra and diagrams are not shown in this work, but their results were only discussed herein in correlation with the adsorptive properties.
2.2. Thermal programmed desorption
The retention strength and CO2/water retention capacities (CRC and WRC, respectively) were assessed through thermal programmed desorption (TPD). The retention strength was regarded as being proportional to the desorption temperature (desorption peak), while the CRC was defined as the area described by the TPD pattern and expressed in terms of micromole CO2 desorbed per gram of dry clay material between 20 °C and 200 °C. This upper temperature limit was determined by TG-DTG measurements, which revealed a thermal stability threshold of up to 240 °C for NaMt-H30. Preliminary investigations showed that optimum amount (50 mg) and particle size (0.01–0.1 mm) of the adsorbent sample allowed preventing diffusion phenomenon during TPD runs under nitrogen stream not exceeding 15 mL⋅min−1. Prior to TPD measurements, each sample was dried in a 10 mm tubular glass reactor under a 15 mL⋅min−1 dry nitrogen stream at 160 °C for 1 h, and then cooled to 20 °C. At this temperature, CO2 was injected without nitrogen (static mode) for accurate CRC assessment. After saturation, the non-adsorbed CO2 excess was evacuated by the nitrogen stream at the throughput selected for TPD until no CO2 is detected by Li-840A CO2/H2O Gas Analyzer (Li-COR Bioscience Inc., USA) at the TPD device outlet after 40–60 min. TPD measurements were performed between 20 °C and 200 °C at a heating rate of 5 °C⋅min−1 under 1–5 mL⋅min−1 nitrogen stream. Here, care should be taken in CRC measurements, because higher nitrogen flow rates during saturation were found to remove the adsorbed CO2 by mere convection even without heating.
2.3. Adsorption capacity modeling
Thus, 27 CO2 adsorption attempts were made according to a 33 experiment factorial design, by varying the nitrogen flow rate from 1 to 15 °C⋅min−1 (X1), contact time from 1 to 12 hours (X2) and quantity of carbon dioxide from 1 to 6 mmol (X3) in suitable parameters ranges (Table 1).
Parameter levels and ranges for 33 factorial design at T = 25 °C
| Parameter level | Minimum | Medium | Maximum | |
|---|---|---|---|---|
| Coded value (non-dimensional) | Symbol | −1 | 0 | +1 |
| Nitrogen throughput (mL⋅min−1) | X1 | 1 | 8 | 15 |
| Contact time (h) | X2 | 1 | 6.5 | 12 |
| Injected CO2 (mmol⋅g−1) | X3 | 20 | 70 | 120 |
The model calculations were achieved using non-dimensional or reduced values of these parameters and each parameter was varied on three levels, i.e., (i) −1 for the minimum value, (ii) 0 for the medium value, and (iii) +1 for the maximum value of the respective parameter. The CRC and WRC were considered as optimality criteria for each of the 27 different attempts.
3. Results and discussion
3.1. Structure of NaMt-H30
The structure of NaMt-H30 had been richly investigated in our previous papers [9, 11, 12, 13, 16]. The powder XRD data indicated the transition from a random to a face-to-face parallel layout of the clay sheets and an optimum ratio of 1 wt% H30 for an enlargement of the interlayer spacing without altering the ordered layout of the clay lamellae. The influence of the OH groups from the clay on the incorporated dendrimer was also detailed in our previous work [10, 11, 12, 13, 16, 17, 18]. The uniform H30 spread in the clay surface produced only a slight improvement of the specific surface area from 45–50 m2⋅g−1 to 54 m2⋅g−1, presumably due to slight structure compaction induced by interactions between next-neighboring organoclay lamellae [11, 19].
3.2. Moisture contribution to CO2 capture
The surface basicity and hydrophilic character expressed in terms of CRC and WRC were the main features investigated herein. Given the higher thermal stability of unmodified NaMt up to 550 °C, repetitive CO2-TPD attempts (CO2-TPD1 to CO2-TPD3) without alternate rehydration after each TPD cycle were run between 20 °C and 450 °C. The results obtained revealed significant changes in the TPD profiles for both CO2 and water (Figure 1). The significant CRC decay observed between 220 °C and 450 °C accounts for an advanced removal of medium and strong basicities. Indeed, three successive thermal desorption-cooling-dry CO2 re-injection cycles induced a marked CRC decay for CO2-TPD2 after TPD1 even more pronounced for CO2-TPD3 after TPD2. Simultaneously, a marked depletion of the hydrophilic character for H2O-TPD2 even more accentuated for H2O-TPD3 took place, as reflected by visible CRC decreases in the WRC (Figure 1b).
Repetitive TPD patterns for CO2 (a) and water (b) under 15 mL⋅min−1 nitrogen stream. TPD1, TP2 and TPD3 were recorded after repetitive CO2-adsorption-thermodesorption cycles with rehydration. TPD1 and TPD1-R were recorded after repetitive CO2-adsorption-thermodesorption cycle with alternate rehydration by injecting moisture saturated CO2.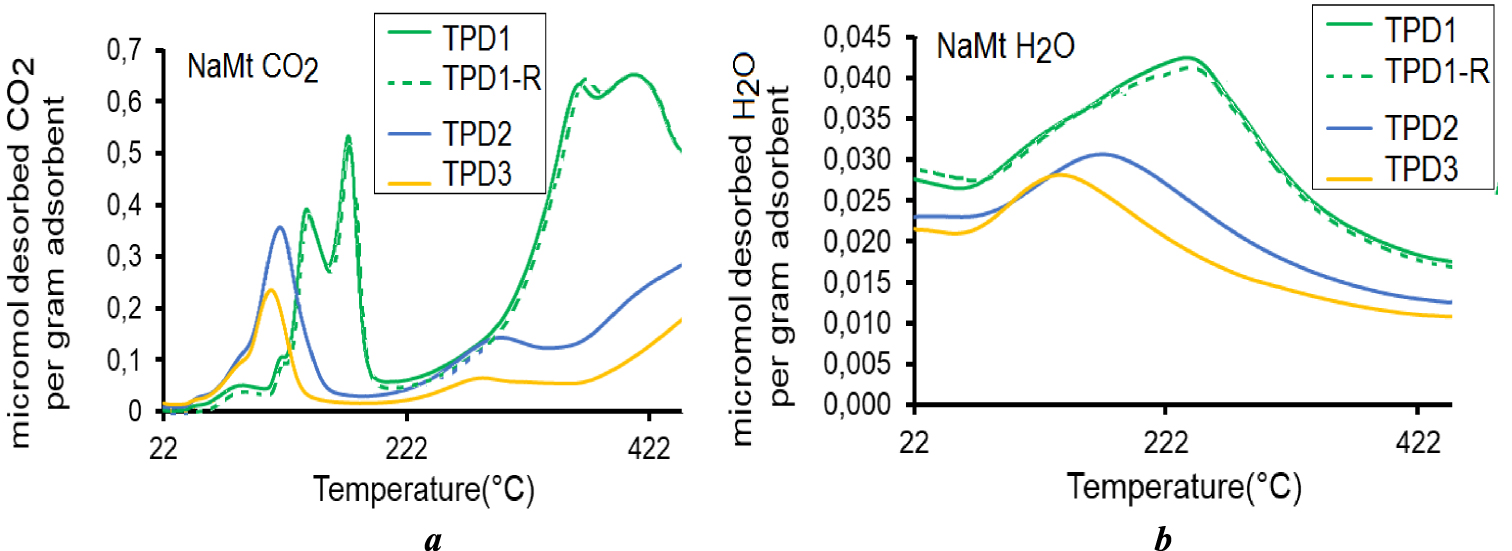
It is worth mentioning that repetitive TPD runs after alternate rehydration by injecting moisture saturated CO2 resulted in TPD patterns (TPD-R) perfectly similar to that of TPD1 for both CO2 and water. This result is of great importance, because it confirms the thermal stability of the starting clay mineral at least up to 450 °C. It is clear that below this thermal stability threshold, NaMt rehydration revives the CRC and that water also contributes to CO2 capture.
3.3. Adsorptive properties of NaMt-H30
NaMt-H30 exhibited appreciable thermal stability, barring dehydration between 80 °C and 140 °C, no degradation of the organic moiety was detected up to 240 °C. Such a thermal stability allowed establishing the temperature range for TPD measurements between 20 °C and 200 °C with high accuracy. TPD measurements were achieved for the 27 attempts involved in the factorial 33 experiment design, by varying three key parameters, namely the carrier gas flow-rate (X1), contact time (X2) and impregnating CO2 quantity (X3). The CRC, expressed in terms of desorbed CO2 amount in the investigated temperature range, showed values in the range 34.4–609.1 μmol⋅g−1 for nitrogen throughputs of 1–15 mL⋅min−1 (Table 2).
33 Parameter combinations and corresponding two response-functions as optimality criteria
| Key-parameters levels (Non-dimensional units) | Response function = Retention capacity (μmol⋅g−1) | |||
|---|---|---|---|---|
| Flow X1 | Contact timea X2 | CO2 amountb X3 | CRC | WRC |
| −1 | −1 | −1 | 386.6 | 1.06 |
| 0 | 385.4 | 1.06 | ||
| 1 | 254.6 | 0.44 | ||
| 0 | −1 | 350.3 | 3.81 | |
| 0 | 441.3 | 2.98 | ||
| 1 | 609.1 | 2.90 | ||
| 1 | −1 | 279.8 | 3.24 | |
| 0 | 304 | 3.18 | ||
| 1 | 366.6 | 4.18 | ||
| 0 | −1 | −1 | 65.7 | 0.64 |
| 0 | 81.7 | 0.24 | ||
| 1 | 73.4 | 0.29 | ||
| 0 | −1 | 39.3 | 0.61 | |
| 0 | 141.2c (143.0; 140.5; 140.0) | 1.38c (1.39; 1.35; 1.50) | ||
| 1 | 169.2 | 3.93 | ||
| 1 | −1 | 48.9 | 0.82 | |
| 0 | 153.5 | 1.59 | ||
| 1 | 185.8 | 1.82 | ||
| 1 | −1 | −1 | 53.1 | 0.24 |
| 0 | 51.2 | 0.18 | ||
| 1 | 49.4 | 0.27 | ||
| 0 | −1 | 49.3 | 1.03 | |
| 0 | 93.4 | 1.02 | ||
| 1 | 111.1 | 0.89 | ||
| 1 | −1 | 44.2 | 1.19 | |
| 0 | 35.3 | 2.10 | ||
| 1 | 34.4 | 1.24 | ||
a The contact time accounts for the saturation time imposed for the sample impregnation with a given CO2 amount.
b The CO2 amount is the injected quantity to be contacted with the dry powder sample for impregnation up to saturation prior to TPD run.
c The average CRC and WRC values for the (0, 0, 0 experiment were assessed by calculation the mean of the three measurements registered at this experimental point and are given herein between brackets. All CRC and WRC values were calculated on the basis of TPD measurements in the range 20–200 °C.
Preliminary observations showed that lowest flow rates, medium saturation time and medium to high amount of injected CO2 gave the highest CRC values (441.3–609.2 μmol⋅g−1). Conversely, high carrier gas throughput resulted in lowest CRC levels (34.4–53.1 μmol⋅g−1), thereby confirming CO2 capture via weak interaction with the OH groups of the organoclay and easy release upon forced convection without heating. The high discrepancy between the highest and lowest CRC levels accounts for 64–94.4% of the nominal CRC value obtained in these experiments. This result is of great importance, because it clearly demonstrates the occurrence of truly reversible capture of CO2, and that forced convection affects CRC assessments.
3.4. Model calculations and accuracy
CO2 retention capacity (CRC) values and water retention capacity (WRC) values were modeled on the basis of the 27 experimental attempts, using a Taylor’s second-order polynomial model [20, 21, 22, 23]. Before model refinement, the general Taylor equation for both the CRC and WRC (denoted as Y ) is given by (1):
| (1) |
Model coefficients and simulated effects upon CRC and WRC assessment
| Model coefficient | Parameter effect on CRC assessment | Parameter effect on WRC assessment | ||
|---|---|---|---|---|
| Value | Simulated effect | Value | Simulated effect | |
| a0 | 156.8 | Dummy variable | 1.709 | Dummy variable |
| a1 | −158.7 | Strongly detrimental individual effect | −0.816 | Detrimental individual effect |
| a2 | 2.86 | Weakly favorable individual effect | 0.829 | Favorable individual effect |
| a3 | 29.80 | Favorable individual effect | 0.184* | Removed from the model |
| a12 | 3.03 | Weakly favorable X1–X2 interaction | −0.350 | Minimum according to X1 |
| a13 | −13.78 | Weakly detrimental X1–X3 interaction | 0.045* | Removed from the model |
| a23 | 28.49 | Favorable X2–X3 interaction | 0.245* | Removed from the model |
| a11 | 110.09 | Sharp minimum according to X1 | 0.465 | Minimum according to X1 |
| a22 | −64.16 | Maximum according to X2 | −0.740 | Maximum according to X2 |
| a33 | −11.29 | Flattened Maximum according to X3 | 0.062* | Removed from the model |
| a123 | −28.11 | Detrimental ternary interaction | −0.194 | Removed from the model |
∗ These coefficients are smaller than the average error on their values (trust range).
The calculations of the model coefficients are not described in the present work, but details about the method used are described elsewhere [21]. The calculated values of the model coefficients (Table 3) are assumed to describe the individual effects of the investigated parameters and their possible interactions. The model adequacy strongly depends on the accuracy of the experiment measurements, where the main errors arise from volume and weight measurements. For this purpose, three additional attempts at the central point (0,0,0) are required for estimating the average error in calculating the value of each coefficient on the basis of the random variance (Table 4).
Model adequacy tests at (0,0,0) point and variance analysis for CRC and WRC assessments
| Feature | Symbol/Equation | Model adequacy | |
|---|---|---|---|
| CRC | WRC | ||
| Parameter number | P | 3 | 3 |
| Level number | L | 3 | 3 |
| Experimental attempt number | N | 27 | 27 |
| Attempt number at (0,0,0) point | n | 3 | 3 |
| Model variance | 𝜈 | 2 | 2 |
| Retention capacity at (0,0,0) point | y01 | 143.0 | 1.00 |
| y02 | 140.5 | 1.35 | |
| y03 | 140.1 | 1.80 | |
| Mean at (0,0,0) point | y0 =∑ y0i∕3 | 141.17 | 1.38 |
| Random variance | 2.583 | 0.16 | |
| Square root of variance | S | 1.607 | 0.40 |
| Risk factor | α * | 0.05 | 0.05 |
| Student’s t test factor | t𝜈,1−𝛼∕2 | 4.3b | 4.3b |
| Average error on the coefficient value | 𝛥ai = ±t𝜈,1−𝛼∕2× (S/N)0.5 | ± 1.33 | ± 0.332 |
| Coefficients to be eliminated | |ai| < |𝛥ai| (Student’s t test) | None | a3, a13, a23 and a33 |
| Number of remaining coefficients | R | 11 | 7 |
| Model response at (0,0,0) | y(0,0,0) = a0 | 157.0 | 1.709 |
| Average yield for the 27 attempts | Ym = ∑Yi∕27 | 179.9 | 1.567 |
| Residual variance | 40,314 | 2.058 | |
| Fisher’s test (Fisher–Snedecor law) | Second test for model adequacy F = Sr2∕S2 | 15,606 > F0.95,3,4 = 6.6 | 12.79 > F0.95,3,4 = 6.6 |
Risk factor: α = 0.05 was arbitrary chosen. In this case, a 95% confidence was regarded as being satisfactory.
t2,0.95 = 4.3 (Student Law with 2 degrees of freedom at a 95% confidence).
F0.95,3.4 = 6.6 (see Fisher–Snedecor tables). To invalidate the hypothesis that all the coefficients of the model are equal to zero or to validate that at least one coefficient is different from zero, the calculated F-test should be higher than the theoretical value of 6.6 provided by the tables.
Model refining using the t-student test gave lower average error of 0.133 than the very coefficient values. Therefore, all coefficients were maintained in the CRC model (2). Application of the same Student’s t test to the WRC model gave higher |𝛥ai| (0.332) than coefficients a3, a33, a13, a23 and a123. Removing these coefficients were removed from the WRC model (3) suggests negligible effect and interactions of their common parameter, namely the injected CO2 amount (X3) on the moisture content.
| (2) |
| (3) |
A method of adequacy test was achieved through the Fisher’s test, expressed in terms of the quotient of the random variance, previously calculated and the residual variance estimated in Table 4. In this case also, both calculated models (with 3 degrees of freedom) are considered to fit the CRC and WRC in the same range, because F ≫ F0.95,3,4 with a 95% confidence.
3.5. Effect simulation and optimization
The individual effects and interactions of the parameters were discussed on the basis of the sign and the absolute value of each coefficient. These coefficient features will define the direction and intensity of the corresponding effect (favorable or detrimental) on CRC and WRC assessment. As expected, the carrier gas throughput displayed the strongest detrimental effect on the CRC and to a lesser extent on the WRC, confirming once again that both CO2 and water are weakly retained and that the occurrence of forced convection affects the assessment both retention capacities.
As a general tendency, increasing nitrogen throughput reduces the CRC. However, increasing contact time during adsorption induced a much weaker influence on the CRC but a favorable individual effect on the WRC. This must be due to stronger diffusion hindrance of non-linear and more polar water molecules within the organoclay entanglement as compared to CO2.
3D plot of CRC as a function of non-dimensional values of X1 and X2 for X3 = 0 (a) and of X1 and X3 for X2 = 0 (b) for centered values of the non-plotted parameters. X1: carrier gas throughput; X2: contact time; X3: Injected CO2 amount.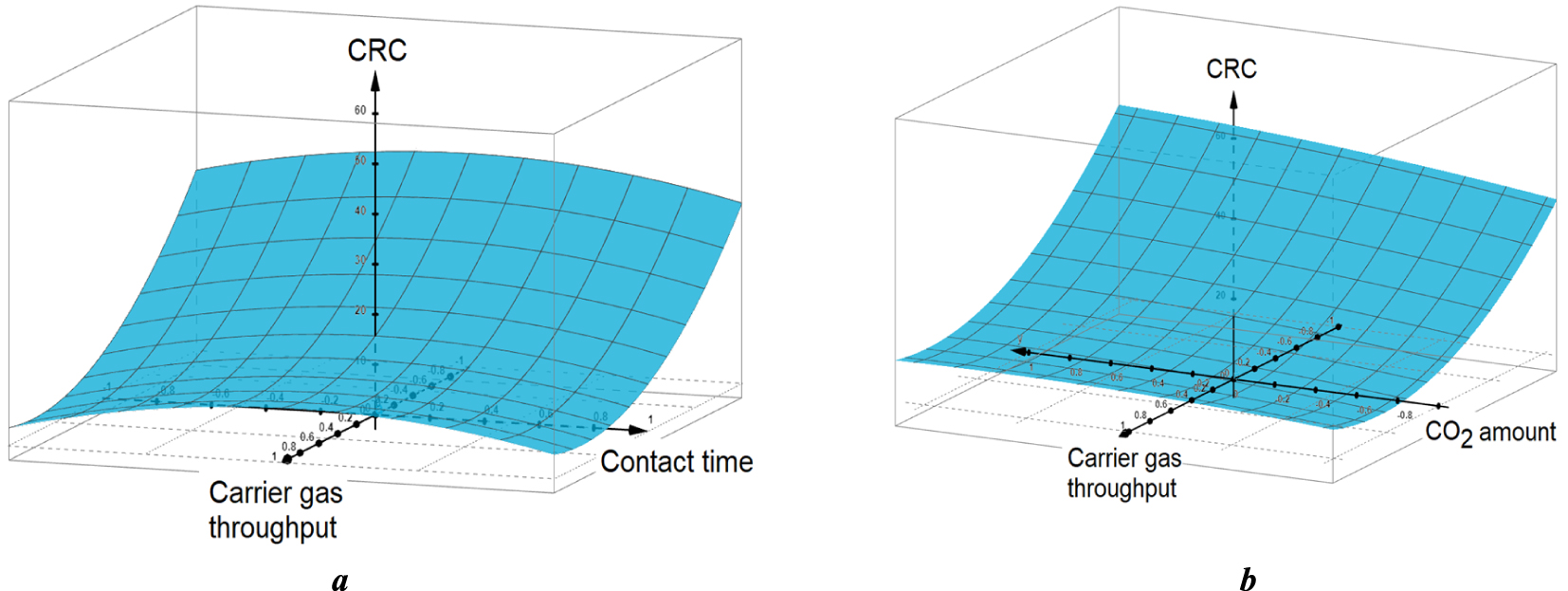
3D CRC plot as a function of non-dimensional values of X2 and X3 for X1 = 0 (a) and for X1 = 1 (b). X1: carrier gas throughput; X2: contact time; X3: Injected CO2 amount.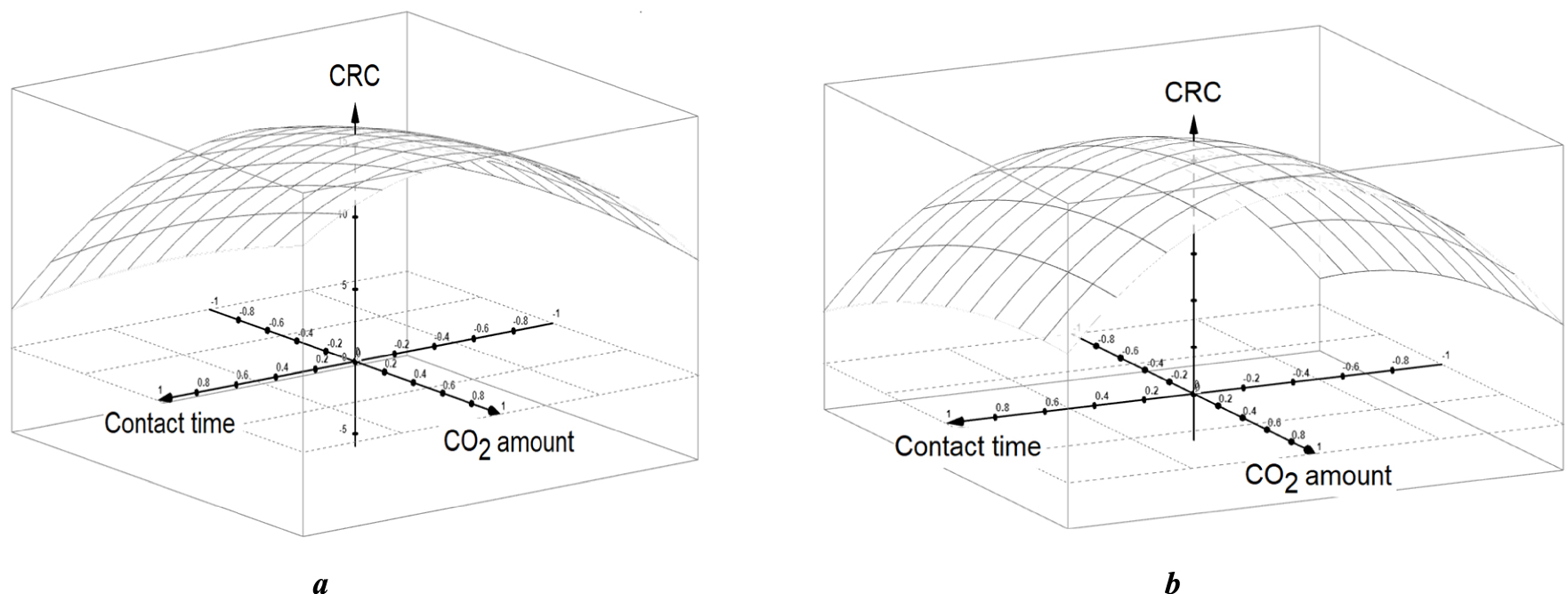
The values of the quadratic coefficients, aii, are essential criteria for estimating the concavity (convexity) of the response surface. The opposite signs of the quadratic coefficients and concavity decrease in the following sequence: |a11|≫|a22| > |a33|, allowed predicting a pronounced minimum of the CRC response-surface with respect to the nitrogen throughput and flattened maximum with respect to the contact time (Figure 2a). A similar but more flattened saddle-shaped response-surface was observed when replacing the contact time (X1) by the injected CO2 (X3) (Figure 2b). This confirms the strong influences of the investigated parameters.
Informative plots were obtained for CRC = f(X2, X3) with X1 = 0 or 1 (Figure 3). The obtained response-surface revealed CRC maxima at optimum values of the contact time (X2) and impregnating CO2 amounts (X3). The occurrence of optimum contact time must be due to slow gas diffusion with the organoclay dendritic entanglement. The fact that the optima are included within the investigated parameters ranges provides clear confirmation of the model validity. Analytical resolution of the equation system resulting from the first derivation of the CRC models for X1 = 0 gave optimum values of X2 = 0.438 and X3 outside the investigated parameter range (1.872).
Similar calculations for X1 = 1 gave optimum X2 = 0.048 and X3 = 0.71. As expected, calculations using these values in the CRC model gave values below 20 μmol⋅g−1 for highest and medium carrier gas throughputs (+1 and 0). This can be explained by the occurrence of forced convection that can release both CO2 and water molecules, in agreement with our previous statements. This suggests that other optimum parameters should occur at the lowest carrier gas throughput. The shape of CRC plot for the slowest throughput of the carrier gas (X1 = −1) allowed predicting a clear optimum (Figure 4). Calculations using the corresponding CRC model resulted in values included within the investigated parameters ranges (X2 = 0.40 and X3 = 0.92). Conversion of these non-dimensional values gave optimum contact time (X2) of 8.7 h and amount of impregnating CO2 (X3) of 24.1 mmoL⋅g−1. Qualitative CRC assessment using these optimum parameters in the model resulted in the highest CRC of 35 μmol⋅g−1 among those calculated for various parameter combinations. This CRC is much lower than those obtained by additional triplicate experiments (65.0, 59.4 and 68.2 μmol⋅g−1) under the above determined optimum parameters.
3D CRC plot as a function of non-dimensional values of X2 and X3 for minimum value of the carrier gas throughput (X1 = −1). X1: carrier gas throughput; X2: contact time; X3: Injected CO2 amount.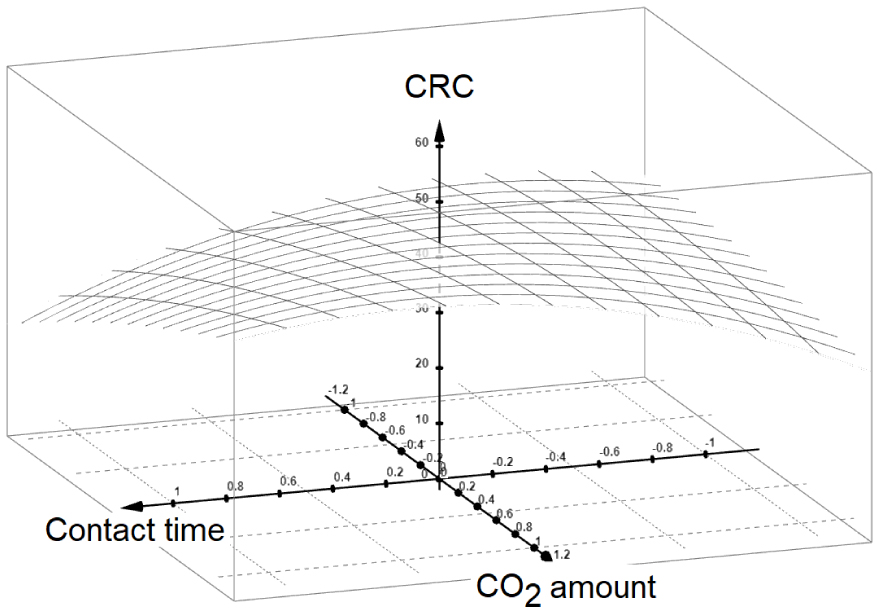
3D WRC plot as a function of non-dimensional values of X2 and X3 for X1 = 0 (a) and X1 = −1 (b). X1: carrier gas throughput; X2: contact time; X3: Injected CO2 amount.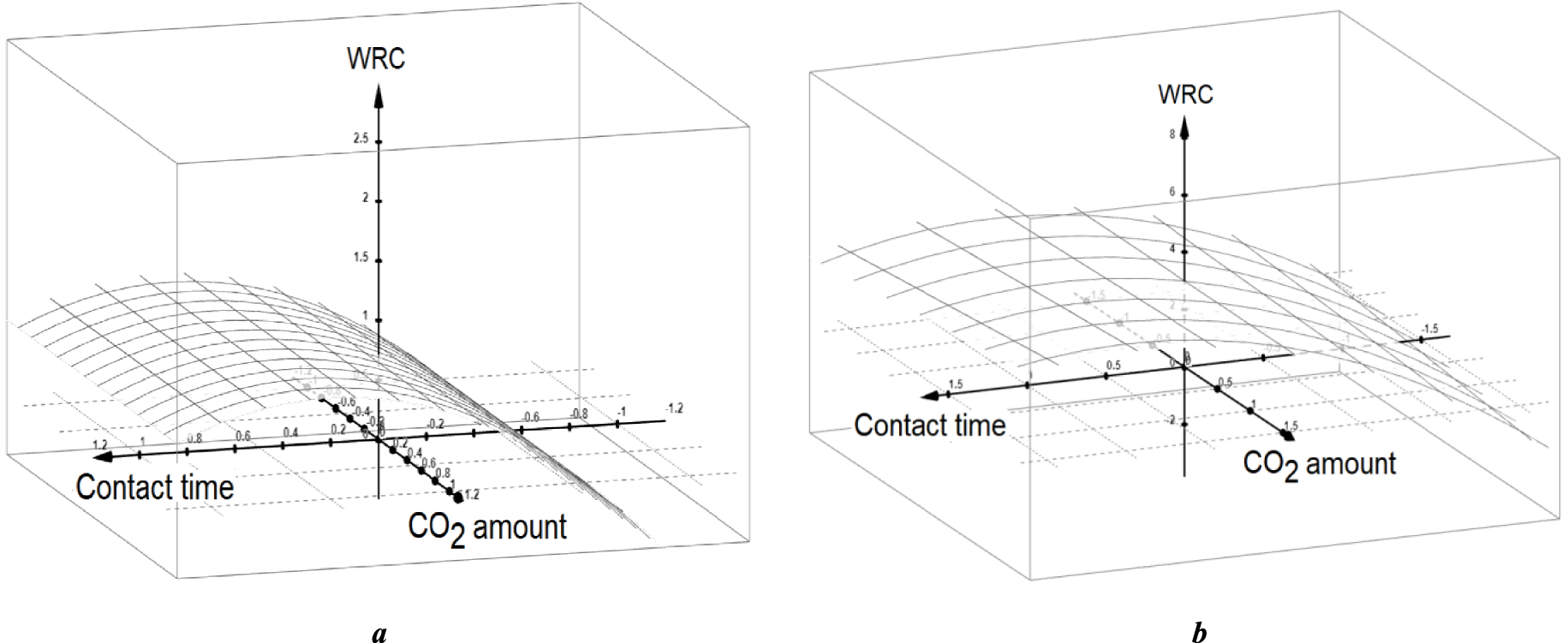
This result confirms once again that the CRC cannot be accurately assessed using such a mathematical model, which is rather intended for parameter optimization. An attempt justified by economic reasons, achieved for minimum contact time (X2 = −1) failed because of even lower estimated CRC values, below 10 μmol⋅g−1. Thus, it is clear that unlike slow gas stream for avoiding forced convection, minimum contact time cannot be an essential requirement for achieving effective CO2 capture on NaMt-H30. Here, the unavoidable diffusion hindrance imposes sufficiently long contact times of such adsorbents, but is not necessarily a major drawback being compensated by the non-stoichiometric capture of CO2. Indeed, a 50 mg NaMt-H30 sample with a 1 wt% polyol H30 (M = 3607.6 g⋅mol−1 and 32 OH/mole) accounts for 88.7 μmoles OH per gram adsorbent.
This is by far lower than the highest CRC value determined in the 33 factorial design (609.1 μmol⋅g−1) (Table 2) and those obtained by additional triplicate experiments (650.0, 594.0 and 682.0 μmol⋅g−1). It results that each OH group in NaMt-H30 can retain more than 13 CO2 molecules. This is a significant result that allows envisaging even higher effectiveness by increasing the number of available OH groups. This can be achieved through higher polyol dendrimer dispersion of the clay surface for minimizing the intermolecular H-bridges. The surprising occurrence of an optimum contact time for the CRC can only be explained a similar phenomenon for the WRC for both medium and slow carrier gas throughput (Figure 5).
Insufficient contact time is assumed to affect the moisture content due to slow water molecule diffusion in agreement with previous statements. Conversely, long contact time should probably favor the diffusion of linear CO2 at the expense of bulkier water molecules. The resulting decrease in moisture content is expected to reduce water–CO2 interaction and subsequently the CRC. This result is or great importance, because it clearly confirms the narrow interaction between the surface basicity and hydrophilic character in such OH-enriched organoclays.
4. Conclusion
Montmorillonite intercalation by dendrimer Boltorn H30 induced an improvement in the affinity towards both moisture and carbon dioxide, with favorable reciprocal interaction between both compounds. The polynomial models describing the capacities for carbon dioxide and water retention showed strong interaction between both adsorbed CO2 and water molecules. Their retention depends on parameter effects and interactions. High nitrogen throughput and low amount of impregnating CO2 induce detrimental diffusion hindrance and mass loss during impregnation through forced convection. Effective CO2 capture requires an optimum compromise between these factors and the moisture content. These results provide a useful tool for envisaging the reversible capture of CO2 by other hydroxylated adsorbents.
Conflicts of interest
Authors have no conflicts of interest to declare.
Acknowledgments
This work was supported by grants from MDEIE-FQRNT (2011-GZ-138312) and FODAR-UQ-2015 (QC, Canada) to AA and RR.




 CC-BY 4.0
CC-BY 4.0