1. Introduction
Rare earth elements (REEs) play a critical role in the global economy due to their numerous applications. They are notably used in electronic and steel industries, as well as permanent magnets, lasers, and batteries. The ongoing development of cleaner energy sources and transportation especially contributes to the sharp increase in REE industrial uses [1, 2, 3]. This rising demand is still mostly met by increasing the extraction from natural minerals [3, 4] despite ongoing efforts in recycling REE, for instance in electronic equipment. Less known and rarer, niobium (Nb) is also a key strategic element for future technologies, and its demand is anticipated to increase by 700% in the next 25 years [1] with about 10% of the market concerning high-purity Nb [5]. Strikingly, about 99% of Nb produced worldwide is extracted from pyrochlore-type materials, which are refractory rocks that also contain REEs.
In this context, the Mabounié (Gabon) deposit discovered in 1986 is an interesting example of a niobium-rich deposit that requires innovative extraction strategies [6]. Indeed, hydrometallurgy is more suited than pyrometallurgy to extract both Nb and REE, but the known fluoride acid route to perform the liquid–liquid extraction is environmentally problematic. This situation stimulated the development of an innovative hydrometallurgical process for the leaching of niobium- and REE-bearing pyrochlore ores and the subsequent separation of Nb from REE [7, 5, 8, 9]. The upstream part of this process produces a raw Nb concentrate through three main steps. First, refractory pyrochlores bearing Nb, REEs, U, and Ta are decomposed by making the non-magnetic ore react with concentrated sulfuric acid (96% H2SO4), yielding a paste that is then further roasted at 250–300 °C. Second, this roasted paste, also named calcinated powder to differentiate it from the untreated ore, is leached with water so that Nb, REE, and other elements from different mineral phases are solubilized in the aqueous phase. As the paste contains a high amount of sulfuric acid, this leaching step occurs at extremely acidic pH. Third, Nb and Ta are selectively thermoprecipitated from REE and U. In the downstream part, the raw Nb concentrate is purified.
However, the optimization of this complex process faced a ubiquitous problem in many hydrometallurgy processes, which is the formation of unfilterable silica gels. For instance, silica gel formation has been reported in hydrometallurgical processes for the extraction of rare earth from eudialyte mineral [2, 10, 11, 12] or from bauxite residue [10, 13]. In hydrometallurgy, the occurrence of silica precipitation and the formation of gelatinous solutions or cakes is a serious drawback for the liquid/solid separation step with deleterious consequences on extraction processes and filterability. Apart from the problematic issue of clogging, the precipitate may blind ore particles from dissolution and reduce leaching kinetics. For instance, in the context of leaching calcium aluminate slags with aqueous HCl, for Al extraction, Tsaousi et al. state that avoiding SiO2 gelation is key to designing robust leaching processes [14].
To facilitate the decomposition of mineral phases before leaching in water solution, pretreatments by reaction with mild to high acid concentration solutions as well as thermal steps are often implemented. However, these strategies are restricted to certain ore types and are typically ineffective for pyrochlore ores. Although silica is initially present in ores, its low solubility in aqueous solutions in both its amorphous and crystalline solid states precludes its involvement in the formation of unfilterable silica gels. Rather, silica gels form in situ during the leaching step due to the release of silicon traces when dissolving certain minerals, leading to their subsequent precipitation as silica. Furthermore, at the high ionic strength of the leaching solution, colloidal metastability is compromised due to charge screening, which leads to aggregation and thus gelation [15, 16]. Gelation, a rheological transition, stems from a structural transition, which is the formation of a three-dimensional percolated network. Silica gels display a multiscale structure that notably depends on pH, a key parameter controlling its solubility and reactivity [16]. The mesostructure that corresponds to supramolecular and colloidal length scales (1–100 nm) is especially relevant to filtration [17].
In this article, we investigate strategies to avoid clogging during the filtration step that follows the acidic leaching of the ore. We first evaluate the extraction yield of the different elements over time. We notably highlight the existence of a characteristic time for the extraction of valuable elements and unveil silicon extraction from dissolved mineral phases and its precipitation as silicates in solution. We then discuss simple parametric approaches to hinder this silica precipitation, such as decreasing the extraction time or increasing the relative amount of leaching solution. We show that although these approaches are efficient, they are costly, polluting, and fragile. We then pivot to a different strategy that consists in rather mastering the mesostructure of the forming silica gel since this mesostructure underlies the overall filterability of the slurry. We present a pathway consisting of deliberately adding more silicates, but at a basic pH, before shifting back to acidic conditions to maintain the solubility of valuable elements prior to filtration. We show that this pathway indeed associates with a drastic densification of the mesostructure, yielding a particle-like instead of a polymer-like gel.
2. Results
2.1. Extracting valuable elements through leaching: release and precipitation of silicon into a clogging gel
The acidic leaching of an ore like that from the Mabounié deposit consists of dissolving minerals to solubilize in solution the elements of interest, here rare earth, niobium, and tantalum. This operation is performed at a given liquid/calcinated ratio (L/C), always expressed in this article at the initial time since most of the solid quickly dissolves. We characterized the calcinated powder by X-ray diffraction, which shows it contains essentially mikasaite, rhomboclase, koninckite (REE- and Nb-bearing phases), crandallite, quartz, baryte, and anhydrite. Comparison with the residue after 4 h of leaching shows the disappearance of rare-earth- and niobium-bearing phases (mikasaite, rhomboclase, koninckite) during the leaching and the appearance of sulfate phases. Therefore, while some of the ore is dissolved through the leaching step, allowing the release in solution of elements of interest, the rest of it remains as solids that must be filtered. Yet, filtration is often hindered by the formation of a clogging gel. To elucidate the nature of this gel, it is useful to monitor extraction over time through an elemental analysis by inductively coupled plasma (ICP). Figure 1A displays the extracted percentage of each major mineral element in the supernatant, obtained by centrifugation of the leached solution, measured by ICP at different times of leaching. We first observe a sharp increase in the concentration of all elements, indicating that some minerals dissolve and thus release elements in solution. This correlates to the rapid dissolution of the calcinated ore, with 77% of its mass dissolved in solution after 30 min. An asymptotic value is quickly reached within 1 h for all elements, with typical values of 70% for niobium and 60% for tantalum. However, there is a strong exception to this generic behavior in the case of silicon. Indeed, following the increase in concentration, a strong decrease is observed, indicating that silicon is somehow removed from the solution. This indicates the precipitation of the dissolved silicon into a new solid phase. It is worth noting that this reprecipitating amount is only a very small fraction of the total silicon content in the ore. QEMSCAN analyses indicate that silicon is mostly contained in quartz, which does not dissolve during leaching. They also suggest the formation of amorphous silica in small amounts. Thermodynamically, silicon could not be simultaneously extracted from quartz and then reprecipitated in the same solution as silicates. It must then originate from mineral phases that dissolve during the leaching step in which silicon can be present as traces, consistently with the small percentages of extracted silica during leaching.
(A) Extraction monitoring of each element in solution over time, quantified by ICP and performed at L/C = 1. Reaching a value of 1 means that the whole amount of the element initially present in the calcinated ore was extracted in solution. All elements reach an asymptotic value of the extraction yield (left Y -axis) within 1 h except silicon, which displays a non-monotonic behavior and much lower extraction yields (right Y -axis). Note that after 30 min, 77% of the calcinated mass is dissolved in solution. (B) QEMSCAN field maps from residue samples collected after 0.5 h (top left), 1.5 h (down left), and 24 h (down right) leaching time. Images are field maps from 1 × 1 mm thin polished sections with false color composite images with different assigned mineral phases shown in the legend panel. Quartz and silica are two phases that are difficult to distinguish, but SiO2 is identified on pixels for which the Si content is lower than that expected for quartz. These pixels are found either at the edge of quartz grains (map 0.5 h) or in small isolated grains in the sulfate matrix (anhydrite).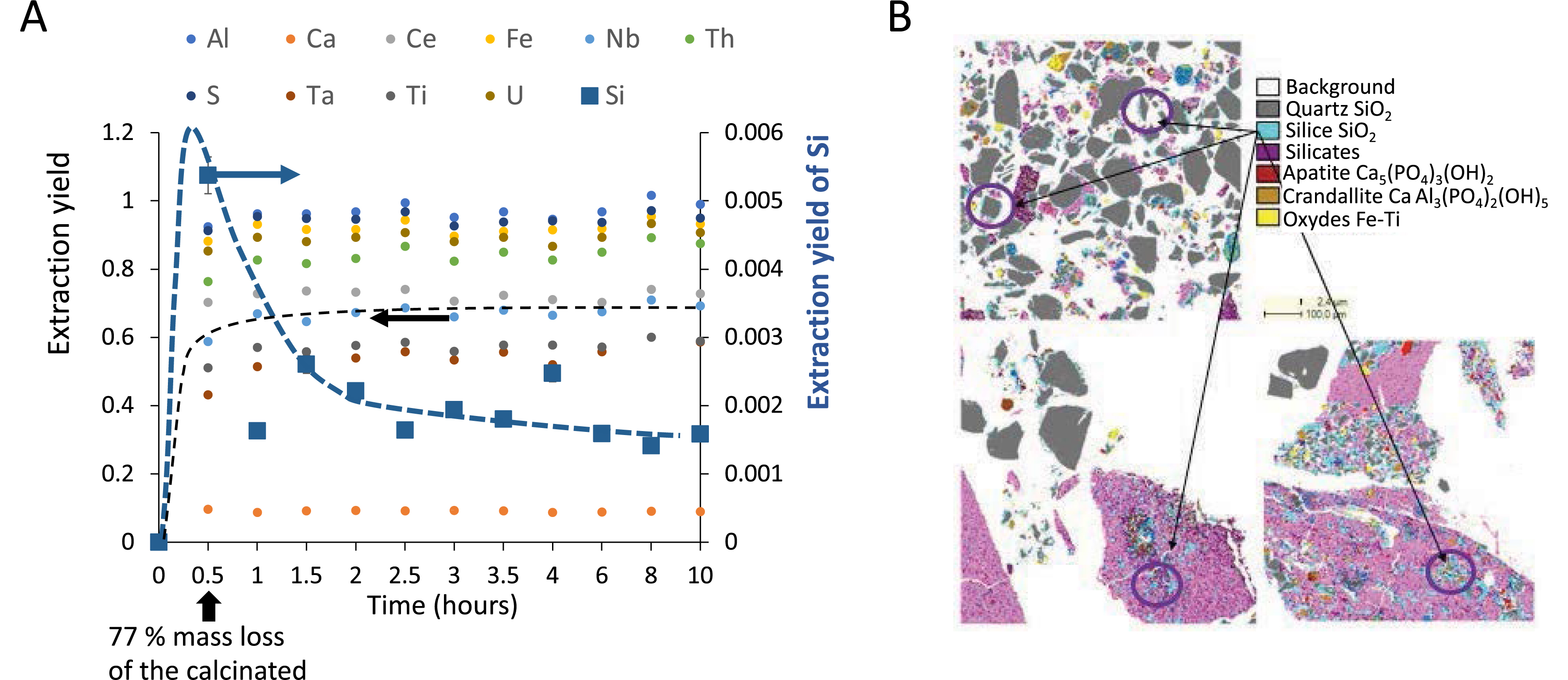
2.2. Precipitation of silica at acidic pH: filterability of slurries
Since the formation of the silica gel is detrimental to filtration, the simplest approach is to avoid or delay its formation, which corresponds to tuning, respectively, thermodynamics or kinetics of silica precipitation. Experimentally, the most straightforward way to play on both is to increase the amount of the leaching solution compared to the ore, which corresponds to increasing the liquid/calcinated ratio (L/C). Silicon extraction and precipitation can then be measured over time by sampling the reactor followed by an ICP analysis. Figure 2A displays the kinetics of silicon leaching and precipitation over time for three liquid/solid ratios of respectively 2, 4, and 8. Qualitatively, the same behavior is observed for all L/C ratios and mirrors the one observed for L/C = 1 displayed in Figure 1A. First, the silica concentration increases as silicon is released from the dissolved mineral phases bearing it as traces, before decreasing at longer times as it precipitates as amorphous silica in solution. However, the extent of this non-monotonic variation decreases sharply upon increasing the L/C ratio and thus increasing the dilution of the ore in the leaching solution. At the highest ratio of 8, the decrease is very mild and occurs over several hours, which is generally too long regarding operating conditions. In that case, silica is nearly at its solubility and the excess precipitates very slowly due to a low supersaturation. Therefore, the extent of precipitation is efficiently tuned by the L/C ratio.
(A) Kinetics of silicon leaching and precipitation for three liquid-to-calcinated ratios L/C. The silica concentration is determined by the molybdenum blue assay in the supernatant of the leached slurry. Initially, silicon is extracted from dissolving mineral phases in solution and eventually precipitates as silica, which explains the non-monotonic variation of the silicon concentration in solution over time. The larger the L/C ratio, the smaller the extent of precipitation. (B) Filtration kinetics for slurries obtained after 0.5 h or 4 h of leaching for three L/C ratios. The linear variation of t/V with V allows us to calculate the specific resistance to filtration, 𝛼 (kg/m3), according to Equation (1). The higher the resistance, the less filterable the slurry.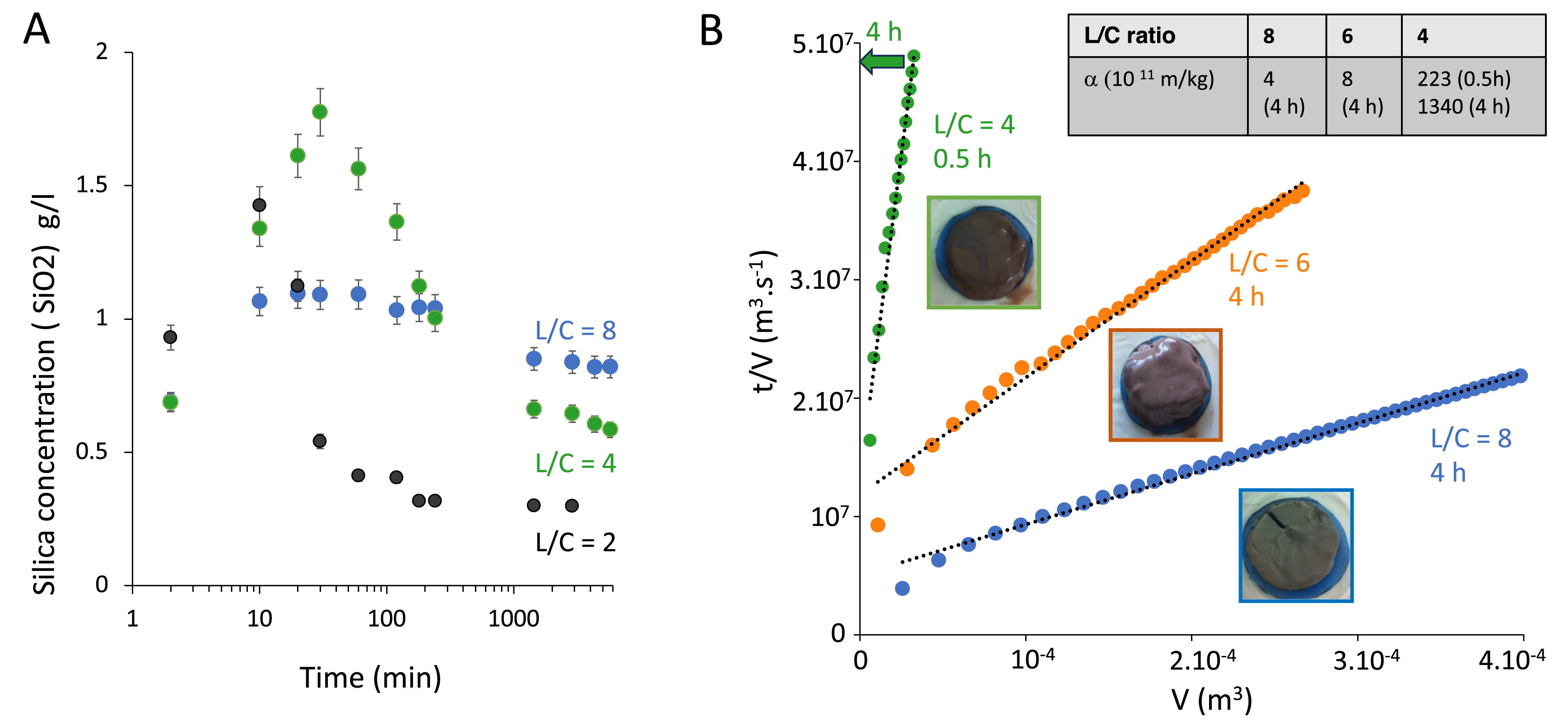
We then investigated the filterability of the corresponding slurries by performing a dead-end filtration at constant pressure. We chose L/C ratios of 4, 6, and 8 to echo the change in the extent of silica precipitation evidenced in Figure 1A. We plot the time-to-volume ratio (t/V ) as a function of filtrate volume (V ) and observe a linear variation for all data. This is consistent with the standard Darcy’s filtration law. Indeed, neglecting the filter cloth resistance and assuming cake incompressibility, we obtain
| (1) |
2.3. Precipitation of silicate solutions at acidic pH: filterability
Since avoiding silica precipitation is not an acceptable option, we turned to a different strategy consisting of mastering the mesostructure of the silica gel, which determines its filterability [17]. However, investigating silica precipitation in slurries obtained from the leaching of the real ore is challenging as the system displays a complex composition. Yet, it is possible as the first approach to start instead from silicate solutions as the source of Si and study the precipitation under given physicochemical conditions. Experiments were conducted under the same highly acidic pH and temperature conditions as for leaching the ore and filtered with the same protocol. This precipitation protocol is therefore quite different from usual synthesis methods that operate at much lower ionic strength. For instance, colloidal silica is typically prepared at a pH of 10, yielding smooth and dense particles and moderate ionic strength, ensuring colloidal stability through ionic repulsions. Therefore, we expect to obtain quite different structures at very low pH and high ionic strength, which can be investigated in detail in this simpler model system with small-angle X-ray scattering (SAXS).
2.3.1. Precipitation of silicates at acidic pH: macro- and mesostructures
The SAXS is a powerful technique to probe mesostructures and was deployed on aliquots sampled over time as silica precipitates. After 60 min, we observe the formation of silica nanoparticles with a finite size evidenced at low q values by the Guinier regime of the scattered intensity (grey curve, Figure 3B). However, at high values and thus small distances, we do not observe the Porod law, which states that for well-defined interfaces, the scattered intensity should decrease as q−4 as is typically observed for colloidal silica prepared under basic conditions [17]. Instead, the scattered intensity decreases as q−2, which can notably correspond to polymeric (so-called fractal) networks. Therefore, the acidic conditions under which silica precipitates drastically impact its resulting mesostructure. At longer times, the q−2 power law extends to lower q values, which highlights an increase in particle size and ultimately the formation of a percolated network that leads rheologically to gelation (black curve, Figure 3B). Interestingly, it means that the silica gel obtained here is structurally a multiscale polymeric network (“polymer gel”), rather than a network of dense colloidal particles (“particle gel”).
(A) Different silica precipitation paths in a hydrometallurgical process. The conventional method is to remain at pH 0. The alternative methods tested are to increase pH to 9 and then add or not silicates, before switching back to pH 0. Note that each step is associated with a color code throughout the figure. (B) After each step, a SAXS spectrum is acquired. Over time, a network forms in solution as visualized by the increase in small wave vector intensity q, which eventually leads to a structure factor decaying as q−2 (grey to black curves). The extension of this slope down to larger wave vectors and thus smaller distances indicates that the whole structure can be seen as a polymeric silica gel. Increasing pH to 9 does not change this structure (blue curve). However, adding silicate leads to the compaction of the mesostructure at small distances, and the Porod law in q−4 is recovered (green curve). This structure is maintained when switching back pH to 0 (orange curve). In contrast, when only the pH cycle is performed without adding silicates, the structure changes only to a smaller extent (purple curve). Note that scattering intensities are not on an absolute scale as the sampling is not achievable at a controlled silica concentration. They were thus scaled by arbitrary factors to highlight similarities and differences. (C) Schemes of the mesostructures obtained depending on the pH cycle used. (D) Filterability of the two different gels obtained (pH = 0 or pH cycle and silicate addition). The sticky gel obtained at pH 0 is strongly clogging while the brittle gel obtained through the pH cycle and silicate addition is much easier to filter. Small length scales thus dictate the filterability, and compacting them is a profitable process modification.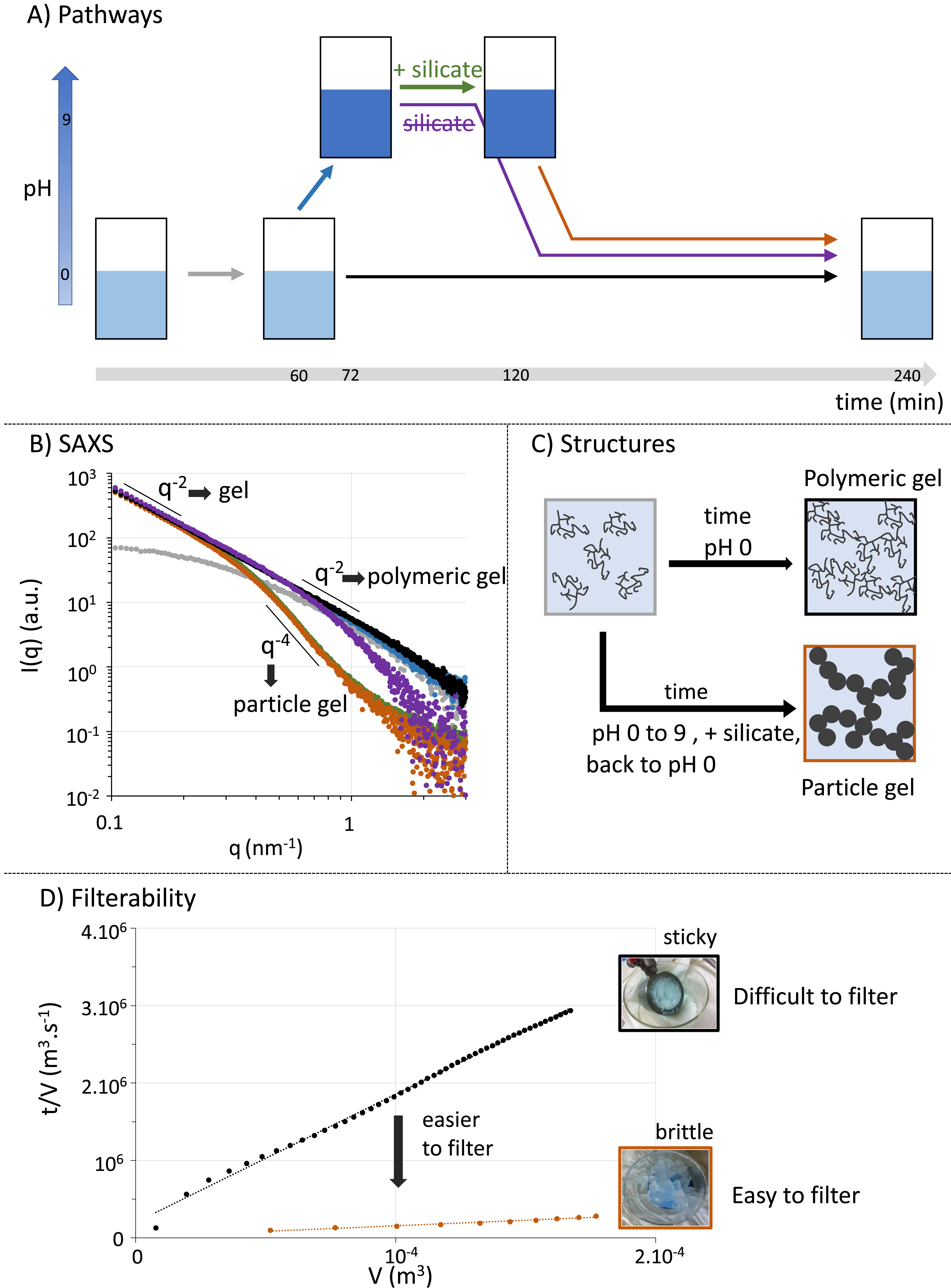
2.3.2. Changing the precipitation pathway by adding silicate ions at basic pH
Following these results, we tried to change the mesostructure by tuning pH during silica precipitation. For this purpose, we increased the pH during precipitation (blue arrow and curve in Figure 3). The resulting SAXS curve at 72 min overlapped with the one obtained after the precipitation of silica under acidic conditions after 240 min, evidencing that the overall mesostructure was not modified but that gelation proceeded faster. The pH was then returned to its original acidic value to dissolve anew the elements of interest (purple arrow and curve in Figure 3). The resulting SAXS data indicates an increase in the exponent of the power law at high q values, which indicates slight densification of the network. To amplify this modification, we devised an alternative pathway in which silicate is deliberately added at basic pH (green arrow) before returning to acidic pH (orange arrow). Strikingly, the two resulting spectra overlap indicating that the mesostructure is then unchanged by the pH variation. Furthermore, the power law then follows the Porod law indicating that silica/water interfaces are now well defined and that the network is denser. Adding silicates at basic pH thus allows for drastically modifying the mesostructure, and can be described as a consolidation of the existing polymeric network, yielding a particle gel. This change in mesostructure cascades to the macroscale, as shown in Figure 3D, which demonstrates that it leads to a drastic improvement in the gel’s filterability. Thus, our counterintuitive strategy, which consists of deliberately adding at the right pH the problematic species in the process, silica, is a powerful means to solve the practical problem of filterability.
2.3.3. Applying the mesostructure shaping strategy to real ore extraction
To verify the feasibility of this strategy in the real system, we applied the same procedure to the ore (see Figure 4A). We first checked that the pH cycle did not compromise extraction yields, as the precipitation of some dissolved elements (Nb, REE, etc.) at basic pH was in fact fully reversible when returning to the initial acidic pH. Figure 4B displays a decrease in specific resistance by two orders of magnitude when tuning silica precipitation through this pH cycle with a consolidation step, similarly to the model system previously presented.
(A) Conventional and alternative precipitation pathways performed on the real ore. In the alternative pathway, silicates are added at basic pH before shifting back the pH to high acidic values. (B) Resulting filterability profiles for both gels were obtained throughout the two pathways. The strong collapse of the specific resistance when performing the silicate addition at the basic pH pathway indicates a tremendous improvement in the filterability. Note that the final liquid/solid ratio is 4. The scheme proposed is the same as in Figure 3 but includes insoluble mineral grains (purple) in addition to the forming silica networks.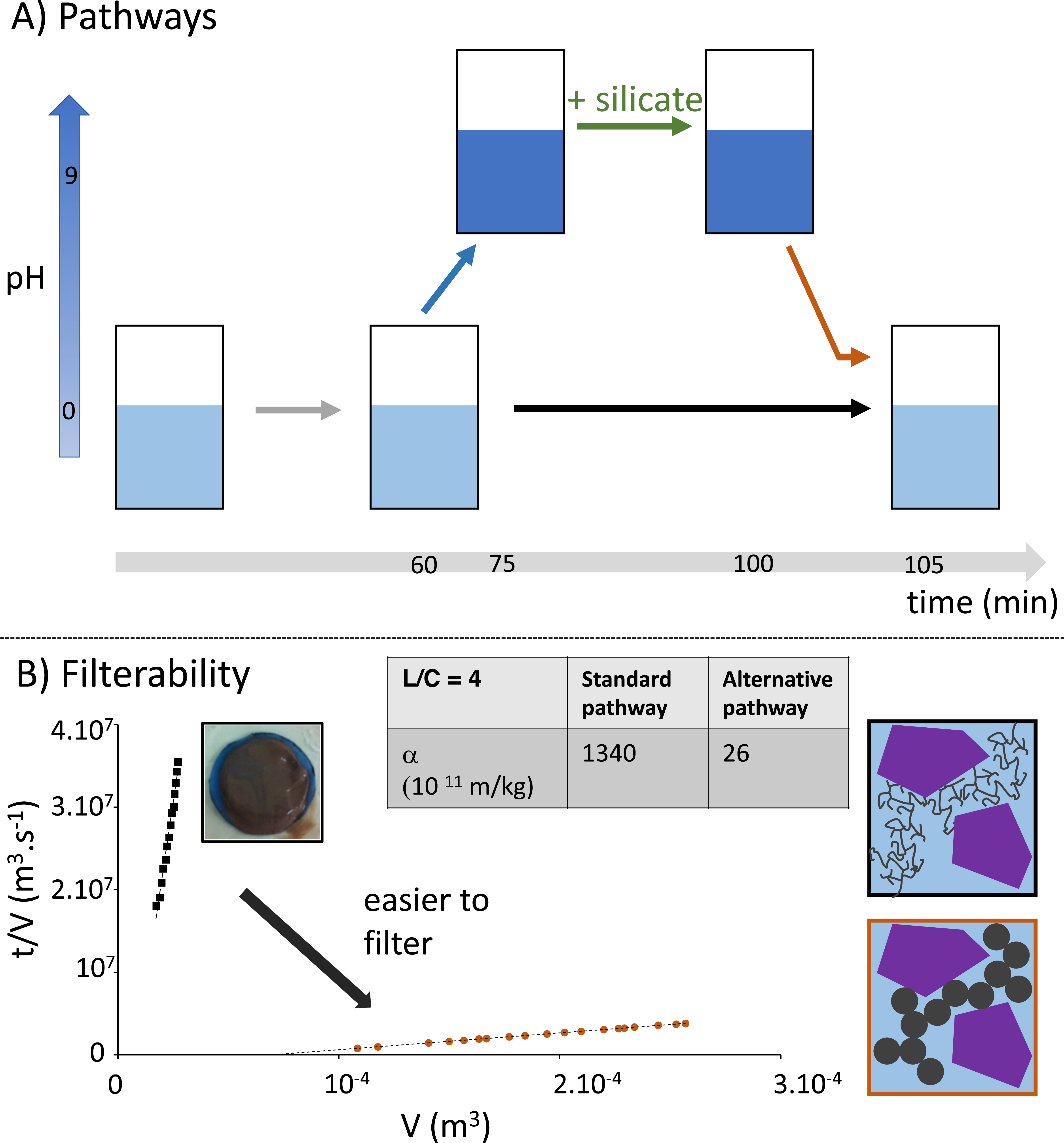
In practice, the pulp thus becomes filterable. It is interesting to stress that the overall procedure leads to a final liquid/solid ratio of 4 and thus would indeed correspond to non-filterable conditions (see Figure 2B). We did not optimize this ratio, but it could be further reduced if more concentrated sodium hydroxide and silicate solutions are used. Overall, this method is thus more advantageous than the dilution strategy tested and presented in Figure 2B, where a ratio of 8 would lead to comparable results but would require a much larger volume and thus decreased profitability. We are confident that this difference could be further increased through optimization, whereas the dilution pathway is bounded by silicate solubility, an equilibrium parameter.
3. Conclusion
In hydrometallurgy, the occurrence of silica precipitation is as ubiquitous as it is deleterious for the design and operation of leaching and downstream stages of the process. Indeed, the resulting gel formation drastically hinders filterability. Although some pretreatment steps have been proposed to restrain silica precipitation through converting silica-bearing mineral phases into an insoluble form, the so-called digestion steps, they are not universal and typically do not apply to the pyrochlore ores we use in this study. Another simpler way is to increase the liquid/solid ratio during extraction by leaching, a dilution step, which eventually leads to operating under conditions where silicates remain solubilized. However, they may eventually precipitate later, which then hugely impacts the overall profitability.
Overall, it is challenging to fight thermodynamics when designing an efficient process. In this work, we shifted our stance to accepting silica precipitation into a gel but rather proposed that by carefully tuning the structure of the gel in the 1–100 nm range, it could be made filterable. Inspired by syntheses of filterable silica performed at basic pH, our idea was to deliberately add the problematic species rather than to remove it by using a pH shift. This may seem counterintuitive, but this addition, when performed at basic pH, leads to a compaction at the smallest length scales of the gel. Indeed, we then transition from a multiscale polymeric network (“polymer gel”) to a network of dense colloidal particles (“particle gel”). This mesostructure change is readily observed in SAXS as a change from a q−2 to a q−4 power law, which is typically observed for smooth objects such as silica at basic pH [17].
We have demonstrated that this strategy, devised on a model system, can be successfully implemented in the extraction of real ores. It is worth stressing that this strategy is generic and not very sensitive to the exact ore used as silica precipitation is mostly controlled by the pH value. Overall, rather than avoiding silica precipitation, we have controlled it at the relevant length scale for filterability, which paves the way for disruptive process modifications in hydrometallurgical processes involving silica precipitation and filtration steps.
4. Materials and methods
4.1. Leaching of calcinated powder
Calcinated powder was provided by ERAMET. It originates from the Mabounié upstream hydrometallurgical process that combines consecutive sulfation and roasting of pristine ore, mostly aimed at converting the pyrochlore mineralogical phase containing the value elements into metallic sulfates to facilitate their leaching. The conditions used to obtain the calcinated powder are described by Beltrami and co-workers in several publications [8, 9, 5]. The mass composition in terms of the main chemical elements in calcinated powder is given in Table 1.
Mass composition of the different main elements in the calcinated powder
| Element | Al | Ca | Ce | Fe | Nb | P | S | Si | Ti |
| Mass percentage | 4 | 1.5 | 0.4 | 10.8 | 1.1 | 2.3 | 17.3 | 4.4 | 1.3 |
Leaching of the calcinated powder was performed in an insulated glass reactor equipped with a three-blade impeller, a pH electrode, and a thermometer equipped with a Pt100 probe. Deionized water was used throughout all the experiments. First, the reactor was filled with 500 ml of deionized water. Then a given mass of calcinated solid particles was introduced. This given mass defines the liquid-to-solid ratio: a liquid-to-solid ratio equal to 1 was obtained by mixing 500 g of calcine powder with 500 ml of water. Right after the calcinated powder addition, the mixture was continuously agitated at 400 rpm. The leaching experiments were conducted at a temperature of 90 °C and for contact times between 30 and 1500 min, starting from the time of powder addition. To ensure the solubilization of valuable elements such as niobium and tantalum from metallic sulfates, leaching has to be performed below pH 2. This condition is easily met without any acid addition thanks to the initial acidity of the calcinated powder. For liquid-to-solid ratios (L/C) ranging from 1 to 4, the solution acidity is equivalent to 1 mol/l H+ in the leaching solution just after the addition of calcinated powder.
In the first series of experiments, the chemical compositions of both solid and liquid phases were monitored over time from 0.5 h to 24 h. First, slurries were collected from the reactor at the end of the experiment and diluted by a factor 2 with deionized water before its centrifugation at 3000 g for 15 min. The yielded sediment was washed twice with 5 mL of deionized water per gram of solid and subsequently dried at 80 °C for 48 h. The resulting powder was analyzed by both X-ray diffraction and scanning electron microscopy (QEMSCAN). Diffraction patterns were obtained using a PANalytical X’Pert Pro diffractometer (Cu K radiation, 1.5406 Å) and identified with the HighScore Software. SEM-QEMSCAN analyses were carried out using an FER Quanta 650 F SEM platform. Separately, the liquid phase obtained after centrifugation was analyzed by inductively coupled plasma atomic emission spectrometry for the compounds with low atomic weight (Al, Ca, Fe, P, S, Si, Ti) and by inductively coupled plasma atomic mass spectrometry for the compounds with high atomic weight (Ce, Nb, Ta, Th, U).
In the second series of experiments, we focused on the kinetics of silica dissolution/precipitation for liquid-to-solid (L/C) ratios of 2, 4, and 8. The same leaching protocol as described above was carried out, but this time, aliquots of slurries were sampled from the reactor at different contact times from a few minutes to several hours. The collected aliquots were diluted by a factor 2 by adding deionized water and then filtered (0.45 μm cutoff) to remove undissolved particles. The filtrates were analyzed by adapting a silicomolybdic acid spectrophotometric method, which is predominantly used for environmental or industrial waters, in order to measure the concentration of silica precursors in the liquid phase at different contact times [18, 19, 20, 21].
4.2. Filtration of slurries
Filtration experiments were conducted with a laboratory filtration cell (Choquenet, France) and filter cloths from Sefar Fyltis (France). The volume of the cell was 102 cm3 and the filtration area was 38.5 cm2. The hydraulic resistance of filter cloths was a hundred times less than the hydraulic resistance of the cakes formed during the filtration experiments, so the resistance of the medium was neglected. The cell was fed with the slurry collected from the leaching reactor and circulating from a guard reservoir maintained at a constant pressure by a regulated air supply. Filtration tests were undertaken just after the slurry reached room temperature and operated at a constant operating fluid pressure of 700 kPa and a temperature of 25 °C. During the filtration, solid particles present in the slurry accumulate on the filter to form a cake. The experiment was terminated when the cake filled the entire space of the cell or when fluid permeation out of the cell was no longer observed. After the filtration, the wet cake was recovered and the mass of solids in the cake was measured by thermogravimetric analysis (Mettler Toledo, Viroflay, France). This mass included the contribution of both solid particles and salts formed during leaching. The mass of salts was determined by measuring the conductivity of a dry pellet redispersed in Milli-Q water. The mass of solid particles in the cake was therefore estimated from the difference between the mass of solids and salt mass. Because we were interested in the permeability of the filtration cakes, we gravimetrically determined the flow rate by recording the mass of fluid permeating out of the cell on an electronic balance at regular time intervals. The cake-specific resistances were directly determined from the variation of the permeating volume V with filtration time t. Filtration experiments were repeated three times to check the reproducibility of the filtration data.
4.3. Precipitation of silicate solutions
Precipitation experiments were carried at T = 90 °C by quickly injecting 100 mL of a sodium silicate solution (pH = 11, [SiO2] = 130 g/L, density 1.39 g/mL) in a reactor filled with 900 ml of an acidic solution (sulfuric acid medium at [H+] = 1 mol/L). The initial silicate concentration is thus of 13 g/L. During precipitation, samples are collected and “quenched” at pH 2 with a soda solution at 1 mol/L to stop the reaction as described in the literature by Iler and Alexander. The arrested samples are analyzed by SAXS on the Xeuss 2.0 platform available in-house.
The alternative pathway consists of increasing pH after 1 h, from pH 0 to 9 by adding 250 mL of a 8 mol/L sodium hydroxide solution at 20.8 mL/min. A consolidation step is then performed by slowly injecting 166 mL of a sodium silicate solution (70 g/L), at 4 mL/min, while maintaining pH at a set value of 9 by adding 40 mL of a sulfuric solution (1 mol/L). After this consolidation step, the pH was decreased back to 0 by adding 100 mL of a sulfuric acid solution at 8 mol/L.
4.4. Monosilicic acid concentration in solution using molybdenum blue methods and ultraviolet–visible light spectroscopy
To titrate the amount of monosilicic acid in the solution, we used a spectroscopic method proposed by Nagul et al. that uses the molybdenum blue reaction [20]. While ICP measures the whole silicon content in solution, this method is more specific to monomeric silica. This method was calibrated using a standardized silica stock solution (99.9% Si(OH)4 monomer, VWR). The monitoring was performed at 800 nm, which corresponds to the absorption by the blue silicomolybdate complex.
4.5. Small-angle X-ray scattering
SAXS experiments were performed on a Xeuss 2.0 laboratory instrument from Xenocs. Samples were injected in disposable quartz capillaries (1.5 mm inner diameter). Azimuthal averaging was performed after mask subtraction, yielding one-dimensional spectra after normalization by transmissions. Since the sampling is heterogeneous, we did not display intensities on absolute scales but rather scaled them by arbitrary factors to highlight scaling laws over the q range.
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.
Acknowledgments
ERAMET Research is thanked for its financial support of the PhD grant to CM. Simon Blancher and Céline Rodriguez are acknowledged for performing the mineral characterization. Dominique Mannoni and Amandine Chabaneix are acknowledged for performing the ICP characterization. Bruno Courtaud, Philippe Ribagnac, and Denis Beltrami are acknowledged for stimulating discussions on this topic. The research federation FERMAT (Université de Toulouse, France) is acknowledged for providing access to the Xeuss 2.0 SAXS instrument (Xenocs) through the CPER IMATECBIO grant with support from Pierre Roblin.




 CC-BY 4.0
CC-BY 4.0