1. Introduction
The growth in world population and industrial activities has resulted in the discharge of various dyes [1, 2], pharmaceuticals and antibiotics [3, 4, 5], numerous organic compounds, especially aromatic compounds [6, 7, 8], and heavy metals [9, 10, 11] into the environment, particularly into aquatic habitats. Among them, heavy metal cations have severe negative impacts on the environment and humans because they tend to accumulate in human tissues without undergoing biodegradation [12, 13, 14, 15, 16]. Ecosystems are polluted by heavy elements through natural or artificial routes. Natural contamination occurs by rainfall and through the release of bedrock and soil into the environment. Artificial routes of contamination include urban and industrial wastes, mining, and agricultural activities [17, 18]. Different industries act as the major source of cadmium (Cd) released into the environment in the form of ceramics, paints, plastics, and pigments and through processes such as electroplating, metallurgy, and battery manufacturing [19]. The risk of human exposure to Cd has risen through the increase in contamination of the food chain [20]. The World Health Organization has set a permissible limit of 0.003 mg/L for Cd in drinking water. Regarding the deleterious effects of Cd on ecosystems, the removal of cations from aquatic systems is inevitable for environmental remediation. In many polluted systems, various contaminants with different permissible limits may coexist. Therefore, the development of a selective separation technique for each pollutant is necessary for achieving their efficient removal from aquatic environments. [19].
Various methods such as ion exchange [21], chemical precipitation [22], flotation [23], ultrafiltration [24], nanofiltration [25], reverse osmosis [26], and electrocoagulation have been used to remove heavy element cations [27]. The adsorption process, among others, proven to be the most practical technique for wastewater treatment [12]. However, preparing adequate sorbents with desirable selectivity and sufficient capacity for the effective removal of target cations remains a key topic of research [19].
Mesoporous materials are widely employed for cation removal due to their large surface area, high porosity, and environmental-friendly properties. To exhibit better performance, the structures of these compounds may be modified by changing the reaction conditions and using various surfactants, organic compounds, and additives [28]. In this regard, SBA-15 is a mesoporous material that is prepared by a triblock copolymer surfactant at low pH levels. The synthesized material has thick silica walls and large pore sizes, facilitating the fast mass transfer of ingoing cations. Furthermore, its high thermal stability enables long-term use of the material. However, SBA-15 gradually loses part of its adsorption capacity due to the absence of a binding group on the surface. To eliminate this drawback, modification of the SBA-15 surface by the grafting of organic groups has been suggested [28]. The strong covalent bonds created by the grafting process strongly hold the grafted groups together, leading to long-time application of the sorbent. Obviously, the grafted groups may reduce the pore diameter of the channels, causing a significant decrease in the diffusion rate of cations and hence a slower kinetic sorption rate. Moreover, the bonded organic groups on the surface of the sorbent limit the access of ingoing cations to sorption sites. Therefore, new studies are required to improve the functionalization method for obtaining more satisfactory adsorption performance for the target cation [28].
In the present study, a new sorbent was prepared by functionalizing mesoporous SBA-15 with 1,5-diphenyl carbazide (DPC) to present a new adsorptive system for the efficient removal of Cd from aqueous solutions. The grafted species is chemically stable, highly hydrophilic, and small in size, yielding desirable performance from the studied cation [28, 29]. To achieve optimum efficiency, the adsorption process was studied by the response surface methodology (RSM) technique. The principles of this experimental design approach have been provided in the literature [30, 31, 32, 33, 34].
Experimental factors and levels in the central composite design for adsorption of Cd(II)
| Factors | Unit | Surface factors | ||||
|---|---|---|---|---|---|---|
| Level | Star point | |||||
| (Low) − 1 | (Central) | (High) + 1 | −𝛼 | +𝛼 | ||
| (A) pH | — | 3 | 5 | 7 | 1 | 9 |
| (B) Adsorbent dose | mg | 3 | 4 | 5 | 1 | 7 |
| (C) Initial concentration | mg/L | 15 | 25 | 35 | 5 | 45 |
| (D) Contact time | min | 15 | 20 | 25 | 10 | 30 |
2. Materials and methods
2.1. Chemical compounds
Pluronic P123 (EO20PO70EO20, Mn = 5800), DPC (C13H14N4O, 97%), hydrochloric acid (HCl, 37%), tetraethylorthosilicate (>99.0%, TEOS), toluene (99.8%), chloropropyltriethoxy silane (CPTES, 97%), ethylene diaminetetraacetic acid (>98.5%), triethylamine (C2H5)3N, >99.5%), and Cd(NO3)2⋅4H2O (98%) were purchased from Sigma-Aldrich.
2.2. Synthesis and functionalization of SBA-15
SBA-15 was synthesized by the hydrothermal method and according to the procedure outlined in [35]. The mixture was prepared by adding 4.00 g of P123 to 85.0 mL of HCl (2.0 M) and then stirring this solution for 2 h at 40 °C. Furthermore, 6.8 mL of TEOS was added, and the mixture was stirred for 18 h, transferred into an autoclave, and finally heated at 100 °C for 22 h. Next, the product was separated, thoroughly rinsed with distilled water, dried at 90 °C, and calcined at 550 °C for 6 h. For functionalization, 50 mL of toluene was added to 1.00 g of the synthesized SBA-15 and stirred for 1 h at 25 °C. After adding 1.0 mL CPTES, the mixture was refluxed for 24 h at 120 °C under N2 atmosphere. Moreover, the chlorinated compound (Cl-SBA-15) was separated and thoroughly rinsed by toluene; it was vacuum-dried at 100 °C. Additionally, 55.0 mL of toluene, 1.2 mL of trimethylamine, and 0.50 g of DPC were then added to 1.0 g Cl-SBA-15. Finally, the mixture was refluxed for 24 h at 115 °C under N2 atmosphere, and the functionalized adsorbent (DPC-SBA-15) was separated and rinsed by toluene and then dried in vacuum at 80 °C [36].
2.3. Adsorption experiments
2.3.1. Statistical and data analysis
The RSM is applied to obtain the optimal response from a limited number of experiments. It is a statistical method for multifactor experiments, and it determines the relationship among various parameters to achieve optimum conditions. In the RSM, the number of experiments (N) is determined by (1) as follows:
| (1) |
In addition, a quadratic equation (2) is employed to describe the performance of the system.
| (2) |
Furthermore, the responses are represented by surface plots showing the interactions between the variables, which determine the optimized conditions of the system. In the present study, the software Design-Expert 7.0.0 is used to evaluate the collective effect of four independent variables (pH, adsorbent dose, initial concentration, and contact time) in sets of 30 experiments. The variables have five levels; the details are presented in Table 1 [40].
2.3.2. Modeling and optimization of adsorption performance
To this end, 40 mL of the Cd2+ solution was added to the adsorbent having a a degree of concentration that was determined by the software (as presented in Table 4) in 30 runs. The table lists the values of pH, adsorbent dose, and contact time for each run of the adsorption process. After performing each run, the sorbent was separated, and the amount of Cd2+ in the solution was measured by atomic absorption spectroscopy (AAS; AAnalyst 300 PerkinElmer, USA; air–acetylene flame at 𝜆 = 228.8 nm). To achieve optimum conditions for the maximum capacity of Cd(II) adsorption (qe) by DPC-SBA-15, all variables (pH, adsorbent dose, initial concentration, and contact time) were set at the determined range. The response (adsorption efficiency) was considered to be maximized in the numerical optimization menu of Design-Expert 7.0.0 [41, 42].
2.3.3. Determination of point of zero charge (pHpzc)
The pH of the surrounding electrolyte determines the surface charge of the adsorbent, which can be calculated by measuring the pHpzc. Five beakers containing 25 mL of NaCl (0.01 M) solution were prepared to determine the pHpzc. This was followed by adding 0.02 g of DPC-SBA-15 to the solution and adjusting the pH to 1, 3, 5, 7, and 9 by adding 0.1 M NaOH or 0.1 M HCl. The solutions were kept under N2 flow for 3 h, and the final pH of each solution was measured accordingly. Then, the pHpzc was obtained by plotting the final versus initial pH values [43, 44, 45, 46].
2.3.4. Adsorption kinetics
The uptake rate of an analyte is a suitable parameter for selecting an adsorbent for application purposes. A series of adsorption experiments was carried out with 40 mL of Cd2+ 25.39 mg/L solutions added to 4.55 mg of the adsorbent at pH 5.75, which was an optimized condition obtained from the software (Table 5), and in a time interval of 0–25 min at 298 K. To investigate the best-fit equation, experimental data were evaluated by the pseudo-first-order and pseudo-second-order kinetic models [47].
2.3.5. Thermodynamics
Some studies have confirmed the effects of temperature on the removal process for obtaining the thermodynamic factors [48, 49]. The corresponding distribution coefficient (Kd) is determined by (3).
| (3) |
| (4) |
| (5) |
2.3.6. Adsorption isotherms
The type of adsorption has been determined from the energy of the sorption process in the literature [51, 52]. Isotherms have also been used to describe the distribution of the adsorbate between aqueous solutions and the solid adsorbent surface. Langmuir, Freundlich, and Dubinin–Radushkevich (D–R) models are the isotherms most commonly used for elucidating the nature of adsorption processes. The Langmuir model indicates that monolayer adsorption occurs and that the adsorbed surface is homogeneous [51, 52]. On the other hand, the Freundlich model determines that the phenomenon is multilayer adsorption and that the surface is heterogeneous [47]. The D–R isotherm suggests that ionic adsorbates bind to the most energetically favorable sites. Then, multilayer adsorption can be observed. This isotherm is applied for determining whether the adsorption mechanism is physical or chemical [51, 52].
To analyze sorption isotherms, 40 mL of the Cd2+ 25.39 mg/L solution was added to 4.55 mg of the adsorbent at pH 5.75 for 21.50 min, which was an optimized condition according to the results obtained from the software (Table 5). The parameters required for substitution in Langmuir, Freundlich, and D–R models were estimated, and calculations were performed accordingly.
2.3.7. Adsorbent regeneration and reusability
For this purpose, 40 mL of the Cd2+ 25.39 mg/L solution was added to 4.55 mg of the adsorbent at pH 5.75 for 21.50 min, which was determined as an optimized condition by the software (Table 5). After cation adsorption, the adsorbent was separated and the solid was dried at 60 °C. Finally, regeneration was separately performed using 5 mL HCl and HNO3 at 0.1, 0.2, and 0.3 M concentrations for 120 min. The regenerated adsorbent was reused six times successfully.
2.3.8. Adsorption selectivity
A series of solutions with a Cd2+ concentration of 25.39 mg/L (an optimized condition) and some common competing ions (Na+, Ca2+, Mg2+, Ba2+, Zn2+, Co2+, Mn2+, and Pb2+) in different concentration ranges (5, 10, 15, 20, 40, and 100 mg/L) were prepared in this regard. Then, 40 mL of these solutions was added to 4.55 mg of the adsorbent at pH 5.75 for 21.50 min, which was an optimized condition provided by the software (Table 5). After performing the adsorption process for each competing ion, the sorbent was filtered and the concentration of Cd ions in the solutions was determined by AAS.
3. Results and discussion
3.1. Sample characterization
X-ray diffraction (XRD) is a useful tool for studying the phase purity of solid samples [53, 54]. To this end, small-angle XRD patterns of SBA-15 and DPC-SBA-15 at 0.8–10° 2𝜃 with a rate of 0.05°/s were recorded using an X’PertPro, D8 ADVANCE, Bruker X-ray diffractometer (with a Ni-filtered Cu-K𝛼 radiation source at 1.5406 Å, 40 kV, 30 mA; Netherlands). This is illustrated in Figure 1. The SBA-15 sample displayed three characteristic diffraction lines at 2𝜃 values of 0.83, 1.47, and 1.78°, which originated from (100), (110), and (200) diffraction planes, respectively. Based on the results, no diffraction lines were observed beyond a 2𝜃 value of 2°, indicating that the material was completely amorphous. The pattern was identical to the reference sample corresponding to an ordered two-dimensional hexagonal mesoporous structure [55]. For the DPC-SBA-15 sample, a small shift was observed for the diffraction lines associated with a slight decrease in the d-spacing value, which was related to the grafting of DPC into the SBA-15 structure. Moreover, the intensity of reflection lines decreased in the functionalized sample [56].
XRD patterns of reference sample SBA-15 [55] (a), synthesized SBA-15 (b), and DPC-SBA-15 (c).
FTIR spectra of synthesized SBA-15 (a), 1,5-diphenyl carbazide (b), and DPC-SBA-15 (c).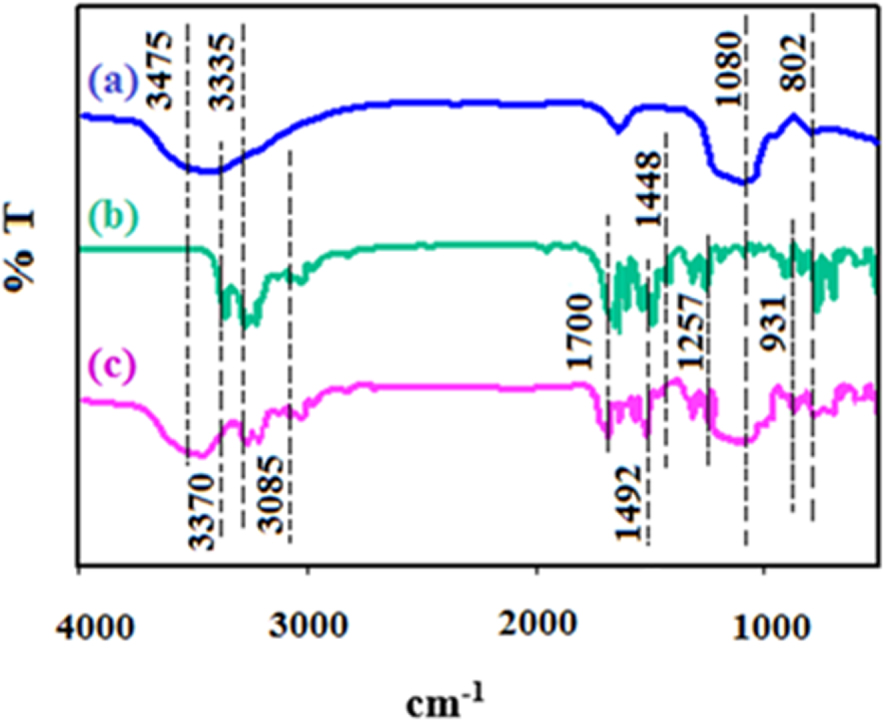
SEM images of reference sample SBA-15 (Rehman et al. 2017) (a), synthesized SBA-15 (b), and DPC-SBA-15 (c).
EDAX spectra of synthesized SBA-15 (a), DPC-SBA-15 (b), and Cd-DPC-SBA-15.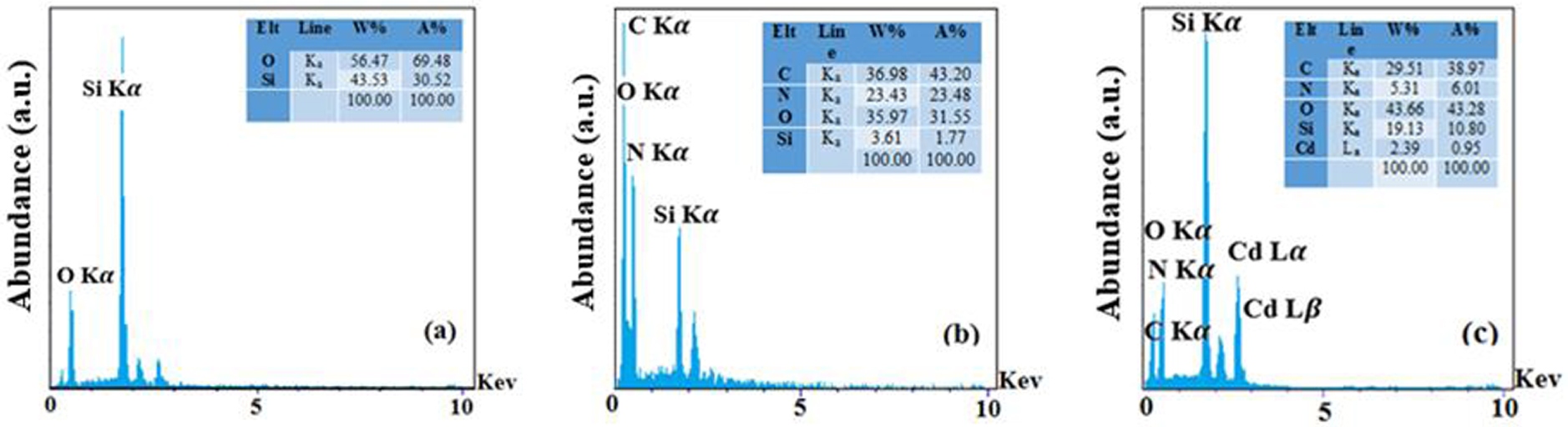
In addition, Fourier transform infrared (FTIR) spectra of the synthesized SBA-15 are recorded by an FTIR spectrophotometer (6300 Jasco, Japan) in the range of 350 −−4000 cm−1 (a resolution of 8 cm−1 and a scan number of 6) by using a KBr pellet (Figure 2a). The absorption bands at 802 and 1080 cm−1 are attributed to the symmetric and asymmetric oscillations of Si–O–Si, respectively. Similarly, the bands at 3475 and 3370 cm−1 correspond to the vibration of –OH. Silanol groups are also observed in the DPC-SBA-15 spectrum [57], which is depicted in Figure 2c. In the FTIR spectrum of DPC (Figure 2b), the absorption bands at 931 cm−1 and 1257 cm−1 are attributed to C–C ring breathing and N–H in-plane bending, respectively. The bands at 1448 and 1492 cm−1 are related to C–C vibrations in benzene, and the bands appearing at 1700 and 3085 cm−1 correspond to C =O and =C–H bonds, respectively. In addition, the band at 3335 cm−1 is related to N–H symmetric stretching [58, 59]. In the spectrum of DPC-SBA-15 (Figure 2c), absorption bands attributed to the Si–O–Si and –OH vibrations of silanol groups are observed, indicating that the ligand was grafted into the SBA-15 structure and that the functionalization procedure was performed properly (Figure 2c).
Surface area, pore volume, and pore diameter of SBA-15 and DPC-SBA-15 samples
| Adsorbent | BET surface area (m2∕g) | Pore volume (cm3∕g) | Pore diameter (nm) |
|---|---|---|---|
| SBA-15 | 907.65 | 1.44 | 3.22 |
| DPC-SBA-15 | 524.36 | 0.82 | 3.01 |
BET, Brunauer–Emmett–Teller.
Figure 3 displays the scanning electron microscopy (SEM) images of the reference SBA-15, synthesized SBA-15, and DPC-SBA-15 samples recorded by TESCAN MIRA3 LMU (Czech Republic). The parallel finger-like appearance of the particles of synthesized SBA-15 is approximately identical to that of the reference sample SBA-15. Due to the immobilization of DPC on the surface of SBA-15, the morphology of the DPC-SBA-15 sample becomes smoother and the thread-like structures are fastened to each other [60].
Furthermore, the energy-dispersive X-ray (EDAX) spectra of the synthesized SBA-15, DPC-SBA-15, and DPC-SBA-15 samples loaded with Cd recorded by TESCAN MIRA3 LMU (Czech Republic) are shown in Figure 4. In the spectrum of SBA-15, constituent elements are detected, including O and Si. The presence of carbon and nitrogen is detected in the spectrum of DPC-SBA-15 in addition to peaks related to O and Si, indicating that the ligand was grafted into the SBA-15 structure. Furthermore, the peaks correspond to O, Si, C, and N. The peak related to Cd is observed in the spectrum of DPC-SBA-15 loaded with Cd. Accordingly, the spectra show that the functionalization process was successfully performed and that the functionalized adsorbent adsorbed the target cation (Figure 4).
The thermal curves (thermogravimetric analysis–differential thermogravimetry [TG–DTG]) of the DPC-SBA-15 sample are recorded in nitrogen atmosphere and at 10 °C/min by a NETZSCH STA 409 PC/PG instrument in the range 25–800 °C (Figure 5). The observed weight loss at 25–110 °C is related to the dehydration of H2O molecules adsorbed on the surface of the samples. Moreover, the detected weight loss peak at 160–220 °C is attributed to the decomposition of the ligand [61].
TG–DTG curves of synthesized DPC-SBA-15.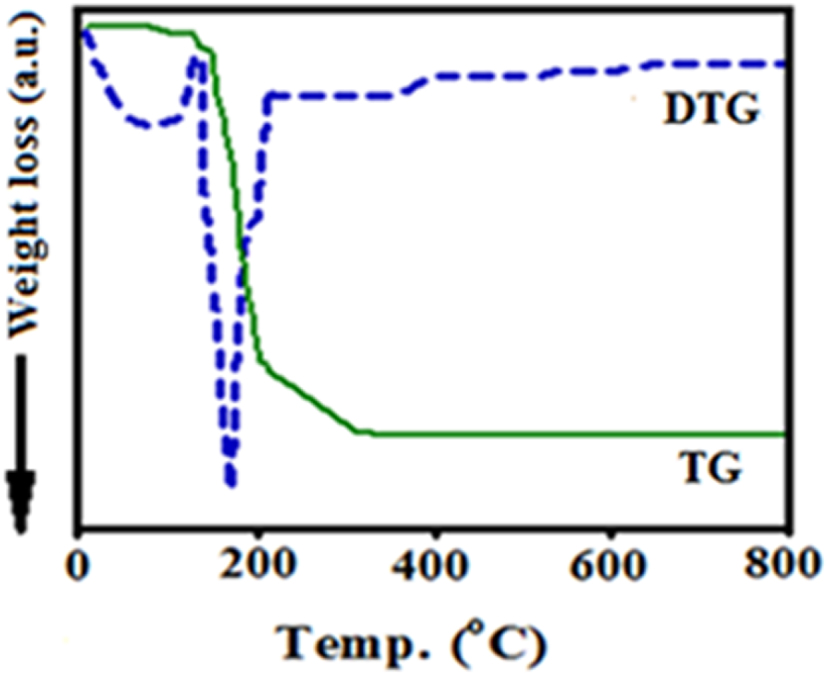
Nitrogen adsorption–desorption isotherms of SBA-15 (a) and DPC-SBA-15 (b). The inset shows the BJH pore size distribution.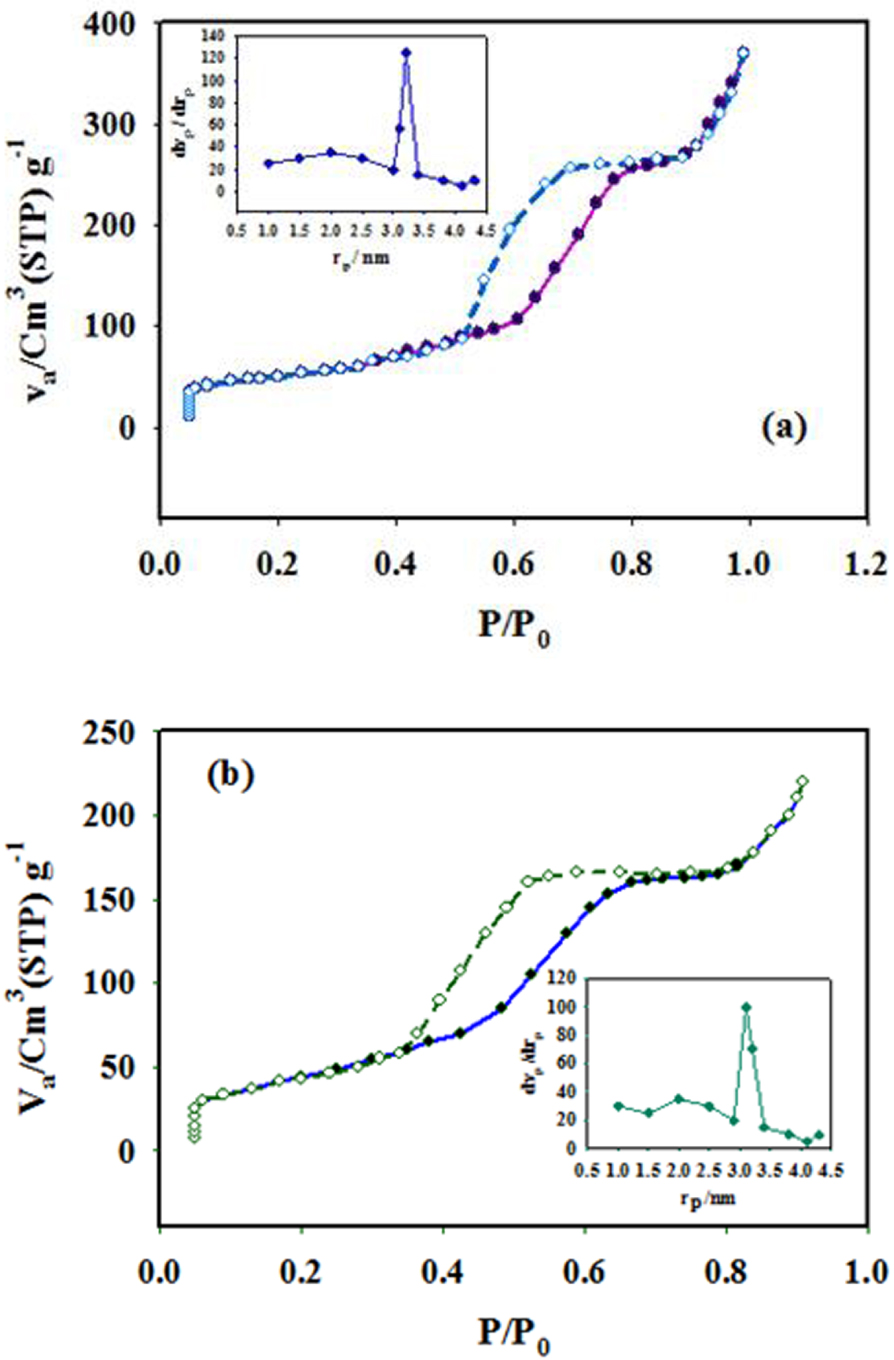
Analysis of variance for Cd(II) adsorption capacity (Q)
| Source | Sum of squares | df | Mean square | F-value | p-value | |
|---|---|---|---|---|---|---|
| Prob > F | ||||||
| Model | 49194.88 | 14 | 3513.92 | 2073.79 | <0.0001 | Significant |
| (A) pH | 2301.04 | 1 | 2301.04 | 1357.99 | <0.0001 | |
| (B) Adsorbent dose | 759.38 | 1 | 759.38 | 448.16 | <0.0001 | |
| (C) Initial Cd concentration | 27270.04 | 1 | 27270.04 | 16093.80 | <0.0001 | |
| (D) Time | 425.04 | 1 | 425.04 | 250.84 | <0.0001 | |
| AB | 3.06 | 1 | 3.06 | 1.81 | <0.1988 | |
| AC | 10.56 | 1 | 10.56 | 6.23 | <0.0247 | |
| AD | 1.56 | 1 | 1.56 | 0.92 | <0.3521 | |
| BC | 18.06 | 1 | 18.06 | 10.66 | <0.0052 | |
| BD | 0.063 | 1 | 0.063 | 0.037 | <0.8503 | |
| CD | 1.56 | 1 | 1.56 | 0.92 | <0.3521 | |
| A2 | 7308.00 | 1 | 7308.00 | 4312.92 | <0.0001 | |
| B2 | 2922.86 | 1 | 2922.86 | 1724.97 | <0.0001 | |
| C2 | 12470.86 | 1 | 12470.86 | 7359.85 | <0.0001 | |
| D2 | 1421.07 | 1 | 1421.07 | 838.67 | <0.0001 | |
| Residual | 25.42 | 15 | 1.69 | |||
| Lack of fit | 18.58 | 10 | 1.86 | 1.36 | <0.3864 | Not significant |
| Pure error | 6.83 | 5 | 1.37 | |||
| Total correction | 49220.30 | 29 | ||||
The N2 adsorption is recorded by PHS1020, and pretreatment is performed under N2 atmosphere at 150 °C in the relative pressure of 88 kPa. The resulting N2 adsorption–desorption isotherms are presented in Figure 6. These isotherms are identical to type IV isotherms, as defined by the International Union of Pure and Applied Chemistry, which is characteristic of mesoporous materials [62]. Based on the obtained data, the inflection position of SBA-15-DPC has slightly shifted to lower pressures, indicating that the pore size decreased after the grafting of DPC on the SBA-15 surface. Additionally, the distributions of the calculated pore from the Barrett–Joyner–Halenda (BJH) plot (inset of Figure 6) show that the diameter of DPC-SBA-15 pores is slightly smaller than that of the SBA-15 pores [63, 64]. Similarly, the specific surface area (524.36 m2∕g) and the pore volume (0.82 cm3∕g) of DPC-SBA-15 are smaller than those of SBA-15 (907.65 m2∕g and 1.44 cm3∕g). However, no significant changes are observed in the pore structure of SBA-15 when it is converted to DPC-SBA-15. This is highly advantageous for ingoing cations with regard to reaching adsorption sites (Table 2).
3.2. Statistical analysis
The analysis of variance (ANOVA) was employed to evaluate the interactions among important variables (Table 3). The data related to the influence of independent variables on the adsorption process were obtained from 30 runs of experiments (Table 4).
Central composite design experiment matrix and experimental results for Cd removal
| Std | Run | pH | Adsorbent dose (mg) | Initial concentration (mg/g) | Time (min) | Adsorbent (mg/g) |
|---|---|---|---|---|---|---|
| 22 | 1 | 5.00 | 4.00 | 45.00 | 20.00 | 61 |
| 23 | 2 | 5.00 | 4.00 | 25.00 | 10.00 | 6 |
| 26 | 3 | 5.00 | 4.00 | 25.00 | 20.00 | 159 |
| 18 | 4 | 9.00 | 4.00 | 25.00 | 20.00 | 129 |
| 2 | 5 | 7.00 | 2.50 | 15.00 | 15.00 | 129 |
| 9 | 6 | 3.00 | 2.50 | 15.00 | 25.00 | 89 |
| 21 | 7 | 5.00 | 4.00 | 5.00 | 20.00 | 80 |
| 30 | 8 | 5.00 | 4.00 | 25.00 | 20.00 | 113 |
| 7 | 9 | 3.00 | 5.50 | 35.00 | 15.00 | 145 |
| 20 | 10 | 5.00 | 7.00 | 25.00 | 20.00 | 159 |
| 12 | 11 | 7.00 | 5.50 | 15.00 | 25.00 | 60 |
| 4 | 12 | 7.00 | 5.50 | 15.00 | 15.00 | 137 |
| 5 | 13 | 3.00 | 2.50 | 35.00 | 15.00 | 150 |
| 14 | 14 | 7.00 | 2.50 | 35.00 | 25.00 | 158 |
| 25 | 15 | 5.00 | 4.00 | 25.00 | 20.00 | 75 |
| 3 | 16 | 3.00 | 5.50 | 15.00 | 15.00 | 138 |
| 6 | 17 | 7.00 | 2.50 | 35.00 | 15.00 | 159 |
| 8 | 18 | 7.00 | 5.50 | 35.00 | 15.00 | 157 |
| 28 | 19 | 5.00 | 4.00 | 25.00 | 20.00 | 160 |
| 17 | 20 | 1.00 | 4.00 | 25.00 | 20.00 | 77 |
| 24 | 21 | 5.00 | 4.00 | 25.00 | 30.00 | 126 |
| 16 | 22 | 7.00 | 5.50 | 35.00 | 25.00 | 53 |
| 27 | 23 | 5.00 | 4.00 | 25.00 | 20.00 | 107 |
| 29 | 24 | 5.00 | 4.00 | 25.00 | 20.00 | 137 |
| 10 | 25 | 7.00 | 2.50 | 15.00 | 25.00 | 69 |
| 13 | 26 | 3.00 | 2.50 | 35.00 | 25.00 | 61 |
| 1 | 27 | 3.00 | 2.50 | 15.00 | 15.00 | 6 |
| 19 | 28 | 5.00 | 1.00 | 25.00 | 20.00 | 159 |
| 15 | 29 | 3.00 | 5.50 | 35.00 | 25.00 | 129 |
| 11 | 30 | 3.00 | 5.50 | 15.00 | 25.00 | 129 |
Optimum conditions derived by RSM design for Cd(II) removal by DPC-SBA-15
| Optimum conditions | Adsorption capacity (mg/g) | ||||||
|---|---|---|---|---|---|---|---|
| Ion | Adsorbent dose (mg) | pH | Ion concentration (mg/L) | Contact time (min) | Qp | Qe | |
| Cd(II) | 4.55 | 5.75 | 25.39 | 21.50 | 162.832 | 160 | |
In addition, the R2 value is used to study the quality of the polynomial equation, and the statistical significance of the model is evaluated by the F-test. Small p-values (<0.0001) indicate that the model is significant and thus can be used for distinguishing statistically significant parameters. The calculated p-values smaller than 0.05 indicate that the results are predicted at a 5% confidence interval. The lack of fit (LOF) is an important parameter that is related to pure error [65, 66, 67]. In the present study, the LOF value of 1.36 for Cd indicates that the model is suitable for predicting adsorbent performance (Table 3).
The second-order polynomial equation shown in (3) is developed using experimental data, and statistically insignificant coefficients (p-values greater than 0.1) are excluded from calculations [65]. The results (Table 3) reveal that A, B, C, D, AC, BC, A2, B2, C2, and D2 are significant model terms.
Furthermore, the quadratic equation is employed to find the optimum value. The empirical equations between adsorption capacity and input factors in the coded terms are substituted in (6), which is followed by excluding insignificant coefficients (p-values greater than 0.1) according to [68, 69].
| (6) |
The plot of actual Q versus predicted Q values for Cd.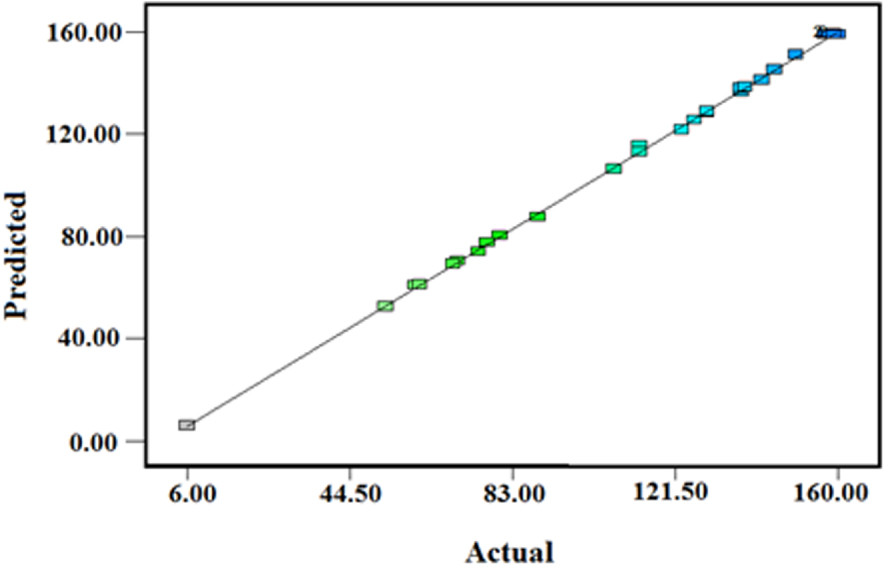
3.3. Response surface plots
Graphical plots are used to evaluate the interactions among the studied variables and to obtain the optimum effect of each variable for the maximal adsorption uptake [40]. Figure 8 displays the plots depicting the adsorption of Cd versus pH, adsorbent dose, and the initial concentration.
Response surface plot for Cd removal. (a) Interaction of pH and initial concentration, (b) interaction of adsorbent dosage and initial concentration.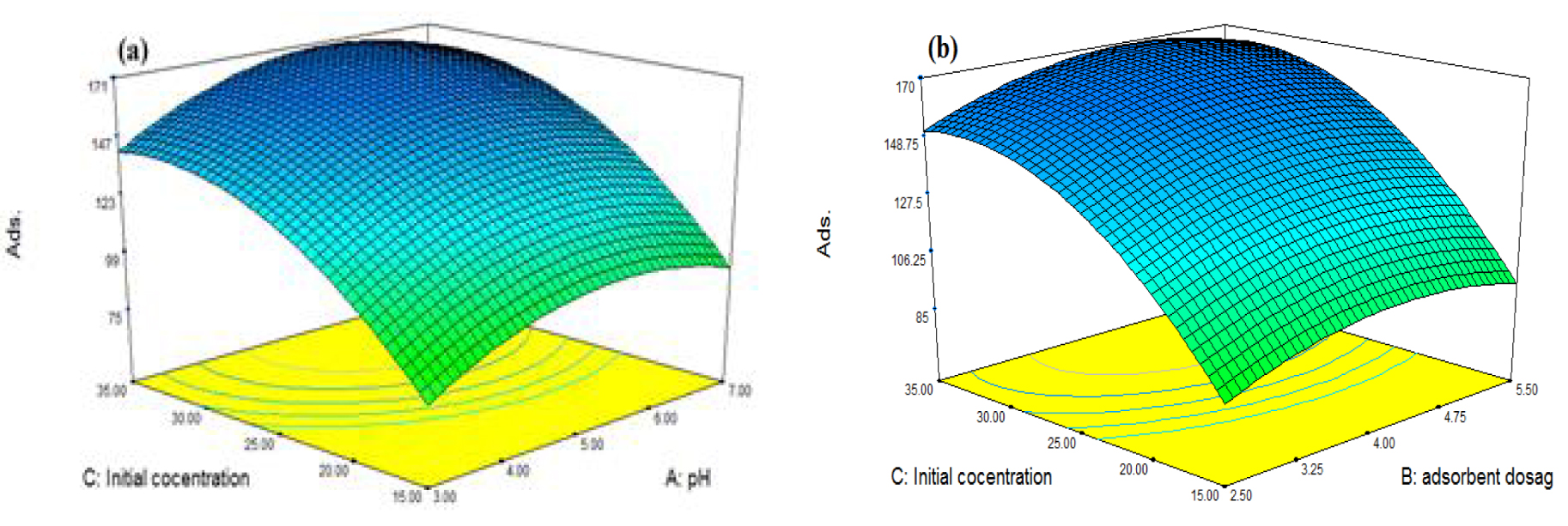
(A) Typical curve for the estimation of the pHpzc of DPC-SBA-15. (B) Schematic diagram showing Cd2+ removal by the DPC-SBA-15 adsorbent.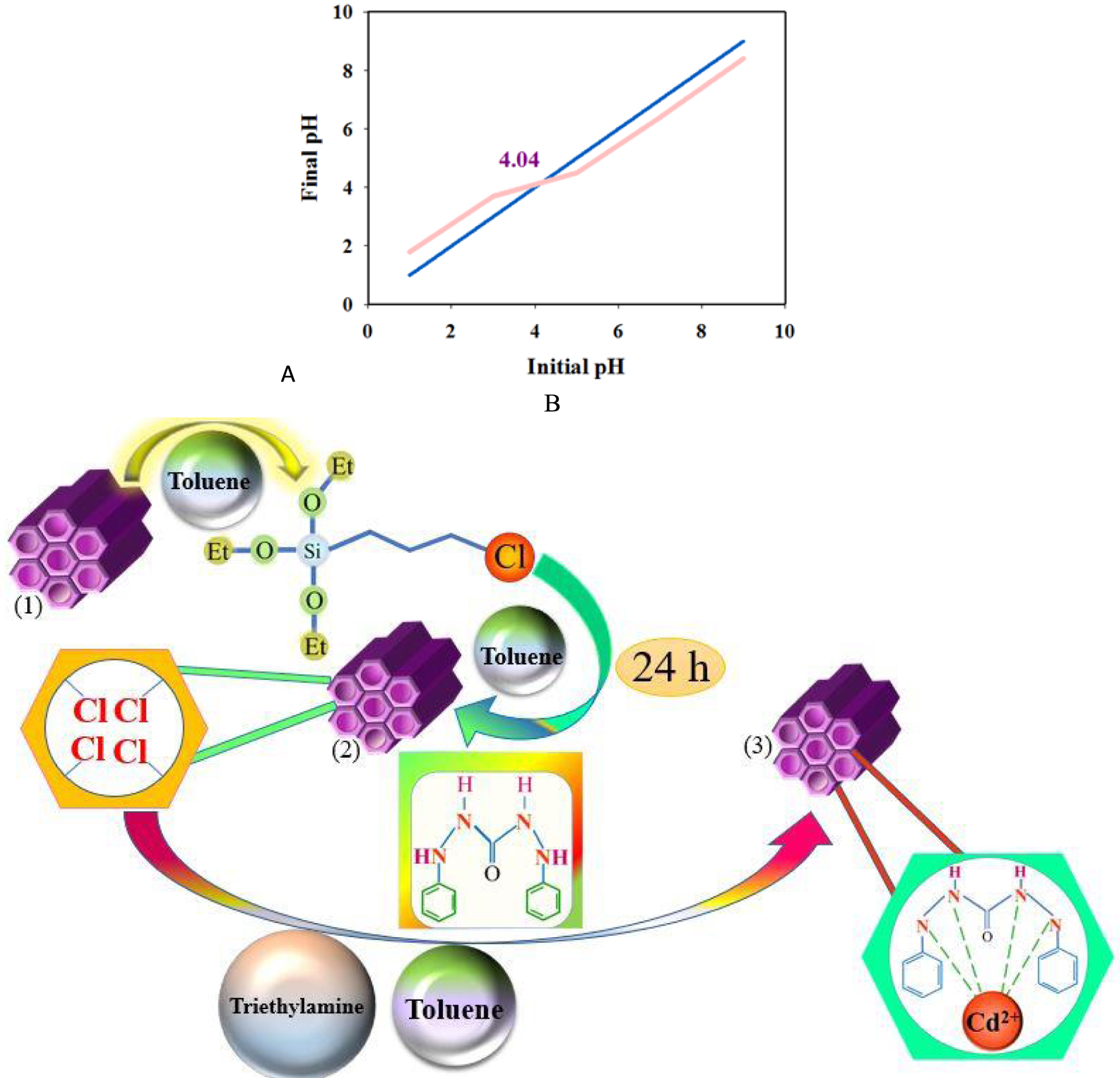
Figure 8a shows the influence of pH and concentration on Cd adsorption in the pH range of 3–7. The sorption capacity of Cd increases up to a pH of 5.75 and then remains nearly constant until a pH of 7. In addition, the measured value of pHpzc indicates that the sorbent surface charge is zero at pH = 4.04 (Figure 9). However, the surface charge is positive at a pH of <4.04, and the uptake of cations is limited because of the repulsion of cations by the positive surface of the adsorbent and the high concentration of H3O+. At pH values higher than the pHpzc, the adsorbent surface charge becomes negative and adsorption gradually increases. Nonetheless, no increase is observed at pH > 6, which is attributed to the partial conversion of Cd2+ to Cd(OH)2 [72]. This is in line with the results obtained by the software (Table 5).
By increasing the initial concentration, the extent of the adsorbed Cd increases and reaches a constant quantity at higher concentrations. This increase is ascribed to the driving force that is created at higher concentrations between adsorption sites and the ingoing cation. Nevertheless, the increase stops at certain concentrations and a steady state is developed, which can be justified by a higher ratio of Cd ions to active sites. The software results (Table 5) perfectly corroborate this conclusion. Finally, the maximal sorption capacity is obtained at 25.39 mg/L of Cd [73].
Figure 8b depicts data on the effect of Cd concentration and sorbent dose. The increase in the uptake of Cd with increasing concentration and sorbent dose is attributed to higher available sorption sites and a higher number of Cd ions. Furthermore, the maximal uptake is observed at 25.39 mg/L of Cd (Table 5). Based on the results, the uptake of Cd increases and then reaches a constant amount with increasing sorbent dose. This increase is ascribed to higher vacant sorption sites although the concentration of the Cd ion is insufficient to engage all adsorption sites with further increase in the amount of the adsorbent. Therefore, the optimized value is obtained with an adsorbent dose of 4.55 mg (Table 5). According to [74], the sorption capacity can be calculated by (4). The typical mechanism for removing Cd2+ cations is shown in Figure 9B.
3.4. Sorption kinetics
The kinetics of the process is studied by a series of experiments performed in the time interval of 0–25 min at 298 K (Figure 10). Equilibrium is attained in 21.50 min, indicating that the process is relatively fast. Then, the data are evaluated by pseudo-first-order and pseudo-second-order kinetic models, respectively, using (7) and (8).
| (7) |
| (8) |
Kinetic parameters of pseudo-first-order and pseudo-second-order
| Kinetic models | Parameters | DPC-SBA-15 |
|---|---|---|
| Pseudo-first-order | (qe)p (mg∕g) | 140.58 |
| k1 (g/mg/min) | 0.3262 | |
| R2 | 0.9583 | |
| Pseudo-second-order | (qe)p (mg∕g) | 161.40 |
| k2 (min−1) | 0.00036 | |
| R2 | 0.9964 | |
Effect of contact time and adsorption kinetics on Cd uptake by DPC-SBA-15. The inset shows the linear plot of (5).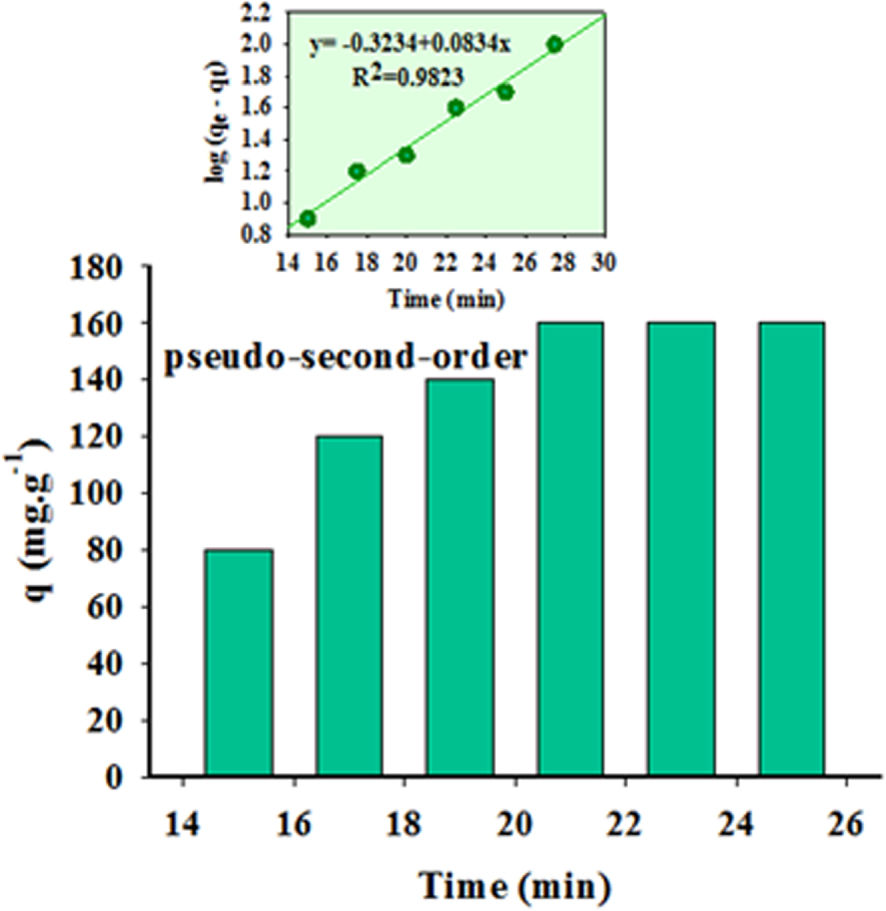
3.5. Equilibrium sorption isotherms
The experimental data are analyzed by Langmuir, Freundlich [77], and D–R models. In the Langmuir isotherm, it is assumed that monolayer sorption occurs and the sorbent surface has a finite number of sorption sites with uniform energy [78], which is computed by (9).
| (9) |
Langmuir adsorption isotherms for Cd.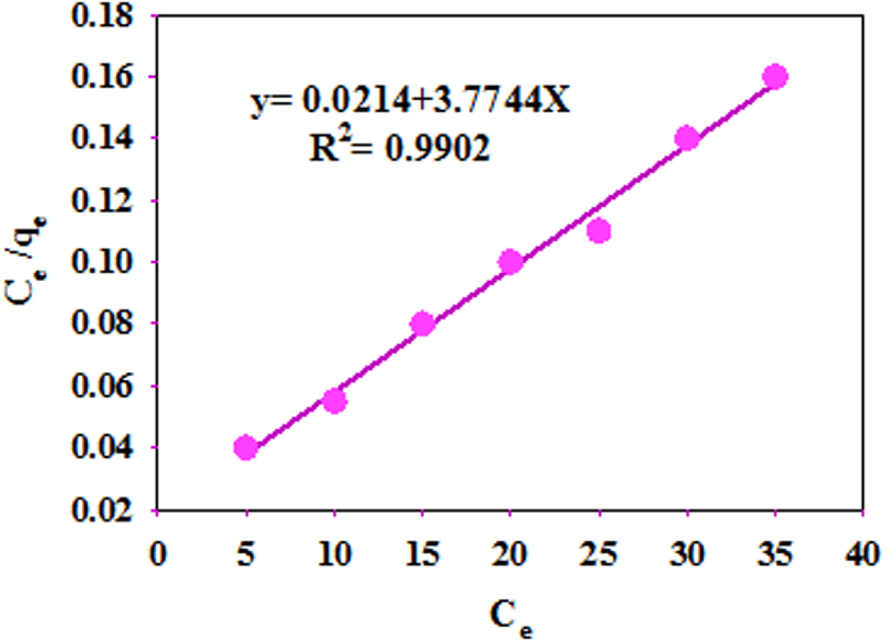
The parameter RL is a dimensionless constant and is determined according to (10):
| (10) |
In the Freundlich isotherm, it is assumed that the sorption of cation occurs on the heterogeneous surface and is commonly represented by (11):
| (11) |
In the D–R model, it is postulated that first the species binds with the most energetical sites and multilayer sorption takes place accordingly. Furthermore, the model describes the sorption on homogeneous and heterogeneous surfaces in low concentration ranges, and the data of this model are used to determine the physical and chemical adsorption of the process. The D–R model is defined according to (12):
| (12) |
| (13) |
| (14) |
As presented in Table 7, the data corroborate the results of the Langmuir model, showing monolayer sorption on a homogeneous surface with no interaction between Cd ions [78].
Parameters for the Langmuir, Freundlich, and Dubini–Radushkevich isotherms
| Isotherm models | Parameters | Cd(II) |
|---|---|---|
| Langmuir | qm (mg∕g) | 130 |
| RL | 0.0471 | |
| b (L∕mg) | 0.0063 | |
| R2 | 0.9902 | |
| Freundlich | Kf (L∕mg) | 36.4325 |
| R2 | 0.9782 | |
| n | 1.739 | |
| Dubinin–Radushkevich | 𝛽 (mol2∕K1⋅J2) | 0.2504 |
| qm (mg∕g) | 23 | |
| R2 | 0.9722 | |
| E | 11.38 | |
Thermodynamic parameters of Cd(II) adsorption by DPC-SBA-15
| Cation | T (K) | 𝛥G0 (kJ∕mol) | 𝛥H0 (kJ∕mol) | 𝛥S0 (kJ∕mol⋅K) | R2 |
|---|---|---|---|---|---|
| Cd(II) | 298 | 23.57 | − 0.036 | − 0.064 | 0.9427 |
Effect of eluents on desorption recovery for metal ions adsorbed on DPC-SBA-15
| Eluent | C (M) | Recovery (%) (n = 3) |
|---|---|---|
| HNO3 | 0.1 | 92 ± 1 |
| 0.2 | 94 ± 1 | |
| 0.3 | 94 ± 1 | |
| HCl | 0.1 | 84 ± 2 |
| 0.2 | 86 ± 2 | |
| 0.3 | 86 ± 2 | |
Effect of potentially interfering ions on Cd(II) removal
| Interfering ion | Cion (mg∕L) | q-Error (%) | Interfering ion | Cion (mg∕L) | q-Error (%) |
|---|---|---|---|---|---|
| Na+ | 0 | — | Zn2+ | 0 | — |
| 5 | − 2.24 | 5 | − 3.02 | ||
| 10 | − 4.11 | 10 | − 4.57 | ||
| 15 | − 8.30 | 15 | − 9.60 | ||
| 20 | − 12.25 | 20 | − 14.02 | ||
| 40 | − 19.48 | 40 | − 19.25 | ||
| 100 | − 28.18 | 100 | − 22.71 | ||
| Co2+ | 0 | — | Mg2+ | 0 | — |
| 5 | − 3.25 | 5 | − 3.68 | ||
| 10 | − 4.70 | 10 | − 4.41 | ||
| 15 | − 7.03 | 15 | − 9.27 | ||
| 20 | − 10.25 | 20 | − 14.45 | ||
| 40 | − 16.37 | 40 | − 18.90 | ||
| 100 | − 22.12 | 100 | − 23.41 | ||
| Mn2+ | 0 | — | Ba2+ | 0 | — |
| 5 | − 3.17 | 5 | − 3.11 | ||
| 10 | − 4.10 | 10 | − 4.10 | ||
| 15 | − 10.71 | 15 | − 7.33 | ||
| 20 | − 18.09 | 20 | − 9.68 | ||
| 40 | − 23.41 | 40 | − 14.44 | ||
| 100 | − 35.53 | 100 | − 18.72 | ||
| Ca2+ | 0 | — | Pb2+ | 0 | — |
| 5 | − 3.19 | 5 | − 4.56 | ||
| 10 | − 4.28 | 10 | − 6.87 | ||
| 15 | − 6.44 | 15 | − 12.78 | ||
| 20 | − 14.37 | 20 | − 19.31 | ||
| 40 | − 20.21 | 40 | − 26.51 | ||
| 100 | − 29.57 | 100 | − 37.37 | ||
3.6. Thermodynamics of the process
To determine the spontaneity of the process, the calculation of thermodynamic parameters is necessary. Equations (15) and (16) are used in this regard.
| (15) |
| (16) |
Determination of toxic metals in real samples
| Sample | Spiked (μg∕L) | Found (μg∕L) | Recovery (%) |
|---|---|---|---|
| Tap water | 0 | Not detected | — |
| 20 | 19.41 | 96.25 | |
| River water | 0 | Not detected | — |
| 20 | 18.90 | 97.30 | |
| Mineral water | 0 | Not detected | — |
| 20 | 19.37 | 95.02 | |
| Water and | 0 | Not detected | — |
| wastewater | 20 | 19.32 | 95.26 |
In addition, negative 𝛥S0 indicates lower randomness of the adsorbed species on the surface of sorbents, arising from strong bonds formed between cations and adsorption sites. Negative 𝛥H0 and positive 𝛥G0 represent the exothermic nature of the process and the nonspontaneous sorption of the cations, respectively. It is reported that the value of thermodynamic parameters is closely related to the type of sorbent, ingoing species, and the type of bonds formed between the adsorbate and the adsorbent surfaces [80, 81, 82, 83].
3.7. Regeneration of the used adsorbent
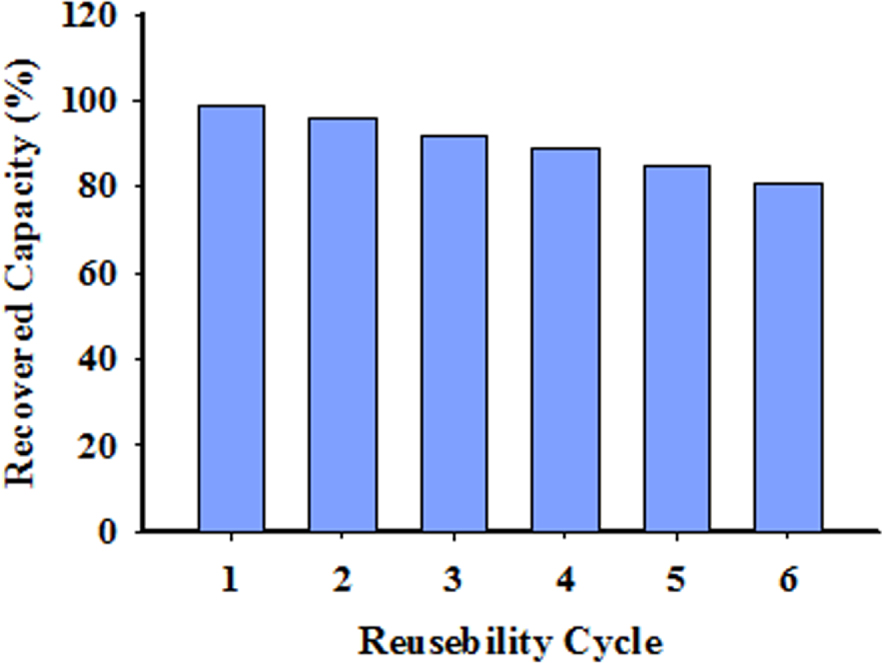
The study of the regeneration performance of a sorbent determines its potential for repeated applications in wastewater treatment processes. Acidic solutions are typically used for the regeneration of sorbents impregnated with cations. In the present study, Cd is eluted by different acids. The results show that HNO3 is the most effective solution. After adsorption of cations, the adsorbent is separated by filtration; then, the solid is dried at 60 °C and regenerated by the evaluated acids. Next, the regenerated sorbent is used for removing the Cd at optimized conditions (4.55 mg adsorbent dose, a pH of 5.75, an ion concentration of 25.39 mg/L, and a contact time of 21.50 min). Based on the data in Table 9, HNO3 (0.2 M) is the most effective reagent for sorbent regeneration.
After the elution of Cd, the XRD test results reveal that the regenerated sorbent retains its initial form without any significant deterioration. In the first adsorption cycle, the adsorption capacity is 160 mg/g, whereas it decreases to 149 mg/g after six cycles. The related data are displayed in Figure 12 [84].
3.8. Selectivity of sorbent
According to their complexation ability, charge density, and hydration degree, the coexisting cations may nearly compete with Cd for adsorption on the surface of DPC-SBA-15. Therefore, this study investigates the potential interfering effect of commonly competing cations. Among the studied cations (Na, Ca, Mg, Ba, Zn, Co, Mn, and Pb), the highest interference effect is exhibited by Pb2+ (Table 10), which can be attributed to the similarity of the radius of its cation to that of Cd. Nonetheless, the interference effect is lower for the remaining cations [85]. To examine the sorbent performance in real samples, the sorbent is used for removing Cd from some real samples. Then, the adsorbent capability is tested on solutions spiked with an intended amount of Cd (Table 11). The results indicate that the recovery is 95%, which is satisfactory [86].
4. Conclusion
Regarding the statistical analysis conducted by Design-Expert 7.0.0 software, Cd adsorption by synthesized DPC-SBA-15 relies on several parameters such as pH, adsorbent dose, initial concentration, and contact time. The results show that a pH of 5.75, an adsorbent dose of 4.55 mg, a Cd concentration of 25.39 mg/L, and an adsorption capacity of 160 mg/g are obtained at optimized conditions. In addition, adsorption by DPC-SBA-15 is a good fit to the pseudo-second-order kinetic model. Furthermore, the experimental data best fit the Langmuir isotherm model, indicating monolayer adsorption on a homogeneous surface. The regenerated sorbent is used for six consecutive cycles, and most of its initial capacity is retained. Finally, the interference of many coexisting cations on Cd removal is negligible in real samples.



 CC-BY 4.0
CC-BY 4.0