1 Introduction
The use of metal ions to control the assembly of organic structural components into supramolecular assemblies is a well-established methodology that has allowed access to a wide range of novel architectures. By a programmed matching of the coordination number and geometry of metal ions with the number and spatial arrangement of donor atoms within ligands, it has been possible to prepare topologically and topographically novel species such as double helicates, triple helicates, catenates, knots, grids, racks and ladders 〚1〛. Although initial studies were concerned with establishing the algorithms and ensuring a precision of the matching of the properties of the metal and ligand components, more recent attention has centred upon fuzzy systems in which ambiguities in the algorithm allow the preparation of static or dynamic libraries of compounds 〚2–8〛.
Although the basic algorithms are frequently described, it is a truism that many systems do not behave in the ways initially predicted. In this paper, we report studies that investigate the influence of structural changes within components which should have no effect upon the self-assembly process but which turn out to have profound and unexpected effects.
The first example of a molecular grid was a 〚2 × 2〛 species reported by Osborn and co-workers as the product obtained from the reaction of a copper(I) salt with 3,6-bis(2-pyridyl)pyridazine (dppz) 〚9〛 (Fig. 1). Subsequently, Lehn and Baxter used expanded analogues of dppz for the preparation of a family of 〚n × n〛 grids 〚10–15〛. An analysis of the algorithms for the assembly of the 〚2 × 2〛 grid from dppz is instructive. The ligand presents two didentate N2 domains which can only bind separate metal centres, as opposed to the same metal, and the copper(I) centre has a preferred tetrahedral coordination geometry which results in the orthogonal alignment of two dppz ligands at each metal centre. If a discrete molecular species is to be formed, as opposed to a polymeric compound, the algorithms lead to the observed 〚2 × 2〛 grid in which each metal centre is four-coordinate and bonded to a didentate domain of two different dppz ligands. In this paper, we investigate the effect of replacing dppz by the closely related ligand 3,6-bis(2-pyridyl)-1,2,4,5-tetrazine (dptz) upon the assembly of metallosupramolecular structures (Fig. 1).
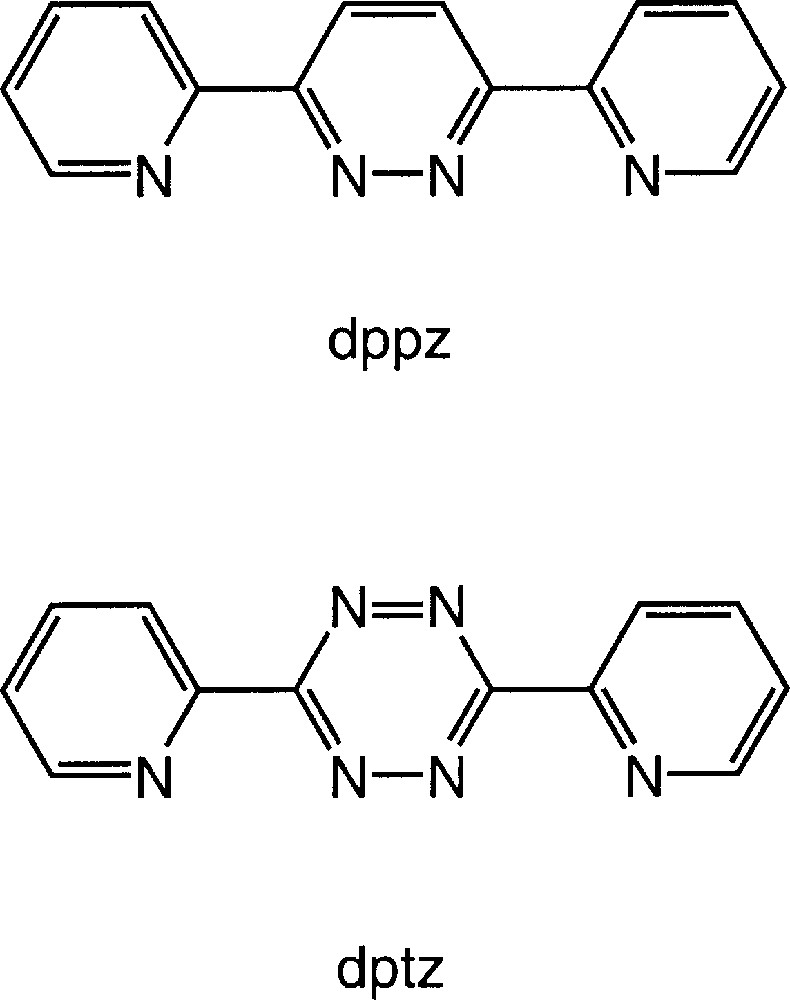
Structures of dppz and dptz.
2 Results and discussion
2.1 The ligand 3,6-bis(2-pyridyl)-1,2,4,5-tetrazine dptz
Ligand dptz could adopt a number of bonding modes as shown in Fig. 2. Prior to our work, examples of a mononucleating-bonding mode had been reported but not structurally characterised 〚16〛, and all structurally characterised species exhibited the bridging transoid mode 〚17–22〛, although some of these species are best formulated as containing ligand radicals. All of the examples of the bridging mode are found in discrete species containing either dinuclear moieties or self-assembled tetranuclear or pentanuclear complexes.
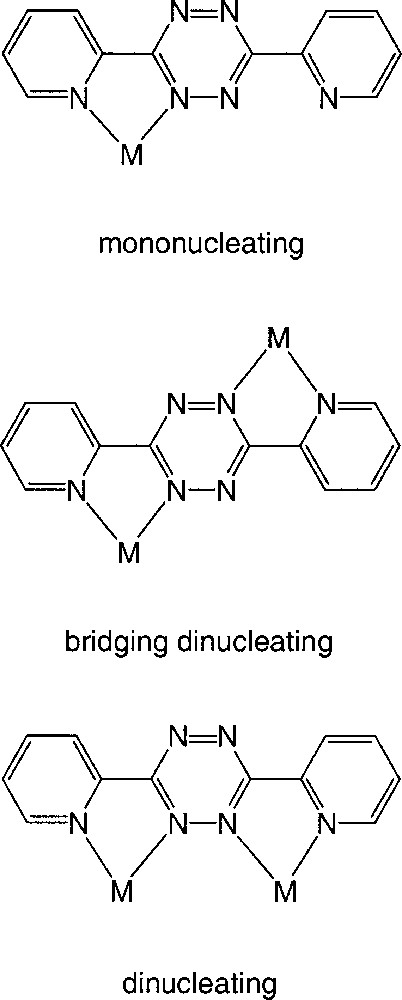
Possible bonding modes for the dptz ligand.
2.2 Silver(I) complexes of dptz
The coordination chemistry of copper(I) and silver(I) generally resemble one another, with a tendency to form complexes with low coordination numbers (usually two, three or four). The d10 electron configuration means that there is no ligand-field imposed influence upon the coordination geometry, and that the observed geometries are close to that predicted by VSEPR models. Neutral ligands which are not sterically demanding generally lead to tetrahedral complexes, as is seen in the widespread use of copper(I) centres for the self-assembly of two 2,2’-bipyridine (bpy) or 1,10-phenanthroline (phen) metal-binding motifs in a range of topologically novel supramolecular chemistry 〚23, 24〛. Silver(I) complexes with two simple bpy or phen ligands follow a similar pattern, although as a detailed analysis of the copper(I) complexes shows, the cations never exhibit a perfectly orthogonal arrangement in the solid state; in the case of silver(I) complexes, interplanar angles between the two ligands lie in the range 57.86–75.52° 〚25–29〛. On the basis of this, we anticipated the formation of a tetranuclear 〚2 × 2〛 grid from the reaction of dptz (Fig. 3).
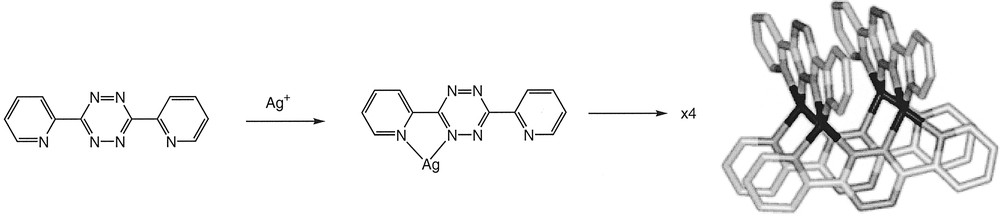
Schematic showing the assembly of the tetranuclear 〚2 × 2〛 grid expected from the reaction of dptz with silver(I).
The reaction of purple dptz with equimolar amounts of AgBF4, AgNO3 or Ag(CF3SO3) in acetonitrile or nitromethane solution gave pink–purple solutions from which purple solids could be obtained upon evaporation of the solvent 〚30〛. Recrystallisation of the triflate salt from acetonitrile by the diffusion of diethyl ether vapour into the solution gave well-formed purple crystals of 1:1 stoichiometry. We initially believed these compounds to be the expected 〚2 × 2〛 grids. The 1H NMR spectra of solutions of the various silver salts were identical in a range of solvents and differed from those of the free ligand. Furthermore, the 1H NMR spectrum of a CD3CN solution of equimolar amounts of Ag(CF3SO3) and dptz was identical to that of the isolated purple solids and exhibited a single pyridine environment indicating that, on the NMR time-scale, a highly symmetrical solution species was present. However, the 1H NMR spectrum of CD3CN solutions of a 1:2 mixture of silver(I) salt and dptz was also identical to that of the isolated silver complex or the 1:1 mixture, leading us to the conclusion that the dominant solution species is 〚Ag(dptz)2〛+. No species other than dptz and the symmetrical silver complex were detected by 1H NMR spectroscopy.
Solutions of the complexes in methanol exhibited highest mass peaks assigned to 〚Ag(dptz)2〛+ in their electrospray mass spectra, whilst acetonitrile solutions of the triflate or tetrafluoroborate exhibited in addition to these peaks, a new cluster of ions exhibiting the correct isotopomer distributions for {Ag2(dptz)2(CF3SO3)}+ (m/z 837) and {Ag2(dptz)2(BF4)}+ (m/z 775) species. No evidence was found by ES MS or FAB MS for tetranuclear species.
2.3 Solid-state structure of the 1:1 silver(I):dptz complex
The above data for the reaction at 1:1 stoichiometry support a dynamic system in which the dominant solution species is 〚Ag(dptz)2〛+, but suggest that 〚Ag2(dptz)2}2+ might be present in MeCN. To confirm this, we have determined the crystal structure of the triflate salt. The structural determination confirmed the overall 1:1 stoichiometry of the crystalline material and established the formation 〚Ag2(dptz)2〛(CF3SO3)2 in the solid state. The structure of the 〚Ag2(dptz)2〛2+ cation is presented in Fig. 4 and relevant structural data in Table 1; the dication is near planar with each silver coordinated to a didentate domain of each of two ligands. The Ag2N4 ring is close to planar with all atoms lying within ±0.009(8) Å of the mean plane. Three of the Ag–N bonds are typical (Ag1–N9, 2.403(9) Å; Ag1–N2 2.417(7) Å; Ag1–N6B 2.323(9) Å) with the remaining Ag1–N3B contact being significantly longer (2.552(8) Å). The coordination geometry is irregular with bite angles for the bpy domains of 70.5(3) and 70.9(3)°. The sum of Ag–N bond angles about the silver is 701.4° and the geometry about the silver is distorted planar. There are longer non-bonding contacts with the oxygen atoms of the triflate counter-ions lying above the dinuclear units (Ag1–O3, 2.969(8) Å; Ag1–O1, 2.806(9) Å) and which preclude any intercation silver–silver interactions and the shortest such distance is 5.430 Å. There is extensive π-stacking within the lattice, involving the terminal pyridine rings of ligands in adjacent sheets, which are coplanar with centroid-to-centroid distances ≈ 3.5 Å (Fig. 5).
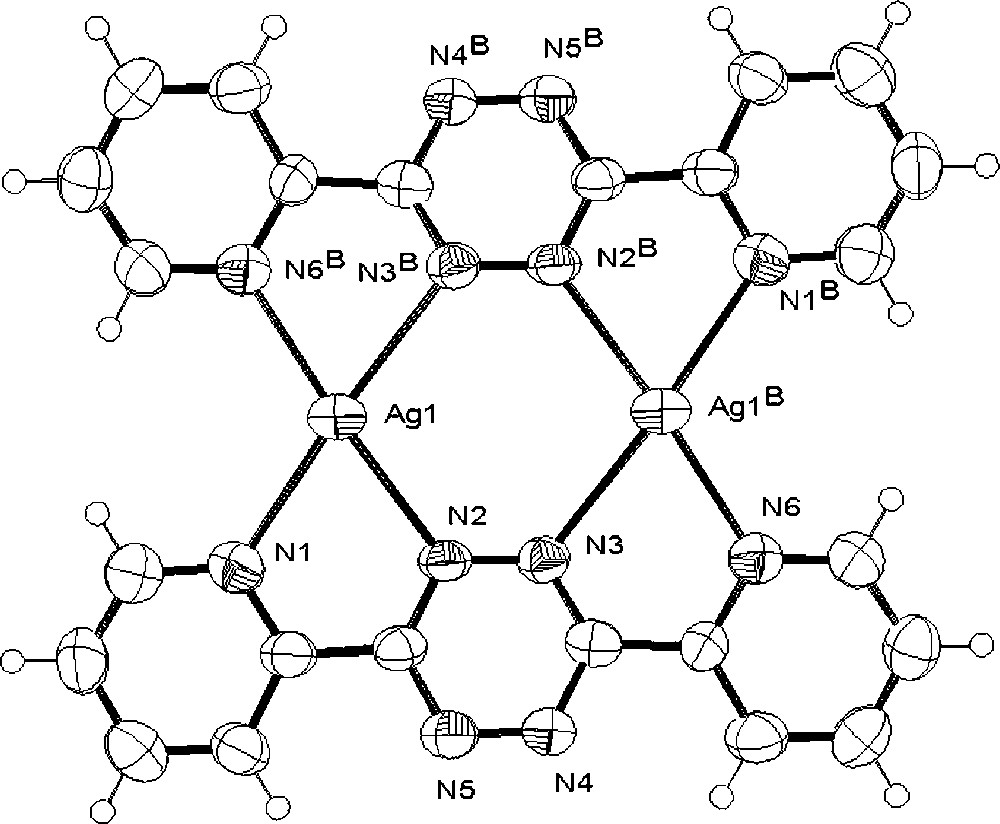
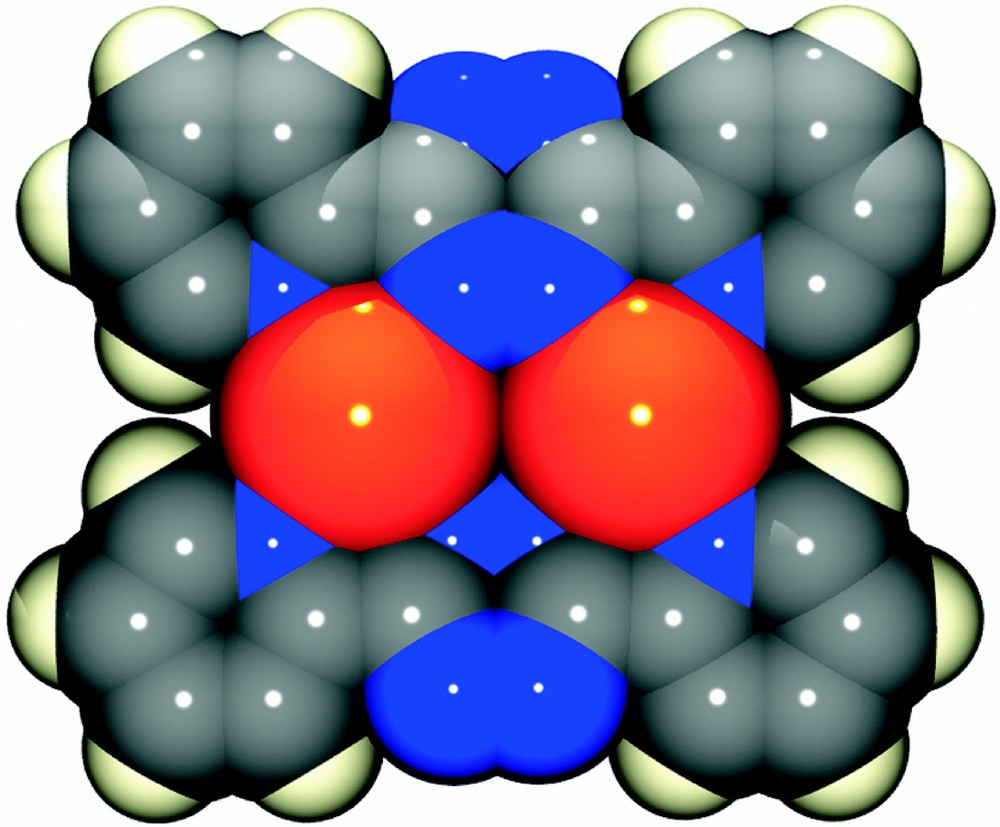
a. The solid-state structure of the 〚Ag2(dptz)2〛2+ cation present in 〚Ag2(dptz)2〛〚CF3SO3〛2, showing the numbering scheme adopted. b. A space filling representation of the same cation.
Selected bond lengths (Å) and angles (°) of 〚Ag2(dptz)2〛〚CF3SO3〛2.
| Ag1–N1 | 2.403(9) |
| Ag1–N2 | 2.417(7) |
| Ag1–N3a | 2.552(8) |
| Ag1–N6a | 2.323(9) |
| N2–Ag1–N3a | 106.3(2) |
| N2–Ag1–N6a | 169.9(3) |
| N3a–Ag1–N6a | 70.9(3) |
| N1–Ag1–N3a | 169.9(3) |
| N1–Ag1–N6a | 113.9(3) |
| N1–Ag1–N2 | 70.5(3) |
A view of 〚Ag2(dptz)2〛〚CF3SO3〛2 showing the extensive π-stacking in the lattice and the role played by the counter-ions in preventing short silver-silver contacts. Hydrogen atoms have been omitted for clarity.
It is useful to compare this complex with related four-coordinate silver(I) complexes. The planarity is usefully represented by the sum Σ of the six inter-bond angles for a four coordinate complex – for a planar complex Σ = 720°, for tetrahedral Σ = 657°, etc. A search of the Cambridge Crystallographic Data Centre yielded a total of 166 four-coordinate silver centres with four nitrogen donors (macrocyclic ligands in which a planar geometry was imposed were omitted). The mean and median values of Σ are 661.8 and 662.7°, indicating that the original assumption of a near tetrahedral geometry for silver(I) is valid. These data are presented in Fig. 6, which shows a plot of the frequency of occurrence against Σ for four-coordinate silver complexes. Two polymeric species containing approximately square-planar silver centres with Σ over 700° are known 〚31, 32〛. The dptz ligand imposes the extremely unusual near-planar geometry upon the silver centre.
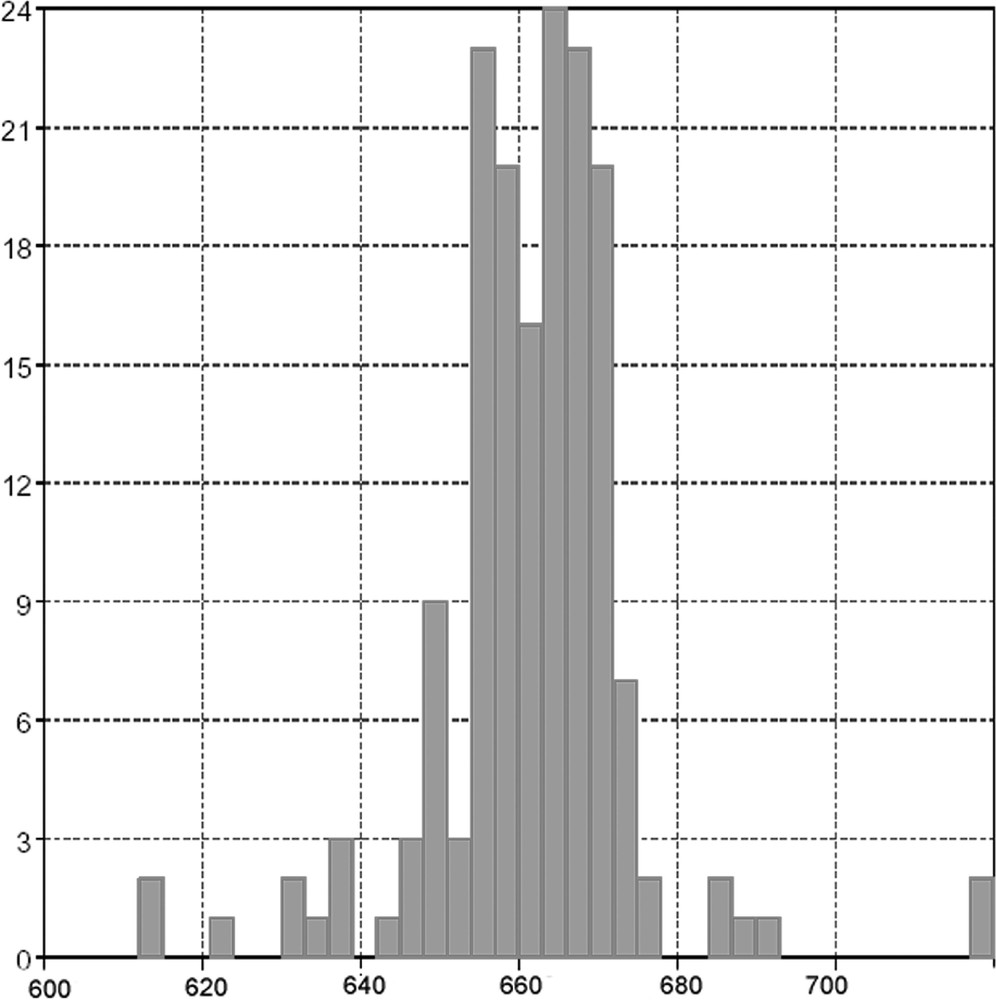
A plot showing the sum of all Ag–N bond angles for all four-coordinate silver(I) compounds in the Cambridge Crystallographic Data Base. Compounds with planar macrocyclic ligands that impose an N4 donor set have been omitted. The mean and median values of Σ are 661.8 and 662.7° indicating that the original assumption of a near tetrahedral geometry (Σ = 657°) for silver(I) is valid.
2.4 Solid-state structure of the 1:1 silver(I):dptz complex
The reaction of silver(I) tetrafluoroborate with one equivalent of dptz in nitromethane resulted in a purple pink solution with an 1H NMR spectrum identical to that of the 2:2 complex discussed above. Microanalysis of the isolated solid species indicated a 1:2 ag:dptz stoichiometry. We expected the 1:2 complex to be a discrete molecular species with an {Ag(bpy)2} coordination motif. The crystal structure analysis revealed that the complex was more complicated and more interesting. Firstly, the silver is best described as six-coordinate and coordinated to a didentate domain from each of three dptz ligands (Fig. 7). Relevant structural data are presented in Table 2. One of the dptz ligands is coordinated to a single silver and exhibits long Ag–N bonds (Ag1–N1, 2.516(15) Å; Ag1–N2 2.559(13) Å) with the remaining didentate domain non-coordinated and with a trans arrangement of the free terminal pyridyl ring with respect to the coordinated pyridyl. The two remaining dptz ligands act in a bridging mode with each presenting a very asymmetric didentate domain to the silver with one short (Ag1–N9, 2.387(12) Å; Ag1–N7 2.322(15) Å) and one very long (Ag1–N10, 2.622(14) Å; Ag1–N8 2.691(13) Å) contact. The silver is in a unique environment that possesses none of the symmetry found in the small number of other six-coordinate silver(I) complexes with pyridine-type donors 〚33–35〛. There are no short contacts between the counter-ions and the cations.

Part of the solid-state structure of the 〚{Ag(dptz-N,N’)(μ-dptz)}n〛〚BF4〛n, showing the coordination about silver and the numbering scheme adopted.
Selected bond lengths (Å) and angles (°) of 〚{Ag(dptz-N,Nˈ)(μ-dptz)}n〛〚BF4〛n.
| Ag1–N9 | 2.388(12) |
| Ag1–N10 | 2.623(13) |
| Ag1–N2 | 2.558(13) |
| Ag1–N7 | 2.322(15) |
| Ag1–N1 | 2.515(14) |
| N9–Ag1–N10 | 65.5(4) |
| N1–Ag1–N9 | 119.4(5) |
| N1–Ag1–N10 | 85.2(4) |
| N2–Ag1–N7 | 120.5(5) |
| N2–Ag1–N9 | 87.3(5) |
| N2–Ag1–N10 | 122.3(5) |
| N1–Ag1–N2 | 64.7(5) |
| N1–Ag1–N7 | 92.0(5) |
| N7–Ag1–N10 | 107.7(5) |
| N7–Ag1–N9 | 145.8(5) |
The bridging dptz ligands lead to the formation of a one-dimensional polymeric structure as indicated in Fig. 8. The packing of the polymeric chains in the lattice is of considerable interest. Each chain has the unique didentate dptz ligands oriented along one face, like one strand of a zip fastener. In the lattice, a second chain completes the zip-fastener in the closed configuration by intercalation of the didentate dptz ligands into a π-stacked array.
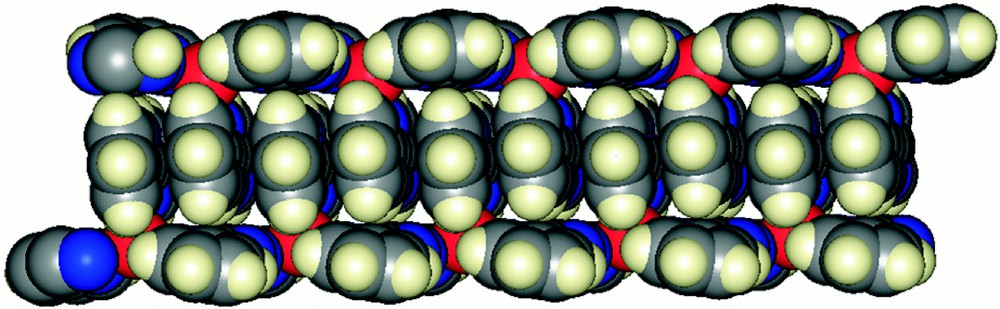
A view of 〚{Ag(dptz-N,N’)(μ-dptz)}n〛〚BF4〛n, showing the extensive π-stacking in the lattice as the unique didentate dptz ligands intermesh to give a closed zip-fastener motif.
2.5 Conclusions
The above results lead us to be very cautious about the generalisation of self-assembly algorithms in metallosupramolecular chemistry. The assumptions that we started with are undeniably correct – silver(I) ions generally resemble copper(I) ions and dptz can behave in the same way as dppz. However, the algorithms will fail if other bonding modes are possible. This is the case with the 1:2 complex, which embodies a bonding mode that we had identified from the start as a possible outcome. However, in the case of the 2:2 complex, the bonding mode of the ligand is identically that which should lead to the 〚2 × 2〛 grid. In this case, the as yet unexplained desire of the silver(I) centre to adopt a planar coordination dominates. To confuse matters further, the dppz motif has been successfully used by Lehn and Baxter for the assembly of higher order grids 〚11, 14, 15〛, although the presence of peripheral methyl groups may play an important role in ensuring orthogonal coordination of the ligands.
3 Experimental
3.1 Synthesis of 〚Ag2(dptz)2〛〚CF3SO3〛2
Silver triflate (0.038 g, 0.15 mmol) was added to a solution of dptz (0.035 g, 0.15 mmol) in nitromethane (5 ml) and the mixture sonicated for 1 min and then stirred for a further 10 min. The solvent was then evaporated in vacuo and the purple solid recrystallised from acetonitrile to produce purple crystals. Yield quantitative. Found: C, 31.9; H, 1.4; N, 16.9. C26H16Ag2F6N12O6S2 requires C, 31.7; H, 1.6; N, 17.0%.
3.2 Synthesis of 〚{Ag(dptz-N,N’)(μ-dptz)}n〛〚BF4〛n
A solution of AgBF4 (0.022 g, 0.113 mmol) in nitromethane (2 ml) was added to a stirred solution of dptz (0.027 g, 0.113 mmol) in nitromethane (10 ml). The solution immediately changed colour from red to purple and was stirred for 24 h, after which the solvent was evaporated to give a purple solid. 1H NMR (CD3CN): δ 9.04 (d, J = 4.4 Hz, d, H6), 8.86 (d, J = 7.7 Hz, 2H, H3), 8.23 (dt, 2H, J = 7.7, 1.4 Hz, H4) 7.88 (dd, J = 7.7, 4.8 Hz, 2H, H5). The NMR solution deposited purple crystals on standing for 24 h. Found: C, 42.5; H, 2.2; N, 24.5. C24H16N12AgBF4.0.5 H2O requires C, 42.6; H, 2.5; N, 24.9
3.3 X-ray structure determination of 〚Ag2(dptz)2〛〚CF3SO3〛2
A single deep red plate (0.10 mm × 0.15 mm × 0.20 mm) of 〚Ag2(dptz)2〛〚CF3SO3〛2 was obtained from a cooled acetonitrile solution of the complex. C26H16N12Ag2F6O6S2, M = 986.39, triclinic, space group , a = 11.712(3) Å, b = 9.111(2) Å, c = 8.040(2) Å, α = 102.20(2)°, β = 93.151(8)°, γ = 72.670(9)°, V = 800.5(4) Å3, Z = 1, μ(Mo Kα) = 1.453 mm–1, F(000) = 484. Data were measured at 296 K on a Rigaku R-axis IIc diffractometer with graphite monochromated Mo Kα radiation (λ = 0.710 69 Å). A total of 4494 (2521 independent) reflections was measured with 2383 with I > 2.0σ(I). Data reduction was carried out by teXsan, structure solution and refinement were done by SHELXS-86 and SHELXL-93. Hydrogen atom positions were calculated and subsequently riding. The cation lies about an inversion centre. Final R1 = 0.0817 (all data), 0.0781 (obs.), wR2 = 0.2263 (all data), 0.2129 (obs.).
3.4 X-ray structure determination of 〚{Ag(dptz-N,N’)(μ-dptz)}n〛〚BF4〛n
A single deep red plate (0.20 mm × 0.15 mm × 0.090 mm) of 〚{Ag(dptz-N,N’)(μ-dptz)}n〛〚BF4〛n was obtained by slow diffusion of a layer of diethyl ether into an acetonitrile solution of the complex. C24H16N12AgBF4, M = 667.17, monoclinic, space group P21/a, a = 13.201(5) Å, b = 25.125(9) Å, c = 7.834(2) Å, β = 102.64(2)°, V = 2535.4(15) Å3, Z = 4, μ(Mo Kα) = 0.867 mm–1, F(000) = 1328. Data were measured at 296 K on a Rigaku R-axis IIc diffractometer with graphite monochromated Mo Kα radiation (λ = 0.710 69 Å). A total of 5755 (2807 independent) reflections was measured with 1948 with I > 2.0 σ(I). Data reduction was carried out by teXsan, structure solution and refinement were done by SIR92 and SHELXL-93. Hydrogen atom positions were calculated and subsequently riding. Final R1 = 0.1444 (all data), 0.0978 (obs.), wR2 = 0.2791 (all data), 0.2453 (obs.).
Supplementary material
The supplementary material has been sent in electronic format to the Cambridge Crystallographic data Centre, 12 Union Road, Cambridge CB2 1EZ, UK under deposition numbers CCDC 171146 and 181881.
Acknowledgements
This paper is dedicated to the memory of John Osborn – a great scientist and a good friend that we will miss. We would like to thank the University of Birmingham and the EPSRC for support of this work.



