1 Introduction
Detailed studies of intramolecular magnetic exchange and spin-frustrated lattices is a current topic of focus in magnetochemistry [1–3]. It thus seems desirable to make available precise data on such lattices but with simple and well-characterized structures. One of the simplest model systems of a frustrated lattice would consist of three spin 1/2 metal ions or free radical fragments bonded together in an equilateral triangle geometry. On general grounds, complexes of Cu2+ ions would be expected to provide such examples [4]. Indeed, three such examples have recently been reported [5–7]. Padilla et al. [5] have investigated [L3Cu3(Im)3](ClO4)3, L = 1,4,7-trimethyl-1,4,7-triazacyclononane and Im = imidazolate, in which the Cu36+ core forms a quasi-equilateral triangle. López-Sandoval et al. [6] reported on [Cu3(cpse)3(H2O)3]·8.5 H2O, cpse = doubly deprotonated form of N-[2-hydroxyl-1(S)-methyl-2(S)-phenylethyl]-N-methyl glycine, composing a truly equilateral Cu2+ triangle. These studies employed EPR spectroscopy, in addition to magnetization measurements, since EPR provides more precise data on the molecular orbital of the unpaired electron. However, neither study was able to resolve spin–spin splitting (fine structure) from the three electrons, or any electron-nuclear hyperfine structure from the Cu nuclei, possibly because of the use of low frequency EPR in [5] or of only powder samples in [6]. More recently, Cotton and coworkers [7] reported the synthesis and characterization of the new compound Cu3(O2C16H23)6·1.2 C6H12, which also contains a Cu36+ core, and in which three Cu2+ (3d9) ions are bridged together in a triangular geometry with three-fold symmetry, Fig. 1 depicts a schematic of the molecule, highlighting the positions of the three Cu2+ ions. The individual Cu2+ ions display a slightly distorted square planar geometry with four oxygen atoms from the carboxylate moieties of the 2,4,6-triisopropylbenzoic acid ligand. As is well established [1–10], Cu2+ ions bonded via oxygen atoms exhibit antiferromagnetic interactions. The Cu3 trimer here thus represents a good model for a three-way spin-frustrated lattice. In such a case, the three spins can exist in either a doubly degenerate doublet (Stotal = 1/2) state or a quartet state with Stotal = 3/2. Based on DC magnetization measurements, it was concluded [7] that this Cu36+ triangle indeed comprises a frustrated-spin triangular lattice with a doublet ground state, and a quartet excited state located 3 J = 324 K above it. Additional data on this rather fascinating compound, using in particular EPR spectroscopy, seemed to be desirable, which provided the main impetus for this undertaking. Here we report EPR measurements using the X-band (9.5 GHz), Q-band (34.5 GHz), and W-band (95 GHz) spectrometers, single crystal and powder samples, and temperature range from 294 down to 4 K. The EPR data confirm the earlier magnetic susceptibility results on the relative disposition of the doublet and quartet states [7], but in addition provide detailed, quantitative information on the symmetry and magnetic parameters of both the doublet and quartet states. They show also that at temperatures lower than about 30 K, the Cu3-triangle settles down in the doublet ground state, and the unpaired electron becomes localized on only one of the three Cu2+ ions, with concomitant loss of the three-fold symmetry. New magnetic susceptibility measurements indicate that this unexpected localization is likely the result of weak inter-cluster antiferromagnetic interactions between the Cu36+ cores which become manifest at cryogenic temperatures, but this point needs additional theoretical investigation.
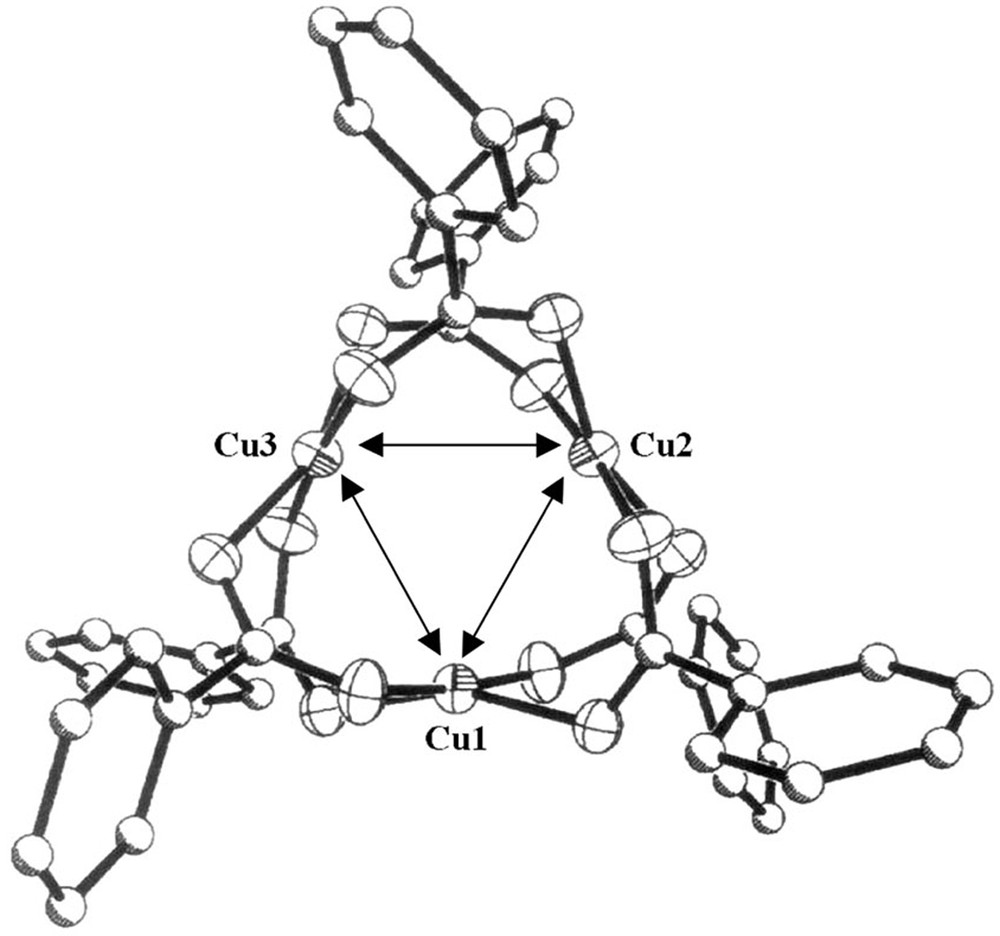
The molecular structure of Cu3(O2C16H23)6·1.2 C6H12. The arrows indicate the equilateral triangle formed by the three Cu2+ ions separated by 3.131 Å, bridged by two carboxylate groups.
2 Results and discussion
2.1 Evidence of zero-field splitting: frequency dependence of the EPR spectra
Fig. 2 shows some typical EPR spectra from single crystals, with the magnetic field aligned along the crystal’s three-fold symmetry axis. The frequencies used are as marked: (a) W-band, 95 GHz (b) Q-band, 34 GHz and (c) X-band, 9.5 GHz. The spectra consist of triplets, with the triplet splitting essentially the same at all the three frequencies, and hence also not dependent on the magnetic fields employed. This observation demonstrates that the triplet must arise from a field-independent interaction, either an electron spin–spin splitting, the so-called D and E parameters, or electron-nuclear hyperfine structure. Because of the strong Cu···Cu spin exchange within the triangle, as shown by the earlier [7] magnetic susceptibility measurements (J = –108 K), we can safely assume that all hyperfine splittings are averaged out for the quartet state, and the triplet structure arises from D-splitting due to the presence of axial symmetry (E = 0). The spin Hamiltonian then becomes very simple, and for the case of the field along the principal axis of the D-parameter (z-axis), it becomes [11,12]
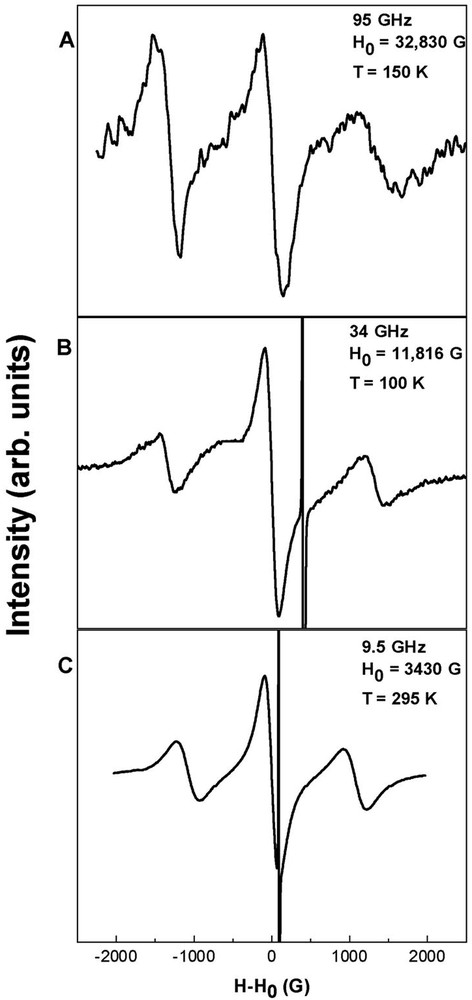
The θ = 0° spectra at 95 (A), 34 (B) and 9.5 GHz (C). The triplet structure in the spectrum is field/frequency independent. It is also notable that the S = 3/2 state is appreciably populated even at 100 K, such that the triplet components are still resolved. The narrow line is DPPH at g = 2.0037.
| 1 |
Interestingly, the zero-field splitting is large enough in this case to allow for resolution of the fine structure into a triplet from the three expected S= 3/2 excited state transitions centered at g = 2.057. The peak-to-peak linewidths, DHpp, of the three components are 296 and 189 G for the outer and central lines, respectively. The smaller line width of the central peak is ascribed to the fact that the central peak from a S = 3/2 state, the MS = –1/2 to +1/2 transition, is always sharper because it is the least susceptible to strain and quadrupole-related broadening. More importantly, in the present case, this peak is slightly asymmetric and more intense than the outer peaks, because it is overlapped by the EPR signal of the S = 1/2 ground state, as will be discussed in section 2.2 below.
2.2 Temperature dependence of the EPR spectrum
Temperature variation of the EPR spectra quickly established that the triplet components could be observed only at temperatures of about 50 K. As may be noted from the 34.5-GHz spectra shown in Fig. 3, they are strongest at the highest temperature, implying that the S = 3/2 state is indeed the excited state of the Cu3 trimer under investigation. Below 50 K, the triplet is replaced by the singlet peak. This singlet becomes stronger at lower temperature, in conformity with it being assigned to the S = 1/2 ground state. These observations suggested that we could measure the spin population changes in these two states by analyzing their corresponding signal intensities (see section 2.3 below).

Variable temperature 34-GHz measurements on a single crystal. The outer lines that arise from zero-field splitting (D) of the thermally excited state decrease in intensity with the temperature until only a single, slightly asymmetric peak is observed at 4 K. The narrow line is DPPH (g = 2.0037).
Another significant observation was that for this H//z orientation, as we lowered the temperature, the lowest-field component of the triplet became much stronger than that at the highest field. This was the case also for the measurements at higher field, as can be noted from the W-band spectrum at 150 K shown in Fig. 2a. This observation clearly implies [11,12] that the sign of the D parameter is negative, i.e., in the quartet state the MS = ± 3/2 states lie lower than the ±1/2 states.
2.3 Temperature dependence of the EPR intensity ratios
The temperature dependence of the relative intensities of the peripheral vs inner lines in the spectrum was analyzed to estimate the doublet–quartet separation. The experimental data are shown as the points in Fig. 4. The analysis used the usual approximation that the EPR intensities are proportional to their respective spin susceptibilities. As discussed by Cotton et al. [7], for a system consisting of a ground state with S = 1/2, and an excited state with S = 3/2, the magnetic susceptibility is given by equation (2):
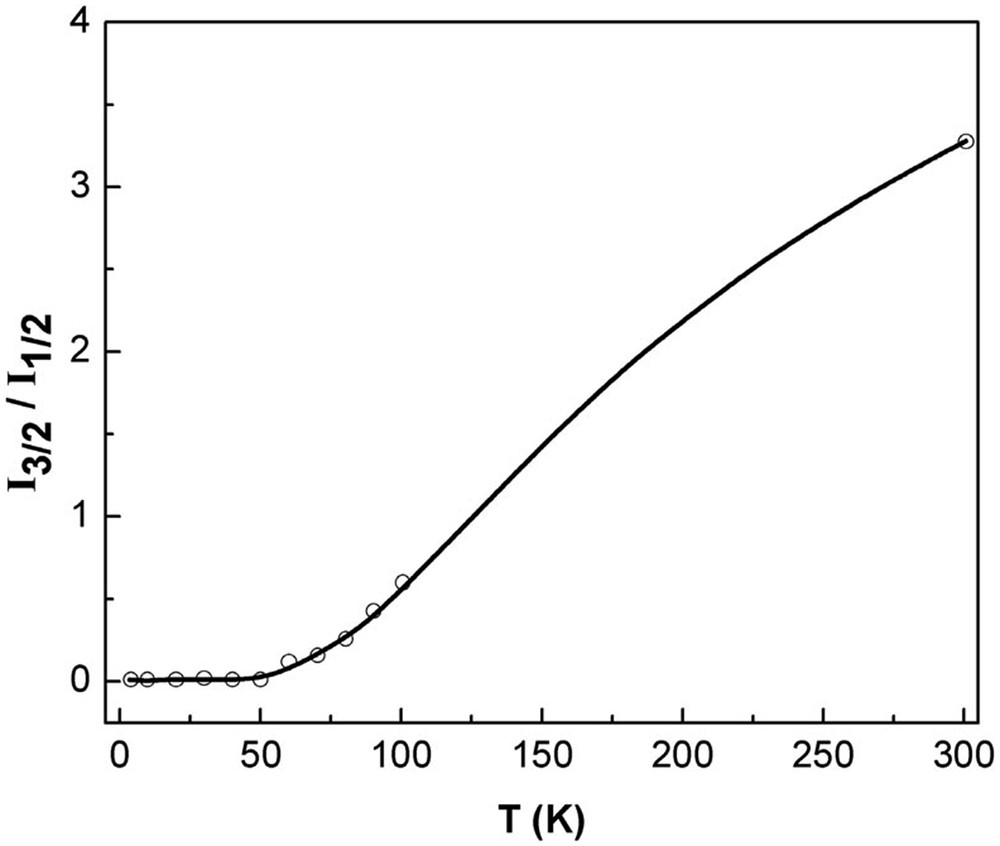
The intensity ratios of the S = 3/2 and S = 1/2 components of the θ = 0 spectrum obtained at different temperatures (open circles) reveal J = –107 ± 6 K from the theoretical fit (dark line).
A fit of equation (3) to the observed intensity ratios is shown in Fig. 4. From the fit, we calculate the exchange parameter J = –107 ± 6 K, which is in accord with the value of J = –108 K derived from the magnetic susceptibility data [7], providing as additional support for the interpretation of the EPR results.
2.4 Magnetic parameters of the S = 3/2 excited state
While the data in Figs. 2–4 enable the identification of the basic designation of the spin states, additional angular variation measurements were made in order to obtain the magnetic parameters of these states. Such measurements were made first at room temperature for the quartet state. Fig. 5 shows the angular variation of the triplet spectra as a function of the orientation of a crystal relative to the applied magnetic field. Here θ = 0 corresponds to the orientation of the magnetic field along the direction perpendicular to the plane of the Cu3 triangle. Clearly the angular variation exhibited roughly a (3 (cosθ)2 – 1) behavior. We then analyzed the whole plot using the standard [12] equations for an S = 3/2 state, given by equation (4) below.
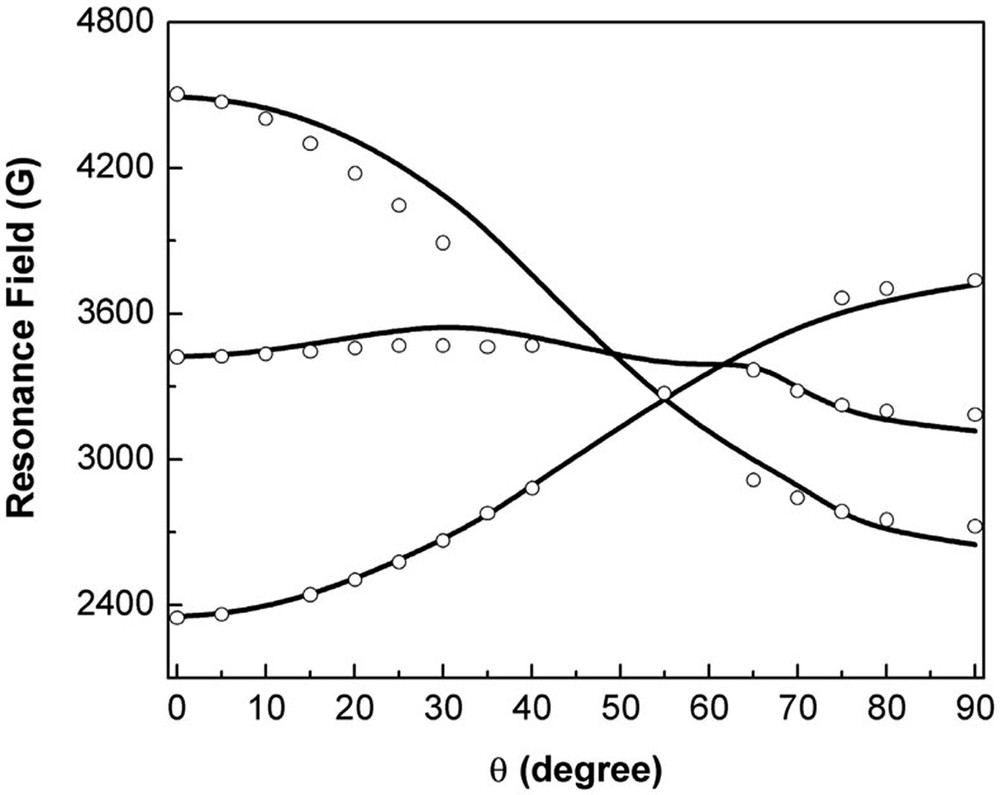
The angular dependence of the 9.5-GHz single-crystal EPR spectrum displays the axial anisotropy expected for a system with three-fold symmetry. The dark lines mark the theoretical behavior expected from equation (4).
Here WMS – WMS–1 is the energy of the transition under consideration, g2 = g⊥2 sin2(θ) + g//2 cos2(θ), D = – 535 ± 10 G, g // = 2.209 ± 0.0005, g ⊥ = 2.057 ± 0.0005, H = resonance field, and S = 3/2, and MS is the corresponding spin-projection quantum number. The continuous lines are the theoretically calculated curves. In particular, it can be noted that the fine structure can be seen to collapse into one broad peak (ΔHPP = 464 G) near θ = 55° as expected based on the 3 cos2θ – 1 dependence of the splitting related to D. We consider the agreement between measured and calculated line positions to be satisfactory. The parameters thus obtained are collated in Table 1.
EPR parameters of the excited (S = 3/2) and ground (S = 1/2) states of the Cu36+ core of Cu3(O2C16H23)6·1.2C6H12
| S = 3/2 | S = 1/2 | J | z J′ |
| g// = 2.057 | gxx = 2.005 | –107 K | –0.15 K |
| g⊥ = 2.209 | gyy = 2.050 | (–7.96 × 105 G) | (–1.1 × 103 G) |
| D = –535 G | gzz = 2.282 | ||
| E = 0 | A// = 157 G |
2.5 Magnetic properties of the S = 1/2 ground state
Detailed angular variation measurements were carried out for the middle peak of the spectra, which at 4 K was assignable solely to the ground state with S = 1/2. In general, as the orientation was changed from that for θ = 0°, the peak split broadly into four, as expected from the three chemically equivalent but magnetically distinct Cu2+ sites in the unit cell. In particular, around θ = 60°, the lowest-field component exhibited a quartet hyperfine structure, characteristic of a single Cu2+ nucleus, with the nuclear spin I = 3/2. Note that from an equilateral triangle containing a spin on each vertex, we expect an equal probability for each vertex of the triangle to contain the single unpaired spin. If this were the case, the hyperfine structure of the spectrum would be expected to consist of 10 peaks, considering three equivalent I = 3/2 Cu nuclei. Fig. 6a reveals the presence of only four hyperfine lines, indicating that in its S = 1/2 ground state, the unpaired spin density must be localized on a single Cu nucleus, in contrast to being spread with equal probability over the three Cu nuclei in the Cu3 core (as was found at T > 50 K for the quartet state). In order to ensure that this splitting did not arise from site splitting in a possibly broken or misaligned crystal, we recorded spectra from a powder sample. The 4-K, 35-GHz powder spectrum (Fig. 6B) confirms the presence of only four hyperfine lines (A// = 157 G) and the presence of the gxx component of the g-tensor due to reduction of axial symmetry. Based on Fig. 6B, the ground state of this system is described by gxx = 2.005, gyy = 2.050, gzz = 2.282, A// = 157 G, and DHPP = 116 G. The EPR parameters for the S = 3/2 and S = 1/2 states are also presented in Table 1.

(A) Rotation of the crystal at 4 K reveals three components in the 34-GHz spectrum. The presence of only four hyperfine lines is unexpected for an equilateral triangle. The three-fold symmetry is removed through inter-trimer antiferromagnetic coupling. (B) The 4-K powder spectrum confirms the presence of only four hyperfine lines.
At low temperatures, thus, the symmetry of the molecular orbital containing the unpaired spin must be reduced from the three-fold symmetry present at room temperature. The magnetic data [7] reveal that at low temperatures the system exhibits antiferromagnetic exchange between trimer units as is the case with another well characterized equilateral Cu(2+) triangle of López-Sandoval et al. [6]. Other authors have proposed that the degeneracy of the two doublet states is removed through inter-cluster exchange based on their experiments on a Cu2+ triangle encapsulated in a metal oxide cluster [13]. We thus reinvestigated the magnetic susceptibility around the 4 K temperature regime, as discussed below.
2.6 Estimation of the inter-trimer exchange parameter
Fig. 7 displays the new magnetic moment data over the range of 1.8–100 K. The data confirm the earlier results on the existence of the plateau between 15 and 50 K, and in addition reveal a significant drop in the moment below 10 K. This drop could be well fitted with an extra exchange constant, J′, representing an antiferromagnetic interaction between the Cu3 cores with z nearest neighbours. The data were corrected for the diamagnetic contribution, using an extrapolation of the data below 50 K, which was also consistent with the estimation based on Pascal’s constants [7]. Our new model for the magnetic susceptibility of this system is similar to that of equation (1) in [6]. We also use the exchange Hamiltonian as H = –2 J (S1·S2 + S1·S3 + S2·S3), which utilizes the convention of writing 2 J rather than J in the coefficient (in contrast to some others [6]). The resultant equation describing the magnetic behavior is given by equation (5):
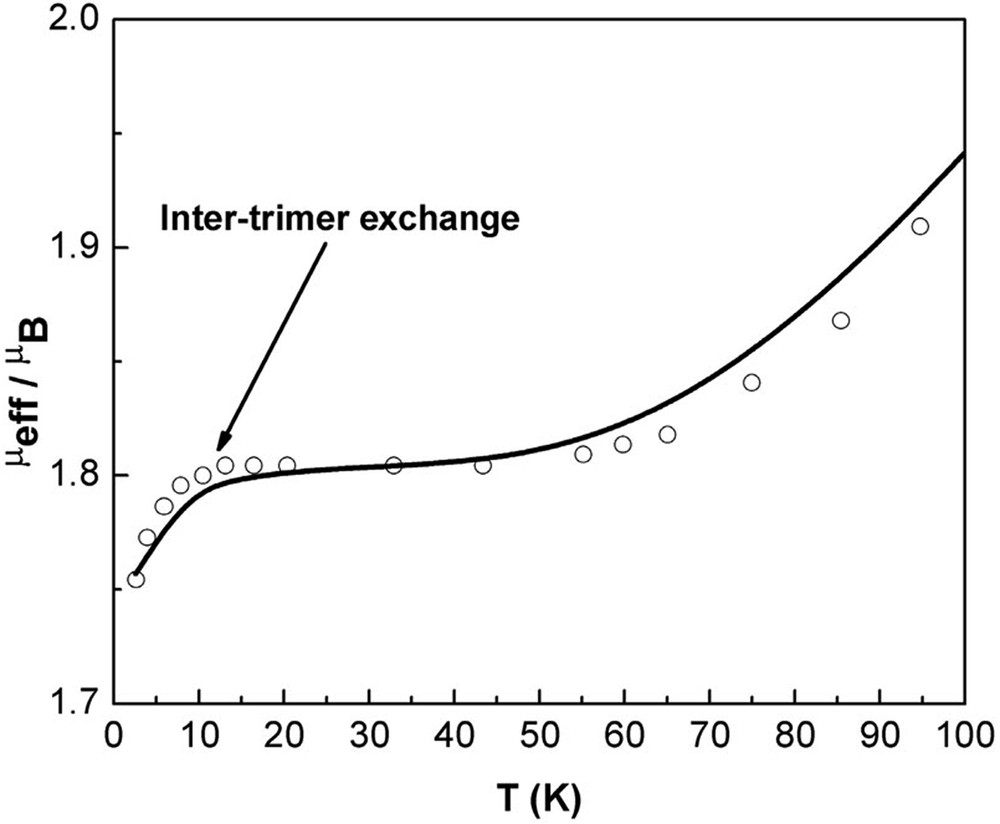
The low-temperature region of the effective magnetic moment. The symmetry-lowering mechanism of the unpaired spin’s molecular orbital arises through inter-trimer exchange. The solid line is a best-fit yielding an exchange constant between trimer units of J′ = –0.15 K.
3 Conclusions
EPR spectroscopic measurements using frequencies up to 95 GHz were made on the model, spin-frustrated triangular system, in the Cu36+ core of Cu3(O2C16H23)6·1.2 C6H12. The spectra confirm the presence of a thermally accessible S = 3/2 excited state intra-trimer exchange parameter J = –107 ± 6 K, in agreement with earlier [7] magnetic data. The excited state spectra exhibit properties of axial symmetry as expected for an equilateral triangle of spins, and a zero field splitting of D = –535 G. The spectra of the S = 1/2 ground state show that the three-fold symmetry present at high temperature is reduced, and the single unpaired electron is now localized on only one of the Cu2+ ions of the Cu36+ core. The results are summarized in Fig. 8. Magnetic susceptibility measurements indicate that this symmetry lowering is caused by the presence of an inter-trimer magnetic exchange that becomes manifest below 30 K. This aspect, however, needs additional investigations.
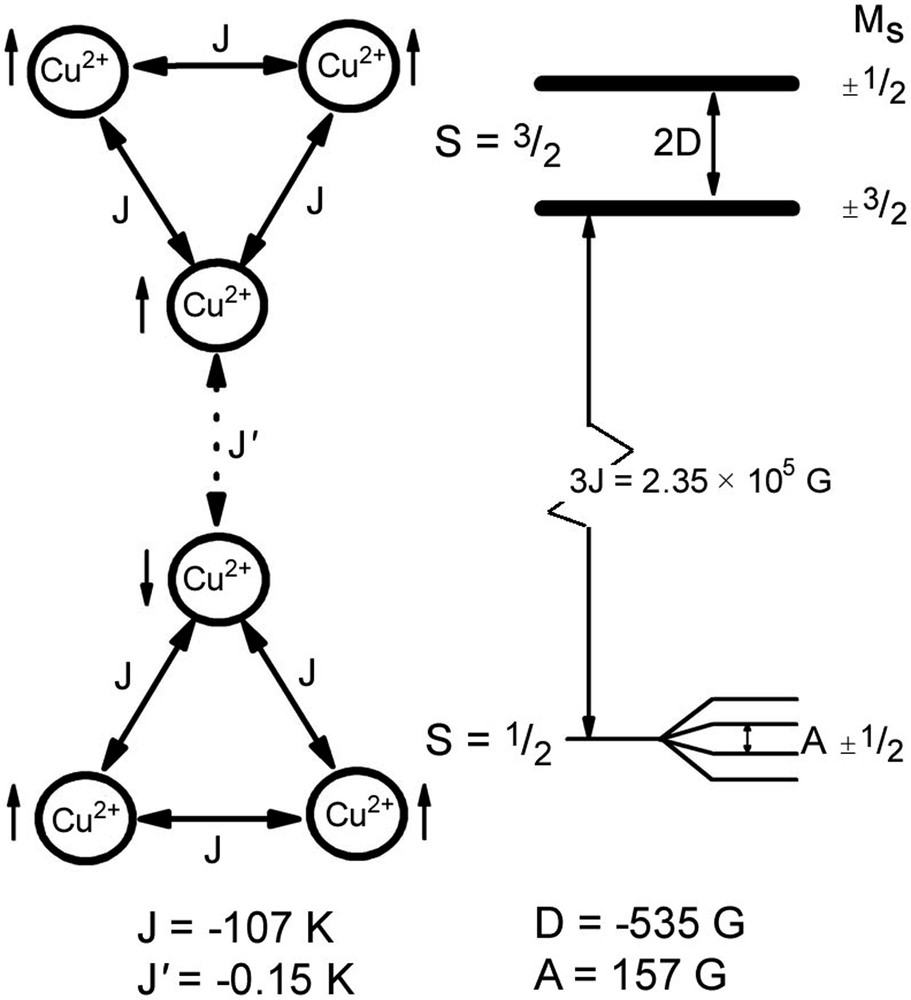
A summary of the results discussed within this paper. The dotted arrow is only active at temperatures where inter-trimer exchange occurs. The up and down arrows mark the electronic configuration of the excited and ground states.
The Cu3(O2C16H23)6·1.2 C6H12 system has been found to be unique among other triangular exchange systems due to (a) its high temperature three-fold symmetry, (b) simplest magnetic system with just three electrons on the triangle, (c) ease of obtaining high-quality single crystals, and (d) nearly optimum Cu–O–Cu bonding that yields well dispersed EPR spectra from both the doublet and quartet spin multiplicities. This molecule constitutes a textbook example of spin frustration and the present study should motivate additional theoretical as well as experimental investigations.
4 Experimental
4.1 Sample preparation
Cu3(O2C16H23)6·1.2 C6H12 was prepared [7] by refluxing 0.993 g of 2,4,6-triisopropyl benzoic acid (HTiPB) and 0.884 g of CuCO3·Cu(OH)2 in ethanol to yield a blue–green solution, which was then filtered over Celite. Evaporation of the solvent in vacuum resulted in the formation of a blue–green solid, which was heated to remove the remaining HTiPB and axially ligated ethanol. The resultant dark green solid was dissolved in cyclohexane and placed in a refrigerator for approximately one week, after which, dark-green single crystals of Cu3(O2C16H23)6·1.2 C6H12 were collected. The crystals were thick plates with well-developed faces, with the Cu3 triangle lying in the plane of the plates, as previously [7] shown by X-ray crystallography.
4.2 EPR studies
9.5-GHz EPR spectra were obtained on powders and single crystals on a Bruker Elexsys-500 EPR spectrometer equipped with a goniometer for angular dependence studies. For precise measurements of the g-values and splittings, the magnetic field was calibrated with a built-in Bruker NMR gaussmeter, and the frequency was measured with a digital frequency counter. The same spectrometer was used in all 34-GHz experiments on powders and single crystals. The temperature of the 34-GHz measurements was controlled to an accuracy of about ±0.1 K with an Oxford continuous flow He cryostat within a range from room temperature to 4 K. 95-GHz experiments on single crystals were performed on a locally built microwave bridge inserted into a Quantum Design PPMS 9 Tesla magnet described in more detail elsewhere [14,15]. These high-frequency measurements were used to confirm the presence of zero-field splitting at much higher frequencies. In all cases, DPPH [16] was used as an additional g-value marker.
4.3 Magnetic measurements
DC magnetic susceptibility measurements were made with a Quantum Design SQUID magnetometer over the range of 1.8 to 100 K. The data were corrected for diamagnetic susceptibility by extrapolating the data below 30 K. This was consistent with the correction using Pascal’s constants [7].



