1 Introduction
Many cellular functions such as catalysis, molecular recognition and information storage are mediated by biomacromolecules that reversibly fold into compact, three-dimensional conformations [1, 2]. Controlling the long-range conformational equilibria of non-biological structures may permit functions that lie outside the biological realm to be realized. Therefore, the precise modulation of conformational equilibria in synthetic oligomers over length scales approaching the nanoscale regime has emerged as a crucial objective in the development of functional materials. Accordingly, there has been tremendous interest in developing linear oligomers, called ‘foldamers’, that fold into well-defined secondary structures [3, 4]. However, functional biomolecules such as proteins tend to exhibit globular three-dimensional morphologies not easily replicated by synthetic linear structures.
Dendrimers provide a potential oligomeric scaffold that superficially replicates the globular morphology of folded protein structures because their highly branched connectivity creates a three dimensional structure that becomes increasingly globular at higher generations [5]. Further, the constitutional monodispersity of these macromolecules ideally suits them to studies aimed at elucidating the structural characteristics necessary to design materials that fold into compact, three-dimensional structures in a process that resembles protein folding. However, the goal of developing dendrimers that display higher levels of structural order has been severely hampered by the conformational flexibility that most dendrimers exhibit [6]. Accumulated structural evidence suggests that in the absence of attractive or repulsive secondary interactions between otherwise flexible dendritic subunits, most dendrimers are conformationally quite flexible especially at lower generations [7, 8]. Accordingly, numerous chiroptical studies of chiral dendrimers have indicated that stable secondary structural order was not present in the dendrimer branch segments [9, 10, 11, 12]. These studies strongly implied that conformationally rigidity would be a crucial factor in creating secondary structural order in a dendritic molecule.
2 Compacting flexible dendrimers in aqueous media
Global compaction of a denatured protein into a condensed conformational state occurs early in the folding process of a protein into its native conformational state and is thought to be an important step in the folding reaction [13, 14]. In fact, early lattice model studies suggested that non-local interactions that drive protein collapse are strongly coupled to the formation of secondary structure and that compaction alone is sufficient to create secondary structure in proteins [15, 16]. Therefore, we constructed water-soluble polyarylether dendrimers, based on 3,5–dihydroxybenzyl alcohol as the repeat unit, to determine whether compaction induced by the hydrophobic effect in water would be sufficient for the induction of local secondary structure (chiral conformational order) in dendrimers (Fig. 1, left). However, contributions to the chiroptical properties from the dendron branch segments were not evident in water or organic media suggesting that chiral substructures were not developing in the branch segments of the dendrimers [17, 18]. Multi-angle light scattering studies revealed that the dendrimers experienced significant aggregation in aqueous media that decreased at higher generations [19]. This behavior could be rationalized by a shift in conformational preference from a disc-like conformation at low generations to a more globular conformation at higher generations. The disc-like conformation at lower generations maintained a greater hydrophobic surface area exposed to solvent that was minimized by aggregation in contrast to the globular conformation in which the hydrophobic portions are segregated from the aqueous solvent in the monomeric state. These conformational studies indicated that global compaction in water was not a sufficient criterion to induce local secondary structure in dendritic molecules composed of repeat units without secondary structural propensities.
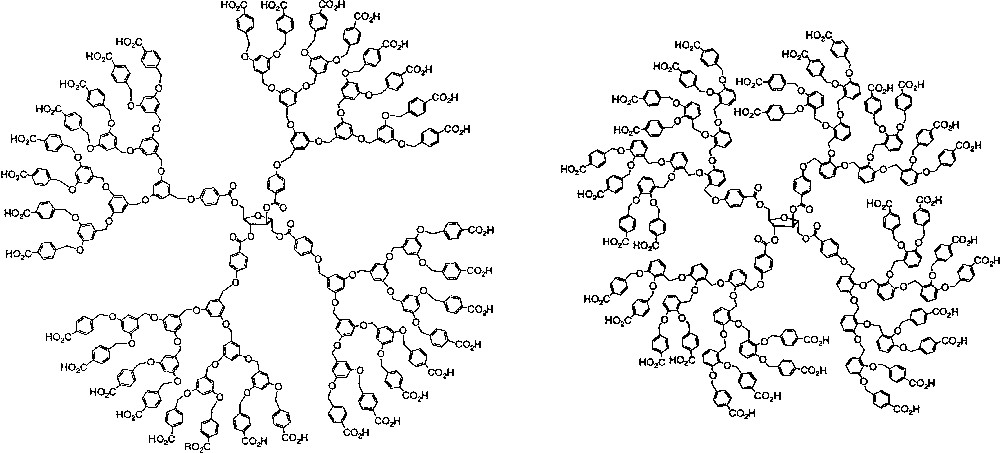
Chiral, amphiphilic dendrimers based on 3,5- and 2,3-dihydroxybenzyl alcohol.
Modeling studies indicated that dendrons constructed using 2,3-dihydroxylbenzyl alcohol as a repeat unit exhibited a slight conformational propensity to fold into a more compact, coiled conformation. The synthesis of dendrimers up to the third generation was undertaken to investigate the effect of compaction on flexible systems with a slight conformational bias in the repeat unit (Fig. 1, right) [20]. Circular dichroism studies indicated that a transfer of chirality from the central core to the achiral branch segments did not occur at any generation in THF [21]. However, a temperature-dependent Cotton effect associated with the 2,3-dialkoxybenzyl ether branching subunit appeared at the first generation in water consistent with a transfer of chirality from the chiral core to the dendrons-this was the first example of chirality transfer in a flexible dendrimer. This effect disappeared at the second and third generations suggesting greater conformational flexibility at higher dendrimer generation consistent with our previous studies in the 3,5-branched systems. The increased flexibility at higher dendrimer generation was rationalized by a decrease in hydrophobic compression at higher dendrimer generation due to the more globular conformation. This work highlighted the importance of compaction in the creation of chiral secondary structure in dendrimers. We could conclude from these systems that compaction could enhance small local conformational preferences; however, compaction alone, as evidenced in the 3,5-branched dendrimers, was not sufficient to create short-range conformational order. Further, this work suggested that a significant local helical conformational propensity in the branched repeat unit would be necessary to create long-range conformational order in dendrimers
3 The synergy of local secondary structure and conformational cooperativity
The intramolecular self-organization necessary to induce a protein to fold into a specific three-dimensional structure is driven by the cooperative interplay of multiple molecular recognition processes such as hydrogen-bonding, van der Waals, electrostatic and solvophobic interactions [22]. These interactions organize the protein structure in a manner that induces conformational cooperativity to occur over large distances causing small energetic differences relating conformational states to be dramatically magnified, leading to highly stable folded materials. In fact, the extremely tight packing of the protein interior in the folded conformational state is thought to engender conformational cooperativity and, therefore, is an important determinant of protein stability [23]. Consequently, improvements in packing efficiency usually impart increased stability to the protein [24]. This phenomenon is commonly observed in biomacromolecules; however, there are relatively few examples of synthetic materials exhibiting this behavior. One example of such cooperativity in a synthetic system occurs in helical linear polymers such as polyisocyanates [25, 26]. In these systems, the sense of helicity can be greatly biased by the use of chiral, non-racemic monomers that exhibit an immeasurably small chiral helical preference prior to polymerization. The small chiral bias of these monomers becomes greatly enhanced in the polymer leading to the predominance of a single helical sense. Green explained the process by which the helical bias develops as the ‘majority rules’ principle [27, 28]. The driving force for predominance of the major helical sense of the backbone is derived from cooperative effects of the monomer units along the backbone that increase the energetic difference between the two helical states in favor of the conformation in the ‘majority’. We hypothesized that inducing such conformational synchronization in a dendrimer system would be an effective method to amplify small energetic differences relating competing conformational states and would result in stable secondary structural order.
4 How to create local secondary structure in a dendrimer system?
In order to induce the dendrons to fold into a well-defined secondary structure, we needed to achieve two objectives: (1) rigidification of the dendron backbone to reduce terminal group backfolding so that pairwise non-bonded interactions occur at the periphery of dendron; (2) induction of a local secondary structural propensity within the dendron structure whose conformational equilibria could be shifted via synchronized motion that occurred at the periphery of the dendron. Accordingly, dendritic structures were constructed using an AB2 repeat unit, based on 4-aminopyridine-2,6-dicarboxamide, to preorganize the interior of the dendrons in a manner that localized the terminal anthranilamide groups rigidly at the periphery. The preorganization imparted to the dendron relied on the preference of this branched repeat unit to exist predominantly in the syn-syn conformation rather than either the higher energy syn-anti or anti-anti forms (Fig. 2) [29]. The syn-syn conformation is lowest in energy because this conformation places the amide NH groups in close proximity to the pyridine-N, which permits intramolecular hydrogen bonding interactions to occur and; further, this orientation of the amides minimizes the repulsive electrostatic interactions between the amide oxygens and the pyr-N that are present in the anti-anti and syn-anti forms [30]. These hydrogen-bonding interactions, in conjunction with the preference of the terminal amides to exist in an s-trans conformation, constrain the system such that the terminal anthranilamide substituents are positioned above and below the plane of the molecule resulting in a local helical structure (Fig. 3, top). The helical antipodes experience a highly dynamic equilibrium that interconverts the M and P conformations quickly relative to the NMR timescale. Although the barrier could not be measured in dendrons having terminal amides, we have recently measured a barrier of 12.3 kcal mol-1 in a related pyridine-2,6-diamide system using NMR lineshape analysis [31]. This barrier most likely represents an upper limit for the dendrons described in this review indicating that a highly dynamic conformational equilibria exists in these dendrons.
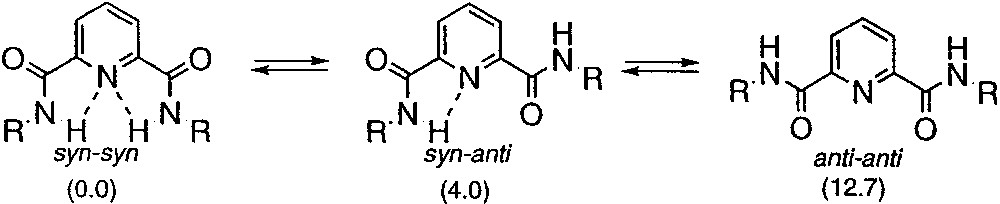
Conformational preference of pyridine-2,6-dicarboxamide (R = C6H5). Relative energies (kcal mol–1) predicted by AM1 are shown in parentheses.
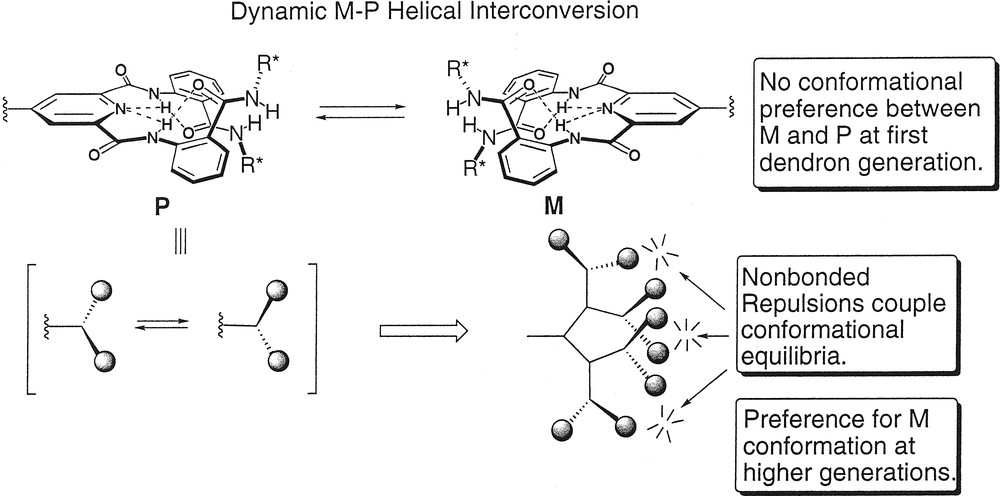
Conformational cooperativity in dendrons.
We hypothesized that, provided the monodendrons were conformationally constrained at each generational shell by the syn-syn preference of the branched repeat unit, pairwise non-bonded interactions between adjacent termini at higher generations would couple the helical interconversions due to the development of a correlated propeller-like rotation of the peripheral anthranilamide groups (Fig. 3) [32]. Each pair of termini, considered as ‘blades’, should twist in the same sense to minimize steric repulsions thereby coupling the motions and conformations of each pair of termini. If such sympathetic motion were operative, the helical preference of each anthranilamide pair would be amplified, because cooperativity in the conformational equilibria of the peripheral subunits would cause small energetic differences between conformational states to be magnified leading to a greater helical bias similar to the ‘majority rules’ conformational behavior of helical polyisocyanate polymers.
5 Design and structure of dendrons
We constructed two different classes of dendrons (Types I and II) differing in the nature of the linkage connecting each generational shell (Fig. 4) to test these hypotheses. The Type-I series were constructed using 4-aminopyridine-2,6-dicarboxamides as the exclusive branching AB2 unit with anthranilamide groups at the periphery. This series was designed to probe whether the helical equilibria relating the anthranilamide groups at the periphery would shift toward a single helix sense as packing interactions at the periphery synchronized the helical interconversions as depicted in Fig. 3. Type-II dendrons employed an anthranilamide ‘turn unit’ at each generational shell to fold the dendrons into a more tightly packed conformation that expressed helical order at each generational shell.
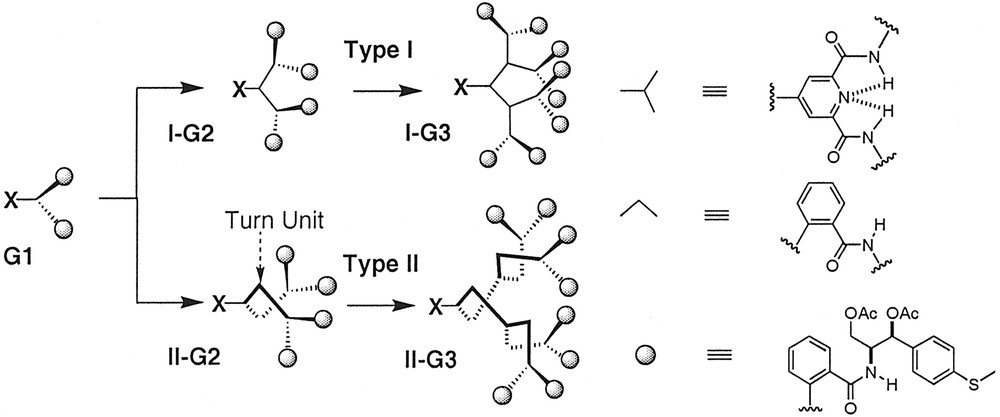
Schematic depiction of Type-I and Type-II dendron designs.
5.1 Type-I dendrons
Preliminary support for the hypothesis that the syn-syn conformational preference of the branch unit would induce cooperative motion at the periphery of the Type-I dendrons was observed in the solid state by X-ray diffraction of second-generation dendron 1 with methyl ester termini [33]. The X-ray crystal structure indicated a propeller-like conformation in which the ‘blades’ encountered pairwise steric interactions, resulting in a propeller-like shape (Fig. 5). The asymmetric unit was actually a dimer composed of two virtually identical, interdigitated monodendrons with two associated molecules of CH2Cl2. Each monodendron displayed all six of the expected bifurcated hydrogen bonds between the amide NHs and the pyridine-N. The relatively flat conformation of each pair of terminal anthranilamides suggested that more sterically bulky groups would be necessary to create a local helical conformation.
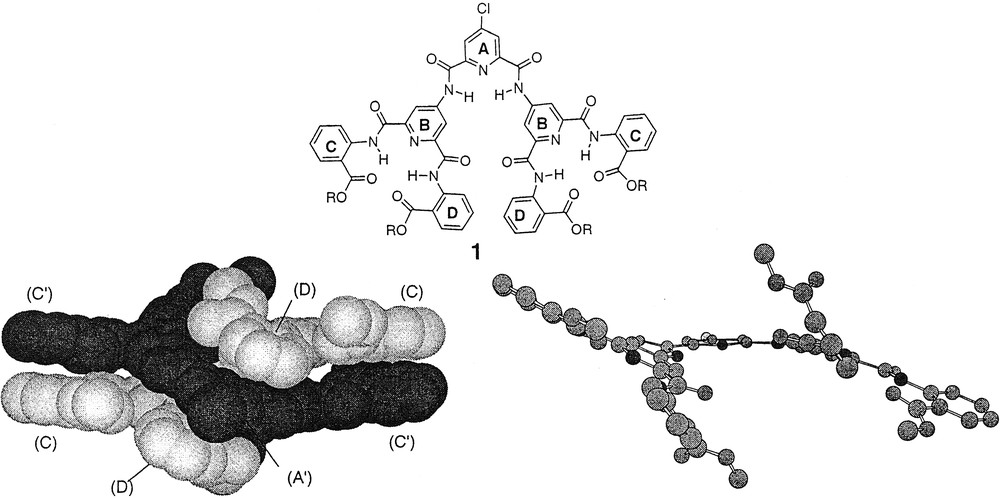
X-ray structure of Type-I second-generation dendron.
Therefore, conformational studies in solution were investigated in dendrons having bulky amide groups placed at the periphery. Further, in order to investigate the conformational properties of the dendrons in solution, chiral, non-racemic anthranilamide groups were employed as termini to cause the M and P helical conformations at the periphery to be related as diastereomeric conformations (Fig. 6). The position of equilibrium of helical conformations could then be measured as a function of generation by circular dichroism (CD) [34].

Structure of Type-I dendrons.
The position of the equilibria interconverting two diastereomeric helical conformations (M and P helices, see Fig. 3) depended on solvent, temperature and dendrimer generation. Specifically, the transition that occurred in the CD spectrum of I-G1, I-G2, and I-G3 in the region of 300-340 nm was due to a π→π* transition centered at 316 nm of the 2-acylaminobenzamide chromophore, as determined by time-dependent density functional theory calculations using the B3-LYP functional. This transition corresponded to a simple Cotton Effect (CE) at the first generation, I-G1, that was temperature and solvent insensitive, and indicated that an extremely small helical bias was present (Fig. 7A). However, the transition became an excitonic couplet at the second generation, I-G2, consistent with a shift in the helical equilibrium toward a major helical sense (Fig. 7B). The electric transition moment associated with this transition runs along the axis containing C3 and C6 of the anthranilamide ring (Fig. 7, top left). Therefore, the absolute sense of helical chirality between each pair of anthranilamide chromophores at the periphery of the Type-I dendrons could be assigned to be M, as shown in Fig. 7. The magnitude of this couplet increased significantly in poor solvents, such as CH3CN and hexane/CH2Cl2 (2:1), which forced the dendron structure to compress in an effort to minimize unfavorable interactions with the solvent. This structural compression increased sympathetic motion of the peripheral units in a manner that amplified the intrinsic helical bias of a pair anthranilamide groups. At the third generation, I-G3, the increased number of synchronized conformational equilibria at the periphery caused that the conformational preference of the termini to become intrinsically more biased toward the M helix and, therefore, was much less sensitive to solvent and temperature as compared with the second generation dendron, I-G2 (Fig. 7C). These observations confirmed that creating correlated conformational equilibria in preorganized dendrimer structure was an effective strategy to enhance intrinsic energetic differences relating conformational states resulting in highly-biased folded structures.
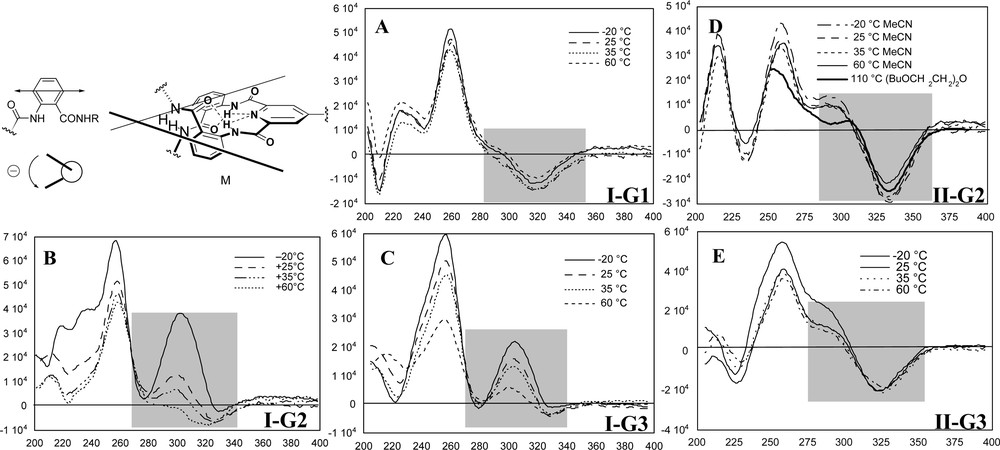
Selected CD spectra of Type-I and Type-II dendrons as a function of temperature in acetonitrile. CD spectra (not shown) of I-G2 and I-G3 become much more temperature sensitive in CH2Cl2 (good solvent) and much less temperature sensitive in hexane/CH2Cl2 (2:1) (poor solvent) in contrast the II-G2 and II-G3 that exhibit no solvent dependence.
5.2 Type-II dendrons
The increased thermal stability of thermophilic proteins has been associated with extremely tight packing of the protein interior and modification of this packing density of proteins often leads dramatically different conformational stability [23]. The helical bias that occurs in I-G2 and I-G3 was limited to the peripheral groups and was highly temperature sensitive, resulting in significant denaturation at 60 °C in CH3CN. Moreover, the increase in helical bias in the Type I dendrons that occurs at higher generations and in poor solvents suggested that increasing the packing efficiency of the dendron structure would create a more stable helical bias by inducing more sympathetic motion of the terminal groups. Therefore, Type-II dendrons were constructed by employing an anthranilamide turn unit to link each generational shell to increase packing efficiency and to extend the peripheral helicity to the internal regions of the dendrons (Fig. 8) [35]. This modification induced the dendrons to fold into a more tightly packed conformation that expressed helical order at each generational shell as shown in the model of II-G2 in Fig. 9, generated by Monte Carlo conformational searching.
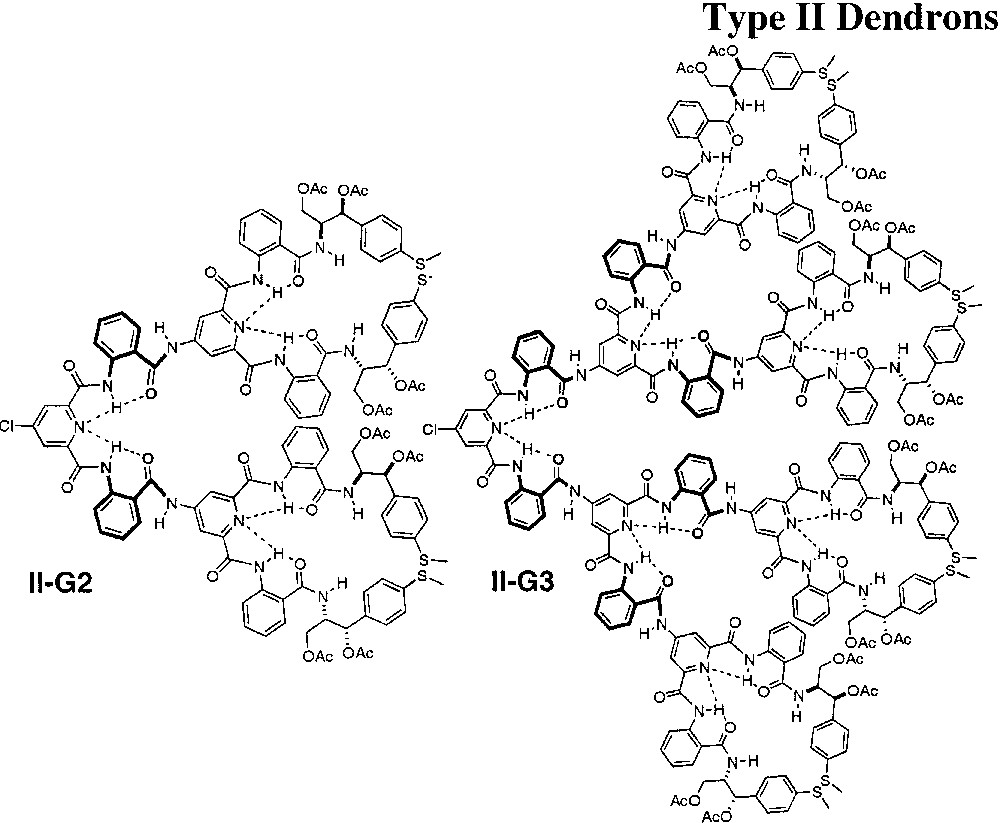
Structure of Type-II dendrons.

Stereo depiction of lowest-energy conformer of II-G2Cl by MM2.
Furthermore, we reasoned that the stability of the dendron secondary structure would increase if internal helical equilibria were sympathetically correlated with the peripheral helicity. The model suggested that (1) that the dendron would adopt a more efficiently packed structure and (2) the helical sense of the inner shell anthranilamide linkages would be of the M-type identical to the peripheral anthranilamides and, therefore, the two shells would be sympathetically correlated. This prediction was verified by CD and NOESY studies, which revealed that the extent and stability of helical secondary structure present in these dendrons was dramatically enhanced by linking each generational shell through an anthranilamide turn unit. For example, several nOe enhancements were observed up to 50 °C in C6D6 in II-G2, supporting this conformational preference. In contrast to the loss of helical bias at 60 °C, in CH3CN, experienced by I-G2, the folded conformation of II-G2 remained stable up to 110 °C in bis(2-butoxyethyl)ether by CD! Similar studies for II-G3 indicated that the helical conformational fold relating the anthranilamides at the focal shell was less compact than at the internal shells. At the focal shell, the syn-syn conformation of the pyridine-2,6-dicarboxamide repeat unit may be destabilized relative to the syn-anti forms in the dendrons at the focal positions as a consequence of the steric bulk of the dendritic branches linked through the repeat unit.
6 Chirality transfer from the central core to the periphery of a dendrimer
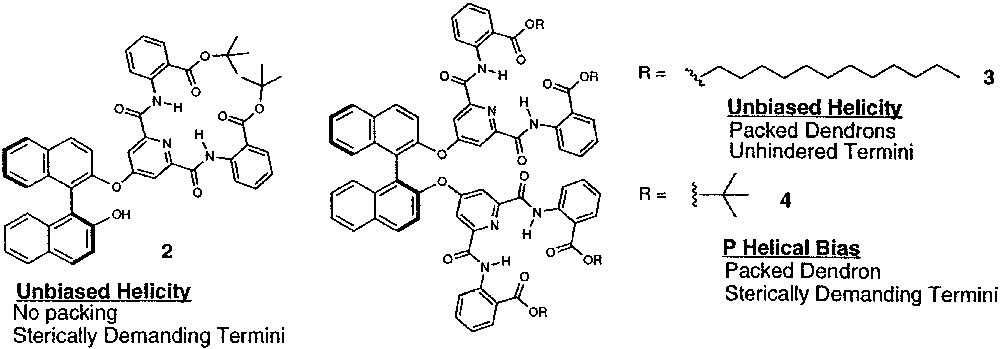
In the previous examples, the relatively weak helical bias imparted to the dendron by the chiral termini was amplified by the synchronized/cooperative motion that correlated the conformational equilibria along the dendron periphery in a manner resembling the ‘majority rules’ behavior observed in linear polymer systems. The ability to faithfully transmit small amounts of chiral information over increasingly greater length scales will be critical in developing highly responsive macromolecular materials that function through their supramolecular conformations. However, controlling the helical bias at the periphery of a dendrimer using a chiral subunit placed at the central core requires transmission of chiral information over a longer distance to more achiral groups than placement at the periphery requires. Therefore, biasing the conformation of a dendrimer with a single, chiral central core is significantly more difficult than with several chiral peripheral groups (Fig. 10) [36]. For example, attaching a single dendron to (S)-1,1′-bi-2-naphthol, as in 2, fails to create a helical bias relating the terminal anthranilate groups, as evidenced by CD spectroscopy (Fig. 11). The lack of sufficient nonbonded interactions between the core and the terminal groups likely creates a very small energetic difference between the two helical conformers. However, linking two [G1]-dendrons to the (S)-1,1′-bi-2-naphthol core synchronizes their conformational equilibria and amplifies this small energetic difference resulting in a strong P helical preference, identical to that of (S)-1,1′-bi-2-naphthol, which can also be considered as a P-type helix [37]. Interestingly, this effect requires sterically bulky terminal t-butyl esters, as in 4; whereas, incorporating primary esters such as dodecyl esters, as in 3, does not create a helical bias even if second generation dendrons are employed. From these preliminary experiments, we concluded that transmitting the central core chirality to distant segments of the molecule requires that the small helical bias imparted by the central core must be amplified through cooperative conformational equilibria and is further enhanced by employing sterically bulky terminal groups that rigidify the helical secondary structure.

Placement of chiral, non-racemic subunit at central core or termini to bias dendron conformation.
Dendrimeric compounds constructed form a chiral, non-racemic central core.
7 Conclusion
Several of the structural requirements necessary to induce a dendrimer to adopt well-defined, chirally-biased secondary order emerge from this work. Most importantly, we found that the dendrons must be preorganized in a manner that forces adjacent subunits to pack in a mutually complementary arrangement. This ordered molecular packing plays an extremely important role in stabilizing dendron secondary structure because it creates non-bonded interactions within the dendrimer that couple the motions and conformational preferences of multiple structural subunits. Such synchronized motion amplifies small energetic differences relating competing conformational states and leads to the predominance of single helical conformation and, consequently, to a more stable secondary structure. Accordingly, increasing the packing efficiency, as in the Type-II dendrons, enhances these effects and dramatically improves thermal stability of the chiral, helical bias of the dendrons. These effects are similarly critical in controlling conformation over longer distances from a single, chiral influence at the focal point because, at a remote site, the effective chiral bias is intrinsically weak and must be amplified through coupled conformational equilibria. Therefore, molecular packing appears to be most important factor in creating folded dendrimer structures with well-defined conformational order.
Proteins rely on their three-dimensional structure for function and the reversible interconversion between different conformations is often the means by which function is modulated or changed. Synthetic macromolecules with higher levels of structural self-organization provide a tremendous potential to develop materials with novel functional capabilities and properties not present in natural biomacromolecules. However, several important questions remain to be answered by further research in the area of macromolecular structure and stereochemistry. For example, cooperativity in the folding of multiple elements of secondary and tertiary structure in proteins is an important driving force in the folding process. How can several elements of secondary structure, represented in this case by the folded dendrons, be combined in a manner that would create tertiary structural order? What effect would this tertiary order have on the secondary structural preferences of the dendrons? Understanding how the conformational equilibria of a particular element of secondary structure is perturbed by non-local elements would greatly facilitate the development of highly ordered macromolecular structures. Similarly, how can the folded structures be induced to reversibly interconvert between two conformations by an external stimulus such as light or pH? This capability may provide the basis for development of molecular switchs, optical storage devices and drug delivery vehicles among other trigger-modulated devices. Current efforts are underway in our laboratory to answer these questions.
Acknowledgements
This work was supported by the National Science Foundation CAREER program (CHE-98-75458) and acknowledgement is made to the donors of the Petroleum Research Fund, administered by the American Chemical Society, for partial support of this work. JRP is grateful for a dedicated group of coworkers who made this work possible.


