1 Introduction
The bonding and structure in organometallic transition-metal clusters is generally well understood within the framework of the polyhedral skeletal electron pair (PSEP) theory. [1] This theory provides simple rules, also known as the Wade–Mingos rules within the organometallic community, which describe the relationship between the geometry of the cluster core and its number of valence electrons. For example, the PSEP theory predicts that a 5-vertex cluster will adopt the triangular bipyramidal structure if it bears six skeletal electron pairs (SEP), whereas a 6-vertex cluster will be octahedral if it possesses seven SEPs. Changing the electron count of these clusters is expected to change their polyhedral shapes. Although very powerful in rationalizing the structure of organometallic clusters, the Wade–Mingos rules have limitations. The more severe limitations are themselves the consequences of the limitations of the closed-shell principle and the isolobal analogy [2] which the PSEP theory is based on. Other limitations arise when skeletal isomerism occurs, [3] as for example in mixed transition-metal (M)/main-group (E) clusters [3]c, d. Indeed, there are often several ways to distribute atoms of different nature on the different vertices of a given polyhedron. For example there are three possible skeletal isomers for a 5-vertex/6-PES closo species with an M3E2 core (Fig. 1). Each of them obeys the Wade–Mingos rules, but the PSEP theory is unable to predict their respective stability. Similarly, there are two possible skeletal isomers for a 6-vertex/7-PES closo species with an M4E2 core (Fig. 1). It turns out that there are numerous clusters of bipyramidal M3E2 and octahedral M4E2 cores which have been isolated and structurally characterized. Selected examples, all of them obeying the Wade–Mingos rules, are given in Tables 1 and 2 [4–45]. In this paper, we use density functional theory (DFT) calculations to evidence the periodic trends governing the respective stability of the different skeletal isomers in both series of closo compounds. Two series of models, namely M3(CO)9E2 (M = Fe, Ru; E = Bi, As, P, N, AsH+, PH+, NH+, S+, Se+, CH, SiH, BH–) and M4(CO)12E2 (M = Fe, Ru, Os; E = Bi, As, P, N, AsH+, PH+, NH+, S+, Se+, CH, SiH, BH–) have been investigated. This work generalizes a limited study by some of us on the octahedral series M4(CO)12E2 (M = Fe, Ru, Os; E = Bi, As, P, N, SiH and CH) [46].
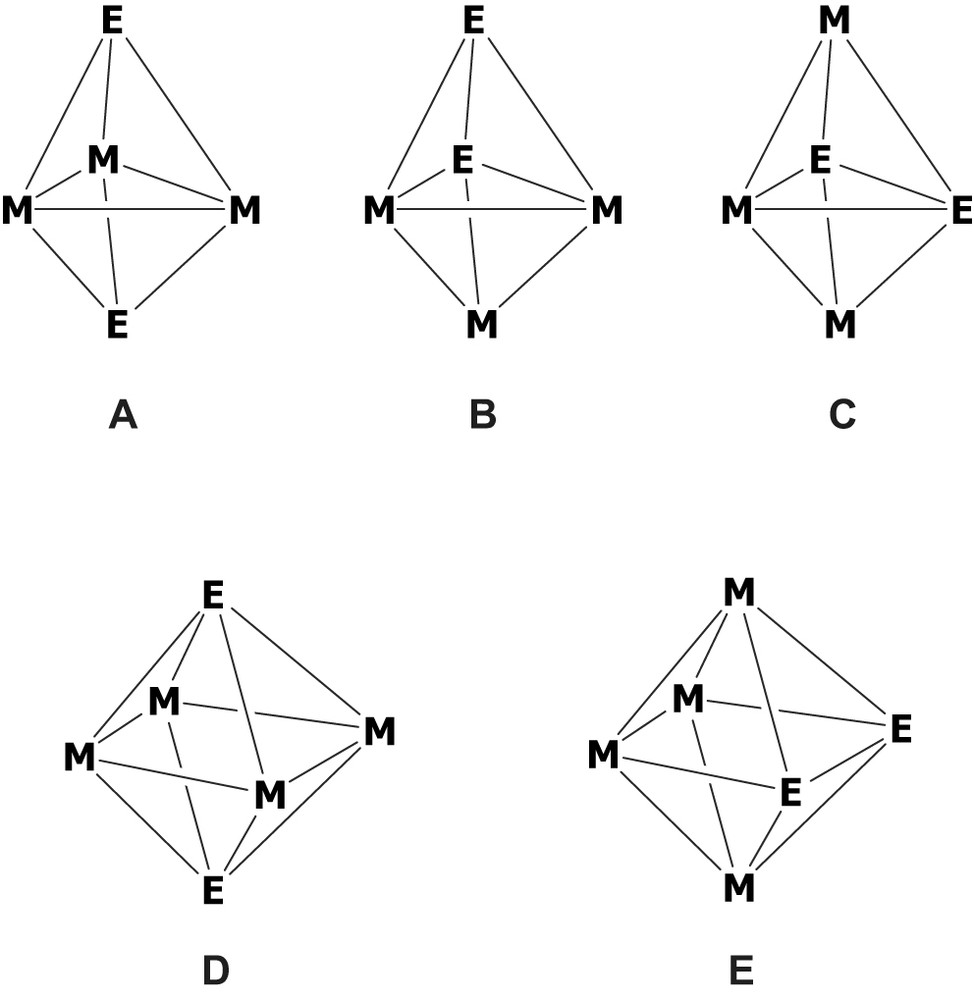
The three possible skeletal arrangements for a 5-vertex/6-PES closo species with an M3E2 core (A, B, and C) and the two possible skeletal arrangements for a 6-vertex/7-PES closo species with an M4E2 core (D and E).
Examples of structurally characterized 6-SEP closo clusters having an M3E2 core
| Compound | Isomer type (see Fig. 1) | Reference |
| Fe3(CO)9Bi2 | A | [4] |
| Ru3(CO)9Bi2 | A | [5] |
| Fe3(CO)13Sb2Mn2(Cp)2 | A | [6] |
| Fe3(CO)9As2 | A | [7] |
| Fe3(CO)9P2[Mn(CO)2Cp]2 | A | [8] |
| Fe3(CO)9[P(Mn(CO)2Cp)][P(Fe(CO)4)] | A | [8] |
| Fe3(CO)9(C2Ph2) | B | [9,10,11,12] |
| Fe3(CO)9(C2Et2) | B | [11] |
| Ru3(CO)7(dppm)(C2Ph2) | B | [13,14] |
| Fe3(CO)9(CMe)(COMe) | A | [15] |
| Fe3(CO)9(CH)(CCO2 Me) | A | [16] |
| Fe(CO)3(CoCp)2(CPh)2 | A | [17] |
| Fe3(CO)9[SnRe(CO)5]2 | A | [18] |
| Fe3(CO)19[GeRe(CO)5]2 | A | [19] |
| Fe3(CO)9(GeEt)2 | A | [20] |
| Fe3(CO)9[SiFe(CO)2Cp]2 | A | [20] |
| Fe2Ru(CO)9(C2Ph2) | B | [21] |
| FeW2(Cp)2(O)(CO)5(C2Tol2) | B | [22] |
| FeW2(Cp)2(CO)6(C2Tol2) | B | [22,23,24] |
| Os3(CO)9(CPh)(COMe) | A | [25] |
| Co3Cp’3P2 | A | [26] |
| Co3(Cp*)3(CMe)2 | A | [27,28,29] |
| Co3Cp*3H2(BH)2 | A | [30,31] |
Examples of structurally characterized 7-SEP closo clusters having an M4E2 core
| Compound | Isomer type (see Fig. 1) | Reference |
| Ru4(CO)12Bi2 | D | [5] |
| Os4(CO)12Bi2 | E | [5] |
| Fe4(CO)11(PpTol)2 | D | [32] |
| Ru4(CO)11(PPh)2 | D | [33] |
| Ru4(CO)9[P(Me)2Ph]2S2 | D | [34] |
| Fe4(CO)11(NEt)2 | D | [35] |
| Fe4(CO)12(C2Me2) | E | [36] |
| Ru4(CO)9(dppm)Se2 | D | [37] |
| Ru4(CO)12(C2Me2) | E | [38] |
| Ru4(CO)12(C2Ph2) | E | [39] |
| Os4(CO)12(C2H2) | E | [40] |
| Os4(CO)12(HC2Et) | E | [40] |
| Fe4(CO)11Se2 | D | [41] |
| Fe4(CO)11S2 | D | [42] |
| [Ru4(CO)10Te2]2– | D | [43] |
| Co4Cp4 H2 (BH)2 | E | [44] |
| [Mn4(CO)12Te2]2– | D | [45] |
2 Computational details
DFT calculations [47] were carried out using the Amsterdam density functional (ADF) program [48]. The Vosko–Wilk–Nusair parameterization [49] was used to treat electron correlation within the local density approximation. Nonlocal exchange and correlation corrections of Becke [50] and Perdew [51], respectively, were included. Compounds containing atoms with Z ≥ 44 were calculated with added relativistic corrections by the use of the zeroth order regular approximation (ZORA) scalar Hamiltonian [52]. The numerical integration procedure applied for the calculations was developed by te Velde [47]d. A triple-ζ Slater-type orbital (STO) basis set was used for C, N and O 2s and 2p, Si and P 3s and 3p. As 4s and 4p, Bi 6s and 6p, extended with a single-ζ polarization function 3d for C, N and O, Si and P, 4d for As and 4f for Bi. A triple-ζ Slater-type orbital (STO) basis set was used for Fe 3d and 4s, Ru 4d and 5s, Os 5d and 6s. A single-ζ STO was used for Fe 4p, Ru 5p and Os 6p. The frozen core approximation was used to treat core shells up to 1s for C, N and O, 2p for Si and P, 3p for As, 5d for Bi, 4p for Ru and 4d for Os [47]a. Geometry optimizations were carried out using the analytical gradient method implemented by Versluis and Ziegler [53].
3 Bipyramidal triangular 6-SEP M3(CO)9E2 clusters
The calculations have been made for M = Fe and Ru and for E = Bi, As, P, N, AsH+, PH+, NH+, S+, Se+, CH, SiH, and BH-. For each compound the geometries of the three isomers have been fully optimized. Examples of the molecular structure of the three isomers obtained for Ru3(CO)9Bi2 and Fe3(CO)9(CH)2 are given in Fig. 2. In all the cases, isomers A, B and C have the C3h, Cs and Cs symmetry, respectively. The relative energies of the three isomers for each compound are given in Table 3 and the pertinent interatomic distances are given in Table 4. A comparison of the available experimental bond distances with the corresponding optimized ones (Table 4) reveals a somewhat overestimation (by 2–6%) of the optimized bond lengths involving heavy atoms. This is a common feature of this type of nonlocal DFT calculations on complexes of transition-metal in low oxidation states [46,54].
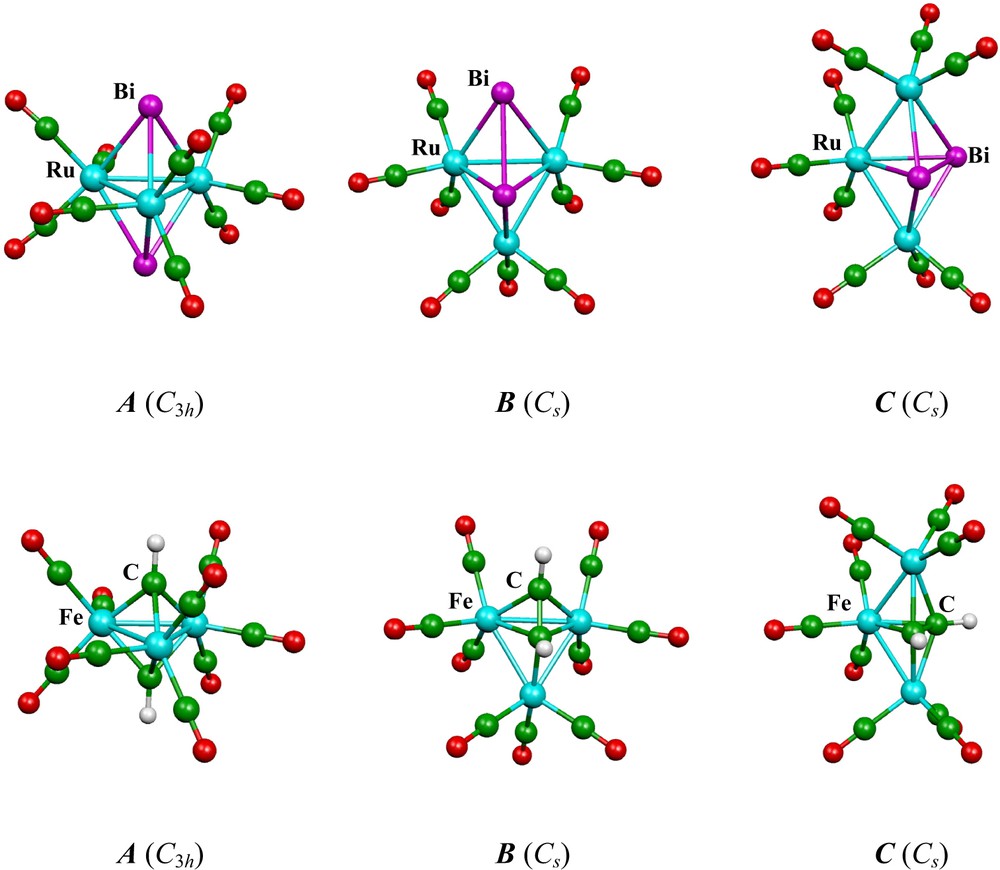
Optimized structures of the three skeletal isomers of Ru3(CO)9Bi2 and Fe3(CO)9(CH)2.
Relative energies (kcal/mol) of skeletal isomers A, B and C for the 6-SEP closo clusters M3E2(CO)9 (M = Fe, Ru; E = Bi, N, P, N, AsH+, PH+, NH+, S+, Se+, CH, SiH, BH–)
| Fe | Ru | |||||
| Isomer type | A | B | C | A | B | C |
| Bi | 0.0 | 14.5 | 6.9 | 0.0 | 10.9 | 11.9 |
| As | 0.0 | 15.2 | 16.1 | 0.0 | 12.1 | 14.0 |
| P | 0.0 | 11.7 | 7.6 | 0.0 | 9.9 | 6.4 |
| N | 39.6 | 0.0 | 14.2 | 40.9 | 0.0 | 18.8 |
| AsH+ | 0.0 | 29.7 | 31.6 | 0.0 | 28.0 | 30.5 |
| PH+ | 0.0 | 30.9 | 35.7 | 0.0 | 30.5 | 37.4 |
| NH+ | 0.0 | 40.2 | 51.9 | 0.0 | 33.6 | 43.8 |
| S+ | 0.0 | 37.8 | 30.0 | 0.0 | 32.1 | 28.5 |
| Se+ | 0.0 | 32.7 | 29.3 | 0.0 | 33.6 | 25.1 |
| CH | 6.9 | 0.0 | 17.5 | 8.5 | 0.0 | 18.4 |
| SiH | 0.0 | 25.6 | 29.2 | 0.0 | 21.2 | 27.8 |
| BH- | 0.0 | 5.1 | 19.9 | 0.0 | 1.2 | 17.7 |
Major optimized averaged interatomic distances (Å) for the three skeletal isomers of the M3E2(CO)9 (M = Fe, Ru; E = Bi, N, P, N, AsH+, PH+, NH+, S+, Se+, CH, SiH, BH–) series. Available experimental values for related species are given in parentheses
| Fe | Ru | |||||||||
| Isomer type | M–M | M–E | E–E | M–M | M–E | E–E | ||||
| Bi | A | 2.808 | (2.745)a | 2.720 | (2.628)a | 4.369 | 2.984 (2.930)b | 2.848 (2.750)b | 4.535 (4.336)b | |
| B | 2.700 | 2.818 | 3.012 | 2.905 | 2.947 | 3.053 | ||||
| C | 2.630 | 2.839 | 3.324 | 2.812 | 2.963 | 3.174 | ||||
| As | A | 2.720 | (2.623)c | 2.439 | (2.362)c | 3.734 | 2.919 | 2.543 | 3.809 | |
| B | 2.670 | 2.514 | 2.466 | 2.869 | 2.618 | 2.404 | ||||
| C | 2.870 | 2.445 | 2.608 | 2.879 | 2.600 | 2.528 | ||||
| P | A | 2.651 | 2.304 | 3.443 | 2.882 | 2.439 | 3.565 | |||
| B | 2.647 | 2.362 | 2.159 | 2.853 | 2.499 | 2.148 | ||||
| C | 2.930 | 2.289 | 2.290 | 3.019 | 2.442 | 2.295 | ||||
| N | A | 2.485 | 1.923 | 2.560 | 2.763 | 2.066 | 2.628 | |||
| B | 2.643 | 2.033 | 1.210 | 2.836 | 2.267 | 1.192 | ||||
| C | 2.676 | 1.934 | 1.365 | 2.880 | 2.083 | 1.400 | ||||
| AsH+ | A | 3.013 | 2.379 | 3.248 | 3.324 | 2.531 | 3.298 | |||
| B | 2.910 | 2.704 | 2.527 | 3.105 | 2.883 | 2.533 | ||||
| C | 3.166 | 2.510 | 2.548 | 3.433 | 2.263 | 2.552 | ||||
| PH+ | A | 2.909 | (2.639)d | 2.234 | (2.279)d | 2.946 | 3.195 | 2.396 | 3.059 | |
| B | 2.820 | 2.285 | 2.180 | 3.079 | 2.478 | 2.179 | ||||
| C | 2.662 | 2.352 | 2.248 | 2.900 | 2.567 | 2.243 | ||||
| NH+ | A | 2.608 | 1.917 | 2.376 | 2.921 | 2.090 | 2.471 | |||
| B | 2.622 | 2.014 | 1.393 | 2.861 | 2.228 | 1.389 | ||||
| C | 2.482 | 2.082 | 1.414 | 2.738 | 2.287 | 1.418 | ||||
| S+ | A | 2.751 | 2.248 | 3.182 | 3.083 | 2.430 | 3.308 | |||
| B | 2.699 | 2.567 | 2.126 | 2.879 | 2.780 | 2.107 | ||||
| C | 3.276 | 2.308 | 2.185 | 3.431 | 2.586 | 2.134 | ||||
| Se+ | A | 2.830 | 2.411 | 3.547 | 3.107 | 2.579 | 3.706 | |||
| B | 2.744 | 2.733 | 2.524 | 2.943 | 2.934 | 2.466 | ||||
| C | 3.312 | 2.484 | 2.520 | 3.399 | 2.750 | 2.456 | ||||
| CH | A | 2.554 | 1.958 | 2.576 | 2.840 | 2.107 | 2.644 | |||
| B | 2.587 | (2.579)e | 2.032 | (2.048)e | 1.391 | (1.409)e | 2.846 (2.710)g | 2.235 (2.172)g | 1.379 (1.409)g | |
| (2.566)f | (2.062)f | (1.391)f | ||||||||
| C | 2.488 | 2.069 | 1.399 | 2.723 | 2.250 | 1.400 | ||||
| SiH | A | 2.788 | (2.666)h | 2.298 | (2.292)h | 3.280 | 3.060 | 2.447 | 3.388 | |
| B | 2.814 | 2.535 | 2.208 | 3.020 | 2.730 | 2.401 | ||||
| C | 3.070 | 2.371 | 2.406 | 3.336 | 2.529 | 2.461 | ||||
| BH– | A | 2.606 | 2.104 | 2.941 | 2.837 | 2.353 | 3.150 | |||
| B | 2.654 | 2.308 | 1.721 | 2.875 | 2.464 | 1.754 | ||||
| C | 3.011 | 2.151 | 1.689 | 3.300 | 2.330 | 1.660 |
We look first at the compounds in which E is a bare atom of group 15. Little difference in the isomer relative energies is found between the heavier Bi and As derivatives, for which isomer A is found to be the most stable, in agreement with the fact that only this form has been isolated and structurally characterized so far (see Table 1) [4,5,7]. In the case of E = P, A is still preferred, but the energy difference with the other isomers is lower than in the case of the heavier Group 15 elements. Moreover, C is more stable than B, as in the case of the Fe/Bi derivative. Going to the E = N species leads to a switching in the isomer relative stabilities: B is found to be largely preferred, especially with respect to A which is by far the less stable isomer. Thus, going up the group 15 column, the preference for isomer A decreases up to E = P and switches to isomer B for E = N.
Changing E = N into E = NH+ reverses the isomer preferences. In the latter case, A is strongly preferred and B and C are strongly disfavored. A related trend is found when changing P into PH+, where a significant reinforcement of the preference for isomer A is found. This trend is also observed, but to a weaker extent, when As is changed into AsH+. Clearly, the protonation of a bare E atom has a significant stabilizing effect on isomer A and this effect is particularly strong in the case of nitrogen. This effect is related to the repulsion between the main-group lone pairs in isomer A. In the case of E = N, the small nitrogen atoms lie close to the M3 triangle and consequently somewhat close to each other. The overlap between their lone pairs across the M3 triangle is significant and tends to destabilize the cluster. On the other hand, this lone-pair repulsion disappears upon changing N into NH+. This is clearly evidenced by the comparison of the N…N distances in the A isomers of M3(CO)9N2 and [M3(CO)9(NH)2]2+ (Table 4). In the former, they are ~ 0.2 Å longer than in the latter. It follows that the M–N bonds are also longer (thus weaker) in the E = N case. A similar effect is found with phosphorus for which the P…P distance in the A isomer of M3(CO)9P2 is ~ 0.5 Å longer than in their protonated relatives.
Despite of their size similarities, NH+ and CH behave differently. Whereas isomer A of [M3(CO)9(NH)2]2+ is by far the most stable, isomer B is preferred in the case of M3(CO)9(CH)2. The reason is likely to be related to the particular strength of the CC bond. However, with E = CH isomer A is only 6.9 and 8.5 kcal/mol less stable than B for M = Fe and Ru, respectively. This is in agreement with the fact that closo compounds of the type M3Ln(CR)2 have been isolated either with form A or B (see Table 1). Changing CH into SiH reverse the energy preference between A and B, but isomer C of M3(CO)9(SiH)2 is slightly more stable than isomer B. This is in agreement with a Si–Si bond being weaker than a CC bond. Consistently with the fact that a BB bond is almost as strong as a CC bond, the relative energies of the [M3(CO)9(BH)2] [2-] isomers are comparable to those of M3(CO)9(CH)2, with isomer B being preferred.
Finally, the E = S+ and Se+ compounds give energy results qualitatively similar to their E = P and As relatives, but with a stronger preference for isomer A.
4 Octahedral 7-SEP M4(CO)12E2 clusters
Calculations on the Fe4(CO)12E2 (E = As, P, N, CH, SiH), Ru4(CO)12Bi2 and Os4(CO)12E2 (E = Bi, As, P) series have been published previously by some of us [46]. We have performed additional calculations in order to analyze the whole series M4(CO)12E2 (M = Fe, Ru, Os; E = Bi, As, P, N, AsH+, PH+, NH+, S+, Se+, CH, SiH, BH–). For all these compounds, the relative energies of both isomers D and E (Fig. 1) are given in Table 5 and the main interatomic distances are given in Table 6, together with some experimental values for comparison. It should be noted that, depending on the nature of the cluster, two different carbonyl arrangements can be found for the D isomer: 4 bridging carbonyls (D4h symmetry) and only terminal or semi-bridging carbonyls (C4h symmetry) [46]. Only the more stable of these two conformations, which are often close in energy, is considered here. Isomer E is of C2v symmetry. Examples of these three arrangements are shown in Fig. 3.
Relative energies (kcal/mol) of the D and E skeletal isomers of the 7-SEP closo clusters M4E2(CO)12 (M = Fe, Ru, Os; E = Bi, As, P, N, AsH+, PH+, NH+, S+, Se+, CH, SiH, BH–)
| Fe | Ru | Os | ||||
| Isomer type | D | E | D | E | D | E |
| Bi | 0.0 | 9.6 | 0.0 | 5.5 | 0.0 | 5.1 |
| As | 0.0 | 6.6 | 0.0 | 3.5 | 0.0 | 3.2 |
| P | 0.0 | 3.8 | 0.2 | 0.0 | 0.0 | 1.7 |
| N | 15.5 | 0.0 | 27.7 | 0.0 | 27.0 | 0.0 |
| AsH+ | 0.0 | 33.9 | 0.0 | 1.6 | 0.0 | 33.9 |
| PH+ | 0.0 | 25.9 | 0.0 | 27.8 | 0.0 | 28.8 |
| NH+ | 0.0 | 41.0 | 0.0 | 42.0 | 0.0 | 35.0 |
| S+ | 0.0 | 37.4 | 0.0 | 37.8 | 0.0 | 34.2 |
| Se+ | 0.0 | 36.0 | 0.0 | 38.3 | 0.0 | 34.3 |
| CH | 15.6 | 0.0 | 18.2 | 0.0 | 25.1 | 0.0 |
| SiH | 0.0 | 6.3 | 0.0 | 5.8 | 0.0 | 7.0 |
| BH– | 2.9 | 0.0 | 18.0 | 0.0 | 18.6 | 0.0 |
Major optimized averaged interatomic distances (Å) of skeletal isomers D and E of the M4E2(CO)12 (M = Fe, Ru, Os; E = Bi, N, P, N, AsH+, PH+, NH+, S+, Se+, CH, SiH, BH–) series. Available experimental values for related species are given in parentheses
| Fe | Ru | Os | ||||||||
| Isomer type | M–M | M–E | E–E | M–M | M–E | E–E | M–M | M–E | E–E | |
| Bi | D | 2.794 | 2.781 | 3.916 | 2.967 (2.908)a | 2.948 (2.837)a | 4.142 | 2.986 | 2.970 | 4.147 |
| E | 2.740 | 2.792 | 3.058 | 2.933 | 2.955 | 3.114 | 2.936 (2.880)b | 2.979 (2.862)b | 3.107(3.016)b | |
| As | D | 2.698 | 2.517 | 3.350 | 2.932 | 2.665 | 3.348 | 2.908 | 2.701 | 3.502 |
| E | 2.726 | 2.495 | 2.508 | 2.939 | 2.642 | 2.557 | 2.917 | 2.642 | 2.560 | |
| P | D | 2.656 | 2.420 | 3.036 | 2.880 | 2.581 | 3.171 | 2.862 | 2.574 | 3.183 |
| E | 2.706 | 2.397 | 2.274 | 2.924 | 2.551 | 2.283 | 2.909 | 2.530 | 2.359 | |
| N | D | 2.447 | 2.060 | 1.413 | 2.672 | 2.250 | 2.443 | 2.689 | 2.267 | 2.469 |
| E | 2.657 | 2.116 | 1.267 | 2.876 | 2.400 | 1.213 | 2.825 | 2.252 | 1.341 | |
| AsH+ | D | 2.809 | 2.482 | 2.975 | 3.028 | 2.638 | 3.082 | 3.018 | 2.623 | 3.050 |
| E | 2.842 | 2.443 | 2.512 | 3.132 | 2.563 | 2.591 | 2.957 | 2.620 | 2.493 | |
| PH+ | D | 2.732 | 2.357 | 2.701 | 2.952 | 2.524 | 2.835 | 2.948 | 2.507 | 2.786 |
| E | 2.807 | 2.282 | 2.216 | 3.014 | 2.460 | 2.209 | 2.968 | 2.920 | 2.302 | |
| NH+ | D | 2.456 | 2.067 | 2.244 | 2.712 | 2.247 | 2.345 | 2.749 | 2.259 | 2.304 |
| E | 2.662 | 2.053 | 1.423 | 2.892 | 2.279 | 1.399 | 2.839 | 2.264 | 1.453 | |
| S+ | D | 2.583 | 2.376 | 3.040 | 2.875 | 2.569 | 3.141 | 2.872 | 2.555 | 3.100 |
| E | 2.730 | 2.293 | 2.310 | 2.956 | 2.516 | 2.219 | 2.902 | 2.451 | 2.541 | |
| Se+ | D | 2.667 | 2.515 | 3.327 | 2.927 | 2.686 | 3.427 | 2.924 | 2.692 | 3.447 |
| E | 2.762 | 2.465 | 2.416 | 2.973 | 2.648 | 2.556 | 2.913 | 2.630 | 2.720 | |
| CH | D | 2.469 | 2.084 | 2.267 | 2.712 | 2.254 | 2.368 | 2.737 | 2.263 | 2.348 |
| E | 2.669 | 2.077 | 1.432 (1.440)c | 2.864 (2.773)d | 2.266 (2.223)d | 1.418 (1.450)d | 2.845 (2.804)f | 2.227 (2.190)f | 1.476 (1.550)f | |
| (2.750)e | (2.218)e | (1.503)e | (2.778)g | (2.198)g | (1.540)g | |||||
| SiH | D | 2.767 | 2.355 | 2.367 | 2.961 | 2.560 | 2.943 | 2.949 | 2.556 | 2.958 |
| E | 2.641 | 2.307 | 2.342 | 2.990 | 2.507 | 2.392 | 2.958 | 2.500 | 2.383 | |
| BH– | D | 2.570 | 2.191 | 2.447 | 2.820 | 2.351 | 2.491 | 2.826 | 2.343 | 2.443 |
| E | 2.685 | 2.157 | 1.742 | 2.910 | 2.280 | 1.743 | 2.898 | 2.287 | 1.773 |
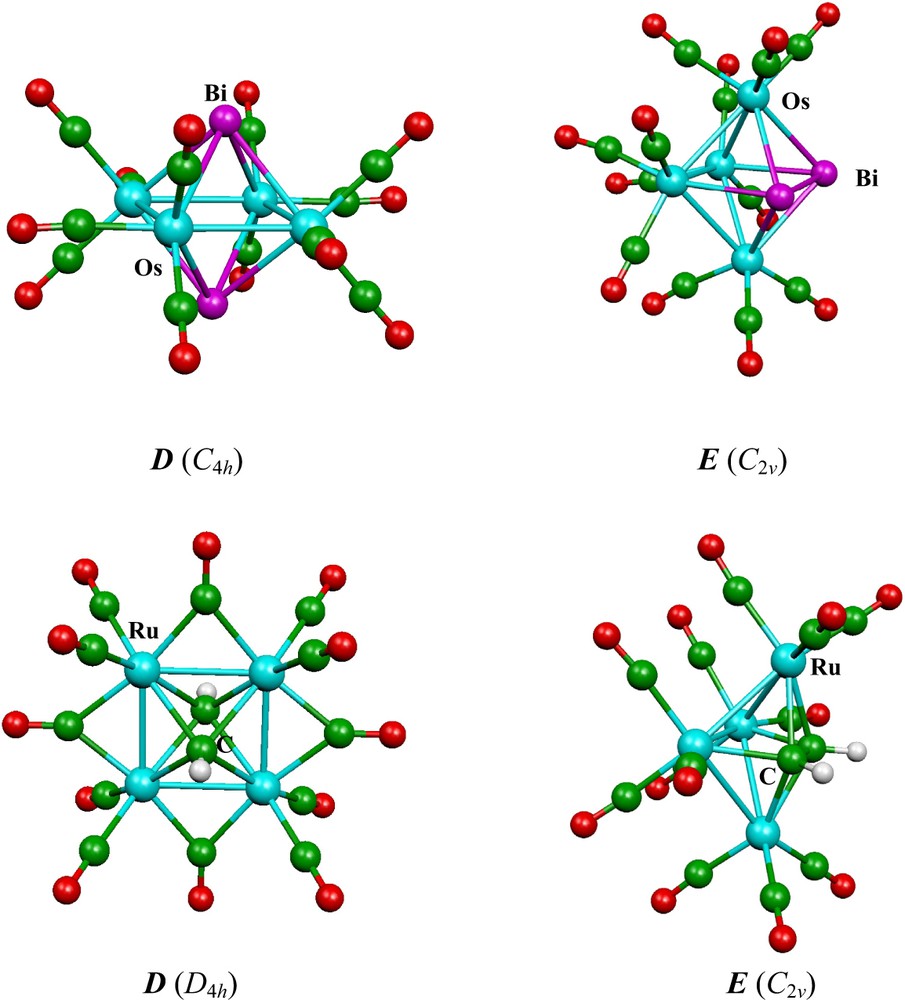
Optimized structures of skeletal isomers D and E of Os4(CO)12Bi2 and Ru4(CO)12(CH)2.
Looking first at the compounds with E being a bare atom of group 15, results similar to those of the M3(CO)9E2 series are obtained. Isomer D, in which no E–E bond is present, is favored for the heavier Bi and As elements, regardless of the nature of M. In the case of E = P, D and E are very close in energy, whereas D is largely disfavored for E = N. Lone-pair repulsion through the cluster center destabilizes strongly isomer D in the case of E = N and reduces its relative stability in the case of E = P. The protonation of E cancels this lone-pair repulsion and isomer D becomes strongly preferred in the case of E = NH+ and PH+. This effect can clearly be traced by comparing the E…E distances in the protonated and unprotonated D relatives (Table 6).
As for the M3(CO)9E2 series, in the case of E = CH, the most stable isomer is the one which contains a CC bond, i.e. E. With E = SiH, there is a slight preference for isomer D, while with E = BH- results similar to the E = CH case are found. Finally, with E = S+ or Se+ D is strongly preferred over E.
All these results are consistent with the known experimental structures of 7-SEP closo M4LnE2 clusters, except for Os4(CO)12Bi2 which has been isolated as its E isomer [5], but which is computed only 5.1 kcal/mol above D (Table 5). In particular, all the known 7-SEP clusters having E = S, Se or PR adopt the D structure, while all the numerous E = CR species adopt structure E. Unique examples of structure E with E = BR, [44] and Bi [5] are also known (Table 2).
5 Discussion and conclusion
Various parameters play a role in the relative stability of mixed transition metal/main-group clusters:
- • The relative M–M, M–E and E–E bond strengths, since the number of these bonds are different in different isomers. In particular, our results suggest that, at least with group 15 metals, strong E–E bonds, such as C–C or B–B bonds, favor isomers exhibiting an E–E bond. This could not be so straightforward for other types of clusters since the number and strength of the three types of bonds can vary in many ways.
- • The relative size of M and E. This parameter favors the isomer for which the connectivity allows the possibility of realistic bond distances and angles.
- • The lone-pair repulsion effect. This is also in part a size effect. When two bare main-group atoms of small size bi-cap a metallic polygon, they come somewhat close to each other. The strong axial overlap between their lone pairs which arises from this proximity tends to destabilize the structure. This effect is clearly evidenced by our calculations in the case of E = N. One should note that lone-pair repulsion between two main-group atoms forming an edge of the polyhedral cluster cage is much weaker.
- • The electronegativity effect. When the polyhedral cage exhibits different types of vertices, the more electronegative atoms tend to occupy one particular type of vertices. The more electropositive atoms tend to occupy the other vertices. For example in the case of a triangular bipyramid, the more electropositive atoms will tend to occupy the axial (capping) sites.
- • When possible, CR, NR and PR groups prefer to be tetravalent and sp3-hybridized. This is one of the reasons why isomer C of the M3(CO)9E2 series is particularly disfavored for these E units.
All these parameters are acting independently from each other in such a way that it is often difficult to make a priori predictions on the relative stability of skeletal isomers. Only quantum chemical calculations can help in this regard. From this point of view, the data of Tables 4 and 6 indicate that in many cases energy differences between isomers are not very large and that more than one skeletal structure should be characterized for one single compound. This is particularly true for isomers A and B of M3(CO)9(CH2) (M = Fe, Ru) and Ru3(CO)9Bi2 as well as for isomers D and E of Ru4(CO)12Bi2. In the former case the interconversion between A and B corresponds to a C–C bond activation reaction. [55] We are currently investigating this mechanism at the DFT level.
Finally, one could argue that the peripheral ligands should also play some role in the energy difference between skeletal isomers, in particular the shape of the ligand sphere could act on the shape of the cluster cage. One may wonder if the tendency of Fe for CO bridging in structure D and the preference of Os for terminal carbonyls play some role in determining the skeletal isomer preference. Obviously this is not the case, as exemplified by the similar trends afforded by Fe, Ru and Os in Table 5. One may also wonder, if, for example, isoelectronic closo clusters such as Fe4(CO)12E2 and Co4(CO)10E2 (E = 3-electron capping unit) would have the same skeletal preference. Again, one should note that except for the closo clusters of the M3Ln(CR)2 and the M4LnBi2 (M = Ru, Os) types where, depending on the nature of the metal, either the A or B (D or E) isomer has been isolated, all the other M3LnE2 or M4LnE2 compounds have been isolated in a single skeletal form for a particular nature of E, regardless of the nature of M and the number and nature of L. The exception of the M3Ln(CR)2 and M4LnBi2 (M = Ru, Os) series is well understood from the small energy differences computed for the A or B (D or E) isomers of M3(CO)9(CR)2 (M = Fe, Ru) and Os4(CO)12Bi2.
Acknowledgements
We thank the Algerian and French governments for a research grant (CMEP 01 MDU 515). Computing facilities were provided by the Pôle de Calcul Intensif de l'Ouest (PCIO) of Rennes and the Institut de Développement et de Ressources en Informatique Scientifique du Centre National de la Recherche Scientifique (IDRIS–CNRS) of Orsay.


