1 Introduction
In the course of an interdisciplinary research program aimed at the synthesis of new classes of molecule-based quantum magnets – enabling their fundamental physical properties to be explored systematically upon variations of physical or chemical parameters – novel CuII-containing coordination compounds have been prepared based on hydroquinone-derived linkers. It has been shown that this class of bridging ligands is able to mediate a magnetic exchange between CuII ions of moderate strength, i.e. of the order of 10 K [1]. Most importantly, the hydroquinone linker can be chemically modified in a way that influences the coordination geometry of the CuII ions while keeping the magnetic exchange at a moderate strength. We were able to synthesize a whole series of low-dimensional quantum-spin systems, cf. Fig. 1, including an isolated CuII dimer (TK 102), coupled-dimer systems (TK 91/TK 251), and with CuII-2,5-bis(pyrazol-1-yl)-1,4-dihydroxybenzene (CuCCP), a 1-D uniform antiferromagnetic S = 1/2 Heisenberg spin chain system. For the latter material we have performed experiments across the saturation field gμBBS = 2|J| which marks, at T = 0, the endpoint of a quantum-critical line in the B–T plane. It has been found that crossing BS is accompanied by a distinct magnetocaloric effect. In addition, a pronounced acoustic anomaly has been observed close to BS and identified as a generic property of the uniform antiferromagnetic S = 1/2 Heisenberg chain with a finite spin–lattice coupling [2]. The focus of the present work lies on a comparison of the magnetic properties of TK 91, TK 102, TK 251 and CuCCP and on an assessment of structure/property relationships; syntheses and details of the X-ray crystal structure analyses are reported elsewhere [3].
Molecular units of the modified 1,4-hydroquinone-based new quantum magnets: the isolated CuII-dimer compound TK 102, coupled-dimer systems TK 91/TK 251 and with CuII-2,5-bis(pyrazol-1-yl)-1,4-dihydroxybenzene (CuCCP), a 1-D uniform antiferromagnetic S = 1/2 Heisenberg spin chain.
2 Structural aspects
In the isolated-dimer compound TK 102, the CuII ions have a distorted square-planar coordination geometry. Each CuII ion is shielded by isopropyl groups to prevent a coordination number larger than 4. Two CuII ions are antiferromagnetically coupled creating a dimer with a singlet ground state. The isopropyl groups of the TK 102 molecule are marked in light blue in Fig. 2. Also shown in Fig. 2 is one DMF molecule which is part of the CuII-coordination sphere (light orange area). DMF has been used as the solvent during sample preparation. The complex cations and their O3SCF3 anions are connected by weak hydrogen bonds. There are five intermolecular C–H⋯O contacts with H⋯O distances between 2.56 Å and 2.68 Å and two intermolecular C–H⋯F contacts with H⋯F distances of 2.65 Å and 2.67 Å.

Copper dimers in the coupled-dimer system TK 91 and in the isolated-dimer compound TK 102. The CuII ions are indicated by the red circles and the core of the hydroquinone linkers is shown in yellow. Due to the chemical modification (light blue areas) of the hydroquinone linkers the Cu coordination and local environment of the CuII ions are different in the two compounds. The light orange areas indicate DMF molecules coordinated at the CuII ions. For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article. Masquer
Copper dimers in the coupled-dimer system TK 91 and in the isolated-dimer compound TK 102. The CuII ions are indicated by the red circles and the core of the hydroquinone linkers is shown in yellow. Due to the ... Lire la suite
The crystal structure of the O3SCF3 salt TK 91 is rather similar to the structure of the corresponding BF4 salt TK 251. In both compounds, the CuII ions are bridged by the same hydroquinone linker to form CuII dimers. In contrast to TK 102 and as a result of the sterically less demanding hydroquinone sidearms, the CuII ions in TK 91 and TK 251 possess a distorted octahedral coordination geometry. As shown in Fig. 2, the equatorial plane is spanned by the atoms N1, N2, O1, and O2. In addition, there are two long axial Cu–O bonds: a Cu–O3 (DMF) bond of 2.565(2) Å and a Cu–O1 bond of 2.434(1) Å to a neighboring dimer (not shown in Fig. 2). Again, the two DMF molecules in the CuII-coordination sphere of TK 91 are marked in light orange.
As a result of interdimer Cu–O1 contacts, TK 91 establishes a polymeric structure along the crystallographic a-axis corresponding to the needle axis of the crystal. The same is true for the BF4 salt TK 251. A picture of a high-quality single crystal is shown in the inset of Fig. 5. At first glance, both systems (TK 91, TK 251) seem to be dimerized spin chains. However, in both compounds, the cations and anions are connected by a large number of intermolecular C–H⋯O and C–H⋯F hydrogen bonds. In TK 91, there are 13 different C–H⋯O contacts with H⋯O distances between 2.51 Å and 2.75 Å and three different C–H⋯F contacts with H⋯F distances between 2.56 Å and 2.75 Å, whereas in TK 251 there are 12 different C–H⋯F contacts with H⋯F distances between 2.34 Å and 2.75 Å.

ESR resonance for a single crystal of TK 91 at 108 K. The inset displays a picture of the single crystal together with the orientation of the principal magnetic axes of a CuII center. For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.
In CuCCP, the hydroquinone core of the bridging ligand has two chelating pyrazolyl anchor groups as shown in Fig. 1. CuCCP was obtained as a microcrystalline material. Its crystal structure was determined by high-resolution X-ray powder diffraction using the method of simulated annealing [4]. The system has triclinic symmetry with a one formula unit, i.e. one CuII ion per unit cell. In the solid state, CuCCP forms 1-D coordination polymers along the crystallographic c-axis and features CuII ions in a square-planar environment (with an intra-chain Cu–Cu distance of 8.226 Å). Each CuII ion is coordinated by two oxygen and two nitrogen atoms. The individual chains are well separated and interact only through weak van der Waals bonds. Note that the distance between the CuII ions of adjacent chains is 5.169 Å along the a-direction and 7.961 Å along the b-axis [4].
According to the χmol (T) data below 1 K, CuCCP lacks a phase transition into a long-range ordered magnetic state above 0.06 K which highlights its 1-D character [5]. Selected bond length and bond angles for TK 91, TK 251, TK 102 and CuCCP are listed in Table 1 together with key parameters characterizing the magnetic properties of these compounds.
Selected bond length, bond angles and magnetic parameter for the dimer compounds TK 91, TK 251 and TK 102 and the antiferromagnetic Heisenberg spin chain CuCCP
| TK 102 | TK 251 | TK 91 | CuCCP | |
| Bond lengths (Å) | ||||
| Cu–O(1) | 1.880(2) | 1.921(3) | 1.9297(12) | 1.8(1) |
| Cu–N(1) | 1.917(3) | 1.969(5) | 1.9653(16) | 2.0(1) |
| Cu–O(2) | 1.965(2) | 2.012(4) | 2.0010(14) | 1.8(1) |
| Cu–N(2) | 2.076(3) | 2.089(4) | 2.0754(15) | 2.0(1) |
| Cu–O(1)#1 | 2.514(4) | 2.4344(13) | ||
| Cu–O(3) | 2.534(5) | 2.5652(16) | ||
| Angles (deg) | ||||
| O(1)–Cu–N(1) | 94.03(11) | 92.78(16) | 90.85(6) | 97(1) |
| O(1)–Cu–O(2) | 89.77(10) | 87.64(15) | 88.07(5) | 83(1) |
| N(1)–Cu–N(2) | 180(2) | |||
| O(1)–Cu–O(2) | 180(2) | |||
| N(1)–Cu–O(2) | 170.78(13) | 173.24(19) | 175.04(6) | |
| O(1)–Cu–N(2) | 169.88(12) | 172.93(18) | 175.61(6) | |
| N(1)–Cu–N(2) | 86.20(11) | 92.95(18) | 93.51(6) | |
| O(2)–Cu–N(2) | 91.55(10) | 87.16(16) | 87.55(6) | |
| Magnetic parameter | ||||
| gz | 2.22 | 2.27 | 2.14 | |
| gx,y | 2.06 | 2.04 | 2.01 | |
| afm ΘCW | 2.2 K | 3.7 K | 6.6 K | 25.0 K |
| μeff (300 K) | 1.95μB | 1.83μB | 1.91μB | 1.96μB |
| J1/kB | 4.0 K | 7.8 K | 9.9 K | 21.5 K |
| α | 0.00 | 0.05 | 0.10 | 1.00 |
3 Magnetic susceptibility
The magnetic characterization of all samples was carried out by employing a Quantum-Design SQUID magnetometer in the temperature range from 300 K to 2 K and fields up to 5 T. In the temperature range 0.06 K ≤ T ≤ 2.0 K, the magnetic susceptibility was determined with an ac-technique in a top loading 3He/4He dilution refrigerator.
In the temperature range from 300 K to 50 K, the molar magnetic susceptibilities of the dimer compounds TK 102, TK 91 and TK 251 exhibit a Curie–Weiss-like behavior with antiferromagnetic Curie–Weiss temperatures of ΘCW = 6.6 K (TK 91), 3.7 K (TK 251) and 2.2 K (TK 102). The effective magnetic moments at room temperature for all dimer compounds range from 1.81μB to 1.95μB. They are slightly enhanced in comparison to the value of a free CuII ion (1.73μB) and exhibit only a weak temperature dependence down to 25 K. These magnetic parameters are a clear indication that the magnetic coupling constants in these novel dimer compounds are of only moderate strength as expected for the modified hydroquinone linkers employed.
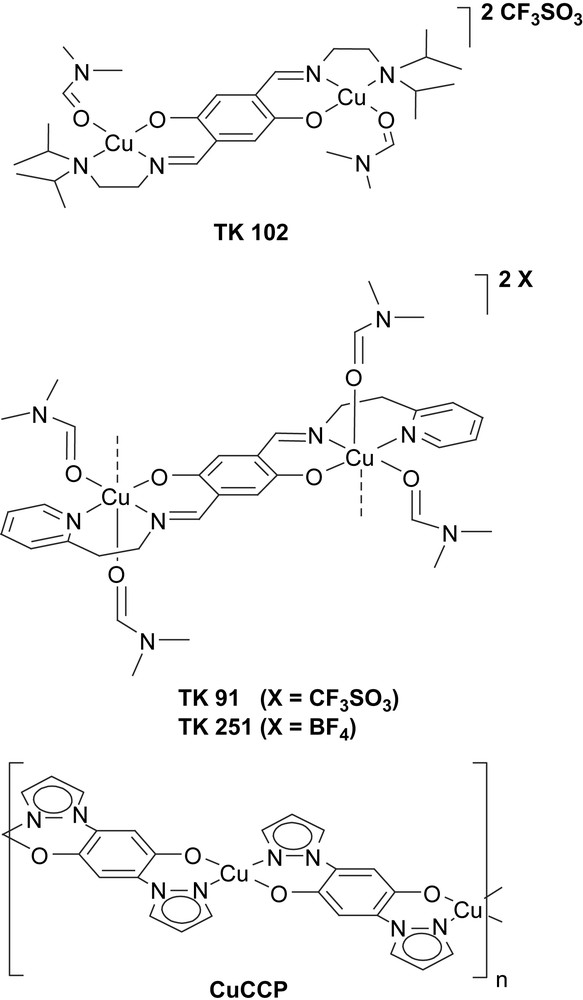
Fig. 3 exhibits χmol (T) for a single crystal of the coupled-dimer compounds TK 91 (open squares) and pressed powder samples of TK 251 (filled triangles) together with the pressed powder sample of the isolated-dimer system TK 102 (open circles). After subtracting the diamagnetic core contribution for the different materials, the data have been fitted by employing a numerical expression given in Ref. [6]. This function has been used to describe especially the low-temperature susceptibility of spin chains with dimerisation parameters α = J2/J1 ranging from α = 0 (isolated dimer) to 1 (uniform Heisenberg spin chain), employing the dominant magnetic coupling constant J1 and α as fit parameters. The Curie-contribution of uncoupled S = 1/2 spins was included in the fitting procedure and had been subtracted from the data displayed in Fig. 3. The content of uncoupled spins in the dimer compounds varies between 0.5% for high-quality single crystals of TK 91 and approximately 40% for both powder samples TK 251 and TK 102.
Magnetic susceptibility as a function of temperature for the different dimer compounds. Open squares TK 91, filled triangles TK 251 and open circles TK 102. The solid lines are fits to the experimental data according to Ref. [5]. The Curie-contribution of uncoupled S = 1/2 spins was included in the fitting procedure. The following amount of uncoupled S = 1/2 spins has been subtracted: TK 91 (single crystal) 0.5%; TK 102; TK 251 (powder) 40%.
The solid lines in Fig. 3 are fits to the experimental data, employing the expression given in Ref. [6]. The so-derived antiferromagnetic coupling constants J1 and dimerisation parameters α are listed in Table 1. The data clearly indicate that J1 and α become reduced on going from TK 91 over TK 251 to TK 102.
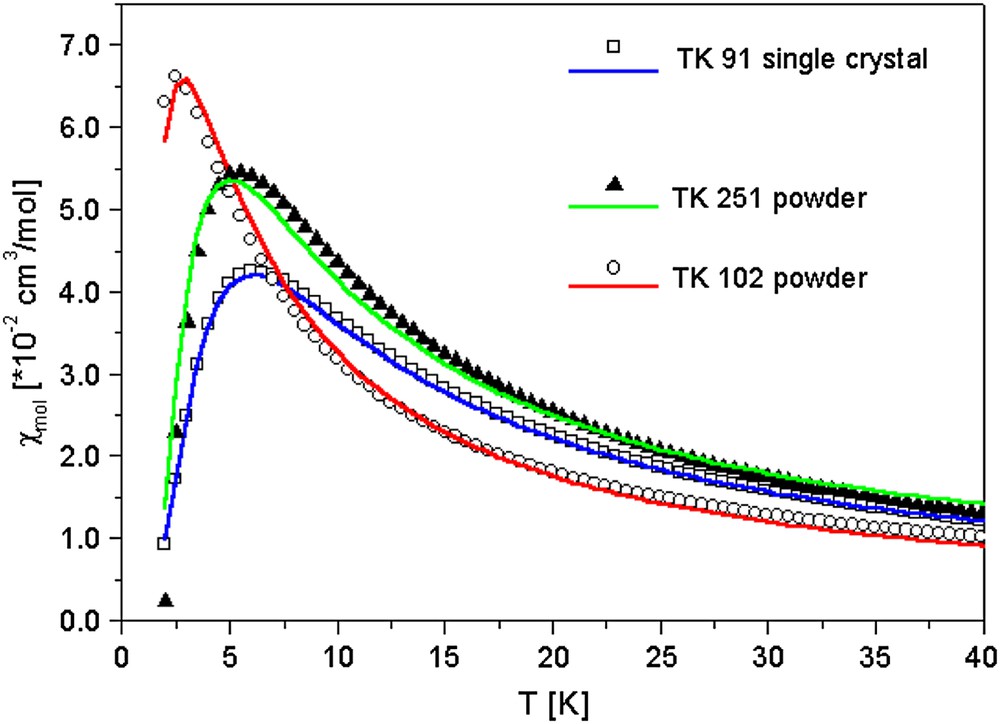
Fig. 4 shows the molar magnetic susceptibility χmol of a pressed powder sample of CuCCP as a function of temperature for T ≤ 80 K, see also Ref. [2]. The data have been corrected for the paramagnetic signal of uncoupled S = 1/2 spins and the temperature-independent diamagnetic core contributions. Fitting the low-temperature data for 0.06 K ≤ T ≤ 1.1 K to a Curie–Weiss-law, we obtained a concentration of 4% uncoupled S = 1/2 spins with a very small antiferromagnetic Curie–Weiss temperature of ΘCW ∼ −10 mK [2,5].
Magnetic susceptibility as a function of temperature of the uniform S = 1/2 antiferromagnetic Heisenberg spin chain CuCCP. The solid line is a fit to the experimental data according to Ref. [5]. The inset shows the effective magnetic moment of CuCCP for temperatures 2 K ≤ T ≤ 320 K. A Curie-contribution of 4% uncoupled S = 1/2 spins has been subtracted from the data.
For high temperatures and down to 120 K, χmol (T) of CuCCP follows a Curie–Weiss-like temperature dependence with an antiferromagnetic Curie–Weiss temperature ΘCW ∼ 25 K. Upon cooling, χmol (T) exhibits a broad maximum around 15 K, typical for a 1-D antiferromagnet [6]. For temperatures below 15 K, χmol (T) slowly decreases, extrapolating to a finite value for T → 0 as expected for a 1-D uniform afm S = 1/2 Heisenberg spin chain [6,7]. The solid line in Fig. 4 is a fit to the experimental data employing the expression given in Ref. [6] from which an antiferromagnetic intra-chain coupling constant J = 21.5 K/kB has been obtained [2]. The absence of a 3-D magnetic ordering down to 0.06 K implies a ratio of inter-chain to intra-chain coupling J⊥/J < 10−4 [8]. According to these distinct magnetic properties, the coordination polymer CuCCP can be considered an excellent model system for a 1-D S = 1/2 antiferromagnetic Heisenberg chain.
The inset of Fig. 4 displays the temperature dependence of the effective magnetic moment of the CuII ions in CuCCP. In the temperature range from 300 K down to 100 K, the effective magnetic moment becomes slightly reduced from 1.95μB to 1.76μB. Below 100 K, the magnetic coupling between the individual CuII ions, which causes the formation of 1-D antiferromagnetic Heisenberg spin chain, leads to the strong reduction of μeff below 100 K clearly seen in the inset of Fig. 4.
4 Ab initio calculations
We have investigated the electronic properties of the Cu-based organometallic systems by performing ab initio density functional calculations within the generalized gradient approximation (GGA) [9]. As a basis set, we considered the linearized muffin tin orbital method (LMTO) based on the Stuttgart TBLMTO-47 code [10]. Our aim has been to get a reliable estimate of the nature of the interaction paths in these compounds based on the ab initio calculations. For this purpose, we applied the tight-binding-downfolding procedure [11] which obtains the effective Cud–Cud hopping parameters by downfolding all the degrees of freedom in the band structure calculation other than the Cud bands at the Fermi level. We analyzed two systems, the polymer CuCCP and the coupled-dimer system TK 91.
The predominant hopping path, t = 79 meV, obtained from the CuCCP system, is between Cu neighbors along the chain. This path is mediated by the hydroquinone linker. The next important hopping term is almost an order of magnitude smaller than t, t′ = 8 meV and defines the effective interaction path between coppers belonging to different chains along the a-direction. This ab initio calculation confirms the experimental observation that CuCCP is a quasi-one dimensional system with weak inter-chain interactions.
A rough estimate of the antiferromagnetic superexchange between the Cu ions along the chain can be obtained by using the expression J = 4t2/Ueff, where Ueff is the effective onsite Coulomb repulsion on the Cu site and t is the ab initio derived hopping integral. Considering usual Ueff values for Cu oxides Ueff = 4–6 eV we get an estimate J ∼ 58 K (Ueff = 5 eV) which is somewhat above the experimental value but remains of the same order of magnitude. A detailed ab initio investigation of this system including structural relaxation studies and chemically modified CuCCP structures has been presented in Ref. [12].
The coupled-dimer system TK 91 was also investigated with the downfolding method. Interestingly, we found that the strongest interaction path t = 43 meV is between coppers that are as far apart as 8.4 Å and linked by the hydroquinone group, while the hopping between nearest neighbor coppers at a distance of 3.4 Å is almost zero. The next relevant hopping term t′ is between fifth nearest neighbor Cu ions along the a-direction t′ = 23 meV. The description of TK 91 concluded from these calculations is that of Cu dimers containing the hydroquinone as bridging ligand. These dimers are weakly coupled within the 3-dimensional structure. An estimate of the intradimer coupling can be obtained – as in the case of CuCCP – by considering the expression J = 4t2/Ueff with t being the intradimer hopping integral. We obtain J ∼ 17 K which, though overestimating the experimental value somewhat, is within the same order of magnitude.
5 Electron-spin resonance
The magnetic resonance experiments were performed in the mm- and sub-mm-wave region between 28 and 420 GHz using Gunn- and IMPATT-diode together with frequency multipliers in a home-built spectrometer. For measurements with frequencies up to 42 GHz, specially designed cavities were used.
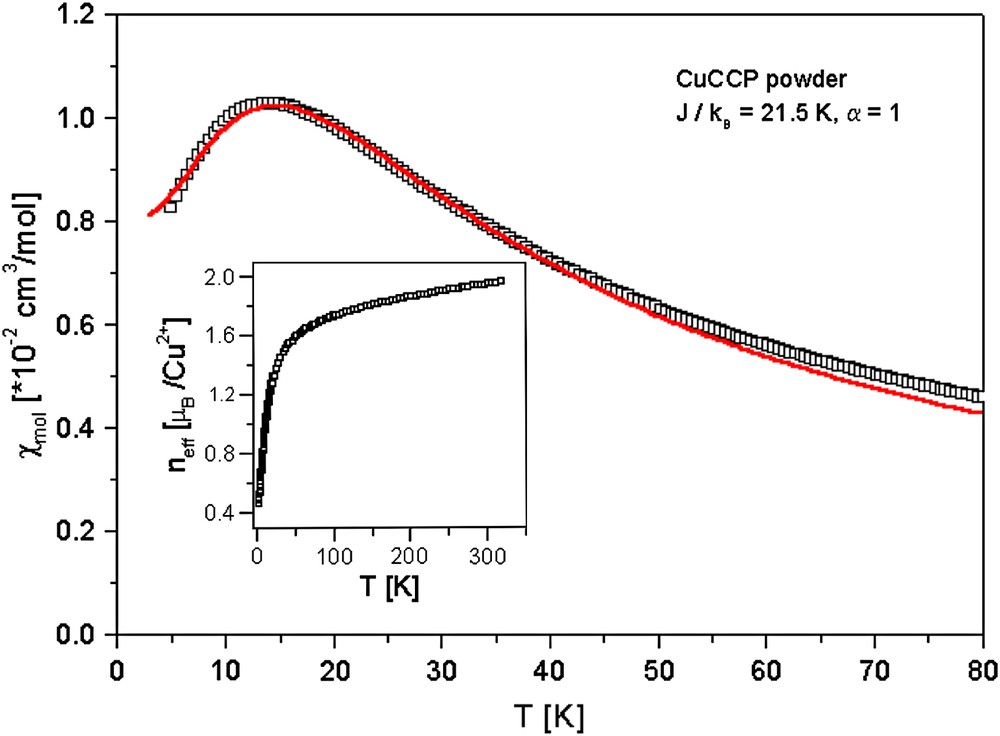
Electron-spin resonance (ESR) experiments on single crystals of TK 91 were carried out in the frequency range 26–40 GHz and for temperatures 4.2 K ≤ T ≤ 140 K. The ESR measurements detect two non-equivalent magnetic centers of copper ions at any orientation of the sample with respect to the applied magnetic field. Each of these has an axial anisotropy with the g-values in the range of 2.04–2.27 at T = 108 K. The local magnetic axes of these centers are almost perpendicular to each other. The axial anisotropy is in accordance with the local environment of this coupled-dimer compound determined by X-ray crystal structure analysis.
Fig. 5 exhibits a typical ESR single-crystal spectrum of TK 91 at T = 108 K and a frequency of 39.852 GHz. The narrow line is the signal of a small amount of the free stable radical DPPH used for calibration. The two non-equivalent CuII centers are clearly visible in the excitation spectrum. The inset of Fig. 5 displays a picture of a single crystal of TK 91. Also indicated in the inset is the orientation of the applied magnetic field (blue arrow) which is tilted by 48.65° with respect to the a-axis of the single crystal. In this orientation, the external field is parallel to one of the principal magnetic axes of a CuII center with g = 2.27. In this field orientation, the second CuII center exhibits a g-value of 2.09. The values of these g-factors are directly connected with the local environment of the CuII ions and they are in the range which is expected for sixfold coordinated copper ions [13].
Fig. 6 shows the typical ESR signal of a powder sample of the isolated-dimer compound TK 102. The data were taken at 2.75 K, i.e., around the maximum of the magnetic susceptibility. The special shape of this broad resonance is due to the averaging of over all possible field orientations of the copper centers in the powdered sample. From the edges of the powder-resonance spectrum, we determined the extremal g-factors gz = 2.22 and gx,y = 2.06, which have a temperature variation of only 0.1% between 120 K and 2 K. These g-factors differ clearly from the values determined for TK 91. The difference is approximately 2.2% for gz and 1.4% for gx,y directly reflecting changes in the coordination and local environment of the CuII ions, on passing from an elongated octahedral (TK 91) structure to a distorted square-planar (TK 102) environment.

ESR resonance of a powder sample of TK 102 at 2.75 K and 35.55 GHz.
Fig. 7 shows the powder spectra for CuCCP taken at the high frequency of 330 GHz and temperatures of 29.7 K and 5.7 K. The temperature dependence of the integrated signal is in accordance with χmol (T). It is obvious that in this temperature range gz and gx,y are temperature independent with values of gz = 2.14 and gx,y = 2.01. These numbers are comparable with g-values expected for a CuII ion in a square-planar coordination [13]. A comparison with the g-factors of TK 102 reveals a difference of approximately 3.7% for gz and 2.5% for gx,y. Again, this behavior indicates the strong influence of the local Cu environment. A deviation from the square-planar CuII coordination to a distorted one leads to these large differences in the g-factors.
ESR resonance of a powder sample of the 1-D Heisenberg spin chain CuCCP at 5.7 K and 29.7 K determined at a frequency of 330 GHz.
6 Discussion
The anisotropies of the g-values found in the ESR experiments for the present series of hydroquinone-based low-dimensional CuII quantum-spin systems are in agreement with the structural investigations on the various compounds. The question at hand is whether there is a correlation between the structural and magnetic properties within this series of compounds. In all systems described in this paper, the dominant magnetic exchange is mediated by the modified hydroquinone linkers. As expected, the magnetic exchange is of moderate size for all systems ranging from J/kB = 21.5 K (CuCCP) to J1/kB = 4.0 K for TK 102. Table 1 indicates that a correlation exists between the size of J/kB and the extent to which the CuII ion is dislocated from the O(1,2)N(1,2)-plane. CuCCP, possessing the largest coupling constant of J/kB = 21.5 K within this new series of low-dimensional spin systems, has its CuII centers in an ideal square-planar coordination environment. Each CuII ion lies precisely within the O(1,2)N(1,2)-plane and the angles N(1)–Cu–O(2) and O(1)–Cu–N(2) are 180° resulting in a magnetic coupling constant of J/kB = 21.5 K. If the position of the CuII ion is slightly above the O2N2-plane as in TK 91, where the angles N(1)–Cu–O(2) and O(1)–Cu–N(2) are 175.04° and 175.61°, respectively, the coupling constant J1/kB is reduced to 9.9 K. This trend continues for TK 102 exhibiting a coupling constant of 4.0 K and bond angles for CuII of 170.78° and 169.88°. Calculating the displacements u of the CuII ions from the distortion angles we obtained a nearly linear dependence between J/kB and u with a value of −(109 ± 9) K/Å.
7 Summary
We have synthesized a new family of low-dimensional quantum-spin systems based on hydroquinone-derived linkers connecting CuII ions carrying a spin of S = 1/2. This family includes isolated CuII dimers, various coupled CuII-dimer systems and a 1-D uniform S = 1/2 Heisenberg antiferromagnetic chain. The antiferromagnetic coupling constants are of moderate strength with values in the range from J/kB = 21.5 K to 4.0 K. By relating the magnetic properties to the structural features of the individual compounds of this family, we have been able to deduce a correlation between the size of the magnetic coupling constant and the position of the CuII ions. An increase of the displacement of the Cu ion with respect to the ideal square-planar coordination leads to a near linear decrease of J within this series of compound, where the magnetic coupling is mediated by modified hydroquinone linkers.
In addition, the first principles calculations performed here are valuable hints for understanding the nature of the microscopic interactions in these organometallic systems.


