In various steps of the nuclear waste disposal appears the need for a good understanding of the chemical properties of radionuclide-containing species, either in molecular forms, aggregates or in bulk materials. The processes under investigation may include ionic recognition for selective extraction of actinides in highly active waste, or confinement and storage. Among the various pathways that chemists may explore to gain insights into the properties of such uncommon and radiotoxic species, theoretical modelling has received particular attention [1–6]. Its added values rely on its capability to rationalize data difficult to understand experimentally otherwise, and on a predictive role, particularly for very hazardous species, provided that the simulation gives reliable data. Fortunately, much progress has been made these last twenty years in the quantum chemical modelling of elements the due to methodological developments adapted to such elements, especially in the Density Functional Theory (DFT) and in the treatment of relativistic effects [7,8].
The present study will be devoted to the theoretical approach for the selective extraction of heavy trivalent actinide (An(III)) species (namely Am and Cm) from highly active nuclear waste, and in particular from non-negligible quantities of trivalent lanthanide (Ln(III)) species. The underlying question for such extracting processes is how to design an organic molecule able to extract An(III) cations selectively from acidic aqueous solutions containing a mixture of Ln(III) and An(III) cations. Among the chemical difficulties to be faced are firstly the high similarity in the coordination properties of both families, which may be classified as hard acidic cations in the Pearson theory of Hard and Soft Acids and Bases (HSAB) [9]. Secondly, their high hydrophilicity leads to a competition between any extracting ligand and water molecules [10,11]. It is now well established that a means to discriminate between 4f and 5f ions is to take advantage of a possible difference in the nature of their bonding towards well-chosen ligands [10]. Quantum chemical calculations are thus well suited to provide more insights into the electronic structure of the bonding.
Within this framework, our main interest lies in the bonding properties of N-heterocyclic ligands towards Ln(III) and An(III) because they have been the subject of numerous studies, either on their interesting selectivity in extracting processes [10,12–16], or on more fundamental topics [3,17–21]. The theoretical description of the bonding between f-element ions and ligands has gained a lot from the use of the coordination chemistry regarding the metal–ligand bond, such as the HSAB theory [9] and the Dewar–Chatt–Duncanson model for donation/backdonation [22,23]. By comparing the coordination properties of various N-donor ligands to Ln(III), U(III) and heavier An(III) cations [6,20,24–26], we have been able to check the reliability of a DFT combined to a quasi-relativistic approach. We have also managed to rationalize some bonding features, especially in Ln(III) and U(III) species, relying on experimental grounds. The main conclusions were that Ln(III), whatever the ligand is, gives strongly ionic bonds, whereas U(III) exhibits a more covalent bonding with π-acceptor ligands due to a significant backdonation. In heavier An(III) such as Am and Cm, experimental data are rather scarce, thus the reliability of calculations have been confronted to more accurate calculations such as multiconfigurational approaches of the wavefunction [27] and topological descriptions of the bonding [25]. For such heavy actinides, the covalent character strongly decreases with respect to uranium, and it thus becomes very difficult to obtain a clear description of the bonding, especially as it seems very dependent on the structure of the complex [2,28].
This article will thus be focused on the following questions. How does the bonding behaviour of possible extracting molecules towards Ln(III) and An(III) (including uranium as well as Am and Cm) depend on the coordination sphere of the f-element cation? How may experimental data provide new insights for theoreticians and support their conclusions, and reciprocally what help theory bring to experimentalists?
To address these issues, we will compare the M–L bonding within several families of complexes, with two limiting cases: the neutral complexes with three counterions of general formula F3M–L (M being Ln(III) or An(III), L being a nitrogen heterocyclic ligand known to give good selective extraction properties), and the triply-charged ML33+ species, which have been experimentally characterized. The intermediate case between these limits will also be examined, i.e. when counterions are lacking, thus giving charged complexes such as [FnM–LSp](3−n)+(n = 2, 1, 0; S being a water molecule and p = 0, 1, 2 or 3). Such stoichiometries are quite frequent with trivalent f cations [2,3,14,15,19].
The calculations have been carried out using the Density Functional Theory (DFT) with the Amsterdam Density Functional package (ADF 2004.01) [29–31], which is widely used for heavy metal complexes. A Generalized-Gradient Approximation (Becke–Perdew) [32,33] functional has been used, combined with a quasi-relativistic treatment through the scalar ZORA formalism [34] applied to valence electrons. Core electrons were kept frozen, with a small core density calculated by a four-component Dirac–Fock method. Finally, the basis sets were the Slater triple-zeta + two polarization function (TZ2P) for light elements and triple-zeta + one polarization function (TZP) for f elements. The spin state was in each case chosen following the first Hund's rule, in agreement with previous multiconfigurational calculations [27,35]: S = 7/2 for Gd3+ and Cm3+; S = 3/2 for U3+ and S = 3 for Am3+. More accurate computational details have been reported elsewhere [24].
1 MF3–L species
The model compounds is of general formula F3M–L, where M is La(III), Gd(III), U(III), Am(III) or Cm(III), and L is one of the investigated N-heterocycles shown in Scheme 1, together with the abbreviation used throughout the paper.

These heterocycles are used as coordinating sites for polydentate extracting ligands, and BTP (2,6-bis(1,2,4-triazinyl)-pyridine) is the model species for alkylated derivatives which are now well-known as powerful selective extractants for An/Ln separation [3,12–15].
The general starting geometry for the model complexes is given in Scheme 2 (for L = py).
Note that for tz124, two possible coordination sites are available, either with the isolated N atom (abbreviated as tzN below) or with an N atom adjacent to another N atom (noted tzNN below).
Such a geometry may be viewed as a model for the experimental triscyclopentadienyl derivatives of Ln(III) and U(III), of formula Cp3M–L, which have been used to compare the M–L bonding properties of Ln(III) and U(III) with various neutral ligands [21,36–39]. We have shown in previous studies that the theoretical modelling of such model complexes with L = pz or CO [6,20,26] was able to reproduce the structural and vibrational trends experimentally observed on these Cp derivatives, or on other families of complexes based on tripodal ligands [20]. The main feature resulting from these experimental and theoretical investigations was, as mentioned above, the presence of a U(III)–L backbonding interaction, whereas Ln(III) species did not exhibit any covalency effect.
Three main properties have been computed, and will be described below: their structures, as obtained by geometry optimizations and frequency calculations, the energetic stabilization, and their electronic structure.
1.1 Geometry optimizations
Geometry optimizations have led to two types of structures, depending on M and L. For ligands py, pz, tz135 and tzN, the final geometry was close to the starting one (Scheme 2), whereas with pydz and tzNN, an η2 coordination mode has been obtained (see Scheme 3 for L = pydz).
The nature of this stationary point has been checked for pydz and tzNN, by calculating harmonic vibrational frequencies, which were found all real. It is interesting to note that such an η2 geometry had been observed for a Cp3 Ce–pydz species by X-ray diffraction [21].
It is necessary at this point to mention that the precision on distances can be evaluated at ca. 0.02 Å, thus differences smaller than this value are not significant. Let us note that the M–F distances for a given metal do not vary with the ligand, and very weak variations are observed with the metal: d(LaF) ≈ 2.15 Å, d(UF) ≈ 2.08 Å, d(GdF) = d(AmF) ≈ 2.09 Å, pointing to the ionic nature of the M–F bond. M–L distances are in contrast more interesting as they provide access to covalency effects. Fig. 1 thus shows the M–L distances for all f elements, in the order of decreasing ionic radius [40], La3+ being the larger one and Gd3+ the smaller cation. For all ligands, a decrease is observed in the d(U–L) distance, reflecting the already known backdonation interaction. La(III)–L distances are the longest ones, in agreement with the highest ionic radii (1.032 Å). For La, Gd and Cm, we can distinctly see two groups of distances; one corresponding to the η1 ligands and the second one with higher distances to the η2 ligands (tzNN and pydz). This behaviour is natural since η2 ligands increase the coordination number in the coordination sphere, and underlines that Cm behaves in the same way as lanthanide counterparts. In contrast, for Am(III) the tzNN and pydz ligands give shorter distances than for the Gd and Cm homologues, whereas for the other ligands, the distances are very similar to those for Gd(III) and Cm(III). This observation may point to a different binding type, compared to La, Gd and Cm.
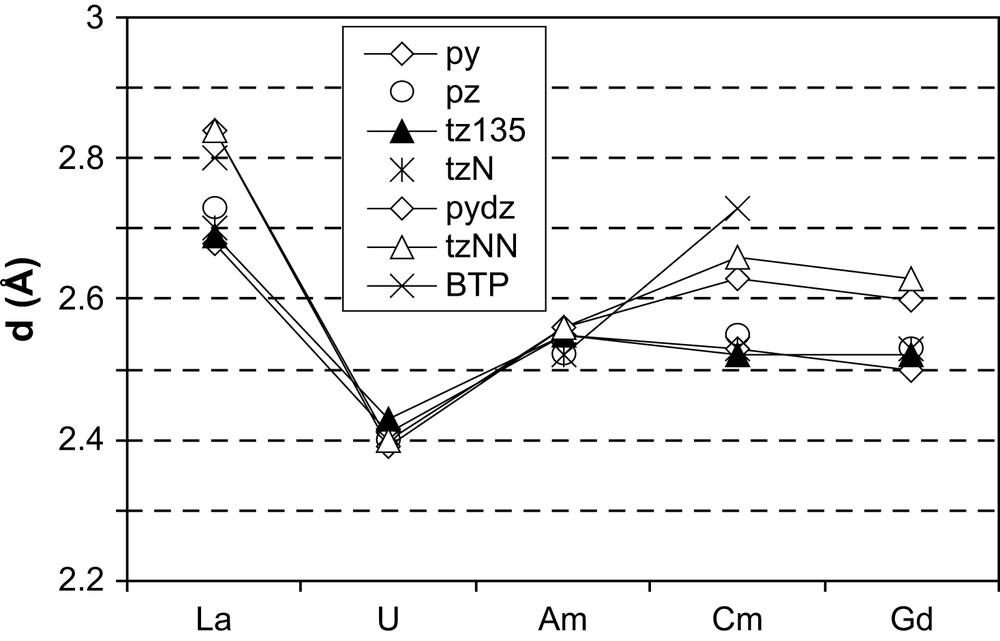
M–L distances (Å) in F3M–L ligands after full geometry optimizations.
As expected, M–L distances increase with BTP as it is a tridentate ligand. At this point, the case of F3U–BTP is quite particular: starting from an electron density corresponding to a U3+ ion, the electronic convergence leads to a U(IV) ion for the fundamental state, and the geometry cannot be directly compared to other F3M–BTP species. This oxidation “in silico” is in good agreement with the experimentally well-known ease of oxidation of U(III) and is consistent with the low π∗ level (LUMO) of the BTP ligand.
1.2 Total bonding energy and decomposition into orbital and electrostatic terms
Although structural parameters may help to identify different bonding features, the description of the bonding needs to take into account the various stabilization factors governing the interaction between MX3 and the L fragments, especially in terms of the electrostatic interaction and a possible covalent contribution. The energy-partitioning scheme available in ADF [31,41] is particularly well suited for this purpose. Indeed, the total bonding energy (TBE) of a complex is the sum of three terms: ΔETBE = ΔEelec + ΔEP + ΔEorb = ΔEster + ΔEorb, where ΔEelec is the electrostatic stabilization energy between MF3 and L when placed in the final geometry, and ΔEP is the Pauli energy due to repulsions between the electron clouds of both fragments in the molecular geometry. Their sum gives the so-called “steric energy” in ADF (ΔEster), and can be seen as the global stabilization or destabilization between MF3 and L fragments positioned at the molecular distance. Finally, the orbital energy (ΔEorb) is the energy gain when the whole electron structure has relaxed, starting from the superposition of the electron densities of both fragments and after the SCF process. It may a priori include internal repolarization within each fragment and a possible covalent interaction between the fragments.
Such an analysis has been performed on all the systems investigated here, and the results are shown in Fig. 2. It is necessary to mention first that due to the precision of calculations and to the BSSE (Basis Set Superposition Error), differences less than 0.04 eV cannot be considered significant. The trends for TBE (Fig. 2a) in both lanthanide complexes (La, Gd) are very similar. For actinides, there are clearly two different behaviours. Uranium species are more stabilized – compared to Ln homologues – and a huge stabilization appears due to the η2 coordinated ligands (pydz and tzNN). In contrast, TBEs for americium and curium species are quite close to those of lanthanides.
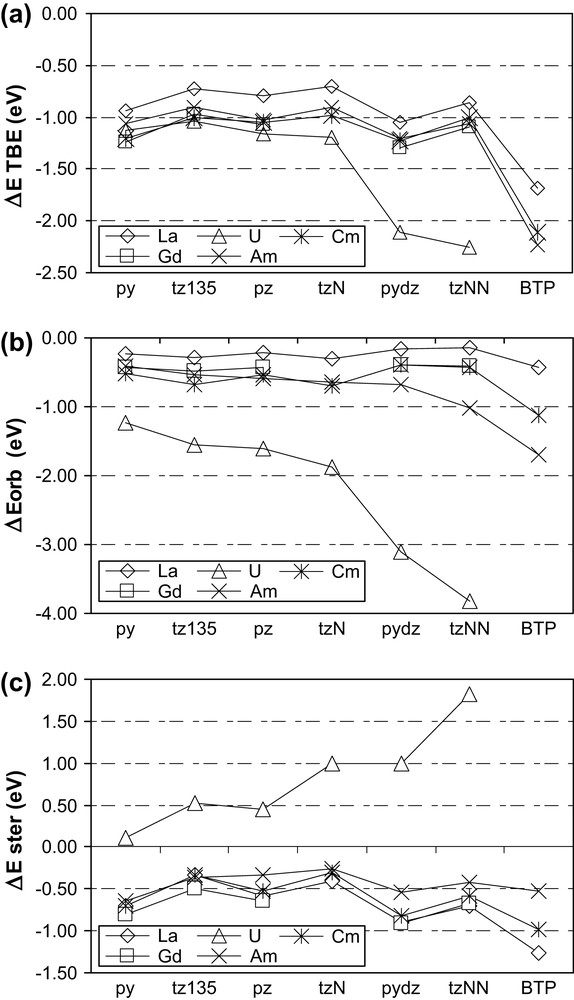
Energetic analysis (see text for definitions of the energy terms) of the formation of MF3–L, starting from the fragments MF3 and L, in the final geometry. (a) Total bonding energies (eV); (b) orbital energies (eV); (c) steric energies (eV).
The orbital contribution (Fig. 2b) for U(III) species is much more negative than for all other f elements, due to the backbonding interaction. This interaction is even strengthened when considering the favorable η2 mode with pydz and tzNN ligands. The orbital terms for both Ln(III) and for Am and Cm are very similar, except for the pydz, tzNN and BTP ligands bonded to Am(III), where a better orbital stabilization appears.
Finally, the “steric” term (Fig. 2c), which accounts for the global stabilization – or destabilization – due only to electrostatic interactions, is also comparable for all Ln(III), Cm(III) and Am(III). For U(III), the steric contribution is always destabilizing, because the U–L distances are always shorter than the hypothetical one obtained if only electrostatic interactions were present. The backdonation effect is responsible for this shortening, which logically increases the Pauli repulsion term, leading to positive steric terms. Thus the steric term increases with ligands favoring backdonation: pydz and tzNN.
1.3 Charge distribution analysis
Mulliken charges have been chosen although it is well known that their values are strongly dependent on calculation parameters. However, their trends, when considering similar species under identical calculation procedures, may reflect some physical features. This had been checked previously on f-element complexes by comparing Mulliken charges to other more “sophisticated” charge analyses, as those obtained from NPA (Natural Population Analysis) or topological approaches (AIM or ELF) [25].
We have reported in Table 1 the variations of Mulliken charges (ΔQ, |e−|) for M and L, associated with the complexation from MF3 to MF3–L. The charge of the counterion F− shows always a very weak decrease (between −0.02 and −0.04 |e−|) upon complexation, whatever the ligand and the metal ion are. Both lanthanides give the same trends, i.e. a very weak increase in electron density, coming from a weak donation of the ligand. This latter effect is also seen on the L charge, which is in the range 0.08–0.13 |e−| for all ligands. For U(III), as can be seen from the negative charge appearing on L, the backbonding interaction is present whatever the ligand may be. The magnitude of this effect drastically increases from py to pz and to tzN, and then to pydz and tzNN. For these latter, the amount of backdonation is enhanced due to the favorable η2 coordination mode. This increase of backdonation is in line with the evolution of the LUMO (π∗) energy level from py to pz and to tz. It should be noted that ΔQL for uranium species is in fact the superposition of the backdonation and donation effects. But as shown in a previous detailed analysis of the bonding in F3U–CO, the backbonding contribution is much stronger than the donation interaction [25].
Variations of the Mulliken partial charges (|e−|) from MF3 to MF3–L for M (ΔQM) and L (ΔQL), for M = La, Gd, U, Am, Cm
| L | La | Gd | U | Am | Cm | |||||
| ΔQM | ΔQL | ΔQM | ΔQL | ΔQM | ΔQL | ΔQM | ΔQL | ΔQM | ΔQL | |
| py | −0.04 | 0.13 | −0.03 | 0.12 | 0.25 | −0.15 | −0.06 | 0.14 | −0.06 | 0.14 |
| pz | −0.03 | 0.12 | −0.04 | 0.11 | 0.37 | −0.28 | −0.02 | 0.09 | −0.05 | 0.13 |
| tz135 | −0.03 | 0.09 | −0.05 | 0.11 | 0.37 | −0.28 | −0.02 | 0.07 | −0.03 | 0.11 |
| tzN | −0.02 | 0.11 | −0.04 | 0.1 | 0.39 | −0.32 | 0 | 0.05 | −0.02 | 0.1 |
| pydz | −0.01 | 0.1 | −0.02 | 0.09 | 0.49 | −0.38 | 0.02 | 0.03 | 0 | 0.08 |
| tzNN | 0 | 0.09 | −0.01 | 0.08 | 0.52 | −0.45 | 0.05 | −0.03 | 0.01 | 0.07 |
| BTP | 0.01 | 0.17 | 0.68 | −0.66 | 0.15 | −0.18 | 0.01 | 0.08 |
Both heavy actinides Am(III) and Cm(III) exhibit more or less the same trends as Ln(III) for almost all ligands. Cm(III) is clearly “lanthanide-like”, whereas Am(III) seems to be intermediate between a lanthanide and uranium. Indeed, a decrease in the L charge for pydz, tzNN and BTP is observed for Am, the latter two being negative, pointing to a very weak backdonation effect. This had been observed in previous detailed analyses (AIM and ELF) [25] where Am(III) was coordinated to a strong π-acceptor ligand (CO). This weak backdonation is consistent with the slight shortening of the Am–L distance compared to other Ln or to the Cm species observed with BTP or η2 ligands, and with the weakly increasing orbital stabilization with these same ligands.
For “UF3–BTP”, the ligand charge (−0.8 |e−|) and the strong increase in the charge on U reflect the oxidation process to a species best described as “F3U(IV)–BTP−”. The KS highest occupied orbitals, not shown here, are clearly consistent with a U(IV) cation (f2 configuration) interacting with a radical anion BTP−.
The main features of the M–L bonding in MF3–L, and more precisely the occurrence of any covalency, can be summarized as follows. For Ln(III) as well as for Cm(III) species, a very weak donation occurs. For U(III), the backbonding interaction from 5f(U) to π∗ (L) is present, and its magnitude clearly parallels that of the LUMO (π∗) level of the ligand. This electron transfer becomes total for L = BTP, with an oxidation from U(III) to U(IV). For Am(III), a backdonation may occur with η2 ligands or with BTP, with similar features (shorter M–N distances, orbital stabilization) than for U(III), but being much weaker. Finally, all along this study, theoretical data (structures, stability, …) have been found fully consistent with experimental findings.
2 ML33+ species (M = La, Gd, U, Cm)
This 1:3 stoichiometry is found in molecular species involved in extraction studies with substituted BTP, and in more fundamental complexation studies with tridentate ligands such as BTP and terpy. We have thus a possible interesting comparison between an M–BTP bond in MF3–L (see above) and in M(BTP)33+. We will summarize here the main results on the latter complexes [24]. The Am(III) homologue could not be obtained due to electronic convergence troubles.
The fully optimized geometries (see Table 2) are consistent with experimental results, either from crystallographic or from EXAFS data [17,18,42]. A shortening from La to U is observed, although their ionic radii are quite similar. This effect is considered once again as the consequence of a backbonding contribution. The Cm species does not show any particular contraction of bonding compared to Gd for instance, as was experimentally found and discussed by Denecke et al. [17].
M–N distances (Å) in calculated optimized geometries of M(BTP)33+ with M = La, Gd, U and Cm and in experimental structures, compared to ionic radii (Å, given for coordination number = 6)
| d(M–Npy) | d(M–Ntz) | Ionic radius for the M3+ cationa | |
| [La(BTP)3]3+ | 2.74 (2.67)b | 2.69 (2.63)b | 1.06 |
| [U(BTP)3]3+ | 2.54 (2.54)b | 2.56 (2.54)b | 1.06 |
| [Cm(BTP)3]3+ | 2.61 (2.57)c | 2.61 (2.57)c | 0.98 |
| [Gd(BTP)3]3+ | 2.58 (2.56)d | 2.59 (2.56)d | 0.94 |
In order to get more insights into the bonding, Mulliken population analyses are displayed in Table 3. We have also reported, for an easy comparison, the data pertaining to the F3M–BTP analogous complex. Both Ln(BTP)33+ show the same behaviour with a charge on the lanthanide around 2 |e−|, and a charge on each BTP of 0.33 |e−|. It points to an increased donation, compared to the neutral F3La–BTP complex, where the BTP charge was two times less (0.17 |e−|). The two uranium complexes are difficult to compare, as the F3U–BTP corresponds in fact to a U(IV) “F3U(BTP−)”. Nevertheless, backdonation is observed with U(BTP)33+, as can be seen from the decrease in fα occupation of −0.5 |e−|. This value represents the sum of the loss due to backdonation and the gain due to donation. The really striking observation is the difference for the curium species. In the F3M–L series, no difference in the M–L bonding could be seen between the Ln and Cm derivatives. In contrast, in the M(BTP)33+ series, a stronger donation is observed with M = Cm compared to that with M = La or Gd, as shown by the BTP and M charges in Table 3. This electron transfer occurs mainly in d orbitals, but also with ca. 20–30% in f orbitals.
Comparison of Mulliken charges for M(BTP)33+ and F3M–BTP, for M = La, U and Cm
| La(BTP)33+a | Gd(BTP)33+a | U(BTP)33+a | Cm(BTP)33+a | F3La–BTP | F3U–BTP | F3Cm–BTP | |
| QBTPb | 0.33 | 0.33 | 0.38 | 0.44 | 0.17 | −0.66 | 0.08 |
| QM | 2.02 | 2.02 | 1.86 | 1.69 | 1.72 | 2.18 | 1.71 |
| Δd | 0.86 | 0.98 | 1.36 | 1.09 | 0.92 | 1.08 | 0.9 |
| Δf | 0.28 | 0.12 | −0.5/0.33 | 0.18 | 0.38 | −0.77/0.52 | −0.06/0.3 |
a See Ref. [24].
b Charge per BTP.
These results are not changed when adding a solvent through a continuum model (Conductor-like Screening Model, COSMO) for water. The structure optimizations and bonding features are not modified, compared to the gas phase results shown above [25].
The absence of counterions and the high 3+ charge in this type of complexes thus drastically change the overall conclusions on the M–L bonding for Am and Cm, compared to what had been obtained with neutral F3M–L systems.
In order to better understand all the parameters of the coordination sphere relevant for a modulation of the M–L bond, we have then systematically varied the number of counterions and the inclusion of either water or ligand molecules. This was achieved on a series of complexes including a metal–pyrazine bond, a ligand chosen because of its “medium” softness among others.
3 Series [ClnM(H2O)p(pz)q](3−n)+ with n = 1,2,3; p = 1–3; q = 1–3
The numerous speciation studies in water that have been published to date on trivalent lanthanide complexes, particularly with several N-heterocyclic ligands, reveal most of the time charged species with coordinated solvent molecules and a variable M:L stoichiometry such as 1:1 or 1:2 [2,3,12,15,19]. The present model species have thus been chosen to evaluate the M–L bonding features within such systems.
The first series: Cl3M–pz, Cl2M–pz+ and ClM–pz2+ allows us to compare the effect of the lack of counterion, without any other donating ligand. Fig. 3 displays the evolution of the pyrazine charge for M = La and U, as well as the amount of electron transferred in the backdonation interaction for U. This latter parameter is the electron amount (|e−|) in the π∗ orbital of pyrazine, coming from U(5f) orbitals, calculated from the percentage of admixture of the π∗ within each 5f α occupied orbital (see ADF documentation) [29].
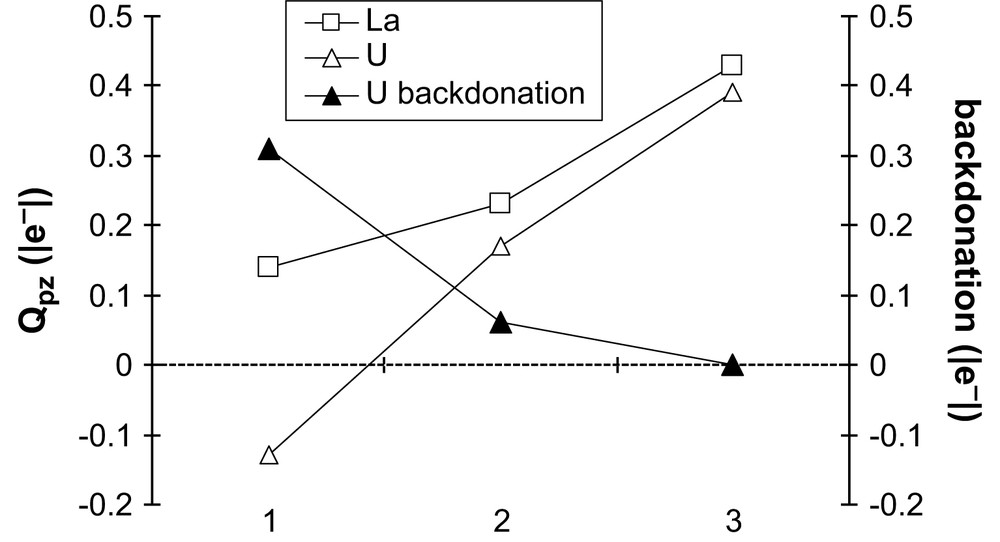
Evolution of the pyrazine charge (Qpz) in [Cl3−nM–pz]n+ for M = La and U and of the backbonding magnitude in the case of the uranium homologue (see text for more details), n, the total charge of the complex.
In both cases, the decrease in Cl− is partly compensated by an increased donation from the pyrazine, resulting in a strong increase of its charge. In the uranium case, backdonation strongly decreases in Cl2U–pz+ and disappears in ClU–pz2+: this may be explained by the difficulty for U to “lose” electrons when counterions are lacking.
The second series: [Cl2Mpz]+, [Cl2Mpz(H2O)]+, [Cl2Mpz(H2O)2]+, [Cl2Mpz(H2O)3]+, allows us to check the influence of donation properties of solvent molecules within a charged complex with two Cl− counterions, with M = La or U. From the examination of the ligand charge (see Fig. 4), it is clear that water molecules partly compensate the loss of one chloride, by transferring ca. +0.1 |e−| per water molecule on the metal center. An interesting consequence is the increasing backdonation in the (hypothetical) aqueous complexes of uranium, when adding donating water molecules: it thus explains the strong Qpz decrease for M = U compared to M = La. It even becomes negative when two or three water molecules are coordinated. The uranium center takes advantage of the donating power of water to retrieve some electron density and to ensure backdonation to pyrazine. But this donating power is limited and does not allow to compensate for the loss of one chloride. Indeed, even with three water molecules, the amount of backdonation in [Cl2Upz(H2O)3]+ is 0.24 |e−|, i.e. less than for Cl3Upz (0.31 |e−|). The uranium derivative in the monochloride series: [ClUpz(H2O)n]2+, with n = 0–3, also supports this conclusion, as backdonation reaches only 0.04 |e−| even with three water molecules. In the latter case, the donation from water molecules is not seen on the metal center, but on the chloride charge, which becomes more negative.
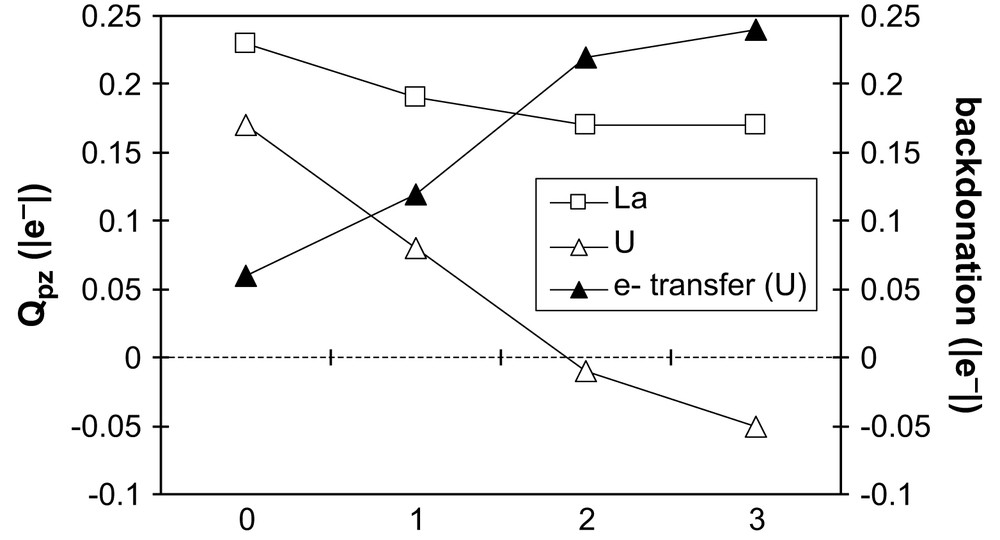
Evolution of the pyrazine charge in the series [Cl2Mpz(H2O)n]+ as a function of n, number of water molecules, for M = La, U and of the electron transfer due to 5f to π∗ (pz) backdonation in the uranium analogue.
The La analogue strengthens this trend: the pyrazine charge is almost constant (+0.17 |e−|), whatever the number of water molecules may be in the first coordination sphere. When adding water molecules, the donated electrons are retrieved by the chloride, whose charge becomes more negative, from −0.26 ([Cl2Lapz]+ to −0.47 |e−| ([Cl2Lapz(H2O)3)+]. We have performed analogous calculations on the curium and gadolinium [Cl2Mpz(H2O)n]+ series, which rigorously behave in the same way as lanthanum.
In order to better check a possible effect of the ligand softness, we have thus considered the evolution of a metal–pyrazine bond in charged complexes when adding more pyrazine ligands. Thus a similar series has been investigated: [Cl2M(pz)]+, [Cl2M(pz)2]+ and [Cl2M(pz)3]+. The charge on the ligand does not depend on the metal within each metal:pyrazine ratio: Qpz ≈ 0.24 |e−| for [Cl2M(pz)]+, and 0.17 |e−| for [Cl2M(pz)2]+ and [Cl2M(pz)3]+. Thus the conclusion on this series is that even a soft ligand as pyrazine is not able to discriminate within such complexes between lanthanides and curium.
This suggests that, apart from uranium, which exhibits a special bonding character, no change can be seen in the metal–ligand bond for lanthanides or for a heavy actinide, when chloride anions are present. From these series, it seems that counterions in the first coordination sphere have a “screening” effect on any donation interaction coming from other ligands. Strong polarization effects in these complexes may preclude any fine tuning of a covalent contribution in the metal–pyrazine bond. Thus the metal–pyrazine bond is not sensitive to the nature of the coordination sphere and to the metal itself.
The absence of bonding differences within charged complexes had already been pointed out by Guillaumont [2], in N-donor tridentate species, where almost no covalency could be detected, neither with Ln(III) nor with An(III) complexes.
4 Discussion
We will focus in this part on the differences between lanthanide and actinide bonds. The very first remark is that U(III) always gives a very specific U–ligand interaction, controlled by backdonation from 5f electrons to virtual orbitals of the N-heterocyclic ligand. Changes in the coordination sphere affect more or less the magnitude of this backdonation, on the basis of simple electronic considerations. Indeed, if the U(III) ion experiences a loss of electron density due to the lack of counterions and/or the lack of donating ligands (water or other ligands), backdonation decreases and can reach zero in the case of the [ClUpz]2+ complex. When more donor atoms are present, backdonation increases and may go as far as a complete electron transfer and an oxidation from U(III) to U(IV), as had been experimentally observed. Thus the composition of the coordination sphere strongly modulates the electron transfer between U(III) and the ligand, but the backdonation in itself is always present.
The case of Ln(III) and heavy actinides An(III) is more subtle. Am(III) and Cm(III) complexes are very different from U(III) homologues. The metal–ligand bond for these heavy actinides are rather similar, being always strongly ionic, with a weak covalent effect for Am(III) or Cm(III) in some specific cases. The coordination sphere strongly influences the very nature of the bonding. For instance, in the F3M–L series with L being a good π-acceptor ligand (pyrazine, triazine, BTP), a weak backdonation may be observed for M = Am, whereas for M = Cm, the interaction is purely electrostatic. In contrast, for ML33+ complexes, a stronger amount of donation is observed for M =Cm, compared to M = Ln species. This may be an explanation of the high selectivity observed with the BTP ligand, for which this 1:3 stoichiometry is observed. In intermediate cases, when the complexes are positively charged, there is no way to find any difference.
5 Conclusion
In the light of such analyses, it is clear that uranium(III) is not a good model for the heavier actinides, although it is interesting for structural characterizations or validation of calculations. From the results given here, it is also essential to control the coordination sphere of the species involved in the extracting process for discriminating between Ln(III) and An(III). More precisely, the best coordination should avoid any solvent molecules (water) and counterions. This is the case for the derivatives of BTP, which are able to give a very stable ML33+ system, thus “exalting” the soft character of BTP in order to provide a more covalent effect with An(III) than with Ln(III).
A neutral coordination sphere enhances backbonding effects. Slight discrepancies may indeed appear between Ln(III) and Am(III) with pydz or triazines, but not with Cm(III). So this kind of coordination sphere is not efficient for a good selectivity between both heavy An(III) and Ln(III).
We have shown here that theoretical calculations may reveal quite interesting to obtain further insights into bonding features, an issue which is crucial in the discriminating processes based on ligand (or extractant molecule) selectivity. Nevertheless, it also needs to be always confronted to other experimental data, such as structural or spectroscopic ones, or on reactivity or thermodynamic data. Clearly, it is possible to reproduce experimental data, and this paves the way for future developments and predictive analyses.
Aknowledgements
P.M., L.P. and V.V. wish to thank the Nuclear Energy Division of the CEA for its financial support.


