1 Introduction
The interface between classical and quantum physics has always been an interesting area, but its importance has nevertheless grown with the current explosive thrusts in nanoscience. Taking devices to the limit of miniaturization (the mesoscale and beyond) where quantum effects become important makes it essential to understand the interplay between the classical properties of the macroscale and the quantum properties of the microscale. This is particularly true in nanomagnetism, where many potential applications require monodisperse, magnetic nanoparticles.
In order to put this review into perspective, let us consider Fig. 1, which presents a scale of size ranging from macroscopic down to nanoscopic sizes. The unit of this scale is the number of magnetic moments in a magnetic system. At macroscopic sizes, a magnetic system is described by magnetic domains (Weiss 1907) [1] that are separated by domain walls. Magnetization reversal occurs via nucleation, propagation, and annihilation of domain walls (see the hysteresis loop on the left in Fig. 1 which was measured on an individual elliptic CoZr particle of 1 μm × 0.8 μm and a thickness of 50 nm [2]). Shape and width of domain walls depend on the material of the magnetic system, on its size, shape and surface, and on its temperature [3,4].

Scale of size that goes from macroscopic down to nanoscopic sizes. The unit of this scale is the number of magnetic moments in a magnetic system (roughly corresponding to the number of atoms). The hysteresis loops are typical examples of magnetization reversal via nucleation, propagation, and annihilation of domain walls (left), via uniform rotation (middle), and via quantum tunneling (right).
When the system size is of the order of magnitude of the domain wall width or the exchange length, the formation of domain walls requires too much energy. Therefore, the magnetization remains in the so-called single-domain state. Hence, the magnetization might reverse by uniform rotation, curling or other nonuniform modes (see the hysteresis loop in the middle of Fig. 1). For system sizes well below the domain wall width or the exchange length, one must take into account explicitly the magnetic moments (spins) and their couplings. The theoretical description is complicated by the particle's boundaries.
Magnetic molecular clusters (also called molecular nanomagnets or single-molecule magnets) are the final point in the series of smaller and smaller units from bulk matter to atoms (Fig. 1). Up to now, they have been the most promising candidates for observing quantum phenomena because they have a well-defined structure with well-characterized spin ground state and magnetic anisotropy. These molecules can be regularly assembled in large crystals where all molecules often have the same orientation. Hence, macroscopic measurements can give direct access to single-molecule properties.
This review introduces the basic concepts that are needed to understand the quantum phenomena observed in molecular nanomagnets. Most tunneling studies presented here were performed by magnetization measurements on single crystals using an array of micro-SQUIDs [4]. This review concludes by mentioning new trends towards molecular spintronics using junctions and nano-SQUIDs [5].
2 Overview of molecular nanomagnets
Molecular nanomagnets or single-molecule magnets (SMMs) are mainly organic molecules that have one or several metal centers with unpaired electrons. These polynuclear metal complexes are surrounded by bulky ligands (often organic carboxylate ligands). The most prominent examples are a dodecanuclear mixed-valence manganese-oxo cluster with acetate ligands, in short Mn12 acetate [6], and an octanuclear iron(III) oxo-hydroxo cluster of formula [Fe8O2(OH)12(tacn)6]8+ where tacn is a macrocyclic ligand, in short Fe8 [7]. Both systems have a spin ground state of S = 10 and an Ising-type magnetic anisotropy, which stabilizes the spin states with m = ±10 and generates an energy barrier for the reversal of the magnetization of about 67 K for Mn12 acetate [8–12] and 25 K for Fe8 [13].
Thermally activated quantum tunneling of the magnetization has first been evidenced in both systems [14–18]. Theoretical discussion of this assumes that thermal processes (principally phonons) promote the molecules up to high levels with small quantum numbers |m|, not far below the top of the energy barrier, and the molecules then tunnel inelastically to the other side [19–26]. Thus the transition is almost entirely accomplished via thermal transitions and the characteristic relaxation time is strongly temperature dependent. For Fe8, however, the relaxation time becomes temperature independent below 0.36 K [18,27] showing that a pure tunneling mechanism between the only populated ground states m = ±S = ±10 is responsible for the relaxation of the magnetization. On the other hand in the Mn12 acetate system one sees temperature independent relaxation only for strong applied fields and below about 0.6 K [28,29]. During the last years, many new molecular nanomagnets were presented (see, for instance, Refs. [30–34]) which show also tunneling at low temperatures. The largest molecular nanomagnet is currently an Mn84 molecule [35] that has a size of a magnetic nanoparticle (Fig. 2) and an Mn6 has currently a record anisotropy barrier approaching 100 K [36].
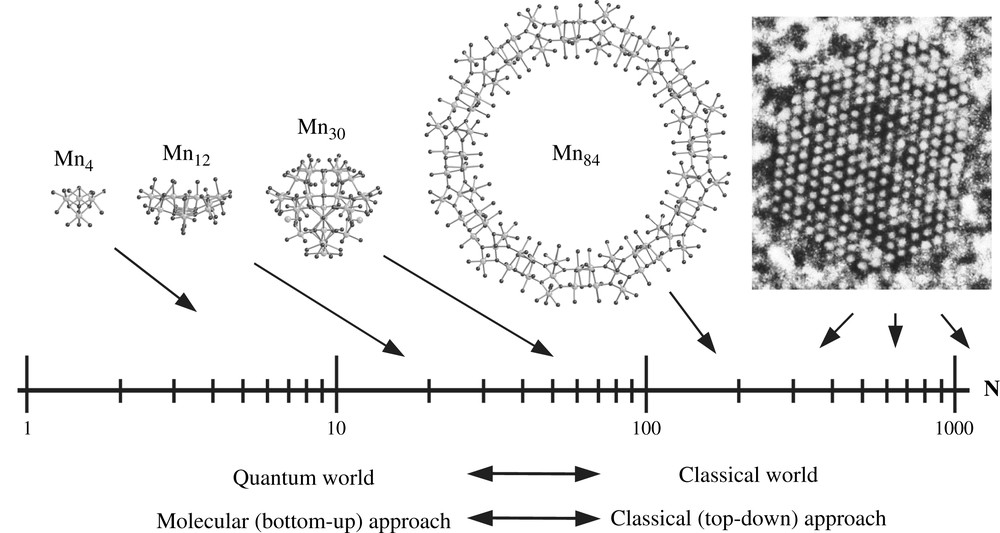
Size scale spanning atomic to nanoscale dimensions. On the far right is shown a high-resolution transmission electron microscopy view along a [110] direction of a typical 3 nm diameter cobalt nanoparticle exhibiting a face-centered cubic structure and containing about 1000 Co atoms [37]. The Mn84 molecule is a 4.2 nm diameter particle. Also shown for comparison are the indicated smaller Mn nanomagnets, which are drawn to scale. An alternative means of comparison is the Néel vector (N), which is the scale shown. The arrows indicate the magnitude of the Néel vectors for the indicated SMMs, which are 7.5, 22, 61, and 168 for Mn4, Mn12, Mn30 and Mn84, respectively.
3 Giant spin model for nanomagnets
A magnetic molecule, that behaves like a small nanomagnet, must have a large uniaxial easy axis type magnetic anisotropy and a large ground state spin. A typical example is the octanuclear iron(III) oxo-hydroxo cluster of formula [Fe8O2(OH)12(tacn)6]8+ where tacn is a macrocyclic ligand (1,4,7-traiazcyclononane), short Fe8 (Fig. 3) [7].

Schematic view of the magnetic core of the Fe8 cluster. The oxygen atoms are black, the nitrogen atoms are gray, and carbon atoms are white. The arrows represent the spin structure of the ground state S = 10.
The internal iron(III) ions are octahedrally coordinated to the two oxides and to four hydroxo bridges. The outer iron(III) ions coordinate three nitrogens and three hydroxyls. Spin polarized neutron scattering showed that all Fe ions have a spin 5/2, six spins up and two down [38]. This rationalizes the S = 10 spin ground state that is in agreement with magnetization measurements.
In principle, a multi-spin Hamiltonian can be derived taking into account of all exchange interactions and the single-ion magnetic anisotropies. However, the Hilbert space is very large (68 ≈ 106) and the exchange coupling constants are not well known. A giant spin model is therefore often used that describes in an effective way the ground spin state multiplet. For a nanomagnet like the Fe8 molecular cluster it has the following Hamiltonian:
| (1) |
Sx, Sy, and Sz are the three components of the spin operator, D and E are the anisotropy constants which were determined via high frequency electron paramagnetic resonance (HF-EPR) (D/kB ≈ 0.275 K and E/kB ≈ 0.046 K [13]), and the last term of the Hamiltonian describes the Zeeman energy associated with an applied field . This Hamiltonian defines hard, medium, and easy axes of magnetization in x-, y-, and z-directions, respectively (Fig. 4). It has an energy level spectrum with (2S + 1) = 21 values which, to a first approximation, can be labelled by the quantum numbers m = −10, −9, …, 10 choosing the z-axis as quantization axis. The energy spectrum, shown in Fig. 5, can be obtained by using standard diagonalization techniques of the [21 × 21] matrix describing the spin Hamiltonian S = 10. At , the levels m = ±10 have the lowest energy. When a field Hz is applied, the energy levels with m < −2 increase, while those with m > 2 decrease (Fig. 5). Therefore, energy levels of positive and negative quantum numbers cross at certain fields Hz. It turns out that for Fe8 the levels cross at fields given by μ0Hz ≈ n × 0.22 T, with n = 1,2,3,…. The insert of Fig. 5 displays the details at a level crossing where transverse terms containing Sx or Sy spin operators turn the crossing into an “avoided level crossing”. The spin S is “in resonance” between two states when the local longitudinal field is close to an avoided level crossing. The energy gap, the so-called “tunnel spitting” Δ, can be tuned by an applied field in the xy-plane (Fig. 4) via the SxHx and SyHy Zeeman terms (Section 3.2).

Unit sphere showing degenerate minima A and B which are joined by two tunnel paths (heavy lines). The hard, medium, and easy axes are taken in x-, y-, and z-direction, respectively. The constant transverse field Htrans for tunnel splitting measurements is applied in the xy-plane at an azimuth angle φ. At zero applied field , the giant spin reversal results from the interference of two quantum spin paths of opposite direction in the easy anisotropy yz-plane. For transverse fields in direction of the hard axis, the two quantum spin paths are in a plane which is parallel to the yz-plane, as indicated in the figure. By using Stokes' theorem it has been shown [39] that the path integrals can be converted in an area integral, yielding that destructive interference—that is a quench of the tunneling rate—occurs whenever the shaded area is kπ/S, where k is an odd integer. The interference effects disappear quickly when the transverse field has a component in the y-direction because the tunneling is then dominated by only one quantum spin path.
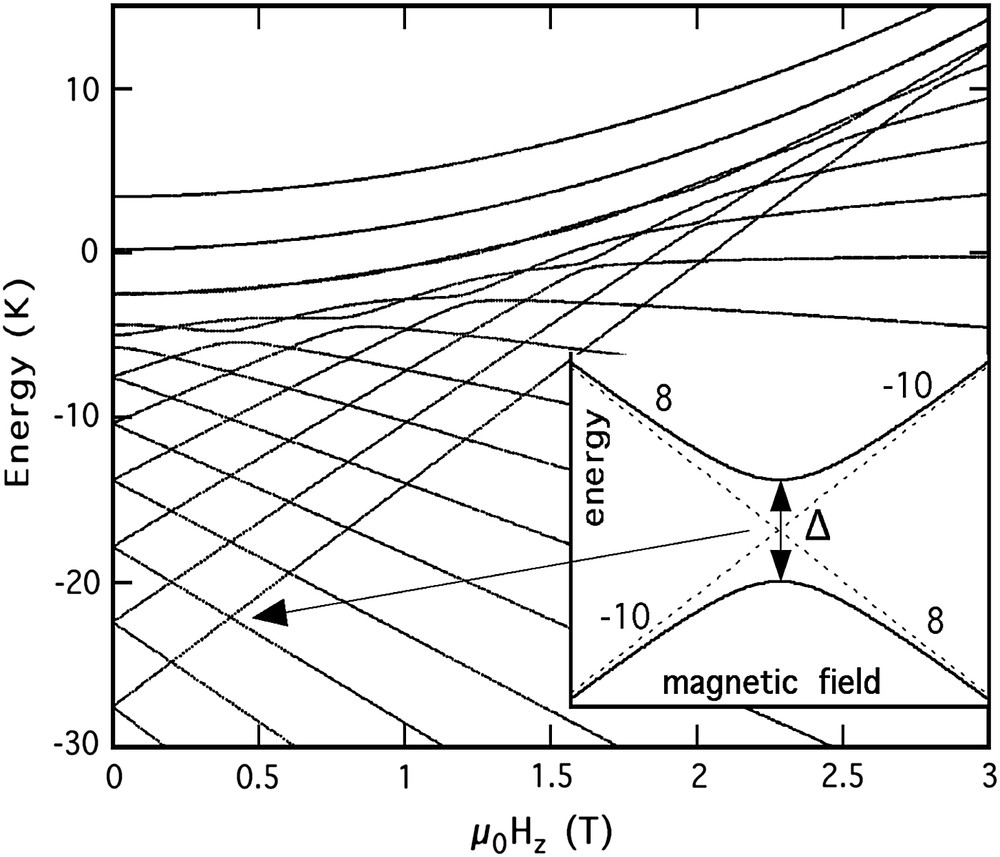
Zeeman diagram of the 21 levels of the S = 10 manifold of Fe8 as a function of the field applied along the easy axis [Eq. (1)]. From bottom to top, the levels are labelled with quantum numbers m = ±10, ±9, …, 0. The levels cross at fields given by μ0Hz ≈ n × 0.22 T, with n = 1,2,3,…. The insert displays the detail at a level crossing where the transverse terms (terms containing Sx or/and Sy spin operators) turn the crossing into an avoided level crossing. The greater the tunnel splitting Δ, the higher the tunnel rate.
The effect of these avoided level crossings can be seen in hysteresis loop measurements (Fig. 6). When the applied field is near an avoided level crossing, the magnetization relaxes faster, yielding steps separated by plateaus. As the temperature is lowered, there is a decrease in the transition rate due to reduced thermal-assisted tunneling.

Hysteresis loops of a single crystal of Fe8 molecular clusters at different temperatures. The longitudinal field (z-direction) was swept at a constant sweeping rate of 0.014 T/s. The loops display a series of steps, separated by plateaux. As the temperature is lowered, there is a decrease in the transition rate due to reduced thermal-assisted tunneling. The hysteresis loops become temperature independent below 0.35 K, demonstrating quantum tunneling at the lowest energy levels.
3.1 Landau–Zener tunneling in Fe8
The nonadiabatic transition between the two states in a two-level system has first been discussed by Landau, Zener, and Stückelberg [40–42]. The original work by Zener concentrates on the electronic states of a bi-atomic molecule, while Landau and Stückelberg considered two atoms that undergo a scattering process. Their solution of the time-dependent Schrödinger equation of a two-level system could be applied to many physical systems and it became an important tool for studying tunneling transitions. The Landau–Zener model has also been applied to spin tunneling in nanoparticles and clusters [43–47]. The tunneling probability P when sweeping the longitudinal field Hz at a constant rate over an avoided energy level crossing (Fig. 7) is given by
| (2) |
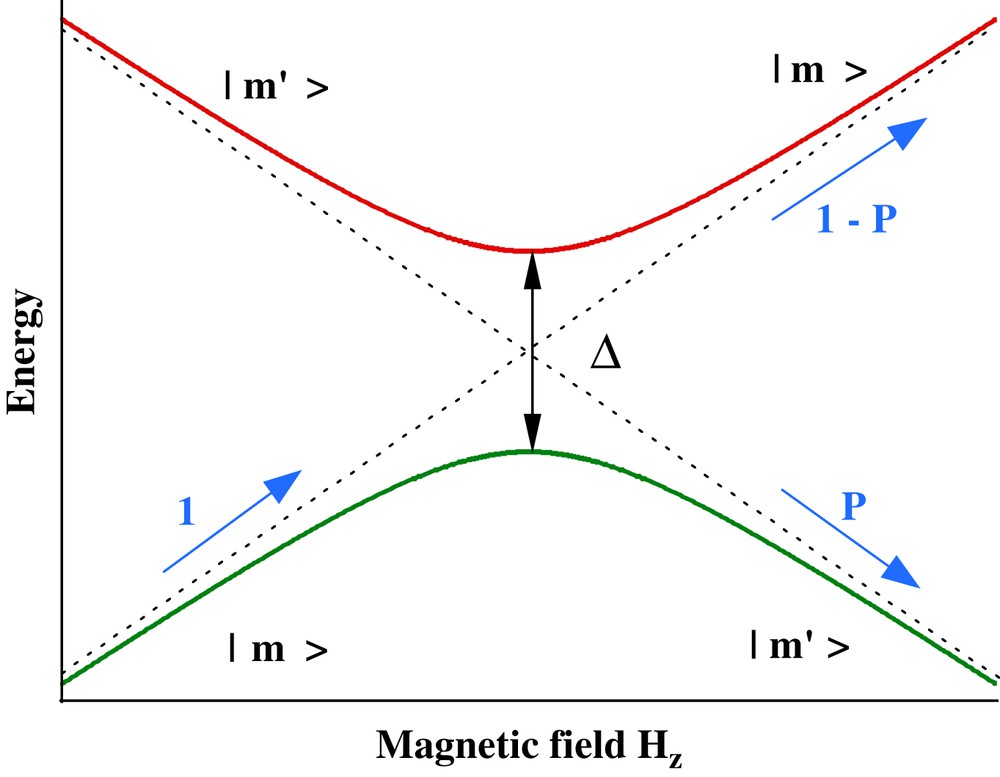
Detail of the energy level diagram near an avoided level crossing. m and m′ are the quantum numbers of the energy level. Pm,m′ is the Landau–Zener tunnel probability when sweeping the applied field from the left to the right over the anticrossing. The greater the gap Δ and the slower the sweeping rate, the higher is the tunnel rate [Eq. (2)].
With the Landau–Zener model in mind, we can now start to understand qualitatively the hysteresis loops (Fig. 6). Let us start at a large negative magnetic field Hz. At very low temperature, all molecules are in the m = −10 ground state (Fig. 5). When the applied field Hz is ramped down to zero, all molecules will stay in the m = −10 ground state. When ramping the field over the Δ−10,10-region at Hz ≈ 0, there is a Landau–Zener tunnel probability P−10,10 to tunnel from the m = −10 to the m = 10 state. P−10,10 depends on the sweeping rate [Eq. (2)]; that is, the slower the sweeping rate, the larger the value of P−10,10. This is clearly demonstrated in the hysteresis loop measurements showing larger steps for slower sweeping rates [48]. When the field Hz is now further increased, there is a remaining fraction of molecules in the m = −10 state which became a metastable state. The next chance to escape from this state is when the field reaches the Δ−10,9 region. There is a Landau–Zener tunnel probability P−10,9 to tunnel from the m = −10 to the m = 9 state. As m = 9 is an excited state, the molecules in this state de-excite quickly to the m = 10 state by emitting a phonon. An analogous procedure happens when the applied field reaches the Δ−10,10−n regions (n = 2, 3, …) until all molecules are in the m = 10 ground state; that is, the magnetization of all molecules is reversed. As phonon emission can only change the molecule state by Δm = 1 or 2, there is a phonon cascade for higher applied fields.
In order to apply quantitatively the Landau–Zener formula [Eq. (2)], we first saturated the crystal of Fe8 clusters in a field of Hz = −1.4 T, yielding an initial magnetization Min = −Ms. Then, we swept the applied field at a constant rate over one of the resonance transitions and measured the fraction of molecules which reversed their spin. This procedure yields the tunneling rate P−10,10−n and thus the tunnel splitting Δ−10,10−n [Eq. (2)] with n = 0, 1, 2, ….
We first checked the predicted Landau–Zener sweeping field dependence of the tunneling rate. We found a good agreement for sweeping rates between 10 and 0.001 T/s [48], that is for LZ tunnel probabilities small than few percent. The deviations at lower sweeping rates are mainly due to the hole-digging mechanism [49] which slows down the relaxation (Section 7.2). In other words, the spin has time to interact with its environment at lower sweeping rates. These interactions are not included in the LZ model and it fails to describe the observed tunneling rates. Our measurements showed for the first time that the Landau–Zener method is particularly adapted for molecular clusters because it works even in the presence of dipolar fields which spread the resonance transition provided that the field sweeping rate is not too small.
3.2 Oscillations of tunnel splitting
An applied field in the xy-plane can tune the tunnel splittings Δm,m′ via the Sx and Sy spin operators of the Zeeman terms that do not commute with the spin Hamiltonian. This effect can be demonstrated by using the Landau–Zener method (Section 3.1). Fig. 8 presents a detailed study of the tunnel splitting Δ±10 at the tunnel transition between m = ±10, as a function of transverse fields applied at different angles φ, defined as the azimuth angle between the anisotropy hard axis and the transverse field (Fig. 4). For small angles φ the tunneling rate oscillates with a period of ∼0.4 T, whereas no oscillations showed for large angles φ [48]. In the latter case, a much stronger increase of Δ±10 with transverse field is observed. The transverse field dependence of the tunneling rate for different resonance conditions between the state m = −10 and (10 − n) can be observed by sweeping the longitudinal field around μ0Hz = n × 0.22 T with n = 0, 1, 2, …. The corresponding tunnel splittings Δ−10,10−n oscillate with almost the same period of ∼0.4 T (Fig. 8). In addition, comparing quantum transitions between m = − 10 and (10 − n), with n even or odd, revealed a parity (or symmetry) effect that is analogous to the Kramers' suppression of tunneling, predicted for half-integer spins [50,51]. A similar strong dependence on the azimuth angle φ was observed for all studied resonances.

Measured tunnel splitting Δ as a function of transverse field for (a) several azimuth angles φ at m = ±10 and (b) φ ≈ 0°, as well as for quantum transition between m = −10 and (10 − n). Note the parity effect that is analogous to the suppression of tunneling predicted for half-integer spins. It should also be mentioned that internal dipolar and hyperfine fields hinder a quench of Δ which is predicted for an isolated spin.
3.2.1 Semiclassical descriptions
Before showing that the above results can be derived by an exact numerical calculation using the quantum operator formalism, it is useful to discuss semiclassical models. The original prediction of oscillation of the tunnel splitting was made by using the path integral formalism [52]. Here [39], the oscillations are explained by constructive or destructive interference of quantum spin phases (Berry phases) of two tunnel paths (instanton trajectories) (Fig. 4). Since our experiments were reported, the Wentzel–Kramers–Brillouin theory has been used independently by Garg [53] and Villain and Fort [54]. The surprise is that although these models [39,53,54] are derived semiclassically, and should have higher-order corrections in 1/S, they appear to be exact as written! This has first been noted in Refs. [53] and [54] and then proven in Ref. [55] Some extensions or alternative explications of Garg's result can be found in Refs. [56–60].
The period of oscillation is given by [39]
| (3) |
3.2.2 Exact numerical diagonalization
In order to quantitatively reproduce the observed periodicity we included fourth-order terms in the spin Hamiltonian [Eq. (1)] as employed in the simulation of inelastic neutron scattering measurements [61,62] and performed a diagonalization of the [21 × 21] matrix describing the S = 10 system. For the calculation of the tunnel splitting we used D = 0.289 K, E = 0.055 K [Eq. (1)] and the fourth-order terms as defined in [61] with B40 = 0.72 × 10−6 K, B42 = 1.01 × 10−5 K, B44 = −0.43 × 10−4 K, which are close to the values obtained by EPR measurements [63] and neutron scattering measurements [62].
The calculated tunnel splittings for the states involved in the tunneling process at the resonances n = 0, 1, and 2 are reported in Fig. 9, showing the oscillations as well as the parity effect for odd resonances.

Calculated tunnel splitting Δ as a function of transverse field for (a) quantum transition between m = ±10 at several azimuth angles φ and (b) quantum transition between m = −10 and (10 − n) at φ = 0° (Section 3.2.2). The fourth-order terms suppress the oscillations of Δ for large transverse fields |Hx|.
3.2.3 Spin-parity effect
The spin-parity effect is among the most interesting quantum phenomena that can be studied at the mesoscopic level in SMMs. It predicts that quantum tunneling is suppressed at zero applied field if the total spin of the magnetic system is half-integer but is allowed in integer spin systems. Enz and Schilling and Van Hemmen and Sütö [64,65] were the first to suggest the absence of tunneling as a consequence of Kramers degeneracy. The Kramers theorem asserts that no matter how unsymmetric the crystal field, an ion possessing an odd number of electrons must have a ground state that is at least doubly degenerate, even in the presence of crystal fields and spin–orbit interactions [66].
The predicted spin-parity effect can be observed by measuring the tunnel splitting as a function of the transverse field [67]. An integer spin system is rather insensitive to small transverse fields whereas a half-integer spin systems is much more sensitive. However, a half-integer spin system will also undergo tunneling at zero external field as a result of environmental degrees of freedom such as hyperfine and dipolar couplings or small intermolecular exchange interaction.
The nicest observation of the spin-parity effect has been seen for two molecular Mn12 clusters with a spin ground state of S = 10 and S = 19/2 showing oscillations of the tunnel probability as a function of a transverse field being due to topological quantum phase interference of two tunnel paths of opposite windings (Section 3.2.1). Spin-parity dependent tunneling was established for the first time in these compounds by comparing the quantum phase interference of integer and half-integer spin systems [68].
3.3 A classical approach with applications to the quantum regime
Recently, the molecular (or bottom–up) approach has reached the size regime of the classical (or top–down) approach to nanoscale magnetic materials [35]. Indeed, a giant Mn84 SMM was reported with a 4 nm diameter torus structure, exhibiting both magnetization hysteresis and quantum tunneling. The study of such large systems is greatly complicated by the fact that the spin Hilbert space is huge and it is impossible to treat such systems with exact matrix diagonalization methods. However, since some SMMs are now as large as some classical nanoparticles, it raises the interesting possibility that classical models commonly employed to study the latter may be used to obtain a first order understanding for large molecular systems [69]. Indeed, we herein propose the use of the classical Néel–Brown model [70–72] of thermally activated magnetization reversal of a magnetic single-domain particle in order to study large SMMs [69]. This method allows us to determine important parameters that characterize the magnetic properties of the SMM: the energy barrier, the magnetic anisotropy constant, the spin, τ0, and the crossover temperature from the classical to the quantum regime. The method is particularly useful for SMMs having low-lying energy states and not showing quantum tunneling steps in hysteresis loops. In such systems, electron paramagnetic resonance (EPR) measurements often exhibit only very broad absorption peaks which do not allow the determination of the magnetic anisotropy.
3.3.1 The Néel–Brown model of thermally activated magnetization reversal
The method is based on the Néel–Brown model of thermally activated magnetization reversal of a magnetic single-domain particle which has two equivalent ground states of opposite magnetization separated by an energy barrier due to magnetic anisotropy [70–72]. The system can escape from one state to the other either by thermal activation over the barrier at high temperatures or by quantum tunneling at low temperatures. At sufficiently low temperatures and at zero field, the energy barrier between the two states of opposite magnetization is much too high to observe an escape process. However, the barrier can be lowered by applying a magnetic field in the opposite direction to that of the particle's magnetization. When the applied field is close enough to the reversal field, thermal fluctuations are sufficient to allow the system to overcome the barrier, and the magnetization is reversed.
This stochastic escape process can be studied via the relaxation time method consisting in the measurement of the probability that the magnetization has not reversed after a certain time. In the case of an assembly of identical and isolated particles, it corresponds to measurements of the relaxation of magnetization. According to the Néel–Brown model, the probability that the magnetization has not reversed after a time t is given by
| (4) |
| (5) |
| (6) |
In order to study the field dependence of the relaxation time τ(T, H) and to obtain the parameters of the model, the decay of magnetization has to be studied at many applied fields H and temperatures T. This is experimentally very time consuming and complicated by the fact that the equilibrium magnetization is temperature dependent and difficult to obtain for long relaxation times. In addition, for fast relaxation times the initial magnetization depends on the field sweep rates to apply the field. The number of exploitable decades for τ values is therefore limited for relaxation time measurements.
A more convenient method for studying the magnetization decay is by ramping the applied field at a given rate [77] and measuring the coercive field Hc (the field value to obtain zero magnetization), which is then measured as a function of the field sweep rate and temperature.
The mathematical transformation from a reversal time probability (Eqs. (4) and (5)) to a reversal field probability was first given by Kurkijärvi [78] for the critical current in SQUIDs. Later, Gunther and Barbara calculated similar expressions for magnetic domain wall junctions [79]. A more general calculation was evaluated by Garg [80]. Here, we use a simplified version [77]: the probability density of reversal of a stochastic process is −dP/dt = P/τ and the maximum of the probability density can be derived from d2P/dt2 = P(1 + dτ/dt)/τ2 = 0. This gives dτ/dt = −1. The application to Eq. (5) leads to . Using Eq. (6) we find Eq. (7). The mean reversal field of an assembly of identical particles or SMMs is approximated by the coercive field Hc:
| (7) |
3.3.2 Application to Mn12 SMMs
The method is here applied to an Mn12 SMMs [69] with a spin ground state of S = 10. Fig. 10 shows typical hysteresis loops with a series of quantum steps separated by plateaus [81]. In order to apply the above method, the temperature and field sweep rate dependences of the coercive fields Hc were measured and plotted in Fig. 11. As expected for a thermally activated process, Hc increases with decreasing temperature and increasing field sweep rate. Furthermore, all measurements showed an almost logarithmic dependence of Hc on the field sweep rate. Hc becomes temperature independent below about 0.6 K.

Hysteresis loops of single crystals of an Mn12 molecular cluster at different temperatures and a constant field sweep rate indicated in the figure. The loops display a series of steps, separated by plateaus. As the temperature is lowered, there is a decrease in the transition rate due to reduced thermal-assisted tunneling. The hysteresis loops become temperature independent below 0.6 K, demonstrating quantum tunneling at the lowest energy levels.
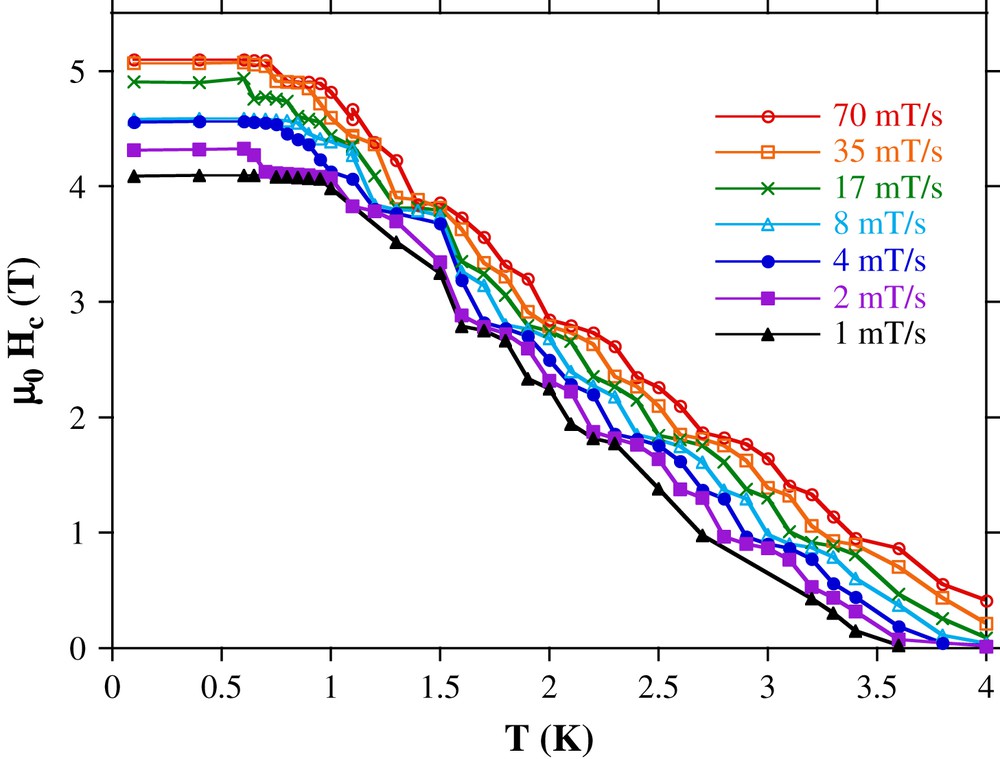
Coercive field Hc for Mn12 as a function of temperature. Note the steps of Hc coming from the resonant tunneling steps in the hysteresis loops 10.
The validity of Eq. (7) was tested by plotting the set of Hc(T, v) values as a function of [T ln(c/v)]1/2 where c = Hc0kBT/τ02E0(1 − Hc/Hc0). If the underlying model is sufficient, all points should collapse onto one straight line by choosing the proper values for the constant τ0. We found that the data of Hc(T, v) fell on a master curve provided τ0 = 2.1 × 10−7 s.
At low temperatures, strong deviation from the master curves is observed. In order to investigate the possibility that these low-temperature deviations are due to an escape from the metastable potential well by tunneling, a common method for classical models is to replace the real temperature T by an effective temperature T∗(T) in order to restore the scaling plot [82]. In the case of tunneling, T∗(T) should saturate at low temperatures. Indeed, the ansatz of T∗(T) as shown in the insert of Fig. 12(b), can restore unequivocally the scaling plot demonstrated by a straight master curve (Fig. 12(b)). The flattening of T∗ corresponds to a saturation of the escape rate, which is a necessary signature of tunneling. The crossover temperature Tc can be defined as the temperature where the quantum rate equals the thermal one. The insert of Fig. 12(b) gives Tc = 0.97 K. The slopes and the intercepts of the master curves give E0 = 72.4 K and Hc0 = 9.1 T. The E0 values are in good agreement with those extracted from Arrhenius plots (69 K). This result allows us to estimate the spin ground state using S = 2E0/(gμBμ0Hc0): S = 11. This differs slightly from S = 10 determined via magnetization measurements. This deviation is due to quantum effects in the thermally activated regime and is considered further below.

(a) Scaling plot of the coercive field Hc(T, v) of Mn12 for field sweep rates between 0.0001 and 0.1 T/s and several temperatures: 0.1 K, 0.4 K, from 0.6 to 1 K in steps of 0.05 K, and from 1 to 4 K in steps of 0.1 K. The arrows indicate the step index n = −(m + m′) where m and m′ are the quantum numbers of the corresponding level crossing. Note the parity effect of the steps: even n have larger steps than odd n. (b) Same data of Hc(T, v) and same scales but the real temperature T is replaced by an effective temperature T∗ (see insert) which restores the scaling below 1.1 K.
Several points should be mentioned: (i) the classical regime of the model corresponds in most SMMs to the thermally activated tunneling regime with tunneling close to the top of the energy barrier. Because all parameters are deduced from this regime, small deviations from the exact values are expected; (ii) the field dependence of the energy barrier can be obtained directly using Eq. (7) and is plotted in Fig. 13; (iii) Eq. (7) is not valid for fields which are close to H = 0 because the model only takes into account the transitions from the metastable to the stable well. However, close to H = 0, transitions between both wells are possible leading to a rounding of the master curve at small fields; (iv) the method can be applied to powder samples with random orientations of the molecules. In this case, α ≈ 1.5, νE0 = DS2 where ν can be calculated [75,76], and the intercept of the master curve gives Hc0/2; (v) in the case of a distribution of anisotropies, different parts of the distribution can be probed by applying the method at different M values; (vi) this method is insensitive to small intermolecular interactions when Hc is larger than the typical interaction field; and (vii) the method can be generalized for 1D, 2D, and 3D networks of spins. In this case, Eq. (6) describes a nucleation barrier.

Field dependence of the energy barrier of Mn12 obtained from Eq. (7) and the set of Hc(T, v) data from Fig. 12. The arrows indicate the step index n = −(m + m′) where m and m′ are the quantum numbers of the corresponding level crossing. Note the step-like reduction of the energy barrier due to resonant tunneling and the parity effect of the steps: even n have larger steps than odd n. The dotted line gives the classical barrier ΔE = E0(1 − H/Ha)2 with E0 = 74 K and Ha = 9.8 T.
4 Quantum dynamics of a dimer of nanomagnets
We present here a new family of dimers of nanomagnets [83] in which antiferromagnetic coupling between two single-molecule magnets (SMMs) results in quantum behavior different from that of the individual SMMs. Each SMM acts as a bias on its neighbor, shifting the quantum tunneling resonances of the individual SMMs. Hysteresis loop measurements on a single crystal of SMM–dimers established quantum tunneling of the magnetization via entangled states of the dimer. This shows that the dimer really does behave as a quantum-mechanically coupled dimer, and also allows the measurement of the longitudinal and transverse superexchange coupling constants [84]. The experimental evidence for entangled states was confirmed by an electron paramagnetic resonance (EPR) study [85].
The compound [Mn4O3Cl4(O2CEt)3(py)3] crystallizes in the hexagonal space group R3(bar) with two Mn4 molecules per unit cell lying head-to-head on a crystallographic S6 symmetry axis [83] (Fig. 14). Each Mn4 monomer has a ground state spin of S = 9/2, well separated from the first excited state S = 7/2 by a gap of about 300 K [86]. The Mn–Mn distances and the Mn–O–Mn angles are similar and the uniaxial anisotropy constant is expected to be the same for the two dimer systems. These dimers are held together via six C–H···Cl hydrogen bonds between the pyridine (py) rings on one molecule and the Cl ions on the other, and one Cl···Cl Van der Waals interaction. These interactions lead to an antiferromagnetic superexchange interaction between the two Mn4 units of the [Mn4]2 dimer [83]. Dipolar couplings between Mn4 molecules can be easily calculated and are more than one order of magnitude smaller than the exchange interaction.

The structure of the [Mn4]2 dimer of [Mn4O3Cl4(O2CEt)3(py)3]. The small circles are hydrogen atoms. The dashed lines are C–H···Cl hydrogen bonds and the dotted line is the close Cl···Cl approach. The labels Mn and Mn′ refer to MnIII and MnIV ions, respectively.
Before presenting the measurements, we summarize a simplified spin Hamiltonian describing the [Mn4]2 dimer [83]. Each Mn4 SMM can be modeled as a giant spin of S = 9/2 with Ising-like anisotropy [Eq. (1)]. The corresponding Hamiltonian is given by
| (8) |
| (9) |
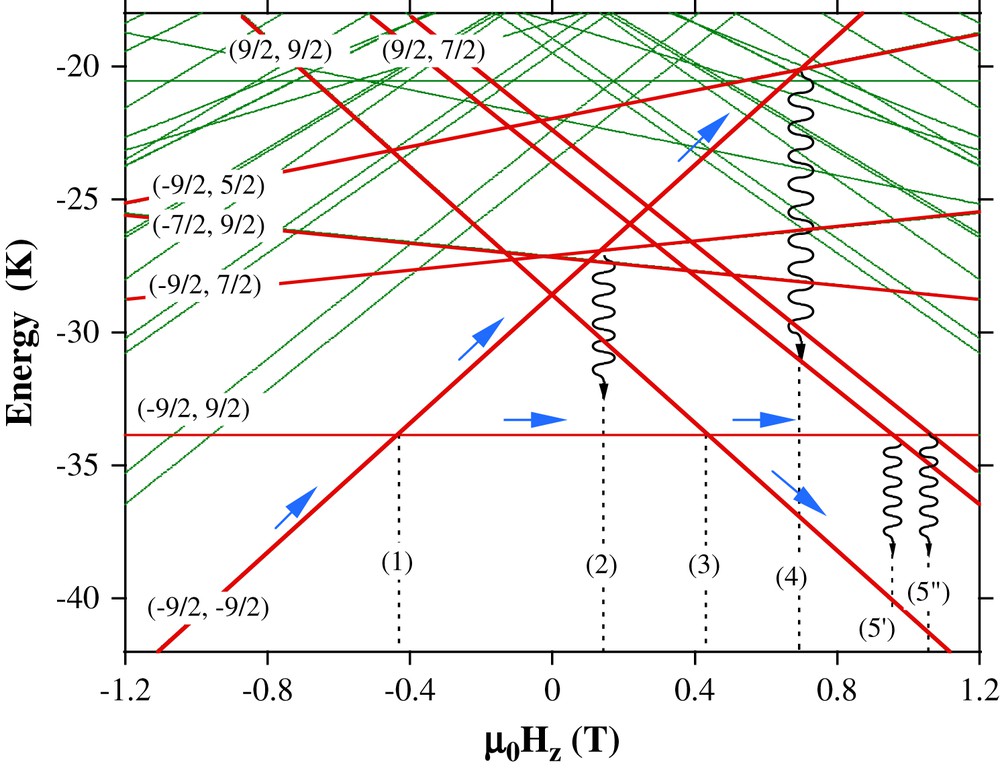
Low-lying spin state energies of the [Mn4]2 dimer, calculated by exact numerical diagonalization using Eq. (9) with D = 0.77 K and J = 0.13 K, as a function of applied magnetic field Hz (Zeeman diagram). The bold energy levels are labelled with two quantum numbers (M1, M2). Dotted lines, labelled 1 to 5, indicate the strongest tunnel resonances: 1: (−9/2,−9/2) to (−9/2,9/2); 2: (−9/2,−9/2) to (−9/2,7/2), followed by relaxation to (−9/2,9/2); 3: (−9/2,9/2) to (9/2,9/2); 4: (−9/2,−9/2) to (−9/2,5/2), followed by relaxation to (−9/2,9/2); 5: (−9/2,9/2) to (7/2,9/2), followed by relaxation to (9/2,9/2). For clarity, degenerate states such as (M,M′) and (M′,M) and lifted degenerate states such as (M, M ± 1), (M, M ± 2), … are not both listed. For example, the (9/2,7/2) and (7/2,9/2) states are strongly split into a symmetric (labelled 5″) and antisymmetric (labelled 5′) combination of (9/2,7/2) and (7/2,9/2) states. This splitting is used to measure the transverse superexchange interaction constant Jxy. Co-tunneling and other two-body tunnel transitions have a lower probability of occurrence and are neglected [87].
Fig. 16 shows typical hysteresis loops (magnetization versus magnetic field scans) with the field applied along the easy axis of magnetization of [Mn4]2, that is, parallel to the S6 axis of the dimer, corresponding to the z-axis of the spin Hamiltonian. These loops display step-like features separated by plateaus. The step heights are temperature independent below ∼0.35 K [83]. The steps are due to resonant quantum tunneling of the magnetization (QTM) between the energy states of the [Mn4]2 dimer (see Figs. 15 and 16 for a discussion of 5 tunnel transitions). QTM has been previously observed for most SMMs, but the novelty for [Mn4]2 dimers is that the QTM is now the collective behavior of the complete S = 0 dimer of exchange-coupled S = 9/2 Mn4 quantum systems. This coupling is manifested as an exchange bias of all tunneling transitions, and the resulting hysteresis loop consequently displays unique features, such as the absence for the first time in a SMM of a QTM step at zero field [83].

Hysteresis loops for the [Mn4]2 dimer at several field sweep rates and 40 mK. The tunnel transitions (manifested by steps) are labelled from 1 to 5, see Fig. 1.
Even though the five strongest tunneling transitions are observed in Fig. 16, fine structure was not observed. For example, the hysteresis loops do not show the splitting of the (9/2,7/2) states (labelled 5′ and 5″), which we suspected might be due to line broadening. Usually, line broadening in SMMs is caused by dipolar and hyperfine interactions [88], and distributions of anisotropy and exchange parameters. In most SMMs, the zero-field resonance is mainly broadened by dipolar and hyperfine interactions because distributions of anisotropy parameters do not affect the zero-field resonance. For an antiferromagnetically coupled dimer, however, this resonance is shifted to negative fields. Therefore, a distribution of the exchange coupling parameter Jz can further broaden this resonance. In fact, we showed that the latter is the dominant source of broadening [84]. We used the ‘quantum hole-digging’ method (see Section 7.2) [49,88–91] to provide direct experimental evidence for the transitions 5′ and 5″, which established tunneling involving entangled dimer states and allowed us to determine Jxy [84].
5 Resonant photon absorption in Cr7Ni antiferromagnetic rings
Magnetic molecules are currently considered among the most promising electron spin based quantum systems for the storing and processing of quantum information. For this purpose, ferromagnetic [92] and antiferromagnetic [93,94] systems have attracted an increasing interest [95,96]. In the latter case the quantum hardware is thought of as a collection of coupled molecules, each corresponding to a different qubit. The main advantages would arise from the fact that they are extremely small and almost identical, allowing to obtain, in a single measurement, statistical averages of a large number of qubits. The magnetic properties can be modeled with an outstanding degree of accuracy. And most importantly, the desired physical properties can be engineered chemically.
The suitability of Cr-based antiferromagnetic molecular rings for the qubit implementation has been proposed [95,96]. The substitution of one metal ion in a Cr-based molecular ring with dominant antiferromagnetic couplings allows its level structure and ground state degeneracy to be engineered [97,98]. A Cr7Ni molecular ring was characterized by means of low-temperature specific-heat and torque-magnetometry measurements, thus determining the microscopic parameters of the corresponding spin Hamiltonian. The energy spectrum and the suppression of the leakage-inducing S-mixing render the Cr7Ni molecule a suitable candidate for the qubit implementation [95,96,99].
In this section we report the first micro-superconducting quantum interference device (micro-SQUID) [100] studies of the Cr7Ni molecular ring [101]. Electron paramagnetic resonance (EPR) methods are combined with high-sensitivity magnetization measurements. We found very narrow resonant photon absorption lines which are mainly broadened by hyperfine interactions. Similar measurement was performed on Ni4 molecules [102] but quantum coherence was not yet directly observed.
The Cr7Ni molecular ring, is based on a homometallic ring with formula [Cr8F8(O2CCMe3)16]. The eight chromium(III) ions lie at the corners of a regular octagon [97]. Each edge of the octagon is bridged by one fluoride ion and two pivalate ligands. There is a large cavity at the centre of the ring. If a single chromium(III) ion is replaced by a metal(II) ion, for example nickel(II), this makes the ring anionic and a cation can be incorporated in the cavity. Thus we can make [H2NMe2][Cr7NiF8(O2CCMe3)16] [98]. If crystallized from a mixture of THF and MeCN the Cr8 and Cr7Ni compounds are isostructural, crystallizing in the tetragonal space group, P4.
The measurements were made in a dilution cryostat using a 20 μm sized single crystal of Cr7Ni. The magnetic probe was a micro-SQUID array [4,100] equipped with three coils allowing application of a field in any direction and with sweep rates up to 10 T/s. The electromagnetic radiation was generated by a frequency synthesizer triggered with a nanosecond pulse generator. This setup allows continuous variation of the frequency from 0.1 Hz to 20 GHz, with pulse lengths ∼1 ns to continuous radiation [103]. Using a 50 μm sized gold radio frequency (RF) loop, the RF radiation field was directed in a plane perpendicular to the applied static field μ0H. The microwave power of the generator could be varied from −80 to 20 dB m (10−11–10−1 W). The sample absorbs only a small fraction of the generator power. This fraction is, however, proportional to the microwave power of the generator. The microwave amplitude BRF can be estimated with the method described in Ref. [100]. We found BRF ≈ 1 mT at 4 GHz and 15 dB m which is more than 1000 times larger than in our previous work on V15 [100].
Fig. 17a shows magnetization versus applied field curves for several field sweep rates at a cryostat temperature of 0.04 K. The magnetization loops exhibit a clear hysteresis which is characteristic for the phonon-bottleneck regime with a spin–phonon relaxation time to the cryostat of a few seconds [104]. Note that the degeneracy of the Kramers doublet is lifted due to internal transverse fields (mainly the transverse hyperfine fields). In order to quantify the out-of-equilibrium effect, Fig. 17b presents the same data as in Fig. 17a but the magnetization M is converted into a spin temperature TS using the following equation [19]:
| (10) |

(a) Magnetization (M) hysteresis loops for several field sweep rates at a cryostat temperature of 0.04 K. The loops are normalized by the saturation magnetization Ms at 1.5 T. (b) Spin temperature TS for field sweeps from negative to positive fields, obtained by inversion of Eq. (10) where M(TS) are the data in (a).
Fig. 18 shows magnetization curves M(H) in the quasi-static regime with a field sweep rate slow enough (0.14 mT/s) to keep the system at equilibrium. During the field sweep, RF pulses were applied to the sample with a pulse length of 1 μs and a period of 4 s between each pulse. Depending on the RF frequency, clear dips are observed which result from resonant absorptions of photons associated with spin transitions between the quantum numbers ms = 1/2 and −1/2. After each pulse, the magnetization relaxes back to the equilibrium magnetization (see the fine structure in the insert of Fig. 18).

Magnetization curves measured with and without irradiation. The cryostat temperature was 40 mK and the field sweep rate of 0.14 mT/s was slow in order to keep the system at equilibrium. The electromagnetic radiation was pulsed with a period of 4 s and a pulse length of 1 μs. The RF frequencies are indicated and the RF amplitude is slightly frequency dependent. Insert: enlargement of the 4 GHz resonance. The fine structure is due to the RF pulses.
Typical relaxation measurements at a constant applied field after RF pulses of different durations are shown in Fig. 19. The relaxation is exponential with the rate independent of the pulse length. Detailed studies showed that the relaxation rate is dominated by the phonon-bottleneck regime, that is the spin–phonon relaxation time to the cryostat.
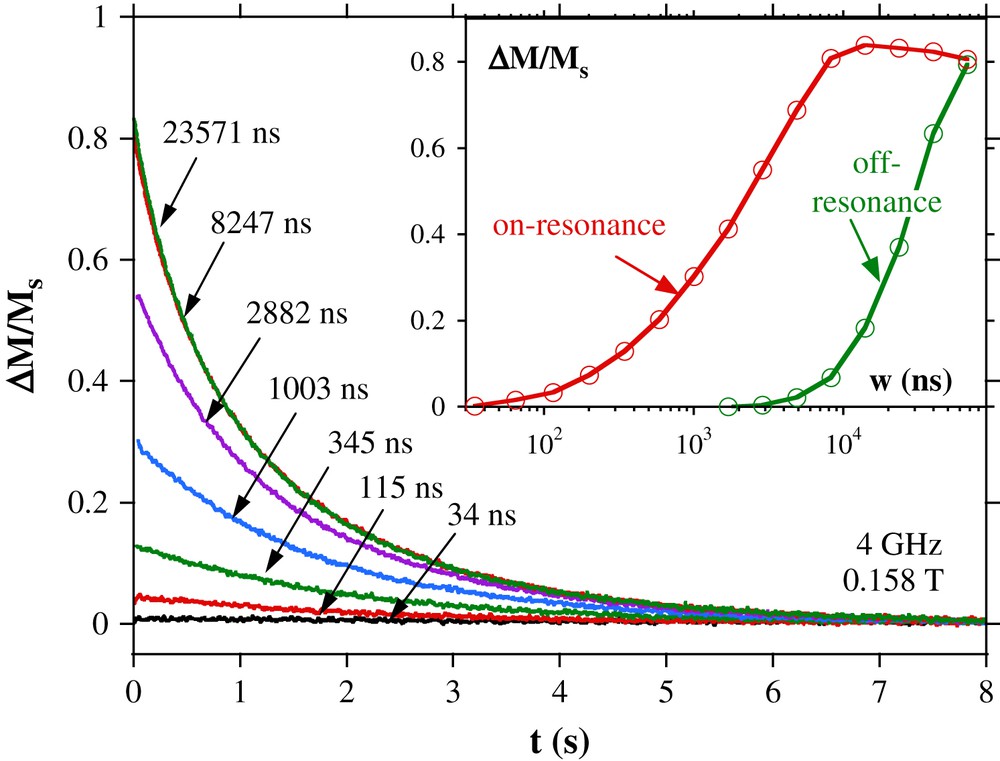
Relaxation of magnetization after a RF pulse of 4 GHz. The pulse lengths w are indicated. Insert: magnetization variation ΔM after a RF pulse versus the pulse length w for an on-resonance field (0.1582 T) and off-resonance field (0.1722 T).
The insert of Fig. 19 presents the change of magnetization ΔM between the magnetization before and after the pulse as a function of the pulse length w.ΔM increases linearly with w for short pulses of few tens of ns. It saturates for w ≈ 10 μs and decrease for very long pulses because of cryostat heating effects. Non-resonant photon absorption is also observed for very long pulses.
The resonant photon absorption lines are often taken to estimate a lower bound on the decoherence time of a qubit. We therefore investigated in more detail the line width observed in Fig. 18. Fig. 20(a) presents a typical power dependence of the line width for continuous irradiation at 4.2 GHz. Resonant photon absorption is clearly visible for a generator power larger than −60 dB m (1 nW). The line saturated at about −20 dB m (10 μW). Fig. 20(b) presents the absorption line for the pulsed technique (see Fig. 18) for several pulse lengths and a generator power of 15 dB m (32 mW, BRF ≈ 1 mT). The resonant photon absorption is clearly visible for pulse lengths longer than 10 ns. Note that the linewidths in Fig. 20(a) are nearly twice as large as those in Fig. 20(b).

(a) Magnetization variation ΔM between the equilibrium curves measured without and with continuous irradiation. The microwave frequency was 4.2 GHz. The microwave powers of the generator are indicated. (b) Magnetization variation ΔM after a RF pulse of 4.2 GHz and several pulse lengths. The cryostat temperature was 40 mK. ΔM is multiplied by a factor two.
In our case of an assembly of identical spins, the line broadening is mainly due to dipolar and hyperfine interactions. The dipolar coupling energy can be estimated with Edip/kB ≈ (gμBS)2/V ≈ 0.1 mK (S = 1/2 and V = 6.3 nm3) [96]. The hyperfine coupling with the nuclear spins can be obtained by considering the dipolar interaction of one Cr ion (s = 3/2) with the neighboring F nucleus having a nuclear spin I = 1/2. With gF = + 5.26 and the distance of d = 0.2 nm between F and Cr ions, the interaction energy is about 0.4 mK for each of the eight F nuclear spins [96]. The hyperfine line broadening of all eight F nuclear spins is about 3 mK which corresponds to 5 mT, in good agreement with the observed Gaussian line widths of about σ = 4 mT in Figs. 18 and 20.
Finally, we discuss the possibility of observing Rabi oscillations with the present setup. Due to inhomogeneous broadening only a lower bound of the coherence time τc can be estimated from the resonance lines in Fig. 20: τc ≈ Bν/(σν) ≈ 10 ns with Bν = 0.166 T, σ = 4 mT, and ν = 4.2 GHz. The corresponding number of coherent flips of the spin system is given by N = τc/τRabi with τRabi = 2π/(γBRF) ≈ 40 ns for BRF ≈ 1 mT. We obtain N ≈ 0.25 showing that there is no hope of seeing Rabi oscillations in the present conditions. In order to get N ≫ 1, it will be necessary to increase further the radiation field BRF, to reduce substantially the hyperfine broadening by substituting the F ions with OH groups, and to minimize the dipolar coupling by doping the crystal of Cr7Ni molecules with Cr8 molecules.
6 Photon-assisted tunneling in single-molecule magnet
It has also been proposed that molecular nanomagnets could be used as quantum computers by implementing Grover's algorithm [92]. For this to occur it is necessary to be able to generate an arbitrary superpositions of eigenstates of these systems. The suggested way to do this was through the use of multifrequency coherent magnetic radiation in the microwave and radiofrequency range. This would first introduce and amplify the desired phase for each mS state and this information could be finally readout by standard magnetic resonance techniques. In this approach, advantage is taken from the non-equidistance of the mS levels of the ground multiplet arising from the large axial anisotropy of these systems, which allows coherent populations of the different mS levels. A theoretical work pointed out that a very accurate control of pulse shape technique, both in amplitude, duration and choice of frequency is needed to fulfill the condition to design quantum computing devices in molecular nanomagnets [105]. In addition to such basic difficulties, we will see below that the total microwave power convoyed onto the samples cannot exceed a critical value above which non-linear effects occur.
In order to investigate the feasibility of the proposed process any preliminary experiment should aim to understand the effects of microwave absorption on the spin dynamics of these systems at low temperature. The measurements were performed using micro-Hall bars [106]. Continuous microwave radiation was generated by a couple of Gunn diodes equipped with calibrated attenuators. With this experimental setup, which has a very good stability of emitted power and a narrow bandwidth (100 kHz), only relative powers at the output of the diode can be known, which will be referred to as ρ in the following. We irradiated the sample using a 6 mm waveguide equipped with infrared filters in order to reduce heating. The circular polarization was maximized around 97%. The study was performed on a 0.1 mm Fe8 single crystal.
As schematically depicted in Fig. 21, microwave radiation with a frequencies of 115 GHz corresponds to the energy separation between the ground states mS = ±S and the first excited states mS = ±(S − 1) of Fe8 in zero applied magnetic field [13,107]. If the radiation is linearly polarized, the populations of the first excited states (mS = ±(S − 1)) in both wells will be enhanced equally (equal transition probability for ΔmS = ±1). On the other hand, the use of circular polarization has the advantage to distinguish between ΔmS = +1 (left polarization, σ− photons) or ΔmS = −1 (right polarization, σ+ photons) [19], and the population of only one of the two excited states will be enhanced (Fig. 21). An excess of tunneling from one well to the other is then expected. Therefore, circular polarization can help to distinguish between spin–phonons relaxation, and spin–phonons relaxation modified by the absorption of photons. The first equally affects the two sides of the barrier, i.e. the two branches of the hysteresis loop, while the second modifies the population of only one side of the barrier, i.e. one branch of the hysteresis loop. Any difference observed between the two branches of the hysteresis loop, has to be traced back to photon absorption.

Schematic representation of photon-assisted tunneling. On irradiating a Fe8 sample with a radiation of wavelength corresponding to the mS = −10 to −9 splitting (vertical arrow), an enhancement of the fraction of molecules that tunnel from the first excited state is expected (horizontal arrow). The use of circularly polarized radiation allows selecting only one side of the well and distinguishing between spin–phonon and spin–photon transitions.
Fig. 22a shows the hysteresis loops of a Fe8 single crystal with the easy axis parallel to the applied field, measured at 60 mK under irradiation. The tunneling transition near zero field is strongly enhanced for a radiation at 115 GHz. This is in agreement with a photon induced population transfer from mS = 10 to mS = 9, and agrees with earlier HF-EPR studies showing strong zero field absorption at about 116 GHz [13,107]. Fig. 22a also shows the expected asymmetry of the hysteresis loops in the presence of circularly polarized radiation. In particular, the height of the zero-field step (first tunnel resonance, n = 0), obtained when sweeping the field from negative saturation, is much less affected than when sweeping from positive saturation. This behavior is completely different from phonon-assisted tunneling (Fig. 22b) and clearly establishes that tunneling is assisted by photons for the matching frequency of 115 GHz. The observation of a more symmetric shape of the hysteresis curve at high microwave power can be explained both by the incomplete microwave polarization and by phonon emission, leading to relaxation on both sides of the barrier.
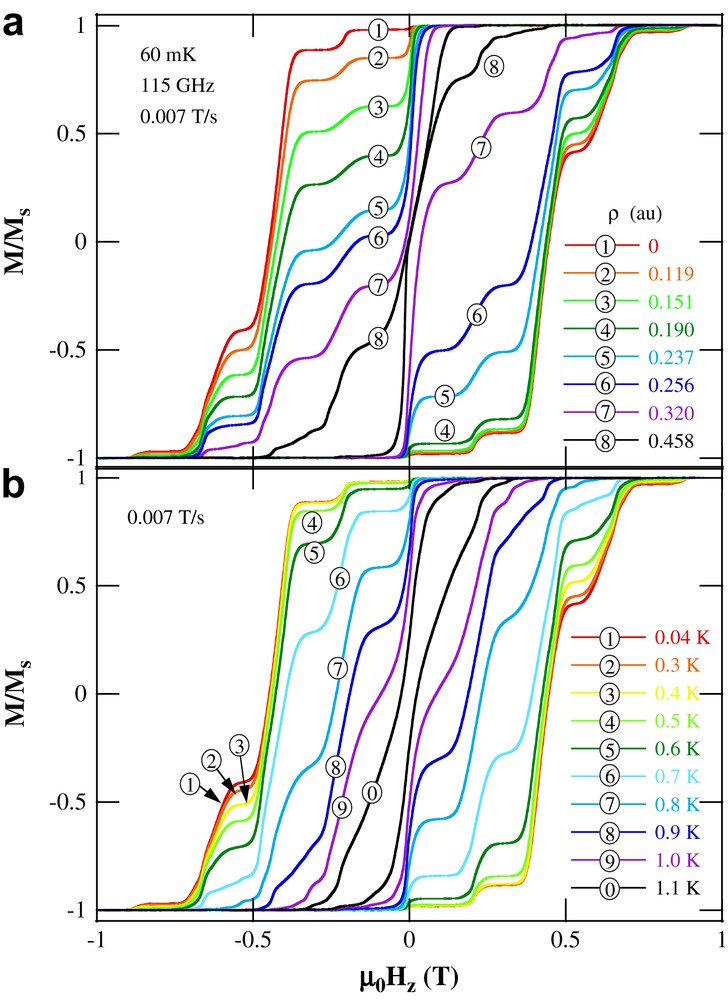
Magnetic hysteresis loops of Fe8 at a field sweep rate of 0.007 T/s and at 60 mK under irradiation with microwaves at 115 GHz and for several microwave powers ρ (a). The easy axis of the crystal is oriented along the applied field and perpendicular to the radiation oscillating magnetic field. The observed increasing of the tunneling rate at zero field, as a consequence of the absorption of photons induced by circularly polarized radiation, becomes evident by comparing the zero-field steps after positive or negative saturation. For comparison, the thermal behavior is presented in (b).
At detailed study showed that at lowest powers, the tunnel probability increases linearly with power, whereas at higher powers a strongly non-linear regime is observed [106]. The latter might be due to multi-spin and coherent photon transitions.
7 Environmental decoherence effects in nanomagnets
At temperatures below 0.36 K, Fe8 molecular clusters display a clear crossover from thermally activated relaxation to a temperature independent quantum regime, with a pronounced resonance structure of the relaxation time as a function of the external field (Section 3). It was surprising, however, that the observed relaxation of the magnetization in the quantum regime was found to be nonexponential and the resonance width orders of magnitude too large [18,27]. The key to understand this seemingly anomalous behavior involves the hyperfine fields as well as the evolving distribution of the weak dipole fields of the nanomagnets themselves [88]. Both effects were shown to be the main source of decoherence at very low temperature. At higher temperatures, phonons are another source of decoherence.
In the following sections, we focus on the low temperature and low field limits, where phonon-mediated relaxation is astronomically long and can be neglected. In this limit, the m = ±S spin states are coupled due to the tunneling splitting Δ±S which is about 10−7 K for Fe8 (Section 3.2) with S = 10. In order to tunnel between these states, the longitudinal magnetic energy bias ξ = gμBSHlocal due to the local magnetic field Hlocal on a molecule must be smaller than Δ±S, implying a local field smaller than 10−8 T for Fe8 clusters. Since the typical intermolecular dipole fields are of the order of 0.05 T, it seems at first that almost all molecules should be blocked from tunneling by a very large energy bias. Prokof'ev and Stamp have proposed a solution to this dilemma by proposing that fast dynamic nuclear fluctuations broaden the resonance, and the gradual adjustment of the dipole fields in the sample caused by the tunneling brings other molecules into resonance and allows continuous relaxation [88]. Some interesting predictions are briefly reviewed in the following section.
7.1 Prokof'ev–Stamp theory
Prokof'ev and Stamp were the first who realized that there are localized couplings of environmental modes with mesoscopic systems which cannot be modeled with an “oscillator bath” model [108] describing delocalized environmental modes such as electrons, phonons, photons, and so on. They found that these localized modes, such as nuclear and paramagnetic spins, are often strong and described them with a spin bath model [109]. We do not review this theory [110] but focus on one particular application which is interesting for molecular clusters [88]. Prokof'ev and Stamp showed that at a given longitudinal applied field Hz, the magnetization of a crystal of molecular clusters should relax at short times with a square-root time dependence which is due to a gradual modification of the dipole fields in the sample caused by the tunneling
| (11) |
| (12) |
7.2 Hole digging method to study dipolar distributions and hyperfine couplings
Motivated by the Prokof'ev–Stamp theory [88], we developed a new technique—which we call the hole digging method—that can be used to observe the time evolution of molecular states in crystals of molecular clusters. It allowed us to measure the statistical distribution of magnetic bias fields in the Fe8 system that arises from the weak dipole fields of the clusters themselves. A hole can be “dug” into the distribution by depleting the available spins at a given applied field. Our method is based on the simple idea that after a rapid field change, the resulting short time relaxation of the magnetization is directly related to the number of molecules which are in resonance at the given applied field. Prokof'ev and Stamp have suggested that the short time relaxation should follow a -relaxation law [Eq. (11)]. However, the hole digging method should work with any short time relaxation law—for example, a power law
| (13) |
- 1. Preparing the initial state. A well-defined initial magnetization state of the crystal of molecular clusters can be achieved by rapidly cooling the sample from high down to low temperatures in a constant applied field Hz0. For zero applied field (Hz = 0) or rather large applied fields (Hz > 1 T), one yields the demagnetized or saturated magnetization state of the entire crystal, respectively. One can also quench the sample in a small field of few milliteslas yielding any possible initial magnetization Min. When the quench is fast (<1 s), the sample's magnetization does not have time to relax, either by thermal or by quantum transitions. This procedure yields a frozen thermal equilibrium distribution, whereas for slow cooling rates the molecule spin states in the crystal might tend to certain dipolar ordered ground state.
- 2. Modifying the initial state—hole digging. After preparing the initial state, a field Hdig is applied during a time tdig, called “digging field and digging time”, respectively. During the digging time and depending on Hdig, a fraction of the molecular spins tunnel (back and/or fourth); that is, they reverse the direction of magnetization. Note that the field sweeping rate to apply Hdig should be fast enough to minimize the change of the initial state during the field sweep.
- 3. Probing the final state. Finally, a field Hzprobe is applied (Fig. 23) to measure the short time relaxation from which one yields Γshort [Eq. (13)] which is related to the number of spins which are still free for tunneling after step (2).

Schema of the hole digging method presenting the time dependence of temperature, applied field, and magnetization of the sample.
The entire procedure is then repeated many times but at other fields Hzprobe yielding Γshort(Hz, Hdig, tdig) which is related to the distribution of spins P(Hz, Hdig, tdig) that are still free for tunneling after the hole digging. For tdig = 0, this method maps out the initial distribution.
7.3 Intermolecular dipole interaction in Fe8
We applied the hole digging method to several samples of molecular clusters and quantum spin glasses. The most detailed study has been done on the Fe8 system. We found the predicted relaxation [Eq. (11)] in experiments on fully saturated Fe8 crystals [27,111] and on nonsaturated samples [49]. Fig. 24 displays a detailed study of the dipolar distributions revealing a remarkable structure that is due to next-nearest-neighbor effects [49]. These results are in good agreement with simulations [91,112].

Field dependence of the short time square-root relaxation rates Γsqrt(Hz) for three different values of the initial magnetization Min. According to Eq. (12), the curves are proportional to the distribution P(Hz) of magnetic energy bias due to local dipole field distributions in the sample. Note the logarithmic scale for Γsqrt. The peaked distribution labelled Min = −0.998Ms was obtained by saturating the sample, whereas the other distributions were obtained by thermal annealing. Min = −0.870Ms is distorted by nearest neighbor lattice effects. The peak at 0.04 T as well as the shoulder at 0.02 T and 0.04 T are originated by the clusters which have one nearest-neighbor cluster with reversed magnetization: the peak at 0.04 T corresponds to the reversal of the neighboring cluster along the a crystallographic axis, which almost coincides with the easy axis of magnetization, while the shoulder at 0.02 T and 0.04 T are due to the clusters along b and c.
For a saturated initial state, the Prokof'ev–Stamp theory allows one to estimate the tunnel splitting Δ±S. Using Eqs. (3), (9) and (12) of Ref. [88], along with integration, we find , where c is a constant of the order of unity which depends on the sample shape. With ED = 15 mT, ξ0 = 0.8 mT, c = 1, and Γsqrt [49,89], we find Δ±10 = 1.2 × 10−7 K which is close to the result of Δ±10 = 1.0 × 10−7 K obtained by using a Landau–Zener method (Section 3.1) [48].
Whereas the hole digging method probes the longitudinal dipolar distribution (Hz direction), the Landau–Zener method can be used to probe the transverse dipolar distribution by measuring the tunnel splittings Δ around a topological quench.
7.4 Hyperfine interaction in Fe8
The strong influence of nuclear spins on resonant quantum tunneling in the molecular cluster Fe8 was demonstrated for the first time [89] by comparing the relaxation rate of the standard Fe8 sample with two isotopic modified samples: (i) 56Fe is replaced by 57Fe, and (ii) a fraction of 1H is replaced by 2H. By using the hole digging method, we measured an intrinsic broadening which is driven by the hyperfine fields (Fig. 25). Our measurements are in good agreement with numerical hyperfine calculations [89,91]. For T > 1.5 K, the influence of nuclear spins on the relaxation rate is less important, suggesting that spin–phonon coupling dominates the relaxation rate.

Comparison of the short time relaxation rates of three different Fe8 samples at T = 40 mK with Htrans = 0 and Minit = 0. The insert displays a typical example of a hole which was dug into the distribution by allowing the sample to relax for the time tdig at μ0Hdig = 14 mT.
8 Molecular spintronics using single-molecule magnets
A revolution in electronics is in view, with the contemporary evolution of two novel disciplines, spintronics and molecular electronics [113–116]. A fundamental link between these two fields can be established using molecular magnetic materials and, in particular, single-molecule magnets, which combine the classic macroscale properties of a magnet with the quantum properties of a nanoscale entity. The resulting field, molecular spintronics aims at manipulating spins and charges in electronic devices containing one or more molecules [117]. The main advantage is that the weak spin–orbit and hyperfine interactions in organic molecules is likely to preserve spin-coherence over time and distance much longer than in conventional metals or semiconductors. In addition, specific functions (e.g. switchability with light, electric field etc.) could be directly integrated into the molecule.
The contemporary exploitation of electronic charge and spin degrees of freedom is a particularly promising field both at fundamental and applied levels. This discipline, called spintronics, has already seen some of its fundamental results turned into actual devices in a record time of 10 years and it holds great promises for the future [113,118,119]. Spintronic systems exploit the fact that the electron current is composed of spin-up and spin-down carriers that carry information encoded in their spin state and interact with magnetic materials differently. Information encoded in spins persists when the device is switched off; it can be manipulated with and without using magnetic fields and can be written using little energy, to cite just a few advantages of this approach.
New efforts are now directed towards spintronic devices that preserve and exploit quantum coherence, so that fundamental investigations are shifting from metals to semiconducting [118–120] and organic materials [121], which potentially offer best promises for cost, integration and versatility. For example, organic materials are already used in applications such as organic light-emitting diodes (OLED), displays and organic transistors. The concomitant trend towards ever-smaller electronic devices (having already reached the nanoscale), and the tailoring of new molecules possessing increased conductance and functionalities are driving electronics to its ultimate molecular scale limit [122], and the so-called molecular electronics is now being intensively investigated.
In experiments of molecular electronics, the measuring devices are usually constituted of two nanoelectrodes and a bridging molecule in between, allowing the measurement of electron transport through single molecules. As the measurement is performed at the molecular level, the observables are connected to molecular orbitals and not to Bloch waves as in bulk materials. Hence, new rules are found for these systems and it becomes possible to probe the quantum properties of the molecule directly. The electron tunneling processes in the electrode-molecule-electrode system can show the presence of Kondo or Coulomb blockade effects, depending on the binding strength between the molecule and the electrodes, which can be tuned by selecting the appropriate chemical functional groups.
In this context, a new field of molecular spintronics is emerging that combines the concepts and the advantages of spintronics and molecular electronics [117,123] which requires the creation of molecular devices using one or few magnetic molecules. Compounds of the single-molecule magnets (SMMs) class seem particularly attractive: their magnetization relaxation time is extremely long at low temperature reaching years below 2 K. These systems, combining the advantages of molecular scale with the properties of bulk magnetic materials, look attractive for high-density information storage and also, owing to their long coherence times [124–126], for quantum computing [92,95,96]. Moreover, their molecular nature leads to appealing quantum effects of the static and dynamic magnetic properties. The rich physics behind the magnetic behavior produces interesting effects like negative differential conductance and complete current suppression [127,128], which could be used in electronics. Last but not least, specific functions (e.g. switchability with light, electric field etc.) could be directly integrated into the molecule.
In order to lay the foundation of molecular spintronics, several molecular devices have been proposed [117]: molecular spin-transistor, molecular spin-valve and spin filter, molecular double-dot devices, and carbon nanotube-based nano-SQUIDs [5]. The main purpose is to fully control the initialization, the manipulation and the readout of the spin states of the molecule and to perform basic quantum operations. The main targets for the coming years concern fundamental science as many issues, experimental, technological and theoretical, must be addressed before applications, for instance in quantum electronics, can be realistically considered.
A double-dot device (Fig. 26) is one possible way to molecular spintronics [117]. It is a three terminal device, where the current passes through a non-magnetic quantum conductor (quantum wire, nanotube, molecule, or quantum dot (QD)). The magnetic molecule is only weakly coupled to the non-magnetic conductor but its spin can influence the transport properties, permitting readout of the spin state with minimal back-action. Several mechanisms can be exploited to couple the two systems. One appealing way is to use a carbon nanotube as a detector of the magnetic flux variation, possibly using the nano-SQUID [5]. Other possibilities involve the indirect detection of the spin state through electrometry. Indeed, a non-magnetic quantum conductor at low temperatures behaves as a QD for which charging processes become quantized, giving rise to Coulomb blockade and Kondo effect depending on the coupling to the leads. Any slight change in the electrostatic environment (controlled by the gate) can induce a shift of the Coulomb diamonds of the device, leading to a conductivity variation of the QD at constant gate voltage. QDs are therefore accurate electrometers. When the QD is coupled, even weakly, with a magnetic object, due to the Zeeman energy the spin flip at non-zero field induces a change of the electrostatic environment of the QD. This effect, called the magneto-Coulomb effect, enables therefore to detect the magnetization reversal of the molecule.
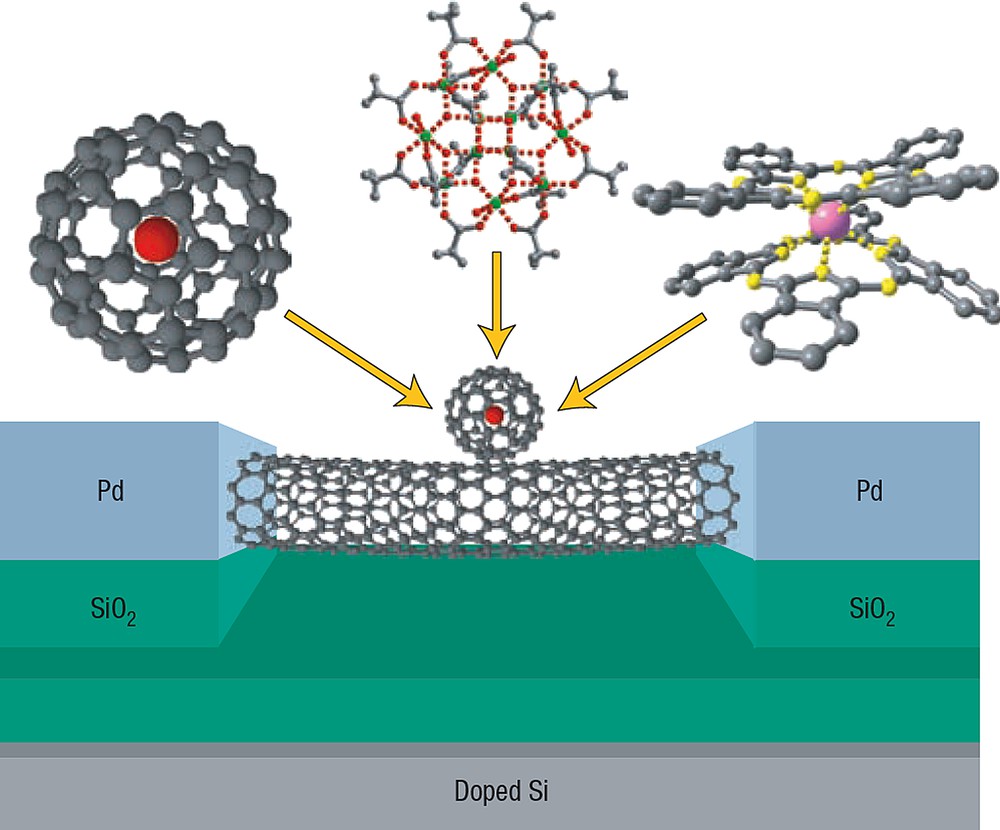
Molecular double-dot devices. Magnetic molecules proposed for grafting on suspended carbon nanotubes connected to Pd electrodes (form left to right): a C60 fullerene including a rare-earth atom, the Mn12 SMM and the rare-earth-based double-decker [Tb(phtalocyanine)2] SMM. The gate voltage of the double-dot device is obtained by a doped Si substrate covered by a SiO2 insulating layer.
Another route is weak exchange or dipole coupling between the magnetic molecule and the QD. It is interesting to probe these effects as a function of the number of trapped electrons because odd or even number of electrons should lead to different couplings. The main advantage of these schemes is that the coupling to the leads and the injected current does not alter the magnetic properties of the molecule. Because coupling is small, these devices might allow a non-destructive readout of the spin states.
9 Conclusion
In conclusion, we presented detailed measurements which demonstrated that molecular nanomagnets offer a unique opportunity to explore the quantum dynamics of a large but finite spin. We focused our discussion on the Fe8 molecular nanomagnet because it is the first system where studies in the pure quantum regime were possible. The tunneling in this system is remarkable because it does not show up at the lowest orders of perturbation theory.
A new family of supramolecular, antiferromagnetically exchange-coupled dimers of single-molecule magnets (SMMs) has recently been reported [83]. Each SMM acts as a bias on its neighbor, shifting the quantum tunneling resonances of the individual SMMs. Hysteresis loop measurements on a single crystal of SMM-dimers have established quantum tunneling of the magnetization via entangled states of the dimer. This showed that the dimer really does behave as a quantum-mechanically coupled dimer. The transitions are well separated, suggesting long coherence times compared to the time scale of the energy splitting [84]. This result is of great importance if such systems are to be used for quantum computing.
Molecules with small spin have also been studied. For example, time-resolved magnetization measurements were performed on a spin 1/2 molecular complex, so-called V15 [129]. Despite the absence of a barrier, magnetic hysteresis is observed over a time scale of several seconds. A detailed analysis in terms of a dissipative two-level model has been given, in which fluctuations and splittings are of the same energy. Spin–phonon coupling leads to long relaxation times and to a particular “butterfly” hysteresis loop [104,130]. We presented magnetization measurements on a crystal of Cr7Ni antiferromagnetic rings with a spin 1/2. Irradiation with microwaves at frequencies between 1 and 10 GHz leads to observation of very narrow resonant photon absorption lines which are broadened by hyperfine and spin–spin interactions.
The use of circularly polarized microwaves allowed us to show for the first time the phenomenon of photon-assisted tunneling in magnetism, using a single-molecule magnet Fe8 [106]. In accordance with the selection rules for EPR spectroscopy [19], circularly polarized radiation promotes the transition mS = 10 to mS = 9 with ΔmS = −1, giving an effect of magnetic dichroism at millimeter wavelengths. At lowest powers, the tunnel probability increases linearly with power, whereas at higher powers a strongly non-linear regime is observed. The latter might be due to multi-spin and coherent photon transitions.
Quantum coherence between states of opposite magnetization has been observed on molecules with small spin [124–126] and without barrier. However, for most SMMs, dipole–dipole and hyperfine interactions are source of decoherence. In other words, when a spin has tunneled through the barrier, it experiences a huge modification of its environment (hyperfine and dipolar) which prohibits the back tunneling. Prokof'ev and Stamp suggested three possible strategies to suppress the decoherence [131,132]: (i) Choose a system where the NMR frequencies far exceed the tunnel frequencies making any coupling impossible; (ii) Isotopically purify the sample to remove all nuclear spins; (iii) Apply a transverse field to increase the tunnel rate to frequencies much larger than hyperfine field fluctuations. Several groups are currently working on such proposals.
Concerning the perspectives of the field of single-molecule magnets, we expect that chemistry is going to play a major role through the synthesis of novel larger spin clusters with strong anisotropy. We want to stress that there are already many other molecular nanomagnets (the largest is currently an Mn84, Fig. 2, and an Mn6 has currently a record anisotropy barriers approaching 100 K [36]), which are possible model systems. We believe that more sophisticated theories are needed which describe the dephasing effects of the environment onto the quantum system. These investigations are important for studying the quantum character of molecular clusters for applications like “quantum computers”. The first implementation of Grover's algorithm with molecular nanomagnets has been proposed [92]. Antiferromagnetic systems have attracted an increasing interest. In this case the quantum hardware is thought of as a collection of coupled molecules, each corresponding to a different qubit [93–96]. In order to explore these possibilities, new and very precise setups are currently built and new methods and strategies are developed. The field of molecular nanomagnets evolves towards molecular electronics and spintronics, which are both rapidly emerging fields of nanoelectronics with a strong potential impact for the realization of new functions and devices helpful for information storage as well as quantum information. New projects aim at the merging of the two fields by the realization of molecular junctions that involve a molecular nanomagnet. In order to tackle the challenge of controlled connection at the single-molecule level, molecular self-assembly on nanojunctions obtained by the technique of electromigration was used [127,128]. Furthermore, a new nano-SQUID with carbon nanotube Josephson junctions was developed [5], which should be sensitive enough to study individual magnetic molecules that are attached to the carbon nanotube. Such techniques will lead to enormous progress in the understanding of the electronic and magnetic properties of isolated molecular systems and they will reveal intriguing new physics [117].


