1 Introduction
Portable NMR has been of interest since the early 1950s for NMR well-logging [1]. At that time, Varian imagined a system consisting of a single coil to polarize the spins, then shut-off quickly in order to record the NMR signal caused by the precession of the spins in the Earth's field [2]. Portable NMR did not draw much attention for a few decades thereafter due to the conflicting requirement for strong fields and portability. The development of new magnetic materials such as NdFeB and SmCo at the beginning of the 1980s [3] have brought new prospects for portable NMR. Previous materials (AlNiCo, ferrites, etc.) did not offer sufficient remanence and coercivity to provide a strong, homogeneous and compact magnet system. Halbach, sensing the possibilities offered by rare-earth magnets, developed his famous multipole structures around these new materials [4]. However, it was only in 1995 that the first truly portable NMR system was proposed, the NMR-MOUSE [5]. This system was among the first to offer the ability to perform NMR outside of a magnet, relaxing standard limitations on samples (e.g., size) applicable to NMR. Such magnets are now called ex-situ magnets, as opposed to the in-situ magnets typically used in NMR and MRI that require one to put the sample inside the bore of the magnet. Several other systems based on permanent magnets have been proposed for both ex-situ and in-situ applications [6–10]. Most of the proposed in-situ systems rely on Halbach's scheme, generating a field transverse to the bore. Although far from an exhaustive list, some examples of such in-situ magnets are the NMR Mandhalas proposed by Raich and Blumler [11], and the more recent homogeneous system proposed by Danieli et al. [12]. Both systems were developed by assembling magnetized cubes.
We propose some theoretical elements for the control of the field produced by a magnet assembly in order to build high-homogeneity magnets for NMR. These were introduced very early by G. Aubert [13] in the context of 3D. Very recently, similar 2D and 3D analytical work has been published [14,15], giving rise to unilateral systems using properly shaped polar pieces. We have used Aubert's theoretical ideas to create a simple system in order to test the feasibility of these theoretical developments. This test-bench is a compact magnet assembly, based on small, inexpensive, magnetized cubes providing a field longitudinal to the bore. This offers better compatibility with current NMR probe designs.
2 Theory
In the case of NMR, the Region of Interest (RoI) lies outside of the field sources region and one can define a magnetic pseudo-scalar potential such that:(1)
This potential verifies the Laplace equation:
| (2) |
In the case we are interested in, and in general for magnetic resonance, it is appropriate to represent the RoI as a sphere. The center of this sphere will be called the origin. The Laplace equation is separable in the spherical coordinate system and one can obtain a unique decomposition of the potential on the spherical harmonics base, centered on the origin. One must keep in mind that the potential exists only in areas of space free of magnetic sources. One can divide the space into two areas where the potential exists: inside the biggest sphere centered on the origin that does not contain any source, and outside the smallest sphere centered on the origin that contains all the sources. Inside the former sphere, one can write this expansion as:
| (3) |
From this equation, one can also infer that a rotationally-symmetric structure will be advantageous, as it will remove all skewed terms. In the case where regular rotational symmetry is not possible, one can still achieve a homogeneity of order n: the presence of a n-fold rotational-symmetry will insure that no skewed terms exist before the axial term of order n. Once skewed terms have been taken care of, one is left with axial terms. Another helpful symmetry is the planar symmetry (anti-symmetry), which will leave only even (odd) axial terms. It is then possible to arbitrarily cancel p orders by properly arranging p + 1 independent sources. We can in principle derive analytical formulas of the expansion for many different source geometries. These formulas are functions of selected relevant parameters of the geometry. Based on these equations, our method provides the optimal parameters for a given geometry and the desired homogeneity. Another benefit of this method is that the solution is scalable: the system can be rendered as large (or as small) as needed, and the field properties (strength and homogeneity) will not change.
3 Test-bench magnet, M0
A particular magnet configuration was proposed in 1991 by G. Aubert to build a permanent magnet system with a longitudinal field [16]. This system features cylindrical symmetry along with plane symmetry (see Fig. 1). However, it is difficult to obtain cylindrical rings with a uniform radial magnetization, making it necessary to segment the ring into discrete elements. We chose to use cubes as they are readily available for a low price. A schematic of the cube-based structure can be seen in Fig. 2. Twelve segments were used to maximize the density of material around a bore of 52 mm diameter. Two rows of cubes are placed in each ring to reinforce the field, requiring a total of 48 cubes. Each cube is 12 × 12 × 12 mm. The resulting assembly is about 66 mm long and has a diameter of roughly 90 mm, with a total weight of about 1 kg.
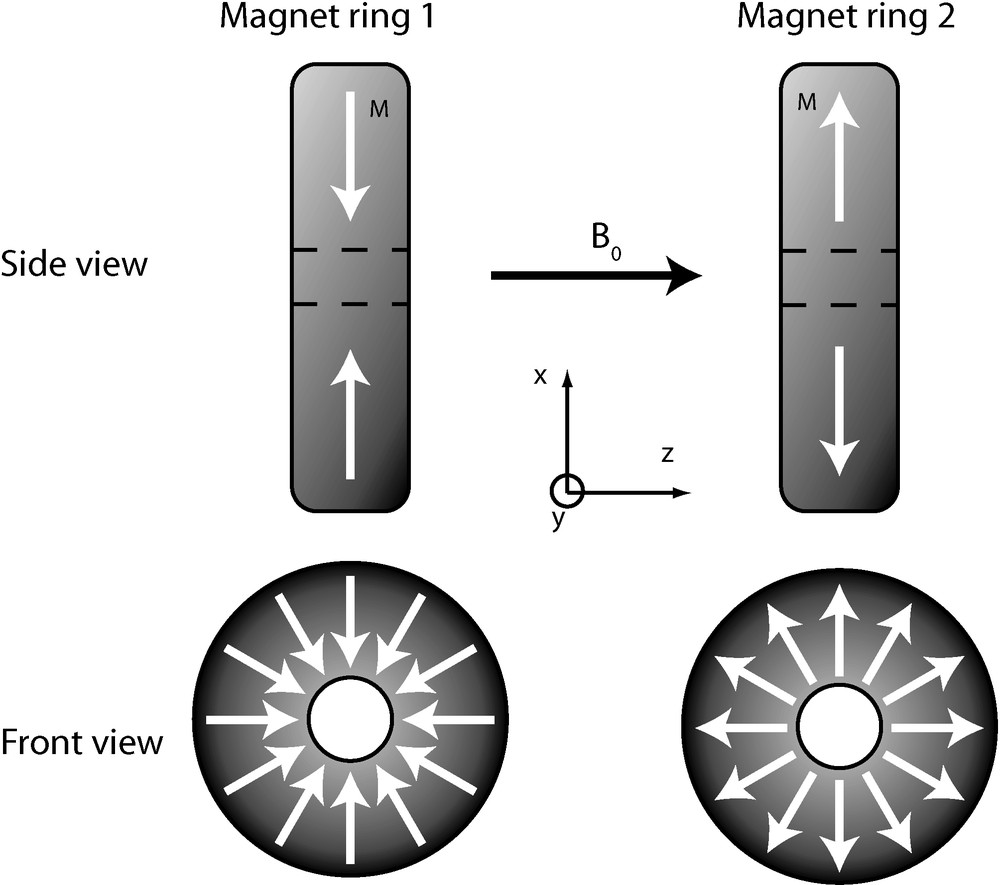
Basic layout of the magnet system. It consists of two rings that are radially magnetized. The combination of these rings creates a longitudinal field in the center of the system and confines the field in the structure.
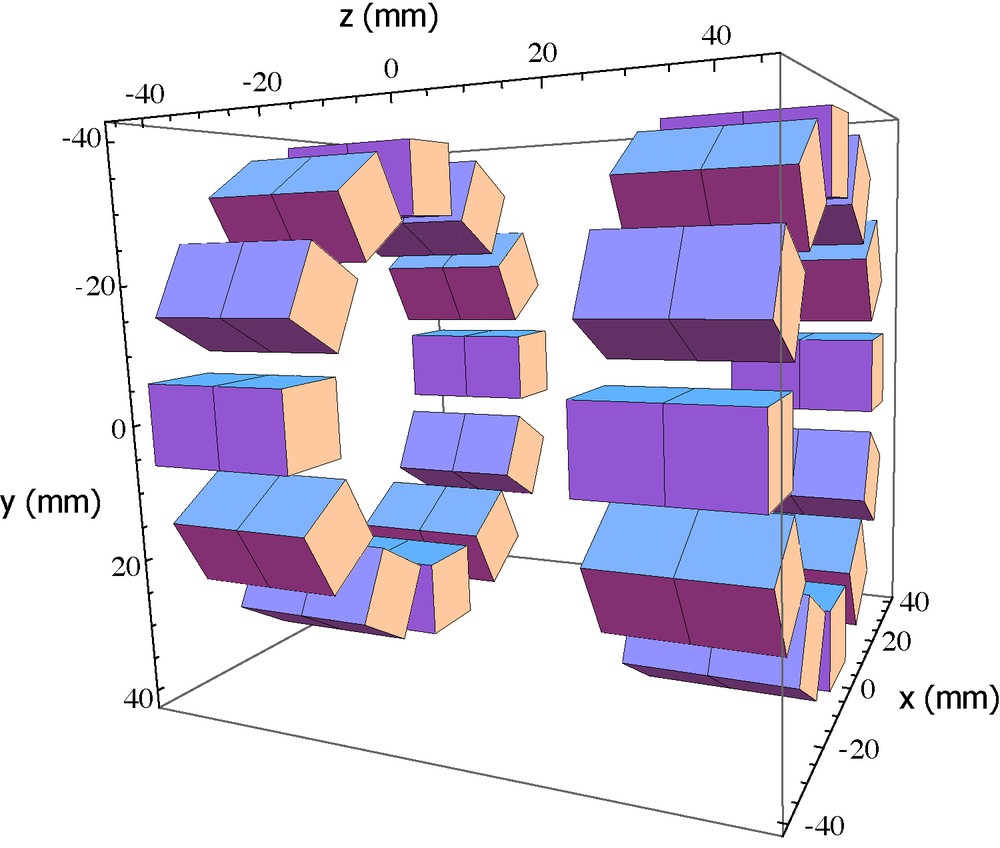
Adaptation of the concept to a geometry using cubic magnets. Each ring is made out of magnetized cubes. Two rows of cubes are used in each ring to reinforce the resulting field in the center. Axes are in mm.
Based on the previous considerations, one can assess the homogeneity that can be potentially achieved by such a system. Starting with the segmentation into 12 pieces (i.e. 12-fold rotational symmetry) of the rings, one can expect that skewed terms will be cancelled up to the 11th order (the first non-zero being the 12th). However, as we have only two rings, only one axial term can be cancelled by adjusting the inter-ring gap. The plane symmetry however, helps us by cancelling all odd terms. As a result, one might expect the homogeneity of this system to be dominated by the axial term of order 4. Given the dimensions of the magnet, this results in a homogeneity of about 15 ppm over a sphere of 3 mm in diameter. This is the best homogeneity achievable by this magnet. Achieving a better homogeneity would imply the addition of a shimming system of significant size compared to the magnet itself. Simulations of the magnetic cube arrangement of Fig. 2, performed using Radia [17] bear this out. A contour plot of the field in the xOz plane (Fig. 3) shows that the variations of the field are indeed dominated by the order 4 and predicts the field at the center to be about 120 mT. However, these results rely on the hypothesis that the cubes are perfectly magnetized. This is generally not the case, especially when using low-cost magnets. As a result, it is necessary to evaluate the magnetization dispersion from one cube to another. After characterization, it might be desirable to discard the poorer magnets and arrange the better ones in a proper manner. We hence decided to buy about 40% more cubes, that is to say 68. The magnets were purchased from Supermagnete.de without any requirements on the mechanical or magnetic tolerances and they were designated as N48.
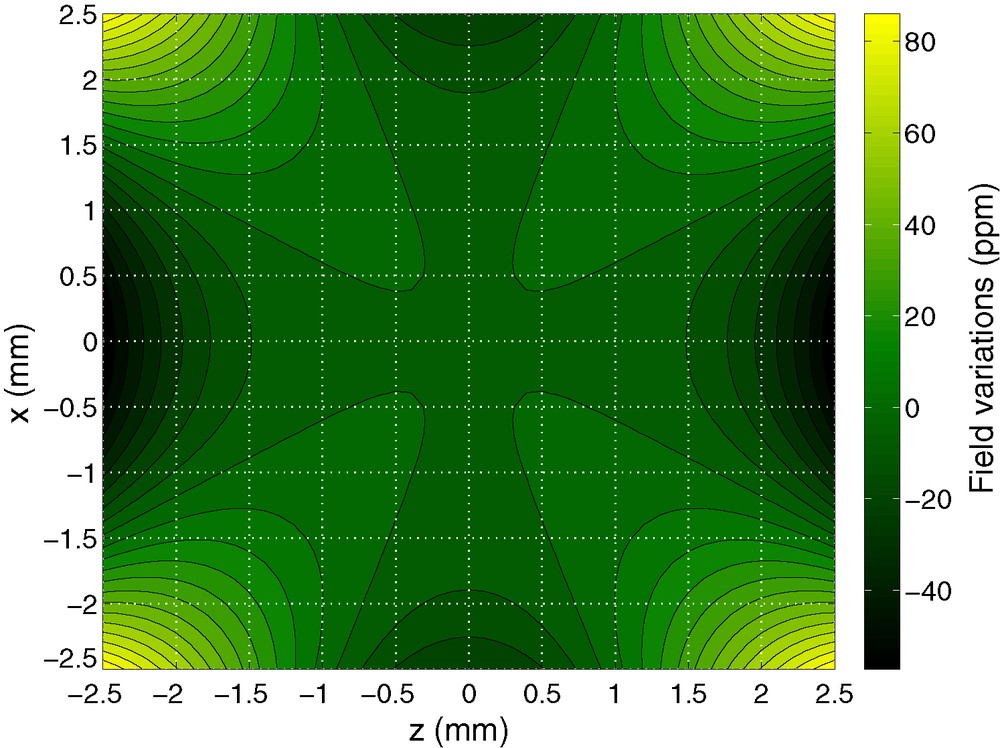
Contour plot of Bz in the xOz plane. One can notice that the variations are dominated by the term of order 4, and are limited to about 140 ppm over a sphere of 5 mm diameter.
4 Magnetization measurements and optimization
We measured the 68 cubes using a Hall probe (Lakeshore 3-axis probe model MMZ-2518-UH with a Lakeshore model 460 3-channel gaussmeter). We developed an automated measurement bench based on three translation stages (Newport, model M-443), operated by three motors (Newport, model LTA-HS). The displacement range is 5 cm in each of the three directions. The motors were controlled by a homemade Labview-based program. The gaussmeter is also interfaced with the Labview-based program so that the positioning/measuring process is controlled by the computer. As a result, an automated scheme was developed to map the field of a cube in a given plane. Along with a dipolar approximation of a cube, such a field map provides the ability to retrieve with a good accuracy the three components of the magnetization of each cube. The field of a dipole is indeed:
| (4) |
with being the unitary vector going from the dipole position O (set to be the origin) to the measurement point P(x,y,z) and R being the distance from O to P. When reducing to the z component of the field, we obtain:
| (5) |
As a result, the knowledge of Bz at three arbitrary points of free space is sufficient to retrieve Mx, My and Mz. However, due to the low precision of a Hall probe (about 10−4) and the uncertainties on positioning and registration of the probe axes to the cube axes, it is necessary to use more than three points. A more detailed description of the measurements will be given in a subsequent detailed publication.2
The retrieved components of the magnetization were converted to spherical coordinates. We achieved a repeatability of 0.5% on the modulus M of the magnetization, 0.5° on θ (angle with the z axis) and 4° on ϕ (angle in the x-y plane). This repeatability was estimated from the repeated measurement of the same cube 60 times. Thermal variations may actually influence the repeatability of the modulus by tenths of a percent. As a result, it is safe to say the accuracy on the modulus is about 1%. The results for the measurements of M, θ and ϕ are presented on Figs. 4–6.
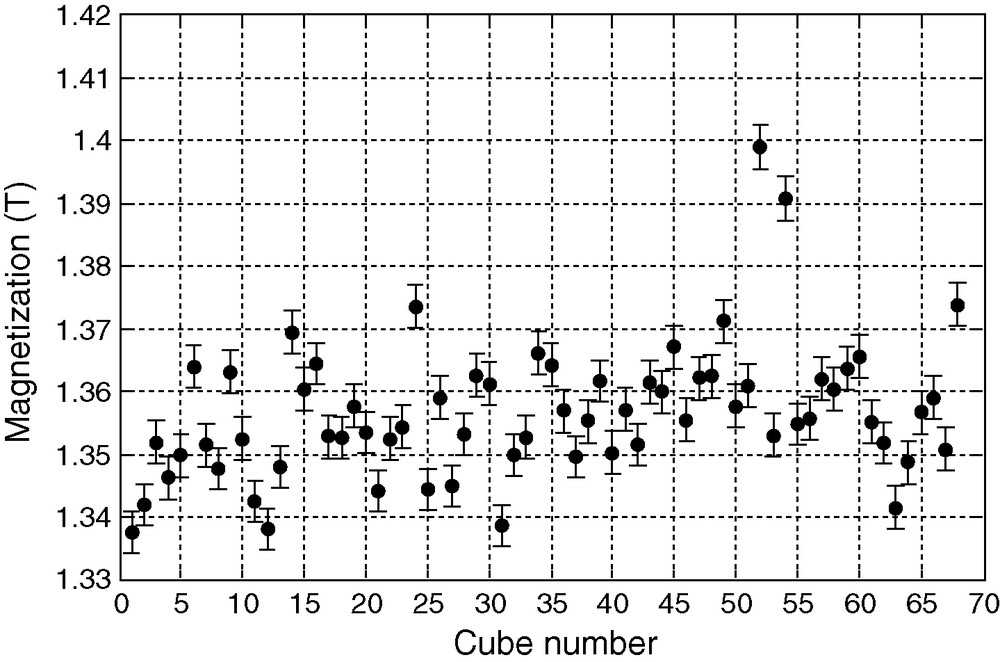
Magnetization modulus as measured using a Hall probe over a 64-point field map for each cube. The dispersion is about ± 2% and the measurement repeatability is about 0.5% on the short term. However, due to the temperature variations during the day in the measurement room, it is safer to consider a 1% repeatability.
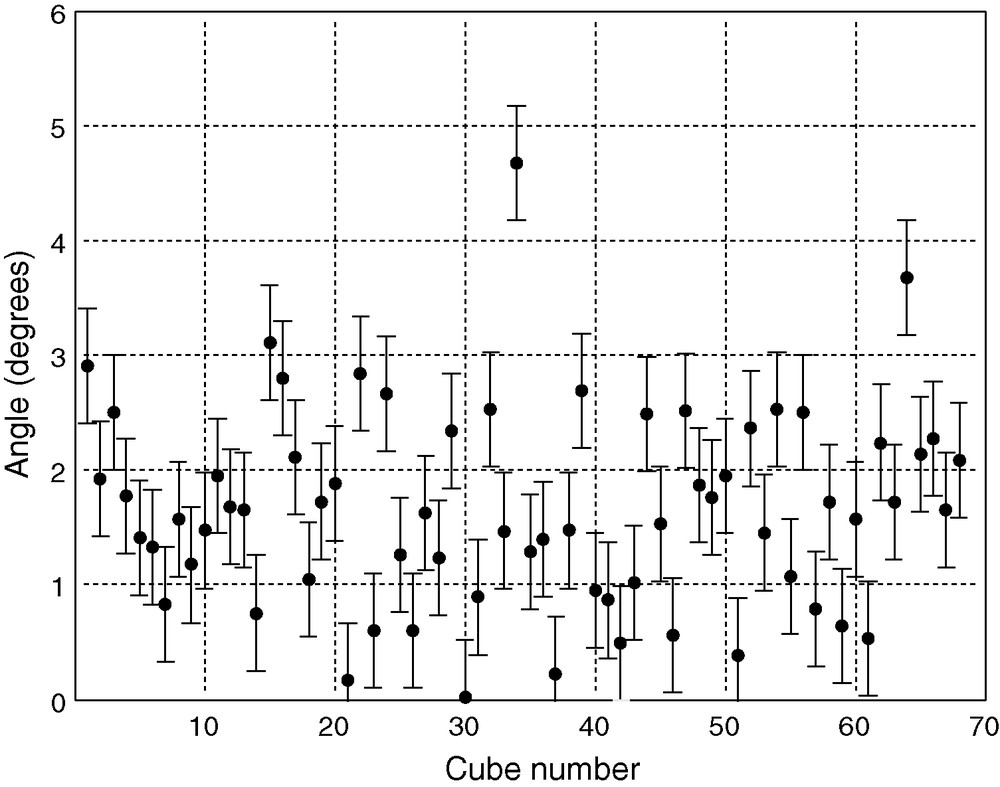
Magnetization angle θ for the different cubes as measured using a Hall probe and a 64 points field map for each cube. The dispersion is about ± 2° and the measurement repeatability is about 0.5°.
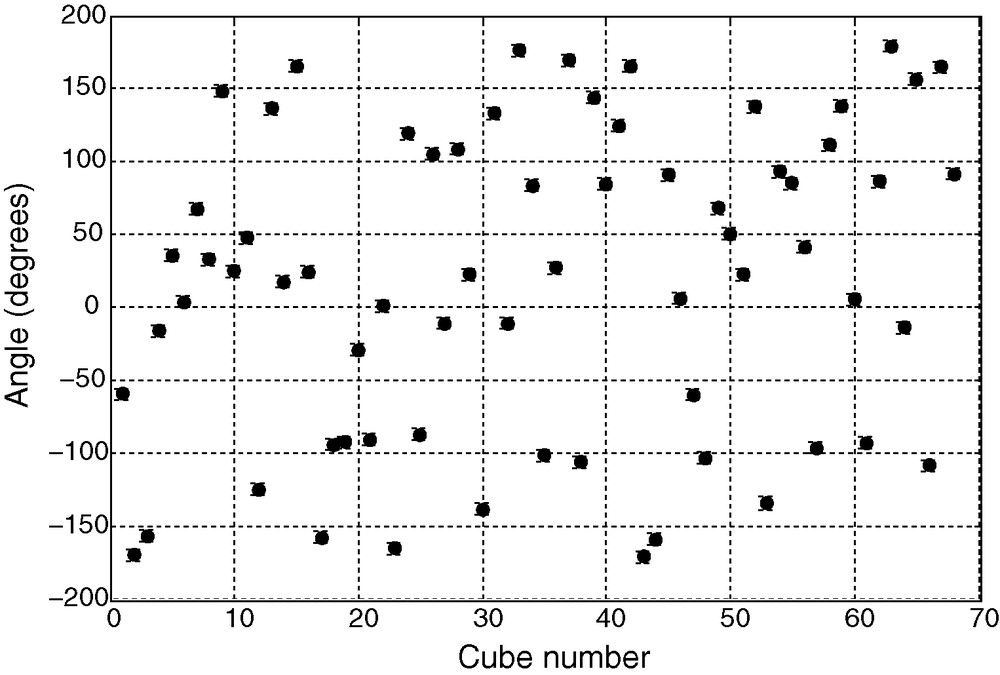
Magnetization angle ϕ for the different cubes as measured using a Hall probe and a 64 points field map for each cube. Giving a dispersion would not make sense as there is an ambiguity when positioning a cube before measurements : one can rotate it around the z axis by π/2, π, 3π or 2π (no rotation) compared to the previous cube, without changing the measurement geometry, nor changing the pole configuration. If the magnetization always had the same absolute ϕ, we would observe four groups of points in the plot. However, the retrieval of ϕ is not very accurate (repeatability around 4°) as θ is quite small and results in a wide dispersion around the four mean values, resulting in an overall 2π dispersion.
The large dispersion of the magnetization from one cube to another leads to imperfections in the symmetries, which were assumed to guarantee the homogeneity of the field at the center of the assembly. It is hence desirable to find an optimum combination of the available cubes which minimizes the inhomogeneities owing to the cube-to-cube variations. This can be done based on the magnetization measurements and analytical formulas for the spherical harmonics expansion of a dipole. The problem of such an optimization is that there are far too many possible combinations. The number of possibilities is governed by , which is reduced by the 12-fold axial symmetry and the planar symmetry to “only” about 4.2474 × 1076 possibilities. It is simply not possible to screen, even numerically, so many possibilities and one can only find a “better” combination, but one cannot guarantee it is the best one. We implemented a simple algorithm for this purpose that generates random combinations. This algorithm evaluates the spherical harmonics expansion at the center of the magnet and computes a quality factor based on the different terms in the expansion and on a weighting function that defined priorities on the terms to be reduced.
5 Experimental results for a non-optimized combination of cubes
Initially, a non-optimized combination of the cubes was put together. The cubes were placed in aluminum mounts (corresponding to a ring) with 12 slots per mount, each slot accommodating two cubes. This first non-optimized system was meant to provide a comparison to an optimized combination. The exact layout was recorded so that it could be simulated using Radia. The magnet system was first mapped with a Hall probe and the gap between the two rings was optimized based on these measurements. The field at the center was about 120 mT and a 2D contour plot in the xOz plane can be seen on Fig. 7a. This plot shows the presence of gradients along z, implying a lack of planar symmetry and the presence of Z1 and Z3 terms in the expansion. The lack of symmetry of the field distribution in regard to the z axis is induced by the lack of axial symmetry of the magnet sources and is associated with the existence of skewed terms of order smaller than 12.

Contour plot of Bz in the xOz plane. (a) Experimental field contours. (b) Simulated field contours. The magnitude and variations of the field are slightly underestimated by the simulation. Overall, the experimental matches reasonably with the simulation. One can notice the presence of local gradients from left to right (z axis) implying the lack of planar symmetry in the magnet. The lack of symmetry from bottom to top (x axis) implies the lack of axial symmetry. These imperfections are due to the cube-to-cube differences. The differences between the simulated and measured field can be attributed to the use of the dipolar approximation in the retrieval of the cube magnetization.
We then simulated the magnet with Radia, taking into account the measured magnetizations of the individual cubes. A 2D contour plot of the simulated field in the xOz plane can be seen on Fig. 7b. Although the simulation does not match the experimental data exactly, one can observe the similarities in the overall variations and span of variations. The lack of correspondence in the smaller scale variations shows that the dipolar approximation is a crude one. The magnetization within each cube might not be homogeneous. Moreover, the distances involved in this assembly are just on the frontier between the legitimate use of the dipolar approximation and the necessity of taking into account the cubes geometry.
However, the homogeneity in this magnet was sufficient to obtain an NMR signal from a water sample, using a small coil. The dimensions of the sample were about 1.2 mm in diameter by 3 mm in length. The coil was a solenoid, wound around a capillary of 1.2 mm i.d. and 1.6 mm o.d. and tuned to 5.1 MHz using a home-made single-channel probe body. After thorough adjustments, we were able to obtain a FWHM of about 40 ppm (Fig. 8). Such a line width is more than sufficient for relaxation-based investigations or some diffusion measurements. The sequence was a simple π/2 pulse followed by the acquisition of 1024 points with a 50 μs dwell time. The SNR on the FID for one scan was about 1.34. Recycle time was 0.1s. FID baseline correction was applied. No apodization was applied in the data processing.
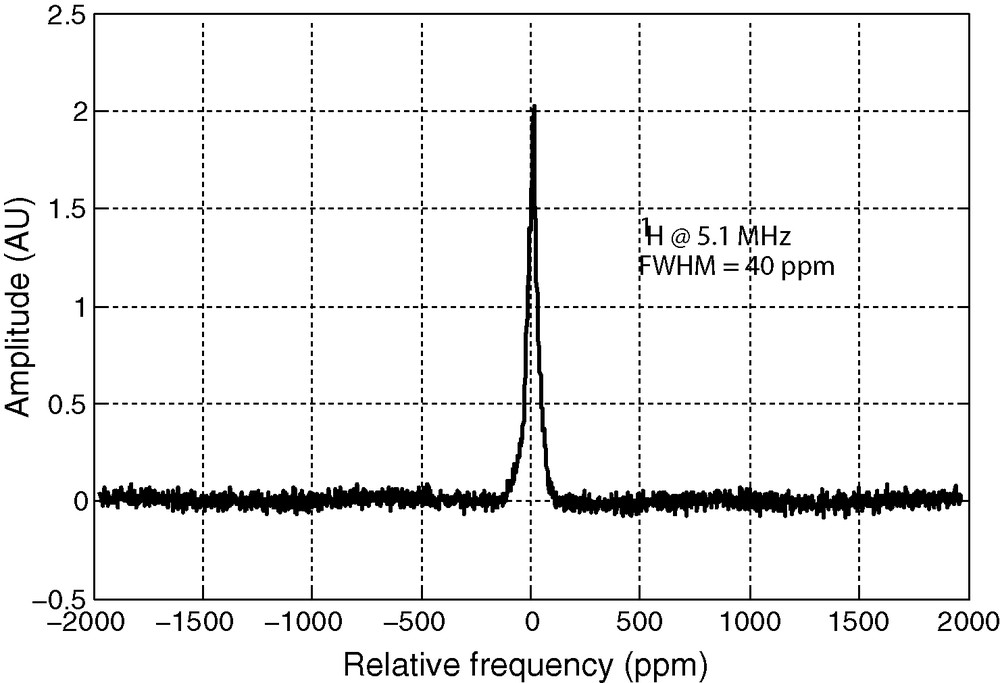
Spectrum of water doped with CuSO4 in the sweet spot of the magnet. The sample was contained in a capillary with i.d. = 1.2 mm. The capillary was sealed with wax to limit the sample length to about 3 mm. A solenoidal coil was wound around the capillary. A 40 ppm FWHM was observed without any shimming of the system.
6 Conclusions
We introduced a general method to design homogeneous magnets based on the spherical harmonics expansion of the field, and applied it to a small test-magnet. As the stated method relies on the assumption that the material features a homogeneous magnetization, we developed a method to assess the magnetization components of each cube based on automated Hall probe measurements, along with a dipolar approximation. These measurements can be parameters in simulations of the field resulting from the assembly of the cubes. The results show that low-cost magnets feature a low repeatability with large deviations of the orientation and modulus of the magnetization. We also developed an algorithm to search for an ideal combination of these cubes based on their measurements and on analytical formulas for the spherical harmonics expansion of the field of a dipole. We have applied these methods to construct a simple, compact and low-cost magnet. The resulting magnet system cannot perform as well as initially predicted because of the wide distribution of magnetization from one cube to another. However, it was still possible to obtain NMR spectra with a linewidth of 40 ppm. This magnet offers accessibility along all three axes and can accommodate a room temperature shim stack in order to eliminate some of the residual inhomogeneities.
The inhomogeneity of the magnetization of each cube, along with the issues of demagnetization during the assembly still have to be explored in order to account for the differences between the simulated and experimental fields. We intend to pursue our work on this magnet by performing passive shimming in order to correct for the magnetization distribution imperfections. One should only pursue the goal of achieving the theoretical homogeneity as going further would result in a shimming system of a significant size compared to the magnet. Better homogeneity over a given volume can be obtained through the scaling of the magnet or through a design allowing the cancellation of more orders in the expansion. As a result, we also intend to pursue our effort of building homogeneous permanent magnet systems based on our method with some higher-order systems built out of higher quality magnets. Such high-performance magnet systems should provide access to NMR spectroscopy and imaging. That a homogeneous longitudinal magnetic field can be generated from such light magnetic system provides new opportunities for pure permanent magnet magic angle field spinning [18]. Work along these directions is currently underway in our laboratory.
Acknowledgements
We would like to thank Jacques-François Jacquinot for insightful discussions during this work, along with Sylvain Foucquart for the machining of the magnet mounts.
The research leading to these results has received funding from the Agence nationale de la recherche contrat ANR-06-JCJ006, the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013), and from ERC grant agreement 205119, IIF grant agreement 237068.
1 A homogeneous field would only contain Z0 in the expansion of the field, as the field is the derivative of the potential, it corresponds to Z1 in the expansion of the potential.
2 C. Hugon, F. D’Amico, G. Aubert, D. Sakellariou. Theory for the design of arbitrarily homogeneous permanent magnet systems for NMR and experimental developments of a simple example (manuscript in preparation).


