Covalent hydration of nitrobenzofurazans compounds from the perspective of the HSAB principle and reactivity–selectivity descriptor

Nadjia Latelli; Malika Mokhtari; Nadia Ouddai

doi:10.1016/j.crci.2011.04.003

Covalent hydration of nitrobenzofurazans compounds from the perspective of the HSAB principle and reactivity–selectivity descriptor

Nadjia Latelli ^1,² ; Malika Mokhtari ³ ; Nadia Ouddai ²

¹ Faculté des sciences, département de chimie, université de Msila, BP 166 Ichbilia, 28000 M'sila, Algeria
² Laboratoire chimie des matériaux et des vivants : activité, réactivité, université El-Hadj Lakhdar Batna, Algeria
³ Laboratoire chimie inorganique et environnement, université Abou Bekr Belkaid, BP 119, 13000 Tlemcen, Algeria

Comptes Rendus. Chimie, Volume 14 (2011) no. 10, pp. 911-915.

Résumé

Global and local DFT-based reactivity descriptors are used to characterize covalent hydration reactions of series of nitrobenzofurazans compounds. The conceptual framework to rationalize the trends observed in reaction rate constants and to explain the main reaction product encountered experimentally is provided by the Pearson's HSAB principle. Molecular hardness of the reactant molecules indicates that the reactions are favored when hard–hard interactions are present. The reactivity–selectivity and the Fukui function are found to be the most efficient descriptors to characterize the regio-selectivity that might be driving the covalent hydration reactions.

Métadonnées

Reçu le : 2011-01-31
Accepté le : 2011-04-13
Publié le : 2011-06-08

DOI : 10.1016/j.crci.2011.04.003

Mots clés : Conceptual-DFT, Nitrobenzofurazans, HSAB principle, Dual descriptors

Affiliations des auteurs :

Nadjia Latelli ^{1, 2} ; Malika Mokhtari ³ ; Nadia Ouddai ²

¹ Faculté des sciences, département de chimie, université de Msila, BP 166 Ichbilia, 28000 M'sila, Algeria
² Laboratoire chimie des matériaux et des vivants : activité, réactivité, université El-Hadj Lakhdar Batna, Algeria
³ Laboratoire chimie inorganique et environnement, université Abou Bekr Belkaid, BP 119, 13000 Tlemcen, Algeria

@article{CRCHIM_2011__14_10_911_0,
     author = {Nadjia Latelli and Malika Mokhtari and Nadia Ouddai},
     title = {Covalent hydration of nitrobenzofurazans compounds from the perspective of the {HSAB} principle and reactivity{\textendash}selectivity descriptor},
     journal = {Comptes Rendus. Chimie},
     pages = {911--915},
     publisher = {Elsevier},
     volume = {14},
     number = {10},
     year = {2011},
     doi = {10.1016/j.crci.2011.04.003},
     language = {en},
}

TY  - JOUR
AU  - Nadjia Latelli
AU  - Malika Mokhtari
AU  - Nadia Ouddai
TI  - Covalent hydration of nitrobenzofurazans compounds from the perspective of the HSAB principle and reactivity–selectivity descriptor
JO  - Comptes Rendus. Chimie
PY  - 2011
SP  - 911
EP  - 915
VL  - 14
IS  - 10
PB  - Elsevier
DO  - 10.1016/j.crci.2011.04.003
LA  - en
ID  - CRCHIM_2011__14_10_911_0
ER  -

%0 Journal Article
%A Nadjia Latelli
%A Malika Mokhtari
%A Nadia Ouddai
%T Covalent hydration of nitrobenzofurazans compounds from the perspective of the HSAB principle and reactivity–selectivity descriptor
%J Comptes Rendus. Chimie
%D 2011
%P 911-915
%V 14
%N 10
%I Elsevier
%R 10.1016/j.crci.2011.04.003
%G en
%F CRCHIM_2011__14_10_911_0

Nadjia Latelli; Malika Mokhtari; Nadia Ouddai. Covalent hydration of nitrobenzofurazans compounds from the perspective of the HSAB principle and reactivity–selectivity descriptor. Comptes Rendus. Chimie, Volume 14 (2011) no. 10, pp. 911-915. doi : 10.1016/j.crci.2011.04.003. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2011.04.003/

Version originale du texte intégral

1 Introduction

It is well known that nitro-2,1,3-benzoxadiazoles, and related oxide derivatives (commonly referred to as nitrobenzofurazans and nitrobenzofuroxans, respectively) are hetero-aromatic substrates possessing high electrophilic character [1–7].

The electrophilic character of nitrobenzofurazans is particularly remarkable in the easy ability to undergo nucleophilic aromatic substitution reactions (S_NAr) [8–11] and nucleophilic addition reactions and the facility of covalent hydration reactions of nitrobenzofurazans or nitrobenzofuroxans to give the corresponding hydroxyl σ-adduct [12,13].

In this paper, we explore how the global and local reactivity of nitrobenzofurazans can be connected to the change in reaction rates. Covalent hydration reactions of the 4-(or 6-) nitrobenzofurazans, 1, variously substituted in -6(or -4) by other electron-withdrawing groups such as CF₃, CN, SO₂CF₃ (Scheme 1) are studied to achieve this goal. The reactions will be rationalized in terms of global and local electronic properties defining the electrophilic and nucleophilic of the interacting systems. The goal of this paper is twofold: on one side we want to rationalize the change in the experimental rate constants in terms of descriptors of chemical reactivity of the interacting molecules; then we want to predict the sites on the electrophiles where nucleophile will attack in order to produce the chemical reaction. For this purpose, several few reactivity descriptors based on Density Functional Theory (DFT) [14] such as chemical potential, hardness, electrophilicity and Fukui function are calculated and analyzed in the light of the Hard-Soft Acids-Bases (HSAB) [15] principle that defines the conceptual framework that will be used to rationalize the nucleophilic-electrophilic interactions.

This article is organized as follows: in section 2, the computational details, the DFT-based reactivity descriptors that will be used in this study are defined; section 3 is devoted to the results and discussion. Finally, some general conclusions are drawn in section 4.

2 Computational details

All calculations were carried out at DFT level using the Gaussian03 program package [16]. All structures were fully optimized and the nature of each stationary point were determined by subsequent frequency calculation at the PBE1PBE/6-31G(d) level of theory [17,18]. The electronic chemical potential μ and the chemical hardness η of a substrate were approximated in terms of the one electron energies of the frontier molecular orbitals (FMO) HOMO and LUMO, E_H and E_L respectively, at the ground state (GS) using [14,19]:

μ = \frac{E_{H} + E_{L}}{2}

(1)

η = E_{L} - E_{H}

(2)

Starting from the chemical potential and hardness, the global electrophilicity index (ω), measuring the stabilization in energy when a system acquires additional electronic charge (ΔN) from the environment, was defined by Parr as [20]:

ω = \frac{μ^{2}}{2 η}

(3)

This index basically quantifies the tendency of a molecule to accept an electron from a generic donor.

Indeed, all the above-mentioned indexes are global electronic properties useful to understand the reactivity of molecules in their ground states. To this end, local electronic properties can be introduced, the condensed Fukui function defined as [21,22]:

f_{k}^{+} = q_{k} (N + 1) - q_{k} (N)

(4)

f_{k}^{+}

represents the ability of atoms k to reacts with a nucleophile. A high value of

f_{k}^{+}

indicates that atom k presents an electrophilic character thus indicating a high probability for a nucleophilic attack.

3 Results and discussion

3.1 Global reactivity indexes

All rate and equilibrium measurements pertaining to Scheme 1 were made at 25 °C and constant ionic strength of 0.2 M⁻¹ maintained with KCl in aqueous solution. Dilute hydrochloric acid, various buffer solutions and dilute potassium hydroxide were used to cover a pH range of 0.8 to 13.0.

Experimental nucleophilic rate constants for covalent hydration reactions with series of nitrobenzofurazans 1a–1f displayed in Scheme 1 are quoted in Table 1.

Substrates	pKa	$k_{1}^{H_{2} O}$ (s⁻¹)	$k_{2}^{O H^{-}}$ (M⁻¹ s⁻¹)
1a	2.94	0.16	32,571
1b	4.95	2.7 10⁻⁴	1417
1c	6.85	6.4 10⁻⁴	2041
1d	7.84	9.5 10⁻⁷	159.3
1e	7.77	1.2 10⁻⁶	175.5
1f	10.07	4 10⁻⁸	31
DNBZ^a	3.92	0.020	15,300

^a Ref. [12]

It is of special relevance here to introduce the $k_{1}^{H_{2} O}$ parameter to assess the degree of participation of H₂O as a nucleophile in the substrats 1a–e system (Scheme 1). Following an approach developed by Bunting et al. for pseudobase formation from quinolinium and napthyridinium cations [23], the $k_{1}^{H_{2} O}$ parameter could be readily derived from a dissection of the observed pH–rate profile for the combined formation and decomposition of the adducts 2a–e (k_obsd) into its k_f and k_d components [24]. Hence, there is no doubt that the water reaction is the sole effective pathway for the formation of the adduct 2a–e at low pH. At higher pH, the OH⁻ pathway ( $k_{2}^{O H^{-}}$ ) becomes predominant, as expected [24].

Table 1 reveals that the pKa values for the conversion of 1a–1f into the adducts 2a–2f fall in the range 2.94–10.07. The substitution of one of the two NO₂ groups of the DNBZ affects very strongly the thermodynamic of σ-complexation and this, in a different way according to whether substitution intervenes in ortho or para position of carbon-7, site of the addition of ion OH⁻.

The substitution of group 4-NO₂ by groups CN or CF₃, of which the attractive characters increase, thus generates a very significant reduction in stability. The pK_a associates at the formation of the complexes 2c and 2e derived from the 1c and 1e are equal to 6.85 and 7.77 respectively, which corresponds to stabilities respectively 850 and 7500 times lower than that of the complex of the DNBZ.

It can be observed that strong variation on the rate constants values occurs when going from substrate 1a to 1b, 1c and very strong variation when compared 1a with 1d, 1e and 1f. In order to rationalize the above observed changes in rate constants, calculation of chemical potential and molecular hardness for the electrophiles were performed, results are quoted in Table 2.

Substrates	μ (kcal/mol)	η (kcal/mol)	ω (eV)
1a	–147	106	4.41
1b	–143	103	4.33
1c	–142	101	4.30
1d	–139	107	3.90
1e	–138	107	3.86
1f	–130	105	3.50
H₂O	–70	242

The chemical potential of the nucleophile is higher than that of the electrophiles confirming the direction expected for the electronic transfer: from the nucleophile with a high chemical potential to an electrophile with a lower chemical potential. The difference of chemical potential among the reacting species Δμ = μ_n − μ_e is a measure of electronic transfer. It indicates that the reaction substrate 1a presents a larger electron transfer than reactions with 1b, 1c, 1d, 1e and 1f substrates. This different behavior might be at the origin of the differences observed in the rate constants quoted in Table 1 (kinetic study).

On the other hand, we can see, when going from 1a to 1f, the chemical potential increases by 16 kcal/mol whereas molecular hardness remains quite constant. This indicates that substitution of the H by the SO₂CF₃ group makes the system more reactive; this is in agreement with the experimental results (Table 1). When going from 1a to 1d, the effect is quite similar; here the chemical potential increases by about 8 kcal/mol.

Assuming that the effect of the position of the NO₂, CF₃ or CN groups is not relevant for local or global reactivity, it is interesting to notice that when going from 1b to 1c and from 1d to 1e, molecular hardness remains quite constant and chemical potential increases slightly.

Qualitatively, we can note that all computed electrophilicity of all substrates (in the range between 3.50 and 4.41 eV) are in the range of strong electrophiles within the ω scale [25]. Furthermore, the large electrophilicity index computed for the substrates accounts for its facile participation in these addition reactions. Electrophilicity values of the electrophiles quoted in Table 2 show that 1a presents a higher capacity to attract electrons than 1b, 1c, 1d, 1e and 1f; this result confirms that the presence of SO₂CF₃ group increase the electrophilic character of the carbocyclic ring of the benzofurazans structures. Charge transfer seems to explain at least qualitatively the change in the nucleophilic rate constants as a function of the substrate molecule.

3.2 The HSAB principle at play

The observed change of the rate constants with respect to changes of the substrates (1a–1f in Scheme 1) can be rationalized at least qualitatively in terms of the Pearson's hard-soft acid-base (HSAB) principle [26–28]: for an acid-base interaction, the hard-hard and the soft-soft combinations are thermodynamically and kinetically favored over crossed interactions. Water acts as hard base; as such, it will prefer to react with the hardest electrophile, in this case 1a, thus leading to the largest $k_{1}^{H_{2} O}$ and $k_{2}^{O H^{-}}$ values among the six reactions. The above observations indicate that hardness plays a major role in the rationalization of kinetic data of the covalent hydration reactions under study.

3.3 Site selectivity

The Fukui functions were determined using Eq. (4); when needed, the ionic systems were calculated using the UHF approximation. Local reactivity indexes have been used to characterize the sites for nucleophilic attack; they are quoted in Table 3. This table shows that for all substrates, the higher $f_{k}^{+}$ values are on atom C₇ and corresponds to unsubstituted positions in the aromatic ring. This means that the nucleophilic attack would be preferential on this site. It is not surprising to find high values of $f_{k}^{+}$ in positions C₇ because this is the nitro group that activates the ortho and para positions of the aromatic ring.

Substrates	C₄	C₅	C₆	C₇
1a	0.080	0.064	0.051	0.148
1b	0.079	0.066	0.062	0.137
1c	0.111	0.018	0.051	0.145
1d	0.075	0.095	0.042	0.138
1e	0.101	0.011	0.057	0.144
1f	0.069	0.109	0.032	0.135

On the other hand, the reactivity–selectivity descriptor Δf (r), introduced by Morell et al. [29,30] characterizes the variations of the absolute hardness when the external potential changes, upon, for instance, an approach of reactants during a bimolecular reaction. It is defined as:

Δ f (r) = f^{+} (r) - f^{-} (r)

(5)

Accordingly, when Δf (r) > 0, then the point r favors a nucleophilic attack, whereas if Δf (r) < 0 then the point r favors an electrophilic attack. Therefore, positive values of Δf (r) identify electrophilic regions within the molecular topology, whereas negative values of Δf (r) define nucleophilic regions. This descriptor has been calculated and the results are shown on Fig. 1. It can be seen that the Δf (r) descriptor is positive for the C atoms (red). Fig. 1 displays, also, a map of the nucleophilic/electrophilic behavior of the different sites within the molecule according to the Δf (r) descriptor. The regions with Δf (r) > 0 (red) where a nucleophilic reaction should take place are located in positions ortho and para. For both substrates 1c and 1e, the regions with Δf (r) > 0 (red) where a nucleophilic reaction should take place are located in position ortho (C₇). For substrates 1b,1d, and 1f, the region with Δf(r) > 0 (red) are located in positions ortho (C₅) and para (C₇). These results are in perfect agreement with experimental results said; that the NO₂ is an electron withdrawing group (EWG) and ortho- and para-orienting group and it has been clearly demonstrated in the literature that a para nitro group plays a leading role in stabilization of the negative charge on σ-anionic complex [1,2]. For the substrate 1a, the region with Δf (r) > 0 (red) is observed only in position para (C₇), that in this case there is the SO₂CF₃ group which appears as more electro attractor compared to the NO₂ groups.

Fig. 1
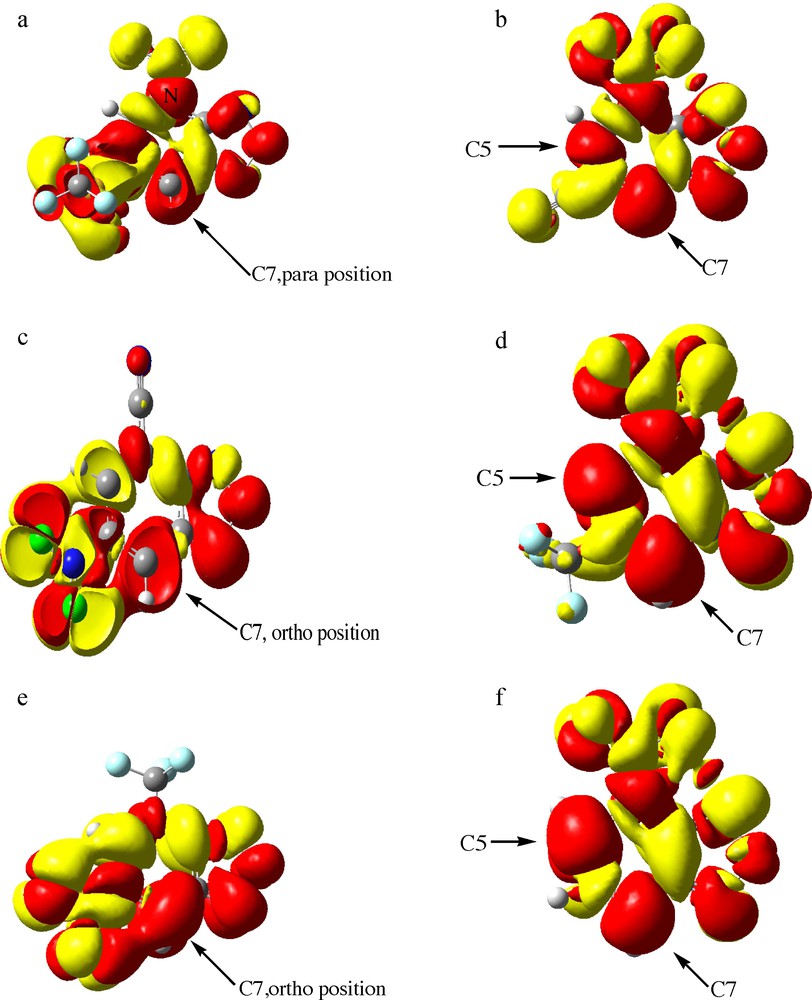
Δf (r) calculated at the PBE1PBE/6-31G(d) level.

4 Conclusion

Global and local DFT-based reactivity descriptors of the nitrobenzofurazans substrates have been used to rationalize experimental kinetic data. Pearson's HSAB principle provided a conceptual framework to rationalize the trend observed in reaction rate constants and to explain the main reaction product encountered experimentally. Chemical potential, molecular hardness and electrophilicity indexes of the reacting species emerge as key elements in the rationalization of experimental rate constants whereas the Fukui function and the dual descriptors appears to explain the specific interactions that produce the expected species as product of the chemical reactions under investigation.

5 Experimental

Stopped-flow determinations were performed on a Applied-Photophysics SX-18MV spectrophotometer, the cell compartment of which was maintained at 25 ± 0.1 °C. Other kinetic determinations were made using a conventional HP8453 spectrophotometer. All kinetic runs were carried out in triplicate under pseudo-first conditions with an electrophile concentration of ca. (3–6) × 10⁻⁵ M⁻¹.

Acknowledgements

The authors acknowledge Pr. François Terrier for permitting the realization of kinetics study in his laboratory (SIRCOB, University of Versailles). The authors thank Pr. Henry Chermette (UCBL, University of Lyon) for the application of the dual descriptor.

Bibliographie

[1] F. Terrier Nucleophilic Aromatic Displacement (H. Feuer, ed.), VCH, New York, 1991

[2] F. Terrier Chem. Rev., 82 (1982), p. 77

[3] E. Buncel; J. Dust; F. Terrier Chem. Rev., 95 (1995), p. 2261

[4] .F. Eckert; G. Rauhut; A.R. Katritzky; P.J. Steel J. Am. Chem. Soc., 121 (1999), p. 6700

[5] F. Terrier; E. Kizilian; J.C. Hallé; E. Buncel J. Am. Chem. Soc., 114 (1992), p. 1740

[6] E. Buncel; R.A. Manderville; J.M. Dust J. Chem. Soc. Perkin Trans., 2 (1997), p. 1019

[7] M.R. Crampton; L.C. Rabbitt; F. Terrier J. Chem. Soc. Perkin Trans., 2 (2000), p. 2169

[8] S. Uchiyama; T. Santa; T. Fukushima; H. Homma; K. Imai J. Chem. Soc. Perkin Trans., 2 (1998), p. 2165

[9] S. Féry-Forgues; C. Vidal; D. Lavabre J. Chem. Soc. Perkin Trans., 2 (1996), p. 73

[10] A. Chattopadhyay Chem. Phys. Lipids., 53 (1990), p. 1

[11] J.W. Nichols Biochemistry, 27 (1988), p. 3925

[12] S. Lakhdar; R. Goumont; T. Boubaker; M. Mokhtari; F. Terrier Org. Biomol. Chem., 4 (2006), p. 1910

[13] M. Mokhtari; R. Goumont; J.C. Hallé; F. Terrier ARKIVOC., xi (2002), p. 168

[14] R.G. Parr; W. Yang; H. Chermette J. Comput. Chem., 20 (1989), p. 129

[15] R.G. Pearson Chemical hardness: application from molecules to solids, Meinheim, Germany, 1997

[16] Gaussian 03, Revision B. 05, M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, J.A. Montgomery Jr. T. Vreven, K.N. Kudin, J.C. Burant, J.M. Millam, S.S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G.A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O., Kitao, H. Nakai, M. Klene, X. Li, J.E. Knox, H.P. Hratchian, J.B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R.E. Stratmann, O. Yazyev, A.J. Austin, R. Cammi, C. Pomelli, J.W. Ochterski, P.Y. Ayala, K. Morokuma, G.A. Voth, P. Salvador, J.J. Dannenberg, V.G. Zakrzewski, S. Dapprich, A.D. Daniels, M.C. Strain, O. Farkas, D.K. Malick, A.D. Rabuck, K. Raghavachari, J.B. Foresman, J.V. Ortiz, Q. Cui, A.G. Baboul, S. Clifford, J. Cioslowski, B.B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R.L. Martin, D.J. Fox, T. Keith, M.A. Al-Laham, C.Y. Peng, A. Nanayakkara, M. Challacombe, P.M.W. Gill, B. Johnson, W. Chen, M.W. Wong, C. Gonzalez, J.A. Pople, Gaussian, Inc., Wallingford, C.T., 2004.

[17] J.P. Perdew; K. Burke; M. Ernzerhof; C. Adamo; V. Barone J. Chem. Phys., 77 (1996), p. 3865

[18] W.J. Hehre; R. Ditchfield; J.A. Pople J. Chem. Phys., 56 (1972), p. 2257

[19] R.G. Parr; R.G. Pearson J. Am. Chem. Soc., 105 (1983), p. 7512

[20] R.G. Parr; L. Szentpaly; S. Liu J. Am. Chem. Soc., 121 (1999), p. 1922

[21] F. Bulat; E. Chamorro; P. Fuentealba; A. Toro-Labbe J. Phys. Chem. A., 108 (2004), p. 342

[22] P. Senet J. Chem. Phys., 107 (1997), p. 2516

[23] J.W. Bunting; D.J. Norris; J.W. Bunting; D.J. Stefanidis; J.W. Bunting; W.G. Meathrel Can. J. Chem., 91 (1977), p. 1189

[24] F. Terrier; F. Millot; W.P. Norris J. Am. Chem. Soc., 98 (1976), p. 5883

[25] P. Arroyo; M.T. Picher; L.R. Domingo J. Mol. Struct., 45 (2004), p. 709

[26] R. Pearson J. Chem. Educ., 45 (1968), p. 981

[27] P.C. Ford Coord. Chem. Rev., 187 (1999), p. 3

[28] P.W. Ayers J. Chem. Phys., 122 (2005), p. 141102

[29] C. Morell; A. Grand; A. Toro-Labbé J. Phys. Chem. A., 109 (2005), p. 205

[30] C. Morell; A. Grand; A. Toro-Labbé Chem. Phys. Lett., 425 (2006), p. 342

Commentaires - Politique