1 Introduction
A new development in the area of electron-deficient aromatics in the last two decades is the discovery of very powerful electrophilic heteroaromatic structures, such as 4,6-dinitrobenzofuroxan (DNBF) [1–8].
The pKa for the formation of the hydroxy σ-adduct 1 according to Eq. (1) in Scheme 1 is 3.75 at 25 °C, as compared with a pKa value of 13.43 for formation of the analogous adduct 2 of 1,3,5-trinitrobenzene (TNB), the conventional reference aromatic electrophile in σ-complex chemistry [9]. Extensive studies have revealed that DNBF is stronger electrophile than the positively charged 4-nitrobenzenediazonium cation (3) [6].
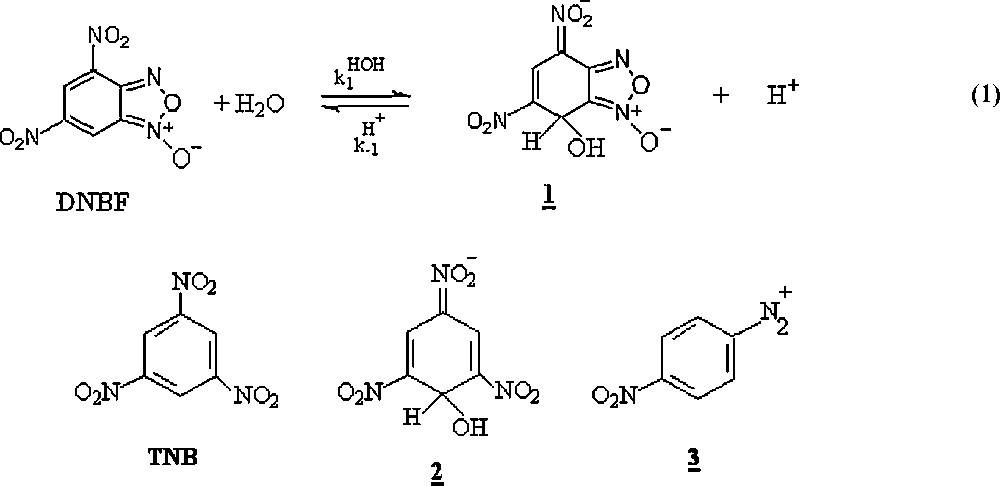
pKa for the formation of the hydroxy σ-adduct 1 of 4,6-dinitrobenzofuroxan DNBF, with the adduct 2 of 1,3,5-trinitrobenzene TNB.
Recently, Mokhtari et al. kinetically studied the covalent hydration of 4-nitro-6-trifluoromethanesulfonylbenzofuroxan 4a to give the corresponding hydroxy σ-adduct in aqueous solution. Among the most significant results that they obtained, the discovery which the 4-nitro-6-trifluoromethanesulfonylbenzofuraxan is the most stable hydroxyl σ-adduct to date (pKa = 2.95) and that its even more electrophile that DNBF [10].
In this article, we report the results of the a kinetic study of the covalent hydration of the 4-(or-6) nitrobenzofuroxans, 4, variously substituted in 6-(or 4-) by other electron-withdrawing groups such as CF3, CN, SO2CF3 [10] in aqueous solution, to give the adducts 5 according to Scheme 2.
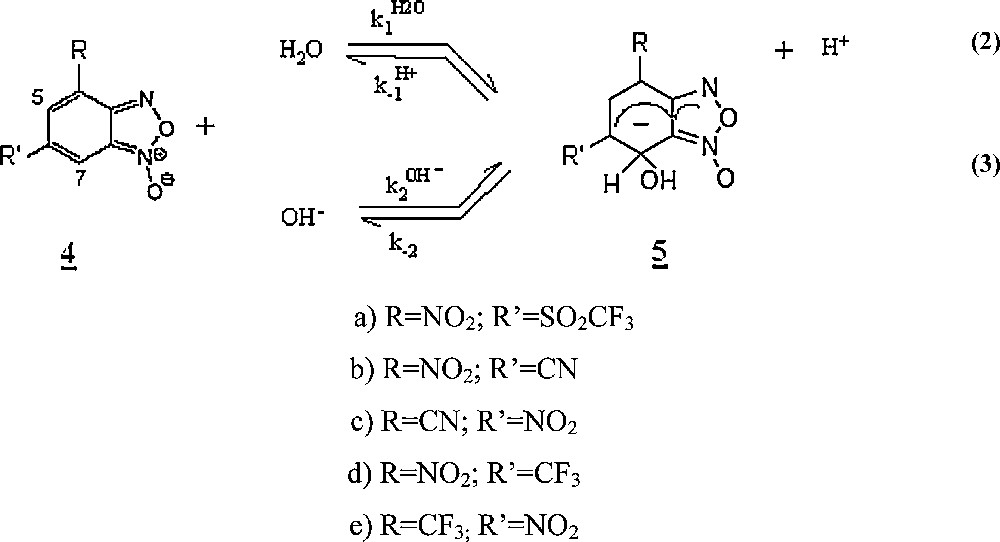
Covalent hydration reactions of the 4-(or 6-) nitrobenzofurazans, 4, variously substituted in -6(or -4).
Another objective of this work is to explore how the global and local reactivity of nitrobenzofuroxans can be connected to the change in reaction rates. The goal of this paper is twofold, on one side we want to rationalize the change in the experimental rate constants in terms of descriptors of chemical reactivity of the interacting molecules; then we want to predict the sites on the electrophiles where nucleophile will attack in order to produce the chemical reaction. For this purpose, several reactivity descriptors based on Density Functional Theory (DFT) [11] such as chemical potential, hardness, electrophilicity are calculated and analyzed in the light of the Hard-Soft Acids-Bases (HSAB) [12] principle that defines the conceptual framework that will be used to rationalize the nucleophilic-electrophilic interactions.
2 Results and discussion
2.1 Kinetic and thermodynamic studies
All rates and equilibrium measurements pertaining to Scheme 2 were made at 25 °C and constant ionic strength of 0.2 M maintained with KCl in aqueous solutions. Dilute hydrochloric acid solution, various buffer solutions and dilute potassium hydroxide solution were used to cover a pH range of 0.8–13. All pH values were measured relative to standard state in pure water accordingly to the relation
2.1.1 pKa values of 4
Using appropriate buffer solutions (see experimental section), the pKa values for the σ-complexation of 4 according to Eq. (2) were readily determined from the observed absorbance variations at λmax ≈ 345–425 nm of the resulting adducts 5 obtained at equilibrium as a function of pH. These actually describe a clear acid-base type of equilibrium, as evidenced by the observation of a good straight line with unit slope, fitting Eq. (4). Results obtained are summarized in Table 1.
| (4) |
Kinetic and thermodynamic parameters for formation and decomposition of hydroxyl σ-adducts in aqueous solution, T = 25 °C, I = 0.2 mol.dm−3 KCl.
| Adducts | pKa | k–2(s–1) | |||||||||
| 5aa | 2.95 | 0.15 | 100.3 | 72150 | 10−6 | ||||||
| 5b | 4.65 | 10−3 | 31 | 1060 | 10−6 | ||||||
| 5c | 5.86 | 2.6·10−3 | 3700 | 2740 | 3·10−5 | ||||||
| 5d | 6.50 | 1.5·10−5 | 39.6 | 270 | 1.1·10−5 | ||||||
| 5e | 8.19 | 6.3·10−5 | 7500 | 502 | 10−3 | ||||||
| DNBFb | 3.75 | 3.45·10−2 | 146 | 33500 | 2.5·10−6 |
2.1.2 pH rate profiles for covalent hydration of 4
The kinetic studies of formation and decomposition of the adduct 4 according to the two pathways of the Scheme 2 were studied in the pH range 0.8–13 by stopped–flow spectrophotometry. The rate measurements were carried out under pseudo first-order conditions with a substrate or adduct concentration of 3–6 × 10−5M. In agreement with the direct equilibrium approach depicted in Scheme 2, only one relaxation time corresponding to the formation (pH > pKa) or decomposition (pH < pKa) of the adducts was observed in all cases were measured at 25 °C and constant ionic strength of 0.2 M maintained with KCl. The variations in the first-order rate constant, kobsd, for the combined formation and decomposition of 5 are plotted in Figs. 1–4 as a function of pH. In the experiments where buffer catalysis was observed, the kobsd values used to draw the pH rate profiles where those extrapolated to zero buffer concentration.
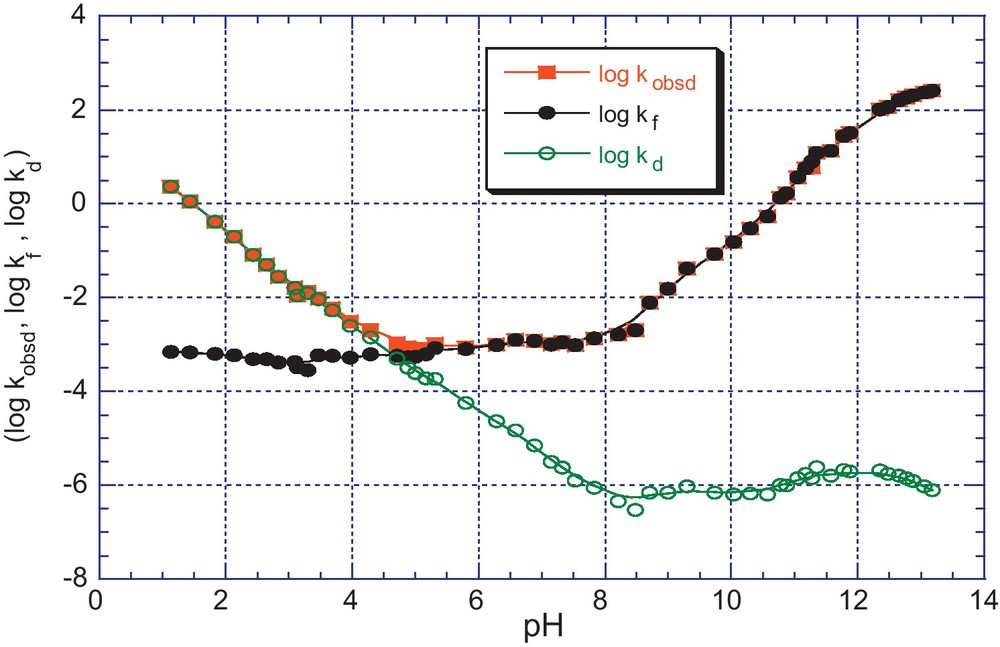
pH dependence of kobsd (s−1) for the formation and decomposition of the adduct 5b in aqueous solution; T = 25 °C, I = 0.2 mol.dm−3 KCl. The (•) and (ο) lines refer to the calculated contributions of the kf and kd components according to Eqs. (6) and (7).
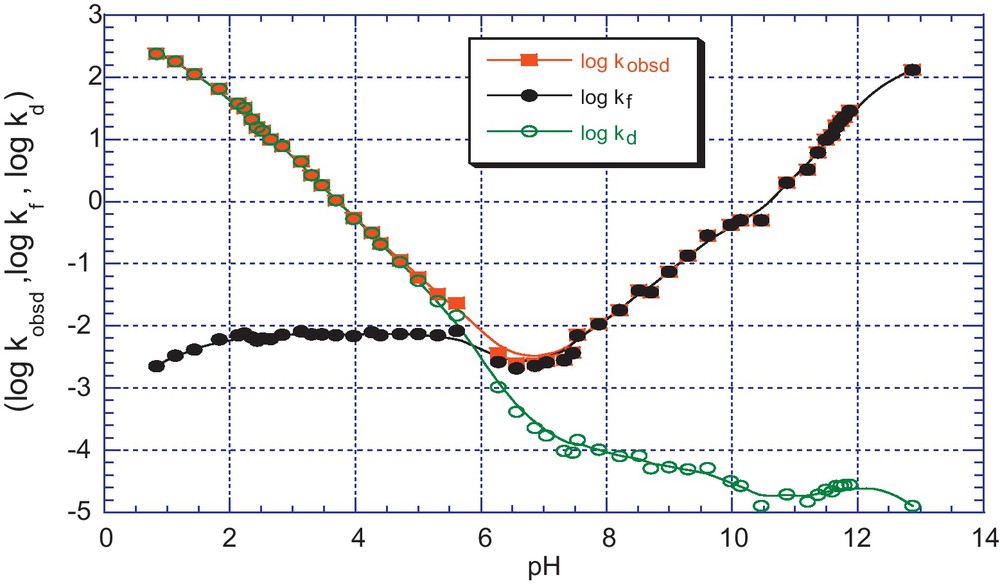
pH dependence of kobsd (s−1) for the formation and decomposition of the adduct 5c in aqueous solution; T = 25 °C, I = 0.2 mol.dm−3 KCl. The (•) and (ο) lines refer to the calculated contributions of the kf and kd components according to Eqs. (6) and (7).
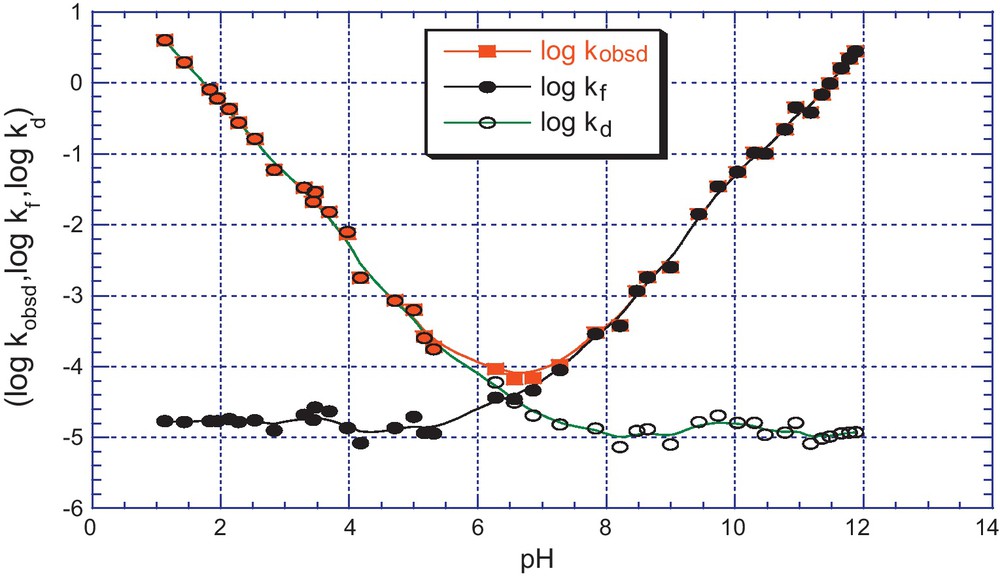
pH dependence of kobsd (s−1) for the formation and decomposition of the adducts 5d in aqueous solution; T = 25 °C, I = 0.2 mol.dm−3 KCl. The (•) and (ο) lines refer to the calculated contributions of the kf and kd components according to Eqs. (6) and (7).
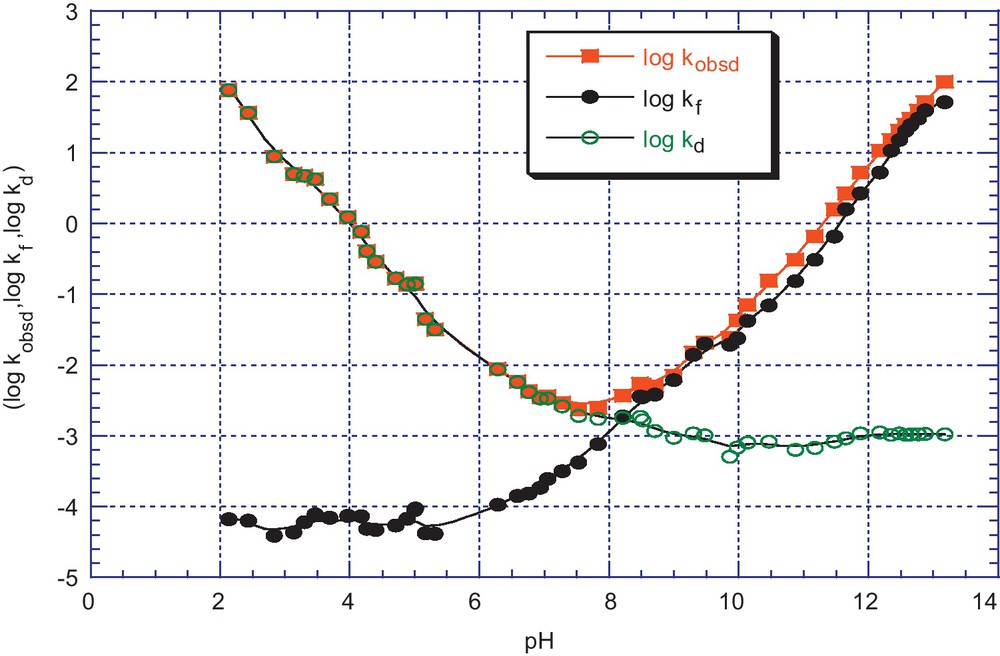
pH dependence of kobsd (s−1) for the formation and decomposition of the adducts 5e in aqueous solution; T = 25 °C, I = 0.2 mol.dm−3 KCl. The (•) and (ο) lines refer to the calculated contributions of the kf and kd components according to Eqs. (6) and (7).
The observed rate constant may be expressed at each pH as the sum of the individual first order rate constant for formation (kf) and decomposition (kd) of 5. Eq. (5). Thus, values of kf and kd can be readily derived from kobsd through Eqs. 6 and 7.
| (5) |
| (6) |
| (7) |
The two corresponding pH rate profiles shown in Figures 1–4 are nicely consistent with Eqs. (8) and (9) respectively, in which the rate constants refer to the various individual pathways depicted in Scheme 2.
| (8) |
| (9) |
Least-square fitting of kf and kd to Eqs. (8) and (9) gave the parameters which are collected together with those for relevant systems, in Table 1.
The Table 1 shows that the substitution of one of the two NO2 groups of the DNBF affects very strongly the thermodynamic of σ-complexation, and this in a different way according to whether substitution intervenes in ortho or para position of carbon -7, site of the addition of ion OH−.
Terrier observed that a para-nitro group plays a dominating role in the stabilization of the negative charge of the σ-adduct [14].
The substitution of group 4-NO2 by groups CN or CF3, of which the attractive characters increase, thus generates a very significant reduction in stability. The pKa associated to the formation of the complexes 5c and 5e derived from the 4c and 4e are equal to 5.86 and 8.19 respectively, which corresponds to stabilities respectively 130 and 27,500 times lower than that of the complex of the DNBF.
The introduction of the CN and CF3 groups on position-6 of the carbocycle of the DNBF decreases the stability of the complexes in a less accentuated way. The pKa related at the complexation of the 4b is equal to 4.65, which corresponds to a stability of the adduct 5b only 8 times weaker than that of DNBF. As for the adduct, its formation is associated to a pKa of 6.50 which is equivalent to a reduction of stability of a factor 560 compared to complex 1.
3 Computational details
All calculations were carried out at DFT level using the Gaussian03 program package [15]. All structures were fully optimized and the nature of each stationary point is determined by subsequent frequency calculation at the B3LYP/6- 31G(d)) level of theory [16]. The electronic chemical potential, μ, and the chemical hardness, η, of a substrates were approximated in terms of the one electron energies of the frontier molecular orbitals (FMO) HOMO and LUMO, EH and EL, respectively, at the ground state (GS) using [11,17]:
| (10) |
| (11) |
Starting from the chemical potential and hardness, the global electrophilicity index (ω), measuring the stabilization in energy when a system acquires and additional electronic charge (ΔN) from the environment was defined by Parr as [18]:
| (12) |
The global maximum charge transfer toward the electrophile was evaluated using [18]:
| (13) |
In order to rationalize the above observed changes in rate constants, calculation of chemical potential and molecular hardness for the electrophile and nucleophile were performed, results are quoted in Table 2.
Values of chemical potential (μ), molecular hardness (η), electrophilicity (ω).
| Molecules | μ (kcal/mol) | η (kcal/mol) | ω (ev) | ΔNmax |
| 4a | –136.34 | 75.69 | 5.33 | 1.800 |
| 4b | –133.26 | 73.50 | 5.25 | 1.813 |
| 4c | –133.02 | 74.44 | 5.15 | 1.786 |
| 4d | –128.69 | 75.88 | 4.73 | 1.696 |
| 4e | –128.69 | 77.01 | 4.66 | 1.671 |
| H2O | –71.68 | 221.80 | ||
| DNBF [20] | –136.53 | 74.00 | 5.46 |
First of all, qualitatively we can note that all computed electrophilicity of all substrates (between 4.66 and 5.33 eV) are in the range of strong electrophiles within the ω scale [19,20]. Furthermore, the large electrophilicity index computed for the substrates accounts for its facile participation in these addition reactions.
Electrophilicity values of the electrophiles quoted in Table 2 show that 4a present a higher capacity to attract electrons than 4b, 4c, 4d and 4e, this result confirms that the presence of SO2CF3 group increase the electrophilic character of the carbocyclic ring of the benzofuroxans structures. Charge transfer seems to explain at least qualitatively the change in the nucleophilic rate constants as a function of the substrate molecule.
Note that, the maximum charges ΔNmax that these systems may acquire from the environment consistly decrease with the global electrophilicity power from 4a to 4e. The only deceiving point being the ΔNmax computed for the 4b is slightly larger than that of 4a while experimentally the contrary holds.
Indeed, one can note that the computed electrophilicity of substrate 4a larger than that of all substrates, thus previewing a reaction kinetically more favorable than that of other substrates.
This fact is further confirmed by the analysis of the chemical potential computed for all substrates. The chemical potential of nucleophile is higher than that of the electrophiles confirming the direction expected for the electronic transfer: from nucleophile with a high chemical potential to an electrophile with a lower chemical potential. The difference of chemical potential among the reacting species Δμ = μn – μe is a measure of electronic transfer, it indicates that reaction substrate 4a presents a larger electron transfer than reactions with 4b, 4c, 4d, and 4e substrates, this different behaviour might be at the origin of the differences observed in the rate constant quoted in Table 1 (kinetic study).
On the other hand we can see, when going from 4a to 4d the chemical potential increases by 8 kcal/mol, whereas molecular hardness remains quite constant. This indicates that substitution of the CF3 by SO2CF3 group make the system more reactive, this is in agreement with the experimental results. Assuming that the effect of the position of the NO2, CF3 or CN groups is not relevant for local or global reactivity, it is interesting to notice that when going from 4b to 4c and from 4d to 4e molecular hardness remains quite constant and chemical potential increases slightly.
3.1.1 Reactivity–selectivity descriptor
The reactivity–selectivity descriptor Δf (r), introduced by Morell et al. [21,22] characterizes the variations of the absolute hardness when the external potential changes, upon, for instance, an approach of reactants during a bimolecular reaction. It is defined as:
Accordingly, when Δf (r) > 0 then the point r favours a nucleophilic attack, whereas if Δf (r) < 0 then the point r favors an electrophilic attack. Therefore, positive values of Δf (r) identify electrophilic regions within the molecular topology, whereas negative values of Δf (r) define nucleophilic regions. This descriptor has been calculated and the results are shown on (Supplementary data, Fig. S1). Fig. S1 displays, a map of the nucleophilic/electrophilic behaviour of the different sites within the molecule according to the Δf (r) descriptor. The regions with Δf (r) > 0 (red) where a nucleophilic reaction should take place are located in positions ortho and para.
For both substrates 4c and 4e, the regions with Δf (r) > 0 (red) where a nucleophilic reaction should take place are located in position ortho (C7). For substrates 4a, 4b and 4d the region with Δf (r) > 0 (red) are located in positions ortho (C5) and para (C7). These results are in perfect agreement with experimental results said, that the NO2 is an electron withdrawing group (EWG) and ortho and para-orienting group and it has been clearly demonstrated in the literature that a para-nitro group plays a leading role in stabilization of the negative charge on σ -anionic complex [1,14].
4 Conclusion
In this work, we have experimentally and theoretically examined the covalent hydration of a serie of nitrobenzofuroxans compounds. Global and local DFT-based reactivity descriptors of the nitrobenzofuroxans substrates have been used to rationalize experimental kinetic data. Chemical potential, molecular hardness and electrophilicity indexes of the reacting species emerge as key elements in the rationalization of experimental rate constants whereas the dual descriptors appears to explain the specific interactions that produce the expected species as product of the chemical reactions under investigation.
5 Experimental
5.1 Rate and pKa measurements
Stopped-flow determinations were performed on an Applied- Photophysics spectrophotometer, the cell compartment of which was maintained at 25 ± 0.2 °C. Other kinetic and pKa determinations were made using a conventional HP8453 spectrophotometer. All kinetic runs were carried out in triplicate under pseudo first-order conditions with a substrates concentration of (3–6) 10−5 M.
5.2 Buffers
HCl and KOH solutions were prepared from titrisol. Buffer solutions were made up from the best available commercial grades of reagents. Buffers used were formate (pH 3–4), acetate (pH 4–5.2), succinate (pH 4.8–5.6), cacodylate (pH 5.6–6.8), phosphate (pH 6–7.5), TES (6.9–7.8), tricine (pH 7.8–8.4), bicarbonate (pH 8.47), DABCO (pH 8.50–9.6), CAPS (pH 10.1–10.4).
Acknowledgements
The authors acknowledge the laboratory SIRCOB, University of Versailles, France, for permitting the realization of the experimental part, and also they thanks the Laboratory of Chemical Physics Theory, University Claude Bernard Lyon1, for the realization of the theoretical part of this article.



Vous devez vous connecter pour continuer.
S'authentifier