1 Introduction
In the last two decades, polynuclear transition metal complexes with large ground spin states (S) and a large zero-field splitting parameter (D) that exhibit Single-Molecule Magnet (SMM) or Single-Chain Magnet (SCM) behaviour have attracted much attention [1–5]. Among the numerous SMM that have been reported, many are based on complexes of manganese mostly in a +III oxidation state or in mixed valence systems, such as the emblematic Mn12Ac [6–11] or the Mn6 [12–15] oximes series that exhibit the highest energy barrier for the reversal of magnetisation. The energy barrier is S2|D| for an integer spin and (S2 - 1/4)|D| for a half-integer spin. Thus the size of the ground spin state S is important but, in order to elaborate a SMM, a negative zero-field-splitting parameter (D) is the main requirement. Thanks to early works on magnetic interactions the relationships between structural parameters and the size of the resultant spin state (S) in polynuclear complexes are quite well understood [16]. This is not yet the case for the factors that govern the strength of the axial magnetic anisotropy and most recent studies are focused on efforts to understand what determines why a complex displays or not a SMM behaviour [17–22]. Different families of manganese clusters have been concerned by such studies; especially noticeable is the Mn6 oximes series for which structural correlation has been found [12–15,23]. However, spin chirality effects have been pointed out [24–27] and the stereo-chemical aspect of chiral SMM has been recently addressed in several publications [28–33]. In continuity with our previous work [27,34], we present here a chiral hexanuclear manganese(III) complex exhibiting SMM behaviour with an energy barrier of slow magnetic relaxation equal to 35 K.
The chiral Mn6 cluster was prepared by reaction of MnII S-mandelato complexes [35–37] [MnII(S-mandelato)2] with 5-methyl-salicylaldoximes (5-Me-saloxH2) in presence of Et3N in ethanol solution.
2 Experimental
All starting materials and solvents were purchased from Aldrich and were used without further purification. IR spectra were recorded on a GX system 2000 Perkin-Elmer spectrophotometer and samples were run as KBr pellets. The Circular Dichroism (CD) spectra were recorded on a Chirascan spectropolarimeter using Chirascan software (Applied Biophysics Ltd., Leatherhead, UK) in KBr pellets.
2.1 Synthesis
To a suspension of MnII S-mandelato complex [35–37] (0.1 g), and 5-Methyl-salicylaldoxim (5-Me-saloxH2) (0.25 g) in EtOH (20 mL) was added NEt3 (0.05 g). The resulting solution was stirred at 60 °C during 2 h. After cooling the color changed to green and the resulting suspension was left upon stirring for 1 h and then filtered. The green solution was left to crystallize by slow evaporation of the solvent. After 3 days dark–brown single crystals suitable for X-ray crystallography analyses were collected by filtration and washed with ether. Yield: 20%. Anal.Calcd (found) for 1: C 49.74 (50.31), H 5.05 (5.32), N 4.58 (4.37).
2.2 Single-crystal X-ray diffraction
Crystal data were collected at low temperature (T = 110 K) using a Geminini Oxford Diffractometer (MoKα radiation, λ = 0.71069 Ǻ) equipped with a CCD camera and using the related software [38]. An absorption correction (analytical) has been applied to all the data sets [39]. The structure was solved by direct methods using the SIR97 program [40] combined with Fourier Difference and the refined against F using the CRYSTALS program [I > 2σ(I)] [41]. All atomic displacements for non-hydrogen atoms were refined using an anisotropic model. Hydrogen atoms have been placed by Fourier Difference accounting for the hybridation of the supporting atoms and the possible presence of hydrogen bonds in the case of donor atoms. Hydrogen atoms have been refined using a riding mode. The Flack parameter has been refined in order to evidence the presence of an enantiopure complex [41]. Details of data collection parameters and crystallographic information for the [Mn6] complex can be found in Table 1. Important bond lengths, bond angles and Mn⋯Mn distances are summarized in Table 2. CCDC 865130 reference contains the supplementary crystallographic data. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.
Data collection details and structure refinement results for 1.
| 1 | |
| Empirical formula | C76H92Mn6N6O26 |
| Molecular weight (g mol−1) | 1835.16 |
| Crystal system | Monoclinic |
| Space group | P21 |
| a (Å) | 12.6053(9) |
| b (Å) | 20.633(2) |
| c (Å) | 15.523(1) |
| β (deg.) | 96.134(7) |
| V (Å3) | 4014.1(5) |
| Z | 2 |
| T (K) | 110 |
| d | 1.518 |
| μ (mm−1) | 0.997 |
| F(000) | 1896 |
| Independent refl. | 19000 |
| Rint | 0.097 |
| R(F) / Rw(F) | 0.0727 / 0.0846 |
| S | 1.10 |
| Reflections | 11223 |
| Parameters / restraints | 1028 / 97 |
| Δρmax / Δρmin (e− Å−3) | 0.90 / −0.63 |
| Flack parameter | 0.02(3) |
| Absorption correction | Analytical |
Important Mn-O,N bond lengths (Å), Mn-O,N-Mn angles (deg.) and Mn⋯Mn distances (Å).
| Mn–O,N bond lengths | |||||
| Mn1-181 | 2.229(8) | Mn1-O191 | 2.293(7) | Mn1-O221 | 1.894(6) |
| Mn1-091 | 1.920(6) | Mn1-O101 | 1.851(7) | Mn1-N110 | 2.015(7) |
| Mn2-O31 | 2.339(6) | Mn2-O71 | 1.955(6) | Mn2-N90 | 1.993(8) |
| Mn2-O141 | 2.112(7) | Mn2-O221 | 1.885(5) | Mn2-O81 | 1.917(5) |
| Mn3-O41 | 2.525(7) | Mn3-O61 | 1.860(6) | Mn3-N70 | 2.033(7) |
| Mn3-O111 | 1.913(6) | Mn3-O201 | 2.172(8) | Mn3-O221 | 1.888(5) |
| Mn4-O31 | 1.963(5) | Mn4-O41 | 1.893(5) | Mn4-N50 | 1.986(7) |
| Mn4-O71 | 2.322(6) | Mn4-O121 | 2.139(8) | Mn4-O222 | 1.873(5) |
| Mn5-O1 | 1.859(7) | Mn5-N10 | 2.002(6) | Mn5-O171 | 2.298(9) |
| Mn5-O51 | 1.924(6) | Mn5-O211 | 2.269(9) | Mn5-O222 | 1.904(6) |
| Mn6-O11 | 1.897(6) | Mn6-O21 | 1.848(6) | Mn6-N30 | 2.004(7) |
| Mn6-O81 | 2.591(6) | Mn6-O161 | 2.286(7) | Mn6-O222 | 1.865(5) |
| Intra-triangle Mn⋯Mn distances | |||||
| Mn1⋯Mn2 | 3.262(1) | Mn1⋯Mn3 | 3.262(1) | Mn2⋯Mn3 | 3.280(1) |
| Mn4⋯Mn5 | 3.243(1) | Mn4⋯Mn6 | 3.261(1) | Mn5⋯Mn6 | 3.266(1) |
| Inter-triangle Mn⋯Mn distances | |||||
| Mn2⋯Mn4 | 3.228(1) | Mn3⋯Mn4 | 3.786(1) | Mn2⋯Mn6 | 3.811(1) |
| Mn-N,O-Mn angles | |||||
| Mn1-O221-Mn2 | 119.3(3) | Mn1-O221-Mn3 | 119.2(3) | Mn2-O221-Mn3 | 120.7(3) |
| Mn4-O222-Mn6 | 121.5(3) | Mn4-O222-Mn5 | 118.3(3) | Mn6-O222-Mn5 | 120.1(3) |
2.3 Magnetic susceptibility
Magnetic susceptibility data (2–300 K) were collected on powdered polycrystalline samples on a Quantum Design MPMS-XL SQUID magnetometer under an applied magnetic field of 0.1 T. Ac measurements were performed in the 1.8–10 K range using a 2.7 G ac field oscillation in 1–1500 Hz range. Magnetization isotherms were collected at 2 K between 0 and 5 T. All data were corrected for the contribution of the sample holder and the diamagnetism of the samples estimated from Pascal's constants [42]. The magnetic susceptibilities have been computed by exact calculations of the energy levels associated to the spin-Hamiltonian through diagonalization of the full matrix with the MAGPACK program package [43,44]. The fitting procedure for AC susceptibility was carried out with an adapted version of Visualiseur-Optimiseur for Matlab® [45,46] using a Lavenberg-Marquard nonlinear least-squares algorithm.
3 Results and discussion
The refined formula for the complex is [Mn6(μ3-O)2(5-Me-salox)6(S-mandelato)2(EtOH)6] (Fig. 1) and it crystallizes in the P21 non-centrosymetrical space group (monoclinic system). The Flack parameter has been refined to 0.02(3) confirming the presence of only one enantiomer in the structure.
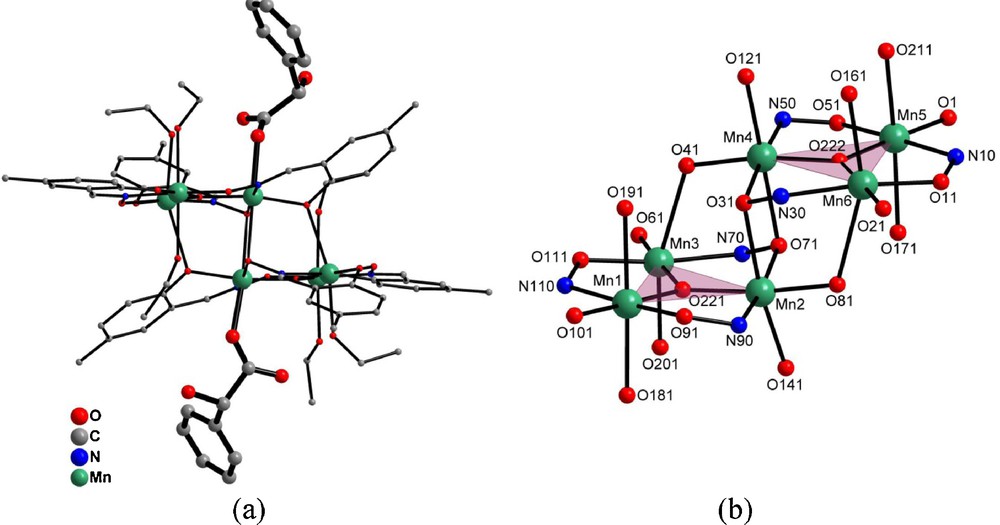
a: molecular structure of chiral [Mn6(μ3-O)2(5-Me-salox)6(S-mandelato)2(EtOH)6] cluster (hydrogen atoms have been omitted for clarity); b: two {Mn3(μ3-O)(5-Me-salox)3(S-mandelato)(EtOH)3} triangular subunits linked together in a head-to-tail manner.
The structure can be viewed as two off-set, neutral stacked {Mn3(μ3-O)(5-Me-salox)3(S-mandelato)(EtOH)3} triangular subunits (Fig. 1) positioned in a head-to-tail manner, and linked together by two phenoxo and two oximo μ3-oxygen atoms belonging to the four double deprotonated oxim groups of the two 5-Methyl-salicylaldoxim ligands. Within each subunit, manganese ions are connected together in a triangular manner by μ3-oxygen atoms. Intra-triangle Mn⋯Mn distances are homogenous, ranging from 3.243(1) Å to 3.281(1) Å (average: 3.262 Å), and are shorter than inter-triangle ones (ranging from 3.228(1) Å to 3.811(1) Å, average: 3.608 Å). Mn-O,N-Mn angles are also homogenous ranging from 119.2(3)° to 121.5(3)°.
All manganese ions are in the +III oxidation state as confirmed by the combination of bond length considerations, BVS calculations [47–49] and charge balance. All MnIII ions display a more or less distorted six-coordinate octahedral geometry associated to a Jahn-Teller elongation. Mn-O,N bond lengths in the square base of the pyramidal environment range from 1.851(7) Å to 2.015(7) Å while Mn-O,N bond lengths along the perpendicular axis range from 2.112(7) Å to 2.591(6) Å. All these Mn-O-Mn angles, Mn⋯Mn distances and Mn-O,N bond lengths are in good agreement with what has been observed previously [14,50–53].
The shortest center to center distance between two neighbouring [Mn6] clusters is equal to 12.6 Å, which indicates that the inter-cluster magnetic interaction can be neglected.
In order to claim the complex enantiopurity, solid-state circular dichroism (CD) (KBr pellets) measurements in absorption mode were performed on crystals of 1 (Fig. S1).
The small intensity CD signals at 600 cm−1 probably correspond to d-d transition generated by C4v octahedral distortion ligand field of MnIII. The more intensive CD signals 520 and 353 cm−1 can be assignment to d-π* and π-π* transitions of the aromatic system.
The results of magnetic susceptibility measurements on the polycrystalline cluster 1 are depicted in Fig. 2. For the chiral [Mn6] (1), at room temperature, the χT product is 17.75 cm3 K mol−1. This value is close to the expected one (18.00 cm3 K mol−1) for six MnIII ions (3.00 cm3 K mol−1, S = 2, g = 2). Upon decreasing the temperature, the χT product at 0.1T continuously increases and reaches 21.90 cm3 K mol−1 at 8.0 K. After 8 K, the χT product decreases rapidly and takes the value of 16.69 cm3 K mol−1 at 2.0 K. The χT evolution indicates the presence of dominant ferromagnetic interactions within the hexanuclear complex.
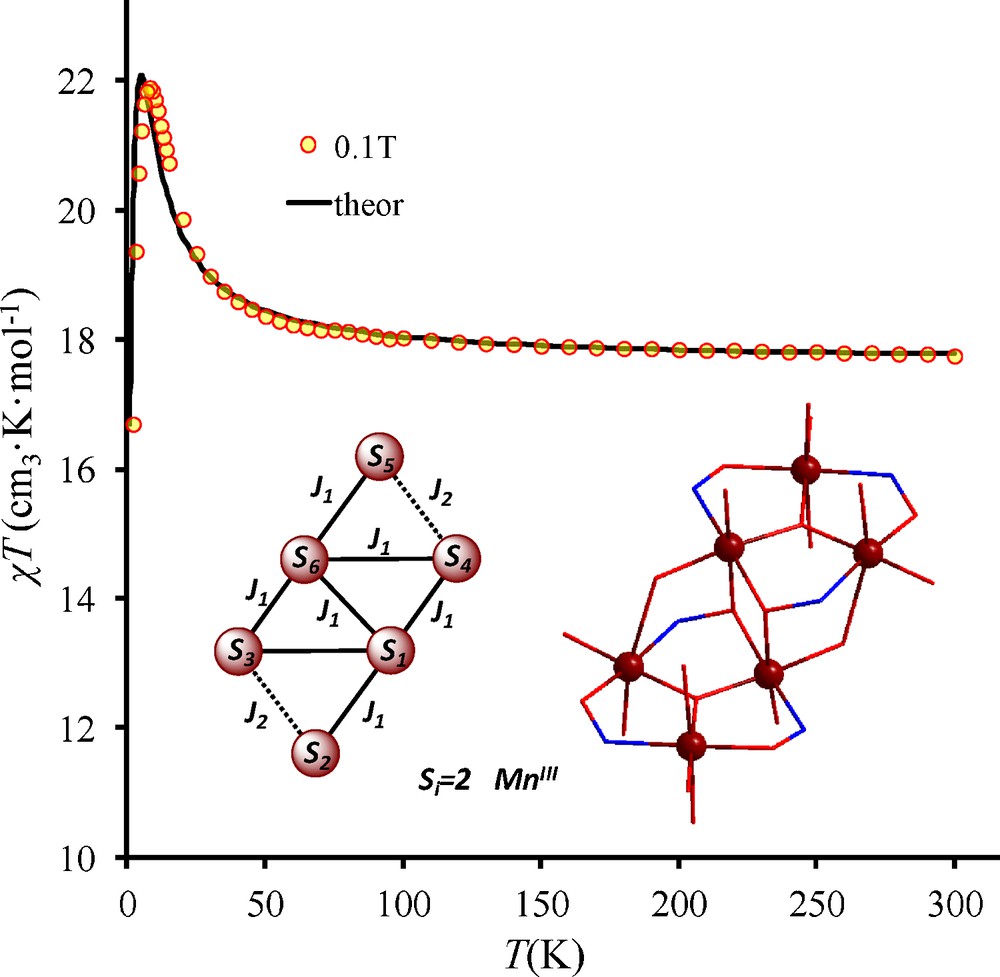
Magnetic susceptibility χT versus T plots data for [Mn6(μ3-O)2(5-Me-salox)6(S-mandelato)2(EtOH)6] (1). The black solid line corresponds to the best fit according to the retained model (see figure and text).
According to the structural features of 1 and to previous magnetostructural studies in Mn6 family, the temperature dependence of the magnetic susceptibility can be calculated using the general spin-Hamiltonian which describes the isotropic exchange interactions in hexanuclear cluster [54].
The experimental values of magnetization at 2,3,4 and 5 K for Mn6 (1) are shown in Fig. S2. The field evolution of magnetization is typical for presence of magnetic anisotropy due to negative ZFS parameters generated by MnIII Jahn-Teller distortion [5,55] and is consistent with a previously published SMM Mn6 family [12–15]. The small magnetic interaction values indicate the possibility of “intermediate” spin ground states which can vary from 4 to 12 [12,50,54,56]. The large versatility of fundamental spin states in Mn6 oxime systems clearly demonstrates a magnetostructural correlation with the torsion angles of the oxime ligand [12,54–56].
Regarding the ac magnetic susceptibility (Hdc = 0) for 1 a strong temperature and frequency dependence of out-of-phase χ” is observed. (Fig. 3 and Fig. S3) We have used the two measuring procedures, the frequency-scan (Fig. 3) and the temperature-scan method (Fig. S3) in order to analyze the relaxation behaviour of the Mn6 compound (1). According to the Glauber's theory [57], the thermal variation of τ is described by the Arrhenius expression:
| (1) |
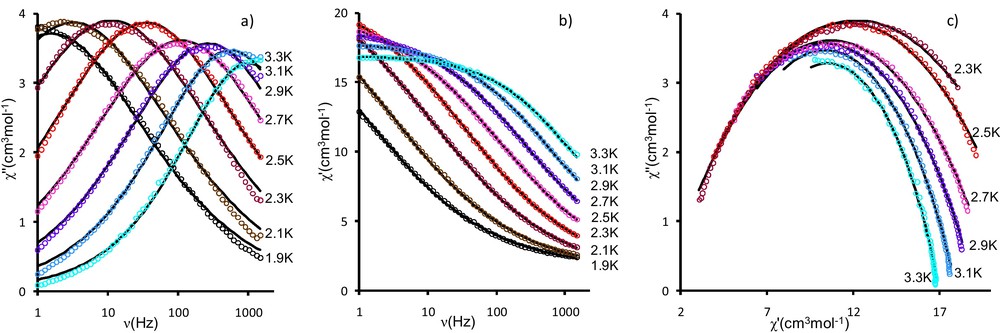
Frequency dependence of out-of-phase χ” (a) and in-phase χ’ (b) susceptibilities at Hdc = 0, Hac = 2.7 Oe; c: Cole-Cole plot for the same data. The solid line is a least-square fitting of the ac data to a single relaxation process as described by generalized Debye model (Eqs (2) and (3)).
The best fit of both data sets (temperature-scan and frequency-scan) gives an effective energy barrier Ueff = 35.3 K and a relaxation time τ0 = 2.7 × 10−9 s (Fig. 4).
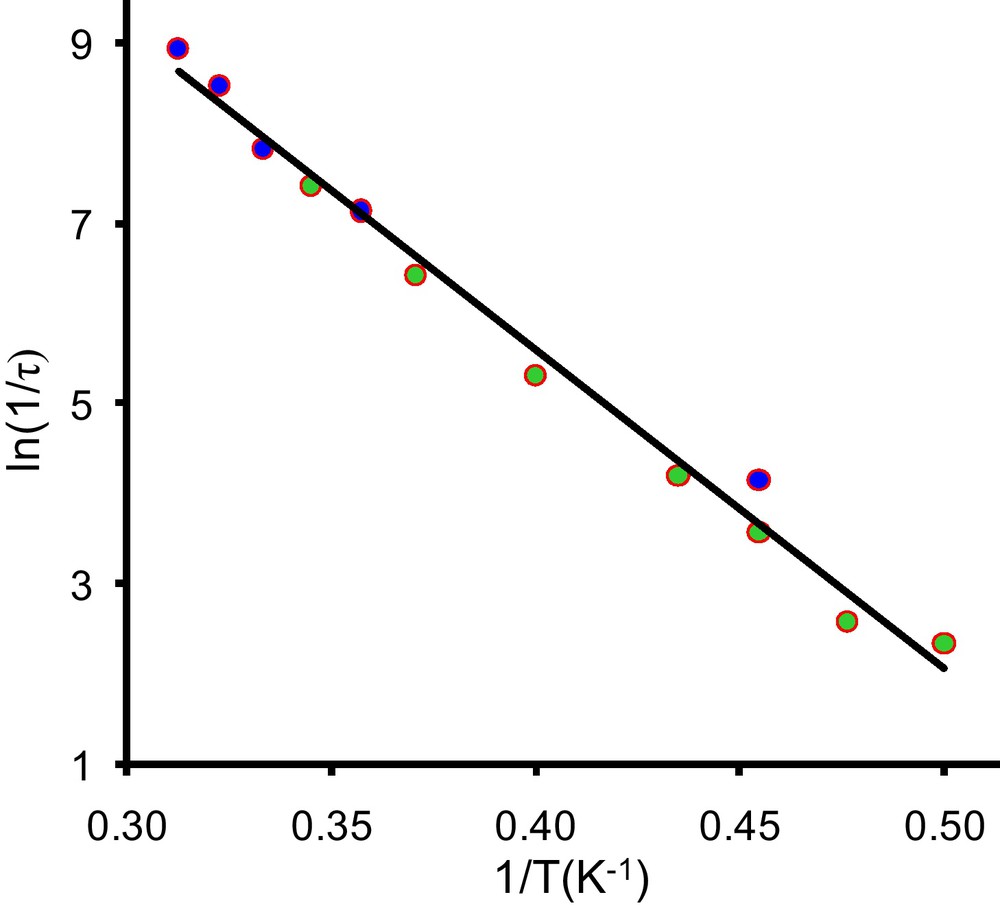
Arrhenius plot for 1 data on a microcrystalline sample. The green points (light grey) are extracted from frequency-scan and the blue points (dark grey) from temperature-scan. The solid line is the best fit of the both data sets by Eq. (1) (Ueff = 35.3 K, τ0 = 2.7 × 10−9 s).
The complex susceptibility can be phenomenological expressed by generalized Debye model (Eqs. (2) and (3)). The Cole-Cole plots [1,58], and the best fits of in-phase and out-of-phase susceptibilities are reported in Fig. 3. Relatively large values were found for α (0.08–0.33). This indicates that more than one relaxation process might be operating here in correlation with the small magnetic interaction values and the possibility of “intermediate” spin ground states.
| (2) |
| (3) |
Such magnetic behavior of 1, characteristic of SMM, is also confirmed by the presence of a hysteresis loop with a 230 Oe coercivity field at 1.8 K (Fig. 5).
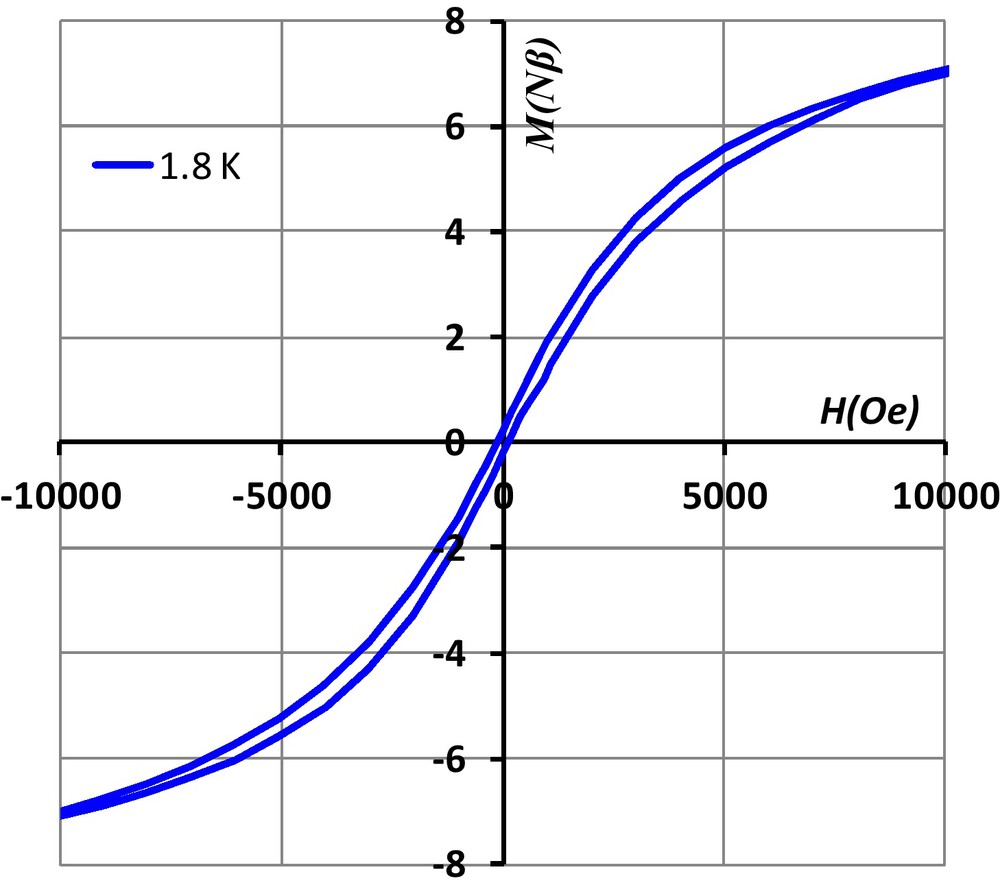
Hysteresis of 1 at 1.8 K.
4 Conclusion
In conclusion by reacting a chiral MnII S-mandelato compound with 5-methyl-salicylaldoxime in a basic solution as starting material, the new chiral MnIII6 cluster has been synthesized and characterized. X-ray analysis confirms a non centrosymmetrical (monoclinic, P21 (no. 4)) structural organization with a refined Flack parameter close to zero. The chirality of bulk material was also proved by circular dichroism spectroscopy in solid state. According to the magnetic measurements, Mn6 represents an enantiopure compound that exhibits SMM properties with an energy barrier of slow magnetic relaxation equal to 35 K.
Acknowledgements
G. Novitchi is grateful to the EU FP-7 for a Marie Curie International Incoming Fellowship.


