1 Introduction
The interest in weak interactions and their properties increases continuously. Amongst the most recent and less known are the pnictogen bonds [1–3]. There are several methods to characterize these bonds: geometries (obtained by crystallography and other techniques), calculated interaction energies, electron densities, IR and UV bands, NMR chemical shifts, etc. [1] NMR spin–spin coupling constants (SSCC) provide important information about their electronic structure. Experimentally, such SSCC termed 1pJPP in the case of both pnictogen atoms being phosphorus, have been observed in intramolecular situations with the unavoidable problem of the transmission of the spin information through the skeleton linking both 31P atoms [1]. A large variety of intermolecular pnictogen complexes [2–7] and one intramolecular case [8] have been calculated theoretically. Closely related to this topic is the σ-hole concept [9].
Although the interaction energies for dimer stabilization are quite large (up to 35 kJ mol−1 for PH2F dimer) [4], there is small hope to measure 1pJPP in solution. In 1988, one of us described 3,4-dimethyl-1-cyanophosphole (1) and described many of its NMR properties (Table 1) [10]. In 2001, the X-ray structure of 1 was reported (Fig. 1) [11]. It is a dimer (12) with a P···P distance of 3.384 Å. In the CSD, the compound received the EDIJOQ refcode [12].
Experimental chemical shifts in CDCl3 (ppm) and SSCC (absolute values, Hz) for monomer 1.
| Atom | Group | Experimental [10] | Experimental (this work) |
| 1H | CH3 | 2.13, 4JHH = |0.7|, 4JHP = |3.6| | |
| 2,5 (CH) | 6.27, 4JHH = |0.7|, 2JHP = |42.0| | ||
| 13C | CH3 | 17.3, 3JCP = |3.6| | 17.8, 1JCH = 127.8, 3JCH ∼ 4.6, 3JCP = |5.0| |
| CN | 115.9, 1JCP = |83.0| | 116.1, 3JCH = 5JCH ∼ 3, 1JCP = |82.9| | |
| 2,5 (CH) | 120.5, singleta | 120.4, 1JCH = 176.5, 3JCH = 6.0 (Me), 3JCH = 3.6 | |
| 3,4 | 155.5, 2JCP = |8.5| | 155.6, 2JCP = |8.8| | |
| 15N | CN | b | |
| 31P (1) | Ring | –54.7 | –52.5, 1JCP = |83.0|c |
a That means that 1JCP ≤ |2| Hz.
b This signal is not observed even after long time.
c Measured on the 13C satellites.
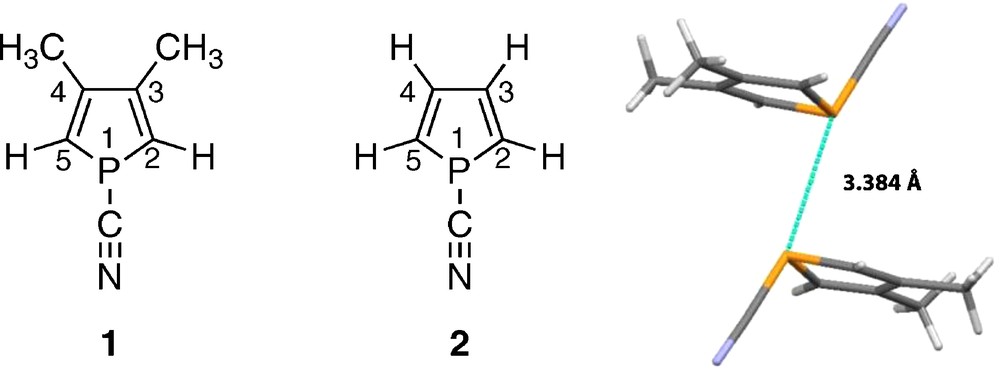
Monomer 1, model compound 2 and structure of the dimer EDIJOQ (12). Color available online.
2 Experimental
2.1 Chemistry
The synthesis of compound 1 was reported in references [10] and [11].
2.2 NMR
Solution NMR spectra were recorded on a Bruker DRX 400 (9.4 Tesla, 400.13 MHz for 1H, 100.62 MHz for 13C, 161.96 for 31P) spectrometer with a 5-mm inverse-detection H–X probe equipped with a z-gradient coil, at 300 K. Chemical shifts (δ in ppm) are given from internal solvent, CDCl3 7.26 for 1H and 77.0 for 13C; for 31P NMR 85% H3PO4 (0.0) was used as the external standard. Coupling constants (J in Hz) are accurate to ± 0.2 Hz for 1H and ± 0.6 Hz for 13C and 31P, respectively.
Solid state 13C (100.73 MHz), 31P (162.16 MHz) and 15N (40.60 MHz) CPMAS NMR spectra have been obtained on a Bruker WB 400 spectrometer at 300 K using a 4 mm DVT probehead. Samples were carefully packed in a 4-mm diameter cylindrical zirconia rotor with Kel-F end-caps. Operating conditions involved 3.2 μs 90° 1H pulses and decoupling field strength of 78.1 kHz by TPPM sequence. 13C spectra were originally referenced to a glycine sample and then, the chemical shifts were recalculated to the Me4Si [for the carbonyl atom δ (glycine) = 176.1 ppm], 31P spectra to (NH4)2HPO4 (AHP) and 15N spectra to 15NH4Cl and then converted to nitromethane scale using the relationship: δ 15N (MeNO2) = δ 15N(NH4Cl) – 338.1 ppm. Typical acquisition parameters for 13C CPMAS were: spectral width, 40 kHz; recycle delay, 5 s; acquisition time, 30 ms; contact time, 2 ms; and spin rate, 12 kHz. In order to distinguish between protonated and unprotonated carbon atoms, the NQS (non-quaternary suppression) experiment by conventional cross-polarization was recorded; before the acquisition, the decoupler is switched off for a very short time of 25 μs [13,14]. Typical acquisition parameters for 31P CPMAS were: spectral width, 100 kHz; recycle delay, 5 s; acquisition time, 30 ms; contact time, 2 ms; and spin rate, 10 and 12 kHz. Typical acquisition parameters for 15N CPMAS were: spectral width, 40 kHz; recycle delay, 5 s; acquisition time, 35 ms; contact time, 6 ms; and spin rate, 6 kHz.
2.3 Computational details
The geometry of the systems has been optimized at the MP2 computational level [15] with the aug′-cc-pVTZ basis set [16]. This basis set is derived from the Dunning aug-cc-pVTZ basis set by removing diffuse functions from H atoms. The absolute chemical shielding and coupling constants of the systems have been calculated with the GIAO method [17] at the B3LYP/aug′-cc-pVTZ level [18]. The Gaussian-09 program has been used for these calculations [19].
The electronic properties of the system have been analyzed through molecular electrostatic potential (MEP), electron density [20], electron localization function (ELF) [21] and natural bond orbitals (NBO) [22] measurements. The MEP has been calculated with the Gaussian-09 program and has been represented on the 0.001 au electron density isosurface with the WFA program [23]. This program has been used to analyze the local minima and maxima of the MEP on the surface. The topological analysis of the electron density has been carried out with the AIMAll program [24]. The topological analysis of the electron density provides the critical points of this property. AIM permits to define the molecular graph of the investigated systems as the ensemble of maxima of the electron density, ρ, associated with the position of the nuclei, saddle points, in which ρ, has two negative and one positive curvatures, the so-called bond critical points (BCPs) and the zero gradient lines connecting them, or bond paths. The ELF function allows to detect those region where the electrons are more concentrated. Thus, information of the characteristics of the different types of bond and lone pair are easily obtained. The ELF function has been calculated with the Topmod program [25]. The natural bond orbital (NBO) method has been used to obtain atomic charges and to analyze the orbital charge transfer between the interactions molecules. The NBO-3 program has been used for these calculations [26].
3 Results and discussion
3.1 NMR spectroscopy
In NMR, using CDCl3 as solvent, monomer 1 is characterized by the data reported in Table 1.
Our attempts to add more data to Table 1 mostly failed: the 15N chemical shifts cannot be measured probably because the signal is a doublet (2JPN) without near H atoms. Moreover, 2JPN cannot be measured on the 15N satellites of the 31P signal because the coupling is buried inside the central peak. In our hands, the 31P NMR signal appears at –52.5 ppm instead of –54.7 ppm [10] (a concentration effect, calculated for the monomer –61.7 and for the dimer –60.3 ppm) and its 13C satellites corresponds to a 1JCP = |83.0| (Fig. 2). An isotope effect of 0.05 ppm (8.1 Hz) between 31P–12C and 31P–13C is also observed in Fig. 2. The 2JNP coupling constant of 18.9 Hz (calculated, Table 2) is lost under the central peak. Since the 1H decoupling was not complete, the lateral peaks due to 2JHP = 42.0 Hz coupling were observed, where these peaks are split by the 4JHP = 3.6 Hz (in principle, a septuplet, but only the three central lines were observed).
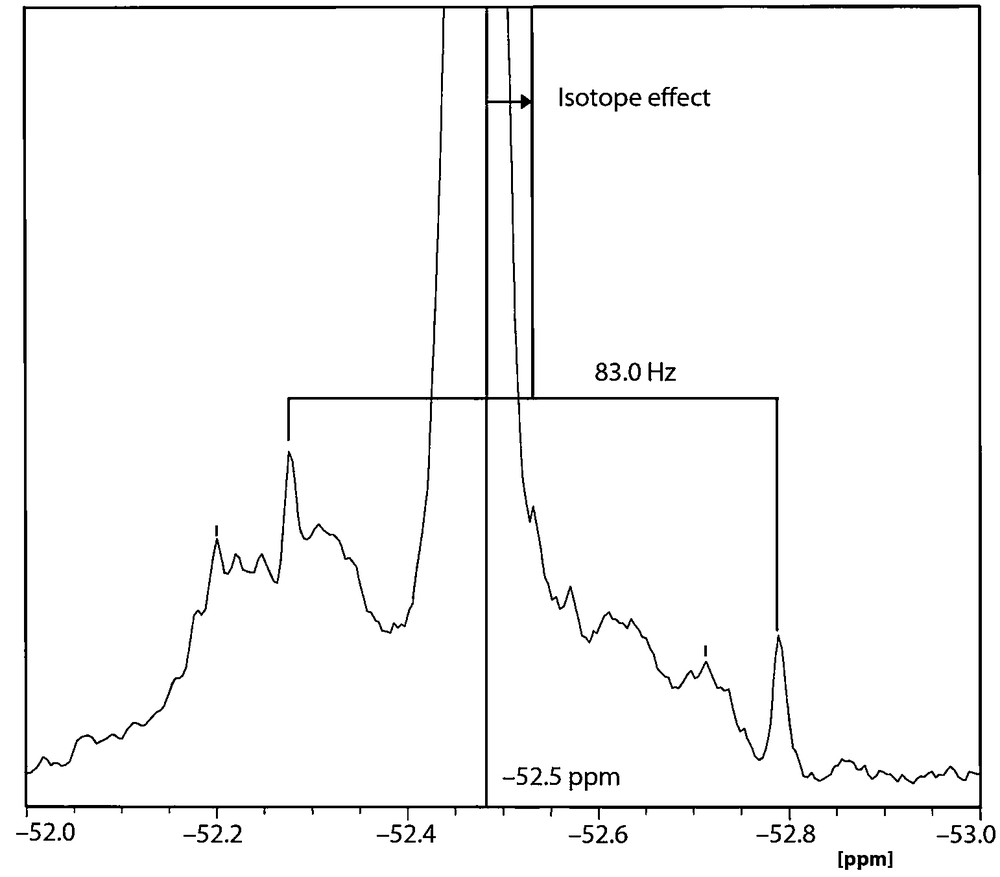
31P [1H] NMR spectrum of 1 in CDCl3 at 161.96 MHz.
Calculated absolute shieldings (ppm) for compound 1 and SSCC (Hz) for compounds 1 and 2.
| Atom | Group | δ 1 | SSCC 1 | SSCC 2 |
| 1H | CH3 | 2.36 | 4JHH = –1.3, 4JHP = +4.8 | – |
| 2,5 (CH) | 6.61 | 4JHH = –1.3, 2JHP = +45.0 | – | |
| 13C | CH3 | 17.8 | 3JCP = +3.4 | – |
| CN | 114.5 | 1JCP = –97.2 | 1JCP = –86.4 | |
| 2,5 (CH) | 126.4 | 1JCP = –8.4 | 1JCP = –10.3 | |
| 3,4 | 156.3 | 2JCP = +10.1 | 2JCP = +12.1 | |
| 15N | CN | –82.2 | 1JCN = –7.6 | 1JCN = –8.0 |
| 31P (1) | Ring | –61.7 | 2JNP = +18.9 | 2JNP = +19.0 |
Then, we calculated theoretically the chemical shifts and coupling constants of 1 (Table 2). The calculations correspond to geometries optimized at the MP2/aug′-cc-pVTZ. On these optimized geometries, we carried out GIAO and SSCC calculations at the B3LYP/aug′-cc-pVTZ level [for references, see Section 2.3].
The calculations afford absolute shieldings (σ, ppm). To transform them into chemical shifts, we have used empirical equations established with many compounds of the largest diversity for GIAO/B3LYP/6-311++G(d,p) calculations. It is important to note that solvent effects are included in these equations since they have been obtained by comparing calculated values in the gas phase with experimental values in solution. Using data of nitriles and isonitriles [27], we have calculated the equation for the 15N chemical shifts of these compounds.
| δ1H = 31.0 – 0.97 * σ1H (reference TMS, 0.00 ppm) [28] |
| δ13C = 175.7 – 0.963 * σ13C (reference TMS, 0.00 ppm) [29] |
| δ15N = –153.4 – 0.744 * σ15N (reference ext., neat MeNO2, 0.00 ppm) [this work] |
| δ31P = 237.0 – 0.81 * σ31P (reference ext., 85% H3PO4 ppm) [30] |
These equations are probably different for B3LYP/aug′-cc-pVTZ calculations but allow us to compare different calculations and, for some nuclei, are rather good. For instance, the experimental chemical shifts of compound 1 in CDCl3 (Table 1) are well correlated with the calculated values of Table 2.
| δexp = (1.7 ± 1.5) + (0.970 ± 0.016) δcalc, n = 7, R2 = 0.999 |
Comparing the values for 1 and 2, we note that the methyl groups at positions 3 and 4 exert a small influence on the coupling constants, the most affected being 1JCP (difference 10.8 Hz).
Both the chemical shifts and SSCC of 1 are acceptably calculated, the worse result concerns 1JCP is calculated to be –97.2 (experimental 83.0 Hz) and –8.4 Hz (experimental < |2| Hz). Thus, we have calculated the SSCC of the dimer (Table 3) to see if the value of 1pJPP was experimentally attainable.
Experimental and calculated [with the minimum (3.21 Å) and the X-ray (3.38 Å) P···P distances] chemical shifts (ppm) for dimer 12.
| Atom | Group | Experimental (CPMAS) | Calculated minimum | Calculated X-ray |
| 13C | CH3 | 18.4 (s) | 17.7 | 17.7 |
| CN | 118.25 (m) | 114.8 | 114.7 | |
| 2,5 (CH) | 120.25 (s) | 128.0 | 126.3 | |
| 3,4 | 158.8 (sa) | 157.1 | 156.5 | |
| 15N | CN | –80.1 (sb) | –80.1 | –78.4 |
| 31P (1) | Ring | –55.6 (sc) | –62.3 | –60.3 |
a C3/C4 (158.8, NQS) is a singlet. This is consistent with 2JCP = 11.4.
b The full width at half maximum (WHM) is about 0.5 ppm, that is, 20 Hz.
c The full width at half maximum (WHM) is about 0.86 ppm, that is, 140 Hz, see Fig. 5.
Using all the available data from the monomer and the dimer, the following equations are obtained:
δexp = (1.6 ± 1.2) + (0.977 ± 0.012) δcalc (minimum), n = 13, R2 = 0.998, predicted, 15N (Table 1) –78.7
δexp = (1.1 ± 1.2) + (0.984 ± 0.012) δcalc (X-ray), n = 13, R2 = 0.998, predicted 15N (Table 1) –79.7
Both equations are very similar even for the predictions for the missing value of the monomer in Table 1.
Concerning dimer 12, if we compare the calculations based on the minimum and on the X-ray geometry, only 2pJCP (1.8 factor) and 1pJPP (1.6 factor) are affected. Comparing 1 with 12 and 2 with 22 (X-ray P···P distance), the most affected SSCC is 1JCP of the CH that decrease to a half (from about –9 to about –4 Hz). The most important result of Table 4 is the sensitivity of the couplings through the pnictogen bond: 2pJCP from +17.5 to +9.7 Hz and 1pJPP from +163.2 to +101.8 Hz.
Calculated (gas phase) SSCC (Hz) for dimers 12 and 22, with the minimum (3.21 Å) and the X-ray (3.38 Å) P···P distances.
| Atom | Group | SSCC 12 minimum | SSCC 12 X-ray | SSCC 22 X-ray |
| 1H | CH3 | 4JHH = –1.5, 4JHP = +4.4 | 4JHH = –1.5, 4JHP = +4.9 | – |
| 2,5 (CH) | 4JHH = –1.5, 2JHP = +42.2 | 4JHH = –1.5, 2JHP = +42.8 | – | |
| 13C | CH3 | 3JCP = +4.4 | 3JCP = +4.6 | – |
| 13C | CN | 1JCP = –96.0 | 1JCP = –94.4 | 1JCP = –84.6 |
| 2,5 (CH) | 1JCP = –4.0, 2pJCP = +0.6 | 1JCP = –3.8, 2pJCP = +0.3 | 1JCP = –5.9, 2pJCP = –0.1 | |
| 3,4 | 2JCP = +9.1 | 2JCP = +11.5 | 2JCP = +11.4 | |
| 15N | CN | 1JCN = –8.2, 2JNP = +19.1 | 1JCN = –8.3, 2JNP = +19.2 | 1JCN = –8.7, 2JNP = +19.0 |
| 2pJCP = +17.5 | 2pJCP = +9.7 | 2pJCP = +12.3 | ||
| 31P (1) | Ring | 1pJPP = +163.2 | 1pJPP = +101.8 | 1pJPP = +133.4 |
The 13C experimental results are shown in Fig. 3 (normal) and Fig. 4 (NQS), while the 31P CPMAS spectrum is depicted in Fig. 5.
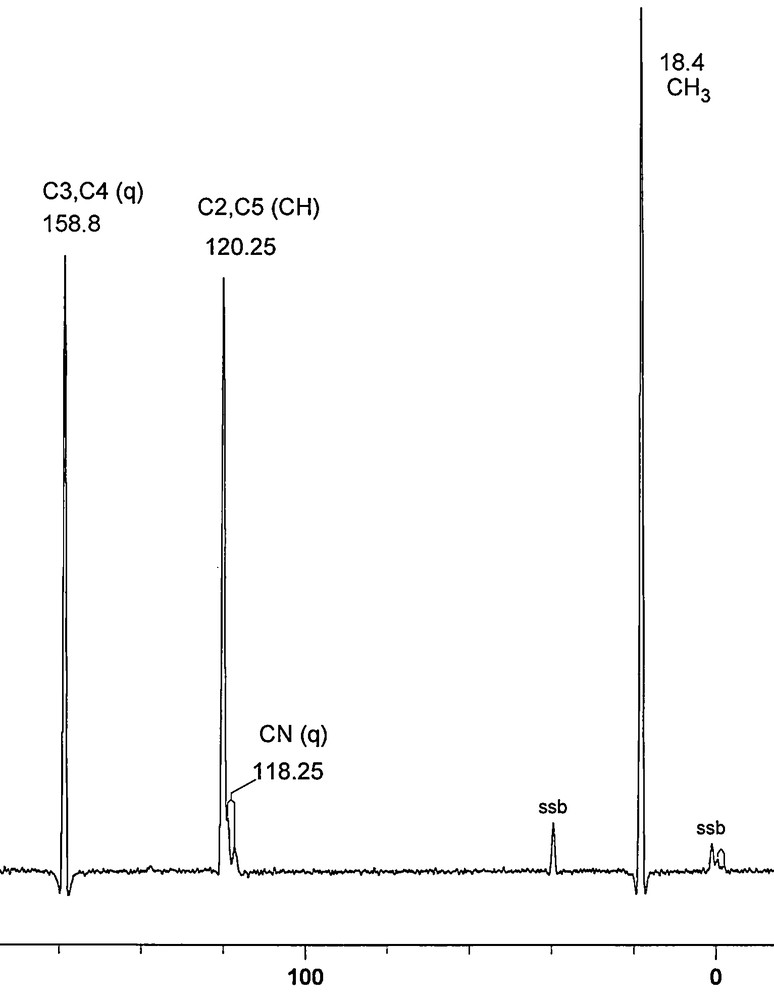
13C/1H CPMAS NMR spectrum of 12.
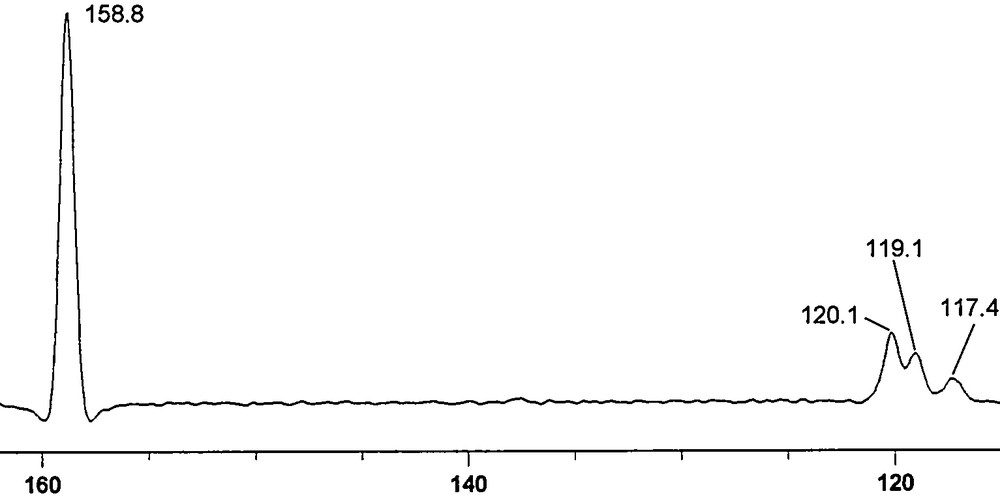
NQS. The 120.1 ppm signal is a residual of the CH. The signals at 118.25 (119.1 and 117.4 ppm) belong to the CN.
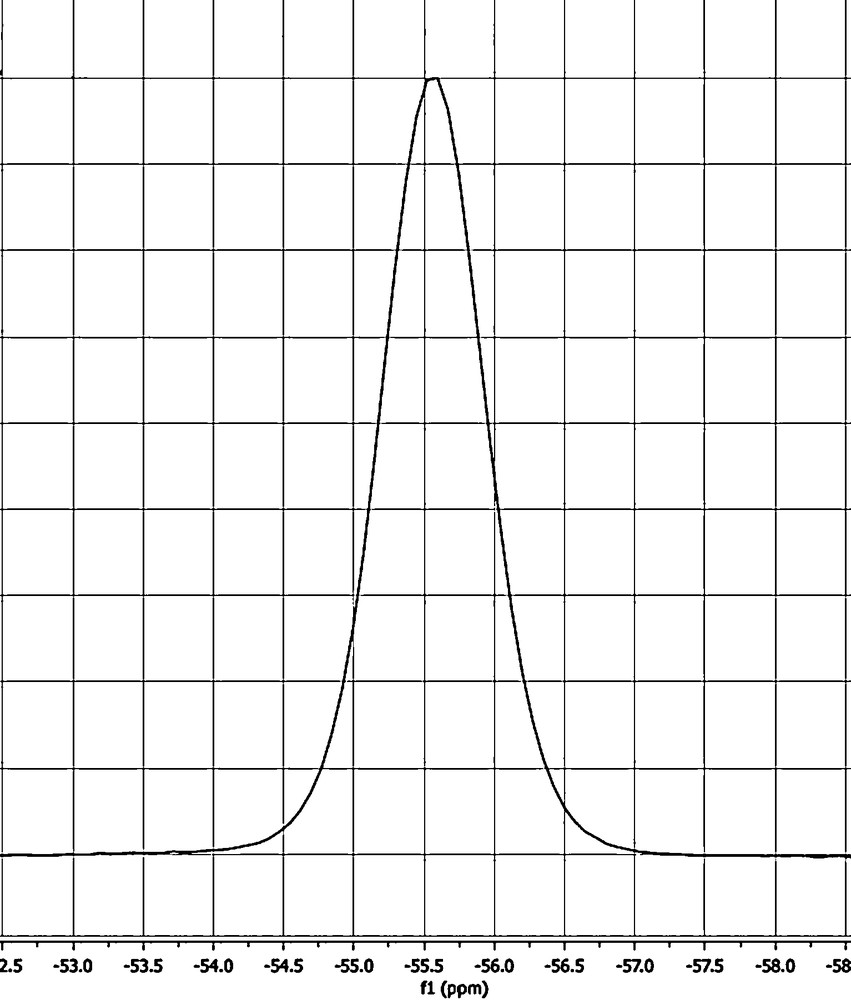
31P CPMAS spectrum of 12.
For determining the 1pJPP in the solid state of the dimer of 3,4-dimethyl-1-cyanophosphole (1), two situations are possible:
- • the symmetry is lifted in the solid state, in spite of the high symmetry obtained by X-ray crystallography (C2h). In this case, the 31P CPMAS spectrum contains two signals. If JP···P is larger than the line width, then one could see an AX or AB spin system and hence, JP···P. That being the easiest case;
- • the symmetry is not lifted in the solid state.
Methods used to measure JP···P:
- • the 31P spectrum shows only a single signal (Fig. 5). Under MAS conditions, it is difficult to measure JP···P. However, by single crystal 31P NMR it would be possible [31] because due to the chemical shift anisotropy, the two 31P will not be chemically equivalent for many different orientations. Unfortunately, single crystals of 1 of suitable size for NMR studies [31] cannot be prepared;
- • another possibility is to try the use of the 13C satellites in 31P NMR. 31P near 12C and 13C have different chemical shifts, but the difference might be small;
- • a better approach would be to analyze the 13C signal of the cyano group, and proceed in a similar way as some of us do previously, using 15N labeled samples [32].
We tried the second method but as it can be seen in Fig. 5, no 13C satellites were observed. Taking into account that the full width at half maximum (WHM) is about 140 Hz and that the calculated values for 1pJPP are ∼102 Hz (X-ray geometry) and ∼163 Hz (minimum geometry), it is not surprising that this approach failed. Then, we tried the third method. In Fig. 4, three signals were observed near 120 ppm: 120.1 ppm corresponds to a residual of the C2, C5 CHs (120.25 ppm in Fig. 3) and 119.1 and 117.4 ppm corresponding to the CN (118.25 ppm in Fig. 3, note that they are apparent in the spinning-side band near 0 ppm). The signal at 119.1 ppm is more intense than that at 117.4 ppm, but this may be due to overlapping with the 120.1 ppm signal; these signals are separated by 169.5 Hz. This cannot be due to the 1JCP because for the monomer its values are 83.0 (experimental, Table 1) and –97.2 Hz (calculated, Table 2) and for the dimer they are –96.0 (calculated, Table 4, minimum geometry) and –94.4 Hz (calculated, Table 4, X-ray geometry). Therefore, this “apparent” doublet is the X part of an AA′X system (A 31P–12C, A′ 31P–13C and X 13C). The difference between A and A′ can be estimated to be Δν ∼ 8 Hz (from the monomer), JA′X = –80/–85 Hz, JAX = 10/20 Hz and JAA′ = 100/160 Hz. But lacking the small transitions of the X part of an AA′X system, it was not possible to carry out an analysis of the spin system to ascertain the values of these couplings.
3.2 Theoretical results
3.2.1 Monomers
It has been shown in the literature that in most weak interactions complexes, the electrostatic term is the most important one [33]. In the case of the pnictogen interactions, the presence of an electronegative group bonded to the P atom generates a region of positive charge, named in the literature as σ-hole [34]. This σ-hole interacts with an electron-rich region, such as a lone pair. In the case of symmetrical P···P interactions, two simultaneous σ-hole:lone pair interactions can be found.
In the systems studied in this paper, the cyano group generates a σ-hole with a value of 0.017 and 0.022 au, for 1 and 2, respectively (Fig. 6).
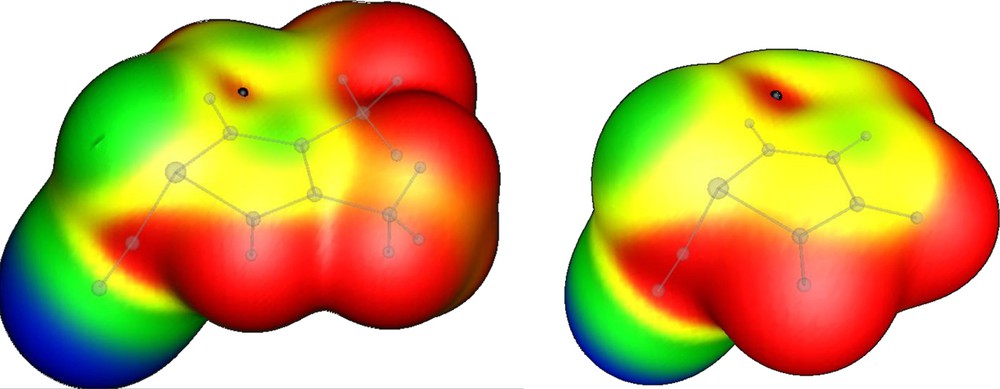
MEP on the 0.001 au electron density isosurface. Left 1, right 2. The black dot indicates the position of the σ-hole. Color code for the MEP (au): red > 0.015 > yellow > 0.0 > green > –0.03 > blue.
3.2.2 Dimers
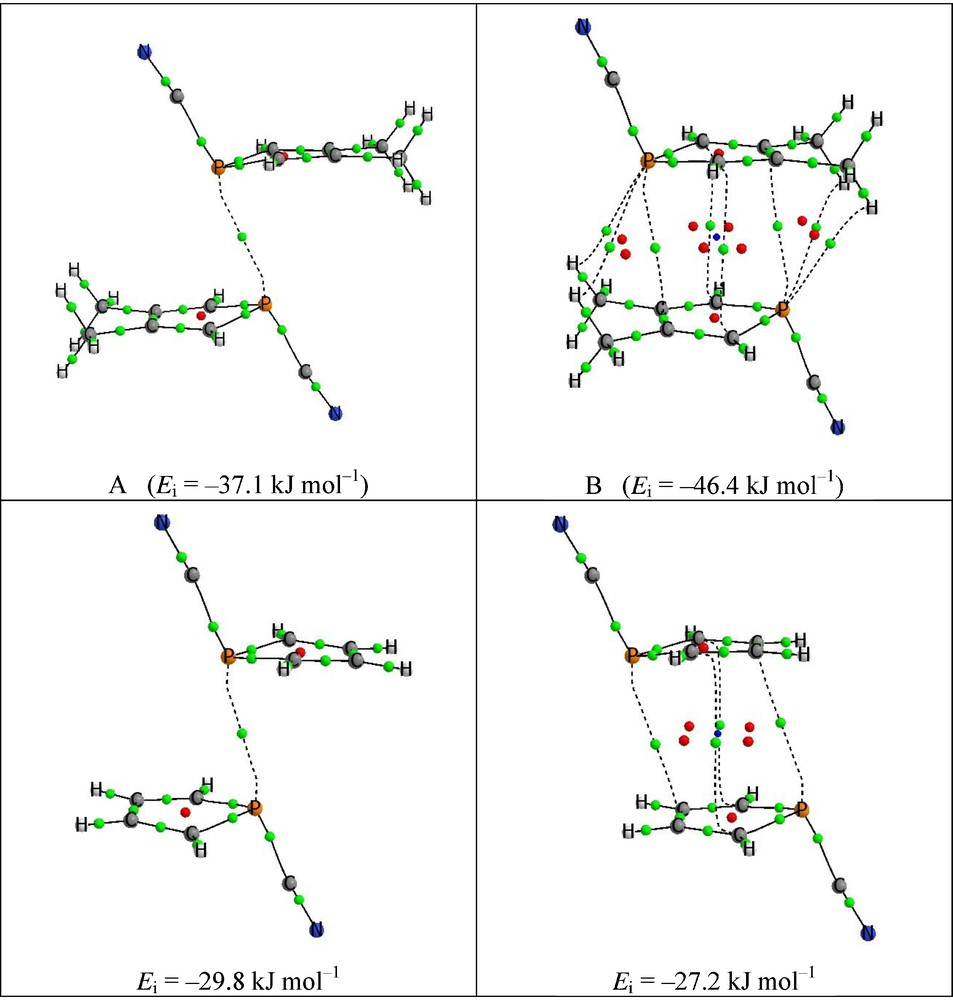
Two minima, A and B, have been found in the optimization of 12 and 22 dimers in gas phase. In the case of 1, the most stable one B corresponds to two P···π pnictogen bond (Ei = –46.4 kJ mol−1). This value of Ei is considerably higher that the stronger Ei reported in the introduction (–35 kJ mol−1). The disposition of the monomers within the dimers studied could favor some extra stabilization similar to the π–π stacking found between aromatic rings.
The second minima (Ei = –37.1 kJ mol−1) is analogous to the one found in the crystal structure and present a P···P pnictogen bond. In the case of 2, the relative stability of the two dimers is reversed and the one with a P···P interaction shows a stabilization energy of –29.8 kJ mol−1 while the one with P···π contacts corresponds to –27.2 kJ mol−1.
The intermolecular P···P distances in 12 and 22 are 3.21 and 3.19 Å, which is approximately 0.2 Å shorter than the distance found in the solid phase. Fixing the intermolecular distance to that in the solid phase, the interaction energies of the dimers obtained are only 1.4 and 1.1 kJ mol−1 less stable, respectively, than the dimers without restrictions.
The topological analysis of the electron density (Fig. 7) shows a P···P bond for the dimers analogous to the one found in the solid phase and two P···π for the alternative dimer and interactions between the heterocyclic rings. In the case of 12, some additional interactions between the methyl groups and the P atoms are also found.
Molecular graphs of the dimers studied. Green, red and blue dots indicate the position of the bond, ring and cage critical points, respectively. The lines connecting the atoms correspond to the bond path.
The NBO analysis shows two degenerate orbital interactions between the lone pair of the P atom of one molecule and the σ* P-C of the other one in the A dimers (12.0 and 14.1 kJ mol−1 for 12 and 22, respectively) while in the B dimers, the charge transfer between intermolecular orbitals are very small (less than 2.5 kJ mol−1).
The representation of the ELF (Fig. 8) shows that the lone pair of the P atoms of one molecule is located in the extension of the NC-P bond of the other molecule, where the σ-hole generated by the NC-P bond should be located.

ELF 0.75 isosurface. The P lone pair basins are indicated. The empty circle indicates the approximate position of the σ-hole. Color available on line.
For the B dimers, the σ-hole points toward the centre of the C3–C4 bond of the phosphole.
4 Conclusions
Although the experimental values of the intermolecular coupling constant between two 31P atoms have not been determined, the study of the dimer of 3,4-dimethyl-1-cyanophosphole (1) has provided interesting information about this complex. The use of NMR, both in solution (monomer) and in the solid state (dimer), coupled with ab initio calculations, has confirmed that 2pJPP coupling constants are large enough to be measured in other complexes. The topological analysis of the electron density and the electron localization function representation illustrates the pnictogen interactions as well as the position of the σ-hole.
Acknowledgments
We thank Prof Hans-Heinrich Limbach and Drs María Luisa Jimeno and Alain Fruchier for valuable discussions on the experimental determination of SSCC in the solid state. Thanks are also given to the Ministerio de Ciencia e Innovación of Spain (Projects CTQ2012-13129-C02-02 and CTQ2010-16122) and the Comunidad Autónoma de Madrid (Project MADRISOLAR2, ref. S2009/PPQ-1533).


