1 Introduction
The development of organic electronics, including organic solar cells (OSCs) and organic light-emitting diodes (OLEDs), has received a significant amount of attention in recent years because of their light weight, of their potential low cost, because they can be used to make large-area flexible and transparent panels, and because the fabrication of the devices is easy [1–7]. Especially, small molecule-based organic electroactive molecules are of increasing importance for their optoelectronic applications in OSCs and OLEDs because they exhibit good light absorption, light-emitting, and charge-carrier transport properties. It is believed that small molecule-based organic electronics are promising for their commercial application in the future. Although enormous progresses have been made recently in the research and the development of new materials, the lower efficiency of small molecule-based organic electronics materials is still the main obstacle to their application. It is therefore necessary to develop novel high-efficiency multifunctional organic materials. They are capable of transporting charge in addition to serving as efficient light-absorption materials in OSCs as well as emitters with excellent performance in OLEDs, respectively [8–13]. Theoretical studies on multifunctional organic materials may provide useful insights into the understanding of the nature of the molecules [14–17]. Among the organic materials, star-shaped conjugated materials have become the most efficient strategy used in the design and synthesis of multifunctional OLEDs and OSCs materials [18–22]. The formation of an ordered, long-range, and coplanar p–p stacking can be prevented by the increased steric hindrance of star-shaped conjugated molecules. This may lead them to be good candidates as charge transport materials. At the same time, the absorption and emission spectra of these materials can be tuned effectively through adjusting the core and arm units, and π-conjugated bridge units or length when applied in organic electronics [23]. Recently, multifunctional star-shaped molecules with triazine core and various bithiophene branches have been reported for light-emitting materials in OLEDs, donor materials in OSCs, and active channels in organic field-effect transistors (OFETs) [24].
In this contribution, we designed a series of star-shaped D–π–A molecules with 1,3,5-triazine (TZ) as the core, aromatic derivatives as end groups, and thiophene or furan π-bridges for applications in organic electronics (Scheme 1). Furthermore, we explored the optical and electronic properties of the molecules with the aim to get a further insight into the relationship between topologic structure and optical as well as electronic properties. This provides a method for the rational design of good candidates for OLEDs and OSCs materials.
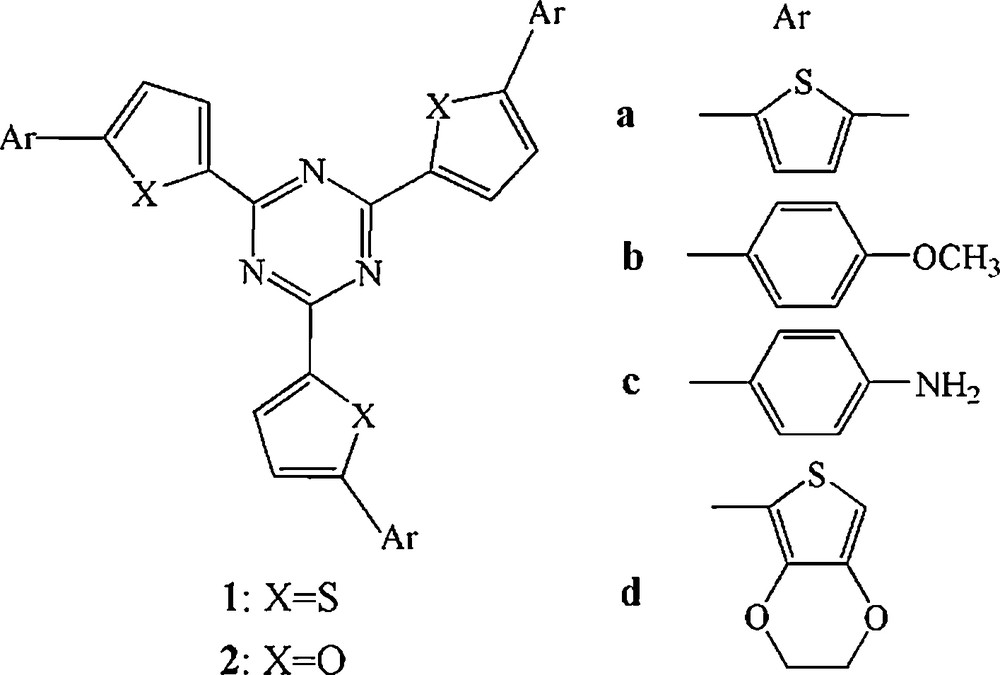
Molecular structures of the investigated molecules.
2 Computational methods
All calculations were carried out with the aid of the Gaussian 09 package [25]. The geometries of the compounds under investigation in ground states (S0) were optimized using the B3LYP method. The corresponding geometries in the first excited singlet state (S1) were optimized using TD-B3LYP. All geometry optimizations were performed using the 6-31G(d,p) basis set. The harmonic vibrational frequency calculations using the same methods as for the geometry optimizations were used to ascertain the presence of a local minimum. The absorption and fluorescent properties of the compounds under investigation were predicted using the TD-B3LYP/6-31+G(d,p) based on the optimized S0 and S1 geometries, respectively. To investigate the influence of solvents on the optical properties for the S0 and S1 states of the molecular systems in toluene as a solvent (dielectric constant: 2.374), we performed polarized continuum model (PCM) [26] calculations at the TD-DFT level.
The charge transfer rate can be described by the Marcus theory [27,28]:
| (1) |
| (2) |
| (3) |
3 Results and discussion
3.1 Frontier molecular orbitals
The qualitative frontier molecular orbitals (FMOs), including the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the investigated molecules (1a–d and 2a–d), are shown in Fig. 1. The total and partial densities of states (TDOS and PDOS) on each fragment of 1a–d and 2a–d around the HOMO–LUMO gaps were calculated based on the current level of theory. The FMOs energies EHOMO and ELUMO, HOMO–LUMO gaps Eg, and the contributions of individual fragments (in %) to the FMOs of 1a–d and 2a–d are given in Table 1. The distribution patterns and contributions of individual fragments (in %) of HOMOs – 1, HOMOs – 2, and LUMOs + 1 for the investigated molecules are given in Fig. SI and Table SI in the Supplementary data, respectively. The FMOs of 1a–d and 2a–d show π characteristics as visualized in Fig. 1. The HOMOs are mainly localized on the aromatic end groups (AR) and conjugate π-bridge fragments (CB) with only minor but nonzero contributions from the TZ fragments. On the contrary, the LUMOs mainly reside at the TZ, CB, and AR fragments of two arms. These results reveal that the different π-bridge units and end groups have obvious effects on the distribution of FMOs for the compounds under investigation. The distribution patterns of the FMOs of the compounds under investigation provide a remarkable signature for the intramolecular charge transfer (ICT) character of the vertical S0 → S1 transition. The results displayed in Table 1 show that the contributions of the TZ fragments to LUMOs are increased, while the corresponding contributions of the CB fragments are decreased compared with those of to HOMOs, respectively. The contributions of AR fragments to LUMOs are decreased, except the corresponding contributions of 1c and 2c, which are increased compared with those of HOMOs, respectively. This indicates that the excitation of the electron from the HOMOs to LUMOs leads the electronic density to flow mainly from the AR and CB fragments to the TZ fragments for 1a, 1b, 1d, 2a, 2b, and 2d, while the corresponding electronic density flows mainly from the CB fragments to the TZ and AR fragments for 1c and 2c. The percentages of charge transfer are the differences between the contributions of the fragments for LUMOs and the corresponding contributions for HOMOs in the compounds under investigation. The percentages of charge transfer from AR and CB fragments to TZ fragments are 33.2–39.7% for 1a, 1b, 1d, 2a, 2b, and 2d. The corresponding percentages of charge transfer from the CB fragments to TZ and AR fragments for 1c and 2c are 38.1 and 44.4%, respectively. The results displayed in Table 1 reveal that the AR and CB fragments serve as donors and the TZ fragments serve as acceptors for 1a, 1b, 1d, 2a, 2b, and 2d. The CB fragments serve as donors and the TZ and AR fragments serve as acceptors for 1c and 2c. Furthermore, the photophysical properties of ICT are well known and highly dependent on the electron donor/acceptor strength [38,39]. The introduction of different donor (acceptor) groups strengthens the electron-donating (-withdrawing) abilities of donors (acceptors). Therefore, the ICT transition in the star-shaped D–π–A molecules becomes much easier after having introduced different donor (acceptor) groups, resulting in the large bathochromic shift in their absorption and fluorescence spectra.
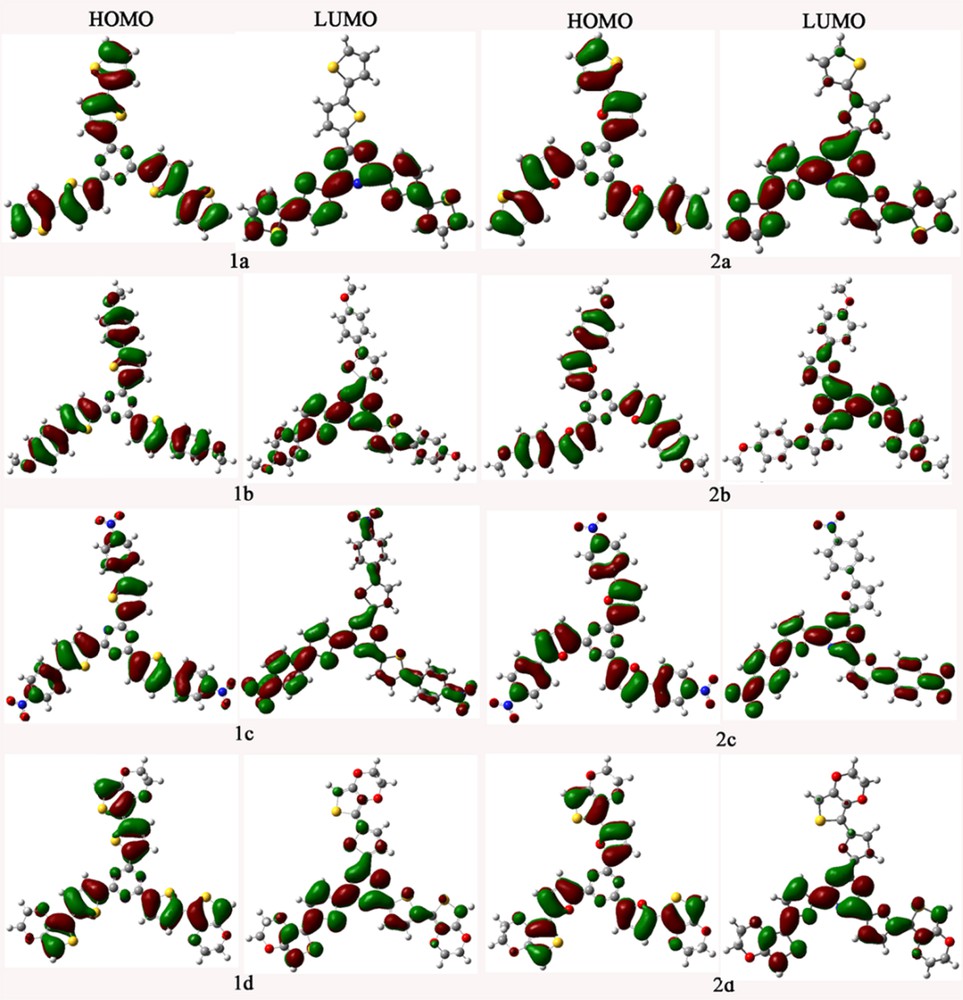
(Color online). The electronic density contours of the frontier orbitals for the investigated molecules at the B3LYP/6-31G(d,p) level.
The FMOs energies EHOMO and ELUMO, HOMO–LUMO gaps Eg (all in eV), and HOMOs and LUMOs contributions (%) of the compounds under investigation at the B3LYP/6-31G(d,p) level.
| Species | HOMO | LUMO | Eg | ||||||
| EHOMO | TZ | CB | AR | ELUMO | TZ | CB | AR | ||
| 1a | –5.595 | 2.8 | 50.8 | 46.4 | –2.167 | 37.1 | 42.2 | 20.5 | 3.428 |
| 1b | –5.386 | 2.6 | 46.7 | 50.7 | –1.822 | 42.3 | 44.5 | 13.2 | 3.364 |
| 1c | –6.602 | 3.6 | 65.4 | 31.0 | –3.044 | 21.5 | 27.3 | 51.2 | 3.558 |
| 1d | –5.164 | 2.7 | 47.2 | 50.1 | –1.872 | 35.9 | 41.2 | 22.9 | 3.292 |
| 2a | –5.461 | 3.2 | 53.9 | 43.0 | –1.932 | 42.1 | 34.1 | 23.8 | 3.528 |
| 2b | –5.187 | 3.0 | 50.5 | 46.5 | –1.603 | 47.0 | 36.2 | 16.8 | 3.584 |
| 2c | –6.453 | 3.7 | 64.5 | 31.8 | –2.985 | 20.7 | 20.1 | 59.3 | 3.469 |
| 2d | –5.034 | 3.0 | 49.9 | 47.1 | –1.614 | 41.1 | 33.5 | 25.4 | 3.420 |
Another way to understand the influence of the optical and electronic properties is to analyze the EHOMO, ELUMO, and Eg values. Inspection of Table 1 reveals that both the EHOMO and ELUMO values of 1b, 1d, 2a, 2b, and 2d increase, while the corresponding values of 1c and 2c decrease compared with those of 1a. The EHOMO values are in the order 2d > 1d > 2b > 1b > 2a > 1a > 2c > 1c. The sequence of ELUMO is 2b > 2d > 1b > 1d > 2a > 1a > 1c > 2c. Thus, the Eg values of 1c, 2a, 2b, and 2c increase, while the corresponding value of 1b, 1d, and 2d decrease compared with that of 1a. The Eg values of 1a–d are in the order 1c > 1a > 1b > 1d, while the corresponding Eg values of 2a–d are in the order 2b > 2a > 2c > 2d. The Eg values of 1d and 2d are smaller than those of 1a–c and 2a–c, respectively. It suggests that the 2,3-dihydrothieno[3,4-b][1,4]dioxine end group is responsible for the smaller Eg value. For the molecules with thiophene and furan π-bridges, the Eg values of molecules with 2,3-dihydrothieno[3,4-b][1,4]dioxine end groups are smaller than that of the corresponding molecules with thiophene, anisole, and 1-nitrobenzene end groups. It reveals that the 2,3-dihydrothieno[3,4-b][1,4]dioxine end group can decrease the Eg value in comparison with the thiophene, anisole, and 4-nitrobenzene end groups when the π-bridges are the same.
It is well known that [6,6]-phenyl-C61-butyric acid methyl ester (PCBM) and its derivatives bisPCBM and PC70BM are excellent acceptors for organic solar cells [40–43]. Therefore, we chose these three fullerene derivatives as acceptors in our work. The FMOs energies EHOMO and ELUMO are listed in Table 2. Comparing the results shown in Table 1 with those in Table 2, one can find that the ELUMO values of 1a–d and 2a–d are higher than those of PCBM, bisPCBM, and PC70BM, respectively, except that the corresponding value of 1c is slightly lower than that of bisPCBM. The differences between the EHOMO of 1a–d and 2a–d and the ELUMO of PCBM, bisPCBM, and PC70BM are larger than 1.917, 2.013, and 1.952 eV, respectively. These results imply that the designed molecules can provide better matches of FMOs to PCBM, bisPCBM, and PC70BM, except that 1c provides better matches of FMOs to PCBM and PC70BM. Therefore, different π-bridges and end groups can tune the FMOs of derivatives more suitable to PCBM, bisPCBM, and PC70BM.
Calculated EHOMO and ELUMO (all in eV) of PCBM, bisPCBM, and PC70BM at the B3LYP/6-31G(d,p) level.
| Species | EHOMO | ELUMO |
| PCBM | –5.670 | –3.117 |
| bisPCBM | –5.474 | –3.021 |
| PC70BM | –5.613 | –3.082 |
3.2 Absorption and fluorescence spectra
The absorption λabs and fluorescence λfl wavelengths, main assignments, and the oscillator strength f for the most relevant singlet excited states of 1a–d and 2a–d are listed in Tables 3 and 4, respectively. The λabs value of 1a is equal to that of the experimental result, while the corresponding value of λfl is in agreement with the experimental results [24]; the deviation is 14 nm. The Stokes shift of 1a is 52 nm, which is comparable to the experimental 66 nm. Thus, this result credits to the computational approach, so appropriate electronic transition energies can be predicted at these levels for this kind of system. For the absorption spectra, the HOMOs → LUMOs transitions play a dominant role for 1a–d and 2a–d. Furthermore, the absorptions of 1b, 1c, 2a, 2c, and 2d also originate from the HOMOs – 1 → LUMOs transitions. The transition of 1a and 2c also corresponds to HOMOs → LUMOs + 1 transitions. The results presented in Table 3 show that the λabs of 1a–c and 2a–d have slight hypsochromic shifts 15, 15, 10, 16, and 8 nm compared with that of the parent compound 1a, respectively. The λabs values of 1d and 2d show slight bathochromic shifts (17 and 3 nm) compared with that of 1a. Moreover, 1a–d and 2b–d have larger oscillator strengths than that of 1a. The f value 2a is slightly less than of 1a. The oscillator strength for an electronic transition is proportional to the transition moment [44]. In general, larger oscillator strength corresponds to a larger experimental absorption coefficient or a stronger fluorescence intensity. This indicates that 1a–d and 2a–d show larger absorption intensity than that of 1a, except for 2a. It suggests that the molecules under investigation could be used as solar cell material with intense absorption spectra.
Longest wavelength of absorption spectrum λabs, corresponding oscillator strength f, and main assignments (coefficient) for the compounds under investigation at the TD-B3LYP/6-31G(d,p)//B3LYP/6-31G(d,p) level, along with available experimental data.
| Species | λabs | f | Assignment |
| 1a | 408 | 0.24 | H → L (0.57) H → L + 1 (0.37) |
| 1b | 393 | 0.88 | H → L (0.68) H-1 → L (0.11) |
| 1c | 393 | 1.36 | H → L (0.55) H-1 → L (0.28) |
| 1d | 425 | 0.37 | H → L (0.69) |
| 2a | 398 | 0.16 | H → L (0.65) H-1 → L (0.18) H-2 → L + 1 (–0.19) |
| 2b | 392 | 0.45 | H → L (0.70) |
| 2c | 400 | 1.06 | H → L (0.48) H → L + 1 (0.42) H-1 → L (–0.20) |
| 2d | 411 | 0.26 | H → L (0.67) H-1 → L (0.13) |
| Expa | 394 |
a The experimental λabs values of 1a in CH2Cl2 were taken from Ref. [24].
The strongest fluorescence wavelengths λfl (in nm), the oscillator strength f, and main assignments (coefficient) of the compounds under investigation at the TD-B3LYP/6-31G(d,p)//TD-B3LYP/6-31(d,p) level, along with available experimental data.
| Species | λfl | f | Assignment |
| 1a | 460 | 0.31 | H ← L (0.70) |
| 1b | 438 | 0.46 | H–1 ← L (0.70) |
| 1c | 447 | 0.24 | H–1 ← L (0.68) H–2 ← L (0.16) |
| 1d | 473 | 0.32 | H–1 ← L (0.70) |
| 2a | 432 | 0.48 | H–1 ← L (0.68) H–2 ← L (0.14) |
| 2b | 422 | 0.74 | H–1 ← L (0.67) H–2 ← L (0.21) |
| 2c | 446 | 0.24 | H–1 ← L (0.68) H–2 ← L (0.12) |
| 2d | 447 | 0.50 | H–1 ← L (0.69) |
| Expa | 460 |
a The experimental λfl of 1a in CH2Cl2 were taken from Ref. [24].
For the fluorescence spectra, the LUMOs ← HOMOs excitation plays a dominant role for 1a, while the fluorescence of 1b–d and 2a–d mainly arises from HOMOs – 1 ← LUMOs. Furthermore, the fluorescence of 1c and 2a–d also originates from the HOMOs – 2 → LUMOs transitions. As shown in Table 4, the λfl values of 1b, 1c, and 2a–d show hypsochromic shifts 22, 13, 28, 38, 14, and 13 nm compared with that of 1a, respectively. The Stokes shifts of 1a–c and 2a–d are 52, 45, 54, 34, 30, 46, and 36 nm, respectively. The λfl of 1d has a bathochromic shift of 13 nm compared with that of the parent compound 1a. Furthermore, the f values of 1b, 1d, 2a, 2b, and 2d are larger than that of 1a, except that the corresponding value of 1c and 2c is slightly less than that of 1a, corresponding to strong fluorescence spectra. This implies that 1a–d and 2a–d have large fluorescent intensity and they are promising luminescent materials for OLEDs.
3.3 Reorganization energy
The calculated reorganization energies for hole and electron are listed in Table 5. It is well known that, the lower the reorganization energy values, the higher the charge transfer rate [10]. The results displayed in Table 4 show that the λh values of 1a–d and 2a–d (0.101–0.224 eV) are much smaller than that of N,N′-diphenyl-N,N′-bis(3-methlphenyl)-1,1(-biphenyl)-4,4′-diamine (TPD), which is a typical hole transport material (λh = 0.290 eV) [36]. It indicates that the hole-transfer rates of 1a–d and 2a–d may be higher than that of TPD. On the other hand, the calculated λe values of 1a–d and 2a–d (0.170–0.267 eV) are smaller than that of tris(8-hydroxyquinolinato)aluminium(III) (Alq3) (λe = 0.276 eV), a typical electron-transport material [37]. It suggests that their electron transfer rates might be lower than that of Alq3. The λh values are predicted in the order 1c < 1a < 1d < 1b for 1a–1d and 2c < 2a < 2b < 2d for 2a–d, respectively. This shows that the thiophene and 4-nitrobenzene end groups lead to the increase of hole-transfer rates for molecules with thiophene and furan π-bridges. For λe, the prediction of λe values is in the sequence 1a < 1d < 1c < 1b for 1a–1d and 2c < 2a < 2d < 2b for 2a–d, respectively. This shows that the introduction of the anisole end group results in a decrease of charger transfer rates for molecules with thiophene and furan π-bridges. Moreover, the difference between λe and λh values for 1a–d and 2a–d are in the region of 0.043–0.081 eV, showing that they have better equilibrium properties for electron and hole transport. Therefore, these molecules are potential ambipolar charge transport materials (electron and hole) under the proper operating conditions for OLEDs and OSCs from the standpoint of the smaller reorganization energy.
Calculated molecular λe and λh (all in eV) of the compounds under investigation at the B3LYP/6-31G(d,p) level.
| Species | λh | λe |
| 1a | 0.159 | 0.196 |
| 1b | 0.224 | 0.267 |
| 1c | 0.152 | 0.227 |
| 1d | 0.166 | 0.214 |
| 2a | 0.123 | 0.190 |
| 2b | 0.153 | 0.234 |
| 2c | 0.101 | 0.170 |
| 2d | 0.158 | 0.229 |
4 Conclusions
In this paper, a series of D–π–A star-shaped small molecules with 1,3,5-triazine as the core, aromatic derivatives as end groups, and thiophene or furan π-bridges have been systematically investigated for OLEDs and OSCs applications. Analyses using FMO and local density of states methods evidenced that the vertical electronic transitions of absorption and emission are characterized as intramolecular charge transfer (ICT). The calculated results show that their optical, electronic, and charge transport properties are affected by the different end groups and π-bridges. The designed molecules can provide better matches of FMOs to PCBM, bisPCBM, and PC70BM except for 1c. Our results reveal that the molecules under investigation, except for 1c, can serve as OSCs donor materials with intense absorption spectra as well as luminescent materials for OLEDs, whereas 1c can be made a luminescent material for OLEDs only. In addition, they are expected to be promising candidates for hole- and electron-transport materials. Furthermore, they have better hole- and electron-transporting balance and can act as nice ambipolar materials. On the basis of our results, we proposed a rational way for the design of charge transport and luminescent materials for OLEDs as well as donor materials for OSCs simultaneously.
Acknowledgements
Financial supports from the Research Program of Sciences at Universities of Inner Mongolia Autonomous Region (No. NJZZ235) and the Natural Science Foundation of Inner Mongolia Autonomous Region (No. 2015MS0201) are gratefully acknowledged.


