1 Introduction
Since a few decades, particles serve as models for atoms and within this context they may be called colloidal atoms (CAs). This analogy turns out to be most rewarding and the origin of several major developments. For instance, the self-assembly of size-monodisperse isotropic CAs in aqueous dispersions helped to clarify crystallization and phase transition mechanisms. Thanks to their mesoscopic size, CAs can be indeed studied in detail on the single-particle level and their dynamics is strongly slowed down in comparison with atomic systems, such that the formation of a crystal nucleus can be followed in detail. Crystallization of CAs into colloidal crystals (CCs) is an entropy-driven process in which configurational entropy and free volume entropy dominate at low and high concentrations, respectively. Concentrating the dispersions allows the disorder-to-order transition; face centered cubic (fcc) and hexagonal close packing (hcp) structures are thermodynamically favored, as they gain more free volume entropy than other packing symmetries. Nevertheless, it requires long time because of the slow relaxation of large CAs and the high viscosity of concentrated suspensions. So, metal crystals and crystallization are quite easily mimicked from the CA self-assembly, especially for evidencing defect formation such as vacancies, macroscopic cracks, polycrystalline domains, and stacking faults.
Mimicking ionic crystals, i.e. crystals made of cations and anions, was also achieved through the self-assembly of binary mixtures of CAs. For instance, mixing oppositely surface-charged and differently-sized CAs and tuning the coulombic attraction through the nature and length of the capping agents enable the fabrication of binary CCs with AB, AB2, AB3, AB4, AB5, AB6 and AB13 symmetries, providing a mesoscale embodiment of NaCl, AlB2, MgZn2, CaB6, NaZn13, etc. crystals [1].
Until now, covalent crystals, i.e. crystals made of pure covalent bonds such as diamond, Si, Ge, and SiC crystals, remain unmimickable at the colloidal scale, because their assembly necessitates highly directional interactions between CAs. Indeed, the diamond structure, with a packing factor of 0.34 against 0.74 for fcc and hcp, is based on tetrahedral arrangements, i.e. fourfold coordination, of atoms displaying a fourfold valence (sp3 orbital hybridization of carbon atoms). So, there exists a huge interest in giving to CAs predetermined “instructions” for the directional assembly by decorating their surface with “sticky patches” and/or topological discontinuities such as “dimples” for locking the neighboring spherical CAs [2–3]. Generally, the robust fabrication techniques use temporary masks for the regioselective modification of the surface. Those masks are often other colloids which shall be previously positioned with the right number and at the right places. This positioning is generally managed by playing with steric repulsions in confinement situations, e.g., within colloidal crystals or droplets, or around a sticky protrusion or a seed.
In this article, we propose to investigate the recent literature in order to make a link between the ongoing modeling efforts that deal with the self-assembly of patchy particles and their fabrication methods. More specifically, we consider the systems predicted by simulations for a given type of patchy particle (i.e. with a fixed number, size, interaction parameters and arrangement of the patches) and we detail the possible or already developed routes to synthesize such particles. As far as we know, this field has never been reviewed from such an angle, but only partially [4–6].
2 One-patch particles
Fantoni et al. considered a fluid of hard spheres bearing one circular adhesive patch in order to analyze the location of the fluid–fluid transition and of the percolation line [7]. Two particles experience an adhesive attraction of Baxter’s type only when they are exactly in contact and when a patch on one sphere touches a patch on the other. This model enabled the study of the influence of the patch surface coverage, as the one developed by Sciortino et al. [8]. They considered particles with a surface divided into two parts: repulsive and attractive, respectively, and studied the phase diagram when the fraction of the surface covered by the attractive patch χ varies from 1 to 0.5. In the latter case, which corresponds to the so-called Janus particles, they evidenced an unconventional phase diagram, in which the fluid–fluid separation competes with the aggregation of particles into micelles or vesicles (see Fig. 1A) [9]. Similar clusters of Janus spheres were obtained through Monte-Carlo simulations and observed experimentally by epifluorescence microscopy by Granick et al. (Fig. 1B) [10–12]. The formation of micelles of amphiphilic polymeric Janus particles was also reported [13].

A. Typical shape of a micelle (a) and a vesicle (b) of Janus particles. Reprinted with permission from [9] Copyright 2009 by the American Physical Society. B. Epifluorescence image and Monte-Carlo computer simulations show the formation of small clusters of Janus amphiphilic particles in the presence of 1-mM KNO3. Reprinted with permission from [10]. Copyright 2008 American Chemical Society. C. SEM images of silica particles whose surface is decorated by gold nanoparticles, except for the circular patch whose surface area can be further modified. Reprinted from [18], with permission from Elsevier. D. Optical microscopy image and schematic of a colloidal macromolecule resulting from the self-assembly of mono-dimpled spheres. Reprinted by permission from Macmillan Publishers Ltd: [24], Copyright 2010.
A plethoric number of routes to fabricate one-patch micro- and nano-particles were developed during the last decade [14–16]. Lin et al. [17] and Perro et al. [18] succeeded in producing asymmetric Janus silica spheres (Fig. 1C) by sequentially arranged particle-embedding and surface-modification processes. Asymmetric Janus polystyrene (PS) [19] and silica [20] particles were also obtained through a combination of etching and deposition processes based on colloidal lithography. Janus PS spheres with a hydrophobic domain of a precise area were obtained by the control of the etching of the gold cap previously deposited on the top of the particles [21]. When the area of the hydrophobic domain was adjusted to allow no more than three neighbors per particle, the patchy spheres self-assemble in the form of monodisperse tetrahedra, as expected. Unlike these previous strategies, Andala and co-workers reported the production of amphiphilic Janus gold nanoparticles by a general method which does not rely on particle immobilization [22]. Instead, the authors demonstrated that the obtained amphiphilic nanoparticles correspond to the thermodynamically favored arrangement of the system’s components resulting from the reduction of the interfacial free energy between two immiscible liquids.
Using Monte-Carlo simulations, Ashton et al. studied the depletion-induced self-assembly of another type of one-patch particles, i.e. spheres with one concave dimple [23]. They showed that such colloids can assemble into chains in the presence of a depletant via lock and key binding in which the convex part of one particle interlocks with the concave part of another. Such a directional assembly of dimpled particles leading to the formation of dumbbells, trimers and colloidal macromolecules has been experimentally observed by Sacanna et al. (Fig. 1D) [24,25]. Micelle-like structures were also obtained through the self-assembly of amphiphilic rod-like particles [26] and of anisotropic PS dimers that consist of one curved, smooth patch on a rough sphere [27].
3 Two-patch particles
3.1 Two identical patches
The assembly behavior of two-patch particles has been extensively studied numerically. Sciortino et al. developed a spot-like patch model to study a simple fluid composed of particles having a hard-core repulsion, complemented by two short-ranged attractive sticky spots at the particle poles [28]. They reported the formation of linear chains, which was in a complete agreement with the predictions of the Wertheim theory. The organization of two-patch spheres into chains whose average size increases smoothly with decreasing temperature was also observed by Zhang and Glotzer who performed a coarse-grained patchy model (Fig. 2A) [29].
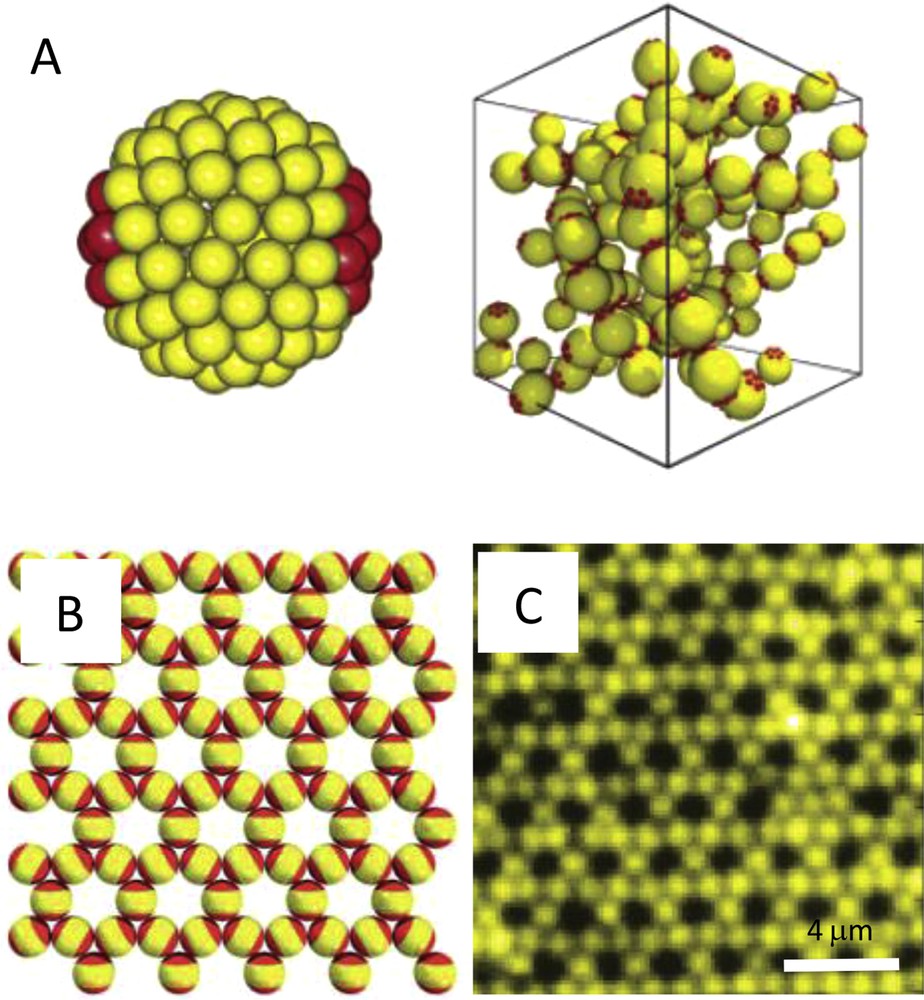
A. Side view of a patchy sphere with two diametrically opposed circular patches and representation of the long chains formed at low temperature. Reprinted with permission from [29]. Copyright 2004 American Chemical Society. B. Snapshot of a Kagome lattice formed by two-patch hard spheres. Reproduced from [32] with permission of The Royal Society of Chemistry. C. Fluorescent image of triblock Janus spheres assembled in a Kagome lattice. Reprinted by permission from Macmillan Publishers Ltd: [33], Copyright 2011.
The influence of the attractive patch surface on the assembly of patchy hard spheres was numerically investigated in details [7,30,31]. It was shown that an appropriate choice of the patch angular width allows for the formation of ring structures which compete with the growth of linear chains at low temperatures [31]. More interestingly, Romano and Sciortino showed that particles with two attractive patches symmetrically arranged as polar caps spontaneously assemble in a two-dimensional (2D) Kagome lattice (Fig. 2B) when the patch width is within the range of values that allows for at most two bonds per patch [32]. This result is in perfect agreement with the experimental observations made by Chen et al. concerning the 2D assembly of triblock Janus particles made up of an electrically charged band in-between two hydrophobic polar caps of a proper size (Fig. 2C) [33,34]. These particles were fabricated by sequential deposition of a metal on a monolayer of latex spheres. After the first vapor deposition, a polydimethylsiloxane (PDMS) stamp was used to lift up the monolayer so that patches are facing down. A second deposition is then performed to create patches on the other pole of the spheres and the grafting of n-octadecanethiol molecules onto the metal made the patches hydrophobic. In order to exploit the idea that consists of limiting the number of bonded neighbors via a proper selection of the patch width for the self-assembly of three-dimensional (3D) crystals, Romano et al. [35] showed numerically that the rational design of patch shape and symmetry can drive patchy particles to crystallize in a single, selected morphology. In particular, they proposed to pattern the colloidal spheres with two triangular patches oriented in a staggered geometry, which is readily achievable by glancing angle deposition [36,37], as such colloids yield via spontaneous crystallization, a pure tetrastack lattice, and a structure with attractive photonic properties [38]. Bianchi et al. modeled the 2D self-assembly of a different type of two-patch particles, referred to as inverse patchy colloids (IPCs) [39,40]. These particles carry two extended charged caps that repel each other and attract the oppositely charged equatorial region of the colloids. By tuning both the confinement conditions of the colloids and the particle–wall and particle–particle interactions, the authors showed different aggregation scenarios of the IPCs, leading to the formation of a gel or of planar aggregates. On an experimental point of view, IPCs could be easily synthesized by adapting the previously described sequential process of Chen et al. [33], starting for instance with negatively charged latex spheres and grafting onto the metal caps a thiol derivative bearing an amine function instead of n-octadecanethiol.
Increasing the anisotropy of the patchy particle shape leads to an increasing complexity of the phases that one may expect. For example Corezzi et al. reported molecular dynamics simulations of the irreversible gelation of a binary mixture composed of ellipsoidal patchy particles with 2 and 5 patches [41,42]. On the experimental point of view, the synthesis and the self-assembly behavior of two-patch polymeric ellipsoids [43] or metallic nanorods [44] were reported. In both cases, the self-assembly of the “pom–pom” anisotropic particles into chains or other hierarchical structures was demonstrated.
3.2 Two different patches
The self-assembly of patchy particles decorated with two patches of different natures and/or sizes was also studied numerically. Villar et al. used a model in which two particles interact via an isotropic Lennard-Jones repulsive core and the directional patch–patch attraction is given by the Lennard-Jones attractive part modulated via a Gaussian angular dependent decay to study the thermodynamics and dynamics of assembly of particles covered by two different patches as model of homomeric protein complexes [45]. In another work, a lattice functional theory method was applied to describe the assembly of a mixture of one-patch, three-patch particles and particles with two different patches into a particular target structure [46].
On the experimental point of view, Chaduc et al. reported the batch synthesis of silica nanoparticles bearing two different polymeric patches by using silica/PS dimers as seeds in the emulsion polymerization of a second organic monomer, i.e. methyl methacrylate [47]. Chen et al. produced triblock spheres with two patches of different sizes by the previously described process [33] followed by an asymmetric etching of the metal caps, enabled by the fact that the PDMS stamp protects from reaction the patch that presses into it [48]. The sequential activation of the bonds through the fine tuning of the ionic strength of the particle suspension allowed the authors to observe the formation of networks of clusters comprising different types of connectivity (Fig. 3).
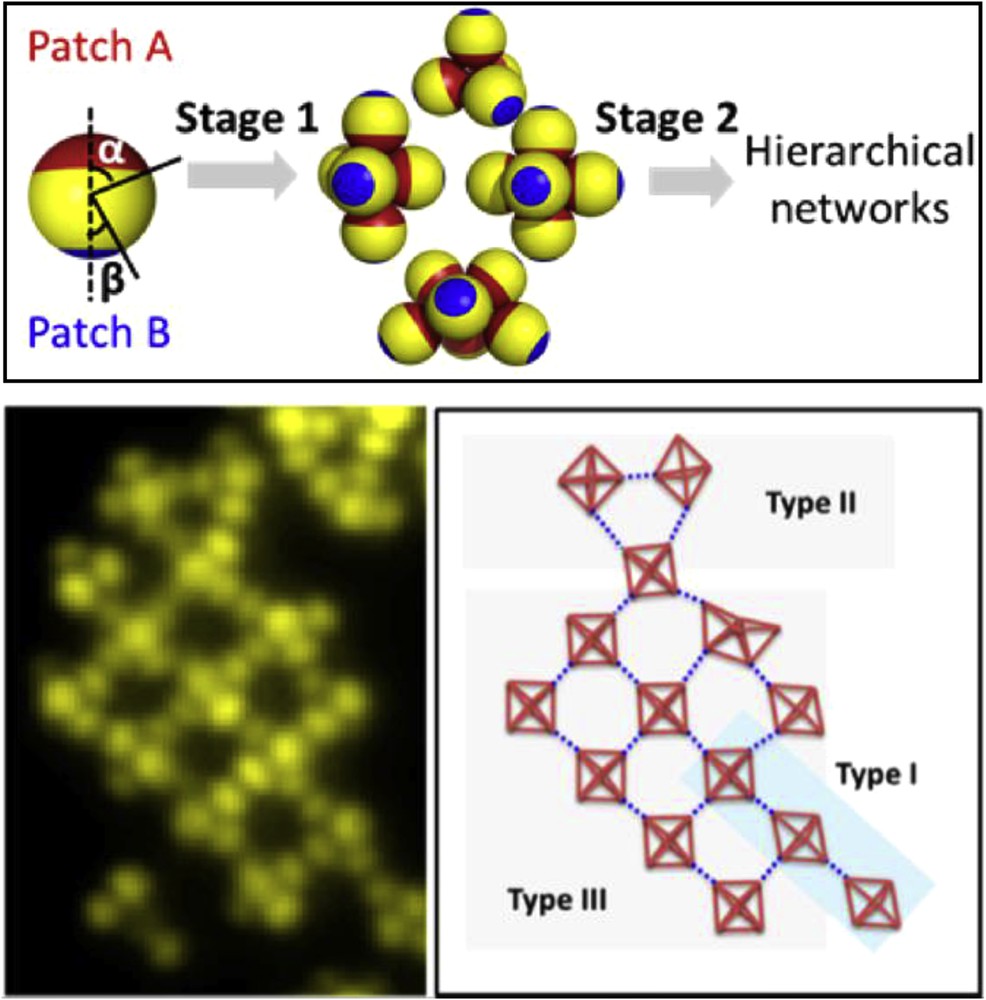
Top. Schematics of the staged self-assembly of triblock spheres. Bottom. Fluorescence image and schematics of a network of clusters comprising different types of connectivities. Reprinted with permission from [48]. Copyright 2012 American Chemical Society.
4 Three-patch particles
Bianchi et al. theoretically and numerically investigated the phase diagram of particles with three regularly arranged attractive patches [49,50]. They mainly showed that the gas-liquid coexistence region in the temperature–density plane is reduced by comparison with particles with a higher number of patches. The self-assembly of particles with three patches located on one of their hemispheres to form tetrahedral, cubic or dodecahedral structures was also studied by the use of a minimal model [51]. Particles with three regularly arranged patches were synthesized using particle-stabilized oil-in-water emulsions in which the oil phase is photocurable [52] and through the assembly of polymer particles with a liquid protrusion and the subsequent polymerization of the liquid [53]. The latter approach also allowed the production of particles with three patches concentrated in a specific region of the particle surface [54].
5 Four-patch particles
Particular attention has been paid to the specific case of four identical patches arranged on a tetrahedral geometry because of its relevance for photonic crystals with diamond symmetry [55]. Models for particles with 4 patches have been initially inspired by the primitive model for water that was introduced by Kolafa and Nezbeda several years ago [56]. The water molecule was depicted as a hard sphere with four interaction sites arranged in a tetrahedral geometry in an attempt to mimic the two hydrogen atoms and the two oxygen lone pairs. This model was also used to show that for such patchy spheres the gas-liquid phase separation is metastable [57]. Indeed, the phase diagram of tetrahedral patchy particles was found to be very rich, with several re-entrant coexistence lines (Fig. 4) [50,58–63]. One can see that the range in density where the diamond phase is actually stable is very narrow, which is a consequence of its low compressibility. Moreover, at low pressures and finite temperatures, the diamond is competitive with a body-centered-cubic (bcc) crystal, both the diamond and the bcc exhibiting similar energies. The diamond solid is only stabilized when the entropy increases, that is when the range of the interactions decreases [58]. Then the self-assembly of tetrahedral patchy particles into a diamond-like crystal might not be so straightforward [64,65]. In fact, crystallization to the diamond structure is greatly favored when a seed crystal is introduced or when an additional term in the potential which induces a relative orientation between particles is added [65].
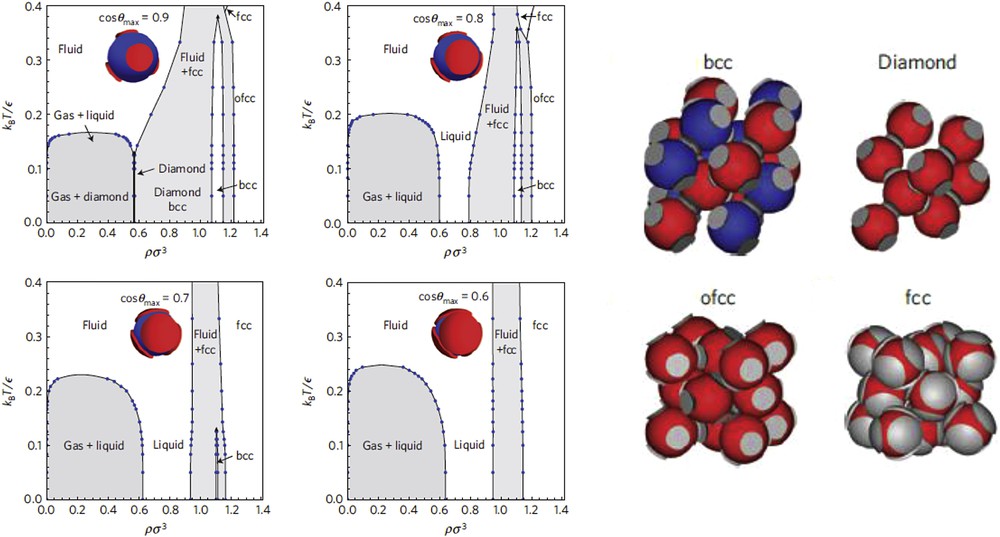
Left. Phase diagrams in the dimensionless density-temperature representation for particles with four tetrahedrally arranged patches and patch widths cosθmax (patch width decreasing when cosθmax increases). Right. Pictures showing the unit cell of body-centered cubic (bcc) crystal phase, consisting of two interlocking diamond lattices, diamond crystal phase, orientationally ordered fcc (ofcc) and disordered fcc. Reprinted by permission from Macmillan Publishers Ltd: [61], Copyright 2013.
As far as we know, no experimental study of the crystallization of tetrahedral patchy particles has been reported yet, even if several routes to produce such colloids exit. A preparation of particles with four patches arranged in a tetrahedral geometry using particle-stabilized oil-in-water emulsions was demonstrated [52]. Colloids with four patches were also produced through the assembly of polymer particles with a liquid protrusion and the subsequent polymerization of the liquid (Fig. 5A) [53]. Also we recently reported a facile chemical route for producing submicrometer biphasic tetrahedral patchy colloids made of four PS latex nodules bound to a silica core (Fig. 5B) [66–68]. By carefully adjusting the experimental conditions, we could obtain tetrahedral colloids at the gram scale with an average yield over 80% [68]. An approach using emulsion droplets as confined geometries and initially developed by Lauga et al. [69] and Pine et al. [70–73] to produce clusters of microspheres was extended by Cho et al. [74,75] and Wang et al. [76] for the production of patchy binary particles with a precise number of patches, especially four in a tetrahedral geometry. The latter functionalized the patches with DNA with single-stranded sticky ends (Fig. 5C) and then assembled different patchy particles, functionalized with complementary DNA, in a controlled manner. For example, by adding particles with four patches to a suspension of one-patch particles with a complementary DNA sequence, methane-like colloidal molecules were formed (Fig. 5D) [76].
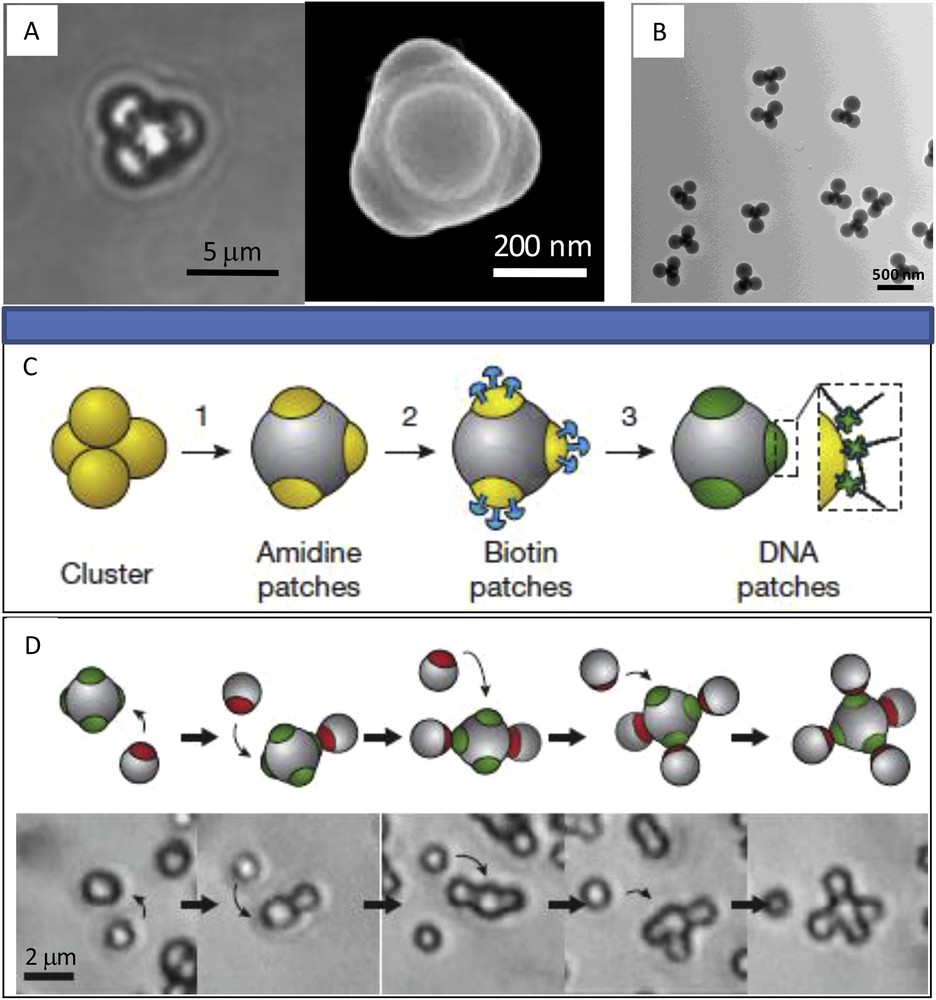
A. Light microscopy image and SEM view of tetrahedral patchy particles created by merging of liquid protrusions. Reprinted with permission from [53]. Copyright 2009 American Chemical Society. B. TEM view of tetrahedral binary patchy particles obtained by seeded-growth emulsion polymerization. C. Preparation of colloidal particles with four DNA-functionalized patches. D. Schematic images and snapshots from videos showing step-by-step attachments of one-patch particles to four-patch particles, forming a methane-like type colloidal molecule. Reprinted by permission from Macmillan Publishers Ltd.: [76], Copyright 2012.
Van Anders et al. have recently introduced the notion of entropic patchy particles and showed how specific self-assembled structures can be targeted by engineering directional entropic forces through the systematic alteration of particle shape [77]. They performed Monte-Carlo simulations and demonstrated that tetrahedrally faceted spheres, i.e. with four concave patches, crystallize to a diamond lattice when the amount of facetting exceeds a certain value (Fig. 6A). One should note that the resulting diamond lattice exhibits a packing fraction higher than 60%, which is noticeably different from one of the open diamond structures obtained from the self-assembly of particles with four enthalpic patches. We recently reported the synthesis of tetrahedrally faceted silica spheres through the selective growth of the silica core of silica/PS tetrapods and subsequent PS dissolution (Fig. 6B) [78]. Both the surface of the multivalent particles and the bottom of the four concave dimples [79] can be regioselectively functionalized, thereby leading to particles with anisotropic geometry and chemistry.
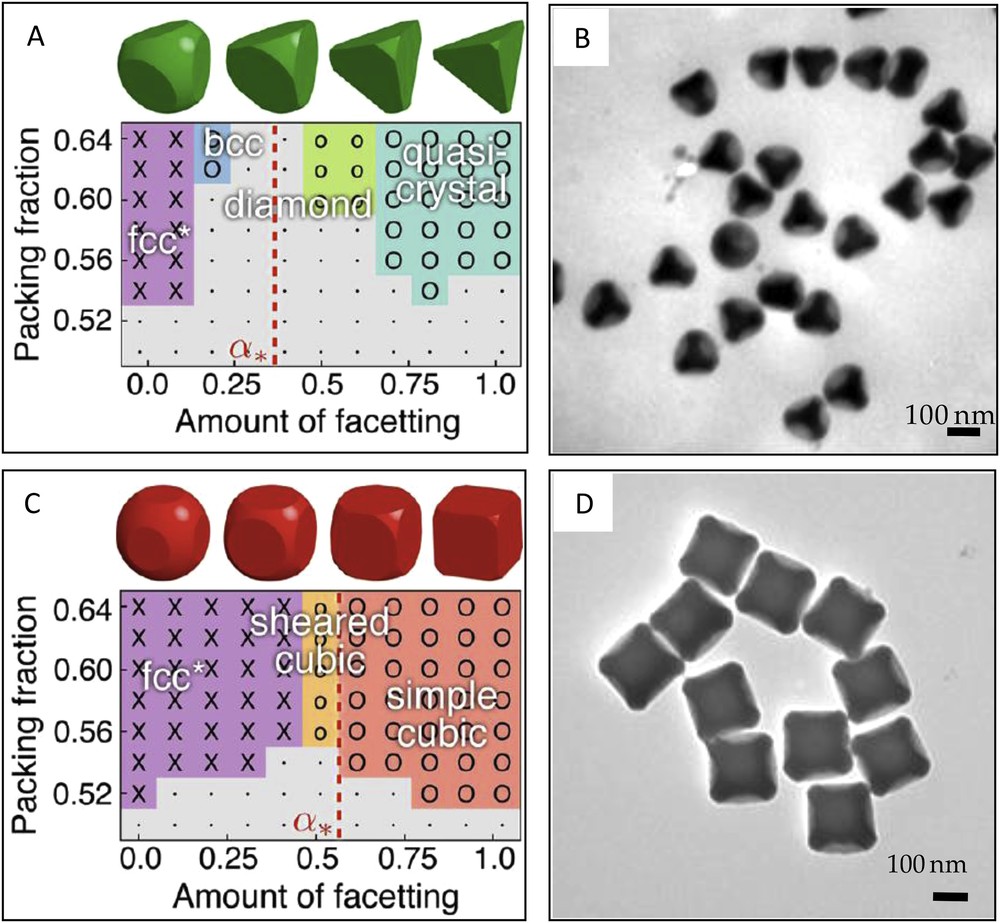
Different crystal structures formed by the assembly of tetrahedrally (A) and cubically (C) faceted spheres as the amount of faceting varies. Reprinted with permission from [77]. Copyright 2014 American Chemical Society. TEM views of dimpled silica particles with four (B) and six (D) concave entropic patches. Reprinted with permission from [78]. Copyright 2013 John Wiley and Sons.
6 Five-patch particles
The phase diagram of particles with five regularly arranged attractive patches was theoretically and numerically investigated by Bianchi et al. [49,50]. Moreover, Wilber et al. performed Monte-Carlo simulations in the canonical ensemble to study the self-assembly behavior of spheres with five patches all located on the same hemisphere [51,80,81]. They showed that the patchy particles reversibly self-assemble into monodisperse icosahedral clusters under optimal conditions. They also found that it is possible to replace the five discrete patches with a single ring patch that should pass through the positions at which the individual patches would otherwise have been placed with no significant loss in yield. The spontaneous formation of icosahedra through the assembly of spheres with a ring-like patch was also demonstrated by Zhang et al. [29]. Such particles with a non-equatorial ring-like patch could be fabricated following the protocol developed by Lin et al. [17] and carefully adjusting the embedding of the spherical particles into the polymer-fiber substrates. Five-patch particles were synthesized by different ways, already described in [52,53,66,75].
7 Six-patch particles
The same protocols [52,53,66,75] and others [67,68] allowed the preparation of six-patch octahedral particles. Several patchy particle models were considered to study the assembly behavior of six-patch octahedral particles [64,82]. A complex phase diagram with competition between multiple solid phases differing both in their density and whether they are orientationally ordered was found [83]. More precisely, a body-centered cubic crystal is more favorable at moderate pressures, whereas an orientationally ordered face-centered cubic structure becomes favorable at high pressures and low temperatures, and a face-centered cubic plastic crystal is the most stable solid phase at high temperatures. The crystal phases of the sticky spots model were carefully investigated by Bianchi et al. considering particles decorated with six patches [63]. By slicing cubically coordinated facets into hard spheres, particles with six attractive entropic patches were created [77]. Monte-Carlo simulations showed that such particles assemble into simple cubic lattices when the faceting amount and packing fraction exceed ∼0.6 and 54%, respectively (Fig. 6C). We recently reported the fabrication at the gram scale of dimpled silica particles with six attractive concave patches by using silica/PS hexapods as templates (Fig. 6D) [78]. The amount of faceting of these slice-like particles could be tuned by modifying the contact angle between the PS nodules and the silica core of the binary seeds and/or the amount of silica precursor added during the conformational growth of the silica core.
8 Particles with more than six patches
The preparation of particles with more than six patches has been reported several times [52,53,66–68,75]. Surprisingly, numerical studies dedicated to the assembly of such particles are rare [77,82], probably because of the fact that the resulting close-packed regular structures are less interesting than open structures that could be obtained through the assembly of particles with lower valence. It was shown by Monte-Carlo simulations that octahedrally facetted spheres, i.e. with eight entropic patches assembled into fcc or sheared bcc crystals depending on the faceting amount [77]. Such faceted particles could be synthesized by following the protocol that we developed recently [78].
9 Towards more complex patchy particles
Recent numerical studies have highlighted the potential interest of more sophisticated patchy particles in order to create new systems. In fact, van Anders et al. [77] pointed out that combining both enthalpic and entropic patchinesses (Fig. 7A) provides opportunities for enhancing particular desired particle alignment or produces competing forces that may give rise to structures of high complexity (Fig. 7B). We recently reported the synthesis of multivalent silica nanoparticles combining both enthalpic and entropic patchiness that could be used as building units to fabricate such structures (Fig. 7C) [79]. Finally, the self-assembly of multi-shell structures from particles with two types of patches was recently simulated (Fig. 8) [84]. This opens the way to better understand not only the basic physical principles of the formation of virus capsids, which are proteinaceous shells with a specific size and structure that are designed to encapsulate the viral genome, but also the design rules for the interactions between the constituent proteins. Indeed, in capsids, the interfaces responsible for the protein–protein interactions shall not only be in contact, but also have the correct relative orientation. The experimental fabrication of particles with two types of precisely located patches has not been realized yet and is a great challenge for the future.
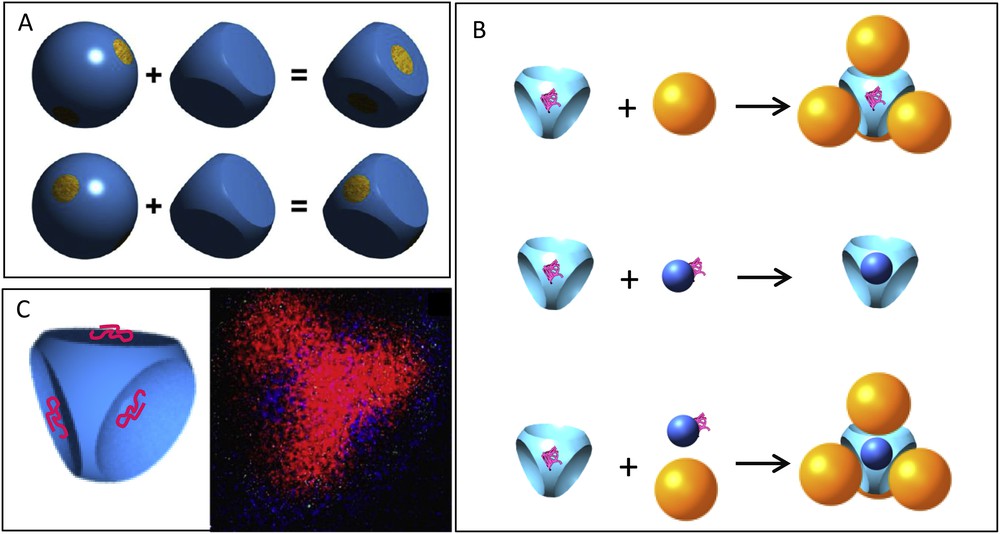
A. Enthalpic patches can be combined with entropic patches. This can be obtained by using the same direction for both types of patches (top) or by using different directions for the entropic patches and the enthalpic patches (bottom). Reprinted with permission from [77]. Copyright 2014 American Chemical Society. B. Synthesis of complex structures from particles with both enthalpic and entropic patches. C. Schematics and STEM EDX mapping (silicon in red and carbon in blue) of a tetrahedral particle with both enthalpic and entropic patchiness. Reproduced from [79] with permission of The Royal Society of Chemistry.
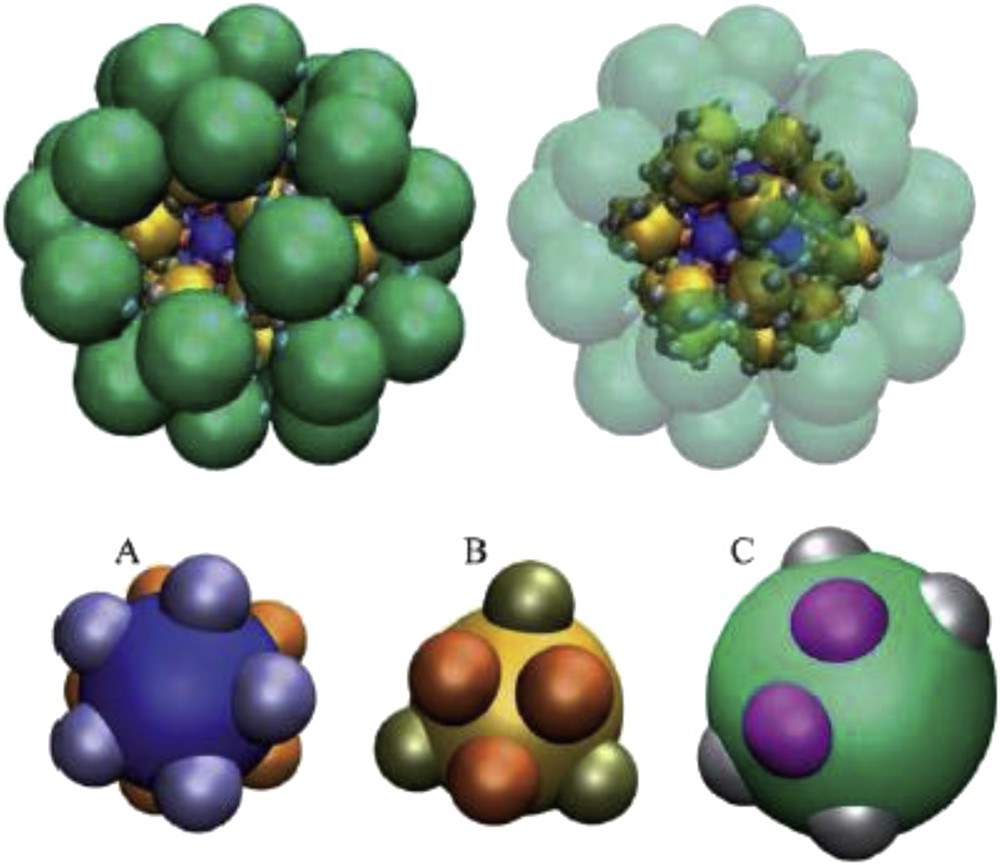
Views of a A12B20C30 multi-shell structure which results from the assembly of the individual particles A, B and C shown underneath. The view on the right has the outer shell partially transparent to give a clearer view of the core. Reproduced from [84] with permission of The Royal Society of Chemistry.
10 Conclusions and perspectives
It appears that enormous efforts have been recently done to model the assembly behavior of particles with a precise number of well-located patches, whose size or interaction capabilities have been considered as variable parameters. On the experimental point of view, a large number of routes to produce patchy particles have been reported and the most common ones are summarized in Table 1. Even if some of them are highly versatile, i.e. liable to lead to particles with two to twelve patches, they are not equal in front of important efficiency criteria such as patch localization and scalability. Taking into account that the patchy particles must be monodisperse in size, patch number and arrangement, and the production yield must be high, these two requirements have only been achieved via several routes presented herein. Indeed, many of them lead to complex mixtures of particles with a different number of patches and the necessary sorting stages, e.g., centrifugation in density gradients, are laborious and time-consuming. Finally, concerning the scalability, it is obvious that the routes derived from industrial processes such as emulsion polymerization should be preferred.
Comparative summary of the features of the most common patchy particle fabrication techniques.
| Fabrication techniques | On a substrate with neighboring particles (glancing angle deposition) | Within emulsion droplets | Around sticky protrusions | On a seed by emulsion polymerization | |
| Size domain | 1–9 μm | ʘ | ʘ | ʘ | |
| 100–999 nm | ● | ● | ʘ | ||
| Accurate control over | Chemical composition | ʘ | ʘ | ʘ | ʘ |
| Relative size | ʘ | ʘ | |||
| Robustness | ʘ | ʘ | ʘ | ʘ | |
| Morphology yield | ʘ | ʘ | |||
| Patch number | ʘ | ʘ | ʘ | ||
| Patch orientation | ʘ | ʘ | ʘ | ||
| Patch stickiness | ● | ʘ | ● | ʘ | |
| Up-scalability up to the gram scale | ● | ● | ʘ |
The experimental study of the 2D self-assembly of patchy particles is still in the infancy stage and no experimental work on the formation of 3D phases has been reported yet, as far as we know. Great efforts must thus be done in these directions.
Finally it shall be emphasized that it is not so common that experimentalists implement some systems that have been studied first theoretically. They are generally not prone to follow theoretical predictions, but just want the latter to confirm or better understand their experiments. When a milestone experimental result is presented, theoreticians usually start modeling the experiments and running simulations to further rationalize the experiment and to find possible extensions or further application of the experimental work. But the reverse is rarely true. Because of the complexity of the assembly of patchy particles capable of developing directional interactions, it is essential that theoretical and modeling experiments run first. Now, for making theoretical and experimental studies converging, some extra physical and chemical considerations shall be now introduced in the simulations, e.g., polydispersity in particle size, patch number and patch position, out-of-equilibrium and kinetic properties. That is at the expense of intensive collaboration that milestone results will arise in this field.
Acknowledgment
C.H. and C.C. were supported by the French Ministry of Higher Education and Research and IdEx Bordeaux (ANR-10-IDEX-03-02), i.e. the Programme Investissement d'Avenir of the French government managed by the Agence Nationale de la Recherche, respectively.


