Theoretical study of the geometry and electronic structure of the trinuclear [AunAgm (HNCOH)3] (m + n = 3) complex

Davood Farmanzadeh; Tahereh Abdollahi; Maryam Jafary

doi:10.1016/j.crci.2015.12.003

Theoretical study of the geometry and electronic structure of the trinuclear [Au_nAg_m (HNCOH)₃] (m + n = 3) complex

Davood Farmanzadeh ¹ ; Tahereh Abdollahi ¹ ; Maryam Jafary ¹

¹ Department of Physical Chemistry, Faculty of Chemistry, University of Mazandaran, Babolsar, 47416-95447, Islamic Republic of Iran

Comptes Rendus. Chimie, Volume 19 (2016) no. 5, pp. 579-584.

Résumé

The structures and properties of different gold and silver mixed-metal trinuclear complexes, [Au_nAg_m(HNCOH)₃] (m + n = 3), were investigated theoretically. The computed properties were compared with those of the [Au₃(HNCOH)₃] complex. The geometries of all complexes were optimized at the B3LYP level of theory using the GEN basis set. The optimization results revealed that the most stable structures of pure Au and Ag complexes are almost similar. In addition, all complexes are flat and highly symmetric. It was shown that the silver substitution had a significant influence on the electronic properties. The metal–metal distances were in the order of: Au–Au < Au–Ag < Ag–Ag. The ionization potential and hardness were found to be decreased while the electron affinity, HOMO–LUMO gap and chemical potential were found to be increased from the [Au₃(HNCOH)₃] to the [Ag₃(HNCOH)₃] complex. The [Au₃(HNCOH)₃] complex was the least reactive in the studied series with the electronic chemical potential equal to −3.98 eV. On the other hand, the value of the chemical potential characterizing the most reactive complex, [Ag₃(HNCOH)₃], was −3.80 eV.

Métadonnées

Reçu le : 2015-10-10
Accepté le : 2015-12-22
Publié le : 2016-02-12

DOI : 10.1016/j.crci.2015.12.003

Mots-clés : Bimetallic gold–silver complex, Trinuclear metal complex, Theoretical study

Affiliations des auteurs :

Davood Farmanzadeh ¹ ; Tahereh Abdollahi ¹ ; Maryam Jafary ¹

¹ Department of Physical Chemistry, Faculty of Chemistry, University of Mazandaran, Babolsar, 47416-95447, Islamic Republic of Iran

@article{CRCHIM_2016__19_5_579_0,
     author = {Davood Farmanzadeh and Tahereh Abdollahi and Maryam Jafary},
     title = {Theoretical study of the geometry and electronic structure of the trinuclear {[Au\protect\textsubscript{\protect\emph{n}}Ag\protect\textsubscript{\protect\emph{m}}} {(HNCOH)\protect\textsubscript{3}]} (\protect\emph{m}\,+\,\protect\emph{n}\,=\,3) complex},
     journal = {Comptes Rendus. Chimie},
     pages = {579--584},
     publisher = {Elsevier},
     volume = {19},
     number = {5},
     year = {2016},
     doi = {10.1016/j.crci.2015.12.003},
     language = {en},
}

TY  - JOUR
AU  - Davood Farmanzadeh
AU  - Tahereh Abdollahi
AU  - Maryam Jafary
TI  - Theoretical study of the geometry and electronic structure of the trinuclear [AunAgm (HNCOH)3] (m + n = 3) complex
JO  - Comptes Rendus. Chimie
PY  - 2016
SP  - 579
EP  - 584
VL  - 19
IS  - 5
PB  - Elsevier
DO  - 10.1016/j.crci.2015.12.003
LA  - en
ID  - CRCHIM_2016__19_5_579_0
ER  -

%0 Journal Article
%A Davood Farmanzadeh
%A Tahereh Abdollahi
%A Maryam Jafary
%T Theoretical study of the geometry and electronic structure of the trinuclear [AunAgm (HNCOH)3] (m + n = 3) complex
%J Comptes Rendus. Chimie
%D 2016
%P 579-584
%V 19
%N 5
%I Elsevier
%R 10.1016/j.crci.2015.12.003
%G en
%F CRCHIM_2016__19_5_579_0

Davood Farmanzadeh; Tahereh Abdollahi; Maryam Jafary. Theoretical study of the geometry and electronic structure of the trinuclear [Au_nAg_m (HNCOH)₃] (m + n = 3) complex. Comptes Rendus. Chimie, Volume 19 (2016) no. 5, pp. 579-584. doi : 10.1016/j.crci.2015.12.003. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2015.12.003/

Version originale du texte intégral

1 Introduction

In recent years, trinuclear metal complexes, because of their unique and interesting properties have been attracting great attention, both experimentally and theoretically. Attention has been given to the syntheses and properties of bimetallic complexes because of their unique catalytic [1], optical, and electronic properties. Small gold-silver complexes have been found to be highly effective in catalysis and medicine [2]. Silver–gold complexes proved to be more effective catalysts than the pure metals because of their increased activity, resistance to poisoning, and selectivity. These materials are considered to be good candidates for electronic nanodevices and biosensors. In addition, there are many fields where these kinds of sensors can be used, such as environmental applications, electronic noses or in the chemical industry [3].

Many bimetallic gold-silver complexes have been synthesized during the past decade [4–7]. The heterobimetallic complex, AgAu(MTP)₂, was synthesized and crystallographically characterized (MTP = diphenylmethylenethiophosphinate) by Fackleret al. [8]. Catalanoet al. [9] reported an Au–Ag complex that is three-coordinate at each metal center, [AuAg(DPIM)₃]²⁺(DPIM = 2-(diphenylphosphino)-1-methylimidazole).

The trinuclear organometallic complex [Au₃(HNCOH)₃], which is presented in this paper, was first synthesized and characterized in 1974 [10,11].In the solid state the minimal unit shows an individual molecule of the planar trinuclear complex (Fig. 1). The intramolecular Au–Au distance is 3.308 Å. The individual molecules form a columnar structure whose intermolecular Au–Au distance is 3.346 Å [12].

Fig. 1
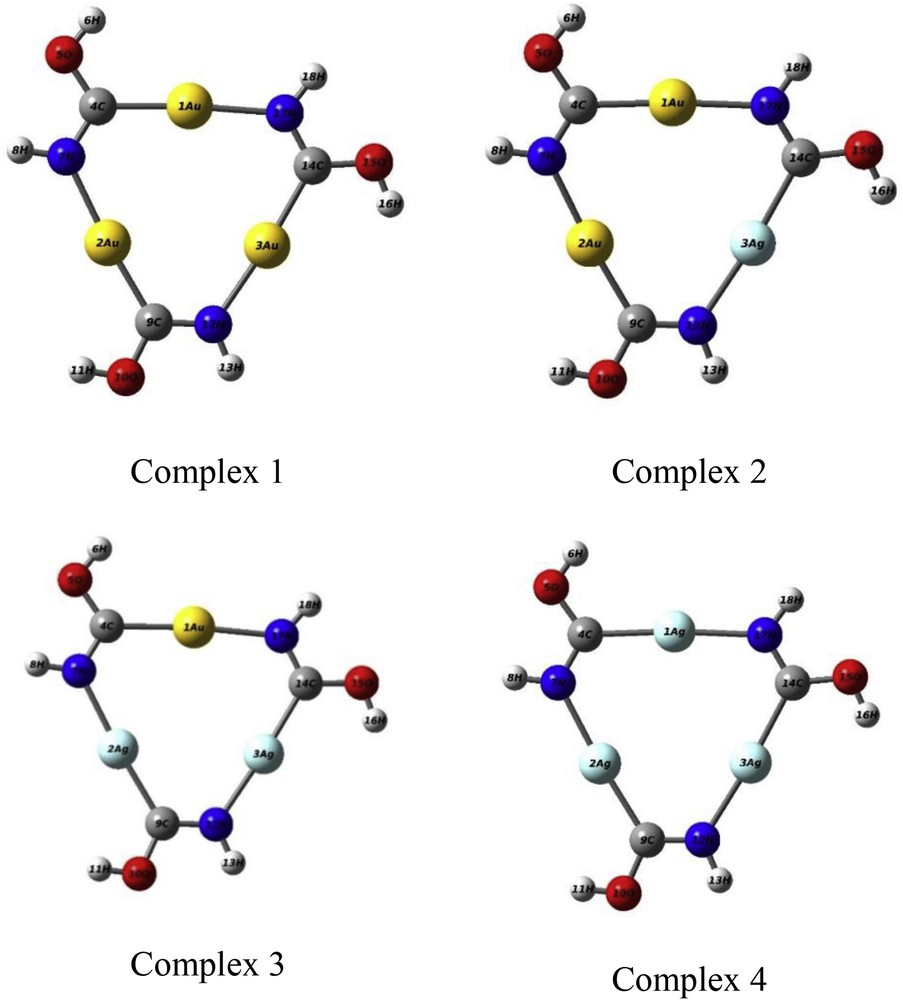
Optimized structure of pure and bimetal complexes of [Au_nAg_m(HNCOH)₃] (m + n = 3).

The structures and chemical properties of these compounds are very attractive. DFT is an affordable method for studying a variety of molecular properties and electronic structures, due to its favorable accuracy to computational cost ratio compared to accurate correlated wave function theory (WFT).There have been several reports of excellent agreement with experimental absorption and emission spectra for different gold complexes [13–16]. There are many complete theoretical studies centered on the triangular gold complex and on the electronic structures and luminescence properties at the MP2, CIS and B3LYP levels [16,17].

However, considering the few theoretical studies on these complexes, our focus in this paper is limited to the influence of silver substitution on the ionization potentials, electron affinities and other molecular properties and electronic structures of the [Au₃(HNCOH)₃] complex. The obtained results are compared with the corresponding properties of the [Au₃(HNCOH)₃] complex.

2 Computational method

The calculations of the geometry and electronic structure were performed using Gaussian 09 at the spin unrestricted DFT wave function (B3LYP) level, i.e., the Becke three-parameter exchange function in combination with the LYP correlation function of Lee, Yang and Parr with a 6-311G* basis set for C, H, N and O atoms, and effective core potential basis set LanL2DZ for Au and Ag atoms. The optimized calculation was confirmed to be local minima by performing harmonic vibration frequency analyses (no imaginary frequency found). No symmetry constrains were applied, and only the default convergence criteria were undertaken during optimization.

Natural bond orbitals (NBO) have been applied to gain insight into the electronic structure of the molecules and the nature of metal- metal and metal-ligand bonds. The popularity of the NBO method comes from its ability to transform the delocalized molecular orbitals into equivalent localized molecular orbitals that recover the expected Lewis bond patterns.

3 Results and discussion

3.1 Geometrical properties

This part of the study is started with the substitution of one silver atom for gold, to establish a series of gold-silver complexes with varying compositions. This replacement continues until the pure silver complex is reached. As the first step, the equilibrium geometries of all [Au_nAg_m(HNCOH)₃] (m + n = 3) complexes are investigated. The results of geometry optimization are reported in Fig. 1.

The results of the optimization process (Fig. 1) show that the most stable structures of pure Au and Ag complexes are almost similar. All the structures are planar. Just the H (hydrogen) atoms are not in the plane. The symmetry point group of these structures is C_3h. Table 1 lists the distances and angles along with the experimental values. Accordingly, comparison with the experimental data reveals a good agreement. The average error in the bond distance was determined to be 0.300 A°. The larger difference, 0.064 A°, is in the Au–N distance. In all of the structures, the C–N bond length is reasonable for a double bond. There is a slight dispersion, considering the angles, compared with the experimental results although the agreement is good. The angles centered at the carbon atom are distorted with respect to the sp² hybridization. On the other hand, the angles centered at N are close to the true value. Therefore, the presence of the metal atom distorts the hybridization of the close adjacent C atom. For these complexes, the intramolecular metal–metal distances with bridging-ligand bonding are in the order of Au–Au < Au–Ag < Ag–Ag. The results were in agreement with the experimentally determined equilibrium geometry. Mohamed et al. [18] have reported the metal–metal distances in the tri-icosahedral structure of the cluster [(PPh₃)₁₂Au₁₂Ag₁₃C_l6]^m+ following the trend of Au–Au < Au–Ag < Ag–Ag.

Complex 1
Bond distances (Å)/[exp]
Au(1)⋯Au(2)	3.494	Au(3)–C(14)	2.013/[2.00]	Au(1)–C(4)	2.013/[2.00]
Au(1)⋯Au(3)	3.494	Au(1)–N(17)	2.093/[2.03]	Au(2)–C(9)	2.013/[2.00]
Au(2)⋯Au(3)	3.495	Au(2)–N(7)	2.094/[2.03]	Au(3)–N(12)	2.094/[2.03]
Bond angles (deg)/[exp]
N(17)–Au(1)–C(4)	178.4/[180.0]	Au(1)–Au(2)–Au(3)	60.00/[60.0]	Au(1)–C(4)–O(5)	123.7/[121.4]
Au(1)–C(4)–N(7)	122.3/[119.4]	N(17)–Au(1)–C(4)–N(7)	0.22/[0.0]
C(4)–N(7)–Au(2)	119.5/[120.6]	Au(1)–C(4)–N(7)–Au(2)	0.01/[0.0]
Complex 2
Bond distances (Å)
Au(1)⋯Au(2)	3.516	Ag(3)–C(14)	2.113	Au(1)–C(4)	2.015
Au(1)⋯Ag(3)	3.503	Au(1)–N(17)	2.088	Au(2)–C(9)	2.013
Au(2)⋯Ag(3)	3.490	Au(2)–N(7)	2.097	Ag(3)–N(12)	2.136
Bond angles (deg)
N(17)–Au(1)–C(4)	176.39	Au(1)–Au(2)–Ag(3)	60.00	Au(1)–C(4)–O(5)	122.42
Au(1)–C(4)–N(7)	122.80	N(17)–Au(1)–C(4)–N(7)	1.22
C(4)–N(7)–Au(2)	122.42	Au(1)–C(4)–N(7)–Au(2)	0.00
Complex 3
Bond distances (Å)
Ag(1)⋯Ag(2)	3.521	Au(3)–C(14)	2.015	Ag(1)–C(4)	2.108
Ag(1)⋯Au(3)	3.524	Ag(1)–N(17)	2.136	Ag(2)–C(9)	2.111
Ag(2)⋯Au(3)	3.526	Ag(2)–N(7)	2.127	Au(3)–N(12)	2.090
Bond angles (deg)
N(17)–Ag(1)–C(4)	175.05	Ag(1)–Ag(2)–Au(3)	60.00	Ag(1)–C(4)–O(5)	124.54
Ag(1)–C(4)–N(7)	121.08	N(17)–Ag(1)–C(4)–N(7)	0.89
C(4)–N(7)–Ag(2)	122.24	Ag(1)–C(4)–N(7)–Ag(2)	−0.36
Complex 4
Bond distances (Å)
Ag(1)⋯Ag(2)	3.549	Ag(3)–C(14)	2.107	Ag(1)–C(4)	2.108
Ag(1)⋯Ag(3)	3.548	Ag(1)–N(17)	2.129	Ag(2)–C(9)	2.109
Ag(2)⋯Ag(3)	3.547	Ag(2)–N(7)	2.128	Ag(3)–N(12)	2.130
Bond angles (deg)
N(17)–Ag(1)–C(4)	175.80	Ag(1)–Ag(2)–Ag(3)	60.00	Ag(1)–C(4)–O(5)	124.00
Ag(1)–C(4)–N(7)	121.64	N(17)–Ag(1)–C(4)–N(7)	4.33
C(4)–N(7)–Ag(2)	122.54	Ag(1)–C(4)–N(7)–Ag(2)	0.15

3.2 NBO charge

The obtained total atomic charge values by natural bond orbital analyses (NBO) are reported in Table 2.As can be seen in the results, all the metal atoms have a net positive charge while nitrogen atoms are negative. The charge of the oxygen atoms is smaller than the charge of the N for all compounds. According to the NBO method, the obtained atomic charge for all complexes shows that the metal atoms have bigger positive atomic charges than the other atoms.

Complex 1	Complex 2	Complex 3	Complex 4
Atom	Charge	Atom	Charge	Atom	Charge	Atom	Charge
Au1	0.365	Au1	0.359	Ag1	0.535	Ag1	0.484
Au2	0.365	Au2	0.351	Ag2	0.540	Ag2	0.484
Au3	0.365	Ag3	0.508	Au3	0.380	Ag3	0.484
C4	0.299	C4	0.298	C4	0.323	C4	0.236
O5	−0.696	O5	−0.698	O5	−0.354	O5	−0.708
N7	−0.875	N7	−0.874	N6	−0.883	N7	−0.889
C9	0.299	C9	0.294	C8	0.335	C9	0.235
O10	−0.696	O10	−0.702	O9	−0.348	O10	−0.708
N12	−0.875	N12	−0.886	N10	−0.876	N12	−0.889
C14	0.299	C14	0.242	N12	−0.871	C14	0.235
O15	−0.696	O15	−0.702	C14	0.377	O15	−0.708
N17	−0.875	N17	−0.881	O15	−0.345	N17	−0.889

Molecular electrostatic potential (MEP) at a point in space around a molecule gives information about the net electrostatic effect produced at that point by the total charge distribution of the molecule[18]. The interaction between the positive charge and some point in the molecule will be attractive if the point is negatively charged; repulsive if it is positively charged, and the strength of interaction will depend on the magnitude of the charge. It is convenient to display this map using the colors of the rainbow from red to blue. Red is the electron-rich end and blue is the electron-poor end.

The MEP surface provides necessary information about the reactive sites. Fig. 2 shows the electrostatic potential counter map of complexes.

Fig. 2
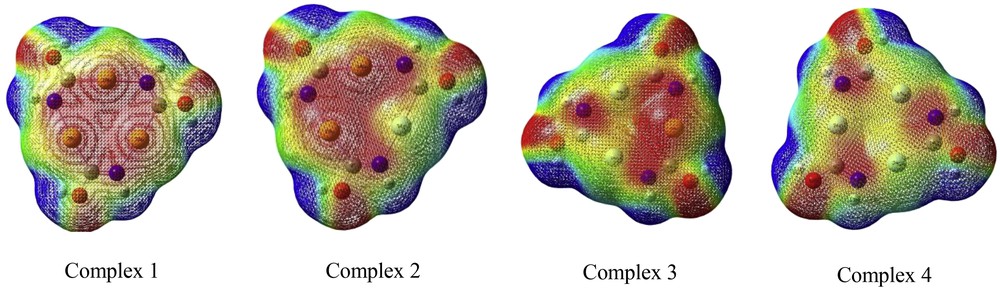
Calculated 3D molecular electrostatic potential contour map of complexes.

3.3 HOMO–LUMO gap

The highest occupied molecular orbitals (HOMOs) and the lowest-lying unoccupied molecular orbitals (LUMOs) are named as frontier molecular orbitals (FMOs). HOMO and LUMO are very important parameters for quantum chemistry. The HOMO and LUMO orbitals are plotted in Fig. 3. In complexes 1,2 and 3,the HOMO belongs to the d atomic orbital of the one gold atom. In complex 4, it belongs to the $d_{z^{2}}$ atomic orbital of the silver atom. Also for all of the complexes, the irreducible representation of the LUMO is shown with e″. As well as the LUMO is located at the carbon and nitrogen atoms, largely.

Fig. 3
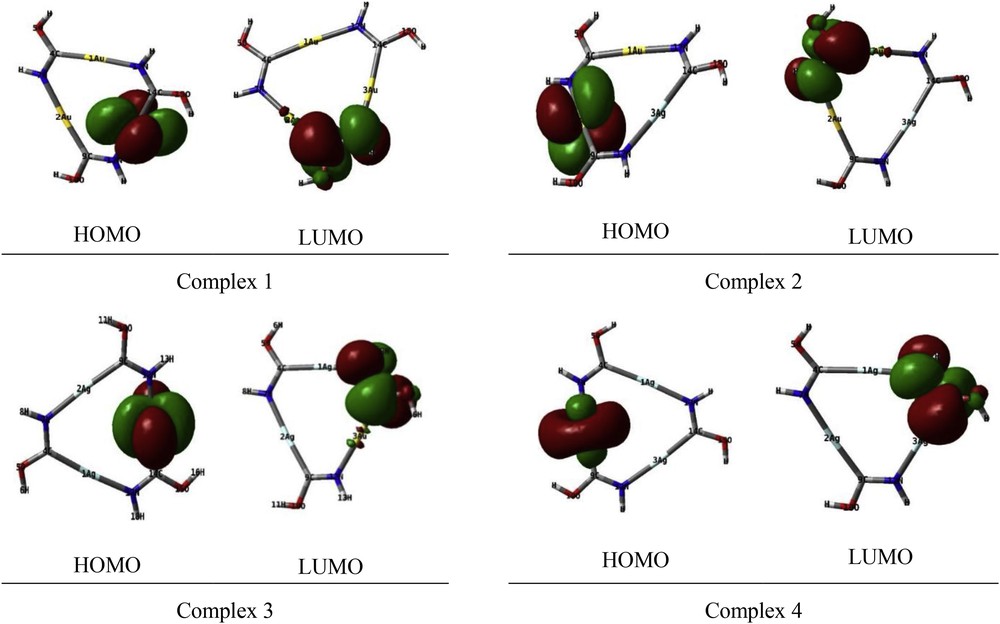
HOMO and LUMO orbitals of complexes.

The computed HOMO–LUMO energy gaps of 1, 2, 3 and 4 complexes were found to be 0.28, 0.30, 0.31 and 0.34 eV, respectively, at the B3LYP/GEN level. Thus the energy gap was found to be significantly increased with increase in the number of silver atoms in the [Au_nAg_m(HNCOH)₃] (m + n = 3) complexes compared to that of complex 1.

3.4 Ionization potential and electron affinity

The ionization potential (IP) is an important parameter to understand the stability towards ejecting out one electron from its HOMO energy level to the continuum. The vertical ionization potentials were computed as the energy required to release an electron from the system at the ground state reference geometry.

The computed first vertical ionization potential of 1, 2, 3, and 4 complexes was found to be 8.50, 8.28, 8.12 and 8.02 eV, respectively. Thus, the first ionization potential is decreased on going from the [Au₃(HNCOH)₃] complex to other [Au_nAg_m(HNCOH)₃] (m + n = 3) complexes; the largest decrease is revealed for the [Ag₃(HNCOH)₃] complex. The vertical electron affinity (EA) of studied systems was also computed. The EA is defined as the amount of energy released when an electron is attached to the system. The computed electron affinities were found to be −0.55, −0.43, −0.39 and −0.32 eV for the 1, 2, 3 and 4 complexes, respectively. Thus, the electron affinity is significantly increased with the increase in the number of Ag atoms.

3.5 Chemical hardness and chemical potential

The computed hardness and chemical potentials of the complexes are listed in Table 3. Chemical hardness[18] which demonstrates the resistance to alteration in electron distribution is given by:

η = \frac{1}{2} (AIP - AEA)

(1)

and is well correlated with the stability and reactivity of the chemical system.

Sample	IP (eV)	EA (eV)	HLG (eV)	Hardness (eV)	Chemical potential (eV)
Complex 1	8.50	−0.55	0.28	4.53	−3.98
Complex 2	8.28	−0.43	0.30	4.36	−3.93
Complex 3	8.12	−0.39	0.31	4.25	−3.86
Complex 4	8.02	−0.32	0.34	4.22	−3.80

Following Parr and Pearson[18], the electronic chemical potential, describing the escaping tendency of an electron from a stable system can be calculated as

μ = - \frac{1}{2} (AIP + AEA)

(2)

We reported here the results of DFT calculations for the global reactivity descriptors (Table 3).The listed values showed that the softest complex was [Ag₃(HNCOH)₃] with the hardness of 4.22 eV, while the maximum hardness of 4.53 eV was found for the [Au₃(HNCOH)₃] complex. The less polarizable species have higher hardness values. The zero hardness corresponds to the most polarizable structure. Considering the chemical hardness, if one molecule has a large HOMO–LUMO gap, it is a hard molecule or if one has a small HOMO–LUMO gap it is a soft molecule. One can also relate the stability of a molecule to hardness, which means that the molecule with the least HOMO–LUMO gap means it is more reactive.

With the Mulliken definition for the chemical potential, the negative μ values correlate with a more stable or less-reactive compound. The μ values (Table 3), indicated that the [Au₃(HNCOH)₃] complex, with μ = −3.98 eV, was the least reactive in this series of compounds. On the other hand, the value of the chemical potential characterizing the most reactive complex, [Ag₃(HNCOH)₃], in this series was −3.80 eV.

The chemical reactivity of [Au_nAg_m(HNCOH)₃](n + m = 3) followed the order of [Au₃(HNCOH)₃] < [Au₂Ag₁(HNCOH)₃] < [Au₁Ag₂(HNCOH)₃] < [Ag₃(HNCOH)₃], which is in agreement with the experimental results. For instance, Hettiarachchi et al. [19] reported the synthesis and characterization of d¹⁰–d¹⁰ heterometallic compounds containing gold and silver, K[Au_xAg_1−x(CN)₂], and compared the results with the corresponding pure systems. They observed that the emission bands in the mixed-metal complexes lay between the emission bands of the pure K[Au-(CN)2] and K[Ag(CN)2].

3.5.1 Second order perturbation analysis

The natural bond orbital (NBO) analysis shows the intermolecular orbital interaction. In this part of study, we examine all possible interactions between donor Lewis-type and acceptor non-Lewis-type NBOs. These interactions lead to donation of occupancy from the localized NBOs of the idealized Lewis structure into the empty non-Lewis orbitals. For this reason, they are denoted as electron delocalization corrections to the zeroth-order natural Lewis structure[20]. The stabilization energy E⁽²⁾ value for each Lewis-type donor (i) and non-Lewis-type acceptor (j), associated with the electron delocalization between i and j (i→j), is estimated as

Δ E_{i - j^{*}}^{(2)} = - 2 \frac{{〈 σ_{i} | \overset{⌢}{F} | σ_{j}^{*} 〉}^{2}}{ɛ_{j} - ɛ_{i}} = - 2 \frac{F_{i j}^{2}}{Δ E}

where

\overset{⌢}{F}

is the effective orbital Hamiltonian and

ɛ_{i} = 〈 σ_{i} | \overset{⌢}{F} | σ_{i} 〉

and

ɛ_{j} = 〈 σ_{j}^{*} | \overset{⌢}{F} | σ_{j}^{*} 〉

acceptor interactions and their stabilization energy. The larger the E⁽²⁾ value the more intense is the interaction between electron donors and electron acceptors, i.e., the more donating tendency from electron donors to electron acceptors and the greater the extent of conjugation of the whole system. The donor–acceptor interaction, however, is considered as an interaction between occupied Lewis orbitals and formally unoccupied non-Lewis orbitals. If any of the values in the E⁽²⁾ column are greater than 20 kcal/mol they are of interest. The important donor–acceptor interactions of complexes are listed in Table 4. The number of donor–acceptor interactions of interest was found to decrease on going from the [Au₃(HNCOH)₃] complex to other [Au_nAg_m(HNCOH)₃] (m + n = 3) complexes. Compared with the other studied complexes, for the complex 2 the BD*(Au1-C4)→LP* Au1 interaction between the Au1-C4 anti-bonding and the Au1 lone pair is the most stable with a stabilization energy of 52.25 kcal/mol.

Sample	Donor NBO (i)	Acceptor NBO (j)	E(2) (kcal/mol)	E(j)–E(i) (a.u.)	F(i,j) (a.u.)
Complex 1	LPO5	BD*(C4-N7)	22.73	0.33	0.111
BD*(Au1-C4)	LP* Au1	23.56	0.03	0.101
LP N7	BD*(Au2-C9)	38.34	0.54	0.184
LP O10	BD*(C9-N12)	22.72	0.33	0.11
BD*(Au2-C9)	LP*Au2	23.39	0.03	0.101
LP N12	BD*(Au3-C14)	38.35	0.54	0.184
LP N17	BD*(Au1-C4)	38.42	0.54	0.184
BD*(Au3-C14)	LP* Au3	23.36	0.03	0.101
Complex 2	LP O5	BD*(C4-N7)	22.58	0.33	0.11
BD*(Au1-C4)	LP*Au1	52.25	0.01	0.097
LPN7	BD*(Au2-C9)	38.28	0.54	0.184
LP O10	BD*(C9-N12)	21.99	0.33	0.109
LP N17	BD*(Au1-C4)	39.64	0.54	0.187
LP O15	BD*(C14-N17)	22.22	0.33	0.109
Complex 3	LP O5	BD*(C4-N7)	21.49	0.34	0.108
LP N7	BD*(Ag2-C9)	20.46	0.53	0.134
LP O10	BD*(C9-N12)	22.12	0.33	0.109
LP N12	BD*(Au3-C14)	39.68	0.54	0.187
LP O15	BD*(C14-N17)	21.88	0.33	0.109
Complex 4	LP O5	BD*(C4-N7)	21.42	0.34	0.108
LP O10	BD*(C9-N12)	21.41	0.34	0.108
LP O15	BD*(C14-N17)	21.41	0.34	0.108

4 Conclusions

In this study, we have performed detailed DFT calculations to study the effect of Ag on the electronic structure and molecular properties of the [Au₃(HNCOH)₃] complex. All the structures are planar. Just the H (hydrogen) atoms are not in the plane. The symmetry point group of these structures is C_3h.

The ionization potential was found to decrease while the electron affinity was found to increase significantly on going from the [Au₃(HNCOH)₃] complex to other [Au_nAg_m(HNCOH)₃] (m + n = 3) complexes; the largest decrease is revealed for the [Ag₃(HNCOH)₃] complex. The [Au₃(HNCOH)₃] complex may protect certain cellular systems which have lower electron affinity and higher ionization potential than that of the studied structures against ionizing radiation and free electrons by ionizing itself or by accepting the electron.

We reported here the results of DFT calculations for the global reactivity descriptors. The results showed that the softest complex was [Ag₃(HNCOH)₃], while the maximum hardness was found for the [Au₃(HNCOH)₃] complex. The μ values indicated that the [Au₃(HNCOH)₃] complex was the least reactive in this series of compounds. Also the donor–acceptor interactions of complexes were investigated.

Acknowledgments

Financial support from the University of Mazandaran is gratefully acknowledged.

Bibliographie

[1] R.K. Das; B. Saha; S.M.W. Rahaman; J.K. Bera Chem.—A Eur. J., 16 (2010), pp. 14459-14468

[2] A.A. Mohamed; R. Galassi; F. Papa; A. Burini; J.P. Fackler Inorg. Chem., 45 (2006), pp. 7770-7776

[3] A.A. Mohamed; A. Burini; J.P. Fackler J. Am. Chem. Soc., 127 (2005), pp. 5012-5013

[4] H.Z. Boon; K. Teo; Xiaobo Shi J. Am. Chem. Soc., 114 (1992), pp. 2743-2745

[5] K.T. Boon; K. Keating Am. Chem. Soc., 106 (1984), pp. 2224-2226

[6] B.K. Teo; H. Zhang; X. Shi Inorg. Chem., 33 (1994), pp. 4086-4097

[7] B.K. Teo; H. Zhang; X. Shi J. Am. Chem. Soc., 115 (1993), pp. 8489-8490

[8] M.A. Rawashdeh-Omary; M.A. Omary; J.P. Fackler Inorganica Chim. Acta, 334 (2002), pp. 376-384

[9] V.J. Catalano; S.J. Horner Inorg. Chem., 42 (2003), pp. 8430-8438

[10] J.E. Parks; A.L. Balch J. Organomet. Chem., 71 (1974), pp. 453-463

[11] F.B. Giovanni Minghetti; Guido Banditelli Inorg. Chem., 18 (1979), pp. 658-663

[12] J.C. Vickery; M.M. Olmstead; E.Y. Fung; A.L. Balch Angew. Chem., Int. Ed. Engl., 36 (1997), pp. 1996-1998

[13] E.J. Ferna; M. Concepcio; A. Laguna; M. Lo; M. Monge; P. Pyykko J. Am. Chem. Soc., 122 (2000), pp. 7287-7293

[14] E.J. Fernández; P.G. Jones; A. Laguna; J.M. López-de-Luzuriaga; M. Monge; J. Pérez; M.E. Olmos Inorg. Chem., 41 (2002), pp. 1056-1063

[15] E.J. Fernández; A. Laguna; J.M. López-de-Luzuriaga; F. Mendizabal; M. Monge; M.E. Olmos; J. Pérez Chem. Eur. J., 9 (2003), pp. 456-465

[16] F. Mendizabal; B. Aguilera; C. Olea-Azar Chem. Phys. Lett., 447 (2007), pp. 345-351

[17] L.E. Sansores; R. Salcedo; A. Martínez; N. Mireles J. Mol. Struct. Theochem, 763 (2006), pp. 7-11

[18] R.G. Parr; R.G. Pearson J. Am. Chem. Soc., 105 (1983) no. 26, pp. 7512-7516

[19] S.R. Hettiarachchi; B.K. Schaefer; R.L. Yson; R.J. Staples; R. Herbst-Irmer; H.H. Patterson Inorg. Chem., 46 (2007) no. 17, pp. 6997-7004

[20] J. Chocholoušová; V. Špirko; P. Hobza Phys. Chem. Chem. Phys., 6 (2004), p. 37

Commentaires - Politique