1. Introduction

Cavitation is related to the growth and the collapse of vapor bubbles or vapor clouds in a liquid. The vaporization of the liquid and the condensation of the vapor are thermodynamic changes of phase of the fluid, involving absorbed and emitted latent heat respectively. Mechanical effects induced by the collapses are also likely to occur. Cavitation differs from boiling in the fact that cavitation results from a pressure drop below vapor pressure at a fixed temperature, when boiling results from an increase of temperature above the temperature of saturation, at a fixed pressure.

Acoustic cavitation occurs when oscillating vapor bubbles are induced by acoustic excitation, and monitored at ultrasonic frequencies ranging from 20 kHz to 1 MHz. A global rectified diffusion of matter from the surrounding liquid toward the bubble, during the expansion phases, enhances an increase of the average size of the bubble until a critical radius, that depends on the frequency and on the acoustic pressure, and above which the collapse of the bubble occurs. The consequences of the collapse depend on the frequency, on the intensity of the pressure field, on the presence of dissolved gases, and on the temperature. Imploding cavities often involve the formation of high-pressure shock waves, and extreme temperatures and pressure may be reached. This might not necessarily result in the formation of a supercritical fluid inside the bubble, therefore supercritical oxidation is not a typical outcome in imploding cavities. Low frequency cycles produce large sized bubbles, giving way to violent collapses. As a consequence, some uncondensed water molecules are splitted and produce hydroxyl radicals ⋅OH. High frequency cycles induce smallest bubbles that collapse with a weaker intensity, but they generate more events and they can help for diffusion of radicals toward the liquid. Hydroxyl radicals can recombine and produce H₂O₂. In contrast, when adding H₂O₂ in the liquid, reaction rates increase [1]. Depending on the hydrophilic or hydrophobic nature of a possible pollutant, the optimum working frequency should be a balance between low or high acoustic frequency. Sonoluminescence is another consequence of the collapse, that is caused by the ionization of rare gases present in the core of the bubbles. It should be noted that the best conditions to observe sonoluminescence are not similar to those enhancing sonochemical activity.

Hydrodynamic cavitation is the consequence of the Bernoulli law, when a flowing liquid passes through a local constriction. The increase of the dynamic pressure 1∕2 ⋅𝜌 u², where 𝜌 is the density of the fluid and u its average velocity, goes with a decrease of the static pressure p, as illustrated in Figure 1. Downstream the constriction, where the velocity of the flow recovers a lower value, the static pressure increases but reaches a smaller level than upstream, because of the singular pressure loss due to the constriction. Inception of cavitation becomes possible if the pressure value falls below a threshold value, which is generally the vapor pressure p_vap. Vapor bubbles and vapor clouds, which arise in the low pressure area, collapse downstream where the static pressure has raised above p_vap.

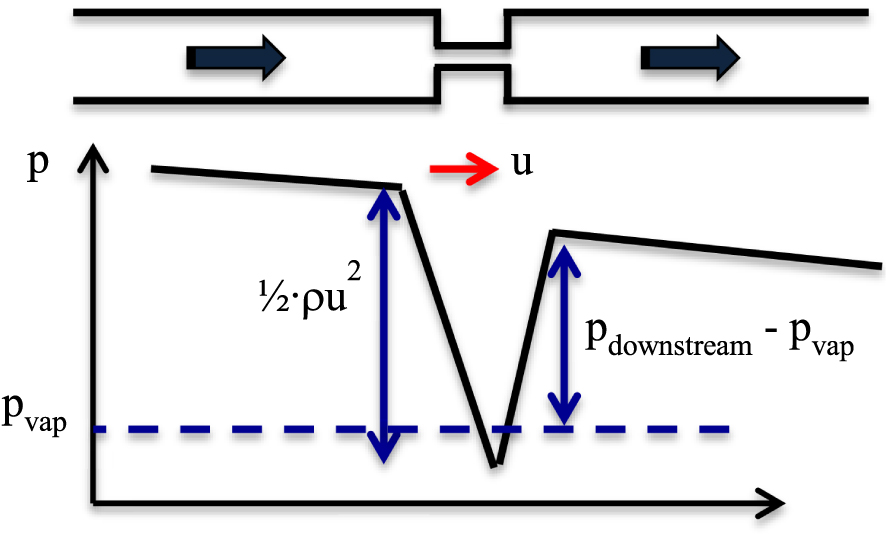
Different flow regimes can induce cavitation: around an emerging liquid jet, around a hydrofoil, through an orifice or a diaphragm, through the throat of a venturi. Shear cavitation is induced in low pressure vortices in shear flows; sheet cavitation appears as a vapor pocket emitting bursts of vapor clouds at a shedding frequency that has no relation with the frequency monitored in ultrasonic cavitation (Figure 2).

Hydrodynamic cavitation is simple to execute. However, the physics of the growth and collapse of multiple cavitating bubbles in a hydrodynamic flow is drastically more complex than in ultrasonic reactors. A cavitation number, noted 𝜎, is a dimensionless parameter that can be used to quantify the possibility for cavitation to occur in a fluid flow system. With the notations of Figure 1, 𝜎 is defined here by:

2. Chemistry induced by hydrodynamic cavitation

Twenty-five years ago, Suslick and co-workers underlined that reports on chemistry induced by hydrodynamic cavitation had been extremely limited [4]. They tested the Weissler reaction, as a dosimeter for chemical reactions, with a solution passed through a high pressure microfluidizer in which cavitation was likely to occur, with working pressures running from 100 bars to 1300 bars. The tri iodide formation rate increased linearly with the upstream pressure. The respective influence of dissolved gases and liquid temperature were also considered, and led to evolutions similar as those observed in acoustic cavitation. That was the first firm demonstration of chemical similarities between acoustic and hydrodynamic cavitation. Unfortunately, the flow rates were not expressed in the paper, and it is not possible to evaluate the hydraulic powers involved in these experiments. Later, Kalumuck and Chahine tested the degradation of p-nitrophenol aqueous solutions in both acoustic and hydrodynamic reactors [5]. They compared the power of the hydraulic set up to the calorimetric power of the acoustic reactor, and concluded to a better efficiency of the hydraulic reactor. Temperature and pH effects highlighted the same trends, in acoustic and hydrodynamic cavitating regimes. The cavitating jet was monitored up to 65 bars. Comparing the application of cavitation reactors for water disinfection, Gogate [6] enhanced an empirical arrangement of multiholes on a plate, taking into account the relative free area offered to the flow. General conclusions were not supported by quantitative values of parameters such as inlet pressure or average maximum velocity. Perhaps in order to treat flow rates higher than what is reachable with high pressure fluidizers, the subsequent efforts, which were consacred, used mild experimental conditions. Wang et al. studied the degradation of rhodamine B using swirling jet-induced cavitation, at an inlet pressure of 6 bars and a hydraulic power of around 600 W [7]. Brauetigam et al. used a design inspired by the multiholes scheme [8, 9] working on a very limited inlet pressure range (from 1.4 bars to 2.6 bars [8], and then up to 10 bars [9]), with hydraulic powers between 60 W and 80 W. They noticed that the centrifugal pump present in the loop could be a source of cavitation, in competition with the reactor. Capocelli et al. undertook simulation and experimental comparison of chemical effects of hydrodynamic cavitation in a Venturi reactor [10]. They conducted degradation tests on p-nitrophenol between 2 bars and 6 bars, and observed a maximum efficiency around 4.5 bars. That optimum was correlated to similar trends obtained by other groups, but with other reactors and other pollutants. Zupanc et al. performed a broad study of shear-induced hydrodynamic cavitation as a tool for pharmaceutical pollutants removal [11]. They stated that the amount of free radicals is related to the aggressiveness of the cavitation, and that shear induced cavitation is more aggressive than sheet cavitation that is formed in the throttle of a Venturi. That conclusion is not shared by Rajoriya et al. [12] who have observed a higher degradation rate of orange-G dye when using slit Venturi at an optimum pressure of 3 bar. The authors state that cavitation in a Venturi profile results into a large magnitude collapse, as long as a choked cavitation regime is not reached. The authors present also an overview of experimental results devoted to waste water treatment by hydrodynamic cavitation through Venturi and orifice nozzles.

A larger spectrum of references may also be found in a short review article published by Tao et al. in the same year of 2016 [13], and more recently by Das et al. [14]. The authors review the possible reactors geometries and list the main operating parameters that are inlet pressure, bulk liquid temperature, effect of pH and of initial pollutant concentration, effect of the initial radius of the nuclei, effect of the surface tension. They agree that qualitative results have been obtained, but they underline the lack of quantitative analysis. Each research team has developed a self-made reactor used to degrade a given pollutant, and it is difficult to draw general conclusions for such a set of data. Similar conclusions have been drawn in most recent review articles [15, 16]. Ciriminna et al. stress that the chemical effects of hydrodynamic cavitation are the consequence of hydroxyl radical formation, and that a direct measurement of such a concentration is hardly possible due to their high reactivity [15]. Hydroxyl radicals are short-lived oxidants that degrade within nanoseconds [17]. Therefore, it is difficult to detect them directly. The dosimetry of hydroxyl radicals comes from indirect measurement, funded on chemical reactions involving new products, or on the emission of light.

3. Dosimetry of hydroxyl radicals produced by hydrodynamic cavitation

Different dosimetry methods have been developed in sonochemistry in order to quantify the chemical activity and the amount of hydroxyls radicals produced by cavitation. Most of them have then been tested in hydrodynamic cavitating flows. The reliability of these techniques, that can only detect radicals which have not been involved in recombination, is still an open question in sonochemistry [18]. The data concerning dosimetry of hydrodynamic cavitating flows are equally scattered.

Iodide dosimetry has been largely used as a test reaction. It has been inspired by the Weissler reaction, where the yield of iodine is proportional to the time of ultrasonic irradiation. When potassium iodide KI is initially present in the solution submitted to cavitation, iodide can scavenge the hydroxyl radicals ⋅OH and form the tri iodide I₃⁻, which is detected by UV visible absorbance at 𝜆 = 353 nm [19, 20]. Otherwise, a part of the processed solution may be withdrawn and mixed with a KI solution. The oxidation of iodide to tri iodide I₃⁻ is then caused by hydroxide peroxide H₂O₂ resulting from the recombination of hydroxyl radicals [21].

But iodide dosimetry is non-specific to ⋅OH radicals, since iodide ions may be oxidised by other radicals and by hydrogen peroxide. The presence of saturated oxygen in the cavitating liquid is likely to help the formation of peroxide hydrogen, and to overestimate the amount of hydroxyl radicals generated by cavitation. Moreover, in a global study devoted to compare the respective efficiencies of acoustic and hydrodynamic cavitation, Morison and Hutchinson enlightened the presence of a consumption reaction in hydrodynamic flows, leading to a limit of the I₃⁻ concentration [20]. That could explain why experiments of Suslick et al. [4] could detect tri-iodide only above very high input pressures. Such a consumption of tri iodide ions occurred even if the flow was driven below the onset of cavitation, but was not present in acoustic cavitation. Their conclusion stated that the Weissler reaction is not reliable in order to know the effectiveness of hydrodynamic cavitation as an advanced oxidizing process.

The Fricke dosimetry is funded on the oxidation of Fe²⁺ to Fe³⁺ [22]. As for the Weissler reaction, other species than ⋅OH radicals may be responsible for the oxidation reaction. Terephtalic acid TA has been used as an ⋅OH radical scavenger [23, 24]. The reaction forms hydroxyterephtalic acid (HTA), which is strongly fluorescent and stable for hours. Terephtalic acid dosimetry is presented as specific for hydroxyl radicals [23]. Matthews, working on the radiation chemistry of the terephtalic dosimeter, observed that the yield of HTA is affected by the oxygen concentration [25]. Oxygenation increases HTA, but in a solution sparged with nitrogen gas, the yield of HTA falls. In acoustic cavitation, the fact that a very low ⋅OH yield is obtained by this dosimetry method is still an open question [18]. In hydrodynamic cavitation, Wang et al. [7] used TA dosimetry to conclude to a synergetic effect between cavitation and H₂O₂ for the degradation of rhodamine B, with fluid pressures ranging from 2 to 6 bars.

Arrojo et al. proposed the application of salicylic acid dosimetry to characterize both ultrasonic and hydrodynamic cavitation [23]. The reaction with ⋅OH produces mainly 2,5 DHB (dihydroxybenzoic acid), that is fluorescent. The reactor was a venturi, developing a hydraulic power around 500 W at a maximum inlet pressure of 4.7 bars. The authors underlined that as salicylic acid is hydrophobic, molecules should migrate toward the bubbles interface. That would enhance the trapping efficiency, as the life time of ⋅OH is very short. A new question then arises, that is to know the ratio between the real number of hydroxyl radicals initially present inside collapsed bubbles, and the effective number of radicals able to react with a hydrophobic or with a hydrophilic molecule present in the liquid phase. Salicylic acid dosimetry was also used by Amin et al. [26], who tested different shapes of orifices (circular, ellipsoidal, rectangular). But unfortunately, there is a lack of hydrodynamic data (such as pressure drop/flow rate relationships, critical pressure drop above which the onset of cavitation occurs), that cannot be related to chemical activity and to the related measurements. More recently, Zupanc and co-workers [27] used salicylic acid dosimetry with a Venturi equipped with a rectangular slit. They highlighted the fact that an excessive concentration of salicylic acid should negatively affect the surface tension and, as a matter of fact, the violence of the collapse. Care must be taken, so that the scavenger should not affect the radical production.

Coumarin dosimetry has been recently used in cavitation. After an exposition to ultrasound waves at 500 kHz, an aqueous coumarin solution has produced hydroxylated products and has presented a decrease of the absorbance of coumarin, that are the consequence of reactions with hydroxyl radicals [28]. Among these products, umbelliferone (also named hydroxylated 7-hydroxycoumarin, 7-OHC) is fluorescent. Coumarin was then used by Srinivas et al. [29] and by De-Nasri et al. [30] to quantify the ⋅OH radical generation in hydrodynamic cavitating vortex diode reactors. Coumarin was also used for the detection of radicals in irradiated solutions [31]. Once again, it is not obvious to know the exact relationship between the amount of ⋅OH molecules involved in the reaction producing the fluorescent 7-OHC component, and the total number of ⋅OH radicals.

A variety of other methods have been published. For example, the transformation of benzene into phenol due to the reaction with hydroxyl radicals can be used as a dosimeter [32]. The correlation between dye degradation experiments, with Congo red used as a reference substance, and chemiluminescence of luminol was used to evaluate degradation effects and cavitation intensity [33].

4. Chemiluminescence of luminol

The above dosimetry methods require a regular extraction of the liquid under test, and do not provide any information neither about the fluid mechanism conditions nor about the localization of the chemical activity. An indirect determination of the presence of ⋅OH hydroxyl radicals and an in-situ visualisation of their localization, may be performed with luminol aqueous solutions. It is known for a long time that aqueous solutions of luminol emit light when exposed to acoustic waves, which are strong enough to generate cavitation, and that such a chemiluminescence results from reactions with hydroxyl radicals [34]. Chemiluminescence of luminol has also been enhanced in single bubble sonoluminescence experiments [35]. The method of chemiluminescence of luminol gives a statement about the spatial distribution of the reaction area and is suitable as a marker for the spatial characterization of the hydroxyl radical concentration, which is also quantifiable for measurements. The observation of the intensity of the radical production becomes possible inside devices equipped with optically transparent walls, because when cavitation occurs and hydroxyl radicals are formed, the decomposition of luminol emits visible blue light above the UV-spectrum.

Surprisingly, using luminol as the working fluid in hydrodynamic cavitating experiments has been firstly presented only six years ago [36]. Gathering relatively high volumes of solution together with transparent reactors able to withstand high pressure levels, is perhaps the reason why there has been such a delay between acoustic and hydrodynamic cavitation experiments using luminol. The measurement of chemiluminescence of luminol is now a well-established proof for hydroxyl radical production by hydrodynamic cavitation even if the number of papers dealing with luminol cavitating flows remains up to now limited. On the one hand, several experiments have been performed under moderate pressure drops through microchannels (hydrodynamic cavitation “on a chip”) [37, 38, 39] and mini channels [40]; on the other hand, another set of experiments at macroscale and under inlet pressures up to 40 bars have been published [33, 41, 42].

The existence of luminescent scavengers of hydroxyl radicals makes possible to count emitted photons directly. However, the relationship between the number of radicals reacting with luminol and the number of collected photons is not obvious. Chemistry of the oxidation of luminol is complex and the emission of light requires both the presence of hydroxyl radicals together with superoxide anion O₂^−° [43, 44]. As a matter of fact, the deficit of superoxide O₂^°−, even if ⋅OH are still present, will stop the luminescence, and one should underestimate the number of ⋅OH radicals. Moreover, when using a photomultiplier tube (PMT) as a photon detector, one has to take into account the correction due to the collection solid angle, the global quantum efficiency of the photocathode of the PMT for the chemiluminescent spectrum, the quantum yield of the luminol chemiluminescence reaction. Whatever the size of the reactor is, the test rig must be completely darkened in order to capture the relatively weakly emitted light. The knowledge of a number of radicals detected during one second, and the knowledge of the hydraulic power required to drive the flow make possible the calculation of the so-called G-value, that is the number of ⋅OH moles produced per Joule of consumed energy. By working with hybrid silicon-Pyrex micro channels with a micro diaphragm inside, Podbevsek et al. calculated a minimum radical production of ≈ 6 × 10⁶ ⋅OH/s for a hydraulic power of ≈ 0.4 W, that corresponds to G ≈ 2.50 × 10⁻¹⁷ mole/J [37].Similar G-values were also recorded with another opto-electronic set up and with other micro reactors (microdiaphragms and micro steps profiles) developing shear rate cavitation [38]. Recently, the chemiluminescence emitted from a larger set of micro- and mini hydrocavitating reactors has been investigated [40]. The devices presented semi convergent–divergent constrictions, with hydraulic diameters ranging from 100 μm to 540 μm. For the largest diameter, the maximum recorded flow rate was 50 L/h under a driving pressure of 10 bars. The flow dynamics was rather different from that inside micromachined silicon-Pyrex devices, because cloud shedding was present at frequencies ranging from 150 Hz to 1400 Hz. It is noteworthy to find that the G-valuescalculated from the reactive oxidising species production were similar (3.6 × 10⁻¹⁷ moles/J  < G < 6 × 10⁻¹⁷ moles/J) to those calculated from former experiments. Moreover, the radical production exhibits a linear evolution as a function of the hydraulic power, and no scale effect was noticeable: the G values of the microreactors were roughly similar to the G values of the minireactors. For a small as for a large device, the G-value was the highest for the smallest constriction under test. To our knowledge, only Arrojo et al. had up to now calculated a G-value from hydrocavitation experiments, and found G ≈ 10⁻¹² mole/J with salicylic acid as a scavenger used in a Venturi [23]. There are five orders of magnitude between these respective G-values. The microfluidics experiments of Podbevsek et al. [37, 39] and of Perrin et al. [38] were mainly devoted to demonstrate the effective presence of hydroxyl radicals inside cavitating flows, and they were performed just above the critical flow rate corresponding to the inception of cavitation, when the cavitating flow was not fully developed. But the recent results obtained at larger scale confirm the former G values [40]. Possible explanations are as follows: the value of the quantum yield of luminol is under evaluated; the luminescence is limited by the superoxide anion production; the hydrophobic salicylic scavenger react with a larger number of radicals, which have disappeared when using luminol. Anyway, complementary experiments at micro and miniscale, with complementary geometries, are scheduled in order to draw firm findings.

Even if chemiluminescence of luminol cannot provide the real number of hydroxyl radicals, it makes possible a mapping of the chemical activity together with a mapping of the two-phase liquid-vapor flow. Supporting the fact that cavitation occurs inside a “lab on a chip”, Podbevsek et al. used a confocal microscope set up to draw a local mapping of the chemiluminescent intensity, enhancing local gradients of intensity. Such mappings could be compared to void fraction mappings, also obtained from confocal microscopy with fluorescent hydrophilic nanotracers [39]. An example of a chemiluminescent mapping is presented in Figure 3, with a snapshot of the corresponding two-phase flow. The main conclusion was that the area where the maximum chemical activity was recorded (due to the presence of both ⋅OH and O₂^−° radicals) is located just downstream the area where the cavitation clouds collapse.

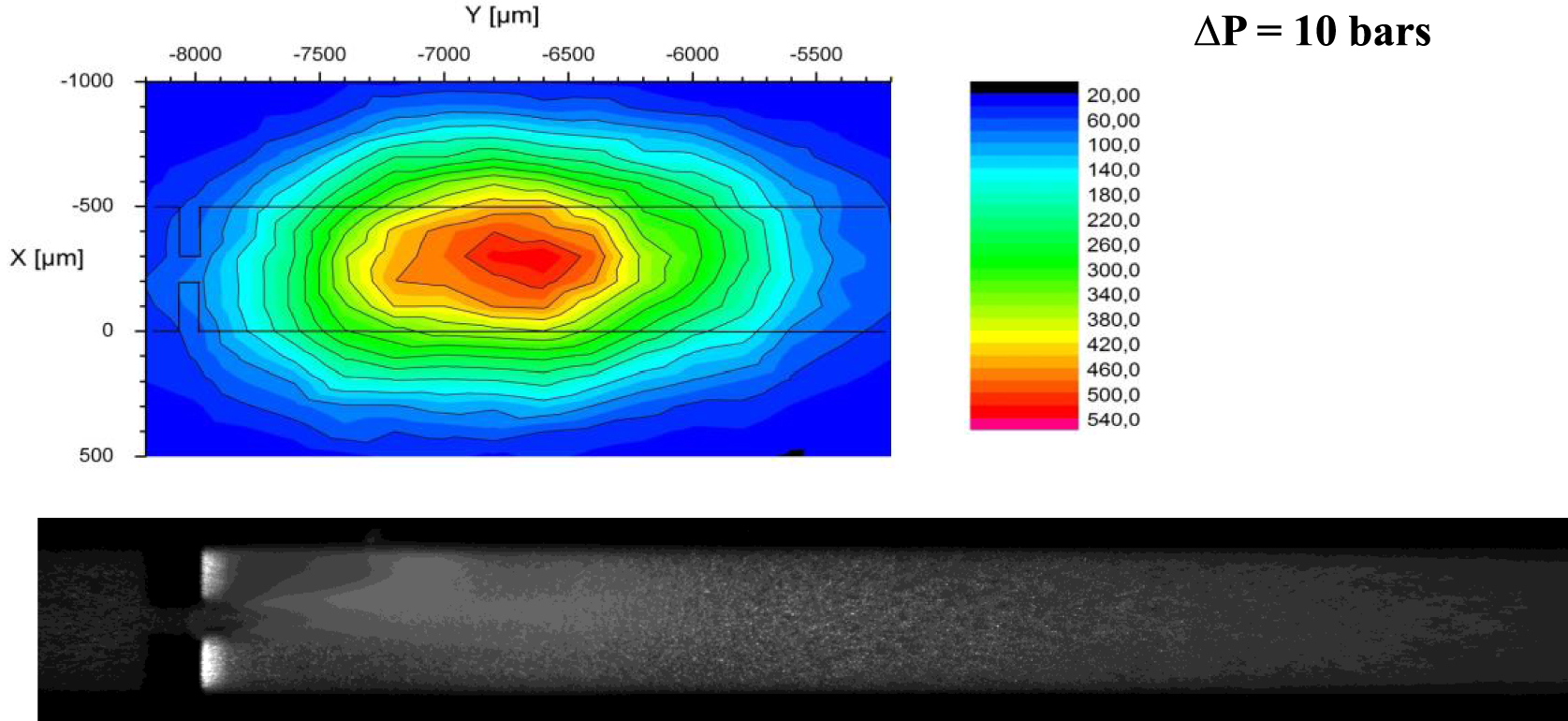
A correlation between the volume of chemiluminescence due to luminol and the volume of cavitation has been studied by Deggelmann et al. [42] and Nöpel et al. [33, 41], but on a larger scale. The authors applied the method of chemiluminescence of luminol, which occurs in the visible range of light due to the reaction with hydroxyl radicals. The emitted light was then recorded with a digital SLR camera.

The investigations about the luminescent area and the cavitating vapor cloud were performed initially in a cylindrical reactor with an inner diameter of 15 mm and a length of 100 mm [41, 42]. The flow was accelerated through a circular orifice with diameter sizes of d = 1 mm or d = 1.7 mm. In [33] same orifice diameters were adapted, but the configuration changed to a rectangular reactor with a cross-sectional area of 15 × 15 mm², leading to less light distortion due to curved surfaces. The measurement configuration of recording the chemiluminescence consisted of a digital SLR camera and a light sensitive lens, which was aligned orthogonally to the reactor walls.

The experimental setup with the reactor was shielded from external light influence. In this darkened room, blue light emission from the chemiluminescence of luminol was recorded by long exposure times of 5 min [41] to 10 min [42]. This method is relatively inexpensive and straightforward to perform. The solution here consisted of 2 g/l luminol and 7.5 g/l sodium hydrogen carbonate, which are both dissolved in deionised water by stirring. The solution has a pH value of pH = 9.3 [41].

The method of measuring the chemiluminescence of luminol involved the digital single lens camera recording an integral value of the blue light emission over the exposure time and space. Figure 4 shows the distribution of vapor bubbles (top) and the distribution of light emission of chemiluminescence by luminol reacting with hydroxyl radicals [33]. In Nöpel et al. [33, 41] the exposure time was set to 5 min without additional substances. A camera with a light sensitive lens (Canon EOS 650D, EF 50 mm 1:1.8 STM) was used for this purpose. A different camera and lens (Canon EOS 1100D, EF-S 18–55 mm IS II) was used in [42] and exposure time was set to 10 min resulting in different area sizes. Also a low amount V = 1 ml of hydrogen peroxide solution (30%) of was added in [42], which enhanced the reaction. The changes towards smaller areas were noted in [42]. This was due to the different measurement equipment.

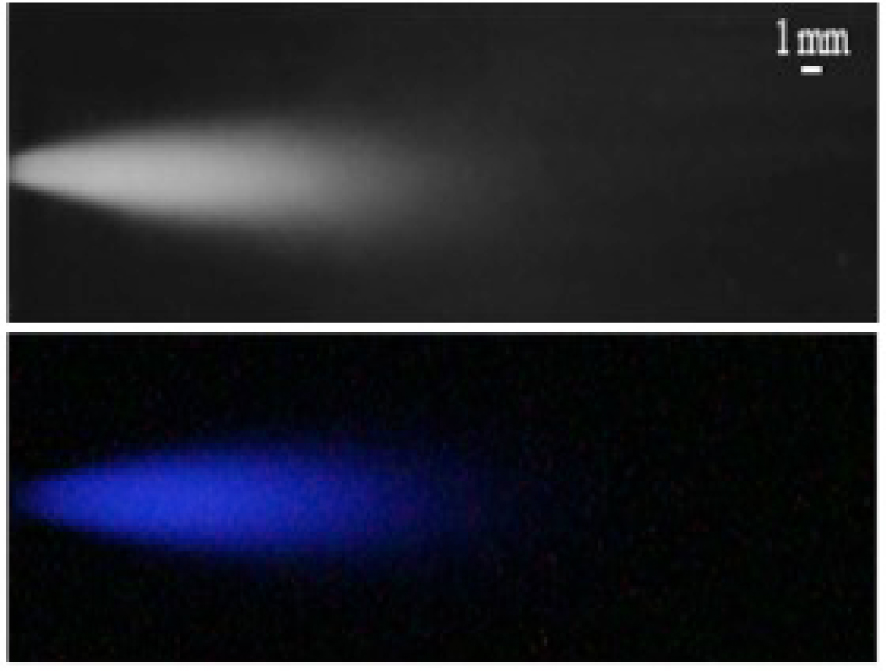
The original images are first brightened and binarized, all similarly, using a threshold for evaluation. From the binary images, the pixel area of the blue light emission can be determined, which represents two-dimensional information about the reaction area. Based on this information, the length extent of the area is used to calculate an approximate volume in which reactions are assumed to be occurring [41].

Figure 5 displays the dependency of the reaction volume marked by chemiluminescence over hydraulic power input. The inception of cavitation occurred at 𝛥p = 7 bar for d = 1 mm. For pressure differences below 10 bar, no light was recorded since the cavitation area was short and vapour density optically low. From 10 bar to 30 bar the optically visible volume of chemiluminescence increases nearly linear.

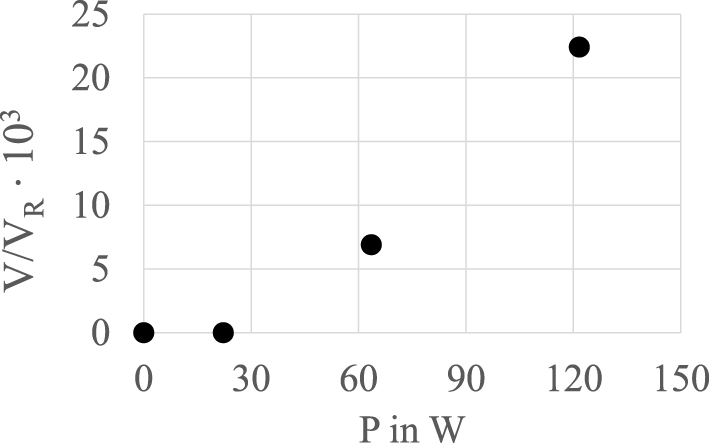
The higher the pressure difference 𝛥p or the hydraulic power P, the greater the cavitation volume of gas bubbles. A larger volume of cavitating bubbles leads to a higher implosion rate, which must tend to produce more radicals. However, the pressure difference increases the fraction of vapour and air bubbles. This may result in differences in the spatial extent of the recorded area of chemiluminescence due to scattering and reflexion of light by the gas fraction. This causes a certain limitation for the application of measuring the strength of cavitation for degradation. In [33] the method is used to proof the occurrence of oxidation as the leading mechanism of degradation.

5. Conclusion

The production of hydroxyl radicals in cavitating flows has been attested by an amount of experiments, each of them performed with a specific hydraulic set up and with a fixed chemical scavenger. Compared with ultrasonic cavitation, that involves a relatively limited number of parameters, hydrodynamic cavitation may be monitored in a lot of kinds of devices, under different complex flow regimes. The number of publications related to chemical activity in hydrodynamic flows has increased these past last years, because possible applications to wastewater treatments are timely. Concerning the hydroxyl radical production, the pros and cons of related scavengers have been now assessed. Recent progresses with luminescent scavengers have made possible live and in-situ observations, facilitating coupled studies between chemistry and fluid mechanics. If the rare quantitative data published up to now agree with the fact that hydrodynamic cavitation could display a low radical efficiency, it is nevertheless believed that any further research programs should develop an experimental, structured and multidisciplinary strategy, in order to reach a full understanding of the physics inside collective collapsing bubbles. For each kind of hydraulic device, the largest number of scavengers should be used and compared, for different cavitating flow regimes. Reciprocally, each scavenger should be tested in different devices, at different scales, and submitted to shear and to sheet cavitation. Ideally, every experiment could be managed in order to rise a quantifiable radical efficiency, expressed in ⋅OH moles/J, that would be a common reference for any comparison.

Conflicts of interest

Authors have no conflict of interest to declare.

Acknowledgments

The authors gratefully acknowledge the support provided by their respective laboratories. Considerable appreciation shall be expressed to Professor J. Fröhlich, Director of the institute and Head of the chair of fluid mechanics and Dr. F. Rüdiger, Head of the group of experimental fluid mechanics, who provided the opportunity for experimental research on cavitating multiphase flows at the institute of fluid mechanics of the TU Dresden. FA, from the Laboratoire des Ecoulements Géophysiques & Industriels, expresses his sincerest appreciation to Dr. L. Perrin, Dr. D. Colombet, Dr. D. Podbevsek and Dr. G. Ledoux for the useful help and effective collaborations that have led to the success of sophisticated experiments devoted to hydrodynamic cavitation on a chip.