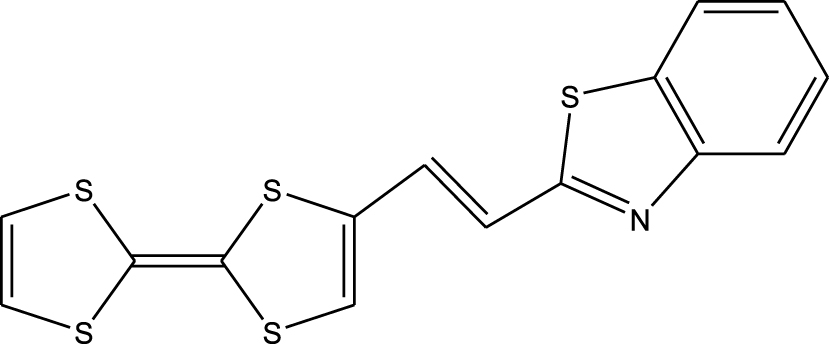
1. Introduction
Tetrathiafulvalene (TTF) and its derivatives, as substituted olefins, are known from both experimental [1] and theoretical data [2] to have excellent donor properties. This is also confirmed by the stable mono-cationic (TTF+∙) and di-cationic (TTF2+) oxidized derivatives obtainable via two sequential and reversible oxidation processes. These capabilities importantly allow useful applications in the chemistry of materials [3], conductors [4] and superconductors [5], adducts with C60 [6, 7], conductive polymers [8], materials for non-linear optics (NLO) [9, 10], cationic sponges [11], ferromagnetic organic magnets [12], liquid crystals [13], dendrimers [14], molecular rotaxanes and catenanes [15]. Recently, TTF-based molecular systems with electron donor (D) and acceptor (A) groups have attracted considerable interest as dyads (D–A). These are used as fluorescence switches such as TTF-PPD (2,5-diphenyl-1,3,4-oxadiazole), which shows strong fluorescence and can be used as an antenna for photoexcitation [16], chemical sensors, molecular rectification, and photovoltaic and NLO applications [17, 18, 19, 20, 21, 22]. This paper mainly aims at a complete description of the molecular geometry and molecular vibrations of the tetrathiafulvalene-1,3-benzothiazole (TTF–CH=CH–BTA) molecule, already discussed in the literature [23, 24, 25] and presented in Scheme 1. In this molecule, TTF was selected as the donor because of the aforementioned properties of its derivatives and the 1,3-benzothiazole ring, which is an essential part of photofunctional organic materials.
In addition, the ultraviolet-visible (UV–Vis) spectroscopic studies along with a highest occupied molecular orbital - lowest unoccupied molecular orbital (HOMO–LUMO) analysis may account for charge transfer effects in the present molecule. In particular, the polarization and charge transfer properties were determined by calculating the atomic polarizability tensor (APT) charges, the molecular electrostatic potential (MEP) and the non-linear optical parameters. The latter, which includes the dipole moment, polarizability and first hyperpolarizability of the molecule, was established in order to gain deeper knowledge about the relationship between molecular architecture and non-linear response, similarly to the work done by other authors [26, 27]. Finally, the natural bond orbital (NBO) method has been applied to analyze the stability of the molecule arising from hyperconjugative interaction and charge delocalization.
Optimized geometric parameters of TTF–CH=CH–BTA
| Bond length (A°) | Calcul | Exp | Angle (°) | Calcul | Exp | Dihedral angle (°) | Calcul | Exp |
|---|---|---|---|---|---|---|---|---|
| S(1)–C(1) | 1.763 | 1.708 | C(6)–C(5)–C(7) | 123.9 | 125.6 | C(7)–C(5)–C(6)–S(4) | 179.0 | 178.9 |
| S(1)–C(3) | 1.786 | 1.752 | S(3)–C(5)–C(7) | 120.5 | 119.0 | S(3)–C(5)–C(7)–C(8) | −5.3 | 1.8 |
| S(2)–C(2) | 1.763 | 1.734 | C(5)–C(7)–C(8) | 125.9 | 124.5 | C(5)–C(7)–C(8)–C(9) | 179.3 | 175.8 |
| S(2)–C(3) | 1.786 | 1.757 | C(7)–C(8)–C(9) | 125.7 | 126.2 | C(7)–C(8)–C(9)–S(5) | −0.9 | 7.9 |
| S(3)–C(4) | 1.782 | 1.756 | C(8)–C(9)–S(5) | 122.5 | 121.6 | C(7)–C(8)–C(9)–N | 179.1 | 172.4 |
| S(3)–C(5) | 1.787 | 1.744 | C(8)–C(9)–N | 122.6 | 123.5 | C(8)–C(9)–S(5)–C(11) | 179.9 | 179.5 |
| S(4)–C(4) | 1.785 | 1.761 | S(5)–C(9)–N | 114.9 | 114.9 | N–C(9)–S(5)–C(11) | −0.1 | 0.9 |
| S(4)–C(6) | 1.746 | 1.718 | C(11)–C(10)–N | 115.6 | 115.6 | C(8)–C(9)–N–C(14) | −179.9 | 178.8 |
| C(1)=C(2) | 1.337 | 1.302 | C(10)–C(11)–S(5) | 109.3 | 108.9 | S(5)–C(9)–N–C(14) | 0.1 | 1.4 |
| C(3)=C(4) | 1.350 | 1.309 | C(9)–S(5)–C(11) | 88.5 | 90.0 | C(15)–C(10)–C(11)–C(12) | 0.0 | 2.0 |
| C(5)=C(6) | 1.354 | 1.335 | C(9)–N–C(10) | 111.7 | 110.6 | C(15)–C(10)–C(11)–S(5) | 179.9 | 177.7 |
| C(5)–C(7) | 1.443 | 1.436 | C(1)–S(1)–C(3) | 94.7 | 95.5 | C(1)–S(1)–C(3)–S(2) | −9.3 | 1.3 |
| C(7)=C(8) | 1.353 | 1.344 | C(2)–S(2)–C(3) | 94.7 | 94.6 | C(2)–S(2)–C(3)–S(1) | 9.3 | 1.4 |
| C(8)–C(9) | 1.446 | 1.436 | C(4)–S(3)–C(5) | 95.0 | 96.1 | C(5)–S(3)–C(4)–S(4) | 13.5 | 1.0 |
| C(9)–S(5) | 1.794 | 1.739 | C(4)–S(4)–C(6) | 94.6 | 95.2 | C(4)–S(3)–C(5)–C(7) | 173.1 | 179.5 |
| C(9)=N | 1.303 | 1.314 | C(6)–S(4)–C(4)–S(3) | −13.0 | 0.9 | |||
| C(10)–N | 1.380 | 1.395 | ||||||
| C(11)–S(5) | 1.752 | 1.737 | ||||||
2. Methods of calculation
All the calculations were performed with the Gaussian 16 package [28]. The Density Functional Theory (DFT) method was employed with the B3LYP functional (Becke’s three-parameter non-local exchange functional with the Lee–Yang–Parr correlation function) [29, 30] and Pople’s [31] basis set 6-31G**. The geometry optimizations were carried out in the gas phase and the minima and were confirmed by frequency calculations; these satisfactorily agreed with experimental structural data. Accordingly, the energies and other chemical–physical properties could be safely compared. Simulated UV–Vis absorption spectra of the molecule TTF–CH=CH–BTA were obtained by the TD-DFT (B3LYP) method along the lines followed by other authors [32]. The corresponding HOMO and LUMO energies were then used to estimate some global chemical reactivity parameters, such as chemical potential (μ), electronegativity (χ), electrophilicity index (ω), and chemical hardness (η) and softness (S) [33, 34]. In addition, the APT partial charges, the molecular electrostatic potential (MEP) map, and the dipole moment of TTF–CH=CH–BTA were similarly derived. The NBO and NLO analyses of specific structures were also carried out for the optimized species.
3. Results and discussion
3.1. Molecular geometry
The optimized structural parameters of the TTF–CH=CH–BTA molecule in Scheme 1 are presented in Table 1. The optimized molecular structure depicted by the Chemcraft software is shown in Figure 1. The optimized computed values have been compared with those of a crystal structure [25]. The 1,3-benzothiazole (BTA) unit is conjugated to TTF by an acetylenic spacer, which eventually acquires ethylenic features. This compound was reported in 2010 by Fujiwara and coworkers. It was considered a switchable conductor useful for the photoelectric conversion of selected materials [23, 24]. In fact, measurements with a single crystal of TTF–CH=CH–BTA suggested the existence of photocurrents along the two stacked TTF and BTA units [25]. An intermolecular electron transfer could be photoinduced with the formation of charge-separated states.
Optimized molecular structure of TTF–CH=CH–BTA.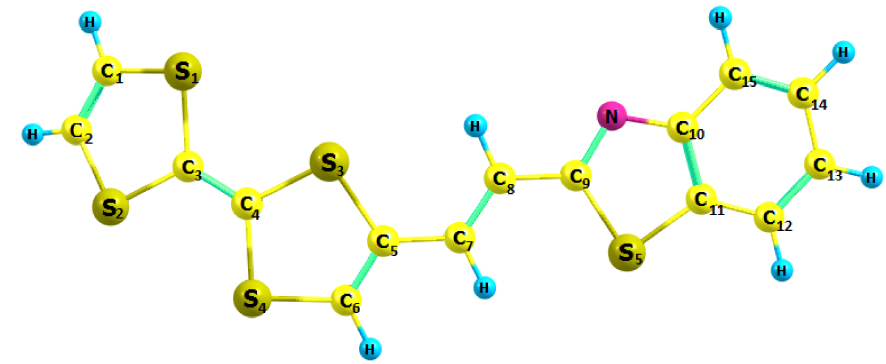
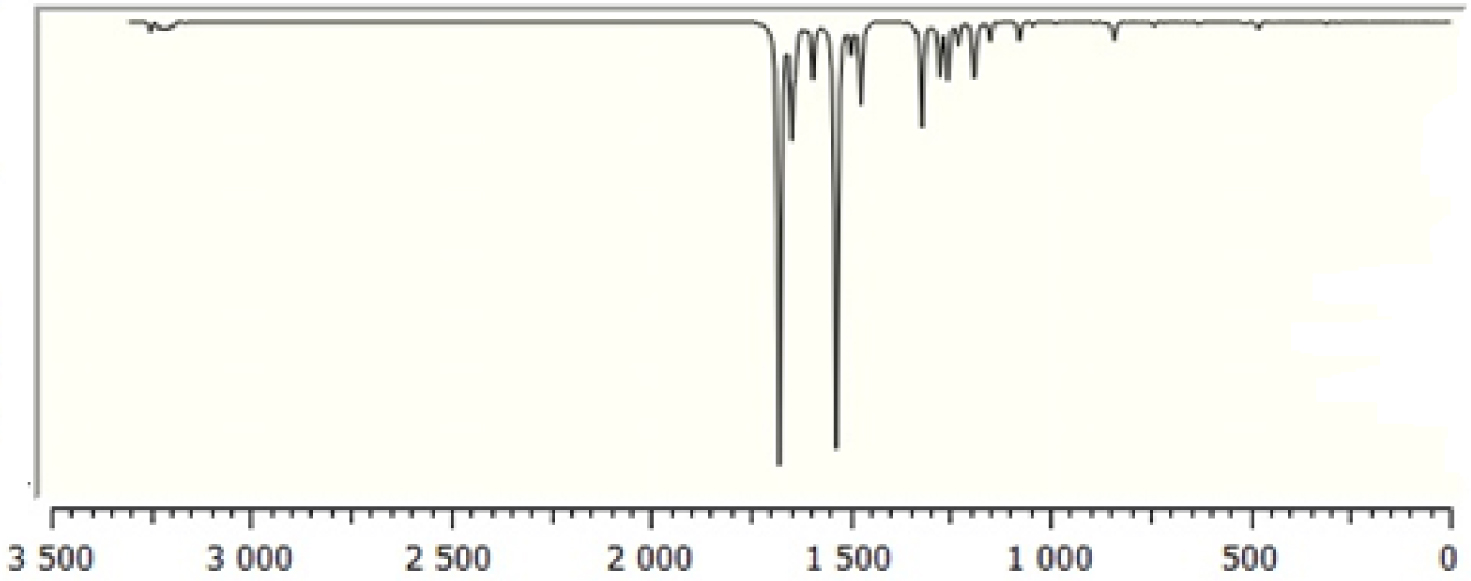
Calculated Fourier-transform infrared (FT-IR) spectra of TTF–CH=CH–BTA.
In general, the observations in Table 1 are indicative of good agreement between calculated structural parameters and experimental data. Minor differences were possibly due to optimized values being obtained in an isolated gaseous phase and experimental values in crystals. Briefly, the average C=C, C–C and C–S bond distances calculated at the DFT/B3LYP/6-31G** level were 1.370, 1.419 and 1.744 Å, respectively, which were slightly larger than average experimental values (1.347, 1.384 and 1.733 Å, respectively). In the BTA unit, the C(9)–N and C(10)=N bond distances of 1.380 and 1.303 Å, respectively, are close to experimental values (1.395 and 1.313 Å, respectively). Furthermore, there is some deviation of the S atom from the plane of the bicycle in the TTF unit, as confirmed by the dihedral angles on the TTF side (C(1)–S(1)–C(3)–S(2) = −9.3, C(2)–S(2)–C(3)–S(1) = 9.3, C(5)–S(3)–C(4)–S(4) = 13.5 and C(6)–S(4)–C(4)–S(3) = −13.0), which does not allow the molecule to be rigorously planar.
Vibrational wavenumbers obtained for the title compound using B3LYP methods with 6-31G** basis set
| Mode | IR | Int | Raman | Vibrational assignments PED (⩾10%) |
|---|---|---|---|---|
| 84 | 3250.47 | 0.22 | 452.21 | 𝜈CH (99) |
| 83 | 3230.84 | 3.60 | 129.81 | 𝜈CH (100) |
| 82 | 3229.62 | 7.21 | 176.94 | 𝜈CH (99) |
| 81 | 3217.68 | 18.45 | 283.99 | 𝜈CH (82) |
| 80 | 3209.37 | 23.69 | 283.45 | 𝜈C15H (12) + 𝜈C12H (81) |
| 79 | 3198.87 | 8.50 | 225.58 | 𝜈CH (91) |
| 78 | 3190.99 | 21.98 | 40.22 | 𝜈CH (98) |
| 77 | 3187.00 | 1.78 | 51.46 | 𝜈CH (83) |
| 76 | 3161.26 | 7.82 | 51.21 | 𝜈CH (98) |
| 75 | 1677.49 | 150.10 | 13930.13 | 𝜈CC (60) + δHCC (10) + δHCC (12) |
| 74 | 1645.66 | 14.39 | 3306.83 | 𝜈C15C14 (23) + 𝜈C11C12 (27) |
| 73 | 1636.75 | 6.41 | 1030.44 | 𝜈CC (69) |
| 72 | 1611.81 | 60.09 | 68.55 | 𝜈CC (64) |
| 71 | 1609.06 | 3.01 | 17.36 | 𝜈CC (52) |
| 70 | 1592.70 | 48.47 | 1666.00 | 𝜈CC (68) |
| 69 | 1534.49 | 129.73 | 12994.84 | 𝜈NC (60) |
| 68 | 1497.79 | 6.62 | 804.22 | 𝜈CC (15) + 𝜈CC (24) + δHCC (45) |
| 67 | 1473.50 | 18.47 | 2427.20 | δHCC (45) + δCCC (15) |
| 66 | 1362.74 | 25.84 | 26.00 | 𝜈CC (64) |
| 65 | 1336.87 | 2.24 | 127.40 | δHCC (58) |
| 64 | 1319.36 | 14.46 | 3052.24 | 𝜈NC (17) + δHCC (22) |
| 63 | 1298.26 | 3.57 | 13.31 | δHCC (63) |
| 62 | 1290.09 | 0.04 | 7.93 | δHCS (83) |
| 61 | 1275.99 | 5.03 | 1488.22 | 𝜈CC (13) + 𝜈NC (20) + δHCC (18) |
| 60 | 1256.08 | 12.53 | 1589.19 | 𝜈CC (20) + δHCC (10) + δHCC (10) + δCCC (18) |
| 59 | 1228.85 | 89.83 | 619.36 | 𝜈NC (11) + 𝜈CC (50) |
| 58 | 1190.28 | 6.24 | 1094.38 | 𝜈CC (13) + δHCS (48) |
| 57 | 1187.32 | 15.51 | 733.15 | 𝜈CC (11) + 𝜈CC (11) + δHCC (57) |
| 56 | 1149.35 | 3.33 | 521.94 | 𝜈CC (35) + δHCC (16) + δHCC (24) |
| 55 | 1125.79 | 0.58 | 16.54 | δHCS (91) |
| 54 | 1076.91 | 2.78 | 506.28 | 𝜈SC (24) + δCCC (12) + δCCC (35) |
| 53 | 1043.91 | 5.53 | 113.98 | 𝜈CC (64) + δHCC (22) |
| 52 | 987.60 | 0.00 | 0.68 | δHCS (66) + τCCCC (22) |
| 51 | 984.14 | 0.20 | 62.28 | 𝜈SC (18) + 𝜈SC (14) + δCCS (42) |
| 50 | 968.61 | 33.53 | 4.47 | τHCCC (87) |
| 49 | 947.92 | 2.40 | 0.27 | τHCCC (87) |
| 48 | 888.91 | 13.39 | 60.34 | 𝜈NC (12) + δCCC (48) + δCCC (13) |
| 47 | 870.48 | 0.75 | 3.92 | τHCCC (85) |
| 46 | 867.94 | 0.11 | 0.71 | τHCSC (95) |
| 45 | 863.44 | 0.33 | 37.23 | τHCCC (64) |
| 44 | 844.33 | 25.76 | 103.25 | 𝜈SC (60) |
| 43 | 838.91 | 24.53 | 434.23 | 𝜈SC (52) + δSCC (15) |
| 42 | 805.56 | 29.01 | 9.58 | 𝜈SC (41) + δHCS (15) + δCCS (31) |
| 41 | 777.10 | 46.02 | 0.49 | 𝜈SC (50) + δCSC (25) |
| 40 | 774.76 | 40.66 | 1.09 | τHCCC (66) |
| 39 | 760.43 | 22.59 | 5.98 | τHCSC (79) |
| 38 | 739.21 | 5.90 | 100.68 | δCCC (50) + δCCS (15) |
| 37 | 739.07 | 10.45 | 6.36 | τHCCC (17) + τHCCC (16) + τCNCC (12) + τCCCC (37) |
| 36 | 736.05 | 4.99 | 6.78 | 𝜈SC (90) |
| 35 | 714.82 | 3.59 | 18.62 | 𝜈SC (30) + δCCS (32) + δCCC (11) |
| 34 | 671.79 | 41.34 | 14.51 | δCCS (15) + δCCN (34) |
| 33 | 649.30 | 56.55 | 10.26 | τHCSC (95) |
| 32 | 629.85 | 2.67 | 35.22 | δCCS (25) + δCCC (17) + δCSC (13) |
| 31 | 627.82 | 9.60 | 29.83 | δCCS (12) + δCCN (18) |
| 30 | 622.62 | 1.72 | 9.74 | τCNCC (28) + τCCCC (12) |
| 29 | 620.70 | 0.97 | 11.18 | 𝜈SC (33) + δCCS (12) |
| 28 | 557.56 | 0.72 | 0.58 | τCCCC (39) + τCCCC (14) + τCCCC (16) |
| 27 | 519.09 | 9.56 | 10.94 | δCCC (26) + γ SCSC (17) |
| 26 | 514.67 | 9.12 | 17.87 | δCCC (13) + γ SCSC (53) |
| 25 | 506.94 | 5.70 | 37.85 | 𝜈SC (14) + δCCS (53) |
| 24 | 488.41 | 1.52 | 4.01 | τCSCC (40) + τCCCC (11) |
| 23 | 478.64 | 2.64 | 175.49 | 𝜈SC (32) + δCCS (11) + δSCC (19) |
| 22 | 444.30 | 3.19 | 7.60 | δCCS (15) + δCCC (31) |
| 21 | 441.29 | 3.40 | 0.53 | τCCCC (69) |
| 20 | 432.53 | 17.84 | 6.28 | 𝜈SC (10) + δCCS (11) + δSCC (16) |
| 19 | 420.07 | 0.03 | 2.95 | τSCCS (88) |
| 18 | 360.02 | 2.52 | 3.18 | δCCS (11) + δCCC (24) + δCCN (12) |
| 17 | 346.79 | 0.34 | 7.33 | γSCCC (72) |
| 16 | 308.22 | 0.88 | 67.12 | δCCS (44) |
| 15 | 286.40 | 0.26 | 1.53 | τHCCC (14) + τCCCS(52) |
| 14 | 278.28 | 0.74 | 20.81 | 𝜈SC (12) + δCSC (23) + τCCSC (21) |
| 13 | 251.68 | 0.63 | 3.19 | τCCSC (51) |
| 12 | 211.09 | 1.86 | 1.84 | 𝜈CC (10) + δCSC (14) |
| 11 | 200.97 | 1.03 | 5.36 | τCCCC (19) + τCCCC (10) + τCSCC (21) + τCCCC (11) |
| 10 | 183.29 | 0.06 | 2.52 | τCCCC (22) + τCCCC (15) + τCCCS (13) + τCCCC (18) |
| 9 | 128.29 | 0.52 | 1.73 | 𝜈CC (11) + δCCC (57) |
| 8 | 105.07 | 0.95 | 2.46 | τCCCS (41) + τCCCC (22) |
| 7 | 90.94 | 0.58 | 1.64 | δCCS (46) + τCSCC (26) |
| 6 | 80.08 | 1.36 | 0.51 | δCCS (24) + τCSCC (54) |
| 5 | 68.46 | 2.84 | 0.36 | τCCSC (75) |
| 4 | 45.27 | 0.19 | 5.92 | τCCCS (10) + τCCSC (50) |
| 3 | 32.34 | 0.34 | 2.56 | δCCC (71) |
| 2 | 21.75 | 0.07 | 1.46 | δCCC (81) |
| 1 | 18.19 | 0.95 | 3.85 | τCCSC (66) |
3.2. Vibrational analysis
The molecule consists of 30 atoms, thus implying 84 normal modes of vibrations, which are active in both infrared (IR) absorption and Raman scattering. The fundamental vibrational wavenumbers of TTF–CH=CH–BTA were calculated by the DFT method with B3LYP as the 6-31G** basis set. The results of IR (vibrational wavenumbers and IR intensities) and Raman activities for the optimized structure are listed in Table 2. The calculated IR and Raman spectra are displayed in Figures 2 and 3. The vibrational assignments were carried out on the basis of the potential energy distribution calculation using the “Vibrational Energy Distribution Analysis” (VEDA) program.
3.2.1. TTF vibrations
In general, non-aromatic compounds show C–H stretching vibrations in the region below 3000 cm−1 while values above 3000 cm−1 are typical of aromatic compounds [35]. In the present study, the modes calculated at 3250, 3231 and 3230 cm−1 are identified as symmetric and asymmetric C–H stretching modes, while the observed wavenumbers occur at 3099 cm−1. Theoretical and experimental data for C–H stretching modes of the TTF part show a very good correlation with the literature [36]. The C=C stretching modes are found in wavenumber range 1565–1495 cm−1. The C–S stretching modes are observed in wavenumber range 935–734 cm−1 and are in good agreement with the general appearance of ν(C–S) stretching modes.
3.2.2. BTA vibrations
Due to the presence of the BTA unit, the spectrum of the compound involves the bands corresponding to C–H, C–C, C–C–C and H–C–C bending as well as C–C–C–C torsion vibrations. The four C–H bonds in BTA correspond to the vibrations at 3209, 3187, 3199 and 3218 cm−1. In-plane C–H bending vibrations are related to C–C stretching vibrations and the vibrations of aromatic molecular structures occurring in the 1500–1100 cm−1 region [37]. In-plane C–H bending vibrations were obtained at 1256, 1187, 1678, 1337, 1319, 1276, 1256, 1149, 1474, 1044, 1678, 1298, 1498 and 1190 cm−1. The C–C stretching vibrations of aromatic structures occur strongly within 1650–1430 cm−1 [37]. In this study, the C–C stretching vibrations were calculated at 1646, 1498, 1149, 1276, 1363 and 1046 cm−1.
3.2.3. C=C vibrations
Conjugated C=C stretching vibration has been reported at 1600 cm−1 [35]. In the present study, the C–C stretching vibrations are calculated at 1678 cm−1.
3.3. Atomic charges (APT)
The atomic charges in TTF–CH=CH–BTA were derived by calculating the Atomic Polar Tensor (APT). This tensor is calculated as the sum of the charge and charge flux tensors that allow to construct a charge–charge flux model [38]. The corresponding atomic charges of TTF–CH=CH–BTA are shown in Table 3.
Atomic charges of the optimized TTF–CH=CH–BTA molecule
| Atom | Charge | Atom | Charge |
|---|---|---|---|
| S(1) | −0.13 | C(8) | −0.24 |
| S(2) | −0.17 | C(9) | 0.69 |
| S(3) | −0.19 | C(10) | 0.09 |
| S(4) | −0.39 | C(11) | −0.03 |
| C(1) | 0.01 | C(12) | 0.03 |
| C(2) | 0.00 | C(13) | −0.08 |
| C(3) | 0.23 | C(14) | −0.09 |
| C(4) | 0.05 | C(15) | 0.08 |
| C(5) | −0.15 | S(5) | −0.20 |
| C(6) | 0.31 | N | −0.52 |
| C(7) | 0.32 | ||
Atomic charge calculations play an important role in quantum mechanical studies of molecular systems because they are used to explain molecular dipole moments, electronic structures and polarizabilities and hence chemical reactivities. From the atomic charge analysis of TTF–CH=CH–BTA, it emerges that the nitrogen atom in the BTA unit has the maximum negative charge of −0.52 e. The sulfur atoms are also negatively charged with values −0.13, −0.20 and −0.39 e. The C(9) atom in the benzothiazole unit is the most positively charged (+0.69 e); most of the other C atoms are also positively charged with the exception of C(5), C(8), C(14) and C(13), which carry negative charges of −0.15, −0.24, −0.09 and −0.08 e, respectively.
Molecular electrostatic potential map of TTF–CH=CH–BTA.
Schematic presentation of the electronic excitation mechanism of TTF–CH=CH–BTA.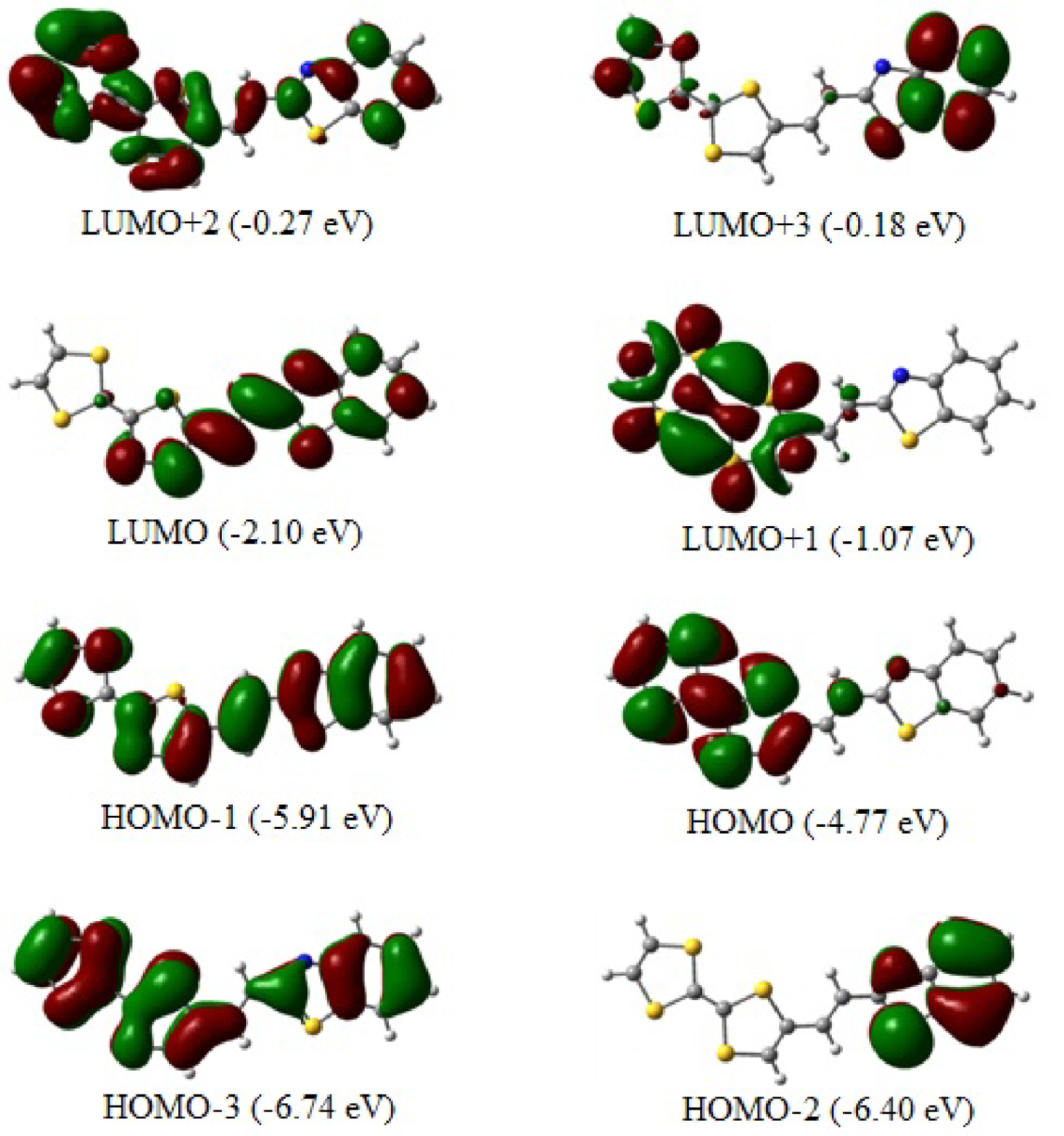
Selected optimized parameters for the TTF–CH=CH–BTA molecule in chloroform solution. The values 𝜆calc, total energy, f and the lower electronic singlet excitations for each transition are reported
| Transitions | 𝜆calc [nm] | Energy (eV) | f | Involved levels |
|---|---|---|---|---|
| S0→S1 | 486.01 | 2.5510 | 0.1708 | HOMO→LUMO (98.4%) |
| S0→S4 | 331.71 | 3.7378 | 0.9534 | HOMO−2→LUMO (2.4%) |
| HOMO−1→LUMO (85.5%) | ||||
| HOMO→LUMO+3 (7.7%) | ||||
| S0→S5 | 307.00 | 4.0385 | 0.1744 | HOMO−2→LUMO (30.3%) |
| HOMO−1→LUMO (2.5%) | ||||
| HOMO−1→LUMO+1 (2.4%) | ||||
| HOMO→LUMO+3 (57.7%) | ||||
| S0→S6 | 302.83 | 4.0942 | 0.1241 | HOMO−2→LUMO (60%) |
| HOMO−1→LUMO (7.5%) | ||||
| HOMO→LUMO+3 (22.1%) | ||||
3.4. Molecular electrostatic potential
The MEP has been typically employed to account for electrostatic interactions in a variety of chemical systems [39]. At any point , the electrostatic molecular potential corresponds to the force acting on a positive test charge (a proton) located at through the charge cloud generated by the molecule’s electrons and nuclei. For the present system, the values were calculated as described previously by using the equation [40]
| (1) |
The MEP of TTF–CH=CH–BTA using DFT-B3LYP/6-31G** optimized geometry was computed, and its surface map is shown in Figure 4. This figure shows electrostatic potential values using a color coded scheme. The most negative value is characterized by red, which suggests the favored sites for a possible electrophilic attack. The most positively charged regions appear in deep blue, which in turn indicates the favored sites for a nucleophilic attack. The determined limits are −5.169e−2 (deepest red) and +5.169e−2 (deepest blue), with the intermediate scale of colors changing from red to orange, yellow, green and blue in order, as shown in Figure 4. The most negative potential is concentrated around the unique nitrogen atom, while positive potentials are peripheral especially at the external H atoms of the TTF unit. The positivity is somewhat less marked for the H atoms of the BTA unit. In conclusion, the MEP mainly suggests a possible electrophilic attack on the nitrogen atom with some possibility also for two TTF S atoms. Conversely, a strong base may have a chance to remove as a proton one of the two H atoms of the HC=CH linker or in other words to transform the corresponding ethylenic moiety into a vinylidene anion at the side of the TTF substituent.
3.5. Frontier molecular orbitals
The top views of the optimized TTF–CH=CH–BTA frontier molecular orbitals (from HOMO−2 to LUMO+3) are depicted in Figure 5 with the HOMO and LUMO playing significant roles in intramolecular charge transfer (ICT). The topological features of these levels are important for interpreting kinetic stability (and consequently, the potential chemical reactivity) as well as other properties such as optical properties [41, 42]. As anticipated, all the involved molecular orbitals have π character which extends on the overall planar molecule.
The calculated HOMO–LUMO gap is as large as 2.67 eV. The TTF moiety mainly contributes to the HOMO. The LUMO is mainly centered at the ethylenic linker, although there is some residual pπ contribution of atoms at both its left and right sides. Conversely, the π character of the HOMO, which is distributed throughout the entire TTF–CH=CH–BTA molecule, indicates how the electron delocalization can involve the entire system also thanks to the π nature of the linker. The HOMO–LUMO energy gap is relatively large, and the corresponding electronic transition implies a significant electron density redistribution in the molecule. In particular, the gap seems to explain the origin of the band shoulder detected in the previously reported experimental UV–Vis spectra [21]. More specifically, the given shape of the spectrum corroborates the ICT between the TTF donor and benzothiazole fragments, with the latter representing the acceptor side of the molecule.
3.6. UV–Vis spectral analysis
The vertical excitation energies were calculated by using the time-dependent DFT (TD-DFT) method [43] in order to define the nature of the electronic transitions and the assignment of the observed bands in the UV–Vis absorption spectra. The computational results are summarized in Table 4 and the simulated spectra are shown in Figure 6.
Simulated electronic absorption spectra of TTF–CH=CH–BTA using the TDDFT-B3LYP/6-31G** method.
From the results in Table 4, it emerges that the most relevant S0→S1 transition that determines the first excited state occurs at 486.01 nm. This essentially involves the HOMO–LUMO electron transfer, given that its weight is evaluated as large as 98.4%. Furthermore, in view of the composition of the levels, the transition highlights how the target of the ICT in TTF–CH=CH–BTA is directed toward the TTF moiety.
The next most intense transition, with an oscillation force constant of 331.71 nm, occurs from the ground state to the fourth excited state (S0→S4). In this case, its main component of 85.5% involves the electron transition from the HOMO−1 to the LUMO, while another 7.7% involves the HOMO and the LUMO+3.
3.7. Global reactivity descriptors
The global reactivity descriptors such as ionization potential (I), electron affinity (A), electronegativity (𝜒), chemical hardness (𝜂), chemical softness (S), chemical potential (𝜇) and electrophilicity index (𝜔) values were examined based on the optimization of TTF–CH=CH–BTA in the gas phase. The parameters provide some information about the chemical stability of the molecule. The numerical reactivity descriptors, which are mainly based on the HOMO–LUMO energies, are summarized in Table 5.
Global reactivity indices of TTF–CH=CH–BTA
| Parameters | Values |
|---|---|
| Ionization potential (I) (eV) | 4.77 |
| Electron affinity (A) (eV) | 2.10 |
| Electronegativity (𝜒) (eV) | 3.43 |
| Electrochemical potential (μ) (eV) | −3.43 |
| Global chemical hardness (η) (eV) | 1.33 |
| Global chemical softness (S) (eV−1) | 0.75 |
| Electrophilicity index (ω) (eV) | 4.42 |
The ionization potential (I) and electron affinity (A) according to the Koopmans theorem can be defined by the following equations [44]:
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
3.8. Local reactivity descriptors
The most important indicator of reactivity is the Fukui function f(r), proposed in 1984 by Parr and Yang [47]. The function at the point r is the derivative of the electron density with respect to the variation of the number of electrons N, given the external potential V (r):
| (7) |
∙ For nucleophilic attacks,
| (8) |
| (9) |
| (10) |
For electrophilic attacks,
| (11) |
| (12) |
| (13) |
For radical attacks,
| (14) |
| (15) |
| (16) |
The parameters of local reactivity in Table 6 indicate that the nitrogen atom is the most reactive site for the attacks of electrophilic and free radical types, while ethylenic C(8) is most prone to a nucleophilic attack.
3.9. Natural bond orbital analysis
The NBO analysis is a reliable method to examine the charge transfer properties and the intra- and intermolecular bonding nature of a given molecule. The π electron delocalization implies that a given Lewis valence orbital (donor) undergoes a decrease in occupancy due to the electron density, which is being shifted toward another region of the molecule (acceptor). The applied second-order perturbation theory shows some energy lowering associated with this effect. For each donor (NBO(i)) and acceptor (NBO(j)), the strength of delocalization interaction or stabilization energy (E(2)) associated with the electron redistribution between the donor and acceptor sides can be formulated as the second-order energy lowering [48, 49, 50]:
| (17) |
The reactive sites for non-hydrogen atoms in TTF–CH=CH–BTA
| Atoms | f− | f+ | f0 |
|---|---|---|---|
| S(1) | 0.059 | 0.368 | 0.213 |
| S(2) | 0.038 | 0.107 | 0.073 |
| S(3) | 0.084 | 0.364 | 0.224 |
| S(4) | −0.177 | 0.736 | 0.279 |
| C(1) | −0.035 | −0.359 | −0.197 |
| C(2) | 0.020 | −0.107 | −0.043 |
| C(3) | 0.192 | 0.698 | 0.445 |
| C(4) | −0.190 | −0.728 | −0.459 |
| C(5) | −0.886 | 0.927 | 0.020 |
| C(6) | 0.680 | −0.788 | −0.054 |
| C(7) | 0.633 | −1.108 | −0.237 |
| C(8) | 0.145 | 1.100 | 0.622 |
| C(9) | −0.461 | −1.072 | −0.766 |
| C(10) | −0.728 | −0.715 | −0.722 |
| C(11) | 0.173 | 0.137 | 0.155 |
| C(12) | −0.286 | −0.197 | −0.241 |
| C(13) | 0.326 | 0.142 | 0.234 |
| C(14) | −0.160 | −0.200 | −0.180 |
| C(15) | 0.329 | 0.281 | 0.305 |
Numerical NBO results derived from the second-order perturbation theory analysis of the Fock matrix for TTF–CH=CH–BTA
| Donor (i) | ED (e) | Acceptor (j) | ED (e) | E(2) kcal/mol | E (j)-E (i) a.u. | F (i.j) a.u. |
|---|---|---|---|---|---|---|
| 𝜋 (C9–C10) | 1.89 | 𝜋∗ (C11–C12) | 0.18 | 14.58 | 0.34 | 0.063 |
| 𝜋 (C11–C12) | 1.84 | 𝜋∗ (C9–C10) | 0.29 | 16.18 | 0.28 | 0.062 |
| 𝜋 (C11–C12) | 1.84 | 𝜋∗ (C13–N30) | 0.35 | 17.71 | 0.28 | 0.066 |
| 𝜋 (C13–N30) | 1.85 | 𝜋∗ (C11–C12) | 0.18 | 11.43 | 0.35 | 0.057 |
| 𝜋 (C13–N30) | 1.85 | 𝜋∗ (C14–C15) | 0.48 | 17.10 | 0.33 | 0.074 |
| 𝜋 (C14–C15) | 1.62 | 𝜋∗ (C13–N30) | 0.35 | 12.85 | 0.26 | 0.052 |
| 𝜋 (C14–C15) | 1.62 | 𝜋∗ (C16–C18) | 0.30 | 16.31 | 0.30 | 0.064 |
| 𝜋 (C14–C15) | 1.62 | 𝜋∗ (C17–C19) | 0.32 | 18.95 | 0.29 | 0.067 |
| 𝜋 (C16–C18) | 1.70 | 𝜋∗ (C14–C15) | 0.48 | 20.51 | 0.26 | 0.069 |
| 𝜋 (C16–C18) | 1.70 | 𝜋∗ (C17–C19) | 0.32 | 19.87 | 0.28 | 0.067 |
| 𝜋 (C17–C19) | 1.69 | 𝜋∗ (C14–C15) | 0.48 | 18.71 | 0.27 | 0.066 |
| 𝜋 (C17–C19) | 1.69 | 𝜋∗ (C16–C18) | 0.30 | 18.34 | 0.29 | 0.065 |
| LP (2) S1 | 1.78 | 𝜋∗ (C5–C6) | 0.21 | 21.84 | 0.26 | 0.067 |
| LP (2) S1 | 1.78 | 𝜋∗ (C7–C8) | 0.40 | 17.47 | 0.25 | 0.062 |
| LP (2) S2 | 1.78 | 𝜋∗ (C5–C6) | 0.21 | 21.70 | 0.26 | 0.067 |
| LP (2) S2 | 1.78 | 𝜋∗ (C7–C8) | 0.40 | 17.34 | 0.25 | 0.062 |
| LP (2) S3 | 1.80 | 𝜋∗ (C7–C8) | 0.40 | 16.06 | 0.25 | 0.060 |
| LP (2) S3 | 1.80 | 𝜋∗ (C9–C10) | 0.29 | 19.81 | 0.25 | 0.064 |
| LP (2) S4 | 1.75 | 𝜋∗ (C7–C8) | 0.40 | 16.16 | 0.26 | 0.060 |
| LP (2) S4 | 1.75 | 𝜋∗ (C9–C10) | 0.29 | 23.11 | 0.26 | 0.069 |
| LP (2) S29 | 1.70 | 𝜋∗ (C13–N30) | 0.35 | 24.32 | 0.25 | 0.071 |
| LP (2) S29 | 1.70 | 𝜋∗ (C14–C15) | 0.48 | 17.74 | 0.27 | 0.064 |
| LP (1) N30 | 1.88 | 𝜎∗ (C13–S29) | 0.09 | 18.61 | 0.52 | 0.088 |
The above results suggest that the most important interaction in the molecule is that between the lone pair S(5) with the 𝜋∗ (C9–N) component and S(4) with 𝜋∗ (C5–C6). In these cases, the corresponding stabilization energies are 24.32 and 23.11 kcal/mol, respectively. Correspondingly, a large energy transfer is observed in these pairwise interactions. In particular, the electron transfers into the 𝜋∗ (C12–C13) and 𝜋∗ (C7–C8) levels induce significant stabilization energies of 18.95 and 14.58 kcal/mol, respectively.
3.10. Non-linear optical properties
The non-linear optical properties of a molecule have been proved to be an important guideline for establishing the molecular structure and assembly of organic materials. These properties have a role in current technologies such as communication and computer processes [51, 52]. The NLO effects result from the interactions of electromagnetic fields with various media which alter features in the incident fields such as phase, frequency, amplitude or other propagation aspects [53]. The NLO effects are important for providing the key functions of frequency shifts, optical modulation, optical switching, optical logic, optical memory, and emerging technologies in telecommunications, signal processing and optical interconnections [54, 55, 56, 57]. Therefore, DFT has been widely used to study NLO organic materials [58, 59, 60, 61, 62].
The dipole moments μ, polarizability α, average isotropic polarizability 〈𝛼〉, the anisotropy of the polarizability Δα and the first hyperpolarizability βtot of TTF–CH=CH–BTA. The polarizability (𝛼ij) and hyperpolarizability tensors (𝛽ijj) have been converted into electronic units (esu) (𝛼; 1 a.u. = 0.1482 × 10−24 esu, 𝛽; 1 a.u. = 8.6393 × 10−33 esu)
| Dipole moment (D) | Polarizability (a.u.) | Hyperpolarizability (a.u.) | |||
|---|---|---|---|---|---|
| 𝜇x | −0.3817 | 𝛼xx | 508.235 | 𝛽xxx | −5173.75 |
| 𝜇y | −0.3028 | 𝛼xy | −21.728 | 𝛽xxy | 468.315 |
| 𝜇z | 2.3528 | 𝛼yy | 255.661 | 𝛽xyy | −13.584 |
| μ | 2.4027 | 𝛼xz | 9.3152 | 𝛽yyy | −9.190 |
| 𝛼yz | −20.169 | 𝛽xxz | −33.632 | ||
| 𝛼zz | 125.862 | 𝛽xyz | 52.649 | ||
| 〈𝛼〉(a.u.) | 296.586 | 𝛽yyz | 35.771 | ||
| 〈𝛼〉a | 43.949a | 𝛽xzz | 44.934 | ||
| 〈𝛼〉b | 43.949b | 𝛽yzz | −13.088 | ||
| 𝛥𝛼a | 49.912 | 𝛽zzz | 15.922 | ||
| 𝛽tot | 5161.57 | ||||
| 44592.368c | |||||
a〈𝛼〉 is given in 10−24 (esu); b〈𝛼〉 is given in (Å3); c𝛽tot is given in 10−33 (esu).
Properties, such as the dipole moment (μ), polarizability (αij) and first hyperpolarizability (βtot), are related to non-linear optical properties. This DFT method used for our purpose has already been proved successful in the study of organic materials with NLO. Our derived values are summarized in Table 8. The equations used to derive the value of the total dipole moment (μtot), the average isotropic polarizability (〈𝛼〉), the anisotropy of the polarizability Δα and the first order of the hyperpolarizability (βtot), respectively, are the following [63]:
| (18) |
| (19) |
| (20) |
| (21) |
The NLO behavior of a molecule is usually determined by comparing the total dipole moment (μtot) and the average first-order hyperpolarizability (𝛽tot) with the corresponding values of urea [64], which are typically used as the threshold values for comparative purposes. The values of μtot, α and βtot of urea according to our calculations are 1,373 debye, 3,831 Å3 and 0.3728 × 10−30 cm5/esu, respectively. From the values above, it can be seen that the μ and βtot values of TTF–CH=CH–BTA exceed those of urea, corroborating the efficiency of TTF–CH=CH–BTA as an NLO agent [65, 66, 67, 68].
Conclusions
In this paper, the molecular structure and vibrational analysis results of the TTF–CH=CH–BTA molecule have been reported together with its electronic properties. The molecular geometry was optimized in the singlet ground state, showing good agreement with the available experimental data. FT-IR and FT-Raman spectral characterizations of TTF–CH=CH–BTA are described for the first time. An analysis of the partial atomic charge distribution revealed a concentration of negative charge at the nitrogen atom, while the adjacent carbon atoms are evidently positively charged. This is in agreement with the features of a MEP surface, which clearly shows the most negative region around the nitrogen atom, as it is highly prone to an electrophilic attack. Conversely, the hydrogen atoms appear the most positively charged, being potentially suited for a nucleophilic attack. A study of the molecular orbital topology showed a HOMO–LUMO energy gap of 2.66 eV, which also explains the origin of the shoulder observed in experimental UV–Vis spectra and the computed one in Figure 6. In particular, the orbital features suggest that an intramolecular charge transfer (ICT) occurs between the TTF donor and the benzothiazole fragment. The basic chemical reactivity descriptors were calculated, indicating that the TTF–CH=CH–BTA molecule is a reasonably soft molecule of high polarizability and chemical activity. These results are also supported by computed UV–Vis spectra. Finally, the computed non-linear optical properties have confirmed the nature of TTF–CH=CH–BTA as a potentially good NLO material.
Acknowledgments
This work was supported by MESRS-DGRSDT and University of Batna 1. The authors are grateful to Institut de Chimie de Nice, Université de Nice-Sophia Antipolis (France) for the use of some computing resources and the continuous encouragement.




 CC-BY 4.0
CC-BY 4.0