Version abrégée
Un tensioactif non ionique est constitué de l'adjonction d'une chaı̂ne alkyl (apolaire) et d'une tête polaire (comme (OCH2CH2)NpOH, dont l'encombrement est comparable, sinon supérieur, à celui de la partie apolaire. En phase aqueuse, ces molécules ont une concentration micellaire critique (CMC) faible en comparaison de celle des tensioactifs ioniques. En présence d'un solide hydrophile, polaire et même hydrophobe, on observe un mécanisme d'adsorption à l'interface solide/solution aqueuse. Cette adsorption a été étudiée depuis plusieurs années en raison de son importance industrielle (flottation, industries des lessives, biochimie des protéines). La compréhension des mécanismes d'adsorption s'est appuyée pendant longtemps sur l'étude des isothermes d'adsorption. Cependant, ce premier niveau d'analyse, bien qu'important, n'est pas suffisant. Une étude directe de la couche d'adsorption est nécessaire. Le but de cet article est de présenter une brève revue de ce sujet. Nous n'évoquerons ici que le cas des solides hydrophiles ou polaires.
Dans une première partie, nous commentons quelques travaux expérimentaux marquants dans l'étude de l'adsorption des tensioactifs non ioniques qui ont été effectués depuis moins de vingt ans. Nous montrons sur la Fig. 1 la forme générale de l'isotherme d'adsorption d'une série de tensioactifs non ioniques à l'interface solide polaire (silice dans ce cas)–eau. On observe en général le développement de l'adsorption légèrement en dessous de la CMC. Le plateau diminue d'intensité lorsque l'encombrement de la partie polaire augmente. La forme sigmoı̈de, généralement associée au caractère associatif de l'adsorption, s'estompe lorsque le degré de polymérisation de la chaı̂ne polaire augmente. Plusieurs expériences macroscopiques [4,18,21] permettent d'établir que le processus d'adsorption implique une interaction « normale » avec le solide polaire relativement faible et un mécanisme d'association des molécules adsorbées relativement important. Le problème est de savoir comment ces associations de surface peuvent être décrites. S'agit-il de la formation d'une phase étendue, ou de la création de clusters de surface disjoints ? Pour répondre à cette question, plusieurs travaux récents ont été réalisés en utilisant la spectroscopie de déclin de fluorescence [15,16], la réflectivité de neutrons [12], la diffusion aux petits angles [8], la microscopie à force atomique [5,7,22]. Comme le montre la Fig. 2, il apparaı̂t que, dans la plupart des cas, la couche d'adsorption est constituée d'agrégats disjoints de tensioactifs. Ces résultats mettent en évidence le fait qu'une interaction faible entre les têtes polaires et la surface solide assure la fixation des tensioactifs sans imposer de sévères restrictions conformationnelles. Ceci permet d'assurer la reformation, en dessous de la CMC, d'agrégats surfaciques de courbure importante. On pourrait résumer en disant que le solide polaire ou hydrophile joue le rôle d'un précurseur d'agrégats micellaires qui se construisent à l'interface solide–liquide pour des potentiels chimiques inférieurs à la CMC.
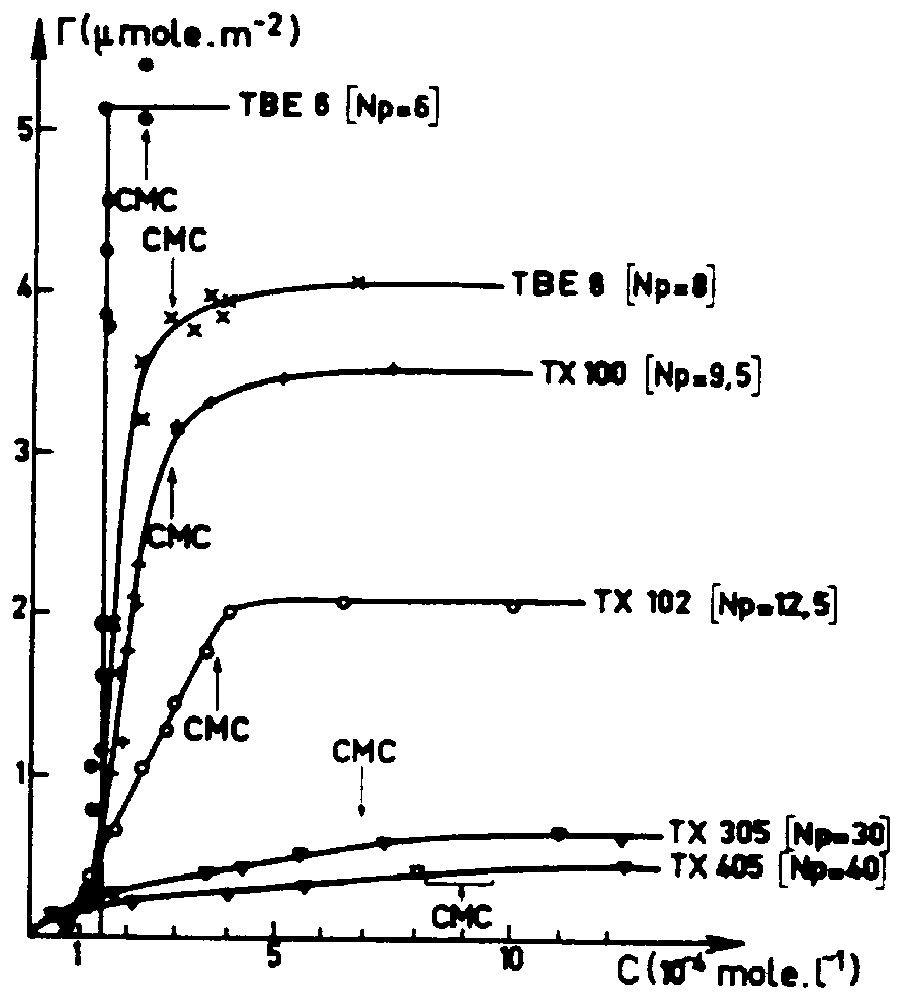
Experimental adsorption isotherms of C8PENp surfactants from aqueous solution on silica (Spherosil XOB015) [15,16].
Isothermes d'adsorption expérimentales des tensioactifs C8PENp en solution aqueuse sur la silice (Spherosil XOB015) [15,16].

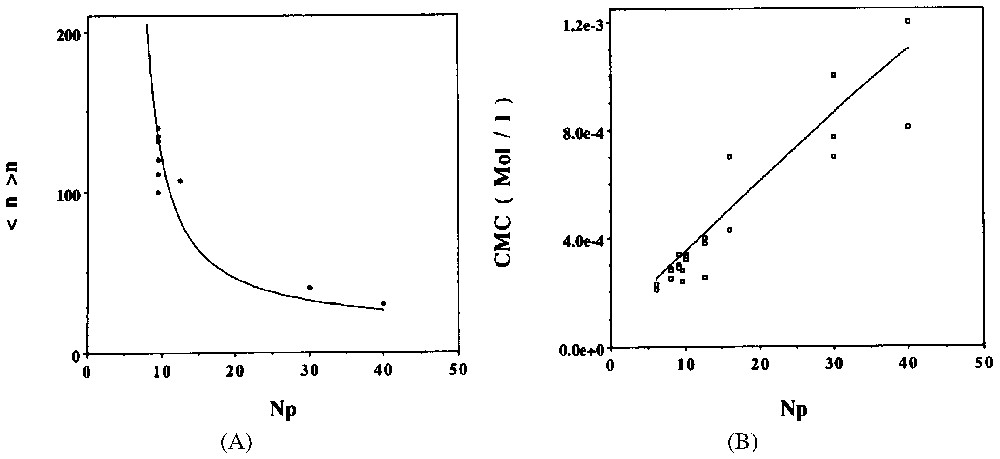
Average aggregation number N of non-ionic surfactants at the Spherosil XOB15–solution interface vs. the apparent surface coverage rate θ. A. Adsorption layer of TX100 (C8PE9.5). B. Adsorption layer of TX102 (C8PE12). C. Adsorption layer of TX300 (C8PE30). For each case, the horizontal dotted line gives the average aggregation number of micelle aggregates at 10−2 M [16].
Nombre d'agrégation moyen N des tensioactifs non ioniques à l'interface XOB15/solution en fonction du taux apparent de couverture θ. A. Couche d'adsorption de TX100 C8PE9,5. B. Couche d'adsorption de TX102 (C8PE12). C. Couche d'adsorption de TX300 (C8PE30).
Dans la deuxième partie de cet article, nous discutons de la possibilité d'une modélisation thermodynamique du processus d'adsorption des tensioactifs non ioniques à l'interface solide hydrophile–solution aqueuse. Nous proposons un modèle simple, permettant de prédire les principales caractéristiques de la micellisation (CMC et taille des agrégats micellaires, cf. Fig. 4), puis de rendre compte du mécanisme d'adsorption agrégatif (cf. Figs. 6 et 7).
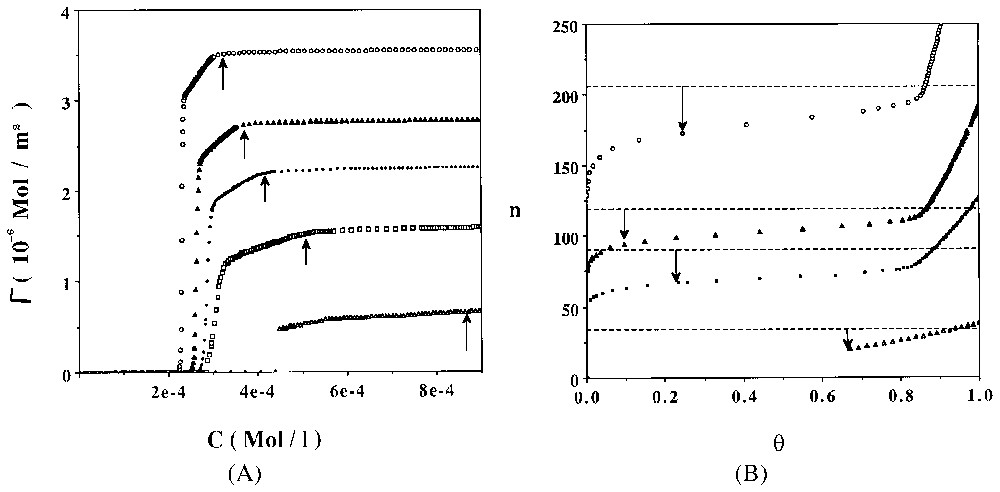
A. Evolution of the mean aggregation number of C8PENp micelles at 289 K and for a total concentration C=10−2 M. Full points: experimental results; full line: theoretical prediction from model ([13] and references inside). B. Comparison between predicted CMC (full line) and experimental determinations (points) for C8PENp homologous series at 298 K ([13] and references inside).
A. Évolution du nombre moyen d'agrégation des micelles de C8PENp à 289 K et pour une concentration totale de C=10−2 M. Points : résultats expérimentaux ; ligne pleine : prédiction théorique à partir du modèle [13]. B. Comparaison entre les CMC prédites (ligne pleine) et les déterminations expérimentales (points) pour la série d'homologues C8PENp à 298 K [13].
A. Computed adsorption isotherms of C8PENp homologous series at 298 K. ξa=−5.0 cal Å−2. Key: open circles Np=8, close triangles Np=10, close circles Np=12, open squares Np=16, open triangles Np=30. Vertical arrows show the theoretical values obtained for CMC. B. Evolution of the computed average surface aggregation number versus the surface coverage rate θ. Key: open circles Np=8, close triangles Np=10, close circles Np=12, open squares Np=16, open triangles Np=30. Horizontal dotted lines and vertical arrows indicate the predicted bulk micelle size at 10−2 M [13].
A. Isothermes d'adsorption calculées de la série d'homologues C8PENp à 298 K. ξa=−5.0 cal Å−2. Symboles : cercles ouverts Np=8, triangles pleins Np=10, cercles fermés Np=12, carrés ouverts Np=16, triangles ouverts Np=30. Les flèches verticales indiquent les valeurs théoriques des CMC. B. Évolution du nombre d'agrégation de surface, calculé en fonction du taux de recouvrement surfacique θ. Symboles : cercles ouverts Np=8, triangles pleins Np=10, cercles pleins Np=12, carrés ouverts Np=16, triangles ouverts Np=30. Les lignes horizontales et les flèches verticales indiquent les valeurs des tailles de micelles en solution à 10−2 M [13].
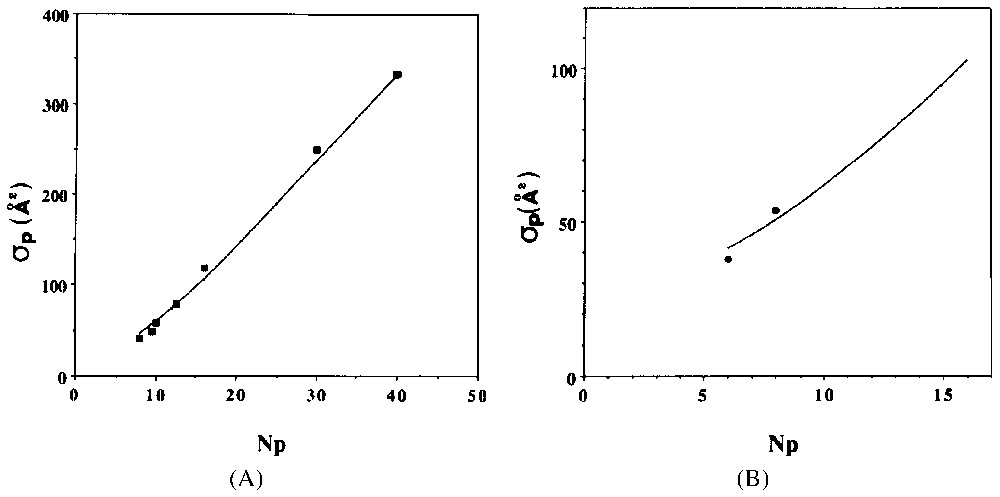
A. Apparent surface per surfactant at the adsorption isotherm plateau for the C8PENp homologous series. T=298 K. Key: points, experimental determination from [4,16,18,21]; continuous line, model from [13]. B. Apparent surface per surfactant at the adsorption isotherm plateau for the C12ENp homologous series. T=298 K. Key: points, experimental determination from [21]; continuous line, model from [13].
A. Surface apparente par molécule de tensioactif, calculée au plateau de l'isotherme d'adsorption pour la série d'homologues C8PENp. T=298 K. Symboles : points, détermination expérimentale à partir des références [4,16,18,21] ; ligne continue, modèle théorique [13]. B. Surface apparente par molécule de tensioactif calculée au plateau de l'isotherme d'adsorption pour la série d'homologues C12ENp. T=298 K. Symboles : points, déterminations expérimentales [21] ; ligne continue, modèle théorique [13].
1 Introduction
Adsorption of non-ionic surfactants from aqueous solutions has been studied for years because of its industrial relevance. These surfactants, made of an aliphatic part attached to a hydrophilic and polar chain, play an important role in diverse applications ranging from ore flotation, paint technology, lubrication, papermaking, oil recovery, and biochemistry of proteins. Relationships between adsorption layer organisation and numerous properties such as colloidal stability or wetting characteristics are presently actively debated in the literature. Modelling of the adsorption mechanisms of surfactants has traditionally been based on the interpretation of adsorption isotherms. However, this first level of investigation is not sufficient for a complete understanding. Direct inspection of adsorbed layer of non-ionic surfactant molecules at the solid–liquid interface is needed. This is an active field of research for almost 15 years, even if the subject is not completely settled down. The aim of this paper is to present a short review of this topic. I will restrict this paper to the case of non-ionic adsorption onto hydrophilic or polar solid interfaces. In the first part, I comment some experimental studies of non-ionic adsorption layers, including fluorescence spectroscopy, neutron scattering and atomic force microscopy. In the second part, a theoretical discussion about thermodynamics of adsorption is presented. A model involving an aggregative adsorption process is proposed.
2 Experimental studies: a short review
Non-ionic surfactants such as alkylNa (CNaENp) or alkyl phenol polyoxyethylene glycol (CNaPENp) have a polar chain length comparable or even larger than the alkyl chain size. During the micellar aggregation, repulsive interactions in the micellar polar corona are relatively weak. Typical value of the critical micellar concentration (CMC), around 10−4 M, is lower than characteristic CMC values of ionic surfactants.
Reversible adsorption of non-ionic surfactants occurs onto hydrophilic or polar solids–water interface below the CMC. As shown in Fig. 1 and in several other experimental studies [4,6,10,14–16,18,21], all adsorption isotherms reach a plateau around the CMC. This plateau decreases when the polar chain length increases. A step isotherm can be observed for very short polar chains, whereas for long polar chains, the adsorption isotherm appears to have a ‘Langmuir shape’ with no clear inflection point. In between, typical sigmoidal shapes can be observed with a rising part always located below but near the CMC. A parallel behaviour is observed in the kinetics of adsorption [3,11]. The adsorption rate is directly correlated to the monomer surfactant concentration in water, as long as the concentration is lower than the CMC and becomes constant as the CMC is crossed. Hence, the equilibrium as well as the kinetics data show that the adsorption layer is built from isolated molecules coming from the aqueous solution and not by direct adsorption of micelles. For solid surface developing amphoteric surface acids, such as SiOH and TiOH, the proximity of the rising part of the isotherms with the CMC (at least for short and medium POE chains) is typical of a ‘weak normal bond adsorption isotherm’. In fact, this is not unexpected, since adsorption merely involves the replacement of one hydrogen bond by another one (for example, a silanol–water hydrogen bond by a silanol–ethoxy hydrogen bond). However, the way that the polar chain interacts with the polar surface cannot explain the global shape of the adsorption isotherm. An interesting experiment [21] is to look at the adsorption of the polar chain of the surfactant, mainly a polyoxyethyleneglycol molecule. Generally, these molecules are weakly adsorbed (with a maximum around the zero point charge of the polar solid) as compared with the adsorption level of the corresponding surfactants.
Several experimental results support the fact that non-ionic surfactant adsorption on polar solid/water interface appears to be a cooperative process involving strong lateral interactions between surfactants and weak interaction with the solid surface.
Following the seminal work of Case and Mutaftschiev [2], it is interesting to compare normalised adsorption isotherms showing how reduced surface coverage θ evolves with the reduced coordinate C/CMC. Normalised isotherms of two surfactants having the same polar head and a slightly different alkyl chain can be superimposed. This property observed [4,15] for the adsorption of C8PE10 and C9PE10 on different type of polar solids (silica, quartz, kaolinite) strongly suggests a local organisation of adsorbed molecules very similar to that of the micelles in solution.
Perhaps one of the most clear macroscopic experiments to support an aggregative adsorption is the differential enthalpy of adsorption measurement. At very low surfactant coverage, the adsorption is essentially exothermic and certainly involves the fixation of polar surfactant chains on polar solid surface via hydrogen bonding. More unexpectedly, the differential enthalpy of adsorption of non-ionic surfactant dramatically drops as the surfactant coverage increases. Above a surface coverage θ of 0.1–0.3 and for a bulk surfactant concentration lower than CMC, an endothermic process is observed. Its amplitude is very similar to the one observed for bulk micellisation above the CMC [4,10,18].
At this level, an important issue is to understand the molecular structure of surfactant adsorption layer. Several organisations can be suggested, involving condensed molecular assemblies on the surface, in the form of either micellar-like aggregates or more extended lamellar phases. In the last 15 years, some (but few) works were published on this topic, attempting a direct inspection of non-ionic adsorption layer.
The fluorescence decay spectroscopy of a built-in chromophore or an extrinsic probe (pyrene) has been used to characterise the adsorbed phases formed by non-ionic surfactants at the solid–solution interface [14–16]. These works give clear evidence that adsorbed molecules are involved in finite surface aggregates. As shown in Fig. 2, the average aggregation number in the adsorption layer below the CMC and above a surface coverage of 0.2 turns out to be in the same range that the size of micellar aggregates observed in water well above the CMC. Later on, the non-ionic adsorption layer on a flat SiO2–water interface was investigated by neutron reflection [12]. From low to high coverage, the local and semi-local structure of the adsorbed phase appears to be a ‘fragmented’ bilayer. Similar conclusions were reached using small angle neutron scattering (SANS) structural determination of a non-ionic surfactant layer absorbed on tri-octahedral clay particles [8]. Finally, AFM was recently used to image the adsorption layer on different hydrophilic supports such as silica, mica or silicon nitride [5,7,22]. Surface aggregates were generally observed with a local bilayer structure. Diverse evolutions of these surface clusters with surfactant concentration or temperature were recorded ranging from polydisperse and flattened ‘micelles’ to extended bilayers.
The major point resulting from these different experimental investigations is that the adsorption process occurs mainly below but near the CMC. It involves a surface aggregative process similar in some respect to the bulk micellisation, taking place in solution above the CMC. The weak normal interaction between surfactant polar groups and solid surface permits to minimise the hydrophobic interaction through an aggregative process and to optimise the surface aggregate curvature, in order to reduce steric repulsion of surfactant polar chains.
3 Theoretical models
Several models [1,13] have been proposed to describe non-ionic surfactant adsorption. For example, the use of the self-consistent field theory [1] seems really appealing. However to our knowledge, no model has tried to analyse the specific properties of a ‘fragmented’ adsorption layer. The aim of this section is to present a thermodynamic model for such an aggregative adsorption [13]. In a first part, thermodynamic properties of non-ionic surfactant aggregates are presented. A simple model of micellisation is proposed and its predictions are compared with available experimental results. In a second part, I discuss the properties of an aggregative adsorption layer in equilibrium with the bulk solution. Using a grand partition function, theoretical adsorption isotherms are then computed and compared with experimental data.
3.1 Non-ionic micellisation
The CMC of non-ionic surfactants are lower than those of ionic surfactants. Polyoxyethylene (POE) chains repulsion on the external part of micelles is much smaller than for ionic surfactants. Generally, ionic charges can be localised on a defined external surface of the aggregate. Several phenomenological models use this approximation to compute ionic micellisation properties. In the case of non-ionic surfactants, POE polar chains have a typical size well above the alkyl chain dimension and fill an extended polar corona, as shown in Fig. 3. An average volume of interaction per polar chain must replace the average surface per ionic head. During the transfer of a POE chain inside this polar corona, two important contributions should be considered: steric repulsion and stretching deformation. Similar problems appear in diblock copolymer micellisation [17]. A non-ionic surfactant can be considered as the low molecular weight limit of a diblock copolymer, the very short alkyl chain playing the role of the solvent-incompatible block and the polyoxyethylene chain that of a small solvent-compatible polymer. Obviously, this approximation is not strictly applicable to low polymerisation indexes Np (Np<8). However, studies using such a hypothesis qualitatively and quantitatively reproduce some important features of non-ionic micellisation [9]. In this part, I will use this approach and try to extend the previous models of Tanford [23], and Nagarajan and Ruckenstein [19,20].

Local structure of a micellar aggregate of a non-ionic surfactant.
Structure locale de l'agrégat micellaire de tensioactif non ionique.
I use a thermodynamical model involving multiple equilibria between monomers and micellar aggregates of size n. The corresponding set of equations is written as:
| (1) |
| (2) |
3.2 Aggregative adsorption at hydrophilic solid/water interface
The perturbation depth of the water phase close to a hydrophilic solid surface (of silica, for example) is generally small (a few nanometres). In the following, I will discuss the properties of the surfactant molecules inside the adsorption layer, even if a part of the adsorption process (especially for interactions between POE chains and solid surface) results from an exchange mechanism with water. In general, adsorption of non-ionic surfactants occurs at very low liquid concentrations. In this condition, the surface excess of surfactants (mainly defined by a conventional Gibbs plane near the solid surface) and the total amount of adsorbed molecules can be considered to be very close. Keeping this approximation in mind, the free energy of an aggregative adsorption layer, FS(A,n,NaS,T) composed of NaS surface aggregates of size n, distributed on a mineral surface A, can be written as:
| (3) |
The standard free energy of transfer of a surfactant molecule from the bulk solution to the surface aggregate can be approximated as the sum of two terms, as:
| (5) |
The second step is to look at the grand partition function of the adsorption layer (μL1=cte). This function is written as:
| (6) |
| (7) |
| (8) |
| (9) |
This equation has an infinite number of solutions (n,NaS). The most probable configuration (and the average one far from a critical point) () is given by:
| (10) |
| (11) |
- • the absolute derivative is always negative; in this case, no aggregation adsorption is predicted; the model fails to give an average configuration of the interfacial system; the physical meaning of this situation is that adsorption of single molecules or the formation of small specific molecular associations must be considered;
- • a local maximum for t(n) exists, but it is not the most probable configuration; the former conclusions apply;
- • there is a global maximum; the more probable and the mean configuration of the adsorption layer is ().
- • the derivative dlnt/dn is always positive; a two-dimensional condensation involving an infinite aggregate occurs.
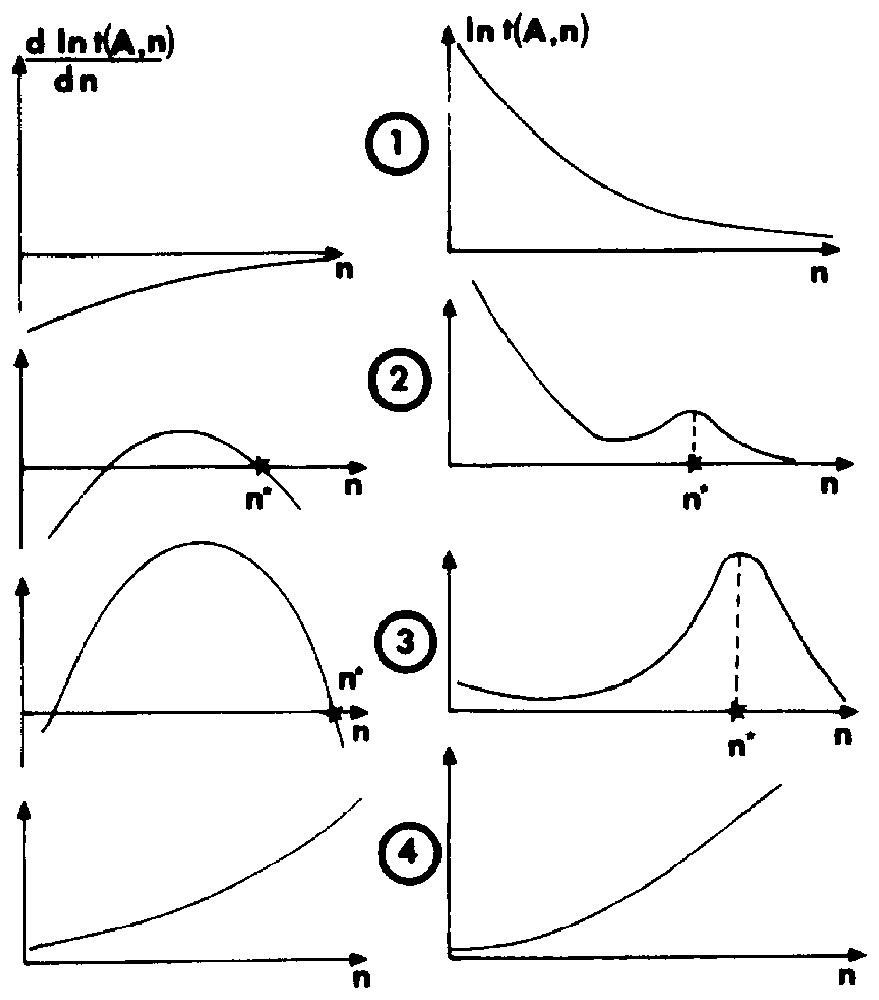
Four stability criteria used in the computation of the most probable configuration of the adsorption layer.
Quatre critères de stabilité utilisés dans le calcul de la configuration la plus probable de la couche d'adsorption.
Straightforward computation of the former model can be done when one chooses a localised adsorption model with surface aggregates interacting according to a hard core potential [13]. Adsorption isotherms of C12PENp homologous series are presented in Fig. 6A for a relatively weak value of ξa (−5.0 cal Å−2). Evolution of the average surface aggregate size is shown in Fig. 6B. The general trend closely follows the experimental results shown in Figs. 1 and 2. I have computed in Fig. 7 the apparent surface per molecule (σp) at the plateau of the diverse theoretical isotherms. A direct comparison with experimental results (on silica) is also shown. A good agreement is observed.
The aggregative adsorption model proposed in this work predicts some important features of the adsorption of non-ionic surfactants at the hydrophilic solid/water interface. The simple description of the bulk micellisation allows a phenomenological analysis of an isolated aggregate independently of the exact nature of the surfactant. Only structural parameters such as Na, Np, VT are needed to predict the micellar properties of a specific surfactant. A basic model of the aggregative adsorption involving a single adjustable parameter, namely ξa, describes how a weak interaction between polar monomers with a hydrophilic surface can generate a set of surface aggregates at equilibrium concentration below but close to the CMC. It is clear that some hypotheses used in this model are oversimplified. This is the case with an assumption concerning the inter-aggregate potential (hard core). For average or long POE chains, the overlapping of the adjacent surface aggregates should be taken into account. On the other hand, and for short polar chain surfactants, coalescence of surface clusters can occur at high surface densities. Certainly, the model does not correctly handle the early stage of the adsorption. Possible isolated and small molecular associations could appear in the first step of the adsorption (θ<0.2). These associations would have some apolar tails oriented toward the bulk solution. This point could explain the slight hydrophobic character of the adsorbed layer at low coverage rates. The global thermodynamic description of these isolated or tiny molecular associations is not straightforward, owing to their specific nature. For example, conformation of the POE chain of an adsorbed isolated surfactant depends on its length and on its interactions with the solid surface. This conformation, especially for long POE chains, can range from a flat to a ‘polymer-like’ configuration where only a small part of the available polar groups are interacting with the solid. I did not attempt to take into account such kind of adsorbed entities. However, it seems to us that the early stages of the adsorption must weakly perturb the ‘extended’ surface aggregation observed later on, except in two cases: (i) when the interaction between solid surface and polar chains is strong; (ii) for surfactants with long POE chains, as already discussed.
4 Conclusion
In conclusion, experimental results and thermodynamical models discussed in this paper present some general properties of non-ionic surfactant adsorption on hydrophilic solids. A more complete description of interaction between a solid surface and surface aggregates is certainly needed. An interesting question concerns the role of the so-called ‘normal interaction’ (surfactant/solid interaction) in relation with the choice of the optimal curvature for the surface aggregates. Non-ionic micellar aggregates exhibit strong curvature due to the interplay of the so-called hydrophobic interaction, which drives molecular aggregation, and the steric repulsion of the polar heads in the corona volume. The weak normal interactions between polar chains and solid surface are one condition to get curved surface aggregates of surfactants below but close to the CMC. This is an example where there is a possible organisation avoiding a complete unfolding (bilayer) of the surface aggregates. However, this unfolding can certainly be observed for surfactants having a short polar chain length.
Understanding the detail of the adsorption process of these surfactants is not simply an ‘academic’ exercise. These molecules constitute approximately one third of the total non-ionic surfactant usage. They are use as emulsifiers, detergents, foam control additives and dispersants. Recently, a large technological program has attempted to use them in the so-called ‘tertiary oil recovery’. The main goal was to increase the potential recovery of exploited oil fields by adjunction of surfactants and polymers in the incoming water flow, in order to decrease surface tension and capillary effects. One of the important advantages of these surfactants is their low sensitivity to an elevation and/or a variation of the ionic strength (generally observed in oil fields). Adsorption on the pore walls is a technological limitation of the process. A good understanding of this adsorption mechanism is necessary to limit this effect. Another topics of interest is related to the stability control of concentrated suspensions and the possibility, without flocculation, to concentrate and to re-dilute a formulation made of colloidal particles of SiO2, Al2O3, TiO2. It is possible to monitor non-ionic surfactant adsorption in order to control particle approach and to avoid direct contact (via a direct interaction between adsorption layers). These few examples show that a good understanding of adsorption processes (thermodynamics and structure) is important in numerous industrial applications.
Acknowledgements
It is a real pleasure to thank Pr J.-M. Cases who brought this subject to my attention (there is now a long time ago).


