Version abrégée
Par suite de leur utilisation industrielle dans des domaines aussi variés que la valorisation des minerais par flottation, la récupération assistée du pétrole, la stabilisation des suspensions, la détergence, etc., les tensioactifs ont fait l'objet, dans le passé, de nombreuses recherches et de nombreux débats et disputes en ce qui concerne leurs modes de fixation sur les surfaces minérales. L'origine des contradictions entre les modèles présentés provenait, d'une part, du désir légitime, chez de nombreux chercheurs, de vouloir proposer un modèle nouveau, souvent dit « unifié », applicable à tous les systèmes dans lesquels les tensioactifs sont utilisés [28] et, d'autre part, dans la plupart des cas, de l'ignorance des contraintes qui imposent et régissent les conditions d'utilisation. La recherche d'un modèle unifié est un leurre, pour quatre raisons fondamentales.
1. Le mode de rétention du tensioactif est différent selon la nature de l'adsorbant. La fixation se fera par la tête du tensioactif, la chaı̂ne étant rejetée vers la solution, dans le cas de l'adsorption sur solide hydrophile, et par la chaı̂ne hydrophobe, dans le cas inverse. Dans le premier cas, l'adsorption du tensioactif conduit à une surface hydrophobe, si l'adsorption est limitée à une monocouche, et, dans le second cas, à une surface hydrophile. Dans les deux cas de figure, la structure des phases adsorbées est différente.
2. L'importance des liaisons latérales entre les chaı̂nes aliphatiques favorise l'existence de phénomènes agrégatifs. La nature des agrégats formés est alors fonction de la conformation de la chaı̂ne aliphatique, c'est-à-dire de la valeur du point de Krafft [6]. Au-dessous de la température correspondant au point de Krafft, la chaı̂ne aliphatique est entièrement étendue, rigide ; chaque liaison CC ne peut prendre que la position trans. Les agrégats de molécules de tensioactifs formés sur la surface ou dans la solution ne peuvent avoir alors qu'une structure lamellaire, due aux fortes liaisons latérales entre les chaı̂nes (il n'a pas deux manières de mettre côte à côte des allumettes) : c'est l'état cristal hydrate [39]. Au-dessus de la température correspondant au point de Krafft, chaque liaison CC de la chaı̂ne peut prendre trois positions correspondant à l'état trans et aux états gauche +, gauche −. Les chaı̂nes deviennent fluides et acquièrent alors deux propriétés apparemment contradictoires, une très grande richesse conformationnelle, qui favorise leur expansion spatiale et les rend apte à occuper tout espace disponible, et des liaisons latérales entre chaı̂nes, qui les forcent à se rapprocher. Le gain entropique à l'équilibre dans ces phases condensées compense la perte d'énergie interne attractive. Les agrégats formés peuvent être, selon la concentration en tensioactifs ioniques, soit des phases micellaires (globulaires, cylindriques...), soit, à plus forte concentration, des phases lyotropes (hexagonales puis lamellaires). Il est évident alors que les conformations possibles de la chaı̂ne peuvent influencer la structure des agrégats superficiels : c'est l'état cristal liquide [2]. La connaissance de la physico-chimie du tensioactif en solution aqueuse est donc d'une importance capitale pour la compréhension des mécanismes d'adsorption [12].
3. L'importance de la liaison normale adsorbat–adsorbant, responsable de la fixation du tensioactif, impose la structure et l'organisation de l'agrégat formé. Si la liaison adsorbat–adsorbant hydrophile est forte, le tensioactif se fixe solidement sur la surface par la tête polaire et par l'intermédiaire de liaisons électrostatiques [1,7] ou chimiques [1,44]. Dans ce cas, les liaisons fortes latérales dans la couche adsorbée favorisent la formation de phases adsorbées condensées de structure lamellaire [1,8,10,12,23–25,57,59]. Dans ce domaine des fortes énergies de liaison de la molécule avec le support, l'hétérogénéité énergétique de la surface joue un rôle fondamental, dans la mesure où la taille des agrégats de surface dépend de la taille des domaines de même énergie qui la compose. La surface devient de plus en plus hydrophobe au fur et à mesure du remplissage de la monocouche (Fig. 1, courbe I). Cette dernière est complète pour des valeurs de concentration d'équilibre très faibles, dans un domaine où l'interface liquide–air n'est que faiblement couverte par les molécules tensioactives. Ce sont les conditions recherchées pour une bonne flottation du solide considéré. À plus forte concentration, la surface peut se recouvrir d'une bicouche et devient alors hydrophile (Fig. 1, courbe II). À l'inverse, les liaisons normales adsorbat–adsorbant faibles permettent, si la température est supérieure a celle du point de Krafft, de minimiser les interactions hydrophobes par l'intermédiaire d'un processus agrégatif et d'optimiser le rayon de courbure des agrégats de surface, qui se forment de manière à réduire les répulsions stériques entre les parties polaires des molécules. Elles permettent la formation sur la surface, à une concentration légèrement inférieure à la CMC, d'agrégats globulaires, dont la taille est voisine de celle des micelles présentes dans la solution au-delà de la CMC (Fig. 1, courbe VI). On rencontre cette possibilité lors de l'utilisation de tensioactifs non ioniques [31–37] en récupération assistée du pétrole. Il s'agit de minimiser les pertes de tensioactifs par adsorption [9] : la liaison normale tensioactif–solide est alors choisie comme étant voisine de la liaison tête polaire–eau. Dans le domaine des très faibles énergies normales d'adsorption, l'hétérogénéité énergétique du solide est un paramètre qui peut être négligé. La surface reste toujours hydrophile lors de l'adsorption.
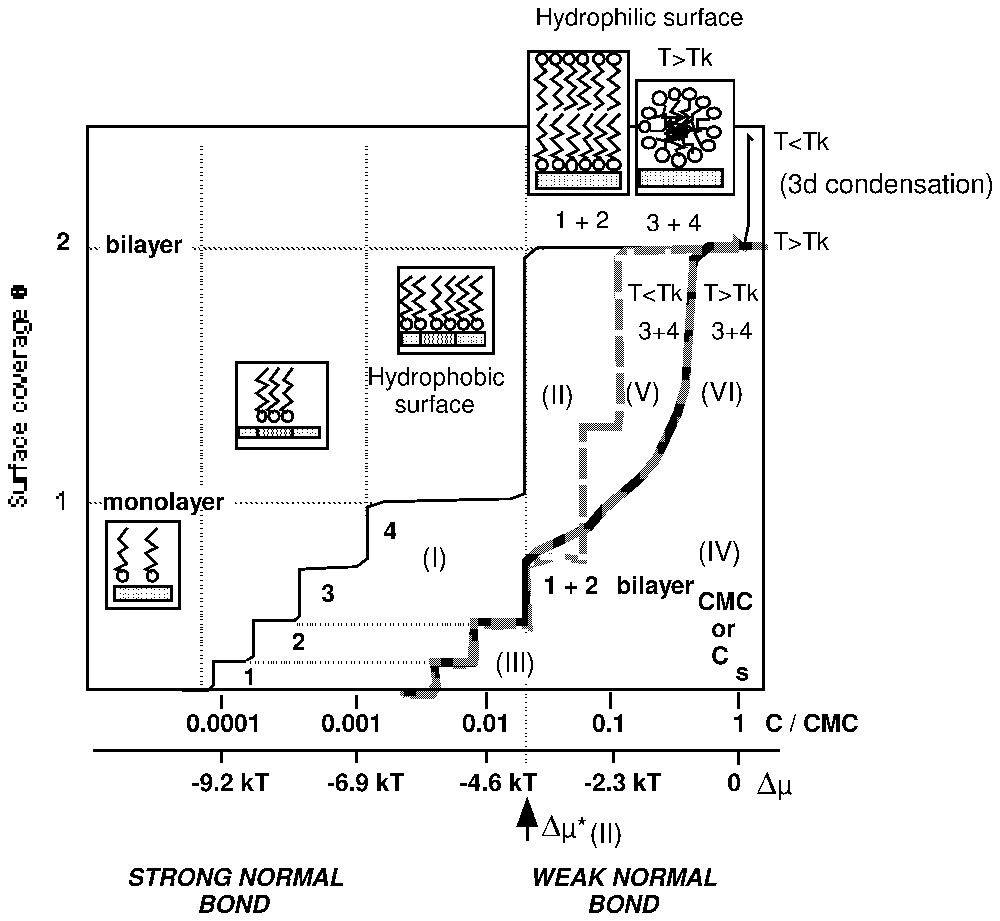
Schematic representation of different shapes of surfactant adsorption isotherms on heterogeneous and hydrophilic surfaces [12].
Représentation schématique des différentes formes d'isothermes d'adsorption des tensioactifs, obtenues sur surfaces hétérogènes des solides hydrophiles [12].
4. Le tensioactif ionique peut réagir avec des ions en solution provenant de la dissolution du solide. Les sels d'acides gras précipitent dans la solution et sur la surface sous forme de sels de calcium lors de la flottation des minéraux de type calcite, fluorine, apatite, scheelite... [41,45,46,50,51]. Les phases précipitées entraı̂nent la formation de couches adsorbées épaisses, alors que le champ de surface n'influence pas le dépôt de multicouches. Les lois de l'adsorption ne sont plus applicables.
Compte tenu de ce qui précède, l'approche thermodynamique ne peut être unique.
1. Dans le domaine de l'adsorption, il est possible d'utiliser la théorie de la condensation bidimensionnelle, en admettant la surface hétérogène [8,10,12] : dans la mesure où si une deuxième couche apparaı̂t, elle correspond toujours à une marche verticale d'extension une monocouche. Cette hypothèse est utilisable quelle que soit la valeur du point de Krafft du tensioactif. Cette approche permet d'utiliser le tensioactif comme sonde pour caractériser l'hétérogénéité énergétique superficielle du solide, pour déterminer l'état des molécules dans les agrégats superficiels (molécules fluides ou rigides), en utilisant : (i) le plan (degré de recouvrement–logarithme de la concentration d'équilibre) pour le calcul de l'enthalpie libre de transfert par groupement CH2 ou la valeur de l'encombrement moléculaire à la monocouche [12] ; (ii) le plan (degré de recouvrement–sous-saturation) qui permet de comparer l'organisation de la couche adsorbée à celle d'une phase de référence connue. Cette approche permet aussi de préciser l'origine de la formation d'agrégats de molécules condensées et le mécanisme de remplissage de la couche adsorbée. Les différents domaines homogènes de la surface se remplissent par ordre énergétique décroissant. La taille des différents domaines homogènes contrôle la taille des agrégats lamellaires à une couche (ou deux couches pour les fortes concentrations d'équilibre et si T<TKrafft, (Fig. 1, courbes III et V). Pour le moment, l'utilisation de cette méthode évite la détermination par le calcul de la structure de la couche adsorbée. Elle permet de prendre en compte l'hétérogénéité de la surface et la détermination de manière directe, à partir de la dérivée de l'isotherme d'adsorption dans le plan (θ=f(Δμ)) de la fonction de distribution des différents domaines énergétiques de la surface. La taille des agrégats condensés doit être telle qu'elle justifie l'usage de la thermodynamique statistique des phases de grandes dimensions. Dans l'élaboration de ce modèle, les auteurs furent influencés par la qualité des travaux ayant conduit à la théorie des hémi-micelles [1,23–25].
2. En cas de précipitation du tensioactif, l'utilisation de la thermodynamique relative à la condensation tri-dimensionnelle sur support et dans la solution aqueuse est recommandée. Ces phénomènes sont complexes (nucléation, croissance, mûrissement d'Ostwald) et sont à l'origine de l'accroissement des temps de mise à l'équilibre [41,45].
3. Dans le cas, de systèmes à interactions faibles avec le support et pour des valeurs de température supérieures au point de Krafft, la thermodynamique utilisable est celle des phases de petites dimensions. Les modèles, tout en rendant compte des effets coopératifs conduisant à la formation d'agrégats, doivent permettre de préciser les caractéristiques de la micellisation, c'est-à-dire de la formation d'objets à faible rayon de courbure.
Il n'est donc pas possible d'aborder les mécanismes d'adsorption des tensioactifs sans un minimum de connaissances sur la physico-chimie de l'adsorbat en solution aqueuse, sur la nature de la phase superficielle du solide, sur les conséquences de son hydratation, sur les modèles théoriques susceptibles d'être appliqués. L'utilisation de méthodes de caractérisation in situ des phases adsorbées doit être, lorsque cela est possible, privilégiée. La complexité des phénomènes présentés ci-dessus montre que l'interprétation des mécanismes de rétention et de transport des substances organiques (acides humiques et fulviques, herbicides, fongicides...) dans la biosphère sont plus complexes que ceux habituellement décrits.
1 Introduction
Studies dealing with surfactant adsorption at the solid–aqueous solution interface have raised numerous arguments and debates concerning the exact retention mechanism of amphiphilic molecules on hydrophilic solid surfaces. Most debates originated from attempts to build a unified theory able to describe surfactant adsorption for all the investigated systems [28]. However, depending on the field of application (flotation, enhanced oil recovery, detergency, paints, cosmetics, pharmaceutical...), i.e., on the adsorbate–adsorbent couple studied, different interpretations can be proposed, leading to the definition of different adsorption mechanisms.
Moreover, it is not possible (and dangerous) to interpret adsorption/abstraction mechanisms without a detailed knowledge of the amphiphile–water systems, since the structure of the molecule and the conformation of the chain impose the organisation of the adsorbed layer. For instance, in the case of long chain ionic surfactants [6], the solubility curve reveals two domains: (i) at temperatures below the Krafft point, a hydrated-crystal phase is in equilibrium with monomers [39]. This condensed phase has a lamellar structure, with the polar heads lying along the interface with water. The arrangement is such that the hydrocarbon chains are rigid, extended in the trans ‘zigzag’ position perpendicular to the interface and each sheet is approximately two hydrocarbon chain length thick; (ii) at temperatures above the Krafft point, the paraffinic chains become flexible. The conformation of the chain can be obtained by trans and gauche (g+, g−) rotations around each CC bond. The chains are then able to fill the irregularly shaped space available to them and the system then presents a rich polymorphism. It is the ‘liquid-like’ state [2]. In sufficiently dilute solutions, only monomers exist but, as the concentration is increased, these monomers associate to form an isotropic solution of micellar aggregates (spherical, ellipsoidal, rod-like) with no long-range intermicellar order. The concentration at which micelles start appearing is referred as the critical micelle concentration (CMC). At still higher amphiphile concentrations lyotropic liquid–crystalline phases form. For example, simple soaps first form a normal hexagonal phase composed of cylindrical aggregates in a hexagonal array. At very high concentration, lamellar (neat) phases appear. It is possible to distinguish between the different states of the chain on the basis of the values of the cross sectional area of the chain and the free energy of transfer of one CH2 group of the chain, Δg, respectively:
This paper aims at clarifying the apparent contradictions of the different models presented in the literature. Therefore, we will describe three important and different situations encountered when dealing with surfactant adsorption corresponding to two extreme application cases: ore flotation (surfactant adsorption on the surface is looked for in order to hydrophobise the solid particles [1]) and in enhanced oil recovery (surfactant consumption by adsorption has to be avoided [9]).
2 Ionic surfactants and ore flotation
Two main types of systems have to be explored.
2.1 Systems with strong normal adsorbate–adsorbent bonds
One of the first industrial uses of surfactants was to improve selectivity in ore flotation. In the case of barely soluble oxidised minerals (oxides, silicates...) long-chain ionic surfactants are preferably chosen. An accurate choice must be based on the affinity of the surfactant ions towards the mineral to be recovered. The normal adsorbate–adsorbent bond (generally electrostatic in nature [1,7]) must be strong, so that the mineral is hydrophobised for the lowest surfactant concentrations. Furthermore, to ensure an efficient adhesion of the ore particles to air bubbles, the solid should be covered, for instance, by a surfactant monolayer prior to saturation of the air/aqueous solution interface by surfactant molecules. This can be achieved at very low surfactant concentrations, much lower than the CMC (C/CMC<0.001; Fig. 1). In such systems, the surfactant cannot precipitate due to the low solubility of the solid phase. Different theories have been proposed to describe such systems.
2.1.1 The hemi-micelle hypothesis
Working on the adsorption of long chain alkyl-ammonium ions on quartz, Fuerstenau and Gaudin [25] proposed the hemi-micelle theory, based on the analysis of zeta potential and adsorption experiments [23,24,57,59]. According to this model, for the lower concentrations the ionic surfactants adsorb as individual ions, the polar heads being fixed on the surface through electrostatic interactions with the opposite charged surface until a certain critical concentration is reached in the double layer. For higher concentrations, the sharp increase in adsorption or the sharp change in the slope of the ζ vs logC curves marks the onset of surfactants association at the surface through lateral interactions between the hydrocarbon chains. The adsorbed ions associate into patches in much the same way they associate to micelles (Harkins cylindrical model) in the bulk solution. Because of the high surface charge, the surfactants ions must be oriented with the charged heads towards the surface and tails sticking out into the aqueous solution.
Other works presented ionic surfactant adsorption through formation of patches on homogeneous surfaces [3–5]. The analysis is based on a self-consistent field lattice (SCFA) theory originally developed to study adsorption and association of long chain flexible polymers and micelles [30,55]. The basic results from calculations using the SCFA theory are the equilibrium volume fraction profiles of the different component perpendicular to the surface that give information on adsorbed layer structure.
On a qualitative point of view, these models could predict most features of the experiments, i.e., growth by patches formation through Van der Waals interactions between the aliphatic tails, but could not explain the origin of aggregates of reduced size on a homogeneous surface and the thermodynamical conditions for bilayer formation.
2.1.2 Two-dimensional condensation on heterogeneous surfaces
In domains where adsorption sites present weak adsorption energy, surfaces could be legitimately considered as homogeneous. Such an assumption should never be applied to high adsorption energy surfaces. The existence of surface heterogeneity is a fundamental feature of mineral surfaces due to faces with different compositions (particularly for clays, basal and edge faces), surface roughness, impurities and grinding [13,15,26]. The fact that natural surface are heterogeneous is still not completely recognised [16,53]. In 1968, Cases and Mutafschiev [10] presented their work on the adsorption of a homologous series (10 to 18 carbon atoms in the chain) of alkylammonium chlorides on biotite. They showed that: (i) in the domain of bilayer formation, isotherms exhibit vertical steps characterising unambiguously two-dimensional condensation of the surfactants on the solid particles at undersaturation values equal to ; (ii) in the domain of monolayer formation, isotherms exhibit a constant slope. Since these isotherms could not correspond to the Temkin isotherm, as the slope would have to change with the increase in lateral bonds, i.e., with the number of carbon atoms in the hydrocarbon chain, the authors concluded that adsorption was due to a two-dimensional condensation on a non-homogeneous surface. This hypothesis was confirmed by the method improve to calculate lateral bonds [8,10,12] and the influence of surface energetic heterogeneity on isotherm shape was unambiguously displayed in numerous adsorbate–adsorbent systems [13,15,26].
On the basis of this interpretation, various treatments can be implemented:
2.1.2.1 Use of ionic surfactants as molecular probes to study surface heterogeneity
Surfactants can be advantageously used for determining the aspect ratio of clay particles [14] or the surface energetic distribution function fi of the adsorbent. The model adopted was the ‘patches’ model [8,10,12,52], which assumes that adsorption sites having the same energy are grouped on a heterogeneous surface into patches. Each patch is large enough to use the thermodynamics of large dimension phases and the state of an adsorption system in which two interacting molecules adsorbed on neighbour patches can be neglected. The adsorption systems can then be considered as a collection of independent systems. On each homogeneous domain i of the surface, monolayer formation corresponds to a first order transition and a domain i is either empty or full (0–1 approximation of the 2D-condensation [10,12]). Each homogeneous domain is characterised by the value of its area Si and the value of the normal molecular potential energy −ϕa,0,i. The surface coverage θ can then be expressed in a simplified way (equation (1)):
| (1) |
The position of a step characterising two-dimensional condensation on a domain i, , the undersaturation is obtained from the reduced form of the Cases and Mutaftschiev equation [8,10,12] (equation (2)):
| (2) |
| (3) |
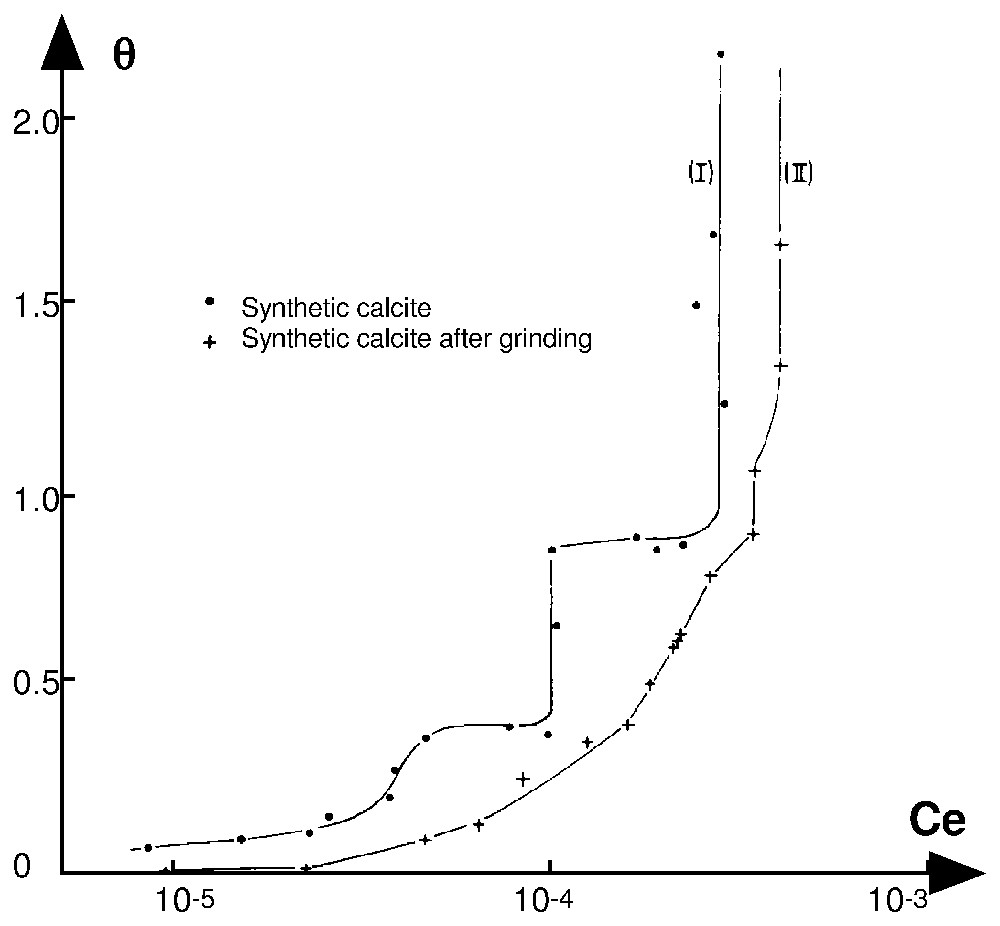
Adsorption isotherms at 25 °C and pH 8.3 of alkyldodecylammonium chloride on synthetic calcite, before (curve I) and after fine grinding (curve II) [26].
Isothermes d'adsorption à 25 °C et pH 8,3 du chlorure d'alkyldodécylamine sur une calcite synthétique, avant (courbe I) et après broyage fin (courbe II) [26].
If the condensation of a second layer is possible, it can be noticed on the adsorption isotherm, by the appearance of a vertical step, at an undersaturation value equal to (Fig. 1, curve II). This step corresponds to the adsorption of surfactant molecules on a surface energetically homogeneous due to the presence of the first layer. Surface phenomena do not influence bilayer formation, as the tail–tail bonds between surfactant molecules are the driving force for such behaviour.
Upon monolayer filling, the surface becomes more and more hydrophobic. In the process presented in Fig. 1 (curves I and II), the surface is hydrophilic for surface coverage values close to 0 and 2, and totally hydrophobic for a surface coverage around 1.
To conclude, it is important to note that micellisation in the bulk solution (C<CMC) and formation of lamellar aggregates at the solid–aqueous solution interface (if the normal adsorbate–adsorbent bonds are strong) are both aggregative processes. However, micellisation generates constant size micelles, whereas the formation of lamellar patches on a surface corresponds to aggregates of various sizes, depending on surface heterogeneity. If the surface of the minerals is very heterogeneous (more than ten domains), the size of the different homogeneous domains is small and if the normal molecular potential energies are continuously distributed, then the isotherm appears as a continuous curve, which is the most frequent case. An example is shown in Fig. 2. Curve I presents the adsorption isotherm of n-dodecyl ammonium chloride on synthetic calcite [26]. It is possible to distinguish two steps in the domain of monolayer formation characterising two homogeneous domains of large extension. The sample was made up of well-developed growth rhomboedra. Their specific area of fits well with the average dimension of the particles (10 μm). The finely dry ground calcite was made up of shapeless sponge-like aggregates without any cleavage plane mixed with a large number of very fine particles. It is a very heterogeneous material and the corresponding isotherm exhibits a quasi-parabolic shape up to an equilibrium concentration of , i.e., an isotherm without discontinuity characterising a highly heterogeneous surface (Fig. 2, curve II). The vertical parts of isotherms correspond to the three-dimensional condensation of n-dodecylammonium carbonate.
2.1.2.2 The use of the θ vs Δμ plot to characterise the state of the adsorbed layer
It was difficult in the past to study in situ the state of the adsorbed layer by direct means of investigation. In contrast, the organisation and structure of either bulk micellar and lyotropic phases or of the hydrated-crystal state were well documented [6,39]. Then, Cases and Mutaftschiev [10] decided to develop an equilibrium equation allowing to compare the state of the adsorbed layer with that of a reference well-known phase. The Frumkin–Fowler isotherm that characterises two-dimensional condensation can be simplified using the following assumptions: (i) a complete adsorption layer (θ=1) on an homogeneous domain has the same structure as the top lattice plane of the surface of a crystal of the same substance (T<TKrafft), hydrated-crystal state (the top bilayer [10]) or as the top lattice plane of the surface of an aggregate of the lamellar lyotropic phase (T>TKrafft, liquid crystal state); (ii) the maximum lateral binding energy per molecule ω is then the same in the adsorbed layer and in the reference phase; (iii) in a first approximation, the difference in entropic terms of kinetics origin between a molecule adsorbed on a foreign substrate and a molecule being part of the top layer of the reference phase of the same substance can be neglected. In other words, surface phenomena do not influence the structure and properties of the adsorbed layer as compared to those of the reference phase. Comparison of the state of the adsorbed layer with that of a reference phase can therefore be accomplished by subtracting the two equilibrium equations, between adsorbed layers on an homogeneous domain i and dilute solutions and between reference phase and bulk solution at saturation (equation (4)):
| (4) |
The equilibrium concentration of the reference phase corresponds to: (i) the saturation concentration of the hydrated crystal phase for a surfactant with n carbon atoms in the hydrocarbon chain Cs,n if T<TKrafft, or (ii) the saturation concentration of the lamellar lyotropic phase C0,L,n if T>TKrafft. This latter value is not known. As the conformation of the alkyl chains for lamellar reference phase is the same as that of micelles [40], the following equation can be written for a homologous series of surfactants (equation (5)):
| (5) |
On an energetically heterogeneous surface, each domain i can be characterised by the position of the step, and the corresponding undersaturation is obtained by posing θ=1/2 in equation (4), because of the evident symmetry of Frumkin–Fowler isotherms with respect to θ=1/2. This leads to equation (2).
Two important inferences can be made: (i) the θ vs Δμ plot can be used to unambiguously determine the surface energetic distribution function fi; (ii) in this plot, if the hypothesis concerning the similarity in organisation and structure of the reference phase and the adsorbed layer are fulfilled, then the isotherms obtained for an homologous series of surfactant on a solid have to superimpose. Such overlapping is often observed [49] (Figs. 3 and 4).
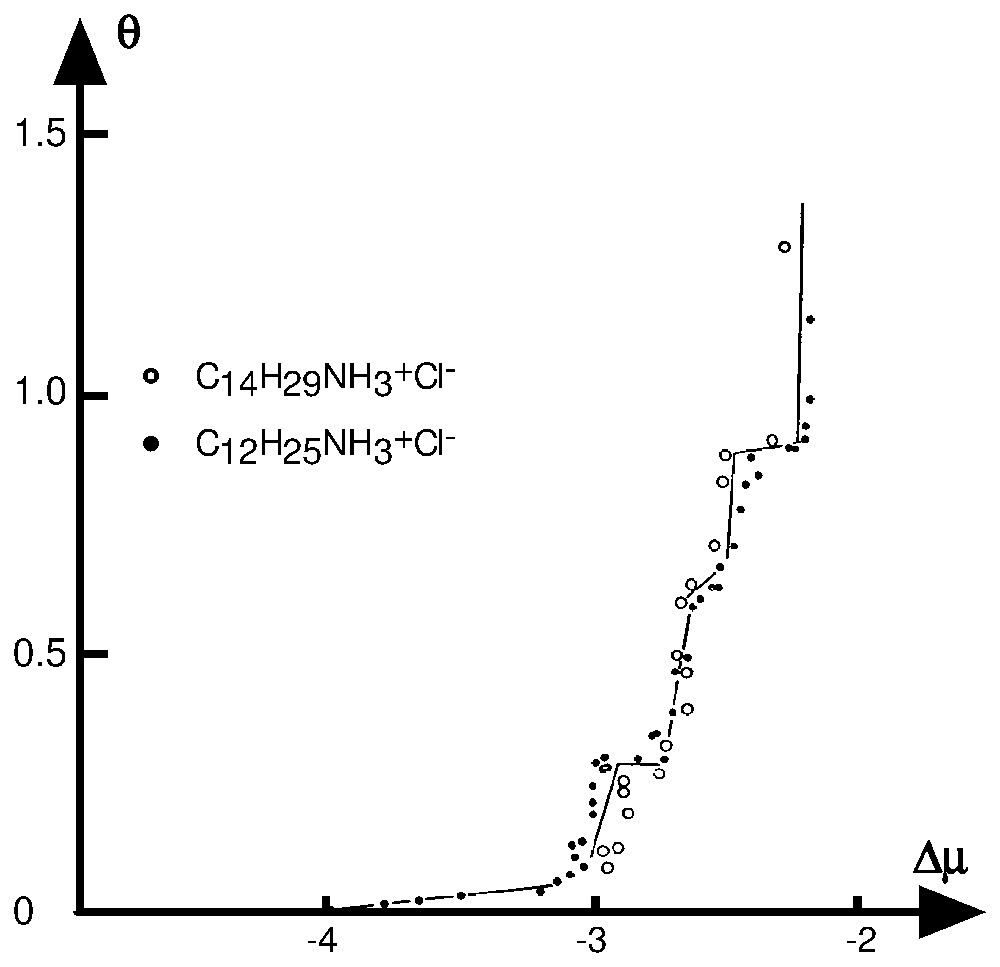
Superimposition in the (θ,Δμ) plot, of the adsorption isotherms at 25 °C and pH 8.0 of alkylammonium chlorides of different chain lengths on calcite [56].
Superposition, dans le plan (θ,Δμ), des isothermes d'adsorption des chlorures d'alkylamine de différentes longueurs de chaı̂nes, obtenues à pH 8,0 et 25 °C sur la calcite [56].

Superimposition in the (θ,Δμ) plot of the adsorption isotherms at 25 °C and pH 8.0 of alkylammonium chlorides of different chain lengths on phosphate oolites [56].
Superposition dans le plan (θ,Δμ), des isothermes d'adsorption des chlorures d'alkylamine de différentes longueurs de chaı̂nes, obtenues à pH 8,0 et 25 °C sur des oolithes phosphatées [56].
2.2 Systems with weak normal adsorbate–adsorbent bonds: three-dimensional condensation on substrate or surface precipitation
The separation of minerals such as apatite, barite, fluorite, magnesite, by flotation from other salt-type minerals such as calcite is extremely complex owing to the close similarity between their physicochemical properties. Up to recently, such problems remained largely unsolved. Some of the most crucial problems were:
- – the real influence of the nature of the normal bond;
- – solubility and its consequences.
The real influence of the nature of the normal bond. These minerals are concentrated by flotation with anionic collectors such as long-chained fatty acid or soaps. It was usually assumed that [1,27,44]: (i) surfactants included in the first adsorbed layer, are chemisorbed at the mineral surface; (ii) in the flotation of these minerals, conditioning is important because time is required for collector–mineral interactions to occur.
Solubility and its consequences. Salt-type minerals are characterised by solubilities that are higher than those of most oxides and silicate minerals. For fluorite-sodium oleate system, calcium cations can precipitate the anionic surfactants, provided the solubility of the calcium salt is exceeded. What are the consequences of this phenomenon?
In this last case, thermodynamic models have to agree with three-dimensional condensation of great dimension phases to take into account the fact that surfactants precipitate in the bulk solution and that, as surfactants can precipitate on the surface (3D-condensation on substrate), the amount of surfactant ‘abstracted’ or ‘retained’ on the surface may go far beyond monolayer capacity.
As the temperature for precipitated phases is always below the Krafft point, the reference phase to take into account is the topmost layer of the hydrated crystal phase. Therefore, to study these systems, two domains have to be taken into account:
- – the domain where the 2D-condensed phases are stable, i.e., Δμ<0 or Ce,n<Cs,n; equation (2) can be written in a simplified form (equation (2′))
in this domain ϕ0,0−ϕa,0,i<0 or ϕ0,0<ϕa,0,i;(2′) - – the domain of 3D-condensation, i.e., Δμ=0 or Ce,n=Cs,n and ϕ0,0=ϕa,0.
This result is of fundamental importance for understanding the formation of two- or three-dimensional condensed layers on a foreign substrate. It means that a condensed two-dimensional phase on a solid, i.e., an adsorbed condensed layer, is possible only if the work necessary to break a normal adsorbate–adsorbent bond is higher than half the separation work needed to break a molecule in the half crystal position of the reference phase [10,12]. In the other cases (Δμ=0 or >0), the formation of a three-dimensional condensed phase on the surface or in the bulk is more favourable. This result is independent of the nature of the normal adsorbate–adsorbent bond.
In addition, special care must be taken for correctly interpreting adsorption experiments:
- – in the range of 3D-condensation, surface coverage loses its physical meaning and terms such as ‘statistical surface coverage’ have to be used; the distribution on the surface of the amount abstracted is not known;
- – 3D-condensation on the surface and its characteristic infinite step (Fig. 2) are not always detected on experimental isotherms, because they depend on saturation concentration, dissolution kinetics of the mineral, volume of solution and surface area of the adsorbent; typically, these two last factors are simultaneously accounted for by changing the ratio solid weight to solution volume; the advent of the maximum often observed [51] on the ‘adsorption isotherms’ is reduced if the solid/liquid ratio is increased and, at high solid–liquid concentrations, the isotherm levels off at the statistical bilayer without any step characterising surface precipitation.
In conclusion, in all cases two-dimensional condensation takes place before three-dimensional condensation.
In order to illustrate the above-mentioned conclusions, it is necessary to present the results obtained by Mielczarski et al. [44,45] on the molecular effects in monolayer formation of oleate on fluorite and on the dynamics of fluorite–oleate interactions:
- – quantitative evaluation of self-assembled monolayers (composition, orientation, adsorbed amount) of oleate on cleaved (111) and polished fluorite surfaces by means of infrared external reflection spectroscopy [44] reveals two types of interaction of oleate groups with calcium surface atoms: (i) on cleaved fluorite surface, a bidentate-like bonding was revealed, with an orientation angle of 80° between the asymmetric stretching vibration of the COO groups and the normal to the surface (position almost parallel to the interface). This bidentate is characterised by an absorbance band at 1536 cm−1. Such a situation is predominant for cleaved fluorite (up to 75% of adsorbed molecules); (ii) the second calcium oleate surface species is the unidentate-like form, with an absorbance band at 1575 cm−1; in that case, the average orientation angle is equal to 56°; the amount of this surface species is related to the number of crystallographic defects present on the natural cleavage plane of fluorite, since their amount increases with polishing;
- – the perturbation found naturally or occurring during polishing or sample preparation of the perfect cleavage plane results in the formation of both bidentate-like and unidentate carboxylate surface complex, as well as the intermediate forms;
- – these first results suggest that in the case of perfect conditions for a well-organised monolayer, only one type of carboxylate group (the bidentate-like form) with the band at 1536 cm−1 should be observed. The importance of this band characterises the order of the lamellar aggregates present on the surface below monolayer capacity;
- – the nature, structure and kinetics of formation of mono and multilayers have also been examined by internal reflection spectroscopy [45].
New and interesting results can be presented as follows (Fig. 5).
- (i) Fluorite immersed in basic oleate solution shows surface phenomena dependent on the initial oleate concentration.
- (ii) At a diluted concentration of 5·10−6 M, the adsorbed amount does not exceed 0.25 of a monolayer after 2 or 6 h of adsorption (2D-condensation domain).
- (iii) In dilute solution, for a concentration equal to 9·10−6 M, a maximum of adsorption of about 4 monolayers is observed after 4 h. Microscopic studies already reveal the presence on the surface of three-dimensional aggregates looking like round and elongated patches. After 19 h of adsorption, the surface species undergo dissolution and the adsorbed amount is about 0.2 statistical surface coverage. At this low coverage, a broad band centred at 1560 cm−1 appears due to a wide distribution of the various conformations of carboxylate surface groups. This seems to agree with the presence of very small patches on the surface, with a high ratio of external, less oriented molecules.
- (iv) At 3.3·10−5 M, the amount of surface precipitated calcium oleate presents a maximum after 6 h adsorption at about 20 statistical monolayers. After 8 h, the amount of calcium oleate abstracted decreases down to 8 statistical monolayers. Microscopic and AFM studies show that the patches already described occupy only a small part of the surface and that their height changes from 10 to 600 nm, i.e., 5 to 285 monolayers in a rigid conformation. These results clearly show that 3D-condensation (nucleation and growth) is responsible for the formation of calcium oleate surface structures. The dissolution of surface products with an increase in adsorption time can then be assigned to Ostwald ripening, which transfers oleate and calcium ions from the surface to the bulk solution to favour the growth of calcium oleate particles more crystallised than on the surface.
- (v) At a concentration of about 1·10−4 M sodium oleate, the intensities of the aliphatic stretching vibration bands in the spectra indicate the monolayer coverage after 30 min of adsorption. The carboxylate absorbance region exhibits a doublet at 1574 and 1537 cm−1 similar to those observed at lower initial oleate concentrations as well as an additional sharp band at 1563 cm−1 assigned to sodium oleate [50], which disappears after 1 h. Longer adsorption time results in the disappearance of the band at 1563 cm−1, whereas the total adsorbed amount increases up to about two statistical monolayers, the highest coverage found at this concentration. After 4 h, lower intensities indicate a coverage of about 1.2 statistical monolayer.
- (vi) Surface products formed at a solution concentration of 5·10−4 M sodium oleate were found to be similar to those formed at 1·10−4 M after a short adsorption time. The difference is that at higher concentrations, the same adsorption products are observed at short and long adsorption times. After 4 h contact with oleate solution, there is still sodium oleate in the surface product. The total amount of oleate abstracted never exceeds a statistical coverage. The microscopic picture shows small three-dimensional patches, unevenly distributed on the mineral surface. At this high concentration, it was suggested that the presence of mixed calcium-sodium oleate micelles in solution prevents the formation of surface aggregates [45]. The unravelling of such complex phenomena was only possible by using in situ real time experiments. These results were later confirmed using other methods [46]. The use of infrared external reflection spectroscopy coupled with AFM and optical microscopy was also successfully applied to study the nature and structure of surface oleate species abstracted on calcite in spite of the overlapping of a small spectroscopic signal from surface species with a very strong absorption signal from the substrate [41].
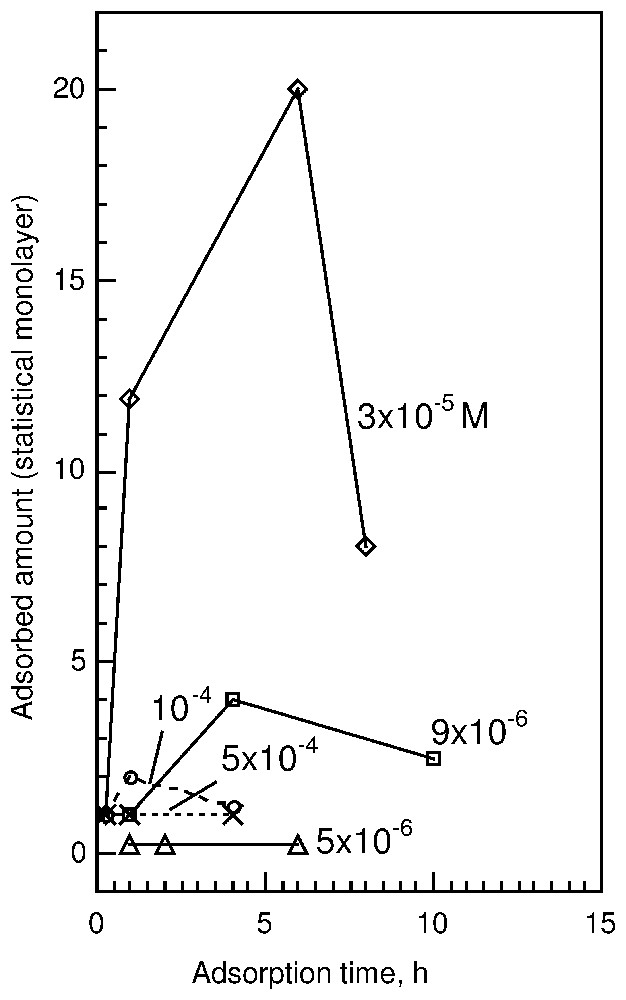
Dynamics of oleate interaction with fluorite at different sodium oleate concentrations in solution, revealed by spectroscopic studies of the mineral surface [45].
Cinétique d'adsorption des ions oléate sur de la fluorine, mise en évidence par l'utilisation de l'interférométrie infrarouge à transformée de Fourier couplée à la réflexion externe.
As thermodynamically predicted, surfactant ions have at first, as much affinity for surface products than for particles that precipitate in solution. For this reason, these systems are considered as systems with weak normal adsorbate–adsorbent bonds. Some of the above-developed considerations can be applied to short chain surfactants, such as potassium xanthates (which are commonly used as collectors in the selective flotation of sulphide minerals) when the mechanisms presented here are not hidden or complicated by associated phenomena resulting from superficial electrochemical reactions [11,60].
3 Enhanced oil recovery and surfactant adsorption
Ionic and non-ionic surfactants have been utilised for optimising enhanced oil recovery techniques [9]. The aim was then to build stable micro-emulsions. For reaching such a goal, the surfactant should have no affinity for the reservoir rocks so that the solutions retain their detergent properties. Two types of surfactants have been investigated: ionic surfactants such as alkyl or alkyl benzene sodium sulfonate for injection in sandstone deposits (quartz and clay surfaces are supposedly having the same electronegative charge as surfactant ions in solution to avoid surfactant adsorption) or non-ionic surfactants. Such systems are referred to as weak normal adsorbate–adsorbent bond [12]. In such systems, adsorption begins for equilibrium concentration between 0.01 and 0.1 of the CMC (Fig. 1, curves III–VI).
3.1 Non-ionic surfactant–solid systems
The retention mechanisms of non-ionic surfactants at the silica surface were carefully described by Klimenko et al. [29] and Levitz and co-workers [31–37]. The adsorption isotherms of alkyl or alkyl phenol polyoxyethylene glycol on hydrophilic silica surface present a ‘Langmuirian shape’ with no clear inflexion point. Reversible adsorption occurs below the CMC (). All the isotherms reach a plateau around the CMC. This plateau decreases when the polar chain length increases. Fluorescence spectroscopy of a built-in chromophore or an extrinsic probe (pyrene) shows that adsorption is an aggregative process. Adsorbed molecules are involved in finite surface aggregates. The average aggregation number between 0.2<θ<0.8 turns out to be in the same range as the size of micelles in solution measured well above the CMC. For higher surface coverage, surface aggregates coalesce to form a bilayer. These results can be understood as follows: these surfactants are anchored to the surface through a direct bond between the POE chains and the solid surface. Normal adsorbate–adsorbent bonds responsible for adsorption are due to hydrogen bonding between surface silanols and oxygen atoms of the ethoxy-groups of the non-ionic surfactant [22] (for this reason, maximum adsorption always occurs at the Zero Point of Charge of the solid [38]). The strength of this bond is similar to that existing between POE chains and water molecules in the bulk solution. This explains why micelles are forming on the surface near the CMC. In contrary to the case described in §2, where the strong bond between the solid and the ionic headgroups of the surfactant directs the hydrophobic tail of the surfactant towards the aqueous solution, non-ionic molecules tend to take a configuration avoiding the direct contact of the hydrophobic tails with the aqueous solution from very low surface coverage values. This can occur through the formation of surface micelles, according to a process described by Levitz and co-workers. In others words, in these systems, ‘the weak normal interaction between surfactant polar groups and solid allows to minimise the hydrophobic interactions through an aggregative process and to optimise the surface aggregate curvature in order to reduce steric repulsion of surfactant polar chains’, as claimed by Levitz [33]. Formation of surface micelles was confirmed by ellipsometry studies [38,58] and other methods [34] including microcalorimetry: upon micelle formation, the differential enthalpies of displacement of water by polyethylenic surfactants on silica and kaolin are slightly endothermic always lower than 10 kJ and close to the values obtained for micellisation enthalpies [19,20].
In these systems, the surface always remains hydrophilic, whatever the apparent surface coverage.
3.2 Ionic surfactant–solid systems
Two different cases can be presented according to the Krafft point.
3.2.1 Adsorption isotherms are carried out at a temperature higher than the Krafft point
The adsorption of sodium octylbenzene sulfonate (TKrafft 18 °C [3]) on alumina at different temperatures (25 and 35 °C), ionic strength (0.1 and 0.3% NaCl) and pH (5 to 9.2) was carefully studied by Denoyel and co-workers using adsorption experiments [19,20] and batch and liquid flow microcalorimetry [20,21]. The general shape of the curves of differential enthalpies of displacement of water by surfactant leads to the following interpretations: (i) up to a surface coverage of 0.2, the differential enthalpy of displacement decreases as expected on heterogeneous surface and is likely to correspond to lamellar surface patches – in this part of the adsorption isotherm, flocculation was observed showing that hydrophobic moieties are forming due to hemi-micelle formation on alumina particles (Fig. 1, curve III) –; (ii) at higher surface coverages, the enthalpies of displacement decrease and become of the same order as micellisation enthalpy – by analogy with non-ionic surfactant adsorption, it was assumed that adsorption in this coverage range is an aggregative process between surfactants molecules, leading to surface micelles on the part of the surface non covered by surfactant (Fig. 1, curve VI) –; (iii) at higher concentrations (θ≈0.9 at 25 °C) on the enthalpy curve, a peak is obtained, which was assigned to the fusion of micelles to form a bilayer. In Fig. 1 (curve IV), the transition between the filling of domains 1+2 (high energy sites, formation of lamellar patches) and 3+4 (formation of globular micelles) corresponds to the formation of bilayers in domains 1+2 (). This hypothesis was not confirmed by microcalorimetry experiments. It seems that bilayer formation is only possible on flat surfaces and not on rough surfaces. These results do not agree with the work of Chandar and co-workers [18] who, on the basis of fluorescence probe studies on the structure of the adsorbed layer of dodecylsulfate at the alumina–water interface at 25 °C, pH 6.5, 0.1 M NaCl, claimed the presence of highly-organised surfactant aggregates (hemi-micelles) on all the concentration range below the CMC, the average aggregation number of the patches increasing along the isotherm from 66 to 356 just below the CMC. These results were discussed earlier [12,17]. In order to clearly discuss these important results, it is necessary to precisely know the Krafft point of the surfactant used. Indeed, the Krafft point of sodium dodecylsulfonate was found about 31 °C [2]. It is a crucial point for understanding surfactant adsorption.
3.2.2 Adsorption isotherms are carried out at a temperature lower than the Krafft point
An adsorbed surfactant ion may be present in a condensed two-dimensional phase in a fully extended form, i.e., the surface patches have a lamellar-type organisation. Since (Fig. 1, curve IV), it was assumed that for , domains 1+2 are covered with bilayers. When adsorption begins in domains 3 and 4, the patches that form are also bilayers (Fig. 1, curve V). The conditions for the filling of a surface by bilayered patches are:
- – surface energetic heterogeneity,
- – weak normal adsorbate–adsorbent bond,
- – temperature lower than the Krafft point.
In the past [28,54] Schechter and co-workers proposed a new theory that they termed the admicelle hypothesis: surfactant aggregation occurs on the surface of mineral oxides in the same way as micelle formation and these formed aggregates are bilayers. They used for this approach the pseudophase separation model for micellisation. In fact this approach fails for two fundamental reasons:
- – if the pseudo-phase separation model applies in this range of high concentrations, i.e., weak normal adsorbate–adsorbent bond, micelles would form and not lamellar patches;
- – then, the temperature is higher than the Krafft point.
Classical adsorption theory sufficiently explains the formation of bilayers [8,10,12]. Overall, it can be seen that for surface coverage higher than the coverage corresponding to , the surface must become and stay hydrophilic.
In these kind of systems, it was also shown that counter-ions play an important part in adsorption phenomena. Adsorption isotherms of sodium tetradecyl sulfonate (TS), sodium dodecylsulfonate (DS) and sodium decylbenzene sulfonate (DBS) on kaolinite, determined at a temperature below the Kraff point, are presented in the θ vs Δμ plot (Fig. 6) [47,48]. In that case, the hydrated-crystal state was chosen as a reference phase. It was assumed (§2.1.2.2) that if the organisation of the adsorbed layer is identical to that of the top reticular plane of the reference phase, the isotherms built with a homologous series of surfactants superimpose. The non-superimposition of the tetradecyl sulfonate isotherm with the two others has to be discussed according to two conclusions:
- – one may assume that the adsorbed layer structure is different from that of the reference phase; this should be assigned to some influence of the kaolinite surface; however, the superimposition of the DS and DBS isotherms does not agree with this assumption; therefore, this hypothesis can be rejected;
- – one may assume that the normal bond between solid surface and the adsorbed surfactant ions is different in the TS-kaolinite system compared to that in the DS- and DBS-kaolinite systems.
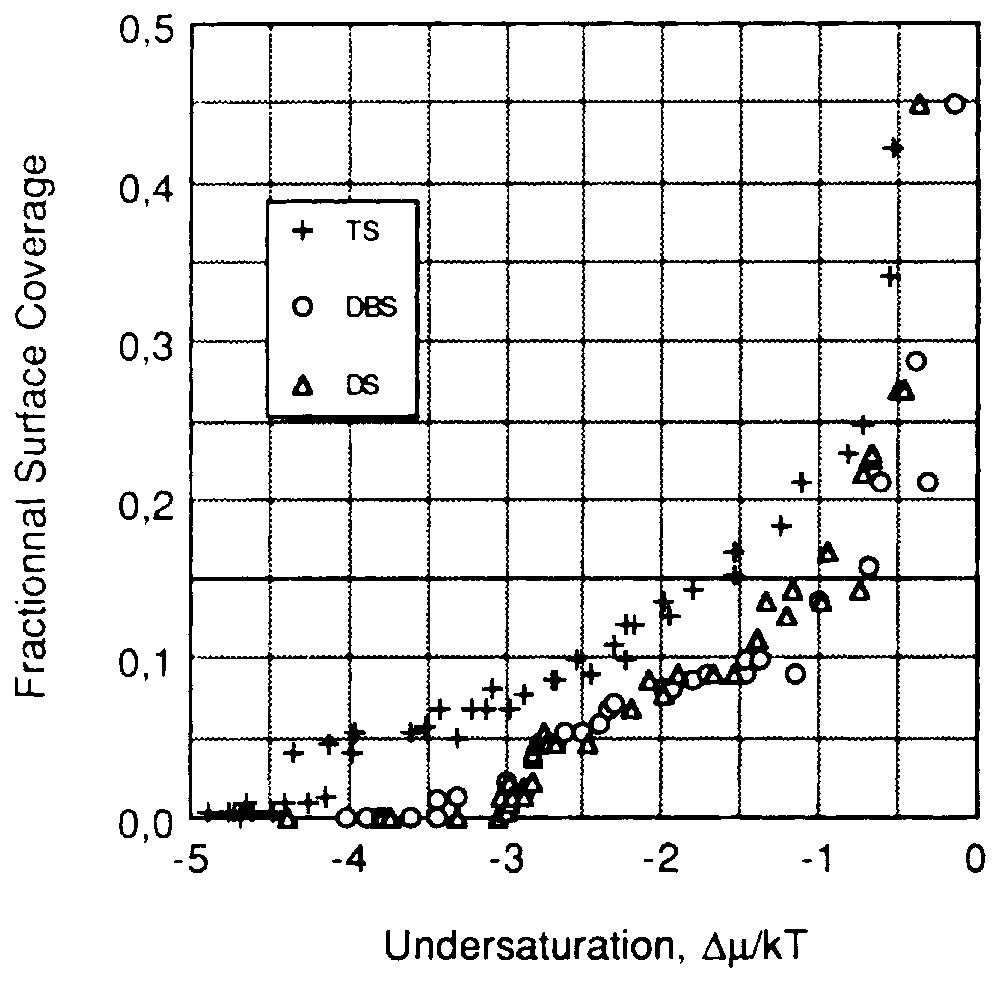
Reduced adsorption isotherm ((θ,Δμ) plot) at 28 °C and natural pH of sodium tetradecyl sulfonate, sodium dodecyl sulfonate and sodium decylbenzene sulfonate onto kaolinite [48].
Isothermes d'adsorption réduites (plan (θ,Δμ)) des ions tétradécylsulfonate, dodécylsulfonate et dodécylbenzène sulfonate sur la kaolinite à 25 °C et à pH naturel [48].
Before discussing this latter hypothesis, attention should be drawn to the following point: (i) the Cationic Exchange Capacity (CEC) of kaolinite is located on edge faces [16]; (ii) the edge faces of the kaolinite sample determined using argon low-temperature adsorption microcalorimetry represent 16.1% of the total surface area ( [47]); (iii) the exchangeable cations of natural kaolinite are calcium ions; (iv) the surfactants used are sodium salts; (v) when surfactant concentration increases, the concentration in sodium ions also increases in the bulk; (vi) a cationic exchange occurs between sodium ions and exchangeable calcium ions.
Complementary experiments revealed that sodium ions do not exchange below a concentration of 0.001 M. For higher sodium concentrations, the mean exchange ratio was one calcium ion for two sodium ions [47]. For a sodium concentration equal to 0.01 M, the exchange was far from complete.
The TS adsorption isotherm is located in a concentration range where no cationic exchange occurs up to a surface coverage of about 0.2, whereas adsorption is due to binding of surfactant ions on the edge faces through calcium and sodium ions mainly for DS and DBS. This result is in agreement with the shift of the TS isotherm towards lower undersaturations. It can be noted that a fractional surface coverage of 0.2 nearly corresponds to the formation of a complete bilayer in a hydrated-crystal state on edge faces. This last case provides a good illustration of the influence of counter-ions and exchange phenomena in this range of concentration.
4 Conclusion
The objective of this review was to present different systems where surfactants are used and the associated constraints that prevent the development of any unified theory for surfactant adsorption due to the complexity of the mechanisms involved. A good understanding of adsorption phenomena requires to know the surface energetic heterogeneity and crystal chemistry of the adsorbent, the structures resulting from the hydration of solid surfaces, the physico-chemistry of surfactants in aqueous solution, including the precise determination of the temperature of the Krafft point for ionic surfactants. The possible existence of surface precipitation phenomena, the application of thermodynamics of large dimension phases and of small phases, i.e., the basic adsorption and the three-dimensional condensation theories, have also to be considered. Micelles and lamellar surface patches involve aggregative processes, but the nature of the surface cannot be ignored, especially in the domain of strong normal adsorbate–adsorbent bonds, where the size of patches depends on surface heterogeneity. This is true even if surface phenomena do not influence the organisation of surface species. When the investigated system is favourable, the use of sophisticated in situ methods for surface characterisation of the adsorbate provides useful complementary information for interpreting adsorption isotherms. These remain the basic tool for a proper understanding of adsorption phenomena [17]. The desire to present a brand new theory for every investigated system, although exciting, may not always push in the right direction for helping to solve industrially relevant problems.
The same general remarks and the same methodology can be applied for a good understanding of very complex mechanisms involved for instance in the adsorption–retention and in the transport of organic compounds as micropollutants in the biosphere. This methodology also seems to be the most appropriate one to solve the real influence of organo-minerals. This phenomenon is central to increase our efficiency in gaining a better knowledge, a better management, and a better conservation of soils and continental water.
Acknowledgements
J.-M. Cases wish to thank Mutaftschiev for his valuable contributions and discussions during so many years with one of them (J.-M. Cases).


