Version française abrégée
1 Introduction
La vitesse de chute de sédiments cohésifs en suspension dans les cours d'eau est très supérieure à celle des grains d'argile individuels. Ceci s'explique par le fait que la plus grande partie de la masse sédimentaire en suspension se rassemble sous la forme d'agrégats [9]. La vitesse de chute synthétise certaines caractéristiques de ces agrégats, telles que la taille, la forme et la masse volumique.
La vitesse de chute intervient dans deux phénomènes sédimentaires de première importance, qui sont la répartition verticale des matières en suspension (MES) et leur flux de dépôt. La vitesse de chute varie principalement en fonction de la concentration locale C [4,5,11]. Pour les suspensions diluées, la vitesse de chute augmente avec C. Pour les suspensions très concentrées
La plupart des auteurs caractérisent la vitesse de chute par sa valeur médiane locale
2 Théorie
Une distribution verticale stationnaire des MES dans un écoulement est théoriquement possible si, à chaque niveau z, le flux solide vertical descendant lié à
Ainsi, si
La dynamique verticale des MES provoque une ségrégation des agrégats, de sorte que les vitesses de chute des sédiments du fond sont plus élevées que celles des sédiments superficiels [2]. Comme la concentration décroît aussi avec z, la variation verticale de
Le profil vertical de C dépend de l'expression retenue pour décrire
De plus, le paramètre r intervenant en (3) et (6) et caractérisant l'étendue de valeurs de W satisfait à l'Éq. (7) [8], où
Si une vitesse de chute locale adimensionnelle est définie par
En régime stationnaire, on peut montrer que si, pour un sédiment donné, la fdp de W au fond est décrite par une loi gamma, alors la variable aléatoire W, à n'importe quel niveau z, est aussi distribuée selon une loi gamma de même paramètre r [1]. Dans ce cas, la variation verticale de
Tous ces résultats sont compatibles avec les expressions usuelles de
Le Tableau 1 donne, pour plusieurs valeurs de r, les valeurs de
Values of
Valeurs de
| r |
|
|
|
| 0.25 | 2.0000 | 5.7243 | 11116 |
| 0.50 | 1.4142 | 2.1981 | 171.3 |
| 1.00 | 1.0000 | 1.4427 | 21.85 |
| 2.00 | 0.7071 | 1.1966 | 7.31 |
| 4.00 | 0.5000 | 1.0893 | 3.83 |
| ∞ | 0.0000 | 1.0000 | 1.00 |
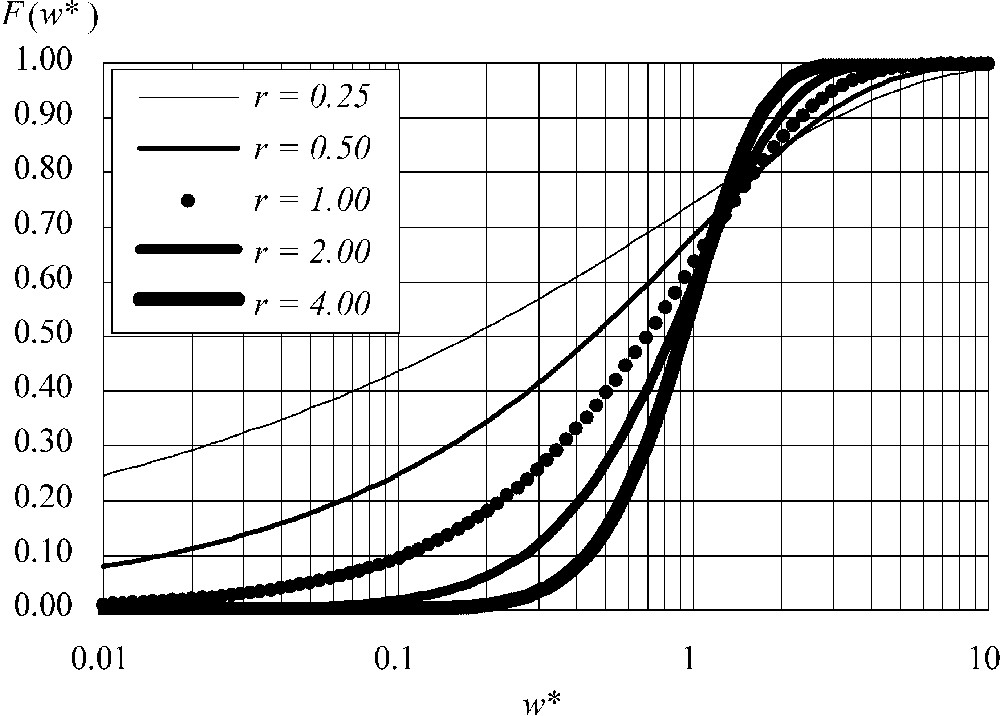
Cumulative distribution function linked to the pdf
Fonction de répartition associée à la fonction de densité de probabilité
À titre d'exemple, la Fig. 2 montre, pour
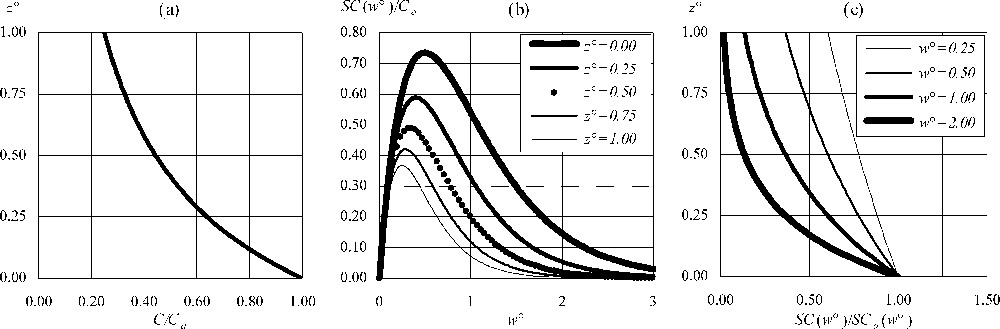
Suspended sediment vertical distribution for
Suspended sediment vertical distribution for
Répartition verticale des matières en suspension pour r=2 et un nombre de Péclet
Répartition verticale des matières en suspension pour r=2 et un nombre de Péclet
3 Méthodes et résultats
Dans le but d'étudier la répartition verticale des MES et leurs vitesses de chute, six tests ont été effectués sur des échantillons prélevés dans l'estuaire de la Loire simultanément au fond, à mi-profondeur et en surface [1] (Tableau 1). La distribution locale des MES en termes de vitesses de chute a été examinée par la méthode du tube de décantation [6].
La Fig. 3 montre les fréquences cumulées expérimentales de
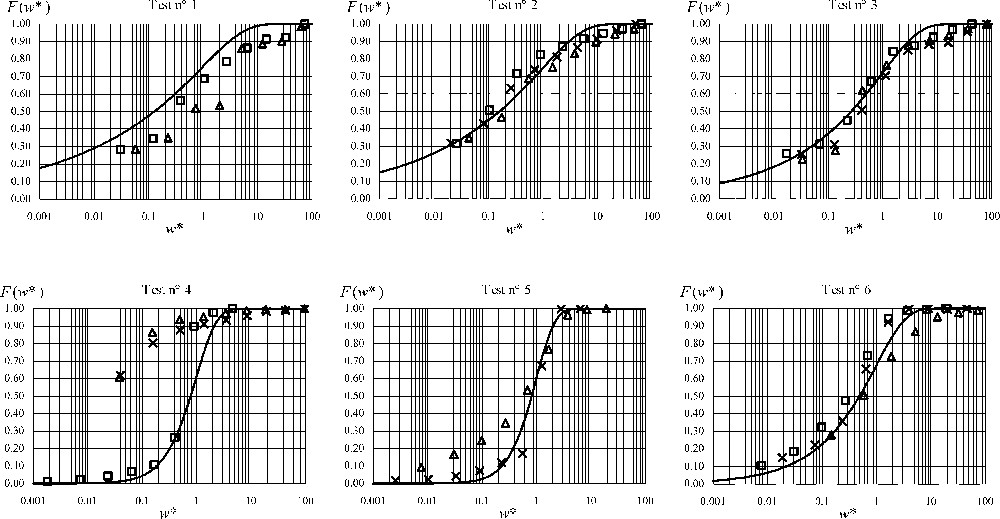
Experimental cumulative frequencies of
Fréquences cumulées expérimentales de
Ces lois sont confirmées par huit autres mesures in situ avec un tube d'Owen
D'une façon générale, pour
On doit noter que, quand une couche de crème de vase recouvre le fond, la concentration de référence
4 Conclusions
En régime stationnaire, si la vitesse de chute des sédiments du fond est distribuée en accord avec la loi gamma, alors la variation verticale de la vitesse de chute moyenne locale
Ainsi, quand la vitesse de chute de la masse de sédiments en suspension près du fond est distribuée selon une loi gamma, la vitesse de chute moyenne
1 Introduction
The settling velocity of cohesive suspended sediments in the natural open surface flows is much higher than that of the elementary clay grains. This is due to the fact that the greatest part of the mass of sediments consists of aggregates, whose weight is largely higher than that of the individual grains [9]. The settling velocity includes a certain number of the characteristics of these aggregates, such as their size, shape and density.
The dynamics of the cohesive sediment is strongly dependent on the settling velocity of the suspended matter. This parameter intervenes in two sedimentary processes of first importance: the vertical distribution of the suspended matter and its deposition rate.
Settling velocity varies mainly with the local suspended sediment concentration C. A great number of field and laboratory measurements [4,5,11] showed that for diluted suspensions, settling velocity increases regularly with the concentration. On the other hand, for the highly concentrated suspensions starting from a concentration of about 10 kg m−3, this velocity decreases when the concentration increases because the sediments are blocked in their fall (hindered velocity). What follows deals with the study of the settling velocity of diluted suspensions for concentrations lower than about 10 kg m−3.
Most of the researchers characterize settling velocity by its median value. In all the cases, the median settling velocity
Settling velocity in sedimentary models is usually represented by a scalar whose value depends mainly on the local suspended sediment concentration [3–5,7,10,11]. However, taking into account the great diversity of aggregates that one can simultaneously find in suspension, the settling velocity is actually a stochastic variable. A random variable W is defined as the settling velocity of a particle of the suspended aggregates of infinitesimal elementary mass.
2 Theory
A steady-state vertical distribution of the suspended sediment in a flow is theoretically possible if at each level z the vertical downwards mass flux due to the local mean settling velocity
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The vertical profile of the concentration depends on the expression used to describe
| (6) |
| (7) |
If a non-dimensional local settling velocity
| (8) |
In steady-state conditions, if, for a given sediment, the pdf of W linked to the bottom sediments is described by a gamma distribution, then, for every level z, W is also gamma distributed with the same parameter r [1]. In this case, the vertical variation of the local mean settling velocity
These results are compatible with the usual expressions of
| (9) |
Table 1 gives, for several values of r, the values of
As an example, Fig. 2 shows for
Another property of the gamma distribution defined by Eq. (6) is that when Eq. (5) is completed by Eq. (9), then, the ratio
3 Methods and results
In order to study the vertical distribution of the suspended sediments and their settling velocities, a series of six tests was carried out on samples collected in the Loire estuary simultaneously at the bottom, half-depth and surface [1]. The local distribution of the suspended matter in terms of settling velocity has been examined by the bottom-withdrawal method [6]. Table 2 recapitulates the characteristic parameters of each of the six tests carried out.
Characteristic parameters of the settling-velocity measurement tests
Paramètres caractéristiques des tests de mesure de la vitesse de chute
| Number of the test | Date | Location | Distance from the mouth | Total depth (m) | River flow (m3 s−1) | Tidal coefficient |
Bottom salinity | Surface salinity | Average temperature | Surface flow velocity (m s−1) |
|
| 1 | 14/03/03 | Couëron | 40 km | 7.00 | 552 | 0.35 | 0‰ | 0‰ | 10.35 °C | 0.620 | 0.021 |
| 2 | 25/03/03 | Couëron | 40 km | 9.00 | 514 | 0.49 | 0‰ | 0‰ | 12.10 °C | 0.428 | 0.028 |
| 3 | 01/04/03 | Couëron | 40 km | 10.00 | 545 | 0.86 | 0‰ | 0‰ | 14.40 °C | 1.008 | 0.064 |
| 4 | 09/04/03 | Paimbœuf | 15 km | 7.00 | 425 | 0.33 | 21‰ | 11‰ | 11.50 °C | 0.945 | 5.596 |
| 5 | 16/04/03 | Paimbœuf | 15 km | 8.50 | 400 | 1.09 | 11‰ | 11‰ | 13.60 °C | 1.251 | 28.11 |
| 6 | 07/05/03 | Couëron | 40 km | 9.50 | 419 | 0.52 | 0‰ | 0‰ | 17.10 °C | 0.262 | 0.322 |
Fig. 3 shows the experimental cumulative frequencies of
| (10) |
| (11) |
These laws are confirmed by eight other measurements carried out in the field using Owen tubes in the range
It must be noted that when a layer of fluid mud covers the bottom, the reference near-bottom concentration
4 Conclusions
In steady-state conditions, if the settling velocity W of the bottom suspended-sediment mass is gamma distributed, the vertical variation of the local mean settling velocity
When the settling velocity of the suspended sediment mass is gamma distributed, the mean settling velocity and the shape parameter r of the distribution are sufficient to describe the vertical dynamics of the whole of the suspended aggregate population. In this case, the local mean settling velocity at the bottom must be connected with the bottom concentration (
Finally, it is to be noted that the theoretical development presented in this article can also model the vertical dynamics of non-cohesive suspended sediments.



Vous devez vous connecter pour continuer.
S'authentifier