Modèles géostatistiques de concentrations ou de débits le long des cours d'eau

Chantal de Fouquet; Caroline Bernard-Michel

doi:10.1016/j.crte.2006.02.002

Résumés

Français
Anglais

Estimer les concentrations ou les débits le long d'un réseau hydrographique nécessite des covariances ou des variogrammes valides sur un support arborescent. Nous généralisons deux modèles récemment proposés dans la littérature, en les étendant notamment au cas intrinsèque. Nous proposons une construction par « rivière », c'est-à-dire sur les chemins reliant les sources à l'exutoire. La combinaison de fonctions aléatoires (FA) monodimensionnelles stationnaires ou intrinsèques fournit, sur le réseau, des modèles stationnaires ou intrinsèques par arête, avec des discontinuités aux confluences. La construction de l'exutoire vers les sources fournit des modèles stationnaires ou intrinsèques par rivière, sans discontinuité aux confluences, avec le variogramme linéaire comme cas particulier. L'extension au modèle linéaire de corégionalisation est immédiate.

Estimating concentrations or flow rates along a stream network requires specific models. Two classes of models, recently proposed in the literature, are generalized, to the intrinsic case in particular. We present a global construction by ‘streams’, i.e. on the whole set of paths between sources and outlet. Combining stationary or intrinsic one-dimensional random functions leads to stationary or intrinsic models on segments, with discontinuities at the forks. A construction from outlet to sources, leads to stationary or intrinsic models on each stream, without any discontinuity at the forks. The linear variogram is found as a particular case. The extension to the linear model of coregionalization is immediate, allowing a multivariate modelling of concentrations.

Abridged English version

Estimating concentrations of pollutants along a stream network makes it necessary to take into account the geometry of the network. Usual geostatistical models as the spherical covariance were developed for Euclidean space, and are no more valid on tree graphs. Generalizing recent models [2,11,12] built on stream segments, we present a construction combining one-dimensional Random Functions (RF) defined on each path between sources and the outlet.

Ver Hoef et al. [12] developed a class of valid models derived from the one-dimensional moving average method. Integrating a kernel function upstream from a location (Eq. (11bis), Annex 2), they obtain a random function Z whose values upstream of any fork are independent on the different parts of the network. The moving average is calculated by distributing the kernel function on the upstream segments with a proper weighting, to ensure that the variance is constant (Fig. 2 and Eq. (12)). On each segment, the covariance $C_{1}$ , derived from the kernel function, is stationary. Between two ‘stream connected’ points $s_{i}$ and $t_{j}$ , the covariance is equal to $C_{1}$ up to a weighting term, depending on the weights attached to the segments ending at the nodes lying between $s_{i}$ and $t_{j}$ (Eq. (6)).

Fig. 2
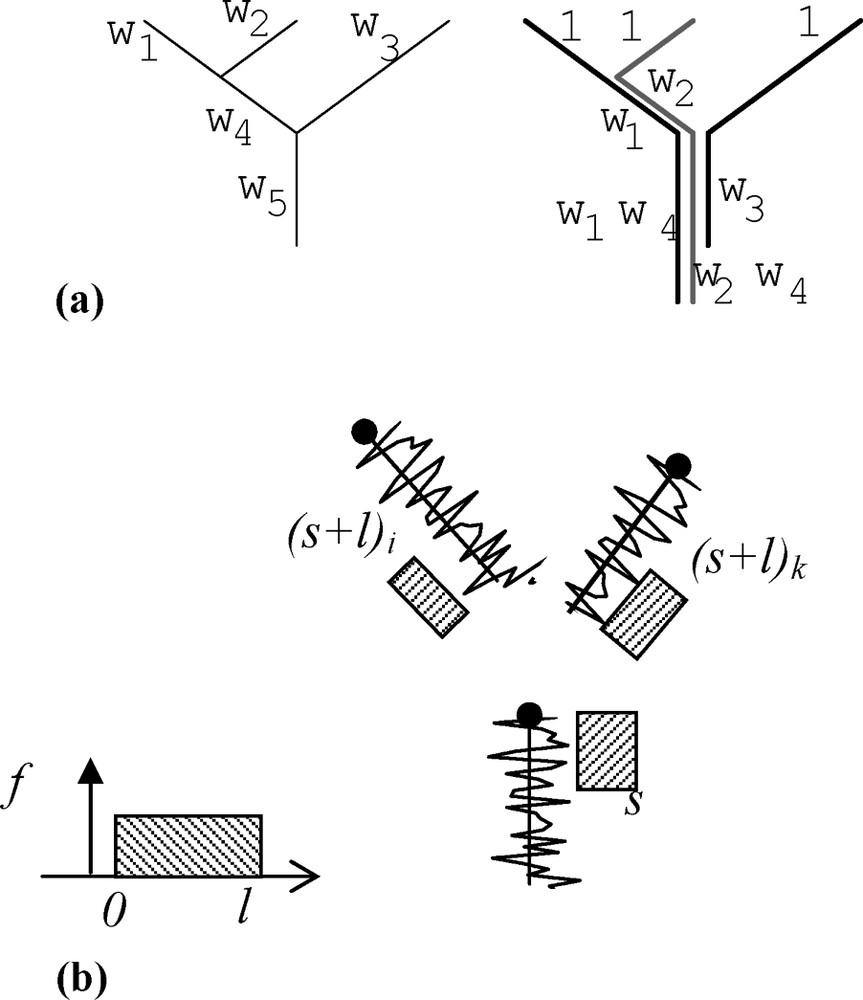
Combinaison par filets (a) ou par arête (b). (a) À gauche, les poids attribués aux arêtes, et à droite, la pondération résultante sur les filets. (b) Moyennes mobiles en une confluence, modèle Ver Hoef. En grisé, le noyau f.
Combining streams (a) or segments (b). (a) On the left, weights assigned to the segments and on the right, resulting coefficients along the streams. (b) Moving average at a fork, Ver Hoef model.

This model can be simplified and generalized, considering the one-dimensional random functions $Y_{I}$ defined on each path linking one source to the outlet. When different paths join at a node, the resulting random function Z downstream is a linear combination of the corresponding $Y_{I}$ (Eq. (1)) using their respective weights. When the kernel function is defined on the half-line, this model is equivalent to the Ver Hoef one. But any one-dimensional random function model can now be used for the $Y_{I}$ : for example, the kernel function can be symmetric. This model is easily extended when the different $Y_{I}$ are spatially correlated: the values of Z on two segments upstream from a node are now correlated. Intrinsic RF $Y_{I}$ can be considered too. This can be useful, for example, to describe flow rates that usually increase along the stream.

In the previous models, the RF Z is discontinuous at each node, in the mean square sense (or equivalently, its variogram or covariance is discontinuous at the nodes) and stationary or intrinsic on each segment between nodes. For points belonging to different segments, the variogram or the covariance depends on the weights.

To obtain RF without discontinuities at the nodes along each stream, Monestiez et al. [11] and Bailly et al. [2] constructed a model running in the opposite sense, from the outlet to the sources. It is based on a conditional independence between parts of the network upstream a node, knowing Z downstream, between the node and the outlet. The covariance of Z along each stream can be any one-dimensional covariance. The covariance between points on two different streams is given in the present paper (Eq. (10)). Extending the model to variograms and thus to intrinsic random functions on each stream, we obtain the linear variogram as a particular case.

We prove that among the covariances or variograms, which only depend on the distance along the tree, only the exponential and the linear scheme are consistent with the conditional independence hypothesis, and can then be constructed this way.

All the previous models can be incorporated in a linear coregionalization model defined on a stream network for a multivariate modeling of concentrations.

1 Introduction

Estimer des flux, des concentrations ou la quantité de matières en suspension [6] dans un réseau hydrographique à partir des mesures aux stations nécessite de tenir compte de la géométrie du réseau. Or les modèles géostatistiques usuels, développés dans des espaces euclidiens de dimensions deux ou trois, voire quatre pour les phénomènes spatiotemporels, ne sont généralement plus valides pour des variables définies sur un « support arborescent ». En effet, les théorèmes de Bochner et de Schoenberg font explicitement intervenir la distance euclidienne dans la caractérisation spectrale des covariances ou des variogrammes (voir par exemple [3]).

Utilisant la distance curviligne le long d'un réseau hydrographique, Ver Hoef et al. [12] montrent ainsi que, pour le schéma sphérique, certaines valeurs propres de la matrice de covariance peuvent être négatives. Comme conséquence pratique, les variances calculées avec ce « modèle » peuvent également devenir négatives. D'où la nécessité de modèles de covariances ou de variogrammes adaptés à la topologie des graphes.

Les fondements théoriques ont été récemment établis pour des fonctions aléatoires (FA) définies sur les sommets d'un graphe [7]. Le problème se pose différemment pour une FA définie sur un support continu, c'est-à-dire en tout point des arêtes du graphe. Seuls les graphes à structure « d'arbre » sont considérés dans la suite, ce qui exclut le cas de canaux reliant différents cours d'eau ou réseaux hydrographiques. Deux classes de FA ont été proposées récemment, fondées sur une construction des sources vers l'exutoire [12] ou, en sens inverse, de l'exutoire vers les sources [2,11].

Nous proposons ici une construction par combinaison de FA monodimensionnelles quelconques. Les modèles ainsi obtenus sur l'arbre présentent des discontinuités aux confluences ; ils généralisent le modèle Ver Hoef [12], qui correspond au cas particulier où la covariance est l'autoconvoluée d'une fonction définie sur la demi-droite. Des résultats complémentaires sont ensuite donnés pour le modèle Bailly–Monestiez [2,11], continu aux confluences. Ces deux classes sont généralisées au cas intrinsèque, les modèles non stationnaires permettant notamment de représenter des débits, généralement croissants dans le sens de l'écoulement.

2 Éléments bibliographiques

2.1 Différents modèles de FA sur un arbre

À la suite de Monestiez [10], pour modéliser le résidu sec des fruits sur un pêcher, Audergon et al. [1] calculent les variogrammes expérimentaux selon quatre distances définies sur l'arbre. Retenant comme distance le nombre d'embranchements entre deux points, les auteurs ajustent une covariance exponentielle, et effectuent un krigeage. Lorsque plusieurs distances apparaissent pertinentes, le choix de la plus appropriée est une étape importante de la modélisation.

Pour modéliser la largeur du fluvisol dans la partie aval du réseau hydrographique de l'Hérault [11] ou les fossés de drainage du bassin de Roujan [2], ces auteurs construisent une FA sur un arbre, de l'exutoire vers les sources, en posant une hypothèse d'indépendance conditionnelle entre points situés sur des cours d'eau différents, connaissant l'ensemble des valeurs à l'aval de leur confluence. Par cours d'eau, tous les modèles de covariance monodimensionnelle sont admissibles ; entre points situés sur des cours d'eau différents, la covariance n'est pas stationnaire. Des simulations conditionnelles sont présentées.

Ver Hoef et al. [12] proposent une construction en sens inverse, des sources vers l'exutoire. Posant une hypothèse d'indépendance entre rivières à l'amont de leur confluence, ces auteurs adaptent le procédé classique des moyennes mobiles, en répartissant sur les arêtes, à l'amont des confluences, le « noyau » défini sur la demi-droite. Ils estiment ensuite par krigeage (ponctuel ou de bloc) la concentration en métaux lourds le long d'un réseau hydrographique. Cressie et al. [5] reprennent ce modèle en combinant distance euclidienne et distance curviligne.

Cressie et al. [4] présentent une modélisation spatiotemporelle de la concentration en nitrates le long d'une rivière drainant un bassin versant. La structure du réseau hydrographique n'intervient pas dans la modélisation effectuée en deux dimensions, le temps et une dimension d'espace, via l'abscisse curviligne le long de la rivière. Une dérive multiple permet de prendre en compte la saisonnalité ainsi que de nombreuses variables décrivant le « milieu ».

Le développement de modèles de FA définies sur un support arborescent répond notamment à la nécessité d'une quantification précise des concentrations en différents polluants le long des cours d'eau. Seul l'aspect spatial est ici examiné.

2.2 Stationnarité

Sauf mention contraire, on examine les propriétés d'ordre deux des FA, c'est-à-dire leur covariance ou leur variogramme.

Une covariance (respectivement un variogramme) est dite stationnaire si elle ne dépend que de la distance curviligne entre deux points du graphe, et non stationnaire lorsqu'elle dépend des deux points séparément. Si la covariance sur les arêtes dépend de leur orientation, celle sur l'ensemble du graphe est considérée comme non stationnaire.

3 Combinaison de FA monodimensionnelles

Sur tout arbre, nous construisons une classe de FA par combinaison de « processus » définis sur des segments.

3.1 Principe de la construction

Soient deux affluents, de débits respectifs $d_{1}, d_{2}$ et de concentrations $c_{1}$ et $c_{2}$ immédiatement à l'amont de leur confluence ; juste à l'aval, le débit $d = d_{1} + d_{2}$ et la concentration $c = \frac{d_{1}}{d_{1} + d_{2}} c_{1} + \frac{d_{2}}{d_{1} + d_{2}} c_{2}$ s'obtiennent par combinaison linéaire des variables définies sur les affluents. À la confluence, le débit et la concentration présentent une discontinuité.

Prolongeons les affluents en les considérant comme des « filets d'eau » distincts, dont la réunion forme les « rivières ». Pour chaque filet, nous définissons, de la source à l'exutoire, un débit et une concentration, fonctions de l'abscisse curviligne comptée depuis l'exutoire. À l'aval des confluences successives depuis les sources, les débits des filets se cumulent pour former le débit total, et la concentration dans la rivière se ramène à une combinaison des concentrations des différents filets, en proportion de leur débit relatif. On en déduit un procédé général de construction de FA sur un arbre.

Lorsque le rapport des débits des « filets » reste constant entre deux confluences, les coefficients de la combinaison linéaire des concentrations des « filets » sont constants par arête, et changent aux confluences. Nous examinerons d'abord ce modèle simplifié.

3.2 Définitions et notations

Nous utilisons la terminologie géographique usuelle, complétée par celle relative aux graphes. Certaines notations sont reprises de [12].

Le réseau hydrographique est représenté par un arbre dont les sommets sont les sources, les confluences ou l'exutoire, supposé unique. Une « rivière » désigne un chemin d'une source vers l'exutoire ; le nombre de rivières est égal à celui des sources. Toute arête est caractérisable par les indices des rivières qui la traversent (Fig. 1a et b).

Fig. 1
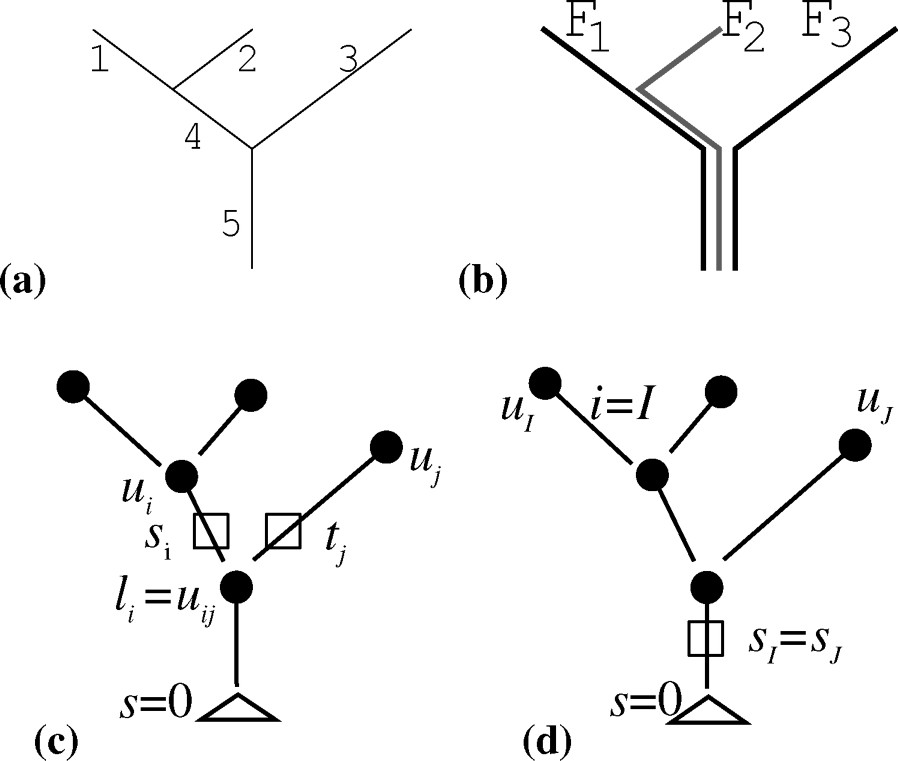
Description de l'arbre. (a) Définition des arêtes, et (b) des « rivières ». (c) Notation par arête ou (d) par rivière.
Description of the tree. (a) Definition of segments, and (b) of streams. (c) Notation from segments and (d) from streams.

Deux points sont reliés (au fil de l'eau), si l'un est à l'aval de l'autre ; ils appartiennent alors à une ou à plusieurs rivières communes. Deux points non reliés sont situés sur des rivières différentes, à l'amont de leur confluence. Par analogie, deux arêtes sont « reliées » si l'une est à l'aval de l'autre, et non reliées dans le cas contraire.

Les rivières sont indicées en majuscules par leur source ; les arêtes sont notées en minuscules. L'arête à l'aval immédiat d'une source est aussi indicée par la source. Toute rivière a donc le même numéro que son arête amont. Tout point du réseau hydrographique, noté $s_{i}$ ou $s_{J}$ , est repérable par sa distance curviligne s, comptée positivement depuis l'exutoire (où $s = 0$ ), ainsi que par le numéro i de son arête ou celui J d'une des rivières passant par cette arête (Fig. 1c et d). Le sommet amont $u_{i}$ appartient à l'arête i ; le sommet aval, considéré comme l'amont de l'arête suivante dans le sens du courant, n'appartient pas à l'arête i. L'ensemble des indices des arêtes à l'amont de l'arête i, excluant i, est noté $U_{i}$ et l'ensemble des indices des arêtes à l'aval de l'arête i, incluant cette arête, $D_{i}$ . L'ensemble $B_{i j}$ des indices des arêtes situées entre $s_{i}$ et $t_{j}$ est :

– vide si les arêtes ne sont pas reliées ;
– égal à $(U_{i} \cup U_{j}) \cap (D_{i} \cup D_{j})$ pour deux arêtes reliées, celle à l'amont étant incluse, et celle à l'aval, exclue.

L'ensemble des indices des arêtes sur la rivière J à l'amont de l'arête i (cette arête étant exclue) est noté $B_{i J} . V_{i}$ désigne l'ensemble des indices des rivières passant par l'arête i. L'abscisse de la confluence des rivières I et J est notée $u_{I J}$ , et l'abscisse de la confluence des rivières passant par les arêtes i et $j, u_{i j}$ . La distance curviligne le long de l'arbre est alors :

• $d (s_{i}, t_{j}) = | s - t |$ sur toute rivière ;
• $d (s_{i}, t_{j}) = (s_{i} - u_{i j})$ ( $t_{j} - u_{i j}$ ) entre points non reliés.

La longueur de la rivière J coïncide avec l'abscisse curviligne $u_{J}$ de sa source. En pratique, toute confluence peut être numérotée par son arête aval.

Dans la suite, la FA $Y_{J}$ représente le débit ou la concentration du « filet » $F_{J}$ , dont le support est un segment de même longueur $u_{J}$ que la rivière J associée. Les « filets » sont en bijection avec les rivières.

La FA Z représentant le débit ou la concentration du réseau hydrographique est définie sur l'arbre indicé par ses arêtes. La covariance de Z est écrite comme une fonction de $s - t$ lorsqu'elle ne dépend que de la distance curviligne entre les points, ou comme une fonction de $s_{i}$ et $t_{j}$ , lorsqu'elle dépend aussi des arêtes.

3.3 Combinaison de FA stationnaires indépendantes

Pour un arbre à N sources, soient N FA ou « composantes » $Y_{J}, 1 ⩽ J ⩽ N$ , centrées et de même covariance $C_{1} (h)$ autorisée en dimension 1.

En toute confluence, attribuons à chaque arête amont k un poids $w_{k}$ (Fig. 2(a)). Dans la combinaison linéaire (1), le coefficient des composantes $Y_{J}$ des filets passant par l'arête i est égal au produit des poids des arêtes situées strictement à l'amont de i, depuis la source $u_{J}$ . Sur l'arbre, la FA Z est définie par :

Z (s_{i}) = \sum_{J \in V_{i}} (\prod_{k \in B_{i J}} w_{k}) Y_{J} (s)

(1)

Les sources sont traitées comme des confluences à une seule arête amont, de coefficient unité. Sur l'arête

i = I

à l'aval immédiat d'une source,

Z (s_{i}) = Y_{I} (s)

Supposons d'abord les composantes $Y_{J}$ mutuellement indépendantes.

Dans la combinaison (1), des points non reliés n'ont aucune composante commune. Les $Y_{J}$ étant spatialement indépendantes, la covariance de Z entre ces points est nulle.

Soient deux points reliés, situés sur des arêtes différentes, i étant à l'amont de j. Seules les composantes des filets communs, ceux passant par l'arête i, ont une contribution non nulle dans la covariance. La covariance de Z entre ces points s'écrit : $s > t$ et $V_{i} \subset V_{j}$

C_{Z} (s_{i}, t_{j}) = C_{1} (s - t) \sum_{J \in V_{i}} (\prod_{k \in B_{i J}} w_{k}) (\prod_{ℓ \in B_{j J}} w_{ℓ})

(2)

Le long de toute rivière, la covariance de Z est proportionnelle à $C_{1} (s - t)$ , le facteur de proportionnalité variant suivant les arêtes i et j. Tous les coefficients des arêtes situées entre les sources et chacun des points interviennent dans (2).

En deux points d'une même arête $i, Z$ est combinaison linéaire des mêmes composantes $Y_{J}$ , $J \in V_{i}$ , et sa covariance s'écrit :

C_{Z} (s_{i}, t_{i}) = C_{1} (s - t) \sum_{J \in V_{i}} \prod_{k \in B_{i J}} w_{k}^{2}

(3)

En particulier,

Var Z (s_{i}) = C_{1} (0) \sum_{J \in V_{i}} \prod_{k \in B_{i J}} w_{k}^{2}

Par arête, la variance de Z est constante et sa covariance est stationnaire. Aux confluences, Z est discontinue en moyenne quadratique, ou ce qui est équivalent, sa covariance est discontinue. Z est non stationnaire par rivière et donc sur l'arbre : sa variance est généralement modifiée à chaque confluence. À même distance curviligne, la covariance dépend des sources communes aux deux points et des confluences intermédiaires, ainsi que des poids affectés aux arêtes.

Ce modèle, construit des sources vers l'exutoire, permet de décrire les concentrations le long d'un réseau hydrographique. Lorsqu'ils sont connus (calculés par exemple à partir de l'aire du bassin versant drainé), les débits relatifs interviennent via les poids aux confluences.

Pour des débits, qui se somment aux confluences, la condition de conservation de masse revient à attribuer un coefficient unité à chaque arête. La FA Z, construite par sommation des composantes indépendantes $Y_{J}$ s'écrit alors :

Z (s_{i}) = \sum_{J \in V_{i}} Y_{J} (s)

(4)

La variance $C_{1} (0)$ étant supposée identique pour tous les filets, la variance de Z est proportionnelle au nombre de filets en un point : constante par arête, elle croît des sources vers l'exutoire.

Supposons qu'en toute confluence d'un nombre n quelconque d'arêtes, la somme des carrés des poids affectés à ces n arêtes amont soit égale à 1 :

en toute confluence à n arêtes amont, \sum_{j = 1}^{n} w_{j}^{2} = 1

(5)

Les démonstrations données dans [12] restent valides pour une covariance $C_{1}$ quelconque. Par récurrence sur les confluences successives depuis les sources, on montre que, sur toute arête, la covariance (3) est égale à $C_{1} (s - t)$ . La variance de Z, égale à $C_{1} (0)$ , est alors constante sur l'arbre. Pour deux points reliés $s_{i}$ et $t_{j}$ séparés par au moins une confluence, seuls interviennent dans la covariance les poids aux confluences situées entre $s_{i}$ et $t_{j}$ :

C_{Z} (s_{i}, t_{j}) = C_{1} (s - t) \prod_{k \in B_{i j}} w_{k}

(6)

Le modèle Ver Hoef [12] correspond au cas particulier où la covariance $C_{1}$ est l'autoconvoluée d'un noyau ƒ défini sur la demi-droite ; les composantes $Y_{J}$ sont construites par convolution d'une mesure aléatoire orthogonale,¹ par le noyau ƒ. L'équivalence de ce modèle avec la combinaison de composantes indépendantes (1) est donnée en Annexe 2. Dans la combinaison par « filets », la covariance $C_{1}$ est quelconque ; dans le cas d'une convolution, le noyau ƒ est par exemple symétrique.

Plus généralement, introduisons une fonction de pondération $a_{J}$ (s) par filet. La combinaison linéaire

Z (s_{i}) = \sum_{J \in V_{i}} a_{J} (s_{i}) Y_{J} (s)

(7)

définit une FA de variance et de covariance généralement non stationnaires, données respectivement par :

Var Z (s_{i}) = C_{1} (0) \sum_{J \in V_{i}} {(a_{J} (s_{i}))}^{2} et C_{Z} (s_{i}, t_{j}) = C_{1} (s - t) \sum_{K \in V_{i} \cap V_{j}} a_{K} (s_{i}) a_{K} (t_{j})

(8)

Le modèle initial correspond à une fonction constante par arête, pour laquelle $a_{J} (s_{i}) = \prod_{k \in B_{i J}} w_{k}$ . Pour des débits $a_{J}$ , (s) est constante et égale à 1 le long de chaque rivière (relations (4) et (7)). Lorsque la pondération est constante par arête, la covariance de Z est stationnaire par arête.

Ce modèle général (7), (8) s'applique également, lorsque le support arborescent est discrétisé.

Remarques :

– (1) pour construire une FA Z d'espérance m constante, on somme m à la combinaison des composantes $Y_{J}$ centrées ;
– (2) une concentration ou un débit étant des variables positives, les composantes $Y_{J}$ sont par exemple les transformées par une anamorphose positive de FA de loi spatiale gaussienne [3] ;
– (3) d'autres modèles de FA sur un arbre sont obtenus en modifiant l'opérateur agissant sur les $Y_{J}$ . La combinaison linéaire (7) peut être remplacée par une moyenne d'ordre quelconque, par le produit, le maximum ou le minimum ;
– (4) les modèles précédents s'étendent à d'autres graphes que les arbres, par combinaison de composantes définies sur tous les chemins reliant une « origine » à une « extrémité » du graphe.

3.4 Combinaison de FA corrélées

Dans un bassin versant, les concentrations dépendent du milieu : nature des sols, type d'agriculture... Les concentrations des affluents drainant des milieux analogues sont alors corrélées. Les modèles multivariables de type dérive externe ou à résidus permettent d'introduire le contexte environnemental dans l'estimation [3,4]. Cependant, l'information correspondante n'étant pas toujours disponible ou n'expliquant pas systématiquement les liaisons observées, il est utile de disposer de modèles tels, que les valeurs entre affluents à l'amont des confluences soient corrélées.

Il suffit pour cela que les composantes $Y_{J}$ soient spatialement corrélées. Tous les modèles de corégionalisation admissibles à une dimension sont utilisables dans la construction suivante.

La longueur d'une rivière étant variable et égale à l'abscisse curviligne $u_{I}$ de sa source, plusieurs « calages » sont possibles. Considérons, en dimension un, N FA $X_{I}$ , de covariances simples et croisées $C_{I J} (s, t)$ . Nous examinons deux cas :

• $Y_{I} (s) = X_{I} (s)$ , les FA $Y_{I}$ étant « calées » depuis un exutoire commun. Les $Y_{I}$ ont alors mêmes covariances croisées que les $X_{I}$ .
• $Y_{I} (s) = X_{I} (u_{I} - s)$ , pour un calage des $Y_{I}$ depuis les sources. Ce calage induit une corrélation croisée différée de $| u_{I} - u_{J} |$ entre les composantes définies sur des rivières de longueurs différentes. Par exemple, avec un modèle multivariable stationnaire et symétrique $C_{I J} (h) = C_{I J} (- h)$ , comme le classique modèle linéaire de corégionalisation, on obtient :
$Cov (Y_{I} (s), Y_{J} (t)) = C_{I J} (u_{I} - u_{J} + t - s)$

Lorsque les composantes $Y_{I}$ sont corrélées, la FA Z définie par (7) admet la covariance :

C_{Z} (s_{i}, t_{i^{'}}) = \sum_{J \in V_{i}} \sum_{J^{'} \in V_{i^{'}}} a_{J} (s_{i}) a_{J^{'}} (t_{i^{'}}) Cov (Y_{J} (s), Y_{J^{'}} (t))

Toutes les covariances simples et croisées des composantes $Y_{J}$ associées aux filets passant par $s_{i}$ ou $t_{i^{'}}$ interviennent dans la covariance de Z.

3.5 Combinaison de FA intrinsèques

En dimension 1, soit R une FA stationnaire d'espérance m et de covariance $k (h)$ . L'intégrale $S (x) = \int_{0}^{x} R (t) d t$ est une FA intrinsèque, de dérive linéaire de pente m et de variogramme $γ (h) = \int_{0}^{h} (h - t) K (t) d t$ [8]. La variance de S, définie en tout point, est non stationnaire :

Var S (x) = \int_{0}^{x} \int_{0}^{x} K (t - t^{'}) d t d t^{'}

Dans le cas limite où R est pépitique (c'est-à-dire est une mesure aléatoire orthogonale), le variogramme de S est linéaire (voir par exemple [3]).

Lorsque R est positive, la FA S, positive et croissante, est un modèle admissible pour décrire un débit à accroissements stationnaires par unité de longueur de la rivière. $Y_{J}$ ( $u_{J}$ ) représentant le débit à la source, le débit du $J^{e}$ filet est $Y_{J} (s) = Y_{J} (u_{J}) + \int_{s}^{u_{J}} R_{J} (t) d t$ et le débit sur le réseau est défini par (7). À l'aval d'une confluence, la somme des RJ, $J \in V_{i}$ , sur les filets passant par $s_{i}$ représente l'accroissement élémentaire de débit, croissant avec l'ordre hydrologique de la rivière.

Plus généralement, soient N FA intrinsèques $Y_{J}$ , indépendantes (pour simplifier), supposées ici de variogramme quelconque $γ_{J} (h)$ associé à la covariance non stationnaire $C_{J} (s, s + h)$ . La FA Z construite suivant (4) en sommant ces composantes à l'aval des confluences est intrinsèque par arête et de variogramme

γ_{Z} (s_{i}, {(s + h)}_{i}) = \sum_{K \in V_{i}} γ_{K} (h)

somme des variogrammes pour les « filets » passant par l'arête. La covariance associée est la somme des covariances non stationnaires de chacun des filets :

C_{Z} (s_{i}, {(s + h)}_{i}) = \sum_{J \in V_{i}} C_{J} (s, s + h)

La variance de Z est finie et dépend du point $s_{i}$ .

Entre deux points reliés situés de part et d'autre d'une confluence, la covariance non stationnaire s'écrit comme une somme portant sur les seuls filets communs aux deux points, c'est-à-dire ceux passant par le point le plus en amont ${(s + h)}_{j}$ :

h > 0, C_{Z} (s_{i}, {(s + h)}_{j}) = \sum_{K \in V_{j}} C_{K} (s, s + h)

Deux points non reliés n'ont aucune composante commune. La covariance de Z en ces points est nulle et le variogramme est alors la moyenne des variances :

γ_{Z} (s_{i}, t_{j}) = \frac{1}{2} Var (Z (s_{i}) - Z (t_{j})) = \frac{1}{2} Var Z (s_{i}) + \frac{1}{2} Var Z (t_{j})

Ce variogramme dépend séparément de

s_{i}

t_{j}

La FA Z présente des discontinuités aux confluences. Ce modèle se généralise aux combinaisons linéaires de composantes intrinsèques, ainsi qu'au cas où les composantes $Y_{I}$ sont spatialement corrélées.

4 FA stationnaires ou intrinsèques par rivière

Le modèle Bailly–Monestiez [2,11] est construit en sens inverse, de « l'exutoire » vers les « sources ». Évitant les discontinuités aux confluences, ce modèle peut décrire des phénomènes variés, comme des caractéristiques végétales. Ces auteurs l'utilisent pour modéliser la largeur du fluvisol ou celle des fossés d'un réseau de drainage. En inversant l'orientation de l'arbre, on peut aussi l'appliquer aux concentrations dans un delta. Enfin, lorsque la dérive prend en charge les discontinuités aux confluences, ce modèle s'applique aux résidus [2,11].

4.1 FA stationnaire par rivière

Dans ce modèle, la covariance est stationnaire par rivière et identique pour toutes les rivières. Pour deux rivières quelconques, les composantes $Y_{I}$ coïncident de leur confluence à l'exutoire, et elles évoluent indépendamment de la confluence vers les sources (Fig. 3). Tandis que dans le modèle Ver Hoef, les valeurs de Z sur les différentes rivières sont indépendantes, dans le modèle Bailly–Monestiez cette indépendance est conditionnelle aux valeurs de Z sur le chemin commun aux rivières.

Fig. 3
Indépendance conditionnelle de $Y_{1}$ et $Y_{2}$ entre la confluence $u_{12}$ et les sources. Trait noir épais, le segment en construction ; trait gris épais, les « données » utilisées pour le conditionnement ; tireté : poids de krigeage nuls.
Conditional independence between $Y_{1}$ and $Y_{2}$ from the fork $u_{12}$ to the sources. Black bold: segment in construction, grey bold: data used for conditioning, dotted line: null kriging weights.

Pour simplifier, et puisqu'il en est ainsi en pratique, le graphe est désormais discrétisé. On se ramène à un arbre un peu particulier, dont la majorité des sommets comporte une seule arête « amont » et une seule arête « aval ».

Le modèle Bailly–Monestiez est le suivant. À une anamorphose près, Z est supposée de loi spatiale gaussienne. La numérotation étant arbitraire, $Z (s_{1}) = Y_{1} (s)$ de covariance $C_{1} (h)$ , est d'abord construite sur la « première » rivière $F_{1}$ , par exemple la plus longue. Z étant supposée construite sur les $J - 1$ premières rivières, soit $x_{J}$ la confluence d'abscisse maximum raccordant $F_{J}$ aux rivières précédemment construites : $x_{J} = \max {u_{J K}, K < J}$ . Entre l'exutoire $s = 0$ et $x_{J}$ , on pose $Y_{J} (s) = Z (s)$ ; entre la confluence $x_{J}$ et la source $u_{J}$ , $Y_{J}$ de covariance a priori $C_{1}$ est construite conditionnellement aux $Y_{J} (s)$ , $0 ⩽ s ⩽ x_{J}$ . Ceci est possible par simulation séquentielle, ou par toute méthode de simulation non conditionnelle à 1D, en conditionnant ensuite par les valeurs entre l'exutoire et $x_{J}$ [3]. En tout point, on pose :

Z (s_{J}) = Y_{J} (s)

(9)

La covariance de Z entre rivières se calcule à l'aide de la loi conditionnelle dans le cas gaussien : l'espérance conditionnelle coïncide alors avec le krigeage à moyenne connue et la variance résiduelle est égale à la variance de krigeage. Pour deux rivières distinctes d'indices $I, J$ de confluence $u_{I J}$ , posons $Y_{I} (s) = Y_{I}^{K} (s) + R_{I} (s)$ et $Y_{J} (t) = Y_{J}^{K} (t) + R_{J} (t)$ , $Y_{I}^{K} (s)$ et $Y_{J}^{K} (t)$ désignant le krigeage à moyenne connue de $Y_{I} (s)$ et $Y_{J} (t)$ par les seules valeurs communes comprises entre l'exutoire et la confluence, désignées désormais comme « données ». Les résidus $R_{I} (s)$ et $R_{J} (t)$ du krigeage à moyenne connue sont sans corrélation avec les « données » $Y_{I} (s) = Y_{J} (s)$ , $0 ⩽ s ⩽ u_{I J}$ . Dans le modèle Bailly–Monestiez, ces résidus sont, de plus, spatialement indépendants pour $I \neq J$ , et la covariance entre $Z (s_{I})$ et Z ( $t_{J}$ ) s'écrit

E [Z (s_{I}) Z (t_{J})] = E [Y_{I}^{K} (s) Y_{J}^{K} (t)] = \sum_{α, β} λ_{s}^{α} C_{1} (s_{α} - s_{β}) λ_{t}^{β}

(10)

λ_{s}^{α}

désignant le poids de

s_{α}

dans le krigeage à moyenne connue, au point d'abscisse s. Cette covariance admet une expression matricielle synthétique : K désignant la matrice de covariance

C_{1} (s_{α} - s_{β})

des « données » sur le tronçon commun

[0, u_{I J}]

K_{s}

(respectivement

K_{t}

) la matrice des covariances

C_{1} (s_{α} - s)

(resp.

C_{1} (s β - t)

) entre « données » et

Y_{I} (s)

u_{I} < s ⩽ u_{I J}

(resp.

Y_{J} (t)

u_{I J} < t ⩽ u_{J}

), un calcul simple montre que :

E [Y_{I}^{K} (s) Y_{J}^{K} (t)] = {}^{t}K_{s} K^{−1} K_{t}

La covariance de Z, généralement non stationnaire entre points non reliés, dépend de la distance de

s_{I}

t_{J}

à la confluence

u_{I J}

Le modèle Bailly–Monestiez comporte la covariance exponentielle comme cas particulier stationnaire sur tout l'arbre. Dans le cas de simulations non conditionnelles, le krigeage à moyenne connue, effectué suivant les abscisses curvilignes croissantes, ne fait plus intervenir que le point aval précédemment construit le plus proche.

Remarque : en l'absence de discrétisation de l'arbre, il convient de considérer le krigeage sur un support continu. Sous réserve de l'existence d'une mesure appropriée (qui n'existe pas nécessairement pour des covariances très régulières, telles que l'exponentielle de Gauss [9]), ce krigeage s'écrit : $s > x_{I}$ , $Y_{I}^{K} (s) = \int_{0}^{x_{I}} Y_{I} (t) λ_{I} (d t)$ . La covariance entre rivières distinctes admet alors une expression intégrale, généralisation immédiate des sommes finies (10) :

E [Y_{I}^{K} (s) Y_{J}^{K} (t)] = \int_{0}^{u_{I J}} \int_{0}^{u_{I J}} λ_{I} (d s) C_{1} (s - t) λ_{J} (d t)

Dans la suite, sauf mention contraire, le support arborescent est supposé discrétisé.

4.2 FA intrinsèque par rivière

La construction précédente s'étend aux FA intrinsèques, en posant de façon analogue une hypothèse d'indépendance des résidus du krigeage intrinsèque sur les rivières distinctes.

Soit toujours Z défini par (9), les $Y_{I}$ étant ici des FA intrinsèques en dimension un, de variogramme $γ_{1} (h)$ quelconque. Entre deux points reliés, $γ_{Z} (s_{I}, t_{I}) = γ_{1} (s - t)$ . Le variogramme de Z est stationnaire le long de toute rivière.

Soient $s_{I}$ et $t_{J}$ non reliés. Notons $Y_{I}^{*} (s)$ le krigeage intrinsèque de $Y_{I} (s)$ par les « données » $Y_{I} (s) = Y_{J} (s)$ , $0 ⩽ s ⩽ u_{I J}$ , et de même pour J. Alors :

γ_{Z} (s_{I}, t_{J}) = \frac{1}{2} Var (Y_{I} (s) - Y_{J} (t))

avec :

Y_{I} (s) - Y_{J} (t) = Y_{I} (s) - Y_{I}^{*} (s) + Y_{I}^{*} (s) - Y_{J}^{*} (t) + Y_{J}^{*} (t) - Y_{J} (t)

Dans le krigeage intrinsèque, les résidus $Y_{I} (s) - Y_{I}^{*} (s), Y_{J} (t) - Y_{J}^{*} (t)$ sont non corrélés aux combinaisons linéaires autorisées des « données », donc en particulier à $Y_{I}^{*} (s) - Y_{J}^{*} (t)$ . Les résidus sur des rivières distinctes étant supposés indépendants, la variance de la somme est la somme des variances :

γ_{Z} (s_{I}, t_{J}) = \frac{1}{2} Var (Y_{I} (s) - Y_{I}^{*} (s)) + \frac{1}{2} Var (Y_{I}^{*} (s) - Y_{J}^{*} (t)) + \frac{1}{2} Var (Y_{J} (t) - Y_{J}^{*} (t))

Le premier et le dernier terme correspondent aux variances de krigeage $σ^{2} (s_{I})$ , $σ^{2} (t_{J})$ de $Y_{I} (s)$ ou $Y_{J} (t)$ par les $Y_{I} (s) = Y_{J} (s)$ , $0 ⩽ s ⩽ u_{I J}$ ; ils dépendent de la position relative de $s_{I}$ et $t_{J}$ par rapport à ces points, en particulier par rapport à la confluence $u_{I J}$ . Le calcul du troisième terme est classique : notant $λ_{s}^{α}$ (resp. $λ_{t}^{α}$ ) le poids de $s_{α}$ dans le krigeage intrinsèque de $Y_{I} (s)$ (resp. $Y_{J} (t)$ ),

Var (Y_{I}^{*} (s) - Y_{J}^{*} (t)) = Var (\sum_{α} (λ_{s}^{α} - λ_{t}^{α}) Y_{I} (s_{α})) = - \sum_{α, β} (λ_{s}^{α} - λ_{t}^{α}) γ_{1} (s_{α} - s_{β}) (λ_{s}^{β} - λ_{t}^{β})

Via les poids de krigeage, ce terme dépend, là encore, de la position de $s_{I}$ et $t_{J}$ par rapport à la confluence. Le variogramme de Z, généralement non stationnaire entre points non reliés, s'écrit finalement :

γ_{Z} (s_{I}, t_{J}) = \frac{1}{2} σ^{2} (s_{I}) + \frac{1}{2} σ^{2} (t_{J}) - \sum_{α < β} (λ_{s}^{α} - λ_{t}^{α}) γ_{1} (s_{α} - s_{β}) (λ_{s}^{β} - λ_{t}^{β})

qui admet également une expression matricielle.

Ce résultat s'étend au cas où le support n'est pas discrétisé, sous réserve de l'existence d'une mesure appropriée pour l'écriture du krigeage.

Considérons le cas particulier d'un processus de Wiener–Lévy (ou mouvement brownien). W désignant une mesure aléatoire orthogonale, l'intégrale $Y (s) = \int_{0}^{s} W d t$ est intrinsèque et de variogramme linéaire (cf. partie 3.5).

On vérifie sans difficulté que « l'effet d'écran » du variogramme linéaire en dimension un se retrouve sur tout support arborescent, discrétisé ou non : quelle que soit la configuration de krigeage, le long de tout chemin passant par le point à estimer, seules les « données » les plus proches de part et d'autre de ce point admettent un poids non nul (Fig. 4).

Fig. 4
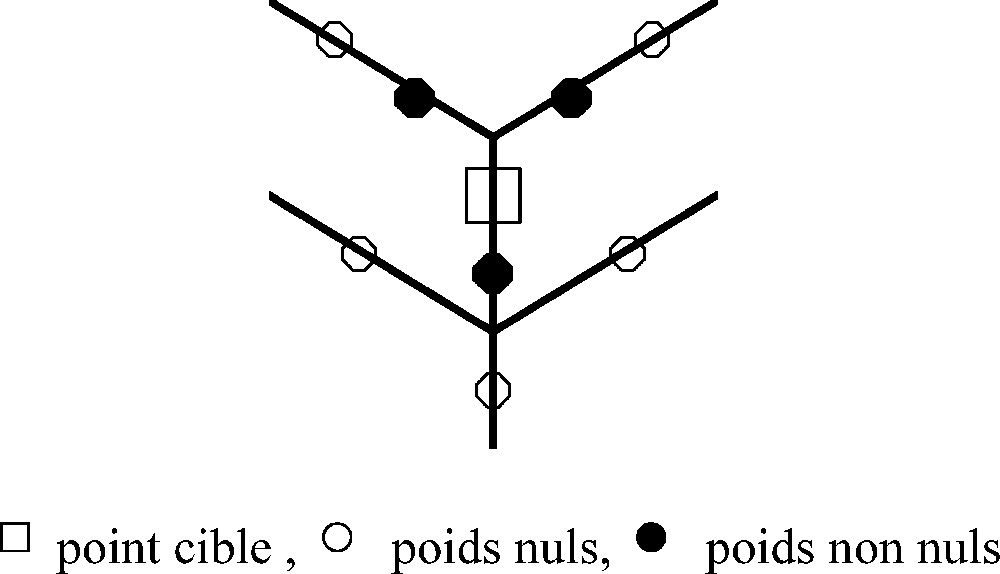
Effet d'écran pour le variogramme linéaire.
Screen effect of the linear variogram for intrinsic kriging.

Sur $F_{1}$ , construisons alors Z de variogramme linéaire. Z étant ensuite supposé de variogramme linéaire sur les $I - 1 ⩾ 1$ premières rivières, soit $x_{1} = \max {u_{I J}, J < I}$ la confluence d'abscisse maximum entre $F_{1}$ et ces rivières. Raccordant Z par continuité en cette confluence, on pose : $x_{1} < s ⩽ u_{I}$ , $Z (s_{I}) = Z_{I} (x_{I}) + \int_{x_{I}}^{s} W_{I} d t$ . Ceci revient à conditionner par l'ensemble des valeurs précédemment construites sur $F_{I}$ .

Les accroissements de Z sur $F_{I}$ à l'amont de $x_{1}$ étant choisis indépendants de ceux sur les I – 1 premières rivières, la variance de la somme de deux accroissements, de part et d'autre de la confluence, est égale à la somme des variances, et le variogramme de Z reste linéaire entre points non reliés. Sur l'arbre, Z est intrinsèque et de variogramme linéaire.

4.3 Indépendance conditionnelle et stationnarité

La covariance exponentielle (voir par exemple [11]), et le variogramme linéaire sont admissibles sur tout support arborescent, discrétisé ou non. Pour ces deux schémas, la construction d'une FA de loi spatiale de type mosaïque est donnée en annexe, sans discrétisation du support.

Dans le cas discret, montrons que ces deux modèles sont les seuls compatibles avec l'hypothèse d'indépendance conditionnelle et stationnaire sur l'arbre (i.e. ne dépendant que de la distance curviligne).

Dans la suite, l'écriture en covariance (et pour une variance unité) correspond au krigeage à moyenne connue, et celle en variogramme au krigeage intrinsèque. Considérons le krigeage en $x^{2}$ à partir de $x_{0}$ et $x_{1}$ séparés par la confluence $u_{12}$ (Fig. 5), $h_{i} = | u_{12} - x_{i} |$ désignant la distance de $x_{i}$ , $0 ⩽ i ⩽ 2$ , à la confluence. Pour $(i, j) = (0, 1)$ ou $(1, 0)$ respectivement, les poids de krigeage s'écrivent selon le cas

λ_{i} = \frac{C (h_{2} + h_{i}) - C (h_{2} + h_{j}) C (h_{i} + h_{j})}{1 - C^{2} (h_{0} + h_{1})} et

λ_{i} = \frac{1}{2} + \frac{γ (h_{2} + h_{j}) - γ (h_{2} + h_{i})}{2 γ (h_{i} + h_{j})}

D'après la condition d'indépendance conditionnelle,

λ_{1} = 0

, et par suite :

C_{Z} (h_{0} + h_{1}) C_{Z} (h_{0} + h_{2}) = C_{Z} (h_{1} + h_{2}) et

γ_{Z} (h_{0} + h_{1}) + γ_{Z} (h_{0} + h_{2}) = γ_{Z} (h_{1} + h_{2})

Fig. 5
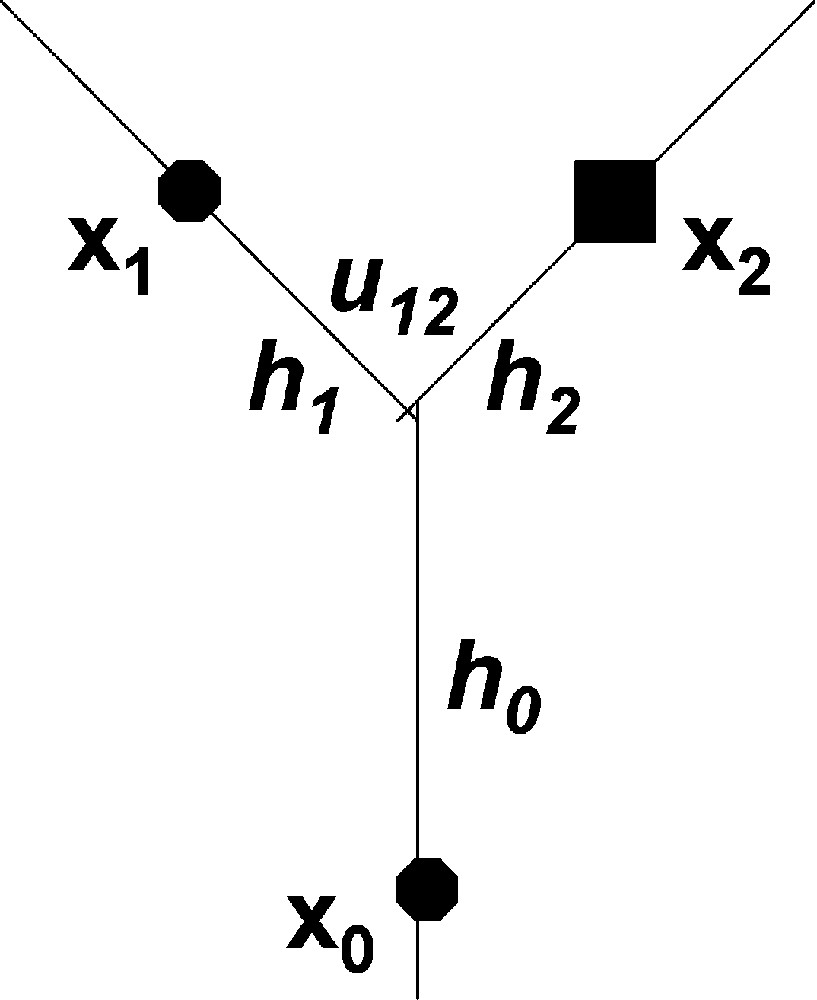
Configuration de krigeage.
Kriging configuration on the node.

Lorsque $x_{0}$ est situé sur la confluence, $h_{0} = 0$ et on retrouve l'effet d'écran en dimension 1. Les relations nécessaires $C_{Z} (h_{1}) C_{Z} (h_{2}) = C_{Z} (h_{1} + h_{2})$ ou $γ_{Z} (h_{1}) + γ_{Z} (h_{2}) = γ_{Z} (h_{1} + h_{2})$ , quels que soient $h_{1}$ et $h_{2}$ bornés, admettent comme solutions la covariance exponentielle et le variogramme linéaire. Lorsque $h_{0} > 0$ , il n'y a pas d'effet d'écran.

5 Conclusion

Les quelques modèles présentés s'adaptent aisément à une modélisation multivariable. Pour représenter les concentrations en différentes substances, par exemple des nutriments (nitrates, phosphates...), on pourra chercher un ajustement en modèle linéaire de corégionalisation. Il est immédiat de vérifier que sur tout arbre, ce modèle s'obtient classiquement par combinaison de facteurs spatiaux mutuellement indépendants [3].

Dans les applications pratiques, une modélisation bivariable débits–concentrations reste à développer, pour les cas où des mesures de débits sont disponibles en certaines stations. Cette modélisation devra tenir compte des valeurs approchées de ces débits, déduites par exemple de la superficie des bassins versants.

L'application aux données réelles pose l'importante question de l'inférence des modèles. Dans les exemples cités, il apparaît une « dérive » marquée des sources vers l'exutoire. Une modélisation de type « dérive + résidu » est alors recherchée pour incorporer au modèle diverses informations sur le milieu et se ramener à une variable stationnaire. Modélisant la largeur de fossés de drainage ou de fluvisols, Bailly et al. et Monestiez et al. calent des dérives qui sont notamment fonction de la longueur cumulée des drains à l'amont d'un point, et ajustent des variogrammes stationnaires pour les résidus.

Ver Hoef et al. montrent que les variogrammes expérimentaux calculés le long des rivières sont structurés et nettement inférieurs à ceux, pépitiques, calculés sur tout l'arbre. Ceci est compatible avec l'hypothèse d'indépendance entre rivières à l'amont des confluences. L'étude des variogrammes expérimentaux sur le réseau devrait ainsi guider la modélisation.

Remerciement

Ce travail a été effectué grâce à la subvention CV02000187 du ministère français en charge de l'Environnement. Les auteurs remercient H. Beucher, J.-P. Chilès, D. Renard et J.-P. Vert pour leur relecture attentive ou leur aide graphique ou linguistique.

Annexe 1 Variogramme linéaire et covariance exponentielle sur un arbre

Nous donnons une méthode de construction, sur tout graphe sans cycle, d'une FA de variogramme linéaire ou de covariance exponentielle, fondée sur le processus de Poisson en dimension 1.

Soient $T_{n}$ les abscisses des points d'un processus de Poisson de densité θ sur la droite, et $A_{n}$ une suite de variables aléatoires identiques en loi, d'espérance m et de variance $σ^{2}$ , mutuellement indépendantes et indépendantes du processus. La FA Y, définie à une constante près comme

– constante entre deux points poissoniens ;
– présentant un saut d'amplitude $A_{n}$ en $T_{n}$ ,

est intrinsèque, de dérive θmh et de variogramme (défini comme la demi-variance des accroissements) linéaire

\frac{1}{2} θ (m^{2} + σ^{2}) | h |

. Si l'on introduit un point d'abscisse

x_{0}

fixée, les propriétés du processus avant et après

x_{0}

restent inchangées.

Il en résulte un procédé de construction d'une FA de variogramme linéaire sur un arbre. On construit un processus de Poisson composé sur tous les chemins du graphe, et on « raccorde » par continuité la FA sur toute nouvelle arête aux chemins précédemment simulés (Fig. 6). En une confluence, la FA admet la même valeur sur toutes les arêtes.

Fig. 6
FA de covariance exponentielle ou de variogramme linéaire, construites sur un processus ponctuel de Poisson. Les valeurs sur les segments contigus sont constantes.
RF with exponential covariance or linear variogram on a tree, built on a Poisson point process. Values are constant on contiguous segments.

Plus précisément, la méthode est la suivante : (1) construire sur les arêtes, des processus de Poisson indépendants, de densité θ ; (2) poser $Y (x) = A_{0}$ en une arête, par exemple celle issue de la racine ; entre deux points du processus, $Y (x)$ est constante, et présente un saut d'amplitude $A_{n}$ aux points de discontinuité $T_{n}$ .

Pour construire sur la droite une FA Y de covariance exponentielle, on implante sur chaque segment, compris entre deux points du processus ( $T_{n}, T_{n + 1}$ ), une valeur constante $Y (x) = A_{i}$ , la FA conservant la même valeur sur toutes les arêtes en une confluence. Comme pour le variogramme linéaire, ce procédé est admissible pour tout graphe sans cycle.

D'après le théorème central limite, la sommation d'un grand nombre de FA indépendantes ainsi construites fournit, au facteur usuel de normation près, une FA de loi spatiale (ou d'incréments) multigaussiens.

Annexe 2 Équivalence de la combinaison de composantes indépendantes et du modèle Ver Hoef

Le modèle Ver Hoef utilise la construction classique par moyennes mobiles. Soit W un « bruit blanc » de variance unité et ƒ une fonction de carré sommable ou « noyau ». En dimension un, la FA définie par

Z (s) = \int ƒ (t - s) W d t

(11)

admet la covariance stationnaire

C_{1} (h) = \int ƒ (t) ƒ (t - h) d t

produit de convolution de f par son symétrisé :

C_{1} (h) = f * \overset{˘}{f}, où \overset{˘}{f} (t) = f (- t)

Dans ce modèle, l'indépendance de Z sur les arêtes à l'amont d'une confluence est obtenue en utilisant un noyau défini sur la demi-droite $R^{+}$ . Dans la relation (11), la moyenne mobile est calculée par pondération de W à l'amont du point courant, la borne supérieure étant conventionnellement mise à +∞, que le support de f soit ou non borné :

Z (s_{i}) = \int_{s_{i}}^{\infty} f (t - s_{i}) W d t

(11bis)

Que devient la moyenne mobile, lorsque t atteint une confluence à l'amont de $s_{i}$ ? Afin d'obtenir une variance stationnaire, Ver Hoef et al. répartissent le noyau f sur les n arêtes à l'amont de la confluence (Fig. 2b), en les pondérant par des poids $w_{j}$ dont la somme des carrés est égale à 1 (relation (5)).

La construction est la suivante : (1) construire un mesure aléatoire orthogonale W en tout point du graphe, indicé par son arête ; (2) effectuer la moyenne mobile en la répartissant sur les arêtes amont, l'intégrale étant conventionnellement étendue à l'infini au-delà des sources :

Z (s_{i}) = \int_{s_{i}}^{u_{i}} f (t - s_{i}) W_{i} d t + \sum_{j \in U_{i}} (\prod_{k \in B_{i j}} w_{k}) \int_{l_{j}}^{u_{j}} f (t - s_{i}) W_{j} d t

La covariance C de la FA Z ainsi construite est :

• nulle entre rivières différentes :
• $C (s_{i}, t_{j}) = C_{1} (s - t) \prod_{k \in B_{i j}} w_{k}$ sur deux arêtes reliées, le deuxième facteur dépendant des confluences entre les arêtes ;
• $C (s_{i}, t_{i}) = C_{1} (s - t)$ sur toute arête.

La covariance C est stationnaire entre arêtes, mais non stationnaire sur l'arbre.

Pour montrer l'équivalence des deux modèles, considérons pour simplifier un arbre comportant n arêtes amont convergeant toutes en une seule confluence d'abscisse u. À l'aval de la confluence, le modèle Ver Hoef s'écrit : 0 $⩽ s ⩽ u$ .

Z (s) = \int_{s}^{u} f (t - s) W d t + \sum_{j = 1}^{n} w_{j} \int_{u}^{u_{j}} f (t - s) W_{j} d t

(12)

Soient alors n FA indépendantes $Y_{j}$ , définies respectivement sur chaque rivière, de la source à l'exutoire, par $Y_{j} (s) = \int_{s}^{u_{j}} f (t - s) W_{j} d t$ . Pour s à l'aval de la confluence, posons :

Y (s) = \sum_{j = 1}^{n} w_{j} Y_{j} (s)

(13)

soit, en introduisant le point de confluence :

Y (s) = \sum_{j = 1}^{n} w_{j} \int_{s}^{u} f (t - s) W_{j} d t + \sum_{j = 1}^{n} w_{j} \int_{u}^{u_{j}} f (t - s) W_{j} d t

Par linéarité de la convolution, le premier terme du second membre s'écrit :

\int_{s}^{u} f (t - s) (\sum_{j = 1}^{n} w_{j} W_{j} d t)

Les n bruits blancs $W_{j}$ étant mutuellement indépendants et de variance unité :

Var (\sum_{j = 1}^{n} w_{j} W_{j} (d t)) = (\sum_{j = 1}^{n} w_{j}^{2}) Var W d t = 1

Les FA Y et Z admettent donc même espérance et même covariance. Lorsque les « bruits blancs » ne sont pas gaussiens, l'histogramme de Z ou de Y n'est plus nécessairement stationnaire, mais dépend de la loi des

W_{j}

, la covariance C restant inchangée.

L'équivalence entre (12) et (13) se généralise à un arbre quelconque, en considérant successivement toutes les confluences depuis les sources. La méthode Ver Hoef revient donc à effectuer la moyenne pondérée suivante, dans laquelle la sommation porte sur les rivières passant par $s_{i}$ :

Z (s_{i}) = \sum_{J \in V_{i}} (\prod_{k \in B_{i J}} w_{k}) \int_{s_{i}}^{u_{J}} f (t - s_{i}) W_{J} d t

la pondération attribuée en $s_{i}$ à la rivière $F_{J}$ dépendant des confluences depuis sa source. L'écriture de Z comme combinaison linéaire, à coefficients variables, de FA indépendantes définies sur les rivières, permet de généraliser ce modèle à la combinaison de FA monodimensionnelles de covariance quelconque.

¹ Une mesure aléatoire orthogonale ou « bruit blanc » W est telle que pour tous $v, v^{'}$ « mesurables », $E [(\int_{v} W {(d x))}^{2}] = α Mes v$ et si $Mes (v \cap v^{'})$ , alors $E [\int_{v} W (d x) \int_{v^{'}} W (d t)] = 0$ .