Une approche innovante pour modéliser la biodégradation des composés organochlorés volatils en aquifères poreux

Fabien Nex; Gerhard Schäfer; Jean-Marie Côme; Timothy M. Vogel

doi:10.1016/j.crte.2006.03.003

Géochimie

Une approche innovante pour modéliser la biodégradation des composés organochlorés volatils en aquifères poreux

Présenté par : Ghislain de Marsily

Fabien Nex ^1,^2,³ ; Gerhard Schäfer ^1,² ; Jean-Marie Côme ³ ; Timothy M. Vogel ⁴

¹ Institut de mécanique des fluides et des solides de Strasbourg, UMR 7507 CNRS–ULP, 2, rue Boussingault, 67000 Strasbourg, France
² Institut franco-allemand de recherche sur l'environnement (IFARE), 23, rue du Loess, B.P. 20, 67037 Strasbourg cedex, France
³ BURGÉAP, 19, rue de la Villette, 69425 Lyon cedex 03, France
⁴ Centre d'écologie microbienne, UMR 5557 CNRS–université-Lyon-1, 69425 Villeurbanne, France

Comptes Rendus. Géoscience, Volume 338 (2006) no. 5, pp. 297-306.

Résumés

Français
Anglais

L'objectif de ce travail a été de développer un module innovant de biodégradation des chloroéthènes, fondé sur une triple approche biologique, thermodynamique et mécanistique. Le schéma de biodégradation proposé repose sur le postulat suivant : à chaque endroit de l'aquifère, un mécanisme de dégradation est dominant, celui qui implique l'accepteur d'électrons le plus énergétique. La sélection du mécanisme de biodégradation actif est ainsi fonction de la concentration des accepteurs d'électrons. Les cinétiques utilisées correspondent à des cinétiques de type Monod, modifiées pour prendre en compte l'influence possible de tous les composés présents sur la biodégradation d'un composé organique donné. Le modèle numérique développé a été appliqué à un cas test simple présenté dans cet article.

The goal of this study was to develop an innovative chloroethene biodegradation module based on biological, thermodynamical and mechanistic concepts. The biodegradation scheme was based on the postulate that in each part of an aquifer only one degradation mechanism is dominant: the one involving the most energetic electron acceptor. Thus, the selection of the active degradation mechanism was a function of the concentration of different electron acceptors. Modified Monod-type kinetics was used in order to take into account the possible influence of some compounds on the biodegradation of a given organic compound. The numerical model developed was applied to a simple test case, whose results are presented here.

Métadonnées

Reçu le : 2006-01-02
Accepté le : 2006-01-18
Publié le : 2006-04-18

DOI : 10.1016/j.crte.2006.03.003

Mot clés : Chloroéthènes, Modélisation, Pollution, Biodégradation, Aquifère, Modèle conceptuel
Keywords: Chloroethenes, Modelling, Pollution, Biodegradation, Aquifer, Conceptual model

Affiliations des auteurs :

Fabien Nex ^{1, 2, 3} ; Gerhard Schäfer ^{1, 2} ; Jean-Marie Côme ³ ; Timothy M. Vogel ⁴

@article{CRGEOS_2006__338_5_297_0,
     author = {Fabien Nex and Gerhard Sch\"afer and Jean-Marie C\^ome and Timothy M. Vogel},
     title = {Une approche innovante pour mod\'eliser la biod\'egradation des compos\'es organochlor\'es volatils en aquif\`eres poreux},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {297--306},
     publisher = {Elsevier},
     volume = {338},
     number = {5},
     year = {2006},
     doi = {10.1016/j.crte.2006.03.003},
     language = {fr},
}

TY  - JOUR
AU  - Fabien Nex
AU  - Gerhard Schäfer
AU  - Jean-Marie Côme
AU  - Timothy M. Vogel
TI  - Une approche innovante pour modéliser la biodégradation des composés organochlorés volatils en aquifères poreux
JO  - Comptes Rendus. Géoscience
PY  - 2006
SP  - 297
EP  - 306
VL  - 338
IS  - 5
PB  - Elsevier
DO  - 10.1016/j.crte.2006.03.003
LA  - fr
ID  - CRGEOS_2006__338_5_297_0
ER  -

%0 Journal Article
%A Fabien Nex
%A Gerhard Schäfer
%A Jean-Marie Côme
%A Timothy M. Vogel
%T Une approche innovante pour modéliser la biodégradation des composés organochlorés volatils en aquifères poreux
%J Comptes Rendus. Géoscience
%D 2006
%P 297-306
%V 338
%N 5
%I Elsevier
%R 10.1016/j.crte.2006.03.003
%G fr
%F CRGEOS_2006__338_5_297_0

Fabien Nex; Gerhard Schäfer; Jean-Marie Côme; Timothy M. Vogel. Une approche innovante pour modéliser la biodégradation des composés organochlorés volatils en aquifères poreux. Comptes Rendus. Géoscience, Volume 338 (2006) no. 5, pp. 297-306. doi : 10.1016/j.crte.2006.03.003. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2006.03.003/

Version originale du texte intégral

Abridged English version

Chlorinated Volatile Organic Compounds (CVOC), especially chloroethenes (tetrachloroethylene (PCE), trichloroethylene (TCE), dichloroethylene (DCE) and vinyl chloride (VC)), are among the most frequently detected contaminants in the subsurface [4]. In soil and groundwaters, they are subject to natural attenuation [3]. Among the different processes involved, such as dispersion, adsorption, volatilisation, chemical and biological destruction, biodegradation is often considered the most important one [19].

Biodegradation is often an oxidation-reduction reaction mediated by microorganisms and involving electron donors and acceptors. In polluted groundwater (and subsurface soils), typical electron donors, species that undergo oxidation reactions to give electrons and other products (carbon dioxide (CO₂) for instance), are petroleum hydrocarbons, BTEX, acetate, methanol, humic acid and the less oxidized CVOC (mainly DCE and VC). Typical electron acceptors, species that undergo reduction reactions by capturing electrons, are inorganic compounds (by order of preference: oxygen (O₂), nitrate $({NO}_{3}^{-})$ , manganese (Mn²⁺), ferric iron (Fe³⁺), sulfate ( ${SO}_{4}^{2 -}$ ), carbon dioxide (CO₂) and the more oxidized CVOC (mainly PCE and TCE). Under reductive conditions, the CVOC undergoes a reduction reaction called reductive dechlorination, that sequentially transforms PCE into TCE, TCE into mainly cis-DCE (the other isomers, trans-DCE and 1,1-DCE are in minority [5]), cis-DCE into VC, and VC to ethene.

However, depending on the bio- and geochemical conditions, not all of the thermodynamically possible reactions, such as oxidation and reductive dechlorination under denitrifying, sulfate-reducing or methanogenic conditions, can be applied to all of the chlorinated solvents.

From a practical standpoint, it is important to characterise and predict the fate of CVOC in polluted sites by using numerical transport codes to model the biodegradation of chlorinated solvents. Numerous commercial analytical or numerical codes exist that can handle the modelling of biodegradation mechanisms, such as RT3D [6] or UTCHEM [7]. However, none of these codes are adjusted strictly for the modelling of the biodegradation of chlorinated solvents and all the required parameters and processes (type of kinetics, notion of ‘sequentiality’...) [16].

The aim of this study was to develop a novel conceptual and mathematical model for the biodegradation of the chloroethene family (PCE, TCE, DCE, VC and ethene) based on a combined mechanistic and biological approach. While the processes involved in biodegradation of CVOCs are quite well known and widely referenced in the literature, the model approach chosen here is original and novel due to the introduction of four concepts, which have been used separately, but never combined in an overall scheme: (i) double role of the inorganic electron acceptors (positive effect due to their successive consumption leading to different redox states; negative effect due to their competition with CVOCs in capturing electrons, thus reducing the kinetics of the CVOCs biodegradation); (ii) limited reaction terms by taking the minimum of two reactions linked to the electron acceptors and electron donors present in the aquifer (this approach is rarely used in common modelling approaches); (iii) competition between electron acceptors and electron donors; and (iv) inhibition of the degradation of one compound by another.

Jeffers et al. [13] and McCarty [14] state that, under natural conditions, the main degradation mechanisms are oxidation and reduction mechanisms, essentially mediated by bacterial metabolism. Furthermore, Vogel et al. [22] describe the scheme of reductive dechlorination of chloroethenes in detail. The selection of possible reactions, based on a thermodynamical approach, is referenced by [1]. The role of inorganic electron acceptors on reductive dechlorination has been thoroughly investigated by Fetzner [12]. These references have been used to elaborate the conceptual model whose main root contains the following postulate: all CVOC do not undergo all of the thermodynamically possible degradation reactions at a given time in a given location, and the reaction involving the more energetic electron acceptor tends to be dominant at a given place of an aquifer. Therefore the approach chosen is based on a ‘double-switch’ system.

Table 1 lists all the compounds included in the proposed conceptual model. The ferric iron and the manganese have not been taken into account in our modelling approach for two reasons: (i) in general, bacterial populations under ferric reducing or methanogenic conditions are not very abundant in polluted sites [2,10,11], (ii) ferric iron and manganese are usually present in the aquifer in the form of oxides or hydroxides, which are not generally bioavailable for microorganisms.

Type de constituant	Nom du constituant
COHV (à la fois donneur et accepteur d'électrons)	PCE (tétrachloroéthylène ou perchloroéthylène)
	TCE (trichloroéthylène)
	cis-1,2-DCE, simplifié en DCE (dichloroéthylène)
	VC (chlorure de vinyle)
	ETH (éthylène, composé non chloré issu de la réduction du chlorure de vinyle)

Accepteurs d'électrons inorganiques	O₂ (oxygène dissous)
	${NO}_{3}^{-}$ (ions nitrate), simplifiés en NO₃
	${SO}_{4}^{2 -}$ (ions sulfate), simplifiés en SO₄
	CO₂ (dioxyde de carbone dissous)

Donneur d'électrons principal	COD (carbone organique dissous) – somme des concentrations en chloroéthènes, éthane et méthane

Produits de dégradation	Cl⁻ (ions chlorure), simplifiés en Cl
	Éthane
	Méthane

Constituants supplémentaires associés aux mécanismes d'oxydation	TCEox
DCEox
	VCox
	ETHox

The first switch corresponds to the selection of one reaction mechanism for the CVOC according to environmental conditions (Table 2). The reaction involving the most energetic electron acceptor is used. Following the thermodynamic principle, the more free energy liberated by the reaction, the more the bacterial population catalysing this reaction is favoured and develops quickly, thus the quicker the degradation. The threshold values used in the model are on the same order of magnitude as the ones that can be measured at industrial polluted sites and found in scientific literature [8,23]. Devol [8] states that the same bacterial population that consumes oxygen can also, via minor metabolic changes, use nitrate when the oxygen concentration becomes very low. Therefore, when the oxygen concentration was between 0 and 0.1 mg/l, we considered that both mechanisms, oxidation and reduction, can occur under denitrifying conditions. As far as the oxygen threshold is concerned, the value, 0.1 mg/l, is consistent with literature values compiled by Van Cappellen et al. [20,21]: the O₂ limit concentration is defined by the concentration above which the main degradation mechanism is the metabolic pathway associated with the concerned electron acceptor. For O₂, this value is between 0.03 and 0.32 mg/l.

Conditions environnementales	Mécanismes considérés
Si $O_{2} > 0, 1 mg / l$	Oxydation sous conditions aérobies

Si $0 < O_{2} < 0, 1 mg / l$ et ${NO}_{3}^{-} > 1 mg / l$	Oxydation sous conditions aérobies et réduction sous conditions dénitrifiantes (compétition entre le COHV et les nitrates pour capter les électrons)

Si $O_{2} = 0 mg / l$ et ${NO}_{3}^{-} > 1 mg / l$	Réduction sous conditions dénitrifiantes (compétition entre le COHV et les nitrates pour capter les électrons)

Si $O_{2} = 0 mg / l$ et ${NO}_{3}^{-} < 1 mg / l$ et ${SO}_{4}^{2 -} > 1 mg / l$	Réduction sous conditions sulfatoréductrices (compétition entre le COHV et les sulfates pour capter les électrons)

Si $O_{2} = 0 mg / l$ et ${NO}_{3}^{-} < 1 mg / l$ et ${SO}_{4}^{2 -} < 1 mg / l$	Réduction sous conditions méthanogènes (compétition entre le COHV et le dioxyde de carbone pour capter les électrons)

The second switch corresponds to the selection of the possible degradation pathways for each CVOC modelled (Table 3).

Composé	Mécanismes de dégradation pris en compte
PCE	Réduction sous conditions sulfatoréductrices ( ${SO}_{4}^{2 -}$ )
	Réduction sous conditions méthanogènes (CO₂)

TCE	Oxydation sous conditions aérobies (O₂)
	Réduction sous conditions dénitrifiantes ( ${NO}_{3}^{-}$ )
	Réduction sous conditions sulfatoréductrices ( ${SO}_{4}^{2 -}$ )
	Réduction sous conditions méthanogènes (CO₂)

DCE	Oxydation sous conditions aérobies (O₂)
	Réduction sous conditions dénitrifiantes ( ${NO}_{3}^{-}$ )
	Réduction sous conditions sulfatoréductrices ( ${SO}_{4}^{2 -}$ )
	Réduction sous conditions méthanogènes (CO₂)

VC	Oxydation sous conditions aérobies (O₂)
	Réduction sous conditions dénitrifiantes ( ${NO}_{3}^{-}$ )

ETH	Oxydation sous conditions aérobies (O₂)
	Réduction sous conditions dénitrifiantes ( ${NO}_{3}^{-}$ )

Assuming that both the biomass concentration is constant and that there is no limiting substrate, the biological degradation of a single compound i, $R_{i}$ , can be written using Monod's law (Eq. (1)). Eq. (1) can become more complex by adding terms, which describe the competition between different compounds to capture the electrons, the inhibition of a compound over another one and the presence of a limiting substrate that reduces the rate of degradation. In our model, a modified version of Monod's law is employed to take into account the competition for electrons between all the compounds present. In other words, it describes the competition between the CVOC and the inorganic acceptors, but also the competition between a given chlorinated solvent and another, which is in the aquifer. As an example, Table 4 summarises the equations used in the model in the case of biodegradation of TCE under sulfate-reducing conditions.

Type de constituant	Équation développée
Accepteurs d'électrons	$R_{TCE} = R_{1_{TCE}} + R_{2_{TCE}}$
	$R_{1_{TCE}} = - V_{\max, TCE} \cdot \min (R_{A}, R_{D})$
	$R_{A} = \frac{C_{TCE}}{C_{TCE} + K_{TCE} (1 + \frac{C_{{SO}_{4}} \cdot E_{{SO}_{4}, TCE}}{K_{{SO}_{4}}} + \frac{C_{PCE} \cdot E_{PCE, TCE}}{K_{PCE}} + \frac{C_{DCE} \cdot E_{DCE, TCE}}{K_{DCE}})}$
	$R_{D} = \frac{C_{COD}}{K_{COD} + C_{COD}}$
	$R_{2_{TCE}} = - Y_{TCE / PCE} R_{PCE}$
	$R_{{SO}_{4}} = - V_{\max, {SO}_{4}} \cdot \min (R_{A}, R_{D})$
	$R_{A} = \frac{C_{{SO}_{4}}}{C_{{SO}_{4}} + K_{{SO}_{4}} (1 + \frac{C_{PCE} \cdot E_{PCE, {SO}_{4}}}{K_{PCE}} + \frac{C_{TCE} \cdot E_{TCE, {SO}_{4}}}{K_{TCE}} + \frac{C_{DCE} \cdot E_{DCE, {SO}_{4}}}{K_{DCE}})}$
	$R_{D} = \frac{C_{COD}}{K_{COD} + C_{COD}}$
Donneur d'électrons	$R_{COD} = α Y_{COD / {SO}_{4}} R_{{SO}_{4}} + β Y_{COD / PCE} R_{PCE} + χ Y_{COD / TCE} R_{1_{TCE}} + δ Y_{COD / DCE} R_{1_{DCE}}$
Produits de dégradation	$R_{Cl} = - Y_{Cl / PCE} R_{PCE} - Y_{Cl / TCE} R_{1_{TCE}} - Y_{Cl / DCE} R_{1_{DCE}}$
	$R_{{CO}_{2}} = - a Y_{{CO}_{2} / COD} R_{COD}$

The conceptual and mathematical model has been implemented in a 1D finite-difference numerical code under steady state flow conditions, where the reactive transport of a dissolved compound i in groundwater is described by the macroscopic mass conservation equation (Eq. (2)). We consider the porous medium as a continuum at the scale of a Representative Elementary Volume (REV). Therefore, only one redox state is possible in a single cell grid. Hence, a larger observation scale introduces mixing processes (such as macrodispersion) and non-uniform reactions in space, which are beyond the scope of this paper.

For the 13 transported compounds considered in the model, a system of 13 coupled differential equations has been solved by finite differences and by the Thomas algorithm [18]. The biodegradation term ( $R_{i}$ ) is formulated in each grid block with an explicit time scheme.

The numerical code was first verified in a simple test in order to check the stability of the numerical solution [16]. As a first stage of validation of the code, the model was tested under ideal biodegradation conditions (Fig. 1): complete degradation of PCE to ethene (via TCE and DCE) and carbon dioxide as the terminal electron acceptor (Table 5). The results of the test show that the code is able to satisfactorily represent the evolution of both the chloroethenes and the inorganic electron acceptors (Figs. 2 and 3) and the transition between the different redox zones at the same time while yielding a very good mass balance.

Fig. 1
Schéma du cas test.
Scheme of the test case.

	Valeur
Concentrations initiales et à l'entrée de l'aquifère
COHV (PCE, TCE, DCE, VC et ETH)	0 mg/l
Oxygène	10 mg/l
Nitrates	20 mg/l
Sulfates	50 mg/l
CO₂	5 mg/l
COD	500 mg/l
Chlorures	0 mg/l
Méthane	0 mg/l
Paramètres cinétiques
Tous les paramètres K, E ainsi que tous les coefficients stœchiométriques $α, β, χ$ ... concernant les réactions de dégradation du PCE, TCE, DCE et VC dans les différentes zones redox	1
Paramètres cinétiques
Tous les paramètres V_max concernant les réactions de dégradation du PCE, TCE, DCE et VC dans les différentes zones redox	5 mg/l/j
Paramètres cinétiques
Tous les paramètres concernant la dégradation des autres COHV	0

Fig. 2
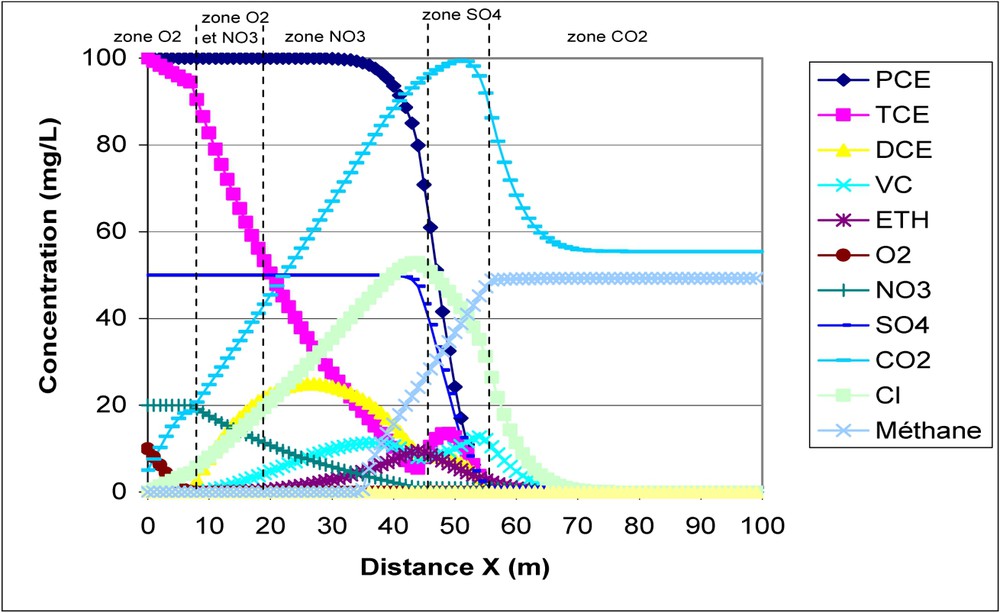
Concentrations à 50 jours.
Concentrations at 50 days.

Fig. 3
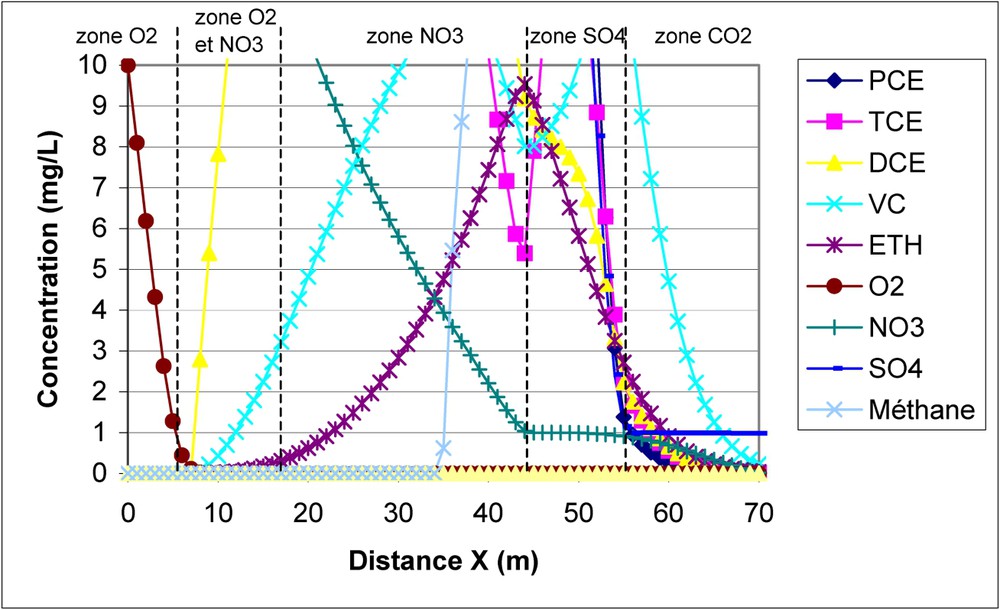
Zoom de la Fig. 2.
Zoom of Fig. 2.

Further validation studies of the biodegradation module are planned via comparison to numerical codes like UTCHEM, which takes into account Monod kinetics and possible inhibition. Within the framework of a R&D project in progress, it is also foreseen to integrate the developed approach into a 3D multiphase transport code.

1 Introduction

Les composés organo-halogénés volatils (COHV), particulièrement les chloroéthylènes ou chloroéthènes – tétrachloroéthylène (PCE), trichloréthylène (TCE), dichloroéthylène (DCE) et chlorure de vinyle (VC ou CV) –, font partie des polluants les plus couramment détectés dans les aquifères [4]. Dans les sols et les eaux souterraines, ils peuvent subir des mécanismes d'atténuation naturelle [3]. Parmi les mécanismes impliqués dans l'atténuation naturelle, comme la dispersion, l'adsorption, la dissolution, la volatilisation, la destruction chimique ou biologique, la biodégradation est le plus important en termes de quantité de pollution dégradée [19].

La biodégradation est souvent une réaction d'oxydoréduction catalysée par des microorganismes, impliquant des accepteurs et des donneurs d'électrons [13,14]. Dans les sols et les eaux souterraines, les donneurs d'électrons typiques, espèces chimiques qui subissent des réactions d'oxydation produisant des électrons et d'autres produits (dioxyde de carbone, CO₂, en particulier), sont les hydrocarbures pétroliers (dont les BTEX – benzène, toluène, éthylbenzène, xylènes et associés), l'acétate, le méthanol, les acides humiques et les chloroéthènes les moins substitués, principalement le DCE et le VC. Les accepteurs d'électrons typiques, espèces chimiques qui subissent des réactions de réduction en captant des électrons, sont les composés inorganiques comme, par ordre de préférence, l'oxygène (O₂), les nitrates ( ${NO}_{3}^{-}$ ), le manganèse (Mn²⁺), le fer ferrique (Fe³⁺), les sulfates ( ${SO}_{4}^{2 -}$ ), le dioxyde de carbone (CO₂) et les chloroéthènes les plus oxydés (PCE et TCE). Sous des conditions réductrices, les chloroéthènes subissent un mécanisme de réduction, appelé déchloration réductrice, qui transforme de manière séquentielle le PCE en TCE, le TCE en cis-DCE (les autres isomères, trans-DCE et 1,1-DCE, sont minoritaires [5]), le cis-DCE en VC, et finalement le VC en éthylène [22].

Cependant, en fonction des conditions bio- et géochimiques, toutes les réactions potentielles de biodégradation, telles que l'oxydation, la déchloration réductrice sous conditions dénitrifiantes, de réduction des sulfates ou méthanogènes, ne peuvent pas s'appliquer à tous les solvants chlorés.

D'un point de vue pratique, sur les sites pollués, il est crucial d'être capable de prévoir et de caractériser le devenir des COHV, ce qui nécessite généralement l'utilisation d'un code numérique de transport prenant en compte la biodégradation des COHV. De nombreux codes commerciaux, analytiques ou numériques, existent qui peuvent modéliser les mécanismes de biodégradation, comme RT3D [6] ou UTCHEM [7]. Cependant, aucun de ces codes n'est strictement adapté à la modélisation de la biodégradation des COHV avec toutes les fonctionnalités requises (type de cinétique, notion de séquentialité...) [16].

L'objectif de ce travail est de développer un modèle conceptuel et mathématique de biodégradation adapté à la famille des chloroéthènes (PCE, TCE, DCE, VC et éthylène), fondé sur une triple approche biologique, thermodynamique et mécanistique. Afin d'être directement applicable en ingénierie des sites et sols pollués, le modèle conceptuel devra intégrer des paramètres et variables d'état quantifiables, de manière opérationnelle, dans le cadre d'une expertise d'un site réel pollué.

2 Modèle conceptuel

Le Tableau 1 liste l'ensemble des constituants inclus dans le modèle conceptuel proposé. La sélection des constituants est fondée sur les hypothèses suivantes :

L'observation, du point de vue biologique, thermodynamique et mécanistique, de la biodégradation des COHV dans les milieux naturels, nous a conduits au postulat suivant, postulat qui représente la base du modèle conceptuel proposé : tous les COHV ne peuvent pas subir tous les mécanismes de dégradation possibles, et le mécanisme impliquant l'accepteur d'électrons le plus énergétiquement favorable pour les bactéries est prédominant [1]. Ainsi, l'approche choisie est fondée sur un système de « double switch ».

Le premier switch correspond à la sélection d'un mécanisme de biodégradation en fonction des conditions environnementales (Tableau 2), celui qui implique l'accepteur d'électrons le plus énergétiquement favorable.

Par ailleurs, à côté des concepts assez bien connus et documentés sur la biodégradation des chloroéthènes, un autre concept a été considéré, qui, bien que documenté de manière séparée, a rarement fait l'objet d'une conceptualisation sous une forme globalisatrice. Il s'agit du concept du double rôle des accepteurs d'électrons inorganiques [12]. Ils possèdent, en effet, un rôle positif, en générant, par leur consommation successive, des conditions réductrices favorables à la déchloration réductrice. Mais ils possèdent également un rôle négatif, en étant en compétition avec les organochlorés quand ils jouent le rôle d'accepteurs d'électrons pour capter les électrons, leur présence induisant alors une diminution de la cinétique de biodégradation des COHV.

Les valeurs seuil utilisées dans le modèle sont du même ordre de grandeur que celles présentées dans la littérature [8,23]. Devol [8] stipule que la même population bactérienne qui consomme de l'oxygène peut également, via des changements métaboliques mineurs, utiliser des nitrates quand la concentration en oxygène dissous devient très faible. Ainsi, quand la concentration en oxygène est comprise entre 0 et 0,1 mg/l, nous considérons que deux mécanismes peuvent agir de pair, l'oxydation et la réduction, sous conditions dénitrifiantes. En ce qui concerne la valeur seuil en oxygène dissous, la valeur retenue (0,1 mg/l) est cohérente avec les valeurs, issues de la littérature, compilées par Van Cappellen et al. [20,21]. Ces auteurs définissent des concentrations limites en accepteurs d'électrons, telles que, lorsque la concentration d'un accepteur d'électrons est supérieure à sa valeur limite, les populations bactériennes utilisent prioritairement cet accepteur. Pour l'oxygène dissous, les valeurs compilées par Van Cappellen et al. [20,21] sont comprises entre 0,03 et 0,32 mg/l.

Le second switch correspond à la sélection des mécanismes de biodégradation potentiels pour chaque chloroéthylène pris en compte (Tableau 3).

Les mécanismes sélectionnés pour chaque composé chloré sont cohérents avec les études existantes de synthèse sur la biodégradabilité des COHV [17,19].

3 Modèle mathématique de biodégradation

Plusieurs lois ont été utilisées pour décrire les cinétiques des réactions de biodégradation. La cinétique de Michaelis–Menten [9], souvent confondue, parfois improprement, avec la cinétique de Monod [15], décrite par une fonction hyperbolique, est connue pour être bien adaptée à la modélisation de la dégradation d'un composé organique, appelé le substrat, par une population bactérienne. Avec l'hypothèse que la biomasse est constante et que le substrat ne soit pas limitant, la dégradation biologique d'un unique composé $i, R_{i}$ , peut s'écrire sous la forme de la cinétique hyperbolique suivante (1) :

R_{i} \equiv \frac{d C_{i}}{d t} = - V_{\max} \frac{C_{i}}{K_{i} + C_{i}}

(1)

avec

V_{\max}

(ML⁻³ T⁻¹) le taux maximum de dégradation et

K_{i}

(ML⁻³) la constante de demi-saturation, correspondant à la concentration de

C_{i}

pour laquelle

R_{i} = V_{\max} / 2

L'Éq. (1) peut être amendée en ajoutant des termes qui décrivent la compétition entre différents constituants pour capter les électrons, l'inhibition de la présence d'un composé sur la dégradation d'un autre, et la présence d'un substrat limitant. Le modèle d'approche retenu privilégie des lois cinétiques de type hyperbolique, les plus couramment utilisées dans le domaine, mais modifiées de manière à prendre en compte trois phénomènes importants et à en conceptualiser certains de manière originale :

– la notion de réactif limitant, par la prise en compte du minimum des deux termes réactifs, l'un lié aux accepteurs d'électrons et l'autre aux donneurs, cette approche étant rarement utilisée dans les codes existants ;
– la notion de compétition entre les accepteurs d'électrons d'une part, et entre les donneurs d'électrons d'autre part ; la conceptualisation de cette notion permet de représenter, de manière réaliste, l'interaction qui peut exister dans l'environnement entre toutes les espèces chimiques présentes pouvant participer au mécanisme de biodégradation ;
– la notion d'inhibition de la dégradation permettant de prendre en compte une cinétique de consommation différente des accepteurs et des donneurs d'électrons, les composés chlorés étant par exemple consommés moins rapidement que les accepteurs d'électrons inorganiques dans le mécanisme de déchloration réductrice.

Ces trois spécificités, prises en compte de façon simultanée, constituent une originalité vis-à-vis des codes de calcul existants.

À titre d'exemple, le Tableau 4 synthétise les équations utilisées pour modéliser la biodégradation du TCE sous des conditions sulfatoréductrices. Dans le Tableau 4, le terme de dégradation du TCE, $R_{TCE}$ , est décrit sous la forme de deux termes : le terme $R_{1_{TCE}}$ exprime la disparition du TCE par biodégradation, le terme $R_{2_{TCE}}$ exprime l'apparition du TCE par dégradation du composé père, ici le PCE. Le terme $\min (R_{A}, R_{D})$ correspond au minimum des deux termes $R_{A}$ , lié aux accepteurs d'électrons, et $R_{D}$ , lié au donneur d'électrons. Cette formulation correspond à la formulation initiale de Monod [9] pour prendre en compte la notion de réactif limitant. Les facteurs $E (-)$ sont des termes d'inhibition ; par exemple, $E_{{SO}_{4}, TCE}$ représente la compétition entre le TCE et les ions sulfate pour capter les électrons disponibles dans le milieu environnemental. Les termes $Y (-)$ sont des termes de croissance (yield en anglais) ; par exemple, $Y_{TCE / PCE}$ représente le rapport entre la masse molaire du TCE et la masse molaire du PCE. $a, α, β, χ$ et $δ (-)$ sont des coefficients stœchiométrique liant l'évolution des accepteurs et des donneurs d'électrons.

4 Test du modèle développé

4.1 Description du modèle numérique

En conditions d'écoulement uniformes, monodimensionnelles et en régime permanent, le transport réactif d'un composé dissous i dans un milieu poreux souterrain saturé est décrit par l'équation macroscopique de conservation de la masse (2) :

R_{i}^{*} \frac{\partial C_{i}}{\partial t} = D \frac{\partial^{2} C_{i}}{\partial x^{2}} - U \frac{\partial C_{i}}{\partial x} + Q_{i} + R_{i}

(2)

avec

R_{i}^{*} (-)

le coefficient de retard du constituant i dû à la sorption sur la surface solide,

C_{i}

(ML⁻³) la concentration du constituant dissous, U (LT⁻¹) la vitesse moyenne de pores, D (L² T⁻¹) le coefficient de dispersion hydrodynamique,

Q_{i}

(ML⁻³ T⁻¹) le terme puits/source, et

R_{i}

(ML⁻³ T⁻¹) le terme de réaction chimique ou biologique (<0 si le composé est dégradé, >0 si le composé apparaît).

Pour les 13 constituants considérés dans le modèle développé (les composés « artificiels » sont traités de manière séparée, étant donné qu'ils ne sont pas transportés), un système de 13 équations différentielles couplées est établi, approché par la méthode des différences finies et résolu par l'algorithme de Thomas [18]. Le terme de dispersion est discrétisé spatialement par les différences finies centrées avec une discrétisation temporelle implicite. Le terme de convection est discrétisé par les différences finies amont avec une discrétisation temporelle explicite. Le terme de biodégradation ( $R_{i}$ ) est formulé par maille avec un schéma temporel explicite. Le code numérique développé a été d'abord vérifié sur un cas test simple, ayant pour objectif de vérifier la stabilité de la solution numérique [16].

4.2 Description du cas test

Le cas test présenté ici consiste à simuler l'évolution d'une source de pollution constituée de PCE et de TCE, soumise aux mécanismes de convection et de biodégradation en conditions aérobies et anaérobies. Dans cet exemple, nous ne modélisons, ni la sorption des différents constituants sur la matrice solide ( $R_{i}^{*} = 1$ ), ni le phénomène de dispersion, pour ne pas masquer le phénomène éventuel de diffusion numérique. Nous supposons, dans cet exemple, que l'éthylène ne se biodégrade pas : la chaîne de dégradation prise en compte est donc PCE → TCE → DCE → VC → ETH.

On considère un aquifère (longueur $L = 100 m$ ), dans lequel l'écoulement est monodimensionnel et où s'effectue le transport des composés organochlorés sous forme dissoute (Fig. 1). Dans les simulations, on suppose que les concentrations en PCE et TCE issues d'une zone source arrivent en $x = 0 m$ dans le milieu poreux initialement non pollué et sont maintenues, pendant toute la simulation, égales à 100 mg/l. La vitesse moyenne de pores est égale à 1 m/j. Les pas d'espace et de temps ont été choisis égaux respectivement à 1 m et 0,01 j. Les concentrations initiales en constituants et leurs valeurs à l'entrée de l'aquifère ainsi que les paramètres cinétiques sont regroupés dans le Tableau 5.

4.3 Discussion des résultats

Les courbes d'évolution des 11 constituants transportés (ne sont pas représentés ni le COD qui est maintenu constant dans l'espace et dans le temps, ni l'éthane qui n'est pas produit, ni les constituants « oxydés ») en fonction de x au temps $t = 50 j$ sont représentées sur les Figs. 2 et 3. La Fig. 3 correspond à un zoom de la Fig. 2 sur une zone permettant de mieux observer les concentrations seuil en accepteurs d'électrons inorganiques, au passage d'une zone redox à une autre, concentrations fixées dans le modèle à 1 mg/l.

Au vu de ces courbes d'évolution des principaux constituants, nous pouvons faire les commentaires suivants :

– L'évolution des chloroéthènes est correctement représentée.

Le PCE ne décroît pas en zones aérobie et mixte aérobie–dénitrifiante. Son début de décroissance en zone dénitrifiante n'est pas dû à un mécanisme de biodégradation, mais au simple mécanisme de diffusion numérique, car le pas de temps choisi correspond à un nombre de Courant très inférieur à 1. Ainsi, le front de concentration à $t = 50 j$ illustre bien un déplacement convectif (la concentration de 50 mg/l est atteinte à la distance $x = 50 m$ pour une vitesse d'écoulement de 1 m/j) avec une diffusion numérique, due au choix de pas de temps, équivalente à une dispersivité longitudinale « apparente » équivalente à la taille d'une demi-maille. La biodégradation du PCE n'est active qu'en zones sulfatoréductrice et méthanogène (terme réactionnel $R_{PCE}$ non nul).

Le TCE décroît dès la zone aérobie, et des ruptures de pente dans sa courbe d'évolution sont bien observées au changement de zone redox. De plus, en zone sulfatoréductrice, l'augmentation de sa concentration s'explique par le fait que, étant donné la forte vitesse de disparition du PCE (biodégradation + arrivée du front à $x = 50 m$ ), la vitesse d'apparition du TCE est localement plus forte que sa propre vitesse de dégradation. Le DCE et le VC n'apparaissent pas en zone aérobie, et ils présentent également un léger pic en zone sulfatoréductrice. L'éthylène est toujours produit et diminue uniquement par arrivée du front convectif à l'abscisse $x = 50 m$ .

– L'évolution des accepteurs d'électrons inorganiques est également bien représentée.

En zone aérobie, définie par une concentration en oxygène supérieure à 0,1 mg/l, les concentrations en nitrates et sulfates sont constantes.

En zone mixte aérobie–dénitrifiante, définie par une concentration en oxygène comprise entre 0 et 0,1 mg/l et une concentration en nitrates supérieure à 1 mg/l, la concentration en sulfates est constante.

En zone sulfatoréductrice, la concentration en sulfates décroît, la concentration en nitrates est égale à 1 mg/l (voir Fig. 3) et la concentration en oxygène est nulle (précisément 10⁻⁹ mg/l, seuil fixé dans le modèle).

La concentration en CO₂ ne commence à décroître qu'en zone méthanogène, où il est consommé en tant qu'accepteur d'électrons. De la même manière que les nitrates en zone sulfatoréductrice, la concentration en sulfates est constante et égale à 1 mg/l en zone méthanogène (voir Fig. 3).

– Le passage entre les différentes zones redox est bien simulé.

Cela se vérifie de deux manières :

• D'une part, le changement de zone redox se produit bien quand les seuils de concentration sont atteints : par exemple, la concentration en sulfates ne commence à chuter que quand la concentration en nitrates passe en dessous de la valeur seuil de 1 mg/l (voir Fig. 3).
• D'autre part, les résultats du modèle incluent les termes réactionnels R pour tous les constituants modélisés. Là encore, nous pouvons observer un bon accord entre le changement de zone et la valeur du terme réactionnel : par exemple, le terme $R_{{SO}_{4}}$ devient non nul dans la maille où la concentration en nitrates devient inférieure à 1 mg/l.

Au vu des résultats de ce cas test, on peut considérer que le code numérique permet de simuler correctement les mécanismes du modèle conceptuel.

5 Conclusions

Un modèle conceptuel, mathématique et numérique, dédié à la biodégradation des chloroéthènes dans les eaux souterraines, a été développé. L'originalité de la démarche tient à la fois aux mécanismes pris en compte (concomitance des notions de réactif limitant, de compétition et d'inhibition) et à l'orientation résolument opérationnelle du modèle (seuls des paramètres et variables mesurables en routine sur site sont considérés).

Testé sur un cas simple schématisant un processus de biodégradation « idéal » (biodégradation totale jusqu'à l'éthylène, CO₂ accepteur final d'électrons), le modèle a permis de représenter de manière satisfaisante l'évolution des chloroéthènes et des accepteurs d'électrons inorganiques ainsi que le passage entre les différentes zones redox.

Compte tenu de ces résultats, le formalisme mathématique de biodégradation sera intégré dans un code numérique 3D, multiphasique, multiconstituant, intégrant l'ensemble des mécanismes d'atténuation naturelle (convection, dispersion–diffusion, adsorption, dissolution, volatilisation, biodégradation) des hydrocarbures pétroliers et des composés organo-halogénés volatils (programme de recherche en cours de réalisation).

Remerciements

Ce travail a bénéficié d'une bourse de thèse cofinancée par l'Ademe (Agence de l'environnement et de la maîtrise de l'énergie) et Burgéap SA.

Bibliographie

[1] O. Atteia; M. Franceschi Conditions chimiques contrôlant l'atténuation naturelle des BTEX et solvants chlorés : un état des connaissances, Rev. Sci. Eau, Volume 14 (2001) no. 4, pp. 419-444

[2] G. Bitton; C.P. Gerba Groundwater Pollution Microbiology, John Wiley & Sons, New York, 1984

[3] H. Benremita; G. Schäfer Transfert du trichloréthylène en milieu poreux à partir d'un panache de vapeurs, C. R. Mecanique, Volume 331 (2003), pp. 835-842

[4] M. Bohy; G. Schäfer; O. Razakarisoa Caractérisation de zones sources de DNAPL à l'aide de traceurs bisolubles : mise en évidence d'une cinétique de partage, C. R. Geoscience, Volume 336 (2004), pp. 799-806

[5] E.J. Bouwer Bioremediation of chlorinated solvents using alternate electron acceptors (R.D. Norris; R.E. Hinchee; R. Brown; P.L. McCarty; L. Semprini; R. Wollast et al., eds.), Handbook of Bioremediation, Lewis Publishers, Boca Raton, FL, 1994

[6] T.P. Clement RT3D, A modular computer code for simulating reactive multi-species transport in 3-dimensional groundwater systems, Pacific Northwest National Laboratory, Richland, Washington, 1997

[7] P.C. de Blanc, K. Sepehrnoori, G.E. Speitel, D.C. McKinney, Investigation of numerical solution techniques for biodegradation equations in a groundwater flow model, in: Proc. 11th Int. Conf. on Computational Methods in Water Resources, 22–26 July 1996, Cancun, Mexico, 1996

[8] A.H. Devol Bacterial oxygen uptake kinetics as related to biological processes in oxygen deficient zones of the oceans, Deep-Sea Res., Volume 25 (1978), pp. 137-146

[9] A.L. Lehninger Biochemistry, Worth Publishers Inc., New York, 1972

[10] D.R. Lovley; F.H. Chapelle; J.C. Woodward Use of dissolved H₂ concentrations to determine distribution of microbially catalysed redox reactions in groundwater, Environ. Sci. Technol., Volume 28 (1994), pp. 1205-1210

[11] S.W. Effler Limnological and engineering analysis of a polluted urban lake: prelude to environmental management of Onondaga Lake, New York, Springer-Verlag, New York, 1996

[12] S. Fetzner Bacterial dehalogenation, Appl. Microbiol. Biotechnol., Volume 50 (1998), pp. 633-657

[13] P.M. Jeffers; L.M. Ward; N.L. Wolfe Homogenous hydrolysis rate constants for selected chlorinated methanes, ethanes, ethenes and propanes, Environ. Sci. Technol., Volume 23 (1989), pp. 965-969

[14] P.L. McCarty Engineering concepts for in-situ bioremediation, Bioremediation: Fundamentals and Effective Applications, Third Annual Symposium of the Gulf Coast Hazardous Substance Research Center, 21–22 February 1991, Lamar University, Beaumont, TX, 1991

[15] J. Monod The growth of bacterial cultures, Annu. Rev. Microbiol., Volume 3 (1949), pp. 371-394

[16] F. Nex, Modélisation numérique de la biodégradation des composés organo-chlorés dans les aquifères, fondée sur des expérimentations in situ. Le cas des chloroéthènes, thèse, université Louis-Pasteur, Strasbourg, 2004

[17] J.F. Pankow; J.A. Cherry Dense Chlorinated Solvents and other DNAPLs in Groundwater: History, Behavior, and Remediation, Waterloo Press, Portland, OR, USA, 1996

[18] G. Schäfer, H. Kobus, DULAMO – Zweischichtiges 1D-Grundwassertransportmodell, Institut für Wasserbau, Universität Stuttgart, Allemagne, PD 90/08, 1990

[19] A. Sinke, I. Le Hecho, Monitored natural attenuation: review of existing guidelines and protocols, TNO-Nicole report, Apeldoorn, The Netherlands, 1999

[20] P. Van Cappellen; J.-F. Gaillard; C. Rabouille Biogeochemical transformations in sediments: kinetic models of early diagenesis (R. Wollast et al., eds.), Interactions of C, N, P, and S Biogeochemical Cycles and Global Change, Springer-Verlag, 1993, pp. 401-445

[21] P. Van Cappellen; Y. Wang Metal cycling in surface sediments: modeling the interplay between transport and reaction (H. Allen, ed.), Metal Contaminated Aquatic Sediments, Ann Arbor Press, 1995, pp. 21-64

[22] T.M. Vogel; C.S. Criddle; P.L. McCarty Transformation of halogenated aliphatic compounds, Environ. Sci. Technol., Volume 21 (1987), pp. 722-736

[23] T.H. Wiedemeier, M.A. Swanson, D.E. Moutoux, J.T. Wilson, D.H. Kampbell, J.E. Hansen, P. Haas, Overview of the technical protocol for natural attenuation of chlorinated aliphatic hydrocarbons in ground water under development for the U.S. Air Force Center for Environmental Excellence, in: Symposium on natural attenuation of chlorinated organics in ground water, U.S. Environmental Protection Agency Report, EPA/540/R-97/504, Office of Research and Development, Washington, DC, 1997, pp. 35–60

Commentaires - Politique

Ces articles pourraient vous intéresser

Mn-oxide: a major source of easily mobilisable Co and Ni under reducing conditions in New Caledonia Ferralsols

Cécile Quantin; Thierry Becquer; Jacques Berthelin

C. R. Géos (2002)

Bioreduction of ferric species and biogenesis of green rusts in soils

Jacques Berthelin; Georges Ona-Nguema; Sébastien Stemmler; ...

C. R. Géos (2006)