Geochemical and microbiological controls on dissimilatory iron reduction

Eric E. Roden

doi:10.1016/j.crte.2006.04.009

Geomaterials (Mineralogy)

Geochemical and microbiological controls on dissimilatory iron reduction
[Contrôles géochimique et microbiologique de la réduction dissimilatrice du fer]

Eric E. Roden ¹

¹ University of Wisconsin, Department of Geology and Geophysics, Madison, WI 53706, USA

Comptes Rendus. Géoscience, Volume 338 (2006) no. 6-7, pp. 456-467.

Résumés

Anglais
Français

Recent experimental studies permit development of conceptual and quantitative models of microbial Fe(III) oxide reduction at circumneutral pH that can be compared to and contrasted with established models of abiotic mineral dissolution. The findings collectively support a model for controls on enzymatic reduction that differs fundamentally from those applied to abiotic reductive dissolution as a result of two basic phenomena: (1) the relatively minor influence of oxide mineralogical and thermodynamic properties on rates of enzymatic reduction compared to abiotic reductive dissolution, and (2) the major limitation which sorption and/or surface precipitation of biogenic Fe(II) on residual oxide and Fe(III)-reducing bacterial cell surfaces poses to enzymatic electron transfer in the presence of excess electron donor. Parallel studies with two well-characterized Fe(III)-reducing organisms (Shewanella putrefaciens and Geobacter sulfurreducens) lead to common conclusions regarding the importance of these phenomena in regulating the rate and long-term extent of Fe(III) oxide reduction. Models in which rates of enzymatic reduction are limited by Fe(III)-reducing bacterial cell density together with the abundance of ‘available’ oxide surface sites (as controlled by oxide surface area and the accumulation of surface-bound biogenic Fe(II)) provide an adequate macroscopic description of controls on the initial rate and long-term extent of oxide reduction.

Des études expérimentales récentes conduisent à l'établissement de modèles quantitatifs de la réduction microbienne des oxydes ferriques à pH neutre, qui peuvent être comparés et doivent être contrastés avec ceux qui décrivent classiquement la dissolution abiotique de ces mêmes minéraux. Les observations convergent pour établir que les différences entre ces deux familles de modèles ont pour cause les deux phénomènes fondamentaux suivants : (i) l'influence relativement mineure de la nature minéralogique et donc des propriétés thermodynamiques de oxydes de fer impliqués sur les vitesses de dissolution observées lorsque la dissolution se réalise par voie enzymatique et (ii) la limitation majeure qu'impose la précipitation et/ou l'absorption du feu biogénique sur les oxydes ferriques résiduels et les cellules bactériennes, lorsque les transferts d'électrons liés à la voie enzymatique ont lieu en présence d'un excès de donneurs d'électrons. Des expériences semblables réalisées avec deux souches bien caractérisées de bactéries ferriréductrices (Shewanella putrefaciens et Geobacter sulfurreducens) montrent que, sur le long terme également, les mêmes phénomènes régulent tant la vitesse que l'importance de la réduction des oxydes ferriques. Il en résulte que les modèles basés sur les limitations imposées à la vitesse de réduction par la densité de cellules bactériennes et l'abondance des sites disponibles sur la surface « accessible » des oxydes ferriques (elle-même contrôlée par la surface spécifique de ces oxydes et par l'accumulation sur cette surface des cations Fe^II d'origine biologique) fournissent une description macroscopique adéquate des paramètres contrôlant, tant la vitesse initiale de la réduction des oxydes ferriques, que son importance sur le long terme.

Métadonnées

Reçu le : 2006-03-07
Accepté le : 2006-03-09
Publié le : 2006-05-30

DOI : 10.1016/j.crte.2006.04.009

Keywords: Iron oxides, Rate of enzymatic reduction, Dissimilatory iron-reducing bacteria
Mot clés : Oxydes de fer, Vitesse de réduction enzymatique, Bactéries ferriréductrices

Affiliations des auteurs :

Eric E. Roden ¹

¹ University of Wisconsin, Department of Geology and Geophysics, Madison, WI 53706, USA

@article{CRGEOS_2006__338_6-7_456_0,
     author = {Eric E. Roden},
     title = {Geochemical and microbiological controls on dissimilatory iron reduction},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {456--467},
     publisher = {Elsevier},
     volume = {338},
     number = {6-7},
     year = {2006},
     doi = {10.1016/j.crte.2006.04.009},
     language = {en},
}

TY  - JOUR
AU  - Eric E. Roden
TI  - Geochemical and microbiological controls on dissimilatory iron reduction
JO  - Comptes Rendus. Géoscience
PY  - 2006
SP  - 456
EP  - 467
VL  - 338
IS  - 6-7
PB  - Elsevier
DO  - 10.1016/j.crte.2006.04.009
LA  - en
ID  - CRGEOS_2006__338_6-7_456_0
ER  -

%0 Journal Article
%A Eric E. Roden
%T Geochemical and microbiological controls on dissimilatory iron reduction
%J Comptes Rendus. Géoscience
%D 2006
%P 456-467
%V 338
%N 6-7
%I Elsevier
%R 10.1016/j.crte.2006.04.009
%G en
%F CRGEOS_2006__338_6-7_456_0

Eric E. Roden. Geochemical and microbiological controls on dissimilatory iron reduction. Comptes Rendus. Géoscience, Volume 338 (2006) no. 6-7, pp. 456-467. doi : 10.1016/j.crte.2006.04.009. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2006.04.009/

Version originale du texte intégral

1 Introduction

The redox cycling of Fe plays a major role in the biogeochemical cycling of many elements in natural systems [9,51]. On the reductive side of the Fe redox cycle, dissimilatory microbial (enzymatic) reduction of Fe(III) oxides has a major impact on the aqueous/solid-phase geochemistry and behavior of natural and contaminant compounds in nonsulfidogenic subsurface sedimentary environments. As a result of the pivotal role of bacterial Fe(III) oxide reduction in surficial and subsurface sediment biogeochemistry, there is great interest in the factors that control the rate and long-term degree of enzymatic Fe(III) oxide reduction. The rate and extent of Fe(III) oxide reduction are governed by complex surface-chemical and physiological interactions which are as yet only poorly characterized [44]. Development of a mechanistic understanding the geochemical and microbiological controls on microbial reduction of soluble and solid-phase metals is a prerequisite for development of reactive transport models of inorganic contaminants and radionuclides in saturated subsurface environments [8]. The studies summarized here explored how the surface chemical (e.g., specific surface area) and thermodynamic properties (e.g., oxide reduction potential) of different Fe(III) oxides influence the rate and extent of bacterial (versus chemical) Fe(III) oxide reduction. The results permit development of conceptual and quantitative models of enzymatic Fe(III) oxide reduction at circumneutral pH that can be compared and contrasted with models of abiotic mineral dissolution and enzymatic soluble metal reduction.

2 Materials and methods

2.1 Fe(III) oxide phases

The Fe(III) oxides employed in this study included a variety of pure synthetic phases [40] as well as three previously characterized Fe(III) oxide-bearing subsoil or subsurface materials (HC, CP, and Oyster). The synthetic oxides were prepared according to standard methods [50]. The HC and CP natural materials are Fe(III) oxide/layered silicate mixtures obtained from Ultisols in Tennessee and North Carolina, respectively. The Oyster material is Fe(III) oxide-coated sand from Pleistocene Age Atlantic Coastal Plain sediments. More detailed descriptions of the properties of these materials are available elsewhere [42,54,55]. The synthetic Fe(III) oxides were freeze-dried and passed through a 100-μm sieve, and their specific surface area determined by multipoint BET N₂ adsorption. The natural materials were air dried and passed through a 2-mm sieve prior to use in experiments.

2.2 Fe(III)-reducing microorganisms

Two well-characterized dissimilatory Fe(III)-reducing bacteria (FeRB) were employed in Fe(III) reduction experiments, Shewanella putrefaciens strain CN32 [14], and Geobacter sulfurreducens strain PCA [3,31]. The procedures used for growth and handling of these organisms for Fe(III) reduction experiments are described in detail in Roden [40] and Jeon et al. [19], respectively.

2.3 Bacterial reduction experiments

The synthetic and natural Fe(III) oxide-bearing solids were suspended in sterile, anaerobic Pipes buffer (10 mM, pH 6.8) contained in sealed serum vials to obtain Fe(III) concentrations of 5 to 250 mmol l⁻¹. Other experiments were conducted with soluble Fe(III) citrate as an electron acceptor. The electron donor for metal reduction was either 100% H₂ in the vial headspace, or 10 mM of either sodium lactate or sodium acetate. The medium was inoculated with ca. 10⁸ cells ml⁻¹ of either S. putrefaciens or Geobacter sulfurreducens cells. Samples for determination of dissolved (0.2-μm filtration and Ferrozine analysis) and total Fe(II) (0.5M HCl extraction and Ferrozine analysis) and pH were collected at 1–10-d intervals.

2.4 Ascorbate and AH₂DS reduction experiments

Table 1

Characteristics of synthetic Fe(III) oxides used in studies of microbial and abiotic reduction experiments. Modified with permission from Table 1 in Roden [40], with kind permission of the American Chemical Society

Caractéristiques des oxydes de fer synthétiques, utilisés pour les expériences de Fe(III) réduction bactérienne et abiotique. Modifié d'après le Tableau 1 de Roden [40], et reproduit ici avec l'aimable autorisation de l'American Chemical Society

Oxide	Assumed morphology^a	% HA–Ext Fe(III)^b	Surface area^c (m² g⁻¹)	Estimated mean particle size^d (nm)	$E_{h}^{0}$ (V)^e
Hydrous ferric oxide	sphere	100 ± 0	600	1.3	+1.230
2-line Ferrihydrite	sphere	14.8 ± 0.2	290	2.6	+0.918
Feroxyhyte	plate	3.61 ± 0.04	176	9.4	+0.888
Lepidocrocite	cylinder	2.55 ± 0.05	63.6	26.7	+0.902
HSA Goethite 1	cylinder	1.75 ± 0.05	211	7.7	+0.844
HSA Goethite 2	cylinder	0.90 ± 0.03	135	12.1	+0.844
Goethite 7 °C^f	cylinder	0.72 ± 0.01	96.3	16.9	+0.811
Goethite 20 °C^f	cylinder	0.34 ± 0.01	73.0	22.4	+0.803
Goethite 30 °C^f	cylinder	0.085 ± 0.003	62.0	26.3	+0.804
Goethite 90 °C^f	cylinder	0.019 ± 0.001	37.6	43.4	+0.787
Mati hematite	sphere	0.53 ± 0.11	18.8	30.3	+0.781
Fisher Hematite	sphere	0.075 ± 0.005	10.3	55.4	+0.774

^a For use in estimating mean particle size from measured surface area.

^b 0.25M Hydroxylamine–HCl/0.25M HCl, 1-h extraction; mean ± SD of triplicate samples.

^c Determined by multi-point BET N₂ adsorption, except for HFO, for which the assumed value is based on discussions and recommendations in Dzombak and Morel [11].

^d Estimated using the oxide densities listed in [6], and assuming the following proportions for plate and cylindrical and particle morphologies: plate diameter: $thickness = 10 : 1$ ; cylinder length: $diameter = 10 : 1$ . Note that particle aggregation is ignored in these calculations.

^e Half-cell reduction potentials (e.g., for reactions such as: $FeOOH + 3 H^{+} + e - = {Fe}^{2 +} + 2 H_{2} O$ ) computed based on the results of abiotic AH₂DS reduction experiments (see Section 2.4).

^f Temperature refers to the temperature at which the mineral synthesis was conducted.

The synthetic and natural Fe(III) oxide-bearing solids were suspended in anaerobic 10 mM ascorbic acid or 10 mM AH₂DS (the reduced form of AQDS, anthroquinone-2,6-disulfonate, prepared by reacting AQDS with 100% H₂ gas in the presence of a palladium catalyst) in 10 mM Pipes buffer. The oxide suspensions were incubated at room temperature on a rotary shaker (250 rpm) and samples were removed with a N₂-flushed plastic syringe at regular intervals. A portion of the sample was passed through a 0.2-μm filter into Ferrozine for Fe(II) analysis, and the remainder used for determination of pH. The final (after reduction ceased) dissolved Fe(II) concentration and pH values achieved in the AH₂DS reduction experiments were used in conjunction with the $E_{h}^{0}$ of the AQDS/AH₂DS couple (+0.23 V) [5] to estimate the reduction potential ( $E_{h}^{0}$ ) of the synthetic Fe(III) oxide phases.

3 Results and discussion

3.1 Initial rates of reduction

Initial (0–3 d) surface area-specific rates of synthetic Fe(III) oxide reduction by S. putrefaciens and G. sulfurreducens did not vary systematically across a wide range of oxide surface area and $E_{h}^{0}$ (Fig. 1A). In contrast, surface area-specific rates of abiotic Fe(III) oxide reduction by ascorbate and AH₂DS were significantly correlated with oxide surface area and $E_{h}^{0}$ (Fig. 1B). These results indicate that initial rates of bacterial Fe(III) oxide reduction are not strongly controlled by oxide crystal thermodynamic properties. An explicit illustration of the relative influence of oxide crystal structural properties on initial rates of biological vs. chemical reduction can be drawn from the results obtained with synthetic lepidocrocite (diamonds circled in Fig. 1). Lepidocrocite possesses a lower degree of crystal order (less negative $Δ G_{f}$ , higher $E_{h}^{0}$ ) than goethites of comparable particle size and surface area [51]. Consequently, lepidocrocite yielded a ca. two-fold higher initial rate of bacterial reduction compared to goethites with similar surface areas (Fig. 1A). However, the effect on the rate of reductive dissolution by ascorbate or AH₂DS was much more dramatic: lepidocrocite with a surface area of 64 m² g⁻¹ was reduced at a rate ca. two orders of magnitude greater than goethites with surface areas of 62 and 73 m² g⁻¹ (Fig. 1B).

Fig. 1
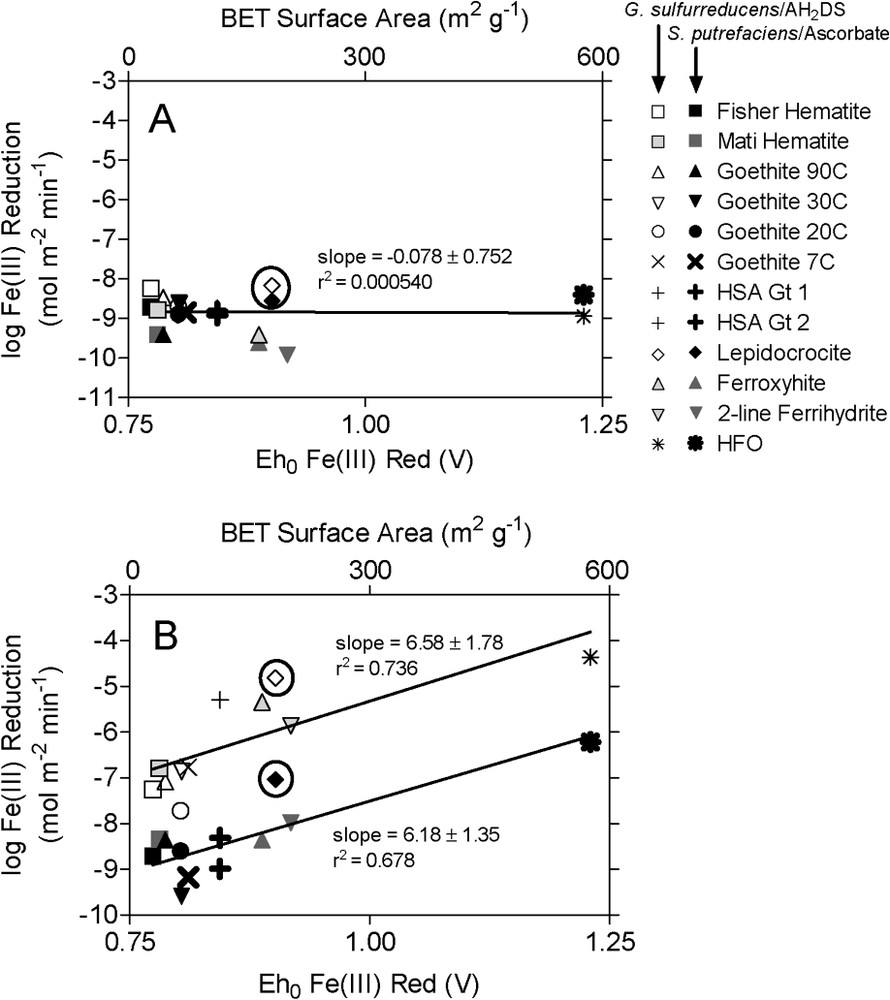
Initial (2–3-day incubation) surface area-specific rates of bacterial (A) and abiotic (B) reduction of synthetic Fe(III) oxides. Different symbols correspond to different Fe(III) oxide phases and reduction systems as indicated in the legend. The temperatures listed with the goethite phases correspond to the temperature at which the synthesis (from ferric nitrate) took place. Starting Fe(III) concentrations in the biotic and abiotic reduction experiments were 10 and 5 mmol l⁻¹, respectively. S. putrefaciens and ascorbate reduction data are reproduced with permission from Fig. 4 in Roden [40]; G. sulfurreducens data are from Roden [41].
Vitesses initiales (incubations pendant 2–3 jours) rapportées à la surface spécifique de la réduction bactérienne d'oxydes ferriques de synthèse. Les différents symboles correspondent aux différents types d'oxydes et de modalités de réduction indiqués sur la figure. Les températures relatives aux goethites correspondent à leurs températures de synthèse (aux dépens de nitrate ferrique). Les concentrations initiales en Fe^III dans les expériences de réduction bactérienne et abiotique étaient de 10 et de 5 mmol l⁻¹ respectivement. Les données relatives aux expériences de réduction en présence de S. putrefaciens et d'ascorbate sont issues de la Fig. 4 de Roden [40], les données relatives à G. sulfurreducens de Roden [41].

Since detachment of a metal ion from an oxide surface site is generally viewed as the rate-limiting step in oxide mineral dissolution [52], it could be argued that because of the tendency for Fe(II) to reassociate (or never become detached in the first place) with oxide surfaces during enzymatic reduction at circumneutral pH (discussed in detail in Roden and Urrutia [47]), the kinetics of the enzymatic reduction system is not controlled by the presence of an obvious leaving group for which the detachment energy (related to the energy required for metal-ligand bond formation and breaking processes [1,47]) is affected by the thermodynamic properties of the oxide phase. However, during the bacterial Fe(III) oxide reduction experiments conducted under simplified aqueous geochemical conditions (i.e. in the absence of ions such as ${HCO}_{3}^{-}$ and ${PO}_{4}^{3 -}$ , which can induce formation of Fe(II) surface precipitates, more than 65% of total (0.5M HCl-extractable) Fe(II) production was accounted for by aqueous Fe(II) accumulation (data not shown). Hence, enzymatic Fe(III) oxide reduction was mainly a reductive dissolution process in these experiments. If Fe(II) detachment from the oxide surface during enzymatic reduction was affected by the thermodynamic properties of the oxide and thus controlled the bulk reduction rate, we would have expected to see a significant correlation between initial surface area normalized reductive dissolution rate and oxide $E_{h}^{0}$ – as was clearly the case for reductive dissolution by ascorbate and AH₂DS. Since this was not the observed, we conclude that the mechanism and/or the rate-limiting step during enzymatic Fe(III) oxide reduction are fundamentally different than that for abiotic reductive dissolution. The simplest explanation is that the rate of electron transfer, rather than Fe(II) detachment, is the rate-limiting step during enzymatic reduction, and that rates of enzymatic electron transfer are not strongly affected by oxide thermodynamic properties.

Ongoing studies with Shewanella [10,12,32–35] and recent studies with Geobacter [24,29,30] have provided direct evidence that low redox potential, outer membrane-associated c-type cytochromes are involved in electron transfer from FeRB to Fe(III) oxides. In addition, a recent atomic force microscopy study by Lower et al. [28] demonstrated apparent molecular “recognition” of Fe(III) oxide surface sites by a putative ca. 150 kDa outer membrane protein of the dissimilatory FeRB Shewanella oneidensis (formerly S. putrefaciens strain MR-1), a close relative of the organism used in this study. Together these findings suggest the possibility that the similarity of surface area normalized electron transfer rates across a broad range of oxide minerals results from the fact that dissimilatory FeRB ‘recognize’ different Fe(III) oxide surfaces more or less equally independent of the underlying crystal structure, such that initial rates of electron transfer subsequent to recognition are not strongly dependent on crystal structure. This suggestion is consistent with an argument presented by Fischer [13] to account for the relatively minor influence of oxide solubility on rates of synthetic Fe(III) oxide reduction by Corynebacteria at pH 7. Fischer [13] reasoned that if the redox potential of the bacterial cells (i.e., their outer membrane c-type cytochromes) is sufficiently negative for reduction of well-crystallized oxide phases like hematite or goethite, each collision (or ‘recognition’) of a FeRB cell with an oxide particle will trigger reduction of a Fe(III) surface site. Therefore, the amount of Fe(II) produced during each collision event will not increase markedly with increasing oxide solubility.

3.2 Long-term extent of reduction

Similar patterns of Fe(II) accumulation were observed during long-term (3-week incubation) reduction of the various synthetic Fe(III) oxides by G. sulfurreducens (Fig. 2A): after an initial period of rapid Fe(II) accumulation, rates of reduction decreased and Fe(II) levels approached an asymptote. pH values correlated directly with aqueous Fe(II) concentrations during Fe(III) oxide reduction (Fig. 2B), as expected from the stoichiometry of Fe(III) oxide reduction coupled to H₂ oxidation:

The measured pH values and aqueous Fe(II) concentrations were used together with the estimated

E_{h}^{0}

values for the different Fe(III) oxides, to compute the free energy of Fe(III) oxide reduction (ΔG values) for the different synthetic phases during the course of the long-term reduction experiments (Fig. 3). The results indicate that the cessation of oxide reduction activity cannot be attributed to free energy constraints posed by dissolved Fe(II) accumulation and pH increase, because reduction rates approached zero at ΔG values substantially lower than the theoretical minimum of ca. −20 kJ mol⁻¹ required for energy conservation during biological energy metabolism [49]. The solid line in Fig. 3 corresponds to a standard transition state theory function that accounts for the influence of thermodynamic driving force on reaction rate [23], modified to account for the minimum free requirement for biological energy conservation as described in Liu et al. [26]. The experimental data clearly do not correspond to this function, in contrast to results obtained in studies of abiotic ligand-promoted dissolution of δ-Al₂O₃ and goethite [21]. Rather, both the total amount of Fe(II) generated and the amount of Fe(II) associated with oxide surfaces (referred to as ‘sorbed Fe(II)’) at the end of the reduction experiments correlated directly with the measured (BET) surface area of the mineral phases (Fig. 4), which suggests that accumulation of Fe(II) on oxide surfaces was responsible for cessation of oxide reduction activity. This conclusion is consistent with many previous studies of crystalline Fe(III) oxide reduction at circumneutral pH, and has be attributed to kinetic and/or thermodynamic impacts of surface-associated Fe(II) on enzymatic electron transfer, including impacts of Fe(II) sorption/surface precipitation on FeRB cell surfaces [47].

Fig. 2
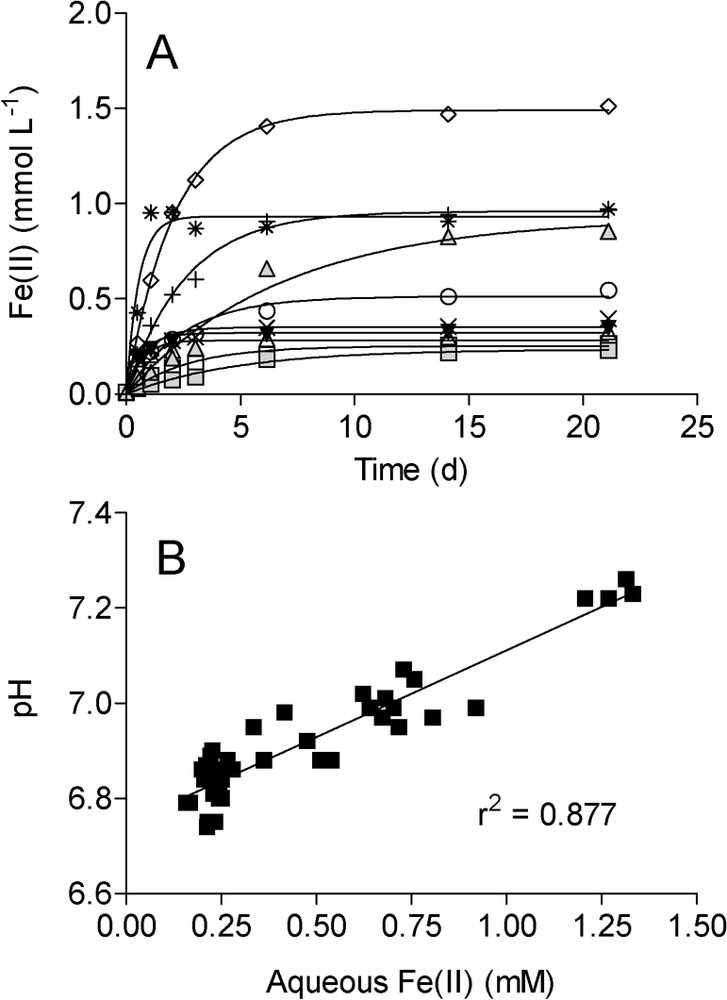
Total (0.5 M HCl extraction) Fe(II) production (A) and relationship between pH and aqueous Fe(II) accumulation (B) during reduction of synthetic Fe(III) oxides by G. sulfurreducens (data from Roden [41]). Symbols as in Fig. 1. Lines in panel A show nonlinear regression fits of the data to the equation depicting the accumulation of end-product of a first-order reaction. Line in panel shows result of a linear least-square regression analysis.
Évolution des concentrations en Fe^II total (extrait par HCl 0,5 M) en fonction du temps (A) et relation entre pH et Fe^II total extrait (B) lors de la réduction d'oxydes de fer de synthèse par G. sulfurreducens [41]. Les symboles sont identiques à ceux de la Fig. 1. Dans la Fig. 2A, les traits pleins montrent l'ajustement des données de régression non linéaire à des équations décrivant l'accumulation des produits de la réaction selon une loi cinétique d'ordre 1. Le trait plein de la Fig. 2B résulte d'une analyse de régression linéaire par la méthode des moindres carrés.

Fig. 3
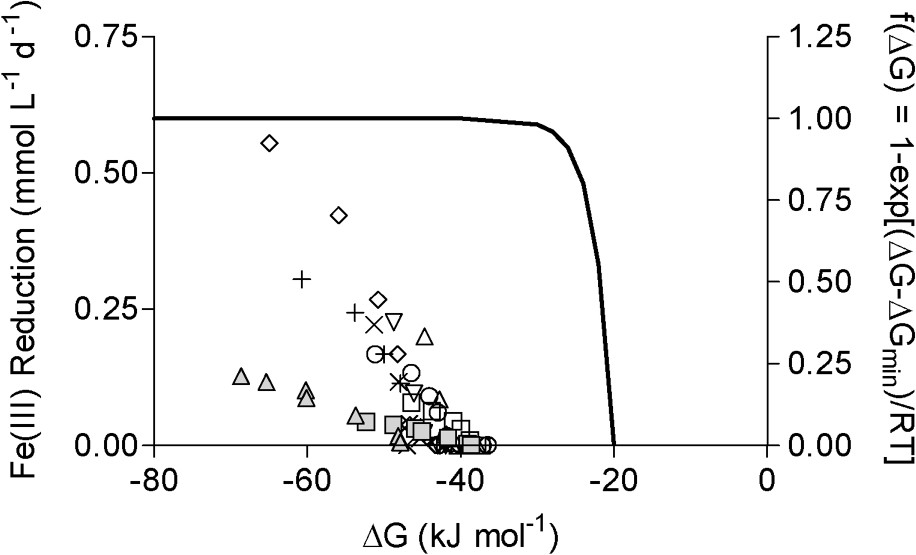
Rate of Fe(III) reduction as a function of the estimated free energy of reaction during long-term G. sulfurreducens experiments (data from Roden [41]). Fe(III) reduction rates were computed from the nonlinear curve fits shown in Fig. 2. Symbols as in Fig. 1. The solid line shows the relationship between reaction rate and energetics predicted based on transition state theory [23], modified to account for the minimum free requirement for biological energy conservation, as described in Liu et al. [26].
Vitesses de réduction du Fe^III en fonction de l'énergie libre estimée de la réaction lors d'expériences de longue durée utilisant G. sulfurreducens. Les vitesses de réduction du Fe^III sont calculées aux dépens des courbes présentées sur la Fig. 2 et les symboles sont ceux de la Fig. 1. Le trait plein montre la relation entre vitesse de réduction et les données énergétiques prédites par la théorie de l'état de transition [23], modifiée pour tenir compte de l'exigence minimale en énergie nécessaire pour la conservation de l'énergie biologique [26].

Fig. 4
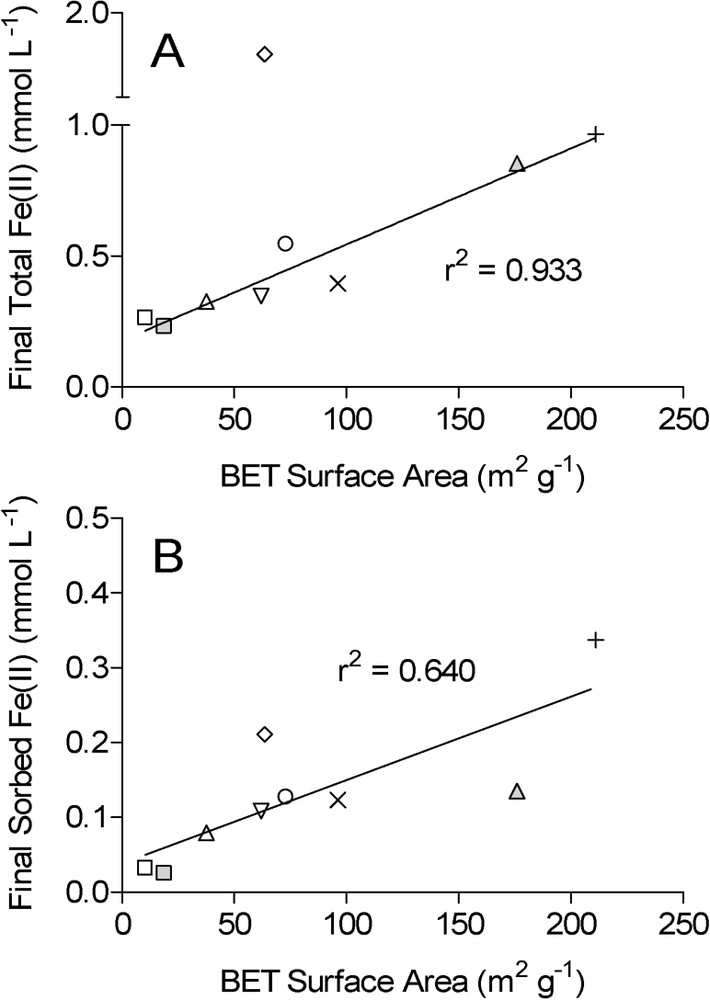
Correlation between oxide mineral surface area and the final concentration of total HCl-extractable Fe(II) (A) and surface-associated (‘sorbed’) Fe(II) (B) during long-term G. sulfurreducens experiments (data from Roden [41]). Symbols as in Fig. 1. Data for the HFO reduction system are omitted, since the mineral was transformed magnetite, which is resistant to further reduction for clearly defined thermodynamic reasons [14,20]. Lines show linear least-square regression fits of the data; data for lepidocrocite (filled diamonds) were omitted in regression in panel A.
Corrélation entre la surface spécifique des oxydes et la concentration finale en Fe^II extrait par HCl (A) ou la concentration en Fe^II adsorbé (B) lors d'expériences de longue durée utilisant G. sulfurreducens. Les symboles sont ceux de la Fig. 1. Les données relatives au système HFO sont omises, car ce minéral se transforme en magnétite, qui résiste à toute réduction ultérieure pour des raisons thermodynamiques bien établies [14,20]. Les traits pleins montrent les ajustements dérivant de régressions linéaires utilisant la méthode des moindres carrés. Les données relatives à la lépidocrocite (losange) ne sont pas utilisées pour tracer la droite de régression apparaissant sur la Fig. 4A.

3.3 Role of amorphous Fe(III) oxide impurities?

It could be argued that the similar surface area-specific rates of reduction observed for the different crystalline Fe(III) oxide phases (Fig. 1A), as well as the correlation between oxide surface area and extent of reduction (Fig. 4), was due to the presence of easily reducible amorphous Fe(III) oxide impurities in the synthetic crystalline Fe(III) oxides, whose abundance could have scaled with oxide surface area. If this were the case, the arguments put forward here and in other recent papers [39,40] regarding surface area vs. thermodynamic control of crystalline Fe(III) oxide reduction would be invalid. Data on initial rates of ascorbate-catalyzed Fe(III) oxide reduction were used to evaluate this question.

Fig. 5 shows time course data for reductive dissolution of hematite, two goethite phases (‘Goethite 30C’ and ‘High Surface Area’ (HSA) goethite), and HFO in the presence of excess (10 mM) of ascorbic acid at pH 3. HFO was fully dissolved within 4 h, whereas much smaller amounts of the crystalline Fe(III) oxide phases were dissolved over a 26-h period. As a result of the much faster kinetics of HFO dissolution compared to the other oxides, it was possible to use the time course data to quantitatively estimate the amount of amorphous HFO impurities present in the crystalline solids. The time course data for the crystalline phases indicated a relatively rapid initial accumulation of Fe(II) during the first few hours of reaction, followed by constant rate of oxide dissolution between 4 and 26 h. This initial rapid Fe(II) production can be attributed to dissolution of HFO impurities. The overall accumulation of Fe(II) during the initial period thus represents a combination of crystalline oxide and HFO impurity dissolution. A simple mathematical model that simulated parallel dissolution of a mixture of crystalline oxide and HFO was developed to estimate the abundance of the HFO impurity. The rate of crystalline oxide dissolution (in % total Fe(III) per hr) was set equal to the linear rate observed between 4 and 26 h, as defined by the least-squares regression analyses shown in Fig. 5A–C:

d [Fe {(III)}_{crys}] / d t = - R

(1)

Fig. 5
Reductive dissolution of Fisher hematite, goethite 30C, HSA goethite, and HFO in the presence of 10 mM ascorbic acid at pH 3. Total Fe(III) oxide concentrations were 6.4, 5.8, 5.7, and 1.1 mmol l⁻¹ for the four oxide phases, respectively. Solid lines in panels A–C show the results of linear least-square regression analyses. Solid line in panel D shows the result of nonlinear least-square regression fit of the data to an equation depicting the accumulation of end-product from a first-order reaction ( $Y (t) = Y_{\max} [1 - \exp (- k t)]$ , where $Y_{\max}$ is the maximum % dissolution, and k is a first-order rate constant). Dashed lines in panels A–C show results of numerical simulations of the oxide dissolution data (see Section 3.3).
Dissolution par réduction de l'hématite Fisher, de la goethite 30 °C, de la goethite HSA et du HFO en présence d'acide ascorbique 10 mM à pH 3. Les concentrations initiales en Fe^III étaient de 6,4, 5,8, 5,7 et 1,1 mmol l⁻¹ pour les différents oxydes. Les traits pleins dans les figures A à C correspondent aux résultats d'analyses de régression linéaire utilisant la méthode de moindres carrés. Le trait plein dans la figure D résulte de l'ajustement des données d'une régression non linéaire à une équation décrivant l'accumulation des produits de réaction selon une loi cinétique d'ordre l, c'est-à-dire : $Y (t) = Y_{\max} [1 - \exp (- k t)]$ , où $Y_{\max}$ est le pourcentage maximal de dissolution et k la constante de vitesse. Les tirets des figures A à C correspondent aux résultats d'une simulation numérique des données relatives à la dissolution de ces oxydes.

The rate of HFO dissolution was modeled as a first-order reaction, using the rate constant (1.37 h⁻¹) derived from the nonlinear least-square regression analysis shown in Fig. 5D:

d [HFO] / d t = - k [HFO]

(2)

Eqs. (1) and (2) were integrated numerically using a standard Runge–Kutta algorithm [38], and total % Fe(III) dissolution was computed as the cumulative sum of crystalline oxide and HFO reduction. The initial fractional abundance of HFO was adjusted to achieve agreement between the observed and simulated % Fe(III) dissolution vs. time data. The results of the analysis are illustrated by the dashed lines in Fig. 5A–C, which reflect estimated HFO impurities of 0.04, 0.10, and 0.32% of the total Fe(III) content of hematite, ‘goethite 30C’, and ‘HSA goethite’, respectively.

The estimated relative abundance of HFO impurities in the crystalline Fe(III) oxides can be compared to the amount of Fe(III) oxide reduction that took place in the G. sulfurreducens reduction experiments in order to constrain the potential contribution of such impurities to the observed Fe(III) reduction activity. The percent of Fe(III) subject to enzymatic reduction ranged from 2.3 to 9.7% for the crystalline hematite and goethite phases; these values are 5- to 95-fold higher than the estimated abundance of HFO impurity in the respective oxide phases. These results verify that enzymatic reduction of crystalline Fe(III) oxide surfaces – rather than reduction of amorphous Fe(III) oxide impurities – was the dominant mode of Fe(II) production in the cultures. The conclusions reached above regarding thermodynamic vs. surface-bound Fe(II) control of long-term crystalline Fe(III) oxide reduction are therefore valid, and they suggest that thermodynamic calculations should be used with caution when interpreting controls on enzymatic Fe(III) oxide reduction in soils and sediments.

3.4 Reduction of natural Fe(III) oxide phases

Data from long-term experiments on bacterial and abiotic reduction of natural Fe(III) oxides (Fig. 6) were interpreted in relation to a standard a generalized rate law for mineral dissolution [22,36]:

J_{t} / m_{0} = k^{'} {(m / m_{0})}^{γ}

(3)

where

J_{t}

is the rate of dissolution and/or reduction at time

t, m_{0}

is the initial mass of oxide, and

m / m_{0}

is the unreduced or undissolved mineral fraction) in order to evaluate changes in the apparent reactivity of Fe(III) oxides during long-term biological vs. chemical reduction. The natural Fe(III) oxide assemblages demonstrated significant changes in reactivity during long-term abiotic reductive dissolution (Fig. 6A), as indicated by γ values in excess of 1 for curve fits of the data to the generalized rate law [22,36]. Even larger changes in reactivity were estimated for the bacterial reduction experiments (Fig. 6B, solid symbols). However, when the analysis was restricted to the long-term ‘microbially reducible’ fraction of the Fe(III) oxide content of the natural solids (Fig. 6B, open symbols), the data could be well-approximated with γ values of ca. 1, i.e. by a first-order rate process.

Fig. 6
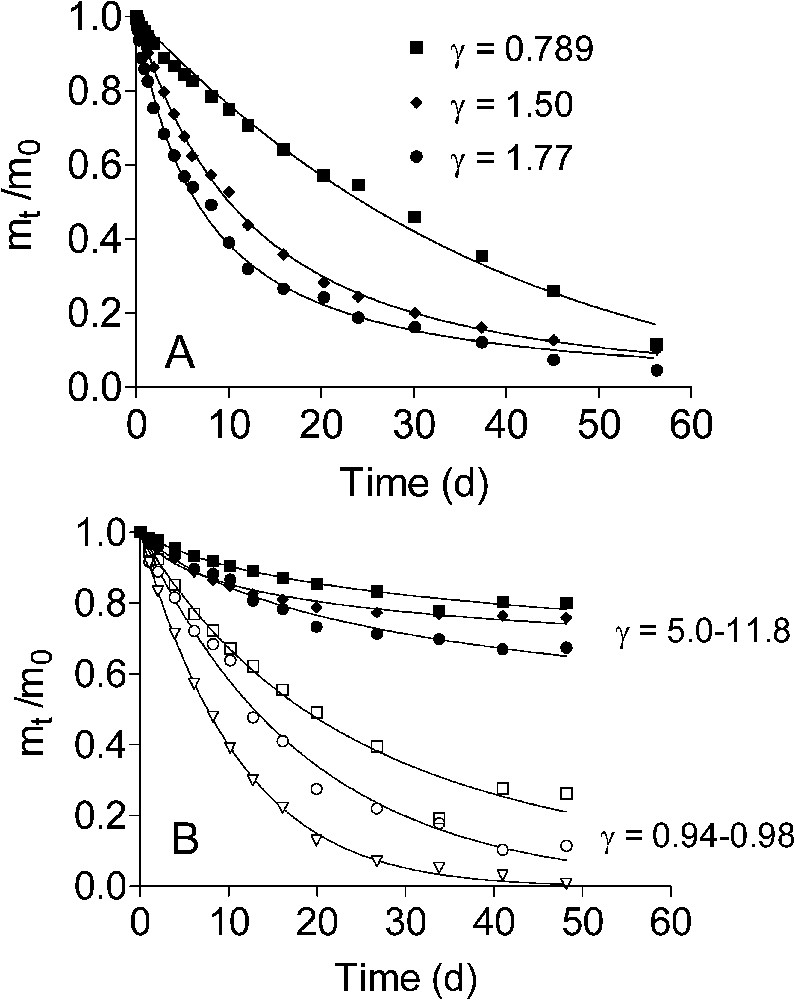
Kinetics of ascorbate (A) and bacterial (B) reduction of natural Fe(III) oxide-bearing materials. Data are reproduced with permission from Fig. 2 in Roden [42]. Squares, diamonds, and triangles represent the HC, CP, and Oyster materials, respectively. Open symbols in panel B refer to reduction of the ‘microbially available’ fraction of the oxide pool. The terms $m_{0}$ and $m_{t}$ refer to the mass (concentration) of Fe(III) oxide present at the start of the experiment and at time t, respectively. Solid lines show nonlinear regression fits of the data to the integrated form of the generalized mineral dissolution rate law (Eq. (3) in text). γ values refer to the results of the nonlinear curve fits.
Cinétique de la réduction d'oxydes de fer naturels par l'ascorbate (A) et des bactéries (B). Les données proviennent de Roden [42]. Les carrés, les losanges et les triangles sont relatifs aux résultats obtenus avec les matériaux dénommés HC, CP et Oyster. Dans la Fig. 6B, les symboles ouverts font référence à la réduction de la fraction d'oxyde définie comme « microbiologiquement disponible». Les termes $m_{0}$ et $m_{t}$ sont les masses (concentrations) des oxydes de fer présents en début de l'expérience et au temps t, respectivement. Les traits pleins montrent les ajustements de régressions non linéaires à la forme intégrée d'une loi générale de la cinétique de dissolution (Éq. (3) dans le texte). Les valeurs de γ sont issues de ces ajustements.

Kinetic and thermodynamic considerations indicated that neither the abundance of electron donor (lactate) nor the accumulation of aqueous end-products of oxide reduction (Fe(II), acetate, dissolved inorganic carbon) are likely to have posed significant limitations on the long-term kinetics of oxide reduction [42]. Rather, accumulation of biogenic Fe(II) on residual oxide surfaces appeared to play a dominant role in governing the long-term kinetics of natural crystalline Fe(III) oxide reduction. This assertion is fully supported by the results of the synthetic Fe(III) oxide reduction experiments (Figs. 3 and 4).

3.5 General conceptual model and rate law for microbial Fe(III) oxide reduction

The experimental findings summarized here point to a conceptual model of bacterial Fe(III) oxide reduction kinetics that differs fundamentally from established models of abiotic Fe(III) oxide reductive dissolution in that oxide surface area, rather than crystal structure and thermodynamic stability, exerts primary control on both the initial rate and the long-term extent of reduction. Numerical simulations of surface area-controlled biotic vs. abiotic Fe(III) oxide reduction indicate that this conceptual model can account for the pseudo-first-order kinetics of reduction of the operationally defined ‘microbially reducible’ fraction of the sediment Fe(III) oxide pool [42]. The explicit surface area control of the initial rate and extent of oxide reduction leads to a general rate law for oxide reduction as a function of electron acceptor and FeRB abundance that differs from those for reduction of chelated Fe(III) and other soluble metal species. As illustrated for synthetic goethite in Fig. 7, initial rates of Fe(III) oxide reduction are a linear function of oxide loading up to relatively high (200 mmol l⁻¹) bulk Fe(III) concentrations, a hyperbolic (Monod-style) function of total FeRB cell density, and a linear function of attached FeRB cell density. The latter relationships are analogous to the well-recognized dependence of abiotic reductive dissolution rate on total and surface-associated ligand concentration [16]. These relationships between oxide reduction rate and oxide/FeRB cell abundance are the opposite of those for reduction of soluble metals, as illustrated for Fe(III)-citrate in Fig. 8: rates of soluble metal reduction are a hyperbolic function of electron acceptor concentration, and a linear function of FeRB cell abundance. Similar patterns hold for reduction of other soluble metals such as U(VI), Co(III), Cr(VI), and Tc(VI) [25,27,43,45,53]. Table 2 provides a summary of rate laws that are appropriate for use in modeling solid-phase and dissolved Fe(III) (and other oxidized metals) reduction.

Fig. 7
Kinetics of synthetic goethite reduction by S. putrefaciens and G. sulfurreducens as a function of oxide loading (A) and FeRB cell density (B). The concentration of cells in the experiments shown in panel A was ca. 10⁸ cells ml⁻¹. The concentration of surface sites used to normalize cell density in panel B was calculated based on oxide mass loading (10 mmol l⁻¹; 89 g l⁻¹), the measured mineral surface area (ca. 55 m² g⁻¹), and an assumed standard mineral surface site density of $3.84 \times 10^{−6} mol sites m^{−2}$ recommended by Davis and Kent [7]. Inset in panel B shows relationship between Fe(III) reduction rate and attached FeRB cell density in the G. sulfurreducens experiment; the abundance of attached cells was determined by direct cell counting as described in Caccavo et al. [4]. Solid lines in panels A and B show results of linear and non-linear least-square regression fits, respectively. The non-linear regression fit in panel B is defined by the following equation (see Table 2): $V_{\max}^{surf} {[FeRB]}_{ssn} / (K_{FeRB} + {[FeRB]}_{ssn})$ ; best-fit values for $V_{\max}^{surf}$ and $K_{FeRB}$ are 1.3 mmol mmol sites⁻¹ d⁻¹ and $1.1 \times 10^{12} cells mmol {sites}^{−1}$ , respectively.
Cinétique de la réduction d'une gœthite par S. putrefaciens et G. sulfurreducens. Les pointillés de la Fig. 7B montrent la densité maximale (normalisée par rapport aux nombres de sites superficiels) de cellules de bactéries ferriréductrices (FeRB) présentes dans les expériences utilisant les différentes charges en oxydes mentionnées sur la Fig. 7A. La concentration en sites superficiels a été calculée en prenant en compte la charge en oxyde (10 mmol l⁻¹), la surface spécifique du minéral (environ 55 m² g⁻¹) et une densité de sites superficiels de $3, 84 \times 10^{−6} mol sites m^{−2}$ [7]. Dans la Fig. 7B, le graphique inséré montre la relation entre la vitesse de réduction du Fe^III et la densité de cellules attachées lors d'une expérience utilisant G. sulfurreducens ; l'abondance de cellules attachées a été mesurée par comptage, comme décrit dans Caccavo et al. [4]. Les traits pleins sur les deux figures montrent les résultats d'ajustement par des régressions linéaire et non linéaire. Sur la Fig. 7B, l'ajustement est décrit par l'équation suivante (Tableau 2) : $V_{\max}^{surf} {[FeRB]}_{ssn} / (K_{FeRB} + {[FeRB]}_{ssn})$ . 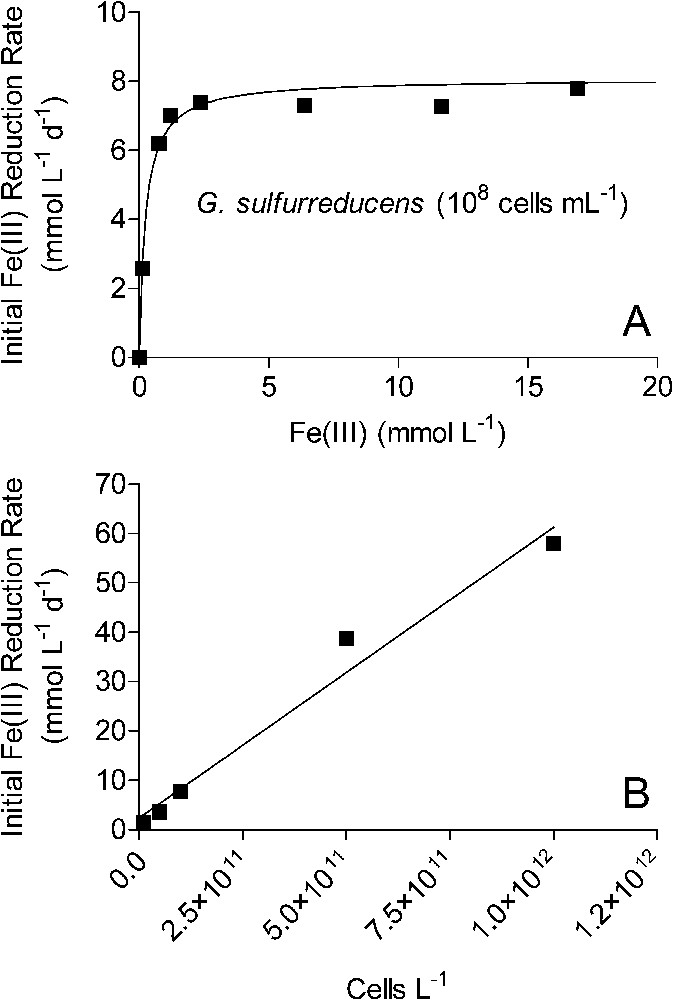Les meilleurs ajustements pour $V_{\max}^{surf}$ et $K_{FeRB}$ correspondent aux valeurs suivantes : 1,3 mmol mmol sites⁻¹ j⁻¹ pour $V_{\max}$ et $1, 1 \times 10^{12} cellules mmol {sites}^{−1}$ pour $K_{FeRB}$ .

Fig. 8
Kinetics of Fe(III)-citrate reduction by G. sulfurreducens. Solid lines in panels A and B show results of linear and non-linear least-square regression fits, respectively. The slope of the line in panel A corresponds to the parameter $α_{FeRB}$ in Table 2; best fit value $= 5.9 \times 10^{−11} mmol {cell}^{−1} d^{−1}$ . The non-linear regression fit in panel B is defined by the following equation (see Table 2): $V_{\max} [Fe {(III)}_{aq}] / (K_{Fe (III)} + [Fe {(III)}_{aq}])$ ; best-fit values for $V_{\max}$ and $K_{Fe (III)}$ are 8.1 mmol l⁻¹ d⁻¹ and 0.25 mmol l⁻¹, respectively.
Cinétique de la réduction du citrate ferrique par G. sulfurreducens. Les traits pleins montrent les résultats d'ajustements utilisant, soit une régression linéaire (B), soit une régression non linéaire (A). La pente de la droite de la Fig. 8B correspond au paramètre $α_{FeRB}$ du Tableau 2 et le meilleur ajustement est obtenu avec la valeur $5, 9 \times 10^{−11} mmol {cellule}^{−1} j^{−1}$ . La courbe calculée de la Fig. 8A est décrite par l'équation suivante (Tableau 2) : $V_{\max} [Fe {(III)}_{aq}] / (K_{Fe (III)} + [Fe {(III)}_{aq}])$ . Pour le meilleur ajustement, $V_{\max} = 8, 1 mmol l^{−1} j^{−1}$ et $K_{Fe (III)} = 0, 25 mmol l^{−1}$ .

Solid phase

R_{Fe (III)} = [Fe {(III)}_{fss}] V_{\max}^{surf} \frac{{[FeRB]}_{ssn}}{K_{FeRB} + {[FeRB]}_{ssn}}

where:

R_Fe(III) = bulk volumetric rate of Fe(III) oxide reduction (e.g., mmol l⁻¹ d⁻¹);

[Fe(III)_fss] = bulk volumetric abundance of ‘free’ (i.e. microbially reducible) Fe(III) oxide surface sites (e.g., mmol sites l⁻¹);

V^surf_max = maximum FeRB cell density-dependent reduction rate constant (e.g., mmol (mmol sites)⁻¹ d⁻¹) (see Fig. 7B);

[FeRB]_ssn = surface site-normalized FeRB cell density (e.g., cells (mmol free surface sites)⁻¹) (see Fig. 7B);

K_FeRB = half-saturation constant for relationship between FeRB cell density and oxide reduction rate constant (e.g., cells/mmol free surface sites) (see Fig. 7B);

Aqueous phase

R_{Fe (III)} = V_{\max} \frac{[Fe {(III)}_{aq}]}{K_{Fe (III)} + {[Fe (III)]}_{aq}}

where:

R_Fe(III) = bulk volumetric rate of Fe(III) oxide reduction (e.g., mmol l⁻¹ d⁻¹);

V_max=α_FeRB [FeRB]_bulk (see Fig. 8A);

[FeRB]_bulk = bulk FeRB cell density (e.g., cells l⁻¹);

α_FeRB = proportionality constant for relationship between bulk FeRB cell density and soluble Fe(III) reduction rate (e.g., mmol cell⁻¹ d⁻¹) (see Fig. 8B);

[Fe(III)_aq] = concentration of aqueous Fe(III) (e.g., mmol l⁻¹).

K_Fe(III) = Half-saturation constant for relationship between Fe(III)_aq concentration and reduction rate (e.g., mmol/l) (see Fig. 8A).

3.6 Implications for natural soils and sediments

Virtually all experimental work to date on bacterial synthetic Fe(III)-oxide reduction indicates that oxide mineral heterogeneity in natural soils and sediments is likely to affect initial rates of bacterial reduction (e.g., during the early stages of anaerobic metabolism following the onset of anoxic conditions) mainly via an influence on reactive surface site density. Although variations in oxide thermodynamic properties may alter rates of enzymatic reduction to some extent (as illustrated by the studies of lepidocrocite vs. goethite reduction), this is likely to represent a secondary effect in relation to the primary controlling influence of oxide surface area. Hence, the surface area of different oxides phases present in a soil or sediment will exert primary control on initial rates of enzymatic reduction.

During the later stages of bacterial Fe(III) oxide reduction in permanently reduced sediments, accumulation of aqueous and surface-bound Fe(II) is expected to exert a dominant control on apparent Fe(III) oxide reactivity toward enzymatic reduction, particularly in situations where removal of Fe(II) end-products is slow compared to the kinetics of reduction [46]. This conceptual model is consistent with a recent analysis of the kinetics of hematite reduction by S. putrefaciens strain CN32 [2,48], which showed that initial rates of reduction were under kinetic control (presumably limited by the rate of electron transfer from FeRB cells to the oxide), whereas the long-term extent of reduction was limited by mass transfer of Fe(II) away from oxide/FeRB surfaces. As discussed above (see Fig. 4), there is a general relationship between oxide surface area and long-term extent of oxide reduction in closed reaction systems, which results from the function of oxide surfaces as a repository for sorbed and/or surface-precipitated biogenic Fe(II). Although the existence of this relationship implies a connection between extent of bacterial reduction and oxide thermodynamic properties, evidence suggests that this connection is not directly related to thermodynamic properties such as $E_{h}^{0}$ or $Δ G_{f}$ , but rather results mainly from the correlation between these properties and oxide surface area.

An important implication of the above findings is that inferences regarding the ability of bacterial Fe(III) oxide reduction to compete with other terminal electron accepting processes (TEAPs) in soils and sediments should be based on estimates of bulk reactive (i.e. microbially accessible) surface site density – rather than the thermodynamic properties of the oxide(s) identified as the dominant phase(s) in a particular soil or sediment. This line of reasoning leads to the provisional conclusion that recent thermodynamic explanations for the coexistence of bacterial Fe(III) oxide reduction and other TEAPs (e.g., sulfate reduction and methanogenesis) in sediments and subsurface environments [17,18,37] have produced reasonable results for mechanistically incorrect reasons. The ability of thermodynamic considerations to explain the coexistence of bacterial Fe(III) oxide reduction and other TEAPs in sediments is likely the fortuitous result of the correlation between oxide thermodynamic properties and surface properties, which, based on current experimental information, actually control the initial reduction rate and long-term availability of Fe(III) oxides as competing electron acceptors for anaerobic respiration. Experiments with a mixed culture of wetland sediment bacteria and a range of synthetic Fe(III) oxides indicate that Fe(III)-reducing bacteria can outcompete methanogens for acetate with equal effectiveness when the different oxides are present at comparable surface area loadings – despite major differences in computed ΔG values for acetate oxidation coupled to Fe(III) oxide reduction [39]. These results emphasize the need for more accurate and robust wet-chemical (e.g., Hacherl et al. [15]) and/or spectroscopic techniques for assessing the surface properties (e.g., specific surface area and reactive site density) of natural Fe(III) oxide assemblages, including ones in which the presence of sorbed or surface precipitated Fe(II) limits the potential for enzymatic electron transfer and thereby controls apparent oxide reactivity toward microbial reduction.

Acknowledgements

This research was supported by grants DE-FG07-ER6321 and DE-FG02-01ER63182 from the US Department of Energy (DOE) Environmental Management Science and Natural and Accelerate Bioremediation Programs, respectively.

Bibliographie

[1] P.L. Brezonik Chemical Kinetics and Process Dynamics in Aquatic Systems, Lewis Publishers, Ann Arbor, 1994

[2] W.D. Burgos; R.A. Royer; Y. Fang; G.T. Yeh; A.S. Fisher; B.H. Jeon; B.A. Dempsey Theoretical and experimental considerations related to reaction-based modeling: a case study using iron(III) oxide bioreduction, Geomicrobiol. J., Volume 19 (2002), pp. 253-292

[3] F. Caccavo; D.J. Lonergan; D.R. Lovley; M. Davis; J.F. Stolz; M.J. McInerney Geobacter sulfurreducens sp. nov., a hydrogen- and acetate-oxidizing dissimilatory metal-reducing microorganism, Appl. Environ. Microbiol., Volume 60 (1994), pp. 3752-3759

[4] F. Caccavo; P.C. Schamberger; K. Keiding; P.H. Nielsen Role of hydrophobicity in adhesion of the dissimilatory Fe(III)-reducing bacterium Shewanella alga to amorphous Fe(III) oxide, Appl. Environ. Microbiol., Volume 63 (1997), pp. 3837-3843

[5] W.M. Clark Oxidation–Reduction Potentials of Organic Systems, The Williams and Wilkins Company, Baltimore, MD, USA, 1960

[6] R.M. Cornell; U. Schwertmann The Iron Oxides, VCH Verlagsgesellschaft mbH/VCH Publishers, Inc., Weinheim/New York, 1996

[7] J.A. Davis; D.B. Kent Surface complexation modeling in aqueous geochemistry (M.F. Hochella; A.F. White, eds.), Mineral–Water Interface Geochemistry, Mineralogical Society of America, Washington, DC, 1990, pp. 177-260

[8] J.A. Davis; S.B. Yabusaki; C.I. Steefel; J.M. Zachara; G.P. Curtis; G.D. Redden; L.J. Criscenti; B.D. Honeyman Assessing conceptual models for subsurface reactive transport of inorganic contaminants, EOS Trans., AGU, Volume 85 (2004), pp. 449-455

[9] W. Davison Iron and manganese in lakes, Earth Sci. Rev., Volume 34 (1993), pp. 119-163

[10] T.J. DiChristina; C.M. Moore; C.A. Haller Dissimilatory Fe(III) and Mn(IV) reduction by Shewanella putrefaciens requires ferE, a homolog of the pulE (gspE) type-II protein secretion gene, J. Bacteriol., Volume 184 (2002), pp. 142-151

[11] D.A. Dzombak; F.M.M. Morel Surface Complexation Modeling: Hydrous Ferric Oxide, John Wiley & Sons, New York, 1990

[12] S.J. Field; P.S. Dobbin; M.R. Cheesman; N.J. Watmough; A.J. Thomson; D.J. Richardson Purification and magneto-optical spectroscopic characterization of cytoplasmic membrane and outer membrane multiheme c-type cytochromes from Shewanella frigidimarina NCIMB400, J. Biol. Chem., Volume 275 (2000), pp. 8515-8522

[13] W.R. Fischer Microbiological reactions of iron in soils (J.W. Stucki; B.A. Goodman; U. Schwertmann, eds.), Iron in Soils and Clay Minerals, D. Reidel Publ. Co., Dordrecht, The Netherlands, 1988, pp. 715-748

[14] J.K. Fredrickson; J.M. Zachara; D.W. Kennedy; H. Dong; T.C. Onstott; N.W. Hinman; S. Li Biogenic iron mineralization accompanying the dissimilatory reduction of hydrous ferric oxide by a groundwater bacterium, Geochim. Cosmochim. Acta, Volume 62 (1998), pp. 3239-3257

[15] E.L. Hacherl; D.S. Kosson; L.Y. Young; R.W. Cowan Measurement of iron(III) bioavailability in pure iron oxide minerals and soils using anthraquinone-2,6-disulfonate oxidation, Environ. Sci. Technol., Volume 35 (2001), pp. 4886-4893

[16] J.G. Hering; W. Stumm Oxidative and reductive dissolution of minerals (M.F. Hochella; A.F. White, eds.), Mineral–Water Interface Geochemistry, vol. 23, Mineralogical Society of America, Washington, DC, 1990, pp. 427-464

[17] R. Jakobsen; H.J. Albrechtsen; M. Rasmussen; H. Bay; P. Bjerg; T.H. Christensen H₂ concentrations in a landfill leachate plume (Grindsted, Denmark): in situ energetics of terminal electron acceptor processes, Environ. Sci. Technol., Volume 32 (1998), pp. 2142-2148

[18] R. Jakobsen; D. Postma Redox zoning, rates of sulfate reduction and interactions with Fe-reduction and methanogenesis in a shallow sandy aquifer, Romo, Denmark, Geochim. Cosmochim. Acta, Volume 63 (1999), pp. 137-151

[19] B.H. Jeon; S.D. Kelly; K.M. Kemner; M.O. Barnett; W.D. Burgos; B.A. Dempsey; E.E. Roden Microbial reduction of U(VI) at the solid–water interface, Environ. Sci. Technol., Volume 38 (2004), pp. 5649-5655

[20] J.E. Kostka; K.H. Nealson Dissolution and reduction of magnetite by bacteria, Environ. Sci. Technol., Volume 29 (1995), pp. 2535-2540

[21] S.M. Kraemer; J.G. Hering Influence of solution saturation state on the kinetics of ligand-controlled dissolution of oxide phases, Geochim. Coschim. Acta, Volume 61 (1997), pp. 2855-2866

[22] O. Larsen; D. Postma Kinetics of reductive bulk dissolution of lepidocrocite, ferrihydrite, and goethite, Geochim. Cosmochim. Acta, Volume 65 (2001), pp. 1367-1379

[23] A.C. Lasaga Kinetic Theory in the Earth Sciences, Princeton University Press, Princeton, NJ, 1998

[24] C. Leang; M.V. Coppi; D.R. Lovley OmcB, a c-type polyheme cytochrome, involved in Fe(III) reduction in Geobacter sulfurreducens, J. Bacteriol., Volume 185 (2003), pp. 2096-2103

[25] C. Liu; Y.A. Gorby; J.M. Zachara; J.K. Fredrickson; C.F. Brown Reduction kinetics of Fe(III), Co(III), U(VI), Cr(VI), Tc(VII) in cultures of dissimilatory metal reducing bacteria, Biotechnol. Bioengin., Volume 80 (2002), pp. 637-649

[26] C. Liu; S. Kota; J.M. Zachara; J.K. Fredrickson; C. Brinkman Kinetic analysis of the bacterial reduction of goethite, Environ. Sci. Technol., Volume 35 (2001), pp. 2482-2490

[27] C. Liu; J.M. Zachara; Y.A. Gorby; J.E. Szecsody; C.F. Brown Microbial reduction of Fe(III) and sorption/precipitation of Fe(II) on Shewanella putrefaciens strain CN32, Environ. Sci. Technol., Volume 35 (2001), pp. 1385-1393

[28] S.K. Lower; M.F. Hochella; T.J. Beveridge Bacterial recognition of mineral surfaces: nanoscale interactions between Shewanella and α-FeOOH, Science, Volume 292 (2001), pp. 1360-1363

[29] T.S. Magnuson; N. Isoyama; A.L. Hodges-Myerson; G. Davidson; M.J. Maroney; G.G. Geesey; D.R. Lovley Isolation, characterization, and gene sequence analysis of a membrane-associated 89 kDa Fe(III)-reducing cytochrome c from Geobacter sulfurreducens, Biochem. J., Volume 359 (2001), pp. 147-152

[30] T.S. Magnuson; A.L. Hodges-Myerson; D.R. Lovley Characterization of a membrane-bound NADH-dependent Fe³⁺ reductase from the dissimilatory Fe³⁺-reducing bacterium Geobacter sulfurreducens, FEMS Microbiol. Lett., Volume 185 (2000), pp. 205-211

[31] B.A. Methe Genome of Geobacter sulfurreducens: metal reduction in subsurface environments, Science, Volume 302 (2003), pp. 1967-1969

[32] C. Myers; J. Myers Outer membrane cytochromes of Shewanella putrefaciens MR-1: spectral analysis, and purification of the 83-kDA c-type cytochrome, Biochim. Biophys. Acta, Volume 1326 (1997), pp. 307-318

[33] C.R. Myers; J.M. Myers Cloning and sequence of cymA, a gene encoding a tetraheme cytochrome c required for reduction of iron(III), fumerate, and nitrate by Shewanella putrefaciens MR-1, J. Bacteriol., Volume 179 (1997), pp. 1143-1152

[34] J. Myers; C. Myers Isolation and sequence of omcA, a gene encoding a decaheme outer membrane cytochrome c of Shewanella putrefaciens MR-1, and detection of omcA homologs in other strains of S. putrefaciens, Biochim. Biophys. Acta, Volume 1373 (1998), pp. 237-257

[35] J.M. Myers; C.R. Myers Role for outer membrane cytochromes OmcA and OmcB of Shewanella putrefaciens MR-1 in reduction of manganese dioxide, Appl. Environ. Microbiol., Volume 67 (2001), pp. 260-269

[36] D. Postma The reactivity of iron oxides in sediments: a kinetic approach, Geochim. Cosmochim. Acta, Volume 57 (1993), pp. 5027-5034

[37] D. Postma; R. Jakobsen Redox zonation: Equilibrium constraints on the Fe(III)/SO₄-reduction interface, Geochim. Cosmochim. Acta, Volume 60 (1996), pp. 3169-3175

[38] W.H. Press; S.A. Teukolsky; W.T. Vetterling; B.P. Flannery, Numerical Recipes in FORTRAN, vol. 1, Cambridge University Press, Port Chester, NY, 1992

[39] E.E. Roden Diversion of electron flow from methanogenesis to crystalline Fe(III) oxide reduction in acetate-limited cultures of wetland sediment microorganisms, Appl. Environ. Microbiol., Volume 69 (2003), pp. 5702-5706

[40] E.E. Roden Fe(III) oxide reactivity toward biological versus chemical reduction, Environ. Sci. Technol., Volume 37 (2003), pp. 1319-1324

[41] E.E. Roden Thermodynamic versus surface area control of microbial Fe(III) oxide reduction kinetics, EOS Trans. AGU (Fall Meet Suppl.), Volume 84 (2003) no. 46 (Abstract B42C-01)

[42] E.E. Roden Analysis of long-term bacterial versus chemical Fe(III) oxide reduction kinetics, Geochim. Cosmochim. Acta, Volume 68 (2004), pp. 3205-3216

[43] E.E. Roden, Unpublished data, 2005

[44] E.E. Roden; Y.A. Gorby Introduction to special issue on microbial Fe(III) oxide reduction, Geomicrobiol. J., Volume 19 (2002), pp. 139-140

[45] E.E. Roden; T.D. Scheibe Conceptual and numerical model of uranium(VI) reductive immobilization in fractured subsurface sediments, Chemosphere, Volume 59 (2005), pp. 617-628

[46] E.E. Roden; M.M. Urrutia Ferrous iron removal promotes microbial reduction of crystalline iron(III) oxides, Environ. Sci. Technol., Volume 33 (1999), pp. 1847-1853

[47] E.E. Roden; M.M. Urrutia Influence of biogenic Fe(II) on bacterial reduction of crystalline Fe(III) oxides, Geomicrobiol. J., Volume 19 (2002), pp. 209-251

[48] R.A. Royer; W.D. Burgos; A.S. Fisher; R.F. Unz; B.A. Dempsey Enhancement of biological reduction of hematite by electron shuttling and Fe(II) complexation, Environ. Sci. Technol., Volume 36 (2002), pp. 1939-1946

[49] B. Schink Energetics of syntrophic cooperation in methanogenic degradation, Microbiol. Mol. Biol. Rev., Volume 61 (1997), pp. 262-280

[50] U. Schwertmann; R.M. Cornell Iron Oxides in the Laboratory, VCH Verlagsgesellschaft mbH/VCH Publishers, Inc., Weinheim/New York, 1991

[51] W. Stumm Chemistry of the Solid–Water Interface, John Wiley & Sons, New York, 1992

[52] W. Stumm; J.J. Morgan Aquatic Chemistry, John Wiley & Sons, Inc., New York, 1996

[53] M.J. Truex; B.M. Peyton; N.B. Valentine; Y.A. Gorby Kinetics of U(VI) reduction by a dissimilatory Fe(III)-reducing bacterium under non-growth conditions, Biotechnol. Bioengin., Volume 55 (1997), pp. 490-496

[54] J.M. Zachara; C.C. Ainsworth; C.E. Cowan; C.T. Resch Adsorption of chromate by subsurface soil horizons, Soil Sci. Soc. Am. J., Volume 53 (1989), pp. 418-428

[55] J.M. Zachara; S.C. Smith; L.S. Kuzel Adsorption and dissociation of Co–EDTA complexes in Fe oxide containing subsurface soils, Geochim. Cosmochim. Acta, Volume 59 (1995), pp. 4825-4844

Commentaires - Politique