Plan
Comptes Rendus
no. 9

Surface Geosciences (Pedology)
Variation of the water-retention properties of soils: Validity of class-pedotransfer functions
[Variation des propriétés de rétention en eau des sols : validité des classes de pédotransfert]

Présenté par : Georges Pédro

Hassan Al Majou1  ; Ary Bruand1  ; Odile Duval2  ; Isabelle Cousin2
1 Institut des sciences de la Terre d’Orléans (ISTO), UMR 6113, CNRS, université d’Orléans, 1A, rue de la Férollerie, 45072 Orléans cedex 2, France
2 Unité de science du sol, INRA, centre de recherche d’Orléans, BP 20619, 45166 Olivet cedex, France
Comptes Rendus. Géoscience, Volume 339 (2007) no. 9, pp. 632-639.

Résumés

Water-retention properties of soils vary according to soil characteristics, and the understanding of their variation remains controversial. Numerous pedotransfer functions (ptfs) that enable prediction of the water-retention properties of soils were developed, but their validity was poorly discussed. In this study, we compare the performances of textural and texturo-structural class ptfs with more sophisticated class and continuous ptfs developed using the same set of soils. We showed that the former led to prediction performances that are better than, or similar to, those recorded with the more sophisticated class and continuous ptfs studied. Thus, textural and texturo-structural class ptfs that are quite easy to establish are potentially worthwhile tools for predicting the water-retention properties of soils, particularly at scales for which semi-quantitative or qualitative basic soil characteristics, such as the texture, are the only characteristics available. More generally, our results pointed out that the discussion of ptfs performance should refer to those recorded with easy to establish ptfs, thus enabling to quantify how much prediction bias and precision can be gained when increasing the complexity of ptfs and, consequently, the number and quality of predictors required.

Les propriétés de rétention en eau des sols varient en fonction de leur composition, et elles sont encore largement discutées. De nombreuses fonctions de pédotransfert (fpt) permettant de les prédire ont été développées, mais leur validité n’a été que rarement discutée. Dans cette étude, nous comparons les performances de classes de fpt texturales et texturo-structurales développées en utilisant un même jeu de données. Nous montrons que les classes de fpt conduisent à des performances de prédiction qui sont meilleures que, ou similaires à celles enregistrées avec les fpt plus sophistiquées étudiées par ailleurs dans cette étude. Ainsi, les classes de fpt texturales et texturo-structurales qu’il est aisé d’établir sont potentiellement des outils utiles pour la prédiction des propriétés de rétention en eau des sols, en particulier aux échelles auxquelles seules des données semi-quantitatives ou qualitatives, comme la texture, sont disponibles. Plus généralement, nos résultats mettent en évidence le fait que les performances des fpt devraient être discutées en prenant comme référence celles enregistrées avec des fpt faciles à établir, comme les classes de fpt texturales. En procédant ainsi, il est alors possible d’apprécier le gain de performance en termes de biais et de précision quand on complexifie les fpt et que l’on accroît le nombre et la qualité des caractéristiques de sols requises.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crte.2007.07.005
Keywords: Texture, Bulk density, Horizon, Structure, Prediction bias, Prediction precision
Mot clés : Texture, Densité apparente, Horizon, Structure, Biais de prédiction, Précision
Hassan Al Majou 1 ; Ary Bruand 1 ; Odile Duval 2 ; Isabelle Cousin 2

1 Institut des sciences de la Terre d’Orléans (ISTO), UMR 6113, CNRS, université d’Orléans, 1A, rue de la Férollerie, 45072 Orléans cedex 2, France
2 Unité de science du sol, INRA, centre de recherche d’Orléans, BP 20619, 45166 Olivet cedex, France 
@article{CRGEOS_2007__339_9_632_0,
     author = {Hassan Al Majou and Ary Bruand and Odile Duval and Isabelle Cousin},
     title = {Variation of the water-retention properties of soils: {Validity} of class-pedotransfer functions},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {632--639},
     publisher = {Elsevier},
     volume = {339},
     number = {9},
     year = {2007},
     doi = {10.1016/j.crte.2007.07.005},
     language = {en},
}
TY  - JOUR
AU  - Hassan Al Majou
AU  - Ary Bruand
AU  - Odile Duval
AU  - Isabelle Cousin
TI  - Variation of the water-retention properties of soils: Validity of class-pedotransfer functions
JO  - Comptes Rendus. Géoscience
PY  - 2007
SP  - 632
EP  - 639
VL  - 339
IS  - 9
PB  - Elsevier
DO  - 10.1016/j.crte.2007.07.005
LA  - en
ID  - CRGEOS_2007__339_9_632_0
ER  - 
%0 Journal Article
%A Hassan Al Majou
%A Ary Bruand
%A Odile Duval
%A Isabelle Cousin
%T Variation of the water-retention properties of soils: Validity of class-pedotransfer functions
%J Comptes Rendus. Géoscience
%D 2007
%P 632-639
%V 339
%N 9
%I Elsevier
%R 10.1016/j.crte.2007.07.005
%G en
%F CRGEOS_2007__339_9_632_0
Hassan Al Majou; Ary Bruand; Odile Duval; Isabelle Cousin. Variation of the water-retention properties of soils: Validity of class-pedotransfer functions. Comptes Rendus. Géoscience, Volume 339 (2007) no. 9, pp. 632-639. doi : 10.1016/j.crte.2007.07.005. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2007.07.005/

Version originale du texte intégral

1 Introduction

Understanding water-retention properties of soil remains a major issue in soil science. Because of the growing demand for soil hydraulic properties, a common solution has been to use pedotransfer functions (ptfs) that relate basic soil properties that are considered as easily accessible to the less often measured soil properties, such as hydraulic properties [1]. A huge number of ptfs was developed over the last three decades and we are facing today the continuous development of ptfs of increasing complexity, with very little or no information about the potential increase in the prediction quality. There is some information available about the performance of continuous ptfs [10,17], very little about the performance of class ptfs [14,17], and even less about the compared performance of these two types of ptfs [15]. The aim of this study is to show that the variation of water-retention properties can be predicted by using stratification based on information about particle-size distribution and structure. We show also that the quality of the prediction is similar to or better than that achieved with much more sophisticated ptfs, despite what is usually admitted.

2 Materials and methods

2.1 The ptfs developed in the literature

Most ptfs published in the literature are continuous pedotransfer functions (continuous ptfs), i.e. mathematical continuous functions between the water content at discrete values of potential or the parameters of a unique model of water-retention curve and the basic soil properties (mostly particle-size distribution, organic carbon content and bulk density) [12,17]. Besides these continuous ptfs that enable continuously the prediction of water content at particular water potentials [13] or estimation of the parameters of models of the water-retention curve [5,10,17], there are class pedotransfer functions (class ptfs) that received little attention, because their accuracy is considered as limited [15]. The existing class ptfs often provide average water contents at particular water potentials, or one average water-retention curve for every texture class [3,11]. Due to the range in particle-size distribution, clay mineralogy, organic matter content, and structural development within each texture class, water-retention properties for individual soils were considered as varying considerably [16]. Despite their possible inaccuracies, class ptfs enable the prediction based on successive stratification using soil characteristics. Moreover, class ptfs are easy to use because they require little soil information and are well adapted to the prediction of water-retention properties over large areas [9,15,16].

2.2 The soils studied

Class and continuous ptfs were developed using a set of 320 horizons, comprising 90 topsoils (from 0 to 30 cm depth) and 230 subsoil horizons (> 30 cm depth) collected in Cambisols, Luvisols, Planosols, Albeluvisols, Podzols, and Fluvisols [8] located mainly in the Paris basin and secondarily in the western coastal marshlands and Pyrenean piedmont plain. A set of 107 horizons comprising 39 topsoil and 68 subsoil horizons was constituted in order to test the ptfs established. These horizons were collected in Cambisols, Luvisols and Fluvisols [8] located in the South of the Paris basin. Basic characteristics and water-retention properties of the horizons were determined as described earlier by Bruand and Tessier [2] (Fig. 1, Table 1). Their bulk density (Db) was measured by using cylinders 1000 cm3 in volume when the soil was near to field capacity.

Fig. 1

Triangle of texture used (a), texture of the horizons used to develop the class and continuous ptfs (b) and texture of those used to test their validity (c).

Fig. 1. Triangle de texture utilisé (a), texture des horizons utilisés pour développer les classes de fpt et les fpt continues (b) et texture des horizons utilisés pour discuter leur validité (c).

Table 1

Characteristics of the horizons of the data set used to develop the ptfs and of the test data set

Tableau 1 Caractéristiques des horizons de l’ensemble de données utilisées pour développer les fpt et de celles utilisées pour en discuter la validité

Particle size distribution (%) OC (g kg−1) CaCO3 (g kg−1) CEC (cmolc kg−1) Db (g cm−3) Volumetric water content (cm3 cm−3)
<2 μm 2–50 μm 50–2000 μm θ 1.0 θ 1.5 θ 2.0 θ 2.5 θ 3.0 θ 3.5 θ 4.2
Horizons used to establish class and continuous ptfs (n = 320)
 mean 28.9 46.2 24.9 5.7 65 14.3 1.53 0.350 0.335 0.316 0.289 0.257 0.220 0.179
 s.d. 15.1 20.8 23.9 4.9 189 8.0 0.15 0.067 0.065 0.070 0.070 0.075 0.074 0.070
 min. 1.9 2.8 0.1 0.0 0.0 0.8 1.00 0.123 0.100 0.080 0.056 0.048 0.033 0.013
 max. 92.9 82.1 90.1 28.8 982 52.8 1.84 0.606 0.596 0.586 0.558 0.510 0.462 0.370
Horizons used to test the ptfs (n = 107)
 mean 30.2 40.6 29.2 6.6 38 15.8 1.51 0.356 0.332 0.312 0.287 0.261 0.224 0.202
 s.d. 15.4 24.3 28.6 5.3 134 10.8 0.13 0.075 0.079 0.082 0.084 0.086 0.083 0.080
 min. 1.9 4.1 1.6 0.0 0.0 0.6 1.10 0.161 0.121 0.099 0.072 0.045 0.041 0.033
 max. 78.7 80.3 91.8 28.2 656 50.2 1.77 0.534 0.498 0.482 0.457 0.440 0.396 0.369

2.3 Analysis of the ptfs performance

In order to discuss the global validity of the ptfs, most studies used the root-mean-square error (RMSE), which is also called root-mean-square deviation or root-mean-square residual [17]. Because the RMSE varies according to both the prediction bias and precision, we computed the mean error of prediction (MEP) that enables discussion of the prediction bias alone, on the one hand, and the standard deviation of prediction (SDP) that enables discussion of the prediction precision alone, on the other hand. We computed MEP and SDP for the whole water potentials as follows:

MEP=1l'⋅l∑j=1l'∑i=1l(θp,j,i−θm,j,i)
SDP=1l'⋅l∑j=1l'∑i=1l[(θp,j,i−θm,j,i)−MEP]21/2
where θp,j,i is the predicted water content at potential i for the horizon j, θm,j,i is the measured water content at potential i for the horizon j, and l is the number of water potentials for each horizon (l = 7 in this study) and l′ is the number of horizons (l′ ≤ 107 in this study). The MEP corresponds to the bias and indicates whether the ptfs overestimated (positive) or underestimated (negative) the water content, whereas SDP measures the precision of the prediction.

In order to discuss the validity of the ptfs at the different water potentials, we computed also the mean error of prediction (MEP′) and the standard deviation (SDP′) of prediction at every water potential as follows:

MEP'=1l'∑j=1l'(θp,j−θm,j)
SDP'=1l'∑j=1l'[(θp,j−θm,j)−MEP']21/2

3 Results and discussion

3.1 The class and continuous ptfs developed

The class ptfs developed in this note were established according to the texture (textural class ptfs) in the CEC triangle [4] and then according to both that texture and Db (texturo-structural class ptfs). The resulting class ptfs corresponded to the average water content at seven water potentials, which was computed within every class of texture (textural class ptfs) (Table 2) and every class combining both texture and Db (texturo-structural class ptfs) (Table 3). More complex class ptfs were established by fitting the van Genuchten's model [6] on the arithmetic mean value of θ at the different values of water potential using the RETC code [7] for every class of texture (VG texture class ptfs) according to the CEC triangle [4] and to the type of horizon (topsoil and subsoil) (Table 4).

Table 2

Textural class ptfs developed

Tableau 2 Classes de fpt texturales développées

Volumetric water content (cm3 cm−3)
θ 1.0 θ 1.5 θ 2.0 θ 2.5 θ 3.0 θ 3.5 θ 4.2
Very fine (n = 15) 0.455 0.437 0.424 0.402 0.385 0.357 0.322
Fine (n = 60) 0.399 0.388 0.373 0.351 0.331 0.301 0.254
Medium fine (n = 96) 0.356 0.342 0.327 0.298 0.254 0.210 0.173
Medium (n = 117) 0.334 0.320 0.302 0.273 0.242 0.203 0.156
Coarse (n = 32) 0.249 0.224 0.181 0.149 0.120 0.100 0.076
Table 3

Texturo-structural class ptfs developed

Tableau 3 Classes de fpt texturo-structurales développées

Volumetric water content (cm3 cm−3)
θ 1.0 θ 1.5 θ 2.0 θ 2.5 θ 3.0 θ 3.5 θ 4.2
Very Fine (n = 15) 1.10 ≤ Db < 1.30 0.498 0.473 0.451 0.423 0.405 0.371 0.330
1.30 ≤ Db < 1.50 0.459 0.439 0.428 0.405 0.385 0.352 0.328
1.50 ≤ Db < 1.70 0.359 0.359 0.361 0.353 0.347 0.340 0.294
Fine (n = 60) 1.00 ≤ Db < 1.20 0.519 0.499 0.494 0.461 0.431 0.373 0.281
1.20 ≤ Db < 1.40 0.452 0.443 0.421 0.385 0.373 0.340 0.271
1.40 ≤ Db < 1.60 0.391 0.378 0.361 0.344 0.321 0.289 0.250
1.60 ≤ Db < 1.80 0.338 0.334 0.325 0.307 0.291 0.275 0.244
Medium Fine (n = 96) 1.20 ≤ Db < 1.40 0.348 0.338 0.323 0.291 0.232 0.188 0.153
1.40 ≤ Db < 1.60 0.359 0.343 0.328 0.298 0.258 0.211 0.175
1.60 ≤ Db < 1.80 0.353 0.345 0.329 0.303 0.263 0.230 0.190
Medium (n = 117) 1.20 ≤ Db < 1.40 0.354 0.337 0.314 0.278 0.245 0.193 0.140
1.40 ≤ Db < 1.60 0.346 0.329 0.310 0.275 0.235 0.193 0.146
1.60 ≤ Db < 1.80 0.320 0.307 0.293 0.270 0.248 0.214 0.167
1.80 ≤ Db < 2.00 0.296 0.289 0.274 0.266 0.258 0.231 0.186
Coarse (n = 32) 1.40 ≤ Db < 1.60 0.241 0.210 0.164 0.135 0.106 0.093 0.075
1.60 ≤ Db < 1.80 0.253 0.231 0.188 0.156 0.126 0.103 0.077
Table 4

Parameters of the van Genuchten's model corresponding to the VG textural class ptfs developed according to the type of horizon (topsoil and subsoil)

Tableau 4 Paramètres du modèle de van Genuchten correspondant aux classes de ptf VG texturales développées en fonction du type d’horizon (horizon de surface et horizon de subsurface)

θ r θ s α n m
Topsoils
 Coarse 0.025 0.397 1.0592 1.1530 0.1327
 Medium 0.010 0.428 0.4467 1.1000 0.0909
 Medium fine 0.010 0.465 0.6860 1.1027 0.0931
 Fine 0.010 0.477 0.6153 1.0652 0.0612
 Very Fine 0.010 0.587 5.9433 1.0658 0.0617
Subsoils
 Coarse 0.025 0.367 1.0535 1.1878 0.1581
 Medium 0.010 0.388 0.1851 1.0992 0.0903
 Medium fine 0.010 0.416 0.1611 1.0978 0.0891
 Fine 0.010 0.437 0.1334 1.0632 0.0594
 Very Fine 0.010 0.472 0.0745 1.0499 0.0475

Continuous ptfs were also developed. They correspond to multiple regression equations as follows:

θ=a+(b×%Cl)+(c×%Si)+(d×%OC)+(e×Db)
with θ the volumetric water content at a given water content, a, b, c, d and e the regression coefficients, %Cl and %Si, respectively, the clay and silt contents, %OC, the organic carbon content, and Db, the bulk density (Table 5). Other continuous ptfs were developed as earlier done by Wösten et al. [16] for the parameters of the van Genuchten's model, using multiple regression equations (VG continuous ptfs, Table 6). For every horizon, the parameters of the van Genuchten's model were computed using the RETC code [7].

Table 5

Regression coefficients and coefficient of determination R2 recorded for the continuous ptfs developed

Tableau 5 Coefficients de régression et coefficients de détermination R2 enregistrés pour les ptf continues développées

Water potential (hPa)
–10 –33 –100 –330 –1000 –3300 –15000
a 0.4701*** 0.3556*** 0.2620*** 0.1301*** 0.0184 –0.0504 –0.0786**
b 0.0026*** 0.0029*** 0.0034*** 0.0038*** 0.0045*** 0.0047*** 0.0045***
c 0.0006*** 0.0008*** 0.0012*** 0.0012*** 0.0008*** 0.0005*** 0.0003***
d –0.0006 –0.0002 0.0002 0.0010 0.0017*** 0.0012** 0.0004
e –0.1447*** –0.0939*** –0.0647*** –0.0084 0.0398* 0.0697*** 0.0710***
R 2 0.59 0.64 0.69 0.74 0.77 0.82 0.86
Table 6

VG continuous ptfs developed for the parameters of the van Genuchten's model

Tableau 6 Relations correspondant aux fpt VG continues développées pour les paramètres du modèle de van Genuchten

θs = 1.1658 − 0.0032 × C − 0.4737 × D + 2 × 10−7 × S2 − 0.0001 × OC2 + 0.0373 × C−1 + 0.0131 × S−1 − 0.0072 × ln(S) + 0.00003 × OC × C + 0.0022 × D × C − 0.0002 × D × OC − 0.0001 × S (R2 = 0.95)
α* = 25.61 + 0.0439 × C + 0.1129 × S + 1.1914 × OC + 32.21 × D − 10.48 × D2 − 0.0009 × C2 − 0.0146 × OC2 − 0.3781 × OC−1 − 0.0178 × ln(S) − 0.1032 × ln(OC) − 0.1 × D × S − 0.6001 × D × OC (R2 = 0.26)
n* = – 15.29 − 0.0659 × C + 0.0115 × S − 0.2115 × OC + 12.33 × D − 1.3578 × D2 + 0.0006 × C2 + 0.0031 × OC2 + 4.0005 × D−1 + 2.2003 × S−1 + 0.1643 × OC−1 − 0.1205 × ln(S) + 0.2693 × ln(OC) − 9.9367 × ln(D) + 0.003 × D × C + 0.0694 × D × OC (R2 = 0.35)

3.2 Validity of the class ptfs

The textural class ptfs underestimated very slightly the water retained (MEP = −0.003 cm3 cm−3) when they were applied to the test dataset without any other stratification than according to the texture. There was no decrease in the prediction bias with the texturo-structural class ptfs (MEP = −0.004 cm3 cm−3), but the bias was already very small with the textural class ptfs studied. However, the precision was slightly better with the texturo-structural class ptfs (SDP = 0.043 cm3 cm−3) than with the textural class ptfs (SDP = 0.045 cm3 cm−3) (Fig. 2a and b). Compared to the textural class ptfs, the VG textural class ptfs showed similar performance. The bias was very small (MEP = 0.002 cm3 cm−3) and the precision poor (SDP = 0.045 cm3 cm−3), as recorded for the textural class ptfs (Fig. 2c). The comparison of the class ptfs performance at every value of water potential showed small bias (−0.008 ≤ MEP′ ≤ 0.007 cm3 cm−3) except for θ4.2 for the textural and texturo-structural class ptfs (MEP′ = –0.020 and –0.019 cm3 cm−3) and for θ1.0 for the VG class ptfs (MEP′ = 0.014 cm3 cm−3), for which it was greater (Table 7). This comparison showed also poor precision for the three class ptfs studied, whatever the water potential (0.040 ≤ SDP′ ≤ 0.047 cm3 cm−3).

Fig. 2

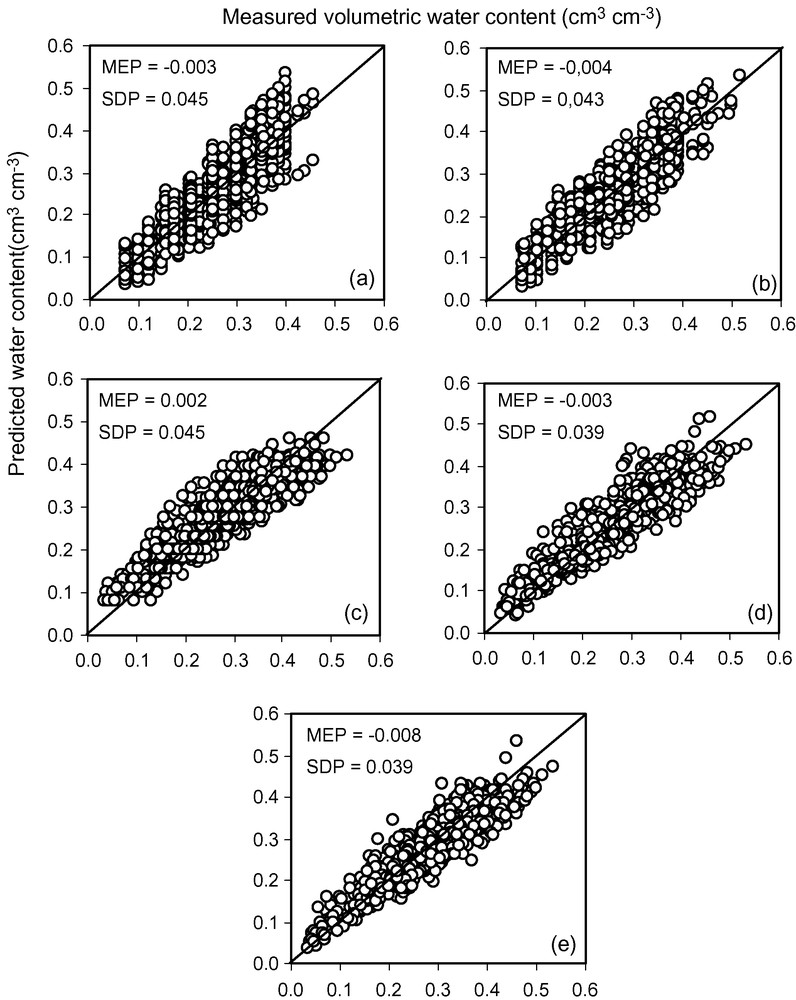
Validity of the textural class ptfs (a), texturo-structural class ptfs (b), VG textural class ptfs (c), continuous ptfs (d), and VG continuous ptfs (e) developed.

Fig. 2. Validité des classes de fpt texturales (a), texturo-structurales (b), et VG texturales (c), ainsi que des fpt continues (d) et VG continues (e).

Table 7

Validity of the continuous and class ptfs according to the water potential

Tableau 7 Validité des classes de fpt et des fpt continues aux différentes valeurs de potentiel de l’eau

Volumetric water content (cm3 cm−3)
Mean error of prediction (MEP’) Standard deviation of prediction (SDP’)
θ 1.0 θ 1.5 θ 2.0 θ 2.5 θ 3.0 θ 3.5 θ 4.2 θ 1.0 θ 1.5 θ 2.0 θ 2.5 θ 3.0 θ 3.5 θ 4.2
Textural class ptfs −0.006 0.004 0.003 0.001 −0.004 −0.001 −0.020 0.046 0.046 0.044 0.045 0.047 0.044 0.042
Texturo-structural class ptfs −0.006 0.002 0.002 0.001 −0.005 −0.002 −0.019 0.042 0.042 0.041 0.043 0.045 0.044 0.041
VG class ptfs 0.014 0.007 −0.003 −0.008 −0.007 0.007 0.002 0.045 0.045 0.045 0.046 0.046 0.043 0.040
Continuous ptfs −0.006 0.001 0.005 0.001 −0.003 0.002 −0.022 0.044 0.044 0.040 0.039 0.036 0.032 0.030
VG continuous ptfs 0.012 0.004 −0.008 −0.017 −0.020 −0.008 −0.016 0.044 0.041 0.038 0.039 0.035 0.033 0.032

3.3 Validity of the continuous ptfs

When applied to the test data set, the continuous ptfs lead to very small bias (MEP = –0.003 cm3 cm−3) and showed poor precision (SDP = 0.039 cm3 cm−3). Results showed a greater bias with the VG continuous ptfs (MEP = –0.008 cm3 cm−3) and similar poor precision (SDP = 0.039 cm3 cm−3) than with the continuous ptfs (Fig. 2d and e). The comparison of the continuous ptfs performance at every value of water potential showed small bias for the continuous ptfs (−0.006 ≤ MEP′ ≤ 0.005 cm3 cm−3), except for θ4.2 (MEP′ = –0.022 cm3 cm−3). For the VG continuous ptfs, the bias was greater for six water potentials with absolute value of MEP′ ≤ 0.020 cm3 cm−3, except for θ1.5 (MEP′ = 0.004 cm3 cm−3) (Table 7). The precision was poor for the simple and VG continuous ptfs (0.030 ≤ SDP′ ≤ 0.044 cm3 cm−3), but results showed that SDP decreased with the water potential.

3.4 Comparison of the class- and continuous ptfs

Results showed very little difference between the ptfs studied. The bias recorded was small (–0.008 ≤ MEP ≤ 0.002 cm3 cm−3) and the greatest absolute value of bias was recorded with the VG continuous ptfs (MEP = –0.008 cm3 cm−3). On the other hand, the precision was poor (0.039 ≤ SDP ≤ 0.045 cm3 cm−3), the greatest precision being recorded with the two types of continuous ptfs studied. If the VG continuous ptfs led to the greatest precision (SDP = 0.039 cm3 cm−3), they led also the greatest bias value (MEP = –0.008 cm3 cm−3).

4 Conclusion

Our results showed that textural class ptfs led to prediction performance that are similar to those recorded with more sophisticated class ptfs and with continuous ptfs. Thus without knowing the particle-size distribution, organic carbon content and bulk density as required by most ptfs, we can predict the water-retention properties with similar prediction quality by using the texture alone. Our results showed also that use of both texture and bulk density slightly increases the precision when compared to the precision recorded with the textural class ptfs. Finally, we showed also that class ptfs, including very simple ptfs, should be still considered as useful tools for predicting the water-retention properties of soils, particularly at scales for which semi-quantitative or qualitative basic soil characteristic such as the texture are the only characteristics available. More generally, our results pointed out that discussion of ptfs performance should refer to those recorded with simple ptfs, thus enabling to quantify how much prediction bias and precision can be gained when increasing the complexity of ptfs and consequently the number and quality of predictors required.

Bibliographie

[1] J. Bouma; H.A.J. van Lanen Transfer functions and threshold values: from soil characteristics to land qualities, Int. Inst. for Aerospace Surv. and Earth Sci. (1987) (pp. 106–111)

[2] A. Bruand; D. Tessier Water-retention properties of the clay in soils developed on clayey sediments: Significance of parent material and soil history, Eur. J. Soil Sci., Volume 51 (2000), pp. 679-688

[3] A. Bruand; P. Pérez Fernandez; O. Duval Use of class pedotransfer functions based on texture and bulk density of clods to generate water retention curves, Soil Use Manage., Volume 19 (2003), pp. 232-242

[4] Commission of the European Communities (CEC), Soil map of the European Communities. Scale 1:1 000 000, CEC-DGVI, Luxembourg, 1985.

[5] H.P. Cresswell; Y. Coquet; A. Bruand; N.T. McKenzie The transferability of Australian pedotransfer functions for predicting water retention characteristics of French soils, Soil Use Manage., Volume 22 (2006), pp. 62-70

[6] M.T. van Genuchten A closed-form equation for predicting the hydraulic conductivity of unsaturated soil, Soil Sci. Soc. Am. J., Volume 44 (1980), pp. 892-898

[7] M.T. van Genuchten; F.J. Leij; S.R. Yates The RETC code for quantifying the hydraulic functions of unsaturated soils, USDA Salinity Laboratory, Riverside, CA, United States, 1991 (Environmental Protection Agency, document EPA/600/2-91/065)

[8] ISSS Working Group RB, World Reference Base for Soil Resources: Introduction (J.A. Deckers, F.O. Nachtergaele, O.C. Spaargaren, Eds.), First Ed., International Society of Soil Science (ISSS), ISRIC-FAO-ISSS-Acco, Leuven, Belgium, 1998.

[9] A. Lilly; J.H.M. Wösten; A. Nemes; C. Le Bas The development and use of the HYPRES database in Europe, Proc. Int. Workshop Riverside, California, 22–24 October 1997 (1999) (pp. 1283–1204)

[10] B. Minasny; A.B. McBratney; K.L. Bristow Comparison of different approaches to the development of pedotransfer functions for water-retention curves, Geoderma, Volume 93 (1999), pp. 225-253

[11] A. Nemes; M.G. Schaap; J.H.M. Wösten Functional evaluation of pedotransfer functions derived from different scales of data collection, Soil Sci. Soc. Am. J., Volume 67 (2003), pp. 1093-1102

[12] Y.A. Pachepsky; W.J. Rawls; H.S. Lin Hydropedology and pedotransfer functions, Geoderma, Volume 131 (2006), pp. 308-316

[13] W.J. Rawls; D.L. Brakensiek; K.E. Saxton Estimation of soil water properties, Trans. ASAE, Volume 26 (1982), pp. 1747-1752

[14] F. Ungaro; C. Calzolari; E. Busoni Development of pedotransfer functions using a group method of handling for the soil of the Pianura Padano–Veneta region of North Italy: water-retention properties, Geoderma, Volume 124 (2005), pp. 293-317

[15] J.H.M. Wösten; P.A. Finke; M.J.W. Jansen Comparison of class and continuous pedotransfer functions to generate soil hydraulic characteristics, Geoderma, Volume 66 (1995), pp. 227-237

[16] J.H.M. Wösten; A. Lilly; A. Nemes; C. Le Bas Development and use of a database of hydraulic properties of European soils, Geoderma, Volume 90 (1999), pp. 169-185

[17] J.H.M. Wösten; Y.A. Pachepsky; W.J. Rawls Pedotransfer functions: bridging the gap between available basic soil data missing soil hydraulic characteristics, J. Hydrol., Volume 251 (2001), pp. 123-150

Commentaires - Politique