1 Introduction
Mobile particles in soils and groundwater aquifers can act as carriers for strongly sorbing chemicals and may enhance contaminant transport. The transport mechanisms of colloids in saturated porous media have been studied in great detail. The knowledge and understanding of the colloid-associated contaminant transport in porous media have increased substantially over the last decade [8,9,13]. However, a limited number of experimental studies have been published to date on the transport and deposition of particles in natural porous media. Understanding the fate and transport of suspended particles in porous media has a great implication on the reduction of the risk of drinking-water-supply contamination. Mobile particles in groundwater aquifers and soils can serve as carriers for contaminants and thereby facilitate contaminant transport [15]. They also contribute to develop internal erosion in dykes and petroleum wells clogging. Owing to their large size and density, the role of suspended particles on solute transport has only recently attracted significant attention [2,6,7,12,19]. During major floods, erosion of alluvial soil causes the occurrence of significant turbidity. Turbid water travels through the alluvium and can reach water supply wells. The alluvial aquifer might be of interest for the understanding of the water pollution risk.
Various restrictions on the movement of suspended particles such as clogging, mechanical straining and filtration were studied. During the flow of the suspension through the medium, particle transport and capture result from several forces and mechanisms depending on particle size, pore distribution, and flow rate. For larger particles, typically more than 10 μm, hydrodynamics, gravity and inertial effects are dominant, while all forces and mechanisms can contribute for smaller particles whose size is ranging between 0.1 and 10 μm [7]. This paper presents an experimental study of the transport of suspended particles (SP) in saturated porous media, aimed at delineating the effects of hydrodynamic and gravity forces on particle transport and deposition rate. This study addresses transport and deposition of suspended particles in two porous media that are different in pore geometry under water-saturated flow conditions. We investigate the various mechanisms governing the process of particle transport, with emphasis on the role of particle deposition. A short-pulse technique was used for measuring particle deposition rate coefficient and collision efficiencies in the two porous media. Suspended particles were injected under saturated flow conditions into a horizontal laboratory column packed with gravel or glass beads. Many experiments were conducted with different flow rates. Particle breakthrough curves (BTCs) were measured on-line using fluorescence and turbidity (dynamic technique) sensors. These curves were well described by the analytical solution of the advection–dispersion equation with a first-order deposition kinetics. The laboratory tests performed with different flow rates and column materials showed that hydrodispersive parameters derived from 1D advection–dispersion models depend on the flow rate and the pore geometry of the porous media.
2 Materials and methods
The column setup used to determine particle transport and deposition rate (Fig. 1), described in a previous paper [2], consisted of a water (pH 6.8) reservoir with constant liquid height, a pump controlling the steady-state flow rate, a pulse injection loop, a Plexiglas column (355 mm length and 89 mm inner diameter) packed with the porous medium, and a detection system for particles and fluorescein connected to a PC for data acquisition. A numerical flowmeter was included between the pump and the column. The particle detection system consists of a turbidmeter previously calibrated for the concentration range used. Some samples of the suspension are analyzed at the outlet column using a Coulter Multisizer particle counter. Two porous media (gravel and glass beads) with quite similar porosity but differences in pore distribution are used alternatively to fill the laboratory column. Eighty percent of the crushed gravel grains ranges from 2.15 mm to 3.15 mm in size, and the glass beads are 3 mm in diameter. The main characteristics of these porous media are given in Table 1. The suspended particles are quartz silt collected from surface formations in Haute-Normandie (France) and their size ranges from 2 to 40 μm, with a 14-μm mode. The concentration of suspended particles is 0.1 g l−1. The injected pulse is chosen very small (2% of the pore volume) in order not to disturb the water flow in the column, even at the lowest rate. It was reported [9] that the step input of suspended particles involves inconveniences owing to the significant quantity of particles introduced into the column. The short-pulse method allows running several experiments on a single column without significant blocking or filter ripening effects. Many experiments were conducted with different flow rates ranging from 0.13 to 4.37 mm s−1 (Darcy's velocity) under steady-state, saturated-flow conditions. In each fresh packed column, ten short-pulse injections were performed, starting from the highest flow rate to the weakest one. The latter technique is chosen in order to avoid a likely release of the suspended particles previously deposited in the porous medium, i.e. the second-order deposition kinetics can be neglected. After each test series, the column was repacked with the same material after washing to remove any suspended particles and drying. To compare suspended particles and fluorescein transport behaviour, the injected pulse consists of a mixture of 0.1 g l−1 of suspended particles and 0.5 × 10−3 g l−1 of fluorescein.
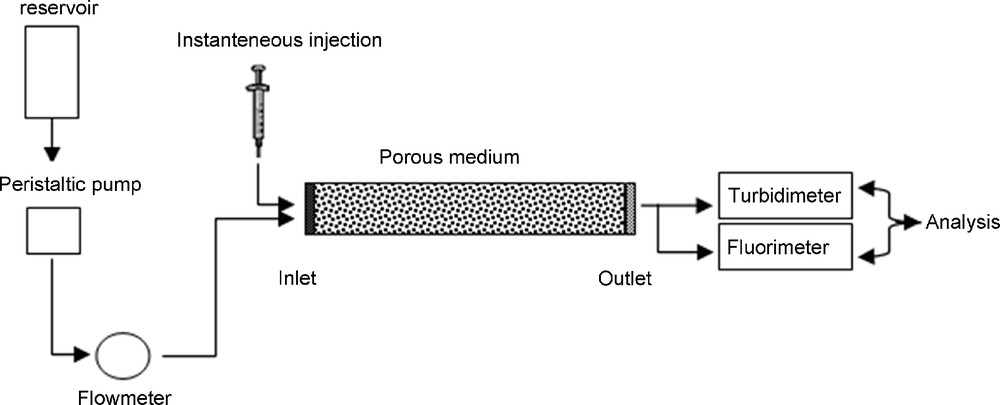
Schematic drawing of the experimental setup.
Fig. 1. Représentation schématique du dispositif expérimental.
Selected properties of the two materials used for column experiments
Tableau 1 Propriétés des deux matériaux utilisés pour les essais en colonnes
| Porous medium | Total porosity | Hydraulic conductivity (mm s−1) | Bulk density |
| Crushed gravel | 0.47 | 23 | 1.37 |
| Glass beads | 0.42 | 21 | 1.49 |
3 Analysis and modelling
The transport of suspended particles through a porous medium is modelled by the advection–dispersion equation including a term of first-order deposition kinetic:
| (1) |
| (2) |
| (3) |
The transport and deposition tests were interpreted with this mathematical model based on equation (3), and the BTCs are fitted with the analytical solution (Fig. 2) using a derivative regression parabolic method, which is appropriate for problems involving three parameters and described in a previous paper [2]. BTCs were well described by the analytical solution of the advective-dispersive equation with a first-order deposition kinetics. For the tracer tests, this method [19] allows immediate determination of the dispersion coefficient (DL), the advection time (tc = L/u, where L is the column length), and the deposition rate coefficient (Kdep). The recovery rate (R) is also estimated by integrating the experimental breakthrough curves (BTCs). In the case of a dissolved tracer (fluorescein), no deposition occurs. Thus, only two parameters were determined (DL and tc).
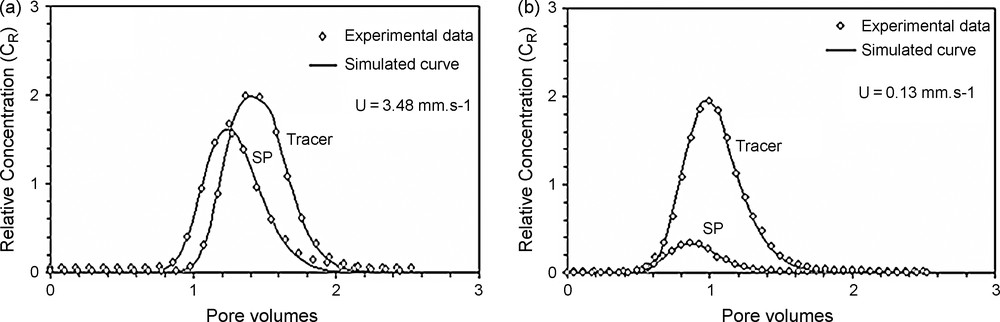
Fitting of the experimental BTCs of suspended particles (SP) and dissolved tracer (fluorescein) with the mathematical model, for high (a) and low (b) Darcy's velocities.
Fig. 2. Ajustement des courbes de restitution des MES et du traceur dissous (fluorescéine) avec le modèle mathématique, pour une forte (a) et une faible (b) vitesse de Darcy.
4 Results and discussion
4.1 Particle transport behaviour
Owing to the high velocities tested (mean pore water velocities ranged from 0.3 to 9.5 mm s−1), low ionic strength (2.6 mM NaCl), large size of suspended particles (a mode of 14 μm), and neutral water pH, electrochemical mechanisms may be neglected. Thus, the present study is restricted to physical (hydrodynamic) mechanisms involved in suspended particle transport and deposition. The laboratory tests performed with different flow rates and column materials showed that hydrodispersive parameters derived from the 1D advection–dispersion model depend on the flow rate and pore size distribution. The breakthrough behaviour of the suspended particles in the two porous media governs the particle transport and deposition patterns. BTCs (Fig. 3) show earlier transport of suspended particles than of dissolved tracer in both porous media. In order to evaluate the earlier breakthrough of suspended particles, Fig. 4 presents the ratio of the suspended particles’ pore velocity uSP to that of the dissolved tracer uDT as a function of the diffusion Péclet number Ped, which is defined as:
| (4) |
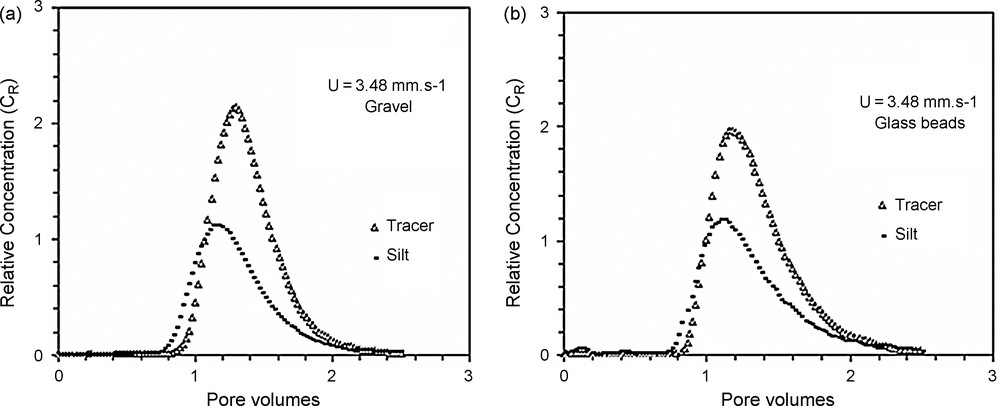
Breakthrough curves of dissolved tracer and suspended particles in gravel (a) and glass-bead (b) columns.
Fig. 3. Courbes de restitution du traceur dissous et des MES dans les colonnes de gravier (a) et de billes de verre (b).
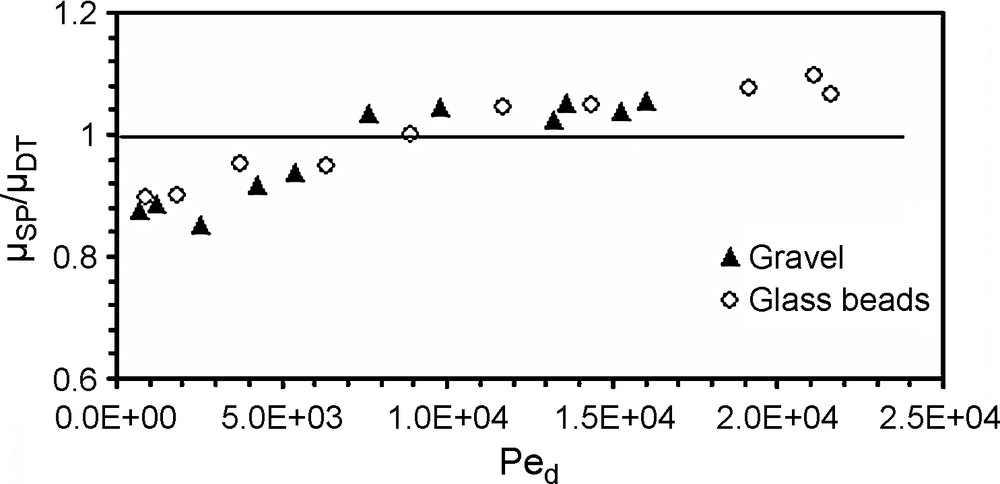
Ratio of the suspended particles pore velocity uSP to that of dissolved tracer uDT versus the diffusion Péclet number Ped.
Fig. 4. Rapport de la vitesse de pore des particules en suspension uSP à celle du traceur dissous uDT en fonction du nombre de Péclet de diffusion Ped.
The results (Fig. 4) demonstrate the existence of a critical Péclet number beyond which particles travel faster than the dissolved tracer does. Increasing flow rates generates earlier breakthroughs of the SP compared to that of a dissolved tracer. The exclusion of particles from the flow zone close to the grain surface is the crucial difference between solute and particle tracer transport. This effect was highlighted [4] into a chromatographic tube and named ‘hydrodynamic chromatography’. Within a cylinder tube, and on the laminar flow regime, the microscopic velocity profile is parabolic, with the maximum velocity at the axis of the tube. Dissolved tracer is transported by all existing velocities in the tube, while the particles are only transported by higher velocities. The size exclusion effect explains the observed behaviour [11]. This exclusion effect seems to be of the same significance in the two porous media. Macropores favour faster movement of suspended particles [1,9,12,18]. The preferential paths become more important for greater flow rates. The earlier breakthrough of particles in comparison with dissolved tracer occurs at Péclet number values of 8.9 × 103 and 7 × 103, respectively for the glass beads and the gravel, corresponding to a similar pore velocity close to 0.30 mm s−1. Below this threshold pore velocity, breakthrough of the dissolved tracer occurs earlier than that of particles. This behaviour can be explained by analysing the granular size distribution of the effluent (Fig. 6). This figure displays the changes in the particle-size distribution during recovery, analysed with a Coulter Multisizer counter. For the greatest flow rate (e.g., 0.021 l s−1) in the gravel column, the recovery of coarser particles is more important than that of the glass-bead column. Thus, for the same flow rate, the largest diameter mode of the recovered particles is 14 μm for the gravel and 8 μm for the glass beads. This result can be explained by the existence of macropore continuity and its importance on preferential transport [1]. The modal size of the recovered particles decreases when the flow rate decreases, i.e., the finest particles are more recovered at low velocities than the coarsest ones. Particle-size distribution of effluents at different flow rates are compared with the initial size distribution in gravel and glass-bead columns. The microgranulometric spectrum mode decreases with decreasing the flow rate. Therefore, lower flow rates favoured transport of smaller suspended particles. Thus, at lower flow rates, the smaller suspended particles transport paths were longer because of the detours in the porous medium before reaching the outlet. In other words, the arrival time (time necessary for the first suspended particles/tracer molecules to reach the column exit) of the suspended particles is greater in comparison with that of the dissolved tracer. In contrast, higher flow rates facilitated mobilisation of the larger suspended particles, but with a significant size exclusion that caused the preferential transport. At lower flow rates, trapping of the larger suspended particles within the porous media is due to settlement in wide pores and clogging in narrower pores. At high flow rates, the recovery of coarser particles is larger in a gravel column that contains a wide range of pores, leading likely to preferential flow paths. The recovery is broadly better for glass beads, although this medium has a porosity value lower than that of the gravel medium. This result shows that global parameters of a porous medium, such as porosity, are not enough to characterize transport of suspended particles. The behaviour difference between gravel and glass-bead media is mainly due to the pore geometry and distribution. Therefore, the gravels’ grain-size distribution favours the mechanical straining of the suspended particles. Indeed, the particle transport in a glass-bead medium was facilitated by the homogeneous pore distribution. The studies conducted on a two-dimensional model [17] demonstrate the role played by high permeability zones in particle transport and deposition. It was also showed [10] that hydraulically equivalent media with exactly the same porosity can produce large differences in the transport of suspended particles if they have different pore-volume distributions.
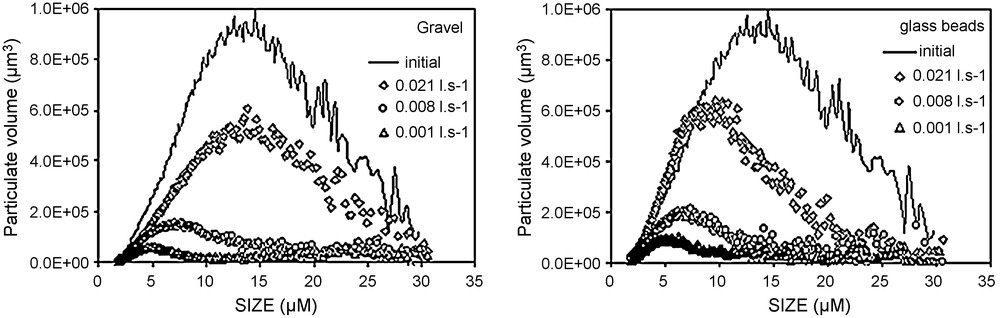
Microgranulometric spectrum of the transported suspended particles in the two porous media.
Fig. 6. Spectre micro-granulométrique des MES transportées dans les deux milieux poreux.
The dispersion coefficient in equation (1) is a simplification of hydrodynamic dispersion, including the processes of mechanical dispersion and molecular diffusion. The mechanical dispersion is caused by a variation in fluid velocity in the pore space of the porous medium and the diffusion is caused by the random motion of molecules. Dispersion is shown to be sensitive to pore-size distribution, pore coordination, and blockage. Several authors [16] noted a non-linear dependence of the longitudinal dispersion on the mean flow velocity. However, our experiments conform to a regime where mechanical dispersion dominates molecular diffusion (300 < Ped < 105). Thus, molecular diffusion is negligible.
The dynamic Péclet number, which is a dimensionless parameter relating the rate of advection of the flow to its rate of dispersion, is defined as:
| (5) |
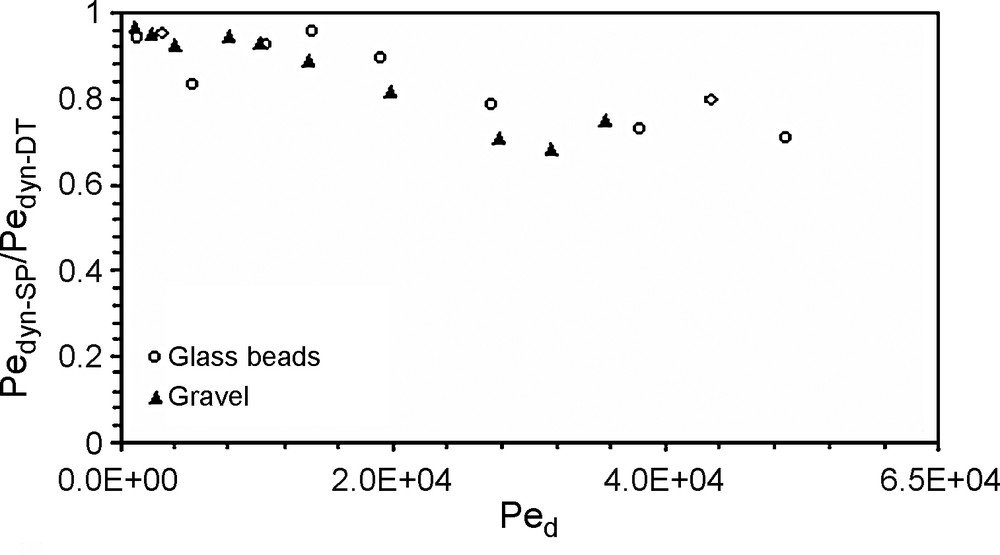
Ratio of the dynamic Péclet numbers of suspended particles and dissolved tracer versus the diffusion Péclet number, for both glass and gravel columns.
Fig. 5. Variation du rapport des nombres de Péclet dynamique des MES et du traceur dissous en fonction du nombre de Péclet de diffusion, pour les billes de verre et le gravier.
4.2 Flow-velocity effect on particle recovery rate and deposition
The recovery rate is obtained by integrating the experimental breakthrough curve area. Results show that the recovery rate decreases when the flow rate decreases, as well illustrated in Fig. 6. Decreasing flow rates result in decreased particle concentrations in the column effluents and decreased total particle recovery. At a given pore water velocity, the particle recovery from the glass-bead column is larger than that from the gravel column. This makes us think of the geometry of the pores and their distribution in the porous medium. In the gravel column, one finds narrow and wide grain sizes, leading to a wide range of pore size distribution and then to the existence of many retention sites, such as constrictions, crevices, and caverns, which participate in particle trapping. On the other hand, the single size of the glass beads leads to a uniform pore distribution. Particle deposition is the primary factor controlling the transport of suspended particles in groundwater. Hence, a thorough understanding of particle deposition is essential for prediction of particulate transport in natural porous media. We focus here on the initial deposition rate onto ‘clean’ solid surfaces before retained particles start to influence the subsequent deposition of particles. The deposition rate coefficient in equation (1) is of first-order kinetic, and no release occurs. This assumption is justified by the amount of particles injected in the column. Fig. 7 shows the corresponding particle-deposition rate coefficients as a function of the diffusion Péclet number, for three duplicated tracer tests with each selected flow rate. The calculations show that particle-deposition rate coefficients increased with increasing Darcy's velocity, with a slope of the log–log relationship close to 0.6. This is consistent with previous experimental studies and theoretical analyses of colloid deposition rates, which predict that at low to moderate flow velocities, the deposition rate increases with flow velocity at the power 0.3 to 0.7 [9,12]. This behaviour is true at low to moderate diffusion Péclet number, but beyond a critical value, the deposition rate presents unexpected changes and then decreases beyond this critical flow. This behaviour is similar for the two porous media (gravel and glass beads), but the deposition rate is larger in gravel because of the wide range pore distribution in this medium, where many retention sites participate in particle trapping. It is known that the distinction in terms of conductance and storage in the respective pore domain are characterized by the fact that: macropores are primary flow paths where both dispersion and advection are prevalent; mesopores are intermediate flow paths where advection becomes dominant; micropores are supplemental flow paths and mass storage spaces where only diffusive flow is manifested. The mechanical filtration is usually neglected when the ratio between the grain size d50 of the porous medium and the suspended particle size dp is greater than 20 [14]. In this study, the ratio d50/dp is 168 and 214 for gravel and glass-bead columns, respectively. Thus, filtration may be neglected in the process of silt particle transport and deposition. However, straining is negligible only if the above ratio becomes greater than 200 [3]. Thus, the gravel medium presents a real susceptibility for particle straining. The decrease of the deposition rate at higher flow velocities makes us think of the flow regime and the validity of Darcy's law. Nevertheless, this does not discard the existence of shear flow able to tear off particles and lower the deposition rate. At low flow rates, the coarser particle deposition is mainly controlled by the sedimentation (gravity effect) and their velocity is no longer that of the fluid; thus, they can be captured in constriction and cavern sites. However, at high flow velocity, the hydrodynamic force, especially drag force, is important and the relative significance of sedimentation with respect to bulk flow is low. Thus, the deposition kinetic decrease can be explained by the fact that the hydrodynamic forces are significant and dominate the gravitational forces applied to the particles.
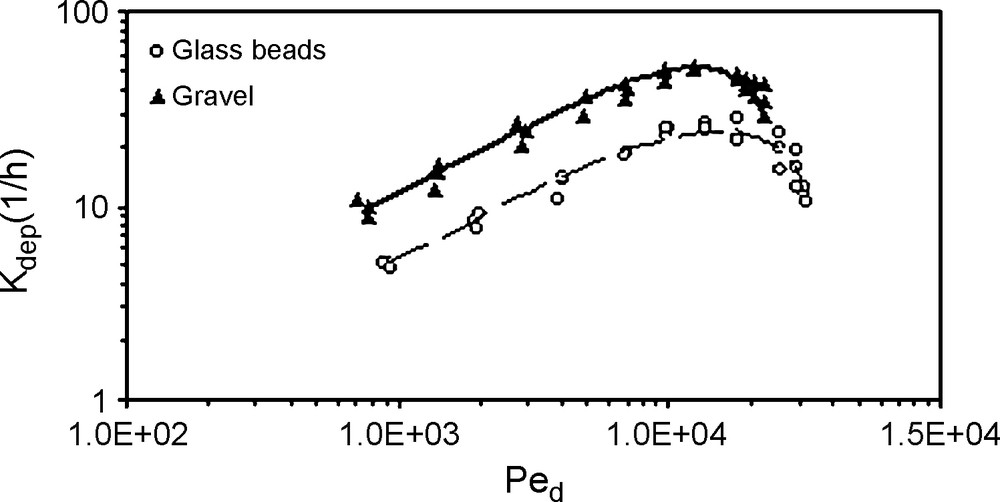
Influence of the Péclet number on the deposition kinetics of silt particles in the two porous media, for three duplicated tracer tests.
Fig. 7. Influence du nombre de Péclet dynamique sur la cinétique de dépôt des particules dans les deux milieux poreux, pour trois essais de traçage dupliqués.
5 Conclusions
This study, devoted to transport and deposition of suspended particles in saturated porous media, shows that the 1-D analytical model can well fit the breakthrough curves from which the hydrodispersive parameters are derived. The response to a short-pulse injection represents an effective method of analysing transport and deposition of particles in a porous medium. Simultaneous tracer tests using a dissolved tracer and suspended particles enable to compare the transport behaviour of particulate and dissolved phases. We provide direct observation of the size-exclusion phenomenon for particles travelling through porous media. Both gravel and glass-bead columns has provided ample evidence that suspended particles can be transported through porous media, under certain hydrodynamic conditions, faster than the dissolved tracer. The recovery rate increases with increasing the flow rate. The amount of particles recovered from the glass-bead column is broadly greater compared to that from the gravel column. Nevertheless, at high velocity, the coarsest particles were mostly recovered. This difference in recovery rate is mainly due to the pore geometry where the throats dimension, tortuosity, and paths connection are the main parameters governing particle transport. The deposition rate presents unexpected changes, depending on the flow rate. The deposition rate increases until a critical flow velocity, beyond which it decreases. This unusual behaviour is attributed to the hydrodynamic forces applied to the particles at high flow rate, which dominate the gravitational forces, thus enhancing lift and drag forces, leading to reduce the suspended particles’ deposition kinetics. Flow velocity was shown to have an effect on the first-order kinetic particle-deposition rate coefficients. For predicting particle transport in subsurface porous media, the kinetics of particle deposition must be known.
Acknowledgements
The research is supported by the ‘Région Haute-Normandie’. Jean-Paul Dupont is gratefully acknowledged for his assistance in acquiring microgranulometric analysis data at the ‘Laboratoire de géologie’, UMR 6143 M2C (University of Rouen, France).


