1 Introduction
Coral skeletons are widely used as recorders of paleo-environmental conditions (for a review: Corrège, 2006; Druffel, 1997). The isotopic composition of oxygen (δ18O) and trace element ratios are thought to vary with temperature (Mitsugushi et al., 1996; Weber and Woodhead, 1972) and thus provide indications of past seawater temperature. These reconstructions are based on empirical calibrations between a proxy (e.g. δ18O) and measured temperature. However, these isotopic compositions and element/Ca ratios differ from the equilibrium values determined for inorganic aragonite (Grossman and Ku, 1986), i.e. due to the so-called vital effects (Urey et al., 1951). Three main geochemical models are proposed to explain the oxygen isotope composition shift in coral skeletons: (1) pH variations in the fluid of calcification, which modifies the proportion of dissolved carbonate species (Adkins et al., 2003); (2) kinetic processes (McConnaughey, 2003; Sinclair and Risk, 2006), in which precipitation occurs before isotopic equilibrium between DIC and water; and (3) Rayleigh fractionation, in which the fluid of calcification is considered as a closed system (Cohen et al., 2006; Gagnon et al., 2007).
From in situ δ18O measurements in scleractinian corals, large variations were documented (Allison et al., 2010b; Blamart et al., 2005; Juillet-Leclerc et al., 2009; Rollion-Bard and Erez, 2010; Rollion-Bard et al., 2003). These observations demonstrate that the vital effect observed in bulk samples mimics the average of micro-scale elemental and isotopic variability in the different parts of the skeleton (Allison et al., 2010a,b; Cohen et al., 2006; Meibom et al., 2003; Rollion-Bard et al., 2003; Sinclair, 2005). Indeed, we have already shown (Rollion-Bard et al., 2003) that pH can control the δ18O values in corals via a change: (1) of the relative fractions of dissolved carbonate species (Usdowski and Hoefs, 1993; Usdowski et al., 1991; Zeebe, 1999, 2007); and (2) of the kinetics of their isotopic equilibration with water before carbonate precipitation (Section 5). The first calculation of the pH from δ11B data in Rollion-Bard et al. (2003) was based on the historical fractionation factor between the two dissolved species (Kakihana et al., 1977). Since 2000, this fractionation factor was revisited (for a review: Pagani et al., 2005), and, based on in situ boron isotope measurements in foraminifera, it has now been shown (Rollion-Bard and Erez, 2010) that this fractionation factor is closed to the value determined by Klochko et al. (2006) – i.e. α4 − 3 = 0.97352.
Here we report a re-calculation of pH from δ11B data in Porites lutea corals (Rollion-Bard et al., 2003) in light of the new fractionation factor between the two boron dissolved species, and new δ11B and δ18O measurements in the same coral sample. We also report δ11B analyses in Mediterranean scleractinian coral, Cladocora caespitosa, grown experimentally under two different atmospheric pCO2, and so in different constant pH in order to observe the variability of the internal pH under constant environmental conditions. This will be interpreted in terms of kinetics of precipitation and in terms of biological control of internal pH by the coral.
2 Samples
To test the influence of environmental parameters on the δ11B variability recorded in the coral skeleton, some measurements were performed on natural sample, P. lutea, and two corals, C. caespitosa, grown under constant laboratory conditions.
The P. lutea sample is a fragment of a modern massive coral collected at the Boulari Reef in New Caledonia in 1994 (166°26’26”E, 22°29’22”S, 5.6 m water depth, mean annual T = 23.15 °C, mean salinity S = 35.75 p.s.u., δ18Osw = 0.46‰). Just after the collection, the sample was dried under the sun, and most of the organic matter was removed by water-jet. It was then cleaned by immersion in an ultrasonic bath in double distilled water, and dried. C. caespitosa is endemic of the Mediterranean Sea (Zibrowius, 1980). Two colonies were collected in the Bay of Villefranche (43°41’N, 7°18’E) at ≈25 m water depth in September 2006. An experiment was set up using two independent aquaria with two different pCO2: ambient pCO2 (i.e. 400 μatm, leading to a solution pH of 8.07) and elevated pCO2 (≈700 μatm, leading to a solution pH of 7.86). The design of the experiments is already described in Rollion-Bard et al. (2009) and in more details in Rodolfo-Metalpa et al. (2010).
Briefly, ambient and elevated pCO2 were obtained by bubbling ambient air and pure pCO2 in two tanks. These conditions were maintained for 1 year. The tanks were continuously filled with Mediterranean seawater pumped from the bay of Villefranche (10 m depth) and then overflowed into the experimental aquaria. Corals were fed two times per week with some Artemia. The temperature, irradiance, and photoperiod were gradually changed in each aquarium in order to mimic the natural changes that occurred at the bay of Villefranche at ca. 20 m depth. At this depth, seawater temperature varied from 13 to 22 °C. pH was measured every 2 days using a Metrohm 862 pH mobile and an Orion electrode. Parameters of the carbonate system (pCO2, CO32−, HCO3−, DIC, and the aragonite saturation Ωa) were calculated from pH, alkalinity, temperature and salinity using the Seacarb program (Lavigne and Gattuso, 2010) with equations from DOE (1994), Frankignoulle (1994), Zeebe and Wolf-Gladrow (2001), and Dickson et al. (2007). At the beginning of the experiment, coral skeletons were stained with Alizarin, which was used as a chronological marker, and was used for measuring subsequent skeletal growth. The colonies were carefully cleaned, and tissues were removed by using of NaOH (1 M).
Parts of the C. caespitosa skeleton above the Alizarin mark were mounted in epoxy and polished with diamond paste down to 1 μm. P. lutea sample was also polished down to 1-μm diamond paste (without epoxy) prior the ion probe analyses, and then gold coated.
3 Methods
Boron and oxygen isotopic analyses were carried out with the Cameca IMS 1270 ion microprobe at CRPG-CNRS, Nancy, France. The analytical settings are described in Blamart et al. (2007) for boron isotope measurements, and in Rollion-Bard et al. (2007) for oxygen isotope analyses. The boron isotopes were measured during two sessions for P. lutea: one in March 2002, and the other one in July 2010, and in one session for C. caespitosa. In summary, for boron isotopic measurements, a primary mass-filtered beam of 16O− ions with an intensity of 60–70 nA was focused into an aperture-delimited spot of approximately 15-μm wide and 30-μm long using Kohler illumination. The analyses were conducted in monocollection mode by peak jumping between the mass 9.5 (background), 10B and 11B. The reference material, WP 22, is an aragonite crystal with a B concentration of 22 ppm and a δ11B value of 21‰. The internal error for δ11B measurements was typically comprised between ±0.3 and 0.6‰ (1σ). Average external reproducibility, estimated from replicate measurements of the aragonite reference, was ±1.1‰ (1σ) for session 1, and ±0.8‰ (1σ) for session 2. These lead to typical total error (1σ) between ±0.9 and ±1.5‰ on δ11B measurements.
For oxygen isotopic measurements, a primary beam of Cs+ ions with an intensity of about 10 nA was focused into an aperture-delimited spot of approximately 15-μm wide and 30-μm long using Kohler illumination. Charge neutralization was achieved using the normal incidence electron gun. Measurements were conducted in multicollection mode using two off-axis Faraday cups (L’2 and H1). All the δ18O values are reported relative to the PDB standard. The reference materials are two calcite crystals (MEX and Carb) and one aragonite grain (Arg) with δ18OPDB of −7.05‰, −19.00‰, and −7.18‰, respectively. The internal error for δ18O measurements was typically less than 0.1‰. Average external reproducibility, estimated from replicate measurements of the carbonate references, was ±0.4‰ (1σ).
All SIMS analyses were performed along the axis of maximum vertical coral growth, and also on trabeculae (vertical skeletal part) and synapticulae (horizontal skeletal part) for P. lutea (Fig. 1).

a: reflected light picture of a gold-coated section of the P. lutea coral after SIMS analyses. Arrow indicates growth direction. RL: reference line; b: reflected light pictures of 2 transects of boron isotope analyses in C. caespitosa: (1) experiment at pCO2≈400 μatm, and (2) experiment at pCO2≈700 μatm. Arrows indicate maximum growth direction.
a : photographie en lumière réfléchie de la section métallisée à l’or du corail P. lutea après les analyses à la microsonde ionique. La flèche indique le sens de croissance. RL : ligne de référence ; b : photographies en lumière réfléchie de la localisation des analyses des isotopes du bore dans C. caespitosa : (1) expérience à pCO2≈400 μatm, (2) expérience à pCO2≈700 μatm. Les flèches indiquent la direction de croissance maximale.
4 Results
4.1 P. lutea sample
Ion microprobe δ18O measurements in Porites coral sample show large variation, from −10.6 ± 0.9‰ to −0.2 ± 0.5‰. This range of variation (≈10‰) cannot be ascribed to changes in environmental parameters since it would represent a temperature variation of about 50 °C (if we consider a temperature dependence of −0.2‰/°C, Epstein et al., 1953). The highest values are close to the isotopic equilibrium value for the aragonite-water system, using an average temperature of 23.15 °C, an average salinity of 35.75 p.s.u., a δ18O (in SMOW) of seawater of 0.46‰ and a pH of seawater of 8.2 (Grossman and Ku, 1986; Zeebe, 2007). Consequently the lowest values show a large and clear O-isotopic disequilibrium.
The δ11B values show also a large variability, from 18.6 ± 1.5‰ to 30.6 ± 1.6‰ during session 1 (March 2002) and between 20.6 ± 0.8‰ and 29.84 ± 0.9‰ during session 2 (July 2010), showing then an overall variability of 12‰ (Fig. 2 and Table 1).

P. lutea SIMS δ11B measurements in function of distance (μm) relative to a fixed point (beginning of the profile). Considering a growth rate of about 22 mm/yr (Rollion-Bard et al., 2003), this profile covers between 2 and 3 months of coral growth.
Mesures de δ11B dans P. lutea par SIMS en fonction de la distance (en μm) par rapport à un point fixé correspondant au début du profil. En prenant un taux de croissance d’environ 22 mm/an (Rollion-Bard et al., 2003), la distance mesurée représente entre 2 et 3 mois de croissance du corail.
Compositions isotopiques de bore, mesurées lors de deux sessions dans un corail moderne Porites lutea et pH calculés à partir de l’Éq. (1).
| δ11B (‰) | Error | pH |
| Session 1 (2002) | ||
| 22.93 | 1.36 | 8.42 |
| 27.06 | 1.40 | 8.68 |
| 27.30 | 1.43 | 8.70 |
| 21.14 | 1.43 | 8.29 |
| 23.66 | 1.47 | 8.46 |
| 30.59 | 1.39 | 8.92 |
| 24.43 | 1.58 | 8.51 |
| 19.41 | 1.38 | 8.15 |
| 27.43 | 1.44 | 8.71 |
| 25.10 | 1.56 | 8.56 |
| 29.80 | 1.40 | 8.87 |
| 22.77 | 1.59 | 8.40 |
| 24.53 | 1.52 | 8.52 |
| 25.58 | 1.53 | 8.59 |
| 28.64 | 1.65 | 8.79 |
| 22.49 | 1.38 | 8.39 |
| 23.29 | 1.51 | 8.44 |
| 18.61 | 1.53 | 8.08 |
| 25.07 | 1.47 | 8.56 |
| 24.62 | 1.53 | 8.53 |
| Session 2 (2010) | ||
| 25.39 | 0.83 | 8.58 |
| 25.57 | 0.80 | 8.59 |
| 23.99 | 0.89 | 8.49 |
| 25.70 | 0.89 | 8.60 |
| 29.84 | 0.87 | 8.87 |
| 27.79 | 0.86 | 8.73 |
| 26.90 | 0.85 | 8.67 |
| 26.36 | 0.80 | 8.64 |
| 21.15 | 0.98 | 8.29 |
| 24.31 | 0.88 | 8.51 |
| 24.06 | 0.83 | 8.49 |
| 26.15 | 0.80 | 8.63 |
| 20.60 | 0.79 | 8.25 |
| 26.20 | 1.59 | 8.63 |
| 24.27 | 1.10 | 8.50 |
| 27.48 | 1.06 | 8.71 |
| 21.59 | 1.06 | 8.32 |
| 25.29 | 0.81 | 8.57 |
| 22.77 | 0.86 | 8.40 |
| 23.23 | 0.76 | 8.44 |
| 28.57 | 0.86 | 8.78 |
| 25.72 | 0.79 | 8.60 |
| 24.69 | 0.81 | 8.53 |
| 23.91 | 0.82 | 8.48 |
| 24.02 | 0.77 | 8.49 |
| 24.83 | 0.89 | 8.54 |
| 25.85 | 0.95 | 8.61 |
| 24.83 | 0.88 | 8.54 |
| 24.08 | 0.78 | 8.49 |
| 23.21 | 0.81 | 8.43 |
| 24.58 | 0.81 | 8.52 |
| 24.35 | 0.79 | 8.51 |
| 23.44 | 0.89 | 8.45 |
| 24.54 | 0.83 | 8.52 |
| 26.08 | 0.83 | 8.62 |
| 23.33 | 0.80 | 8.44 |
| 24.03 | 0.85 | 8.49 |
| 24.10 | 0.92 | 8.49 |
| 27.08 | 0.93 | 8.69 |
| 23.60 | 0.85 | 8.46 |
| 24.46 | 0.82 | 8.52 |
| 24.14 | 0.82 | 8.50 |
| 26.75 | 0.76 | 8.66 |
| 21.69 | 1.02 | 8.33 |
| 29.36 | 0.78 | 8.84 |
In this sample, it was not possible to distinguish the isotopic values of the centres of calcification (CoC) from the fibres, as the CoC are relatively small (less than 5 μm) compared to the ion probe spot (15 μm wide and 30 μm long). By consequence, the δ18O and δ11B values represent either a mixing of CoC and fibres signatures, or only fibres isotopic compositions, and all the values are then taken into account, even if it has been showed that it is unlikely that fibres and CoC derive from a single kinetic process in a common fluid of calcification (Rollion-Bard et al., 2010).
4.2 C. caespitosa samples
Despite the controlled pCO2, leading to a constant pH, δ11B values in each experiment show a large variability from 27.3 ± 0.7‰ to 32.3 ± 0.8 ‰, with an average δ11B of 29.9 ± 1.3‰, for sample grown at pCO2 of ≈400 μatm (i.e. pH = 8.07), and from 27.5 ± 0.7‰ to 31.2 ± 1.0‰, with an average δ11B value of 29.3 ± 1.3‰, for sample grown at pCO2 of ≈700 μatm (i.e. pH = 7.86) (Fig. 3). Both specimens show an overall range of ≈5‰, much smaller than in natural coral, P. lutea. Despite the large variability recorded in cultured C. caespitosa samples, the SIMS average δ11B shows an increase with the surrounding pH, as expected from the relation between δ11B in carbonates and pH of the solution and as shown from bulk coral measurements (Hönisch et al., 2004; Reynaud et al., 2004).

SIMS δ11B measurements in C. caespitosa samples. a: experiment at pCO2≈400 μatm; b: experiment at pCO2≈700 μatm. δ11Btheo represents the δ11B value of B(OH)4− considering δ11Bsw = 39.6‰, T = 18 °C and S = 35 p.s.u. Arrows indicate maximum growth direction. Growth rate of 23 mm/yr was determined from an average calcification rate from Rodolfo-Metalpa et al. (2010).
Mesures de δ11B dans C. caespitosa par SIMS. a : expérience à pCO2≈400 μatm ; b : expérience à pCO2≈700 μatm. δ11Btheo représente la valeur de δ11B de B(OH)4− en considérant δ11Bsw = 39,6 ‰, T = 18 °C et S = 35 p.s.u. Les flèches indiquent la direction de croissance maximale. Le taux de croissance de 23 mm/an a été calculé à partir d’un taux de calcification moyen à partir des données de Rodolfo-Metalpa et al. (2010).
We can also notice a difference of about 5‰ between P. lutea δ11B values and those for C. caespitosa. This difference could be due to different total increase of the pH before the precipitation of the skeleton, and then resulting in different vital effects from species to species, as it was already observed in cultured corals (Pagani et al., 2005, for a review).
5 Discussion
5.1 Boron isotopes as seawater pH proxy?
In seawater, boron is present in the form of two dissolved species: boric acid B(OH)3 and borate ion B(OH)4−. The proportion of these two dissolved species changes as a function of pH. Boron isotopes are fractionated between these two species, B(OH)3 being enriched in 11B by about 27.2‰ relative to B(OH)4− (Klochko et al., 2006 determined at 25 °C and assuming no significant dependence with temperature over the considered range). The use of δ11B of carbonates as pH proxy is in part based on the assumption that only B(OH)4− is incorporated into carbonates (Hemming and Hanson, 1992; Hemming et al., 1995). Nevertheless, in recent studies (Klochko et al., 2009; Rollion-Bard et al., 2011), it was shown by NMR measurements that B(OH)3 species could also be incorporated into biogenic carbonates. As the proportion of B(OH)3 is not known in the coral species studied here, we chose to consider than only B(OH)4−is incorporated into the skeleton and then, the δ11B of carbonates is pH-dependent according to:
| (1) |
Using Eq. (1), a pKB of 8.61 (calculated with the average temperature and salinity at the sampling location from Dickson (1990) equation and the fractionation factor of Klochko et al. (2006), δ11B data result in pH variations at the sites of calcification between 8.12 ± 0.1 and 8.94 ± 0.1. This pH range is smaller and more realistic than the previous one calculated in Rollion-Bard et al. (2003) (7.1 and 9.0). Moreover, it is very close to the pH range measured by micro-electrodes in calicoblastic layers in the scleractinian coral Galaxea fascicularis (from 8.13 to 9.29, Al-Moghrabi et al., 2001).
5.2 Biological control of the internal pH
Large variations of the δ11B data in both coral species are present in only a few micrometers (Figs. 2 and 3). Assuming a linear growth rate of about 2 cm/yr (Rollion-Bard et al., 2003), the δ11B profile covers about 2–3 months of growth and so these variations occur in a very short timescale (less than 5 days, i.e. ≈200 μm). This heterogeneity in tropical corals has been previously reported for Sr/Ca (Cohen and Sohn, 2004; Meibom et al., 2003; Sinclair, 2005), Mg/Ca (Allison and Finch, 2007; Meibom et al., 2004; Sinclair, 2005), U/Ca (Sinclair, 2005), δ18O (Adkins et al., 2003; Allison et al., 2010b; Rollion-Bard et al., 2003) and δ11B (Allison et al., 2010a; Rollion-Bard et al., 2003). No cyclical variation of the δ11B signal seems present, contrary to what has been found for δ18O (Rollion-Bard et al., 2003) and Sr/Ca (Meibom et al., 2003) in tropical corals. These variations are too large to be due to a change in environmental parameters (temperature, salinity, pH). It was also already shown that these variations in δ11B seem to be not due to Rayleigh -evolution process (Rollion-Bard et al., 2010).
In the experimental samples (i.e. C. caespitosa), all the environmental parameters are kept constant (except the temperature, which varies between 13 °C and 22 °C): the corals grew under constant pH of the artificial seawater, i.e. for the experiment at pCO2 = 700 μatm, the measured pH was in average 7.86 ± 0.01, and for the experiment at pCO2 = 400 μatm, the average pH was 8.07 ± 0.03. If the coral δ11B reflects directly seawater pH, then the expected δ11B values would be respectively 15.80‰ at pH = 7.86 and 17.69‰ at pH = 8.07, using Eq. (1) with δ11B of seawater at 39.6‰, pKB = 8.65 (average T = 18 °C, S = 35 p.s.u), and fractionation factor of 0.97352. The measured δ11B values are well above these theoretical values and indicate an elevated internal pH of 8.94 ± 0.09 (for pCO2 = 400 μatm), and pH of 8.87 ± 0.08 (for pCO2 = 700 μatm). These pH values calculated for the sites of calcification imply a strong control of the coral and that internal pH is mostly driven by biological processes, as it was already highlighted by δ11B measurements in natural coral (Fig. 4). This pH increase at the sites of calcification relative to surrounding seawater is probably due to the removal of H+ from the sites of calcification by the Ca2+/H+ ATPase (Dixon and Haynes, 1989; McConnaughey, 1989a; Niggli et al., 1982). It then results in the significant CaCO3 supersaturation required to enhance carbonate precipitation.
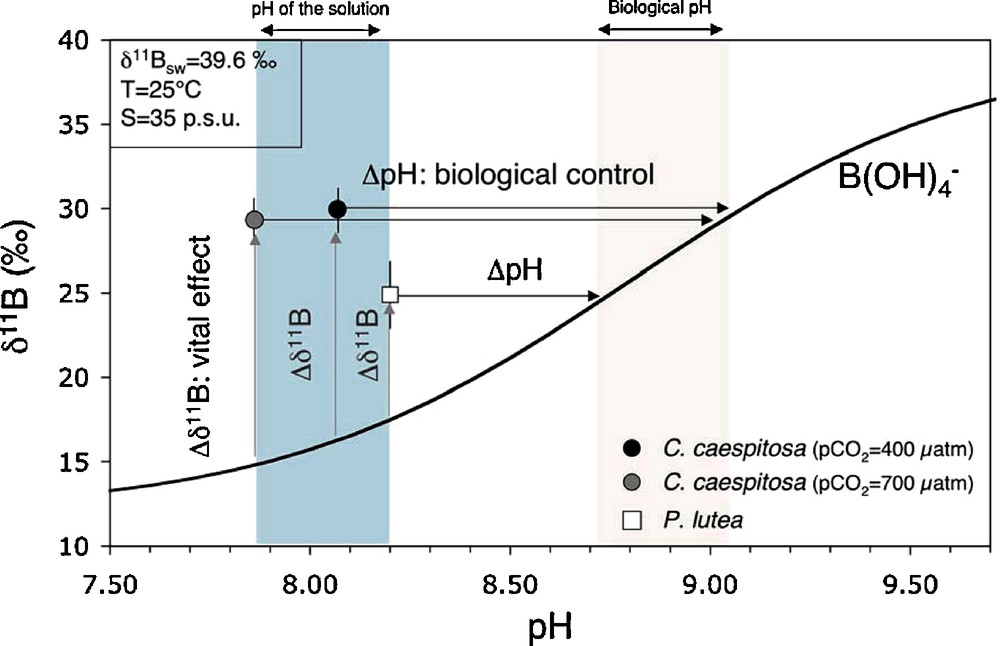
Average δ11B measured in corals versus pH of the solution. The vital effect is represented as the difference between the measured value and the theoretical value of B(OH)4− (black curve), calculated for a seawater δ11B of 39.6‰, temperature of 25 °C and salinity of 35 p.s.u. The biological control of the coral is indicated as the difference between the pH of the surrounding solution in which the coral grew and the pH near the sites of calcification (biological pH).
δ11B moyen mesuré dans les coraux en fonction du pH de la solution. L’effet vital est représenté par la différence entre la valeur mesurée et la valeur théorique de B(OH)4− (courbe noire) calculée pour un δ11B de l’eau de mer de 39,6 ‰, une température de 25 °C et une salinité de 35 p.s.u. Le contrôle biologique exercé par le corail est indiqué par la différence entre le pH de la solution dans laquelle ont poussé les coraux et le pH près des sites de calcification (pH biologique).
5.3 Modelled effect of pH on kinetics of oxygen isotope equilibration between DIC and water
Calcification occurs via the reactions:
| (1) |
| (2) |
| (3) |
| (4) |
All the reactions in the carbonate system are almost instantaneous, and only two reactions (reactions (3) and (4)) can constitute a limiting-step and have to be taken into account in order to calculate the rate of the isotopic equilibration between DIC and water. These two reactions are the production of HCO3− via reaction of CO2 with either H2O (hydration) or OH− (hydroxylation).
Seawater has a δ18O of −29.3‰ relative to PDB, whereas CO2 in equilibrium with water has a δ18O of about 10‰ (Kim and O’Neil, 1997). OH− has a δ18O value of about –67.3‰ (Usdowski and Hoefs, 1993). As a result of isotopic mass balance (2/3 of oxygen coming from CO2, and 1/3 coming from H2O or OH−), HCO3− produced by hydration (reaction (3)) has an initial δ18OPDB of −3.2‰, whereas HCO3− produced by hydroxylation (reaction (4)) has an initial δ18OPDB of −15.8‰. The oxygen isotopic equilibrium of HCO3− value is 3.3‰.
For reactions (3) and (4), the equilibrium constants are calculated for the average temperature and salinity at the sampling location and a total DIC of 2000 μmol.kg−1 using equations from Mehrbach et al. (1973), DOE (1994), Millero and Pierrot (1998), and Zeebe and Wolf-Gladrow (2001). The time required for HCO3− to reach oxygen isotopic equilibration with H2O was then calculated according to McConnaughey (1989b) and Rollion-Bard et al. (2003), for several pH and for the reactions of hydration and hydroxylation (Fig. 5).
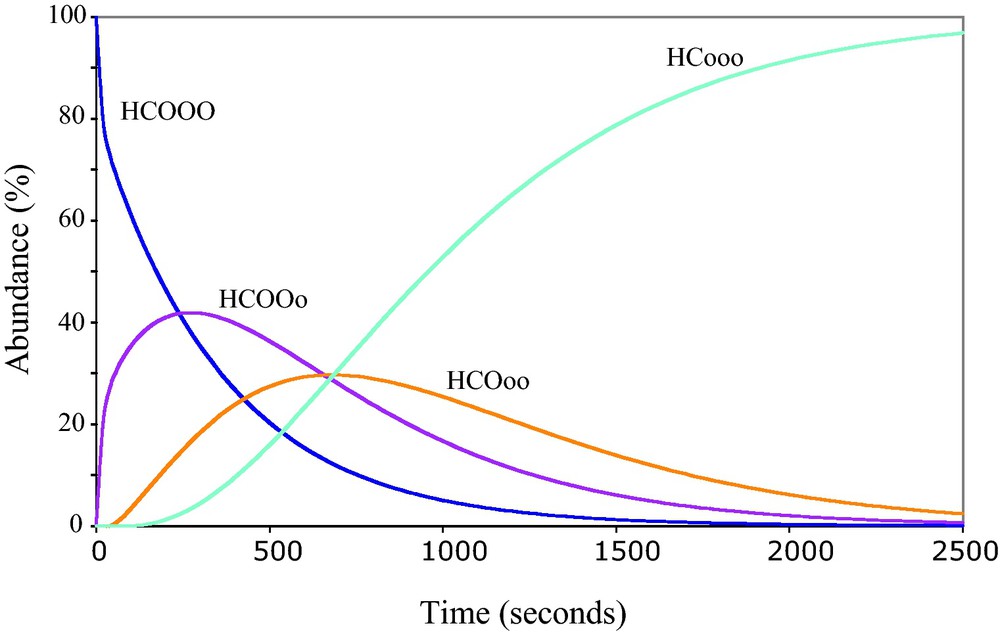
Kinetics of the exchanges between HCO3− and H2O calculated for a water with a pH of 7, temperature of 25 °C and salinity of 35 p.s.u. (DOE, 1994; Mehrbach et al., 1973; Millero and Pierrot, 1998; Zeebe and Wolf-Gladrow, 2001). The curves indicate the remaining fractions in the solution of the different species HCO3− having still 3 (HCOOO), 2 (HCOOo), 1 (HCOoo), and 0 (HCooo) atom(s) of oxygen initially present in HCO3−.
Cinétique des échanges entre HCO3− et H2O, calculée pour une eau à pH 7, une température de 25 °C et une salinité de 35 p.s.u. (DOE, 1994 ; Mehrbach et al., 1973 ; Millero et Pierrot, 1998 ; Zeebe et Wolf-Gladrow, 2001). Les courbes indiquent les fractions restantes dans la solution des espèces de HCO3− ayant encore trois (HCOOO), deux (HCOOo), un (HCOoo) et zéro (HCooo) atomes d’oxygène présents initialement dans HCO3−.
The proportion of HCO3− generated by hydration and hydroxylation is pH-dependent, hydroxylation being dominant for pH higher than 8.4 at 25 °C (Johnson, 1982). If we consider that isotopic equilibrium between B(OH)3 and B(OH)4− is almost instantaneous (Zeebe, 2005) and that the δ11B signature of the carbonate is a proxy of pH at the site of calcification, in the pH range calculated, the fraction of HCO3− produced by hydration and hydroxylation are ≈67% and 33% respectively, at pH 8.1, and 24% and 76% at pH 8.9. Accordingly, the initial oxygen isotopic disequilibrium values for HCO3− would be −7.4‰ and −12.8‰ at pH 8.1 and 8.9, respectively. The δ18O of the carbonate was calculated for different times and different pH values (Fig. 6) from the relative proportions of HCO3− and CO32− in the solution and their δ18O, assuming that they are in isotopic equilibrium as their isotopic equilibration is quasi-instantaneous. H2CO3 is not taken into account as it is negligible for the range of pH considered here.
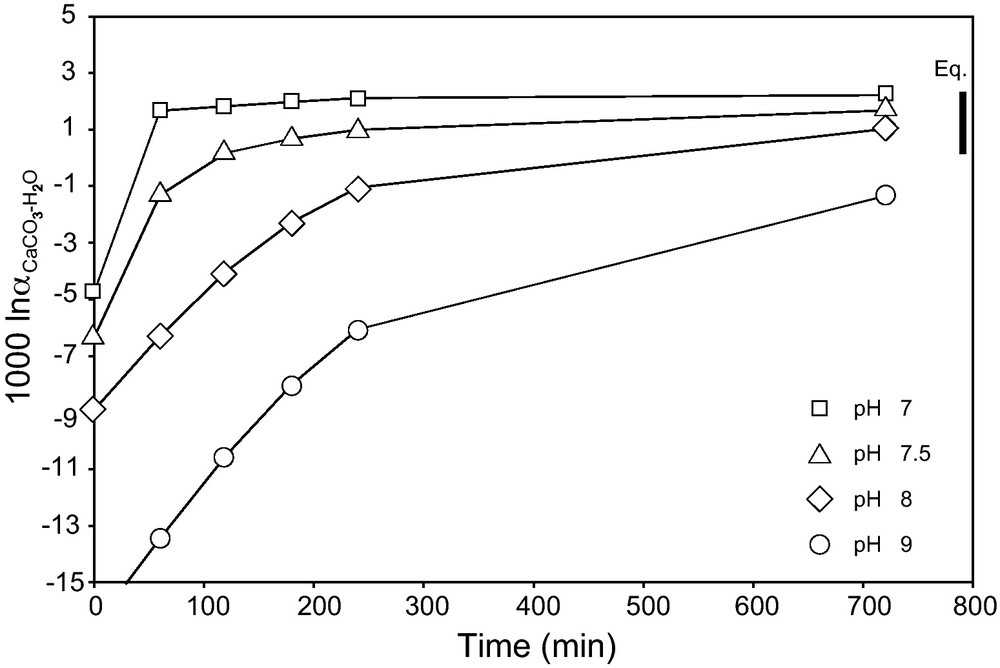
Oxygen isotopic fractionation versus time calculated from the kinetics of the reactions of hydration and hydroxylation and from their proportion relative to the pH of the solution (Johnson, 1982) for a temperature of 25 °C, a salinity of 35 p.s.u., and pH of 7 (square), 7.5 (triangle), 8 (diamond), and 9 (circle). Eq. represents the range of equilibrium δ18O for carbonates precipitated from seawater with pH between 7 and 9 (Usdowski and Hoefs, 1993; Zeebe, 1999, 2007).
Fractionnement des isotopes de l’oxygène en fonction du temps calculé à partir des cinétiques de réaction d’hydratation et d’hydroxylation et de leur proportion selon le pH (Johnson, 1982) pour une température de 25 °C, une salinité de 35 p.s.u. et des pH de 7 (carré), 7,5 (triangle), 8 (losange) et 9 (cercle). Eq. représente la gamme de δ18O pour des carbonates à l’équilibre avec une eau de mer entre les pH 7 et 9 (Usdowski et Hoefs, 1993 ; Zeebe, 1999, 2007).
This calculation can predict the δ18O of a carbonate for different pH and different time of equilibration between DIC and H2O before the precipitation of the carbonate (Fig. 7). The isotopic equilibrium is reached in less than 12 h for pH smaller than 8.4. Almost half the δ18O data measured by ion microprobe can be explained by residence times of less than 4 h (or more rapidly), considering no catalysis reactions; the rest would be precipitated more slowly. This difference in calcification rate could be explained by the significant variation of this rate between day and night, the daytime calcification being higher that the night-time one, the calcification being enhanced by the zooxanthellae (Chalker and Taylor, 1975; Goreau, 1959). This calcification is also different according to the structure of the coral (Clausen and Roth, 1975; Goreau, 1959), nevertheless, in this study, we do not see any evidence of relation with the coral architecture (i.e. synapticulae versus trabeculae).
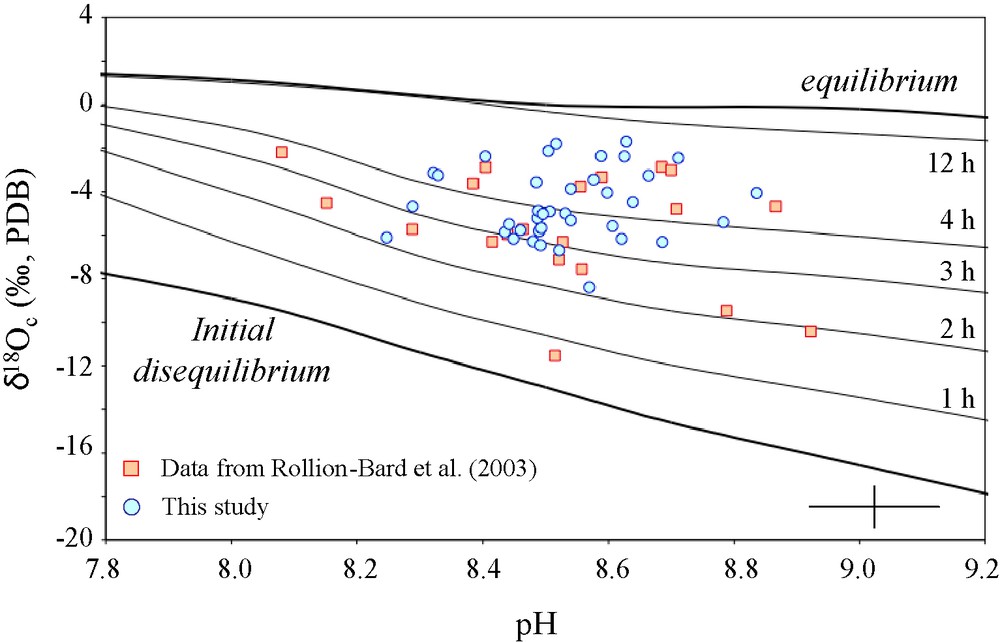
P. lutea δ18O measured by ion microprobe in function of pH calculated from measured δ11B (square: Rollion-Bard et al., 2003; circle: this study). The lines represent the calculated evolution of carbonate δ18O according to the pH of the solution for different time of equilibration of the carbonate species (essentially HCO3− and CO32− at the pH considered) and water. Most of the measurements show that the necessary time for the precipitation of the carbonate constitutive of the coral skeleton would be between 2 and 3 h (without considering any catalysis). Error bars indicate the precision of each analysis (1 σ).
δ18O mesuré par sonde ionique en fonction des pH calculés à partir des δ11B mesurés dans P. lutea (carré : Rollion-Bard et al., 2003 ; rond : cette étude). Les lignes représentent l’évolution calculée du δ18O des carbonates selon le pH de la solution, pour différents temps d’équilibration des espèces carbonatées (essentiellement HCO3− et CO32− aux pH considérés) et l’eau. La majorité des mesures montre que le temps nécessaire à la précipitation du carbonate constitutif du squelette corallien serait entre 2 et 3 heures (en ne considérant aucune catalyse). Les barres d’erreur indiquent la précision de chaque analyse (1 σ).
6 Conclusions
The calculated internal pH is always higher than the pH of the surrounding seawater, which can only result from a strong biological control of the animal. The range of internal pH from δ11B values for P. lutea tropical coral is between 8.1 and 8.9 ± 0.1, in agreement with direct pH measurements by micro-electrodes. Similarly, δ11B measurements in cultured corals C. caespitosa imply a large range of internal pH (from 8.7 to 9.0). A better understanding of the link between pH of surrounding seawater and internal pH is required to improve significantly the use of δ11B as paleo-pH proxy.
Combining δ11B and δ18O measurements in P. lutea sample, and a kinetic model of oxygen isotopic equilibrium between water and DIC, shows that half of the δ18O data can be explained by residence time before the precipitation less than 4 h, the rest being explained by longer times of residence. However, these times of residence are probably too long relative to the typical times calculated from 45Ca incorporation on the order of few minutes (Tambutté et al., 1995), as they do not take into account any catalysis processes (e.g. Ca-ATPase activity). Whatever the catalysis processes involved, the relation between internal pH and δ18O variation is not modified. Even if the temperature controls the rate of reaction and the fractionation factor values, it appears as a second order parameter in the δ18O variations in the coral.
Acknowledgments
We acknowledge the Region Lorraine for financial support. We thank S. Reynaud (Centre scientifique de Monaco) for providing Cladocora caespitosa samples. Two anonymous reviewers are thanked for their constructive comments and suggestions. This is CRPG contribution number 2120.


