1 Introduction
Alteration of silicate minerals is a key process controlling not only the carbon cycle but also the (bio)geochemical cycles of elements, especially of plant nutrient elements (Berner and Berner, 1996; Goudie and Viles, 2012). Presently several major uncertainties remain unresolved that preclude precise quantification of present-day and past impact of silicate alteration on the oceanic budget and on climate variations. In particular, the role of plants, for example during rapid changes of the continental biomass and of vegetation species, on the chemical alteration intensity of silicate minerals is poorly constrained (Amundson et al., 2007; Berner et al., 2004; Lucas, 2001). The onset of vascular plants on the continent during the Late Ordovician and their diversification up to the Devonian (Steemans et al., 2009) is known to have accelerated weathering rates and thereby lowered atmospheric CO2 content (Berner et al., 1983; Berner, 1998; Lovelock and Whitfield, 1982; Moulton et al., 2000). Rooted vascular plants excrete organic acids and chelates that enhance chemical weathering rates in soils (Griffiths et al., 1994). Plants are also known to accelerate chemical weathering processes by mobilizing metals from soils by a factor of two to five compared to the rates when plants are absent; they may also retard metal release to drainage waters by recycling (Berner et al., 2004). Finally, plants cause mechanical fractionation of rocks by increasing their specific surface area and, thus, influence indirectly chemical weathering rates. As a result, plants can control the biogeochemical cycle of nutrients and, therefore, affect their chemical availability in soils: they take up nutrients from the soil solution via their roots, store them in tissues, and finally return them to the soil system via litter fall and organic matter decomposition. While considerable work has been done to understand nutrient fluxes and exchanges between soil-water-plant compartments with classical geochemical tools (Marschner, 1995), developing new tools in this thematic could expand our understanding of these processes.
Instrumental improvements in mass-spectrometry made during the last decade allowed developing more precise isotope measurements of “non-traditional” stable isotopes like Li, B, Mg, Ca and Si in samples from the soil-water-plant interface. A review of Si isotopes is provided separately in this issue (see Opfergelt and Delmelle, this volume). Since Li, B, Mg and Ca have distinct and complementary implications in soil-forming reactions and in vegetation development, their coupled analyses should help gaining insights in mechanisms and rates governing the transfer of matter from bedrocks to surface waters. They are all fluid-mobile, non-subject to redox processes and they present large relative mass differences (from 7.69% for Mg to 16.66% for Ca) between their different stable isotopes. In contrast to Li, B or Mg isotopes that have no radiogenic isotopes, one part of 40Ca originates from the β− radioactive decay of 40K leading to 40Ca excesses compared to other isotopes (Marshall and DePaolo, 1982) but only in case of old samples (> 1 Ga) showing high K/Ca ratios (Nägler and Villa, 2000). They form either ionic (Ca) or covalent bonds with their atomic neighbors, and show variable coordination in solutions and solids, which are the main factors that determine isotope fractionation between solids, complexes and liquids. As a result, Li, B, Mg and Ca are subject to significant low temperature mass fractionations which can provide key information on the nature and quantification of weathering and/or biological processes.
On continents, the weathering of Ca- and Mg-silicates directly influences the carbon cycle by CO2 consumption and releases Ca2+ and Mg2+ cations into the hydrosphere according to the two following reactions (Berner et al., 1983):
These two major alkaline-earth elements are essential nutrients and have physiological and structural key functions in plants. In particular, Ca is necessary for the cell wall stability and acts as an intracellular messenger (Marschner, 1995; McLaughlin and Wimmer, 1999; Taiz and Zeiger, 2010). Mg participates in the activation of more than 300 enzymes for the synthesis of organic molecules and the functioning of chlorophyll (Wilkinson et al., 1990). However, the bio-availability of these two elements can be rapidly limited in soils which developed on base cation-poor bedrocks like granites. Their transfer from the parent mineral to surface water as well as their integration in vegetation tissues is therefore highly sensitive to the nature and extent of the water-soil-plant interactions. In contrast, the alteration of Li- and B-rich minerals does not directly influence the carbon cycle, but these two trace elements are particularly enriched in silicate minerals relative to carbonates, which makes them suitable proxies for quantifying alteration rates of silicate phases at the scale of large mixed lithology basins, or even at the global scale.
Several studies have focused on soil profiles, monolithological and mixed-lithology watersheds for each of these four isotopic systems. They have especially shown isotopic differences of various magnitudes between rivers, silicate rocks and minerals (Chaussidon and Albarède, 1992; Chaussidon and Marty, 1995; Huh et al., 1998; Tipper et al., 2006a, 2010a). Flux-weighted riverine isotopic signatures of these elements are lighter for Ca and Mg (Fig. 1), and heavier for B and Li, compared to the bulk silicate earth value. This suggests that fractionation processes occur on the continents, at local scale of soil profiles and/or during the downstream transfer to the oceans.
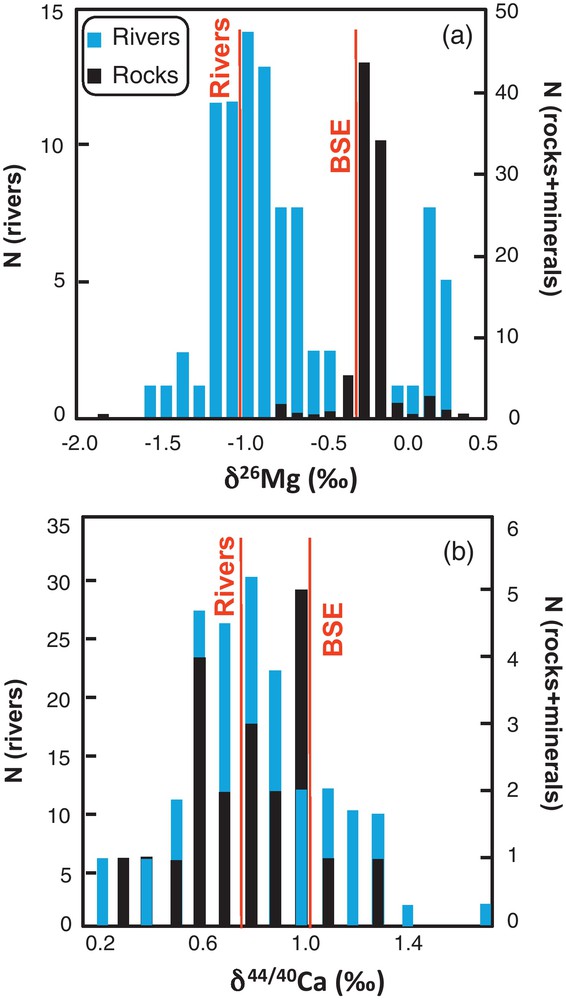
Histogram showing the presently published (a) Mg and (b) Ca isotopic variability in rivers, granite rocks and felsic minerals. Mg isotopic histogramm has been adapted from Tipper et al. (2012). Flux weighted average river and Bulk Silicated Earth (BSE) δ26Mg values from Tipper et al. (2006a) and Bourdon et al. (2010), respectively. Flux weighted average river and BSE δ44/40 Ca values from Tipper et al. (2010b) and Simon and DePaolo (2010), respectively.
Histogramme représentant la variabilité naturelle actuellement publiée dans les eaux de rivière, les roches granitiques et les minéraux mafiques pour les isotopes (a) du Mg et (b) du Ca. L’histogramme présentant les données isotopiques du Mg a été adapté de Tipper et al. (2012). Les valeurs moyennes δ26Mg pondérées par le flux des rivières et la croûte silicatée sont issues de Tipper et al. (2006a) et de Bourdon et al. (2010), respectivement. Les valeurs moyennes δ44/40 Ca pondérées par le flux des rivières et la croûte silicatée sont issues de Tipper et al. (2010b) et de Simon et DePaolo (2010), respectivement.
In the following sections, we will summarize the conceptual advances made by using Li, B, Mg and Ca isotopes to (1) understand and quantify processes controlling the transfer of matter within the silicate soil-water-plant system and (2) identify parameters controlling the isotopic fractionations in small and larger river systems. In the first part, we will present the main analytical aspects for isotope determination. Then, we will discuss the variability of Li, B, Mg and Ca isotopes in soil profiles in order to identify the main factors that control the isotopic fractionations of these isotopic systems. Field observations will be compared to laboratory experiments. Finally, we will discuss the riverine isotopic signature acquired in monolithological and in mixed-lithology watersheds and the parameters that control isotopic fractionations at these scales.
2 Analytical considerations: measurements, uncertainties and notations
Only a very precise determination of the Li, B, Mg and Ca isotopic compositions allows quantification of isotopic fractionations in nature. This was not possible in the past due to the lack of analytical techniques, especially of high-sensitivity mass spectrometers which now allow the precise isotope measurements of these elements. The analytical improvements made in the beginning of the 21st century have allowed enhanced investigation of these isotope systems as environmental tracers. Consequently, during the past decade, analysis of rocks, plants and waters has been performed with variable degrees of accuracy and precision. In nature, it especially appears that B and Li display huge fractionation amplitudes (∼50‰); Ca and Mg are much less fractionated (5–6‰) (Fig. 2), requiring the utmost of analytical precision in order to identify mass-fractionation processes. A summary of the measurement techniques and associated precisions is reported in Table 1.
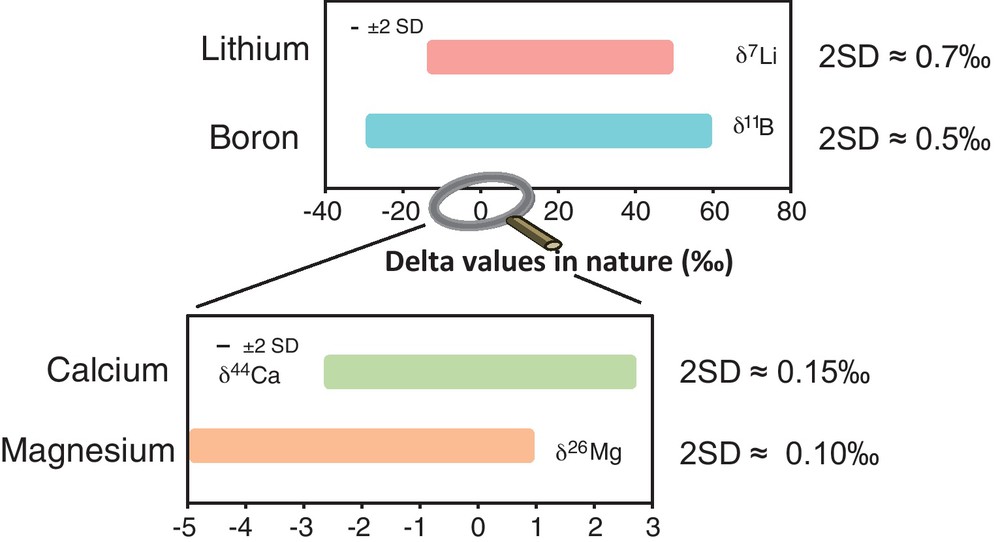
Amplitude of variation and associated reproducibility of Li, B, Ca and Mg isotopes in Earth surface processes.
Amplitude de variation et reproductibilité associée des isotopes du Li, B, Ca et Mg dans les processus de surface.
Résumé de différents protocoles analytiques et de la variabilité naturelle dans les processus de surface.
| Element | Isotopes | Abundance (%) | Mass spectroscopy | Standard | Typical external reproducibility (2SD in ‰)a | Natural variability | |
| Min. delta (‰)b | Max. delta (‰)b | ||||||
| Li | 6Li | 7.52 | TIMS - MC-ICP-MS | L-SVEC | 0.5c | −15 (xenoltihs, Tomascak, 2004) | +45 (carbonates, Tomascak, 2004) |
| 7Li | 92.48 | QUAD ICP-MS | |||||
| B | 10B | 19.82 | P-TIMS (250 ng) | SRM 951 (Catanzaro et al., 1970) | 0.04 | −45 (coal, Williams and Hervig, 2004) | About +60 (brines, Vengosh et al., 1995) |
| N-TIMS (about 1 ng) | |||||||
| MC-ICPMS (about 50 ng) | |||||||
| 11B | 80.18 | ||||||
| Mg | 24Mg | 78.992 | MC-ICP-MS | DSM3 (Galy et al., 2003) | 0.1 | −5.5 (forams, Pogge von Strandmann, 2008) | +0.92 (Sedimentary composite, Li et al., 2010) |
| 25Mg | 10.003 | ||||||
| 26Mg | 11.005 | ||||||
| Ca | 40Ca | 96.941 | TIMS + 42Ca-48Ca | SRM 915a (NIST) (Halicz et al., 1999) | 0.1 | −2.30 (sugar maple roots, Page et al., 2008) | +2.77 (exchangeable soil fraction, Wiegand et al., 2005) |
| 43Ca-48Ca or 42Ca-43Ca | Seawater (Zhu and MacDougall, 1998) | ||||||
| Double spike | Bulk Silicate Earth (DePaolo, 2004) | ||||||
| 42Ca | 0.647 | ||||||
| 43Ca | 0.135 | ||||||
| 44Ca | 2.086 | MC-ICP-MS | |||||
| 46Ca | 0.004 | ||||||
| 48Ca | 0.187 |
a External reproducibilities correspond to 2 × standard deviation obtained for pure solution reference materials.
b The delta values given in the table correspond to δ26MgDSM3, δ44/40CaSRM915a, δ11B and δ7LiL-SVEC. Extraterrestrial samples are not considered here.
c This uncertainty corresponds to MC-ICP-MS measurements.
2.1 Lithium isotope measurement
The first precise Li isotope measurements were performed in the late 1980s by thermal ionization mass spectrometry (TIMS) at the microgram level (Chan, 1987; Xiao and Beary, 1989) following the tetraborate method for Li ionization. Later, with the development of the phosphate method that achieves similar precision but requires much smaller quantities of Li, analyses were performed by TIMS at the sub-microgram level (James and Palmer, 2000; Moriguti and Nakamura, 1998; You and Chan, 1996). TIMS analytical precision (from +0.7 to +1.5‰ at 2σ) is satisfactory with respect to the natural magnitude of δ7Li values (from −15 to +45‰) but requires high levels of Li (Moriguti and Nakamura, 1998). Inductively coupled plasma mass spectrometry (ICP-MS) techniques are a good alternative to TIMS analyses. Over the past 10 years, measurements of Li isotopes were achieved by Quad ICP-MS at the relative precision of 1–2.0‰ (2σ) (Grégoire et al., 1996; Kosler et al., 2001; Misra and Froelich, 2012; Vigier et al., 2008) but may require much smaller amounts of Li (5–10 ng). It has also been shown that rapid and more precise measurements of Li isotopes (0.5–1.0‰ at 2σ) can be achieved by multicollector-ICP-MS for typical quantity of 10 ng Li (Bryant et al., 2003; Millot et al., 2004; Nishio and Nakai, 2002; Tomascak et al., 1999).
Lithium isotope compositions are presented as permil deviation of the measured 7Li/6Li ratio from that of the L-SVEC standard: δ7Li (‰) = [(7Li/6Li)sample/(7Li/6Li)L-SVEC − 1] × 103. L-SVEC standard (Flesch et al., 1973) is a pure lithium carbonate (NIST, RM 8545). IRMM-016 lithium carbonate is also available from the Institute of Reference Materials and Measurements (IRMM, Belgium) and within analytical uncertainty, IRMM-016 has isotope abundances identical to that of L-SVEC (Grégoire et al., 1996; Lamberty et al., 1987; Millot et al., 2004; Qi et al., 1997). Seawater Li isotope composition is very different from that of the L-SVEC standard (δ7Li = +31‰) and has been frequently used as an external standard to validate analytical methods (see for example Millot et al., 2004 and Tomascak, 2004 for a compilation). A chemical purification of Li is required for isotope analyses. This step is performed by ion chromatography, using a cationic resin and diluted HCl as the eluent. A suitable measurement of Li isotopes requires 100% Li recovery. This chemical purification step is, therefore, frequently calibrated and tested by repeated analysis of reference materials and/or of the L-SVEC standard enriched with various cations.
2.2 Boron isotope measurement
Boron isotope analyses show a long history of method developments. The principal issue when analyzing B isotopes comes from its large mass discrimination in the mass spectrometer, which cannot be corrected during the run because of the only two stable isotopes (Table 1). B isotope analyses started in the late 1940s with gas mass spectrometry (BF3), which was in particular developed to separate 10B from natural boron for the need of nuclear facilities, due to its high capacity to capture neutrons (Inghram, 1946). This technique however was subject to important memory effects in the mass spectrometer making it rather impractical for precise measurements of natural materials (Bentley, 1960) and was rapidly replaced by positive thermal ionization mass spectrometry (P-TIMS) of Na2BO2+ (McMullen et al., 1961). Despite an important in-run mass discrimination leading to large analytical errors (4‰, ±2σ), this latter technique was applied with a relative success and furnished all data in boron isotopic geochemistry until its improvement in the mid-1980s. At this time, Na was replaced by Cs, with the result of increasing the mass of the analyzed complex and greatly reducing the instrumental mass discrimination (Spivack and Edmond, 1986). After some later refinements (Lemarchand et al., 2002a; Nakamura et al., 1992), this technique is still recognized as a robust and accurate method for analyzing B isotopes in almost all types of geological materials and waters (0.4‰, ±2σ) with a sample size in the order of 250 ng (Gonfiantini et al., 2003). In parallel, the exceptionally high ionization yield of the ion BO2− was exploited by negative thermal ionization mass spectrometry (N-TIMS) and permitted B isotopic determination at the ng size sample (Heumann, 1982). However, this technique also suffers from important in-run mass discrimination and potential isobaric interference at mass 42 (10BO2) that can be bypassed only by reproducible analytical setup (Foster et al., 2006; Shen and You, 2003). Today, N-TIMS is essentially used for analyzing B isotopes in carbonate samples with perspective of seawater paleo-pH reconstruction (Hönisch and Hemming, 2005; Kasemann et al., 2005) but has also been used in the 1990s to analyse dissolved B (Eisenhut et al., 1996; Vengosh and Hendry, 2001; Williams et al., 2001a). In situ analyses of B isotopes can be performed by secondary ion mass spectrometry (SIMS) for measurements of carbonates and clay mineral transformations (Muttik et al., 2011; Rollion-Bard and Erez, 2010; Rollion-Bard et al., 2011a, 2011b; Williams et al., 2001a, 2001b). Finally, the recent emergence of MC-ICP-MS has changed the way B isotopes are analyzed in a variety of materials and now provide new standards of analytical performances. This technique requires lower sample size than P-TIMS (in the order of tens of ng) is fast (10 to 20 analyses per day) and provides good quality data (0.2‰, ±2σ) (Guerrot et al., 2011; Louvat et al., 2011; Pearson et al., 2009).
B isotopic compositions are expressed as the permil deviation from a standard value: δ11B (‰) = [(11B/10B)sample/(11B/10B)SRM951 − 1] × 103. The standard material SRM 951 is a boric acid provided by the National Institute of Standards and Technology (NIST) with a certified value 11B/10B = 4.04362 ± 0.00137 (Catanzaro et al., 1970). Prior to any B isotope determination, a chemical purification is required to simplify the solution chemical matrix (MC-ICP-MS) and to avoid any trace of alkaline element (P-TIMS). In all cases, a high level of B purification is achieved using the B-specific resin Amberlite IRA 743 (Lemarchand et al., 2002a). For silicate sample digestion, the use of HF is precluded because of the formation of volatile BF3. An alkaline fusion using K2CO3 is performed instead (Cividini et al., 2010; Lemarchand et al., 2012). Water samples can be loaded directly or with a very simplified purification onto filaments and run by the N-TIMS method (Vengosh et al., 1989).
2.3 Magnesium isotope measurement
The development of precise measurements of Mg isotopes is relatively new because it is closely linked to the recent advances in mass spectrometry. The first measurements of Mg isotope compositions of terrestrial materials were performed on various types of rocks and seawater, by TIMS (Catanzaro and Murphy, 1966; Daughtry et al., 1962; Shima, 1964). These first studies pointed to the lack of significant variations of Mg isotope composition on Earth due to limitations linked to the analytical uncertainties (∼0.1 to 0.5%). Recent advances in new generation mass spectrometers such as MC-ICP-MS have allowed 26Mg/24Mg ratio measurements with a precision of ≈ 0.10‰ per amu (at the 2σ level) (Bolou-Bi et al., 2009; Chang et al., 2003; Galy et al., 2001), significantly lower than the observed range on Earth (∼6‰). However Mg isotopes cannot be measured by double spiking because there are only three isotopes. Thus while measurements may be precise, their accuracy is difficult to assess, unless using a standard addition method (Tipper et al., 2008).
Isotopic compositions are currently reported as δ26Mg = [26Mg/24Mg)/(26Mg/24Mg)DSM3 − 1] × 103, where DSM3 (Dead Sea Magnesium) is the reference material developed and provided in solution by the Department of Earth Sciences, University of Cambridge (Galy et al., 2003). New reference materials were recently proposed: organic-rich samples like plants (BCR279, BCR 482, BCR 381), and granitic type rocks (GA, DRN) (Bolou-Bi et al., 2009). Previous studies have underlined the requirement for a preliminary Mg purification step in order to avoid matrix effects during high precision isotope determination by MC-ICP-MS (Galy et al., 2001). It is also necessary to completely recover the sample Mg because significant mass fractionation may occur during separation (Chang et al., 2003). Typically, separation of Mg from samples is performed using anion and cation exchange resins. The various published technical studies present Mg chemical separation procedures performed for specific samples: Chang et al. (2003) for seawater and carbonates, Black et al. (2006) for chlorophyll-a extract from cyanobacteria and Teng et al. (2007) mainly for basalts. Other studies use a modified version of the technique of Chang et al. (2003) for analyzing geological and extraterrestrial samples (Bolou-Bi et al., 2009; Tipper et al., 2006a, 2006b; Young and Galy, 2004). The reference materials used in order to validate these chemical separation techniques comprise granite-type rocks (GA and DRN), basic igneous rocks (basalt: BIR-1, BCR-1, BCR-2, BE-N; dunite: DTS-1), carbonates (Cal-S, JDo-1, JCp-1), solutions (seawater and river water or Mg reference materials doped with various elements) and plants (BCR 279, BCR 482) (Bizzarro et al., 2005; Black et al., 2006; Bolou-Bi et al., 2009; Brenot et al., 2008; Chang et al., 2003; Teng et al., 2007; Wombacher et al., 2009).
2.4 Calcium isotope measurement
The first precise Ca isotope measurements where performed in the late 1970s by TIMS at the microgram level using a 43Ca-48Ca double spike tracer and an exponential law to correct for instrumental mass discrimination (Russell and Papanastassiou, 1978). Several purification protocols using different resins (AG 50W-X8, AG50W-X12, AGMP50, MCI Gel- CK08P), eluents (HCl, HNO3 or HBr) and number of chromatographical steps have been employed (Amini et al., 2009; Chang et al., 2004; Fantle and DePaolo, 2007; Kreissig and Elliott, 2005; Russell and Papanastassiou, 1978; Soudry et al., 2006). A high selectivity automated ionic chromatography separation protocol has also been developed (Schmitt et al., 2009). Loading techniques using single, double or triple filaments, Re, Ta or W ribbons, various activating techniques (H3PO4, Ta2O5, oxidation), amounts of purified Ca (300 ng to 10 μg) and sequences of measurements have also been developed during past decade (Gussone et al., 2007; Hindshaw et al., 2011; Holmden, 2005; Huang et al., 2010; Schmitt et al., 2009; Simon and DePaolo, 2010; Stille et al., 2012). An alternative to Ca isotope measurements by TIMS is the use of MC-ICP-MS instruments. However, the latter technique has only scarcely been used for Ca isotope measurements since it causes isobaric interferences generally preventing the measurement of the major 40Ca isotope (Halicz et al., 1999; Tipper et al., 2006b, 2008, 2010a). Consequently by using this technique, which has been validated using the standard addition technique (Halicz et al., 1999), calcium isotope values are reported as δ44/42Ca. In doing so, 40Ca radiogenic enrichments are avoided and only mass-dependent processes are recorded. Best external reproducibilities are presently achieved using modern TIMS instruments (0.07 to 0.16‰ at 2σ) (Cobert et al., 2011a; Ewing et al., 2008; Farkas et al., 2007; Heuser and Eisenhauer, 2010; Jacobson and Holmden, 2008).
Presently, there exist no international standard for Ca isotopic measurements. Several standards or natural samples (seawater, CaF2 purified salt, SRM915a and SRM915b carbonates from NIST, silicate rocks) have been measured by several laboratories, allowing comparison of the presently published Ca isotopic values (Halicz et al., 1999; Hippler et al., 2003; Russell and Papanastassiou, 1978; Schmitt et al., 2001; Simon and DePaolo, 2010; Wombacher et al., 2009; Zhu and MacDougall, 1998). In this article, calcium isotopes are presented as deviations in parts per thousand of the measured 44Ca/40Ca ratio from that of the SRM 915a pure carbonate standard from NIST as follows:
δ44/40Ca (‰) = [(44Ca/40Ca)sample/(44Ca/40Ca)SRM915a − 1] × 103
3 Mechanisms governing isotope fractionations at the soil-water-plant interface
3.1 Field studies
Soils are complex biogeochemical systems and are often designed as the “critical zone” at the interface of geosphere, hydrosphere, biosphere and atmosphere. Isotopic fractionations of Li, B, Mg and Ca due to secondary biotic and abiotic processes are expected. Plant growth as well as mineral (trans)formation have been identified to cause isotopic fractionation, as summarized in Fig. 3 for Mg and Ca isotopes. So far, only few studies have focused on Li, B, Mg and Ca isotopic fractionations during soil forming reactions (clay (trans)formations, Fe-oxides, calcium carbonates…).
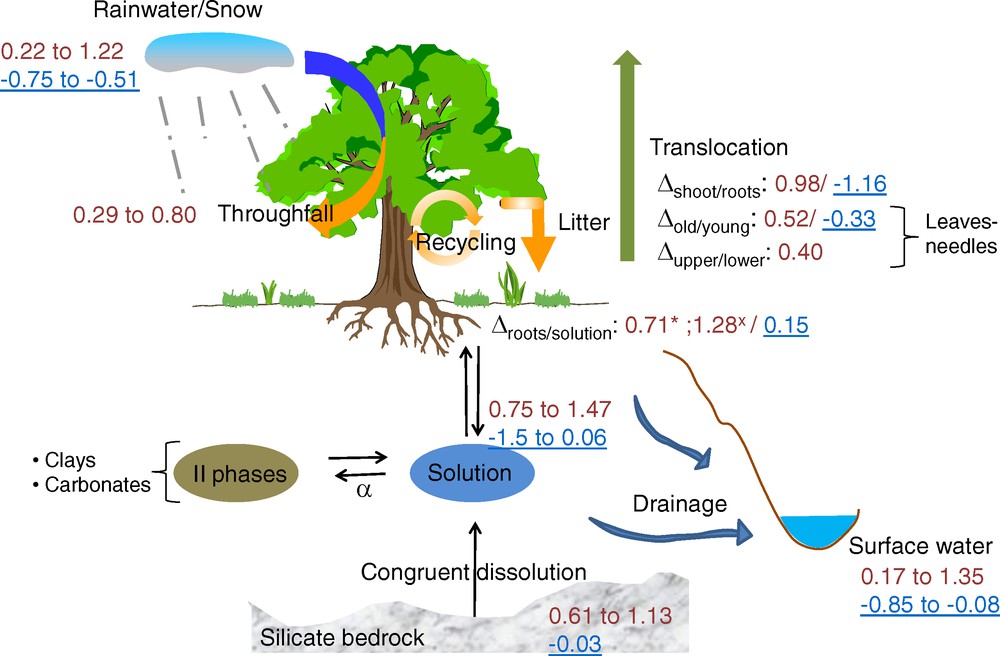
Ca and Mg isotopic compositions in the different reservoirs from the soil-water-plant system. In red: Ca isotope values; in blue underlined: Mg isotope values. *Jack Pine and Spruce; xBeech, Trembling Aspen and Black Spruce. References: for Ca isotopes: Schmitt et al. (2003); Schmitt and Stille (2005); Tipper et al. (2006b); Cenki-Tok et al. (2009); Holmden and Bélanger (2010); Hindshaw et al. (2011); Farkas et al. (2011). For Mg isotopes: Tipper et al. (2010b); Bolou-Bi et al. (2012).
Compositions isotopiques en Ca et en Mg dans différents réservoirs du système eau-sol-plante. En rouge : compositions isotopiques du Ca, en bleu souligné : compositions isotopiques du Mg. *Pin et épicéas ; xhêtre, peuplier et épinette noire. Références : pour les isotopes du Ca : Schmitt et al. (2003) ; Schmitt et Stille (2005) ; Tipper et al. (2006b) ; Cenki-Tok et al. (2009) ; Holmden et Bélanger (2010) ; Hindshaw et al. (2011) ; Farkas et al. (2011). Pour les isotopes du Mg : Tipper et al. (2010b) ; Bolou-Bi et al. (2012).
3.1.1 Plant-induced isotope fractionations
3.1.1.1 Li and B
No plant-induced Li isotopic fractionation has been observed so far (Lemarchand et al., 2010). The non-influence of litter degradation on soil Li-isotope signatures is related to the low Li concentration in vegetation, which is a thousand times lower than in soil, although few concentrations data have been published yet.
Despite the fact that the physiological role of B in plants is rather well documented (see review by Lehto et al., 2010), very little is known about the B isotope fractionation during root absorption, and the few available studies lead to contradictory conclusions (Vanderpool and Johnson, 1992; Wieser et al., 2001). One of the reasons may relate to B bio-availability in soil solutions that affects the way it is absorbed by roots: either passively (channel mediated) or actively (complexation with polyols). Nevertheless, all these studies tend to indicate that the primary factor controlling the B isotope abundance in plants is the influence of local sources (minerals, soils, soil solutions) rather than intrinsic biological effects. Comparison of beech leaves and spruce needles sampled in the Strengbach watershed show similar δ11B values very close to those measured in the soil solutions (Cividini et al., 2010). Moreover, these authors also observed that B concentrations decrease by 80% between soil solutions sampled at 5 and 30 cm depth of a forest soil during the period of plant growth with very little isotopic shift. The absence of a large isotopic shift in these solutions and the strong concentration decrease indicate that the B absorption by plant roots does not cause important isotopic fractionations, at least in the Strengbach watershed.
3.1.1.2 Mg and Ca
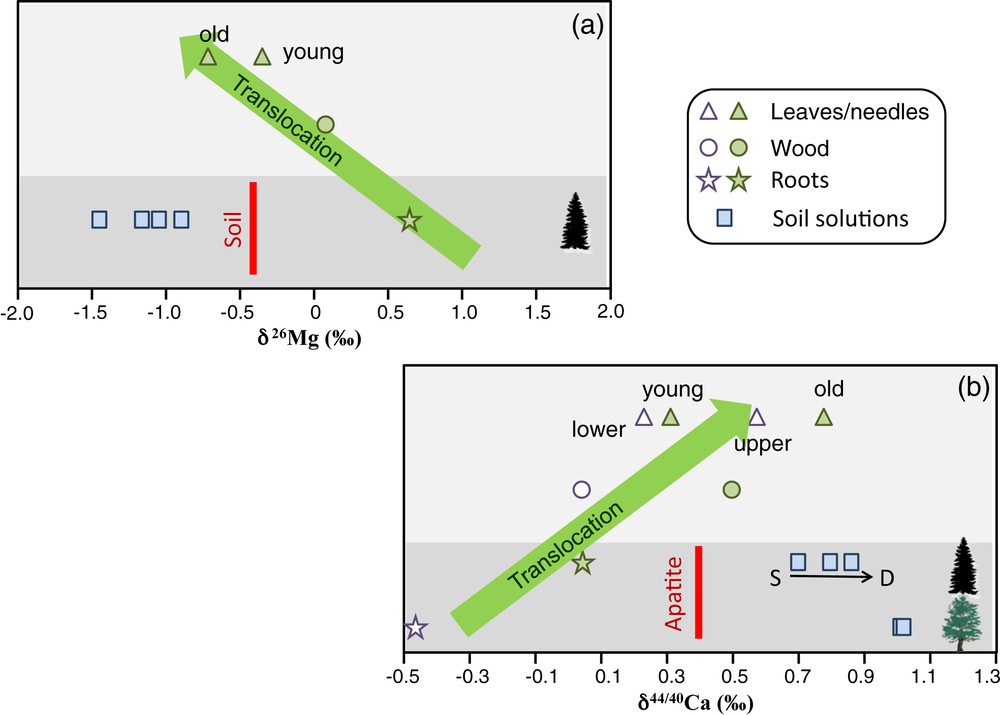
Few is also known about the influence of vegetation on Mg isotope fractionations in field studies. A study has been performed in a small-forested ecosystem developed on sandstones, extremely poor in Mg-bearing minerals (Bolou-Bi et al., 2012). The bulk δ26Mg of trees and grass (−0.32‰ and −0.41‰ respectively) were found to be higher than the average δ26Mg values of the soil exchangeable fraction (−0.92‰ to −0.42‰) and of rainwater (−0.65‰). This systematically heavy signature of plants is mainly carried by roots; the above ground parts are slightly lighter (Fig. 4a). In a Norway spruce, an inverse correlation between needle age and δ26Mg has also been observed. It is explained by internal Mg transfer favouring plant growth on nutrient-poor soils. Soil solution δ26Mg shifts seasonally, suggesting a significant role of vegetation growth on soil water δ26Mg. Similarly, on a soil developed on an uplifted marine terrace from Santa Cruz (California), δ26Mg values of grass samples are greater than those of rain and of the shallow pore-waters (Δ26Mggrass-rain/shallow pore-waters = −0.25‰) (Tipper et al., 2010b).
Dispersion of Ca isotopes (a) and Mg isotopes (b) between 2 mm-roots and soil solutions and between roots and shoots (Schmitt et al., 2003; Cenki-Tok et al., 2009; Bolou-Bi et al., 2012). Green-coloured symbols correspond to spruce trees, whereas white-coloured symbols represent beech trees.
Variabilité des isotopes du Ca (a) et du Mg (b) entre les racines de 2 mm et les solutions de sol et entre parties racinaires et aériennes (Schmitt et al., 2003 ; Cenki-Tok et al., 2009 ; Bolou-Bi et al., 2012). Les symboles colorés en vert correspondent au hêtre alors que les symboles en blanc correspondent à l’épicéa.
About ten articles dealing with Ca isotopes in soils of small-scale watersheds have been published up to now (Cenki-Tok et al., 2009; Farkas et al., 2011; Hindshaw et al., 2011, 2012; Holmden and Bélanger, 2010; Page et al., 2008; Perakis et al., 2006; Schmitt and Stille, 2005; Schmitt et al., 2003; Wiegand et al., 2005). Although data are sometimes difficult to compare with each other (different soil leaching procedures, different vegetation organs, only scarce number of available data…), it appears that vegetation is generally the most 40Ca enriched compartment compared to the surrounding rocks and soils (including soil solutions, soil leachates and bulk soil samples) (Fig. 5). Schmitt et al. (2003) were the first who applied Ca isotopes to a small scale forested granite watershed in the Vosges mountains (Strengbach watershed, France). By analyzing several compartments of this watershed, they observed that the soil solution (δ44/40Ca = 1.77 ± 0.19‰) is enriched in the heavy 44Ca isotope compared to apatite (δ44/40Ca = 0.40 ± 0.10‰) or rainwater (δ44/40Ca = 0.57 ± 0.13 and 1.01 ± 0.15‰) which are supposed to be the two main sources of calcium in this watershed. As a result, the authors concluded that the Ca isotopic signature of soil solutions cannot be explained by a simple weathering flux, which was confirmed by more recent studies (Cobert et al., 2011a; Hindshaw et al., 2011; Ryu et al., 2011). However, Schmitt et al. (2003) suggested that the δ44/40Ca of the soil solutions is the result of biological activity in the surficial soil horizon. They indeed measured two biological samples from the same forest plot, one beech branch (δ44/40Ca = −0.57 ± 0.23‰) and beech leaves (δ44/40Ca = 0.25 ± 0.20‰) and observed that they are the most enriched in the light 40Ca isotope compared to other compartments from the watershed; this observation was in agreement with two previous studies (Platzner and Degani, 1990; Skulan and DePaolo, 1999) (Fig. 5). Later on, several studies confirmed the 40Ca enrichment in vegetation which certainly occurred during the Ca uptake by lateral roots (Cenki-Tok et al., 2009; Holmden and Bélanger, 2010) (Fig. 4b). Thus, similarly to Mg isotopes, Ca isotopes show fractionation between roots and shoots, but the sense of this fractionation is opposite (Fig. 4a–b). The persistence of a heavy soil solution pool and a complementary light biological pool is consistent with a forest that is growing and developing and which is not at steady state. A recent study also indicates that Ca recycling by plants in the Strengbach watershed is not at steady state (Viville et al., 2012). By comparing literature data that refer to similar samples, it can be inferred that Δaverage soil solution/fine roots is equal to 0.71 ± 0.05‰ (N = 3; 2σmean) for Jack Pine and spruces and to 1.28 ± 0.10‰ (N = 6; 2σmean) for beech, trembling aspen and black spruces (Table 2) (Cenki-Tok et al., 2009; Holmden and Bélanger, 2010). This suggests that the intensity of fractionation at the nutrient solution/lateral root interface is species dependent and/or sensitive to the local soil conditions. Wiegand et al. (2005) proposed that the preferential 40Ca uptake by roots through an electrochemical gradient and Ca channels follows a kinetic fractionation. A second fractionation occurs during the Ca translocation from roots to shoots that enriches upper organs in 44Ca: Δroots/shoot = 0.98 ± 0.09‰ (N = 9; 2σmean) (Table 2) (Cenki-Tok et al., 2009; Holmden and Bélanger, 2010). Again, Wiegand et al. (2005) explain the 44Ca enrichment in upper organs by “ion exchange reactions within cell walls of the conducting xylem sapwood”. These explanations were partially confirmed by experiments (Section 3.2).
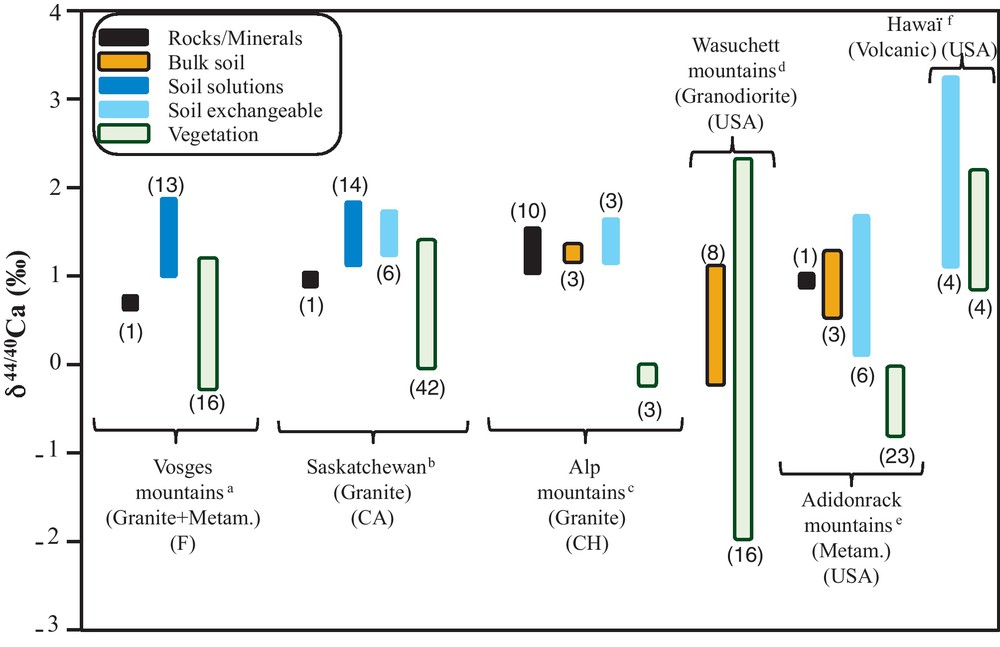
Review of Ca isotopic variations in soils, surface waters and vegetation.
Synthèse des variations isotopiques du Ca dans les sols, les eaux de surface et la végétation. aSchmitt et al. (2003) ; bHolmden and Bélanger (2010) ; cHindshaw et al. (2011) ; dFarkas et al. (2011) ; ePage et al. (2008) ; fWiegand et al. (2005).
Fractionnement isotopique en Ca (δ44/40Ca) (en ‰) entre les racines fines et la solution moyenne de sol pour différentes espèces végétales.
| Watershed | Bedrock | Soil plot | Soil solutions | Average | Tree species | 2 mm roots | Δaverage soil solution/fine rootsc | Reference |
| Strengbacha | Grantitic and metamorphic (Paleozoïc) | BP | 1.00; 0.97 | 0.99 | European Beech (Fagus sylvatica) | −0.48 | 1.47 | Cenki-Tok et al. (2009) |
| SP | 0.69; 0.76; 0.86 | 0.77 | Norway Spruce (Picea Abies) | 0.04 | 0.73 | Cenki-Tok et al. (2009) | ||
| Saskatchewanb | Precambrian shield | Plot 1.1 | 0.86; 1.09 | 0.98 | Jack Pine (Pinus banksiana) | 0.31 | 0.67 | Holmden and Bélanger (2010) |
| Trembling Aspen (Populus tremuloides) | −0.30 | 1.28 | Holmden and Bélanger (2010) | |||||
| Plot 1.2 | 0.83; 1.19 | 1.01 | Trembling Aspen (Populus tremuloides) | −0.15 | 1.16 | Holmden and Bélanger (2010) | ||
| Black Spruce (Picea mariana) | −0.23 | 1.24 | Holmden and Bélanger (2010) | |||||
| Plot 2.1 | 0.85; 1.00 | 0.93 | Black Spruce (Picea mariana) | −0.23 | 1.16 | Holmden and Bélanger (2010) | ||
| Plot 2.2 | 1.05; 1.10 | 1.08 | Jack Pine (Pinus banksiana) | 0.34 | 0.74 | Holmden and Bélanger (2010) | ||
| Black Spruce (Picea mariana) | −0.32 | 1.4 | Holmden and Bélanger (2010) |
After leaves and needles have fallen they become slowly mineralized. Nutrient elements may leave the mineralized substratum and migrate into the soil solutions and become bioavailable again (Likens et al., 1998; McLaughlin and Wimmer, 1999; Taiz and Zeiger, 2010). This process causes 40Ca enrichments in the upper soil compartments (Cenki-Tok et al., 2009; Holmden and Bélanger, 2010; Page et al., 2008). This recycling component needs to be precisely quantified for biogeochemical modeling at the watershed scale. The recycling flux might be especially an important source of Ca for the growth of forests in base-poor and/or acid-rain affected ecosystems. Holmden and Bélanger (2010) showed that in a Canadian forested watershed up to 80% of Ca in trees originates from recycling.
3.1.2 Role of mineral (trans)formation on soil isotope signatures
3.1.2.1 Li and B
Bulk soil signatures of B and Li isotopes seem both to be mainly controlled by mineral (trans)formations and in particular by the ratio between the rate of mineral dissolution and precipitation. These two elements show similar behavior during water-rock interactions. Li isotopes are significantly fractionated during their incorporation into secondary clay minerals. In their study of Hawaiian basalt-derived soils, Huh et al. (2004) reported a large range of Li isotopic compositions for soils (δ7Li varies between −0.4‰ and +13.7‰), compared to the fresh lava they developed on (δ7Li = 4–5‰). In contrast, Pistiner and Henderson (2003) and Kisakürek et al. (2004) found small variations and light isotopic signatures of −4 and +3‰, respectively, in other basaltic soils from Hawaii and from the Deccan traps. Both studies argue for a preferential incorporation of 6Li in secondary clay minerals, but these authors also discussed the possible input of aeolian dusts (having a marine origin) that can also modify the Li isotopic signature at the soil surface. A work on saprolite sequences developed on igneous rocks (granite and diabase) in South Carolina (USA), demonstrated that the soils possess consistently a much lighter Li isotopic composition than the igneous rocks from which they formed (Rudnick et al., 2004) (δ7Li varies between −20‰ and +2‰). More recently, Lemarchand et al. (2010) studied particles and solutions (pore waters) in a soil developed on granite bedrock in the Strengbach watershed (Vosges mountains, France). While the Li isotopic composition of the soils varied only slightly around the isotopic composition of the bedrock (0‰), a significant variation is observed in pore waters; deeper pore waters showing heavy isotope compositions (δ7Li varies between +28 and +33‰) and shallower ones light isotope compositions (δ7Li varies between −17‰ and −5‰) (Fig. 6a). A model of reactive transport, where Li is released by dissolution of soil minerals and then incorporated into secondary phases, has been developed and can explain most of the observed data.

Li isotopic compositions (a) and B isotopic compositions (b) measured in the Strengbach watershed. Data originate from Lemarchand et al. (2010) for Li isotopes and from Cividini et al. (2010) and Lemarchand et al. (2012) for B isotopes. Spruce and beech tree symbols refer to the nature of the vegetation covering each soil profile. The bedrock sample corresponds to the rock outcropping in the middle of the Strengbach watershed. Inversed triangles illustrate the spring waters collected just beneath the corresponding soil profile. B fluxes are calculated from measured concentration and water fluxes.
Compositions isotopiques du Li (a) et du B (b), mesurées dans le bassin versant du Strengbach. Les données proviennent de Lemarchand et al. (2010) pour les isotopes du Li et de Cividini et al. (2010) et de Lemarchand et al. (2012) pour les isotopes du B. Les symboles des épicéas et des hêtres réfèrent à la nature de la végétation couvrant chaque profil de sol. L’échantillon de roche mère correspond à la roche affleurant dans le milieu du bassin versant du Strengbach. Les triangles inversés correspondent aux eaux de source collectées près des profils de sols associés. Les flux de B sont calculés à partir des concentrations mesurées et des flux d’eau.
For their part, B isotopes seem rather to be controlled by amorphous and highly reactive solids in shallow soil horizons, and by clay mineral formation in deeper horizons. First attempts to understand the B isotope distribution in soil were made on a profile developed on the granite Guayana Shield (Spivack et al., 1987); this study showed a very tiny isotopic offset from the bedrock along the 1 m depth profile that was attributed to differences between the boron composition in the labile and refractory minerals. It was also the first time where the absence of isotopic fractionation during mineral dissolution was suggested. Later, a study on sediments and soil solutions from a profile sampled in the Himalaya identified B isotopes as a potential proxy for assessing the chemical budget of soil-forming reactions (Rose et al., 2000). Recently, B isotopes have been monitored for 2 years (between Sept. 2004 and Jan. 2007) in two soil profiles from the Strengbach watershed (Cividini et al., 2010) (Fig. 6b). Seasonal oscillations of δ11B have been observed in soil solutions at 10 cm depth. Given that 10B is preferentially removed from solution to incorporate secondary solids, these oscillations are interpreted as a dynamic process of precipitation (increasing dissolved δ11B during period of vegetation activity, from May to September) and dissolution (release of relative light δ11B in winter) of low-crystallized mineral phases like Fe-oxides. Deeper in the soil, δ11B values reflect the B mass balance between dissolution and precipitation of solids: in the brown acidic soil sampled in the Strengbach catchment (dominated by hydrolysis reactions) δ11B values decrease with increasing contribution from mineral dissolution (low δ11B values) whereas in a podzol from the same site (dominated by complex-hydrolyses reactions) δ11B values increase in line with the preferential incorporation of 10B in neoformed mineral phases. In parallel, bulk soil particles and separated fraction sizes yield additional informations on soil-forming processes (Lemarchand et al., 2012). The major result is that B isotope in soil secondary minerals, especially the clay-size fraction, is mainly controlled by pedogenesis and can be used to investigate soil forming reactions.
3.1.2.2 Mg and Ca
Apart from plant-induced fractionations, some studies suggest that Mg and Ca isotopes are also affected by mineral (trans)formations. Indeed, systematic enrichments in heavy Mg isotopes are observed in alteration products relative to fresh rock or continental crust (Bolou-Bi et al., 2012; Brenot et al., 2008; Tipper et al., 2006a, 2006b, 2008; Teng et al., 2010). However, the mechanisms responsible for these heavy isotopic signatures are not fully understood yet. Tipper et al. (2010b) in their study of the Santa Cruz soil developed on an uplifted terrace show that the Mg profile matches the smectite abundance profile; they interpret the Mg enrichment of pore fluids as a preferential 24Mg leaching from smectite. In contrast, between the C horizon and the upper eluvial (E) horizon of a soil developed on sandstones in the Vosges mountains, δ26Mg values of soils remain close to the bedrock value (0.0 ± 0.14‰), while more than 70% of Mg is lost (due to illite dissolution). Future experimental studies may help to interpret and model these data. In contrast to Mg, enrichments in the light 40Ca isotopes in the solid might occur during precipitation of secondary minerals (travertines and calcium sulphate minerals) compared to the solution it precipitated from, as reported for soils rich in silicate minerals and with negligible vegetation cover (Ewing et al., 2008; Tipper et al., 2006b).
3.2 Laboratory biotic and abiotic experiments
Laboratory experiments help to characterize the individual parameters (temperature, exchange processes, precipitation, dissolution, adsorption, desorption…) that control isotopic fractionations. In field-based studies, it is particularly difficult to determine which process is controlling the measured fractionation since several parameters act together, and sometimes can cancel each other. Several types of parameters have been experimentally investigated, depending on the considered element: dissolution (Li, B, Mg and Ca isotopes), adsorption (Li and B isotopes), clay mineral formation (Li and B isotopes) and biological processes (Mg and Ca isotopes).
3.2.1 Dissolution
3.2.1.1 Li and B
It has been shown that partial dissolution of basalts does not result in fractionation of Li isotopes whereas dissolution of granitic rocks may be responsible for some isotope bias (Pistiner and Henderson, 2003). More recently, Wimpenny et al. (2010) and Verney-Carron et al. (2011) observed in their dissolution experiments of basaltic glass only small Li isotope fractionations. Verney-Carron et al. (2011) have tested the influence of ion-exchange and diffusion processes on Li isotope fractionations at the solid-solution interface. Their experiments indicate that diffusion is important in systems where water-rock interactions occur at moderate temperatures (50–100 °C). In all cases, the leaching process was never associated with the preferential release of the heavy isotope (7Li).
Recently, experiments on biotite, used as a test-mineral for phyllosilicates, were conducted in order to test the fractionation of B isotopes during weathering reactions. These experiments were specially conducted to test whether B isotopes in weathered biotite and the corresponding solution are sensitive to the nature of altering agents typically found in soils (strong and organic acids as well as siderophores) (Voinot et al., submitted). It has been shown that B is released from biotite at pH 3 at a much faster rate than Si with no or tiny isotopic fractionation. At pH 4.5, however, the nature of the altering agent appears to largely influence the fractionation of B isotopes. Citric acid caused no isotopic fractionation, whereas protons or siderophores favored the release of 11B. The authors proposed that the presence of organic acids leads to the dissolution of the biotite mineral whereas protons and especially siderophores promote the release of B from the 11B-rich interlayer sites. The main conclusion from this study is that the mobility of B isotopes in weathered biotite appears to be highly dependent on the chemical nature of the altering agent.
3.2.1.2 Mg and Ca
Mg and Ca isotope fractionations in minerals/rocks were tested during experimental weathering of a Precambrian Boulder Creek granodiorite in a plug flow reactor for 5794 h at pH 1 and T = 25 °C. Concerning Mg, the range of leachate solutions δ26Mg (from −1.59 to −0.27‰) encompasses the value of the bulk granite (−0.73‰), and essentially reflects the isotope compositions of the various mineral phases subsequently dissolved along the course of the experiment, with no significant associated fractionation of the Mg isotopes (Ryu et al., 2011). In contrast, basalt glass and olivine (forsterite) dissolution experiments performed in mixed through-flow reactors at low pH (pH = 2 and 3) resulted in enrichment of the solution in light Mg isotopes, potentially due to kinetic effects during the leaching process (Wimpenny et al., 2010).
Concerning Ca in the Boulder Crek granodiorite, Ryu et al. (2011) demonstrated that, δ44/42Ca reflects mass-dependent isotope fractionation during igneous differentiation and crystallization in accord with previous studies (Amini et al., 2009; Huang et al., 2010). In contrast congruent low-temperature dissolution of the granodiorite minerals does not fractionate Ca isotopes (Ryu et al., 2011). Consequently, Mg and Ca isotopes could be used to trace preferential mineral dissolution. Similarly, experimental congruent dissolution of apatite minerals with two different acids (organic and mineral) and pHs (2 and 3.5) did not cause any observable Ca isotope fractionation in the solution through time (Cobert et al., 2011b).
3.2.2 Adsorption
Adsorption onto natural or synthetic mineral surfaces at low temperature can also be a mechanism of Li and B isotopic fractionation in the hydrosphere (Lemarchand et al., 2005, 2007; Millot and Girard, 2007; Palmer et al., 1987; Pistiner and Henderson, 2003; Taylor and Urey, 1938). For instance, sorption of Li from aqueous solutions by mineral phases at the temperature of the Earth's surface has been highlighted by Taylor and Urey (1938), as well as by Anderson et al. (1989). Li sorption experiments have shown that Li isotope fractionation occurs only when Li is incorporated into the structure of the solid (physical sorption) (Millot and Girard, 2007; Pistiner and Henderson, 2003). When Li is incorporated by stronger bonds (chemical sorption), an isotopic fractionation that is dependent on the chemical structure of the minerals is observable (Anghel et al., 2002). The most significant Li isotopic fractionation factor (Δsolution-solid from +14 to +25‰) has been measured for gibbsite. For Li sorption processes between solution and different solids (clay minerals such as kaolinite and vermiculite, and freshwater sediments), high Li isotopic fractionation factors (Δsolution-solid ∼ +22‰) have also been observed (Zhang et al., 1998). However, a recent study also highlights negligible fractionation associated with adsorption on smectite (Vigier et al., 2008). Voinot et al. (submitted) showed that boron adsorption onto biotite mineral surfaces is achieved through monodentate complexation of boric acid, which contrasts with results observed for other solid surfaces (Lemarchand et al., 2005, 2007). These aspects still need to be investigated in more detail.
No article has presently been published dealing with experimental identification of Mg and Ca isotopes during adsorption.
3.2.3 Clay mineral formation
Li and B isotopes are fractionated during clay formation at low and high temperatures (Fig. 7) (Chan et al., 1992, 1994, 2002; James et al., 1999, 2003; Lemarchand et al., 2005, 2007; Palmer et al., 1987; Seyfried et al., 1998; Williams and Hervig, 2002, 2005; Williams et al., 2001a, 2001b; Zhang et al., 1998). Li isotopic fractionation (Δsolution-clay) estimates range between 0 and +11‰ at high temperature (300–375 °C) (Chan et al., 1993; Seyfried et al., 1998; Williams and Hervig, 2005), and between 0‰ and +29‰ at low temperature (5–20 °C) (Chan et al., 1992; Pistiner and Henderson, 2003; Taylor and Urey, 1938; Zhang et al., 1998). More recently, tri-octahedral Mg-Li smectites (hectorites) were synthesized at temperatures ranging between 25 and 250 °C (Vigier et al., 2008). The Li isotope fractionation factors linked to the incorporation of Li into the octahedral sites, in substitution for Mg2+, were determined. Experimental Δsolution-clay correlates inversely with temperature, as theory predicts, and ranges between +1.6 ± 1.3‰ at 250 °C and +10.0 ± 1.3‰ at 90 °C, and then stays relatively constant down to 25 °C (Fig. 7). The relatively constant isotope fractionation below 90 °C was attributed to high concentrations of edge octahedral in low crystallinity smectites. It was also found that the fractionation factor depends on neither the solution composition nor the amount of Li incorporated into the clay at a given temperature. Similarly, an inverse correlation was found between Δsolution-clay and temperature for B isotopes during illitization of smectite (Williams et al., 2001a, 2001b; Williams and Hervig, 2002, 2005) (Fig. 7).
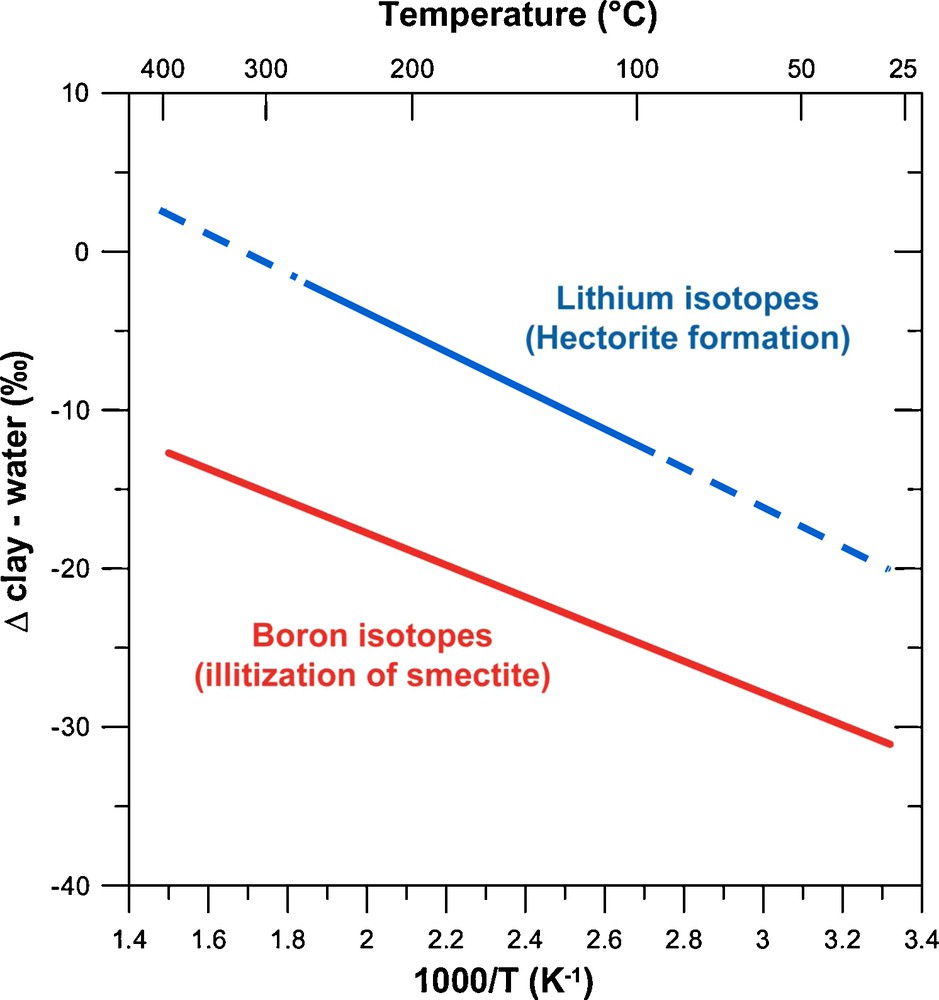
Temperature dependence of B and Li isotopic fractionation during clay mineral (trans)formation. Data from Vigier et al. (2008) and Williams et al. (2001a).
Dépendance avec la température des fractionnements isotopiques du B et du Li au cours de la (trans)formation des minéraux argileux. Les données proviennent de Vigier et al. (2008) et Williams et al. (2001a).
3.2.4 Biological processes
Higher plant growth experiments have been performed in order to identify biological processes that control Ca and Mg isotope fractionations. Hydroponic experiments show that plants are systematically enriched in heavy Mg isotopes, with Δ26Mgplant-solution ranging between +0.2 to +0.4‰ (Black et al., 2008; Bolou-Bi et al., 2010). Bulk clover and rye grass grown under the same conditions exhibit different δ26Mg (by 0.3‰). Adsorption experiments on rye grass roots show that passive Mg binding onto the organic exchange molecules is the main fractionating process that leads to heavy signatures in plants (Bolou-Bi et al., 2010). Mg translocation towards the upper parts of the plants can be associated with enrichments in light isotopes, in particular in the case of Mg deficiency in the source/soil. There is only a small fraction of leaf Mg that is incorporated into the chlorophyll molecule, and part of the remaining Mg is involved in the cell pH regulation or in the formation of organic compounds which are mobile and translocated to roots and younger leaves. If these organic compounds are isotopically heavy, their mobility can essentially explain the light signatures of leaves. The proportion of Mg involved in the formation of organics such as polyphosphates depends directly on the relative amount and availability of Mg and K in the soil. At high K/Mg ratio in soil solution (due to Mg deficiency), more Mg is involved in the formation and transfer of organic compounds in plants, which may explain the significantly lighter signatures of leaves under these conditions (Bolou-Bi et al., 2010).
Hydroponic bean growth experiments have also been performed with nutritive solutions at different Ca concentrations (5 and 60 ppm) and pHs (4 and 6) (Cobert et al., 2011b; Schmitt et al., submitted). The results show that three different fractionation steps occur during Ca uptake by plants (Fig. 8) (Cobert et al., 2011a; Schmitt et al., submitted). The first fractionation occurs when 40Ca is preferentially adsorbed on R-COO− groups of polygalacturonic acids (pectins) which are present on the outer surface of the cell walls of the lateral roots and which can be compared to cation exchange resins. An equilibrium fractionation has been calculated with Δbean-nutritive solution equal to −1.2‰. Then, Ca moves radially apparently without fractionation through the cortex tissues towards the root centre (stele) into the conducting xylem. There, 40Ca is preferentially retained by pectins of the cell wall whereas 44Ca is progressively enriched up the transpiration stream. The last fractionation occurs within reproductive organs that are systematically enriched in 40Ca compared to the other organs, maybe due to chromatographical displacement of Ca within the xylem wall. The fractionation amplitudes (Δnutrient solution-lateral roots: from +0.5 to +0.7‰; Δprimary root/stem-leaves: from −0.6 to +0.4‰) are dependent on the Ca concentration and pH of the nutritive solution. Cobert et al. (2011a) also showed that Ca-oxalates are enriched in the light 40Ca isotope compared to free-Ca in leaves. Further investigations are needed to constrain the impact of the oxalate Ca signature on Ca cycling in watersheds.

Within plant Ca isotopic fractionation (adapted from Cobert et al., 2011a; Schmitt et al., submitted). 1. Nutrient-solution/lateral root interface fractionation. 2. Within xylem sap fractionation. 3. Within reproduction organs fractionation. See text for more details.
Fractionnement isotopique du Ca au sein de la plante (adapté de Cobert et al., 2011a ; Schmitt et al., soumis). 1. Fractionnement à l’interface entre la solution nutritive et les racines latérales. 2. Fractionnement au sein du xylème. 3. Fractionnement au sein des organes reproducteurs. Voir texte pour davantage d’informations.
4 Mechanisms governing isotopic signatures at larger scales
Along with studies seeking to identify the mechanisms of fractionation in the water-soil-plant system, other studies have focused on evaluating the processes controlling the isotopic fractionation at either small monolithological watersheds or larger watersheds draining different lithologies. Indeed, isotopic compositions of river dissolved and suspended loads may integrate signatures from different lithologies, vegetation covers, and drainage systems. Depending on the isotope system and on the spatial and temporal scale of the study, the related information will not be the same.
4.1 Small monolithological watersheds
The study of small-scale monolithological watersheds provides the opportunity to trace isotopic evolution along both soil water and surface water pathway (integrating e.g. atmospheric depositions, leaf litter decomposition, soil waters, and the streamlet close to the sources and at the outlet of the watershed). The fractionation of the different isotope ratios is dependent on reactive transport during water/rock interactions (Li, B and Mg) and/or on seasons and discharge rates (Mg, Ca). The Li, B, Mg and Ca isotopic behavior in rainwater is also discussed in this section.
4.1.1 Reactive transport during water/rock interactions
When rainwater enters the hydrological system of the watershed, it interacts with the vegetation and soil minerals. In the case of the granitic Strengbach watershed, Li and B isotopes in soil solutions and spring water samples reflect water-mineral interactions (Cividini et al., 2010; Lemarchand et al., 2010). Examination of the spatial and temporal variation of spring water chemical composition demonstrates that the weathering regime and the balance between mineral dissolution and secondary phase formation control both the B and the Li isotopic signatures of these waters. This has also been illustrated for glacial (Wimpenny et al., 2010) and basaltic environments (Vigier et al., 2009). For example, the dissolved phase of the Icelandic rivers display heavy isotopic signatures, with δ7Li ranging between +10.1‰ and +23.8‰, while river sediments display a narrower and lower range of values (+3.1‰–+4.8‰) close to that of unweathered MORB (Vigier et al., 2009). High δ7Li values are associated with high K/Li, Na/Li and Mg/Li ratios, and characterize waters draining mainly old and weathered basalts. Rivers with low δ7Li are located in the younger parts of the island. Source-mixing alone between precipitation, Li-rich hydrothermal springs and basalt weathering cannot explain the entire range of δ7Li values. Instead, the Li isotope compositions of both waters and sediments can be explained by a steady-state erosion model where the formation of secondary minerals is associated with significant Li isotope fractionation.
Small stream and river waters draining silicate lithologies like granites, gneiss and sandstones display δ26Mg, which are generally lower than those of fresh bulk rocks or river sediments (Brenot et al., 2008; Bolou-Bi et al., 2012; Tipper et al., 2006a, 2008, 2012; Wimpenny et al., 2010). The main process explaining this bias between dissolved and solid phases is neoformation of clays that may be enriched in heavy 26Mg, as indicated by smectite (Tipper et al., 2006a, 2008) or bulk soil data (Brenot et al., 2008); it may also be caused by preferential 26Mg uptake by plants (Bolou-Bi et al., 2012), or incongruent dissolution (Wimpenny et al., 2010). Water-rock interactions also seem to control Ca isotopes at the watershed scale. In order to equilibrate mass-budget calculations at the Strengbach watershed scale two studies indeed suggested in addition to vegetation uptake and primary mineral weathering a supplementary 40Ca-enriched flux (Cenki-Tok et al., 2009; Stille et al., 2012). This flux could either result from dissolution of secondary clay minerals or Ca desorption (e.g. from the Ca colloidal phase). Similarly, Hindshaw et al. (2011) suggested from leaching experiments that preferential adsorption of 40Ca could occur on organic matter and/or clays at sites older than ∼100 years in their Damma watershed. Moreover, their data indicate that Δ44/40Caexchangeable-bulk soil varies as a function of the sorption site of Ca (mineral versus organic).
4.1.2 Seasonal and discharge controls on isotopic signatures
Three different factors controlling the Ca isotopic fractionation have been identified. Cenki-Tok et al. (2009) observed a season-dependent variation of the δ44/40Ca signature of streamwater that ranges between +0.40 and +0.83‰ at the outlet of the Strengbach watershed. The δ44/40Ca was low in winter and during dry and low water flow rates which they related to chemical weathering of soil minerals such as apatite and feldspar. In contrast, they observed higher δ44/40Ca values in spring, summer and autumn, during wet periods and high flow rates. These heavier δ44/40Ca streamlet values in summer might be caused by increased inflows of 44Ca-enriched soil solutions (depleted in 40Ca taken up by vegetation). The situation is different at an alpine soil chronosequence (Damma glacier) undergoing an initial stage of weathering, where Ca isotope compositions of soils and waters are generally homogeneous (Hindshaw et al., 2011, 2012). Only a slight increase in δ44/40Ca of streamwater is observed during snowmelt, possibly due to adsorption onto soil components in isolated pockets of non-frozen water during winter that is flushed out during snow melt (Hindshaw et al., 2011). Finally, Holmden and Bélanger (2010) observed a strong δ44/40Ca control of river waters by groundwaters (Saskatchewan, Canada; granitic lythology).
4.1.3 Atmospheric contribution to budget calculations
The Li and B isotope signatures of French rainwaters have been characterized by Millot et al. (2010a) over a one-year time period from coastal and inland sites. Li and B concentrations are low in rainwater samples, ranging from 0.004 to 0.292 μmol/L and from 0.029 to 6.184 μmol/L, respectively. δ7Li and δ11B values in rainwaters exhibit a large range of variation between +3.2 and +95.6‰, and between −3.3 and +40.6‰, respectively, over the whole period. These values are clearly different from the signature of seawater (+31‰ and +39.5‰, respectively for Li and B isotopes). Non-sea-salt sources, such as continental crust components and/or anthropogenic activities, have been suggested. At specific places, the influence of anthropogenic fertilizers may also be of importance (Négrel et al., 2010; Qi et al., 1997).
Seasonal variations of soil and river water δ26Mg have also been highlighted and explained by a rapid response to large rain events, due to ion exchange with minerals and/or with organic matter in peaty wetlands (Bolou-Bi et al., 2012; Tipper et al., 2012). Previously, Schmitt and Stille (2005) and Cenki-Tok et al. (2009) pointed out two important Ca fluxes that have often been neglected in watershed studies: rainwater and throughfall, that represent a mixing product of Ca from dissolved atmospheric dust particles and leaf excretions. These studies, performed at the scale of the granitic Strengbach watershed, have shown that only 15% of the Ca watershed budget is atmosphere-derived whereas it can be higher than 50% considering throughfall samples. On the other hand, Holmden and Bélanger (2010) concluded that direct contribution of rain and snow waters to the stream of their studied La Ronge watershed (Canada) are negligible. Similarly, the rainwater contribution in the Dama watershed to the stream water is variable (from 2% in winter to 35% in summer) but seems to have no influence on the Ca isotopic signature (δ44/40Ca varies from +0.88 to +1.24‰) since its δ44/40Ca value remains close to that of silicate rocks (+0.73 to +1.13‰).
4.2 Mixed-lithology watersheds
The study of continental scale watersheds might help to identify the major factors that control riverine and potentially seawater isotopic signatures. There are as yet only a few studies concerning mixed lithology basins. Li isotopes have been investigated in detail for three large areas: the Mackenzie basin (Canada; Millot et al., 2010b), the Himalayan basins (Kisakürek et al., 2005) and the Orinoco basin (Huh et al., 2001). Systematic studies of B isotopes on large-scale watersheds were conducted in the Ganges headwaters (Rose et al., 2000), the Mackenzie basin (Lemarchand and Gaillardet, 2006) and the Chiangjiang rivers (Chetelat et al., 2009). Ca and Mg isotopes have only been scarcely applied at global watershed scale: two studies performed on rivers draining the Himalaya-Tibetan plateau region and one on Vosges basins are currently published (Brenot et al., 2008; Tipper et al., 2006a, 2008).
4.2.1 Lithological control
The Mg and Ca isotopes suggest a lithological control on isotopic compositions of large river waters. Published data of Mg isotope composition of rivers located in mixed lithology basins lead to opposite interpretations: in the Himalayas, no clear lithology (carbonate vs silicate) dependent signature has been observed possibly due to the potential role of other processes such as groundwater contribution or recycling by vegetation (Tipper et al., 2006b, 2008). In eastern France, a combined study of Sr-Mg isotopes shows that the downstream part of the Moselle River can be explained by mixing between tributaries draining carbonates and evaporites on the Lorraine plateau, and Vosgian tributaries draining silicate rocks only (Brenot et al., 2008). These two studies determine that, in mixed lithology areas, 50–90% of the riverine dissolved Mg comes from silicate lithologies.
A study of the tributaries of the Marsyandi river in the Himalaya suggests that the dissolved δ44/40Ca values are not simply the result of mixing between a carbonate and a silicate end-member. They could be related to preferential 40Ca precipitation in secondary carbonate phases such as travertines (Tipper et al., 2006b). Schmitt and Stille (2005) and Farkas et al. (2011) showed that atmospherically derived δ44/40Ca values determined on rain and snow samples collected all over the world are also dominated by carbonate rock signatures. Tipper et al. (2010b) suggest that the Ca isotopic composition of large rivers is dominated by carbonate weathering, which would be consistent with the fact that two-third of present-day world Ca weathering flux is dominated by carbonate weathering (Berner and Berner, 1996; Milliman, 1993). We can notice that the range of variation of presently published bulk carbonate ooze and limestones ranges from +0.10 to +1.5‰ (De La Rocha and DePaolo, 2000; Fantle and DePaolo, 2005, 2007; Sime et al., 2007; Tipper et al., 2006b, 2008). The variability of present-day Ca isotopic signatures in world rivers (Fig. 1b) would then reflect weathering of isotopically different carbonate bedrocks of distinct ages and origins (Farkas et al., 2007).
4.2.2 Silicate weathering rate
Li and B isotopes in large rivers are controlled by the degree of silicate weathering. Li isotopic compositions of waters from the Mackenzie basin show that 7Li is enriched in the dissolved load compared to river sediments, and that the dissolved δ7Li can vary by 20‰ within a large river basin (Millot et al., 2010a). The δ7Li of river particulate load is usually close to that of the bedrock and ranges between −2 and +3‰ for the Mackenzie Rivers. Dissolved Li in river waters is essentially derived from the weathering of silicates, even in carbonate-rich areas, and the Li isotope ratio of the dissolved load is influenced by the regime and the intensity of silicate weathering. The strongest enrichments of 7Li in the dissolved loads are reported for both mountainous and shield areas where soils are thin or absent, and where silicate weathering rates are low (e.g. the Rocky Mountains of the Mackenzie basin, the Canadian Shield, the Andes or the Himalaya (Huh et al., 1998, 2001; Kisakürek et al., 2005; Millot et al., 2010a). In these areas, and in other glaciated environments (Iceland, Greenland), 7Li enrichments are most simply explained by the precipitation of oxy-hydroxides which preferentially incorporate the light 6Li isotope. Another weathering regime characterizes the lowland areas and produces waters with systematically lower δ7Li waters (but still enriched in 7Li compared to bedrocks). In these areas, equilibrium between waters and clay minerals is the most likely mechanism, especially in the case of significant contribution from long-residence time groundwaters (Fig. 9).
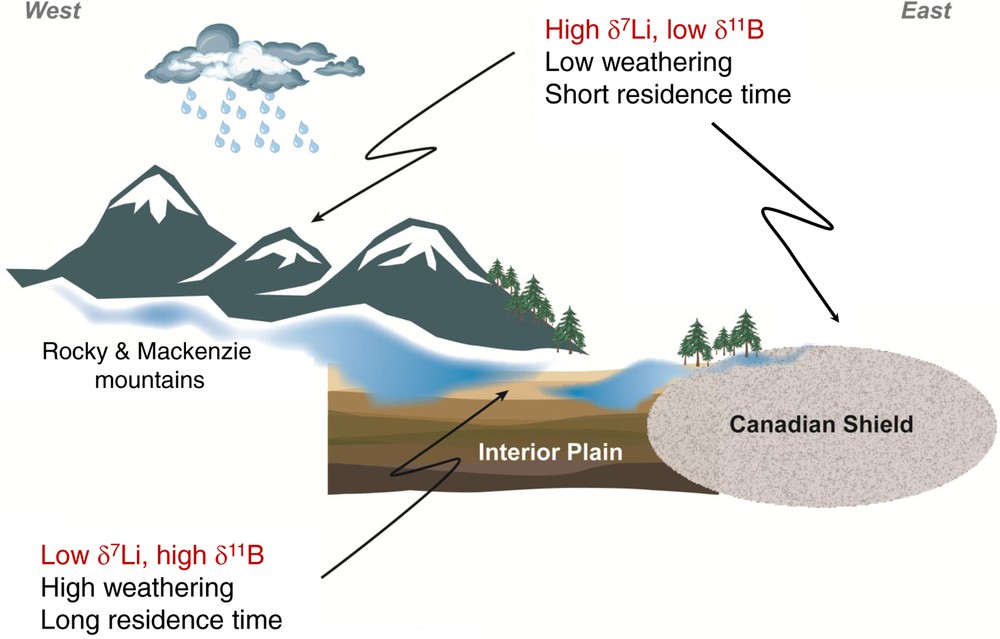
Schematic representation of relationships observed between Li and B isotopic values and weathering rates in large mixed lithology basins (adapted from Lemarchand and Gaillardet, 2006; Millot et al., 2010b).
Relation entre les valeurs isotopiques en Li et en B et les taux d’altération dans de grands bassins versants présentant des lithologies variées (adapté de Lemarchand et Gaillardet, 2006 ; Millot et al., 2010b).
Rivers like Congo or Orinoco, flowing on old silicate shields rich in organic matter and characterized by very low chemical weathering rates (Gaillardet et al., 1999), have δ11B values close to the vegetation end-member (> 40‰, Lemarchand et al., 2000) indicating that the mineral (trans)formation is no longer the parameter controlling the river water chemistry. In the Mackenzie basin, where the bedrock is composed of marine illite-carbonate sediments (North American Shale Composite), the δ11B values of surface waters are shown to be similar to the groundwater and directly related to the size of the watershed (Lemarchand and Gaillardet, 2006). The smaller ones have dissolved δ11B values close to those for bedrock (close to 5‰) whereas the larger ones show large and systematic 11B enrichment (close to 30‰). The authors propose that this relationship between B isotopes and size of the watersheds is driven by the B exchange at the solid surface and the B residence time in groundwaters. The elevated δ11B values are interpreted to reflect a recent increase of the weathering intensity, causing an excess release of dissolved B from the bedrock and a subsequent flux of light B onto solid surfaces. Following this model, the B data in groundwater can be explained by fivefold increase of the weathering rate about 5000 years ago (synchronous with the last deglaciation) (Fig. 9). This δ11B shift of groundwaters is expected to have occurred in all watersheds but only larger ones still keep a record, smaller ones have already reached a steady-state. The magnitude of the B isotopic difference between small and large watersheds can therefore be used as a proxy of post-glacial increase of the weathering rate. This is consistent with marine isotope records of elements having short residence time (Vance, 2011). Increase in the weathering intensity after reactivation of hydrological pathways induces changes in the water chemistry that is propagated in groundwater. In peri-himalayan rivers, δ11B values of the dissolved load is explained by the formation of clay minerals which preferentially capture the light 10B isotope and leave behind complementary solutions enriched in 11B. The gradual increase of δ11B values from headwaters to mouth of continental-scale river watersheds is consistent with the formation of clay minerals in plains (Lemarchand et al., 2000, 2002b). The large peri-himalayan rivers show δ11B values about 4‰ in average lower than the mean world values (10‰); this can be explained by reduced formation of secondary minerals in orogenic belts compared to the plains.
5 Conclusion
Li, B, Mg and Ca isotope data help to elucidate the main factors that control fractionation processes, such as mineral formation/dissolution and biological activity at the soil-water-plant interface. Although the use of these tracers for watershed science is still in its infancy, current studies have allowed us to determine magnitudes of isotope fractionation for these four elements associated with water-rock-plant interaction processes, and the main factors controlling these fractionations. Thus, Li and B isotopes have shown their potential to quantify and trace secondary clay mineral formations in soils and soil solutions. Mg and Ca isotopes can be used to identify plant-mineral interactions and recycling by vegetation. B isotopes are not directly fractionated by the vegetation; nevertheless they can help to characterize the soil pool (depth or reservoir or mineral) in which the vegetation takes up its B. Field investigations suggest fractionation mechanisms, which can be isolated and better quantified through laboratory controlled experiments. Both abiotic processes (dissolution, adsorption, secondary mineral formations) and biotic processes (fractionation processes at the nutritive solution/roots interface and within the plant itself) leading to isotopic fractionation have been identified.
At the scale of monolithological watersheds, Li and B isotope fractionations are mainly controlled by a coupling between mineral dissolution and clay mineral formation. Mg and Ca isotope signatures in soil and river waters vary seasonally influenced by vegetation growth and rain events. In larger scale mixed lithology basins, B and Li isotopes are controlled by the degree of silicate weathering. For Mg and Ca, little work has been done yet at this scale but existing studies highlight a lithological control on river water compositions with Ca isotope signatures of waters being mainly controlled by carbonate phases, and Mg isotopes being controlled by silicate phases.
Further efforts are necessary to improve our knowledge of the processes controlling the isotopic fractionation of these four isotope systems. This includes the extension of the dataset and the study of all types of climatic and geologic environments. In parallel, additional experiments are required for determining more precisely the fractionating mechanisms. This review also points out the potential of coupling Li, B, Mg and Ca isotopes, for developing appropriate alteration models at various scales in space and in time.
Acknowledgements
The authors greatly thank Tom Bullen (USGS) and Ed Tipper (University of St Andrews) for their careful review of this manuscript.


