Scattering enabled retrieval of Green's functions from remotely incident wave packets using cross correlations

Maarten V. de Hoop; Josselin Garnier; Sean F. Holman; Knut Sølna

doi:10.1016/j.crte.2011.06.001

Résumés

Anglais
Français

We analyze the “field-field” cross correlation associated with scattered coda waves, observed at a pair of distinct receivers, to obtain an estimate of the Green's function between the receivers with an emphasis on high-frequency body waves. The scattered waves are generated in a slab with random medium fluctuations by an incident wave packet. Following the dyadic parabolic scaling of wave packets and considering appropriate scaling for the random fluctuations of the medium, we arrive at a description in terms of a system of Itô-Schrödinger diffusion models. Studying the Wigner distributions of the fields and expressing the cross correlation in terms of the Green's function and the Wigner distribution, we can give a complete characterization of the cross correlation using a “blurring” transformation.

Nous analysons la corrélation croisée entre des champs correspondant à des ondes multiplement diffusées et observés en un couple de points distincts, afin d’obtenir une estimation de la fonction de Green entre ces points. Nous prêtons une attention particulière aux contributions des ondes de volume hautes fréquences. Les ondes sont créées par diffusion dans une couche de milieu aléatoire d’un paquet d’ondes incident. En adoptant une mise à l’échelle dyadique parabolique des paquets d’ondes et en considérant un milieu aléatoire avec des échelles appropriées, nous obtenons une description en termes d’un système de modèles de diffusion de type Itô-Schrödinger. En étudiant les distributions de Wigner des champs et en exprimant la corrélation croisée en termes de la fonction de Green et de la distribution de Wigner, nous donnons une caractérisation complète de la corrélation croisée.

1 Introduction

We analyze the notion of “field-field” cross correlations associated with scattered coda waves, observed at pairs of distinct receivers, to obtain an estimate of the Green's function with an emphasis on high-frequency body wave reflections.

As a model configuration for the crust, we consider a slab in which random medium fluctuations occur. The bottom of the slab is bounded by a deterministic discontinuity (a smooth reflector). We consider waves incident from above the slab, and place our receivers within the slab to study the corresponding cross correlations. Otherwise, in the entire configuration, the medium has a deterministic, smoothly varying component. In this general case, the incident wave is decomposed into wave packets. Each wave packet contains a particular scale. The decomposition is used to select a scale in relation to the fluctuations component of the medium in the slab. Through localization in phase space, the propagation and scattering of an incident wave packet can be described by a coupled system of paraxial wave equations written in curvilinear, boundary normal coordinates relative to the support of the wave packet in the deterministic component of the medium. Thus, in principle, each incident wave packet generates its own system of paraxial wave equations. The accuracy of this description can be proven to improve with increasingly finer scales.

In this article, we assume that the background medium is constant, that the slab is flat, and we consider a single wave packet in the limit of fine scales (high frequency). Indeed, we view the cross correlations in the context of parametrix constructions. The paraxial form of the system that we obtain in the limit allows for the use of Itô’s stochastic calculus (for Hilbert-space valued processes) to analyze the scattering due to the random fluctuations; indeed, it enables the closure of the hierarchy of moment equations.

The solution procedure of the coupled system of paraxial wave equations is based on an invariant embedding type approach, generating a transmission and a reflection operator capturing the scattering due to the random fluctuations in the medium. Thus, we arrive at a coupled system of Riccati equations for the two operator kernels. In the limit of fine scales in the sense of distributions, we then obtain a decoupled system of linear Itô-Schrödinger equations for the limiting transmission and reflection operator kernels, with a real-valued Brownian field; to be precise, only the moments of these kernels converge in the limit.

The solutions to the Itô-Schrödinger equations define the transmitted and backscattered fields, at least their statistics. The transmitted field is partly coherent; the backscattered field is weak and fully incoherent in the absence of a smooth (deterministic) reflector, while it is partly coherent in the presence of a reflector. We analyze the Wigner distributions of these fields. We obtain a description of the cross correlation between two points in terms of a blurring transformation of the paraxial random Green's function between these points. This transformation is statistically stable (in the sense that it does not depend on the realization of the random fluctuations of the medium) and it depends on the statistics of the fluctuations of the random medium.

In the past decade, the understanding of how cross-correlating diffuse fields recaptures the Green's function, has been an important topic of research (van Tiggelen, 2003). Cross correlating (diffuse) coda waves as discussed in Campillo and Paul (2003) resulted in the retrieval of surface waves observed at one station and excited at the other station. The idea of using ambient noise for the retrieval of a body-wave reflection response, in a planarly layered medium, dates back to Claerbout (1968). The retrieval of direct and reflected body waves using teleseismic (S-wave) coda was discussed in Tonegawa et al. (2009). The exploitation of a scattering medium in capturing the Green's function by field-field cross correlations was studied by Derode et al. (2003). However, the mathematical analysis of field-field cross correlations in this setting from the point of view of stochastic calculus has just begun. In our paper, we address a scattering regime in which the field is partly coherent and we aim at retrieving the Green's function for the particular realization of the random medium.

2 Scaling and assumptions

We consider acoustic waves propagating in 1+d spatial dimensions. The governing equations are

ρ (z, x) \frac{\partial u}{\partial t} + \nabla p = F, \frac{1}{K (z, x)} \frac{\partial p}{\partial t} + \nabla \cdot u = 0,

(1)

where p is the pressure field, u is the velocity field, ρ is the density of mass, and K is the bulk modulus of the medium;

(z, x) \in ℝ \times ℝ^{d}

denotes the space coordinates. The source is modeled by the forcing term F. We consider a configuration in which a random slab occupies the region

Ω_{r} = {(z, x), x \in ℝ^{d}, - L \leq z \leq 0},

and is sandwiched in between two homogeneous half spaces. The surface z = 0 is the top interface and the surface –L < 0 is the bottom or interior interface. The medium consists of a deterministic component and random fluctuations in the region Ω_r, which vary rapidly in space. To simplify the analysis, the deterministic component of the medium in Ω_r is assumed to be constant.

The medium is assumed to be matched at the top interface z = 0 (transparent boundary conditions). However, the interior interface can act as a smooth reflector and is part of the deterministic component of the medium. This model naturally captures primary reflections if the random fluctuations were absent. Indeed, we consider a mismatch at the bottom of the slab, z = –L < 0, which gives jump conditions at the interior interface. The deterministic component of the medium is thus given by

\frac{1}{K (z, x)} = \{\begin{array}{l} K_{0}^{- 1} & if z \leq - L, \\ K_{1}^{- 1} (1 + ν (z, x)) & if z \in (- L, 0), \\ K_{1}^{- 1} & if z \geq 0, \end{array}

ρ (z, x) = \{\begin{array}{l} ρ_{0} & if z \leq - L, \\ ρ_{1} & if z \in (- L, 0), \\ ρ_{1} & if z \geq 0, \end{array}

where the random field v(z, x) models the medium fluctuations, with correlation length l_K. The deterministic wavespeed for z > –L is

c_{1} = \sqrt{K_{1} / ρ_{1}}

, and for z < –L is

c_{0} = \sqrt{K_{0} / ρ_{0}}

The source, F, is located at z = z_s ≥ 0; we assume, here, that z_s = 0 and write $F (t, z, x) = f_{s} (t, x) δ (z - z_{s}) e_{z}$ , where e_z denotes the unit vector pointing in the z-direction, signifying a body force. We shall refer to waves propagating in the positive z direction as upgoing. The source generates downgoing waves which “propagate” through the random medium, are reflected by the interface at z = –L, and “propagate” up through the medium.

The source is now assumed to be of the form:

F (t, z, x) = χ_{ε} (t, x) δ (z) e_{z}

(2)

The forcing function $χ_{ε} (t, x) = χ (ε^{- 4} t, ε^{- 2} x)$ gives a wave packet oriented in the z direction of scale k, $ε = 2^{- k / 4}$ , corresponding with a dyadic parabolic decomposition of phase space. Here $\hat{χ}$ denotes a window function supported in a box in the $(ω, κ)$ Fourier domain (the support of $\hat{χ}$ is a finite distance away from the ω = 0 axis) and we use the Fourier transforms:

χ (t, x) = \frac{1}{{(2 π)}^{d + 1}} \iint \hat{χ} (ω, κ) e^{- i (ω t - k \cdot x)} d ω d k = \frac{1}{2 π} \int \overset{⌣}{χ} (ω, k) e^{- i ω t} d k

Thus, the transverse width, R₀, of the source function is of order ɛ². This scaling is consistent with the paraxial regime, which will be discussed in the next section, in as much as that it generates the wave solution up to an error of order ɛ². We assume that:

• the correlation length or radius of the fluctuations, l_K, is of the same order as R₀; this regime guarantees non-trivial interaction between the fluctuations of the medium and the waves;
• the propagation distance is of the order of L, which is of order 1; the ratio between the propagation distance and the correlation length of the fluctuations is of order ɛ⁻².

The wave packet has a central frequency of order 2^k. We will establish results, which converge as k → ∞, signifying the high-frequency regime.

Henceforth we shall assume non-dimensionalized units chosen such that the deterministic bulk modulus K₁ and density ρ₁ in the region Ω_r are one and, hence, the deterministic wavespeed $c_{1} = \sqrt{K_{1} / ρ_{1}}$ and impedance $Z_{1} = \sqrt{K_{1} ρ_{1}}$ are equal to one. We assume that $Z_{0} = \sqrt{K_{0} ρ_{0}} \neq 1$ . The medium fluctuations attain the scaled form

\frac{1}{K (z, x)} = \{\begin{array}{l} K_{0}^{- 1} & if z \leq - L, \\ 1 + ε^{3} ν (\frac{z}{ε^{2}}, \frac{x}{ε^{2}}) & if z \in (- L, 0), \\ 1 & if z \geq 0, \end{array}

ρ (z, x) = \{\begin{array}{l} ρ_{0} & if z \leq - L, \\ 1 & if z \in (- L, 0), \\ 1 & if z \geq 0, \end{array}

where v is a zero-mean, stationary random field with correlation length of order one and standard deviation of order one. We write

C (z, x) = E [ν (z^{'} + z, x' + x) ν (z^{'}, x')],

(3)

D (x) = \int_{- \infty}^{\infty} C (z, x) d z

(4)

We assume that v satisfies strong mixing conditions in z. The amplitude ɛ³ of the fluctuations has been chosen so as to obtain an effective limit of order one when ɛ goes to zero. That is, if the magnitude of the fluctuations is smaller than ɛ³, then the wave would propagate as if the medium were homogeneous, while if the order of magnitude is larger, then the wave would not penetrate the slab at all. The scaling that we consider here, controlled by the choice of wave packet, corresponds to the partly coherent regime.

3 Coupled system of paraxial equations, and transmission and reflection operators

We eliminate the transverse components of the velocity field. Because both the medium and the source have transverse spatial variations at the scale ɛ², it is convenient to rescale the transverse coordinates accordingly, that is, ɛ²x → x. In the region Ω_r, we then introduce the directional decomposition in the deterministic medium component,

p (t, z, ε^{2} x) = \frac{1}{2 π} \int ({\overset{⌣}{a}}^{ε} (ω, z, x) e^{i ω \frac{z}{ε^{4}}} + {\overset{⌣}{b}}^{ε} (ω, z, x) e^{- i ω \frac{z}{ε^{4}}}) e^{- i ω \frac{t}{ε^{4}}} d ω,

(5)

with complex amplitudes

{\overset{⌣}{a}}^{ε}

and

{\overset{⌣}{b}}^{ε}

representing, locally, up- and down-going wave constituents, respectively. We have used Cartesian coordinates, since the ray generated by initial conditions corresponding with the center of the wave packet is straight, along the z direction.

The wave-packet source enables the use of the paraxial approximation in the deterministic component of the medium with the above-mentioned estimate, leading to the system for z ∈ (–L,0):

\frac{\partial {\overset{⌣}{a}}^{ε}}{\partial z} = [\frac{i ω}{2 ε} ν (\frac{z}{ε^{2}}, x) + \frac{i}{2 ω} Δ_{x}] {\overset{⌣}{a}}^{ε} + e^{- 2 i ω \frac{z}{ε^{4}}} [\frac{i ω}{2 ε} ν (\frac{z}{ε^{2}}, x) + \frac{i}{2 ω} Δ_{x}] {\overset{⌣}{b}}^{ε},

(6)

\frac{\partial {\overset{⌣}{b}}^{ε}}{\partial z} = - e^{2 i ω \frac{z}{ε^{4}}} [\frac{i ω}{2 ε} ν (\frac{z}{ε^{2}}, x) + \frac{i}{2 ω} Δ_{x}] {\overset{⌣}{a}}^{ε} - [\frac{i ω}{2 ε} ν (\frac{z}{ε^{2}}, x) + \frac{i}{2 ω} Δ_{x}] {\overset{⌣}{b}}^{ε},

(7)

supplemented with the boundary conditions:

{\overset{⌣}{b}}^{ε} (ω, z = 0^{-}, x) = - \frac{1}{2} \overset{⌣}{χ} (ω, x),

(8)

{\overset{⌣}{a}}^{ε} (ω, z = {(- L)}^{+}, x) = R_{0} e^{2 i ω \frac{L}{ε^{4}}} {\overset{⌣}{b}}^{ε} (ω, z = {(- L)}^{+}, x),

(9)

where

R_{0} = (Z_{0} - 1) / (Z_{0} + 1)

. We also have the jump condition across z = –L:

{\overset{⌣}{b}}^{ε} (ω, {(- L)}^{-}, x) = T_{0} {\overset{⌣}{b}}^{ε} (ω, {(- L)}^{+}, x),

where

T_{0} = 2 Z_{0}^{1 / 2} / (1 + Z_{0})

, and across z = 0:

{\overset{⌣}{a}}^{ε} (ω, 0^{-}, x) = {\overset{⌣}{a}}^{ε} (ω, 0^{-}, x) + \frac{1}{2} \overset{⌣}{χ} (ω, x)

In the deterministic case, with v = 0, it can be proven that this system decouples with solutions accurate up to order ɛ².

We invoke an invariant imbedding approach to obtain the representation valid for –L < z < 0:

{\overset{⌣}{b}}^{ε} (ω, {(- L)}^{-}, x) = T_{0} \int \overset{⌣}{T}^{ε} (ω, - L, z, x, x') {\overset{⌣}{b}}^{ε} (ω, z, x') d x',

(10)

{\overset{⌣}{a}}^{ε} (ω, z, x) = R_{0} e^{2 i ω \frac{L}{ε^{4}}} \int \overset{⌣}{R}^{ε} (ω, - L, z, x, x') {\overset{⌣}{b}}^{ε} (ω, z, x') d x',

(11)

where the operators

\overset{⌣}{T}^{ε}

and

\overset{⌣}{R}^{ε}

, defined through their kernels, satisfy a natural coupled system of operator Riccati equations which follow from the equations satisfied by the local amplitudes. In the scaling regime ɛ → 0 we are able to deduce from this system a description in terms of effective white noise models for the transmission and reflection operators, at least on the level of moments. We describe this in the next section.

The formulation generalizes to curvilinear coordinates if the deterministic wave speed in the slab is no longer constant, and the rays are no longer straight, using techniques from microlocal analysis and harmonic analysis.

4 Itô-Schrödinger diffusion models for transmitted and backscattered fields

We centre according to the travel time associated with the deterministic medium component (constant wave speed, here) and define the transmitted and reflected pressure fields by

p_{R}^{ε} (s, x) ≔ p (2 L + ε^{4} s, 0^{+}, ε^{2} x) - \frac{1}{2} χ (\frac{2 L}{ε^{4}} + s, x),

(12)

p_{T}^{ε} (s, x) ≔ p (L + ε^{4} s, {(- L)}^{-}, ε^{2} x)

(13)

The field $p_{T}^{ε} (s, x)$ is the field observed just below the bottom interface at z = (–L)⁻; the field $p_{R}^{ε} (s, x)$ is the field observed just above the top interface at z = 0⁺:

p_{R}^{ε} (s, x) = \frac{1}{2 π} \int {\overset{⌣}{a}}^{ε} (ω, 0^{+}, x) e^{- i ω s} d ω,

(14)

p_{T}^{ε} (s, x) = \frac{1}{2 π} \int {\overset{⌣}{b}}^{ε} (ω, {(- L)}^{-}, x) e^{- i ω s} d ω

(15)

These fields are now characterized via effective scaling limit models for the transmission and reflection operators:

Proposition 4.1 The processes ${(p_{T}^{ε} (s, x))}_{s \in ℝ, x \in ℝ^{d}}$ , ${(p_{R}^{ε} (s, x))}_{s \in ℝ, x \in ℝ^{d}}$ converge in distribution as ɛ → 0 in the space $C^{0} (ℝ, L^{2} (ℝ^{d}, ℝ^{2})) \cap L^{2} (ℝ, L^{2} (ℝ^{d}, ℝ^{2}))$ to the limit processes ${(p_{T} (s, x))}_{s \in ℝ, x \in ℝ^{d}}$ , ${(p_{R} (s, x))}_{s \in ℝ, x \in ℝ^{d}}$ given by

p_{R} (s, x) = - \frac{R_{0}}{4 π} \iint \overset{⌣}{R} (ω, - L, 0, x, x') \overset{⌣}{χ} (ω, x') d x' e^{- i ω s} d ω,

(16)

p_{T} (s, x) = - \frac{T_{0}}{4 π} \iint \overset{⌣}{T} (ω, - L, 0, x, x') \overset{⌣}{χ} (ω, x') d x' e^{- i ω s} d ω,

(17)

where

T_{0}

and

R_{0}

, are the transmission, resp. reflection, coefficient of the interface at z = –L and defined above. Furthermore,

L^{2} (ℝ, L^{2} (ℝ^{d}, ℝ^{2})) = L^{2} (ℝ \times ℝ^{d}, ℝ^{2}) .

The operators

{(\overset{⌣}{R} (ω, - L, z, x, x'))}_{z \in [- L, 0]}

and

{(T (ω, - L, z, x, x'))}_{z \in [- L, 0]}

are the solutions of the following Itô-Schrödinger diffusion models:

d \overset{⌣}{R} (ω, - L, z, x, x') = \frac{i}{2 ω} (Δ_{x} + Δ_{x'}) \overset{⌣}{R} (ω, - L, z, x, x') d z + \frac{i ω}{2} \overset{⌣}{R} (ω, - L, z, x, x') \circ (d B (z, x) + d B (z, x')),

(18)

d \overset{⌣}{T} (ω, - L, z, x, x') = \frac{i}{2 ω} Δ_{x'} \overset{⌣}{T} (ω, - L, z, x, x') d z + \frac{i ω}{2} \overset{⌣}{T} (ω, - L, z, x, x') \circ d B (z, x'),

(19)

with the initial conditions at z = –L:

\overset{⌣}{R} (ω, - L, z = - L, x, x^{'}) = δ (x - x^{'}), \overset{⌣}{T} (ω, - L, z = - L, x, x^{'}) = δ (x - x^{'}) .

The symbol ° stands for the Stratonovich stochastic integral, and B(z, x) is a real-valued Brownian field with covariance

E [B (z_{1}, x_{1}) B (z_{2}, x_{2})] = \min {z_{1}, z_{2}} C_{0} (x_{1} - x_{2})

(20)

Making use of the semigroup property of the effective operators we also find that the joint law for the direct arrival to the two points of observation located at (–L₁, ɛ²x₁) and (–L₂ ɛ²x₂), with –L ≤ –L₂ ≤ –L₁ ≤ 0, can be characterized by

p (L_{1} + ε^{4} s, - L_{1}, ε^{2} x_{1}) \sim - \frac{1}{4 π} \iint \overset{⌣}{T} (ω, - L_{1}, 0, x_{1}, x') \overset{⌣}{χ} (ω, x') d x' e^{- i ω s} d ω,

(21)

p (L_{2} + ε^{4} s, - L_{2}, ε^{2} x_{2}) \sim - \frac{1}{4 π} \iint \overset{⌣}{T} (ω, - L_{2}, - L_{1}, x_{2}, x'') \overset{⌣}{T} (ω, - L_{1}, 0, x'', x') \overset{⌣}{χ} (ω, x') d x' d x'' e^{- i ω s} d ω

(22)

We note that, for –L ≤ –L₂ ≤ –L₁ ≤ 0, the operators

\overset{⌣}{T} (ω, - L, - L_{2}, x, x')

and

\overset{⌣}{R} (ω, - L, - L_{2}, x, x')

are statistically independent of

\overset{⌣}{T} (ω, - L_{2}, - L_{1}, x, x')

and

\overset{⌣}{R} (ω, - L_{2}, - L_{1}, x, x')

, which we exploit in evaluating the cross-correlations. We remark here also that the transmission operator over the sub-slab (–L₁,0) appears in both expressions in (21)–(22) and it is this pairing that will lead to an expression for the cross correlations in terms of a statistically stable filter or transformation below. The general statistical properties of the operators

\overset{⌣}{R}

\overset{⌣}{T}

were studied in Garnier and Sølna (2009a).

5 Characterization of cross correlations

Here, we characterize the “field-field” correlation function between the points (–L₁, ɛ²x₁) and (–L₂, ɛ²x₂). We assume here that $T ≫ L$ and 0 < L₁ < L₂ < L. The field-field correlation function is given by

V_{T}^{ε} (τ) = \int_{0}^{T} p (t, - L_{1}, ε^{2} x_{1}) p (t + τ, - L_{2}, ε^{2} x_{2}) d t .

(23)

The configuration is illustrated in Fig. 1, we compute the cross correlation in between the two points at depth –L₁ and –L₂. We will see that the wave field correlation function concentrates around specific time lags τ that correspond to travel times between the two observation points, and that the time extent of correlation function around these time lags is much smaller, of order ɛ⁴, i.e., of the same order as the source pulse width.

Fig. 1
Configuration. The source is located at the surface z = 0. An interface is present at depth z = –L. We compute the cross correlation between the two points at depth –L₁ and –L₂. The random fluctuations occur in the interval z∈(–L, 0).
Configuration. La source est placée à la surface z = 0. Une interface est présente à la profondeur z = –L. Nous calculons la corrélation croisée entre les deux points aux profondeurs –L₁ et –L₂. Le milieu est aléatoire dans l’intervalle z∈(–L, 0).

Under the scaling assumptions of Section 2, we find that the correlations in (23) has leading contributions at four particular time lags:

V_{T}^{ε} (\pm (L_{2} - L_{1}) + ε^{4} s) / ε^{4} \sim V_{t}^{\pm} (s),

(24)

V_{T}^{ε} (\pm (2 L - L_{1} - L_{2}) + ε^{4} s) / ε^{4} \sim V_{r}^{\pm} (s)

(25)

Here, the amplitude scaling ɛ⁻⁴ corresponds to a re-scaling of the source time traces so that they have order one energy, but plays no significant role as the problem is linear. We shall here focus on the contribution $V_{t}^{+}$ , which corresponds to correlation of wave components directly transmitted in between the points of observation (Fig. 2). The contribution $V_{t}^{+}$ is concentrated around time lag equal to +(L₂–L₁) and it comes from the correlation between the waves that propagate from the surface to the depth –L₁ and then to the depth –L₂. The contribution $V_{t}^{-}$ is concentrated around time lag equal to –(L₂–L₁) and it comes from the correlation between the waves that have been reflected by the interface at z = –L and that propagate from this interface to the depth –L₂ and then to the depth –L₁. We stress here that these wave components have been strongly affected by the multiple scattering in the medium and understanding how this affects the relation of the components V and Green's functions is our main objective. The contributions $V_{r}^{\pm}$ correspond to cross terms and they will be treated in detail elsewhere. We remark here that they give contributions concentrated around times lags that are larger than the ones of the first two contributions (since 2L–L₁–L₂ > L₂–L₁) and they can be used for estimation of the depth L of the bottom interface.

Fig. 2
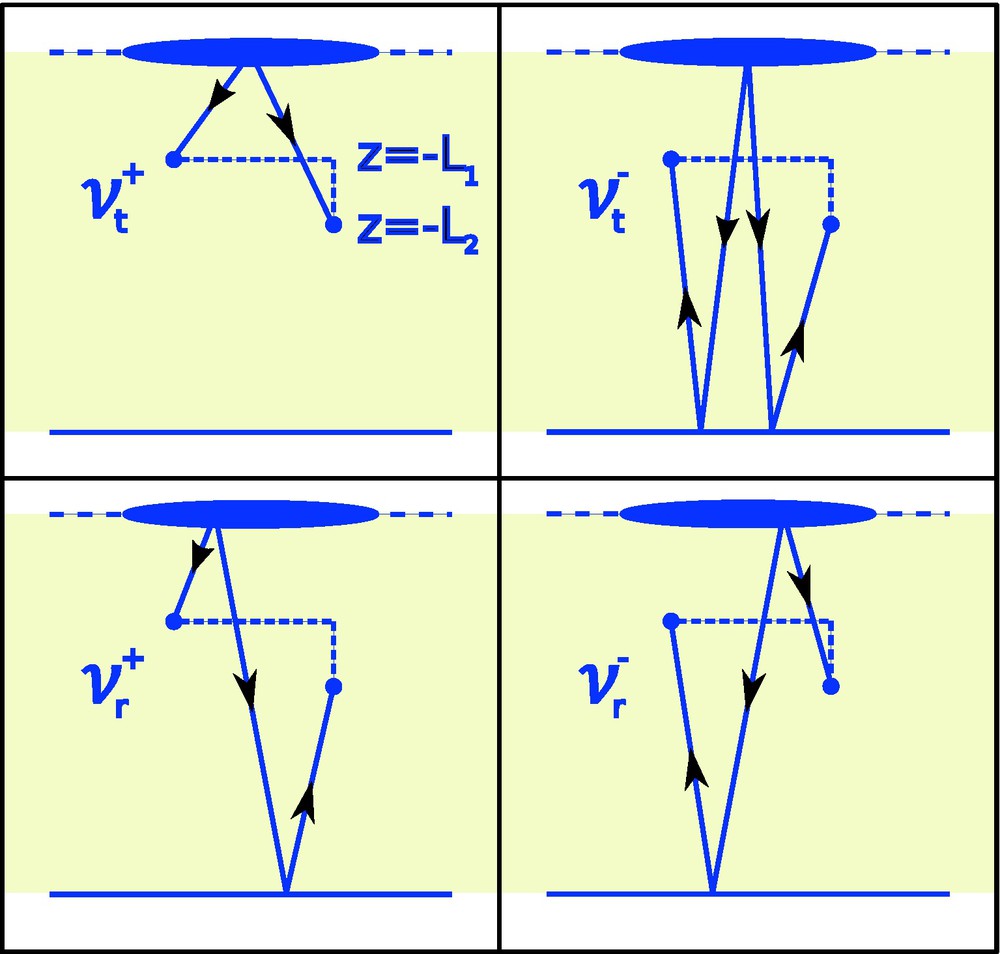
The four contributions to the cross correlation between points (–L₁, ɛ²x₁) and (–L₂, ɛ²x₂).
Les quatre contributions à la corrélation croisée entre les points (–L₁, ɛ²x₁) et (–L₂, ɛ²x₂).

The correlation component $V_{t}^{+}$ can be characterized in distribution in the scaling limit considered in this paper by the following expression using (21), (22) and the definition (23):

V_{t}^{+} (s) = \frac{1}{2 π} \iint Λ_{t}^{+} (ω, x; x_{1}, L_{1}) \times \overset{⌣}{T} (ω, - L_{2}, - L_{1}, x_{2}, x_{1} - x) d x e^{- i ω s} d ω,

(26)

where

\overset{⌣}{T} (ω, - L_{2}, - L_{1}, x, x')

is defined by (19). Remember that

\overset{⌣}{T} (ω, - L_{2}, - L_{1}, x_{2}, x_{1})

is the random paraxial Green's function from the point

(- L_{1}, ε^{2} x_{1})

to the point

(- L_{2}, ε^{2} x_{2})

that we want to estimate. Therefore, (26) reads as a filtered version of the Green's function in between the two points of observation. This filter is

Λ_{t}^{+} (ω, x; x_{1}, L_{1}) = \frac{1}{4} \iint \overset{⌣}{T} (ω, - L_{1}, 0, x_{1} - x, y_{2}) \bar{\overset{⌣}{T} (ω, - L_{1}, 0, x_{1}, y_{1})} \overset{⌣}{χ} (ω, y_{2}) \bar{\overset{⌣}{χ} (ω, y_{1})} d y_{1} d y_{2}

(27)

In the regime considered in this article, the filter $Λ_{t}^{+}$ defining the relevant transformation is self-averaging, see de Hoop and Sølna (2009), in the sense that

Λ_{t}^{+} (ω, x; x_{1}, L_{1}) = \frac{1}{4} \iint E [\overset{⌣}{T} (ω, - L_{1}, 0, x_{1} - x, y_{2}) \bar{\overset{⌣}{T} (ω, - L_{1}, 0, x_{1}, y_{1})}] \overset{⌣}{χ} (ω, y_{2}) \bar{\overset{⌣}{χ} (ω, y_{1})} d y_{1} d y_{2}

In order to characterize the filter $Λ_{t}^{+}$ we introduce the Wigner transform defined by

W_{ω}^{T} (L_{1}, x, x', κ, κ') = \iint E [\overset{⌣}{T} (ω, - L_{1}, 0, x + \frac{y}{2}, x' + \frac{y'}{2}) \bar{\times \overset{⌣}{T} (ω, - L_{1}, 0, x - \frac{y}{2}, x' - \frac{y'}{2})}] e^{- i (κ \cdot y + κ' \cdot y')} d y d y'

The Wigner transforms can be shown to satisfy a set of transport equations that can be integrated, as shown in Garnier and Sølna (2009b), and we find the following integral representation for $W_{ω}^{T}$ :

W_{ω}^{T} (z, x, x', κ, κ') = \frac{1}{{(2 π)}^{d}} \iint e^{- i (κ' + κ) \cdot a - i (x' - x + \frac{κ}{ω} z) \cdot b} e^{\frac{ω^{2}}{4} \int_{0}^{z} D (a + \frac{b}{ω} z^{'}) - D (0) d z^{'}} d a d b

(28)

This gives then an integral expression for the filter. In order to get an explicit form for the filter and characterize the associated resolution scale, or filter support scale, we consider next a particular regime of relatively strong scattering or clutter.

5.1 The strongly cluttered regime

We introduce the correlation length $ℓ$ and the standard deviation σ of the random fluctuations:

C (z, x) = σ^{2} C_{0} (\frac{z}{ℓ}, \frac{x}{ℓ})

With this representation we have:

D (x) = σ^{2} ℓ D_{0} (\frac{x}{ℓ}), D_{0} (x) = \int_{- \infty}^{\infty} C_{0} (z, x) d z

We assume also that the normalized autocorrelation function D₀(x) is at least twice differentiable at x = 0, which corresponds to a smooth random medium.

We introduce the parameter, depending on ω,

β_{L} (ω) = L \frac{σ^{2} ℓ ω^{2}}{4},

(29)

which characterizes the strength of the forward scattering. We shall then assume a subsequent scaling regime corresponding to relatively strong medium interaction, with β_L(ω) being large.

Second, we introduce the frequency-dependent resolution parameter:

Σ_{ω}^{2} (L_{1}) = \frac{16}{ω^{2} γ L_{1}},

(30)

where we defined

γ = - \frac{σ^{2}}{d ℓ} Δ D_{0} (0)

Using the results of Garnier and Sølna (2009a), we find the following expression for the filter

Λ_{t}^{+} (ω, x; x_{1}, L_{1}) = \frac{1}{4} {(\frac{6}{π γ L_{1}^{3}})}^{d / 2} \exp (- \frac{| x |^{2}}{2 Σ_{ω}^{2} (L_{1})}) \int | \overset{⌣}{χ} (ω, y_{1}) |^{2} d y_{1}

(31)

Thus, we have a situation in which a sharp filter and Green's function estimation have been enabled by the medium correlations. We remark that the expression (31) is valid provided $| x_{1} | ≪ \sqrt{γ L_{1}^{3}}$ , which means that the point (–L₁, ɛ²x₁) is in the forward cone of wave energy (Garnier and Sølna, 2009a; de Hoop and Sølna, 2009). Note that this cone is wider than the usual deterministic light cone due to multiple scattering.

We have similarly

V_{t}^{-} (s) = \frac{R_{0}^{2}}{2 π} \iint Λ_{t}^{-} (ω, x; x_{2}, L_{2}, L) \times \overset{⌣}{T} (ω, - L_{1}, - L_{2}, x_{1}, x_{2} - x) d x e^{- i ω s} d ω,

with the filter

Λ_{t}^{-} (ω, x; x_{2}, L_{2}, L) = \frac{1}{4} \iint \overset{⌣}{T} (ω, - L_{2}, 0, y_{4}, y_{2}) \times \bar{\overset{⌣}{T} (ω, - L_{2}, 0, y_{3}, y_{1})}

\times \overset{⌣}{R} (ω, - L, - L_{2}, x_{2} - x, y_{4}) \bar{\overset{⌣}{R} (ω, - L, - L_{2}, x_{2}, y_{3})} \overset{⌣}{χ} (ω, y_{2}) \bar{\overset{⌣}{χ} (ω, y_{1})} d y_{1} d y_{2}

Note that, by reciprocity, we have

V_{t}^{-} (s) = \frac{ℛ_{0}^{2}}{2 π} \iint Λ_{t}^{-} (ω, x; x_{2}, L_{2}, L) \bar{\overset{⌣}{T} (ω, - L_{2}, - L_{1}, x_{2} - x, x_{1})} d x e^{- i ω s} d ω,

(32)

which shows that we obtain a filtered version of the anti-causal Green's function in between the two points of observation.

We can also get a simple expression of the filter in the strongly cluttered regime. Self-averaging implies that

Λ_{t}^{-} (ω, x; x_{2}, L_{2}, L) = \frac{1}{4} \iint E [\overset{⌣}{T} (ω, - L_{2}, 0, y_{4}, y_{2}) \bar{\overset{⌣}{T} (ω, - L_{2}, 0, y_{3}, y_{1})}]

(33)

\times E [\overset{⌣}{R} (ω, - L, - L_{2}, x_{2} - x, y_{4}) \bar{\overset{⌣}{R} (ω, - L, - L_{2}, x_{2}, y_{3})}] \overset{⌣}{χ} (ω, y_{2}) \bar{\overset{⌣}{χ} (ω, y_{1})} d y_{1} d y_{2} d y_{3} d y_{4}

We will again in general have sharp clutter enabled resolution for the filter

Λ_{t}^{-}

, analogously to the situation for the filter

Λ_{t}^{+}

. However, the presence of the reflection operator in the expression for the filter (33) modifies the expression for the filter in a way that depends more critically on the particular scaling regime considered. In particular, one may have scaling situations in which there is a restoration of coherence for the reflected waves which affects the resolution, moreover, a diffusive or incoherent bottom interface condition will affect wave diversity and resolution (Garnier and Sølna, 2009b). These phenomena will be treated in detail elsewhere.

6 Discussion

We presented an analysis for partly coherent and partly incoherent body waves generated by a (teleseismic) wave packet remotely incident on a slab (the crust) containing a medium consisting of a deterministic component and a random field, based on the dyadic parabolic decomposition of phase space coupled to the scaling of the random fluctuations. The deterministic component consists, here, of a planarly layered medium, but can be generalized to contain conormal singularities (discontinuities) combined with smooth wave speed variations. The wave packets provide a frame to represent and study partly coherent wave fields.

To obtain information about the deterministic medium component, one needs to consider “field-field” cross correlations. We showed that these cross correlations are characterized by a transformation (blurring filter) of the random paraxial Green's function, between the points at which the fields are taken, the transformation containing information about the statistics of the random fluctuations. If the points are taken purely transverse to the propagation direction of the wave packet in the deterministic component, the blurring significantly increases, which is consistent with the usual stationary phase arguments. In general our results fully characterize the cross correlation function in the regime in which the source and random medium scaling is such that the waves remain concentrated in phase space.

^☆ This research was supported by NSF ARRA grant DMS 0908274. The authors thank the Mathematical Sciences Research Institute for partial support; they also thank the members of the institute for providing a very stimulating environment during the Inverse Problems and Applications program in Fall 2010.