1 Introduction
Landscape topography is rapidly evolving under the influence of human exploitation of natural resources (including agriculture, mining and habitat), and anthropogenic activities are now cited as the most important geomorphic agent acting on the planet's surface (Wilkinson and McElroy, 2007). Among the various associated activities, agriculture is often reported as a strong determinant of the accelerated erosion processes that lead to significant geomorphological changes (Cerdan et al., 2010; Defersha et al., 2012; Dotterweich et al., 2012; Poesen et al., 2003). At the outlet of river basins, the resulting sediment production (either in the form of dissolved or particulate matter) is exported from the continental areas to the seas. Recent regional quantifications permit the approximation of both the local production and the portion that is exported.
With respect to the soil surface erosion, several studies carried out at the European scale have calculated regional estimates. Kirkby et al. (2008) elaborated a physically based modelling approach known as the PESERA model, which combines a hydrological model with a crop growth model and a sediment transport equation to derive the mean monthly erosion rates at a resolution of 1 ha pixel size. Cerdan et al. (2010) collected an extensive set of observed data to develop an empirical extrapolation of the current mean water erosion rates, which were completed by values for tillage erosion (Van Oost et al., 2009). Despite the local discrepancies in specific contexts, the average regional figures for erosion rates calculated by different methodologies are consistent, on the order of 1–2 t ha−1 yr−1, with variation mainly dependent on land use, topography and soil characteristics. The different estimates also converge on strong spatial heterogeneities of the erosion rates, with high rates only occurring in less than 20% of the area. No such regional estimates exist for the quantification of the distributed local rates of chemical erosion. However, several local quantifications of regolith formation have been carried out in different contexts, which provide a range of reference rates for parent material erosion and soil production and are mostly influenced by lithology, climate and topography (e.g., Heimsath and Korup, 2012). These quantifications are often based on the use of cosmogenic nuclides approaches or more recently on U-series isotopes (Chabaux et al., 2003; Dosseto et al., 2006, 2011; Ma et al., 2010).
At the river basin scale, the calculation of correct sediment budgets is often a difficult task due to the poor availability and reliability of sediment flux data (Meybeck et al., 2003; Walling and Fang, 2003). Various methods can be used to estimate the sediment fluxes and can be divided into three categories: averaging estimators, ratio estimators, and rating curves. In averaging approaches (or interpolations), only the available data for flow rate (Q) and sediment concentration (C) are used to estimate the average sediment loads. Methods based on the ratio estimators are derived from Beale (1962) and account for the covariance between the sediment load and the streamflow values. Finally, rating curves are founded on the establishment of a regression between available values of Q and C, which are subsequently used to extrapolate the C values for the periods with the available Q values. The classical form of a rating curve is a power law in the form of C = aQb, with a and b as the parameters to be calibrated. Classic rating curves are therefore based on the hypothesis of a unique relationship between Q and C and on the assumption that an instantaneous C depends only on Q at any given moment and not on the historical Q. However, the sediment redistribution processes that occur at the origin of sediment fluxes in rivers are not homogeneous in space and time (seasonal variations, flow dynamics, hysteresis, etc.). To take into account these variations, subdivisions can be performed on the datasets; certain authors divide their datasets into two discharge classes of low or high flow (Dolan et al., 1981; Preston et al., 1989; Quilbe et al., 2006). Datasets can also be divided into seasonal classes or the rising limbs (RL) and falling limbs (FL) of the hydrograph (Walling and Webb, 1981) for consideration of temporal variations. Moreover, to take into account the Q chronicle dynamic, an improved rating curve approach (IRCA) was developed by Delmas et al. (2011). The IRCA method was developed to estimate the mean annual specific sediment fluxes (MASSF) from infrequent datasets. This approach differentiates between rising and falling Q and also considers the effect of Q variations. Determination of weather fluxes on large rivers is also often based on short-term monitoring (Gaillardet et al., 1999, 2003), resulting in incomplete time series and low sampling frequencies (e.g. Stallard and Edmond, 1983); few studies consider long-term monitoring (Grosbois et al., 2001; Ollivier et al., 2010; Tipper et al., 2006). Négrel et al. (2007) and Petelet-Giraud and Négrel (2011) defined a dedicated methodology for calculation of weathering fluxes on the Ebro River basin. The aim of this approach was to evaluate the export fluxes for the dissolved loads at the catchment scale over several decades using data compiled from a national databank. The calculations are based on chemical data (Ca, Na, K, Mg, Cl, SO4, NO3, HCO3) and physico-chemical parameters (mainly electrical conductivity, EC) together with discharge values (Q) corresponding to the sampling date over long periods.
The different published rates for sediment exports obviously differ from one river basin to another but are globally one to two orders of magnitude lower than the published rates of local physical soil erosion (e.g., Dupré et al., 2003). As illustrated by Delmas et al. (2012: Fig. 1), a strong decrease in the physical erosion rates is observed when moving from the local scale (m2) to the river basin scale (> 103 km2). The chemical erosion rates are less sensitive to scale and can either decrease or increase with increasing area as a function of lithology, anthropogenic land management and topography (Gaillardet et al., 1999; Granet et al., 2007; Viers et al., 2009).

Theoretical relationship between the spatial scale and published mean sediment concentration derived from erosion rates in agricultural temperate areas of northwestern Europe (over the loess belt) for arable lands with slopes between 2% and 5% after Delmas et al. (2012) ((1) Fox and Bryan, 1999; (2) Leguédois and Le Bissonnais, 2002; Poesen et al., 2003; (3) Cerdan et al., 2004; Van Rompaey et al., 2003; (4) Milliman et al., 1995).
Relation théorique entre l’échelle spatiale et la concentration moyenne de sédiment publiée, dérivée des taux d’érosion des zones agricoles tempérées de l’Europe nord-occidentale (au-dessus de la ceinture loessique) dans le cas des terres arables à pente de 2 à 5 %, selon Delmas et al. (2012) ((1) Fox et Bryan, 1999; (2) Leguédois et Le Bissonnais, 2002; Poesen et al., 2003; (3) Cerdan et al., 2004; Van Rompaey et al., 2003; (4) Milliman et al., 1995).
The relationship between the local soil erosion and the sediment export is therefore non-linear, and most of the sediment budget modelling exercises do not explicitly distribute all of the processes involved; instead, they rely on empirical rating curves (e.g., Gao and Pucket, 2011) or on the empirical sediment delivery ratio concept (e.g., Wilkinson et al., 2009). In this context, the objectives of this article are two-fold:
- • to produce reliable coarse regional estimates of the mean local physical and chemical erosion rates and the mean export of dissolved and suspended matter for the main French river basins; and
- • to investigate the differences between the local and regional scales according to the different lithological and geomorphological contexts of the different basins. To this end, this study will be based on the use of an extensive French database for values of flow and suspended and dissolved matters.
2 Methodology
Calculation of the suspended sediment load for the main French rivers. Discharge data (Q) are available at a daily frequency (automatically calculated from continuous stage records), whereas the collected sediment concentration (C) data are often characterised by infrequent sampling; French water quality monitoring frequency occurs ca. once per month. The IRCA method (Delmas et al., 2011), which uses a sediment stock indicator function S(t), is calculated from Q(t) using a station-independent procedure. Strong reductions of S are assumed to occur during rising flows while smoothed and delayed increases of S occur as the flow decreases. The rating curves used in the IRCA have the following form:
To conduct such an approach independent of the sampling frequency, the number of C-Q pairs must be higher than 120 for estimation of the sediment flux with an uncertainty of ca. 10% (Cheviron et al., 2011). For the main French rivers, the collected data generally cover more than 25 years, and this limitation therefore does not apply. The IRCA method permits the calculation of exports for the Meuse, the Vilaine, the Gaves-Adour, the Loire, the Seine, and the Garonne Rivers. For the Rhône River (19% of the total drained area), a more accurate monitoring exists (from the Rhône River Observatory Station in Arles; Eyrolle et al., 2010) with daily C and Q measurements. From these data, a daily dataset could be constructed from 2001 to the present, allowing the direct calculation of the suspended sediment flux.
2.1 Calculation of the dissolved load for the main French rivers
A selection of monitoring stations was performed to additionally characterise the main French catchments (Meuse, Vilaine, Gaves-Adour, Loire, Seine, Garonne, Rhône). The methodology designed to calculate the dissolved load was detailed by Petelet-Giraud and Négrel (2011). Briefly, the daily river discharge over the longest period is combined with data for electrical conductivity (EC), and the available complete chemical dataset (Ca, Na, K, Mg, Cl, SO4, NO3, HCO3, SiO2) was also used.
The total dissolved solids (TDS, mg L−1) was calculated as the sum of the dissolved major ions and was compared with the electrical conductivity (EC, μS cm−1) because both reflect the water ionic content, i.e., the dissolved load corresponding to the water salinity.
The relationship between the parameters EC and TDS occurs generally in the form of a linear model: TDS (mg L−1) = b × EC (μS cm−1). The annual dissolved load exported by a river corresponds to the instantaneous TDS concentration in the river multiplied by the instantaneous discharge (W) of the river. However, the chemical analyses are not systematically carried out in contrast to the EC, which is measured more frequently, generally on a monthly basis. The correlation between EC and TDS allows assessment of the TDS when only the EC is available. Thus, the co-variation between the daily discharge (W) and the punctual measured EC was investigated, and the best correlation for the Loire River at Nantes was obtained with a power fit equation (EC = a.Wb), as illustrated in Fig. 2.
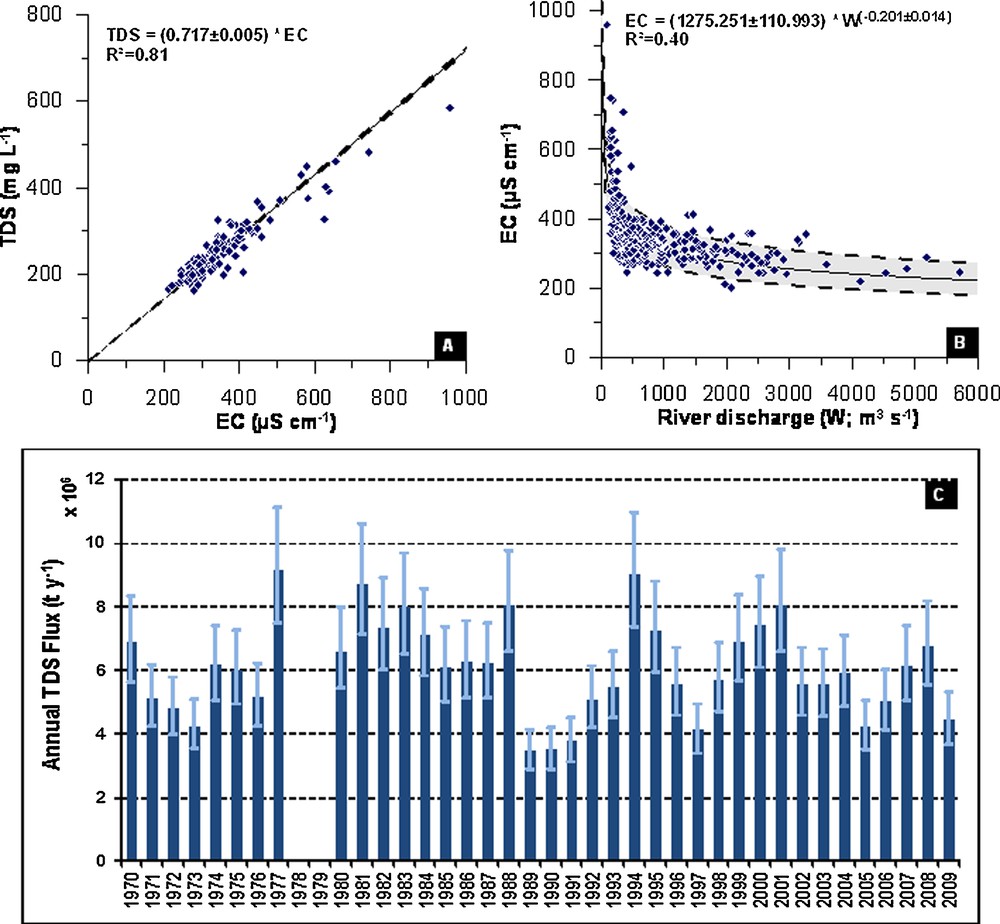
A. Relationship between TDS (mg L−1) and EC (μS cm−1) for the Loire River samples from the Nantes Station. B. Relationship between EC (μS cm−1) and Loire River discharge (W; m3 S−1) at the Nantes Station. C. Annual TDS flux (t y−1) of the Loire River at the Nantes Station over the period 1970–2009.
A. Relation entre TDS (mg L−1) et EC (μS cm−1) pour les échantillons de la Loire en provenance de la station de Nantes. B. Relation entre EC(μ cm−1) et le débit de la Loire (W ; m3 S−1) à la station de Nantes. C. Flux TDS annuel (t an−1) de la Loire à la station de Nantes sur la période 1970–2009).
Finally, the annual flux of the dissolved material can be calculated as the sum of the daily fluxes (F = TDS × W). The robustness of the flux calculations was systematically tested for each step of the flux calculation by adding and subtracting the standard deviation (SD) value to the mean value in both equations EC = (a ± SDa) × W(c ± SDc) and TDS = (b ± SDb) × EC. This process is illustrated in Fig. 2 for the Loire River over the period studied from 1970 to 2009 and was calculated for complete years, i.e., when daily discharge data are available for each day of the hydrological year together with the calculated uncertainty. The annual dissolved flux ranges from 3.5 (± 0.6) × 106 t y−1 in 1989 and 1990 to 9.1 (± 1.8) × 106 t y−1 in 1977 and 1994. The mean annual dissolved flux of the Loire River at the Nantes station is 6.09 × 106 t y−1 (n = 38), and the dissolved flux variation from one year to another one is mainly controlled by the river discharge variations.
2.2 Calculation of the soil production and erosion rates
At the national scale, the soil production is estimated using a soil production function based on soil depth in regions with hard bedrock. This soil production is viewed as a conversion of hard rock to loose material that results in a lowering of the boundary between the rock and the soil. Two main soil production functions can be implemented, and the first shows an exponential decline with increasing soil depth (Heimsath et al., 1997). An alternative soil production function, known as the ‘humped model’, was proposed by Humphreys and Wilkinson (2007). The humped model suggests that the bedrock-lowering rates reach a maximum value for a given soil depth that is not equal to zero. The main idea is that a minimal soil thickness is necessary to permit the water retention that will increase both the chemical and physical weathering of the bedrock. Among the various forms of the humped model, we use the function developed by Minasny and McBratney (2006) in the form of a double exponential model:
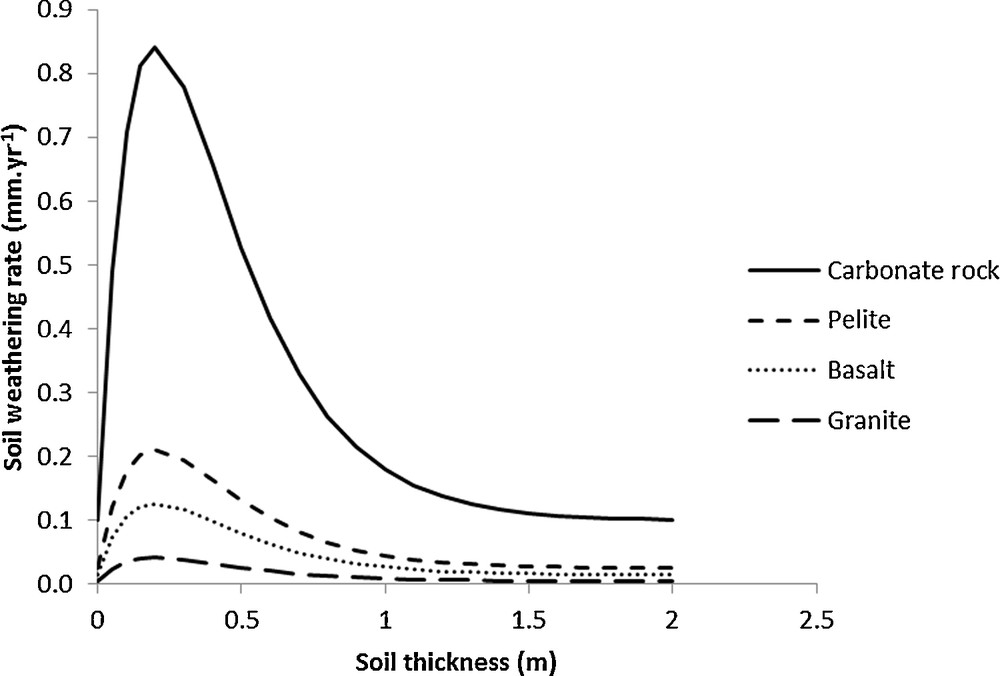
Soil weathering rates according to soil thickness and bedrock type.
Taux d’altération du sol en fonction de l’épaisseur du sol et du type de roche mère.
These relative rates are 1 for granite, 3 for basalts, 5 for pelites, and 20 for carbonate rocks. The 1:1 M French Soil Geographical Database (FAO, 2012) was used to derive the major rock types and soil depths. The database is composed of soil-mapping units (SMU) that regroup the Soil Typological Units (STU) of known mean soil depth. A single mean soil depth is calculated for each SMU according to the soil depth of each STU weighed by its relative area. At the 1:1 M scale, this single mean soil depth for each SMU does not account for the influence of relief, although it is a major factor of soil depth variation (Catani et al., 2010; Saulnier et al., 1997). Therefore, the soil depth value is adapted for each SMU according to the local slope intensity:
The soil erosion rates estimates are derived from a large dataset covering 2741 plot-years from 81 experimental sites located in 19 European countries (Cerdan et al., 2010). Based on this database and on large-scale land use (CORINE), soil (Soil Geographical Database of Europe), and topography (SRTM) datasets for Europe; a water erosion map was produced at a 100-m resolution by applying correction factors for land use, slope gradient, stoniness and slope length using the methods described in Van Oost et al. (2007). The effect of soil texture was also included in this work using the soil erodibility classes for Europe proposed by Le Bissonnais et al. (2005).
3 Results and discussion
3.1 Sediment export
The resulting mean flux of the suspended sediment export to the sea is presented in Table 1. A total of ca. 14 Mt yr−1 is estimated for the main French rivers. The Rhone River contributes 69% to the total sediment export for France, but its contributing area is only 23% of the total considered area. This result highlights the importance of the spatial variability within the drained areas because no relationship is observed between the sediment exports and the catchment area (Fig. 4).
Charges (totales) moyennes annuelles en suspension et dissoutes exportées par les principales rivières de France.
| Rivers | Drained areas (103 km2) | Mean Annual Suspended Loads |
Mean Annual dissolved total Loads (Mt/yr) |
Total export (Mt/yr) |
% of dissolved loads |
| Loire | 115.5 | 0.9 | 6.1 | 7 | 88 |
| Rhône | 83.6 | 9.6 | 15.4 | 25 | 62 |
| Garonne | 71.3 | 1.9 | 4 | 6 | 68 |
| Seine | 64.8 | 0.8 | 8.1 | 9 | 91 |
| Gaves-Adour | 13.1 | 0.5 | 1.8 | 2 | 78 |
| Vilaine | 10.2 | 0.1 | 0.4 | 1 | 80 |
| Meuse | 7.1 | 0.2 | 1.4 | 2 | 88 |
| Total | 366 | 14 | 37 | 51 | 73 |

a: dissolved fluxes – TDS – (t y−1); b: total suspended sediment fluxes – TSS – (t y−1); c: specific dissolved fluxes (t km−2 y−1), d: specific total suspended sediment fluxes (t km−2 y−1) versus the basin area (×106 km2). Literature data are from Gaillardet et al. (1999), except the Loire at Orleans (Grosbois et al., 2000), Ebro_T: Ebro at Tortosa (Négrel et al., 2007), and Garonne (Semhi et al., 2000).
a : flux dissous – TDS – (t an−1) ; b : flux totaux de sédiment en suspension – TSS – (t an−1) ; c : flux spécifiques dissous (t km−2 an−1) ; d : flux totaux spécifiques de sédiment en suspension (t km−2 an−1) en fonction de la surface du bassin (× 106 km2). Les données de la littérature sont tirées de Gaillardet et al. (1999), excepté pour la Loire à Orléans (Grosbois et al., 2000), l’Ebro_T : l’Ebre à Tortosa (Négrel et al., 2007) et la Garonne (Semhi et al., 2000).
The lack of correlation between the specific sediment yield and the basin area also emphasises the importance of considering the spatially distributed parameters in reproduction of the river sediment budget and also shows the limitation of approaches based on the SDR ratio that rely on the existence of such relationships (e.g., Gao and Pucket, 2011). The mean annual total dissolved loads are also presented in Table 1 and Fig. 4. In this study, which focuses on the general regional trends, we consider only the total DSL, including atmospheric inputs and anthropogenic activities. Depending on the catchment land management policies, the DSL resulting from weathering processes may therefore represent only a portion of the calculated exports. As an illustration, Roy et al. (1999) found that 25% of the total DSL is derived from anthropogenic sources for the Seine at Paris. The percentage of the Rhône contribution to the total French DSL (ca. 40%) is less important than that of the SSL, with the collective contribution from the Seine (22%), the Loire (16%) and the Garonne (11%) showing more significance.
The total exports from French rivers amount to ca. 51 Mt yr−1, and the proportion of the total dissolved loads represents ca. 70%, ranging from 60% (Rhône) to 90% (Seine). Several studies (Gaillardet et al., 1999; Millot et al., 2002; Roy et al., 1999; Viville et al., 2012) have shown that the physical erosion rates (i.e., the suspended particulate load) are correlated with the silicate weathering rates (i.e., excluding all other dissolved contributions from carbonate or evaporite). However, in this study, the correlation between a specific DSL and the SSL is rather weak and is only significant if we discard the Meuse River. A first explanation is related to the mode of calculation. In this work, we calculated the total dissolved load fluxes (including the weathering of silicates, carbonates or evaporites) and the anthropogenic contribution, but only silicate weathering fluxes were considered in the other studies (Gaillardet et al., 1999; Millot et al., 2002; Roy et al., 1999). This observation implies that the relationship between the weathering rates and physical erosion rates is only valid for steady-state rivers that are not significantly impacted by human activities. As a supplementary example, in the Loire River, Grosbois et al. (2001) showed that the suspended matter load does not correlate with the dissolved load due to the generalisation of human impacts on the river (agricultural activities, dams, etc.). Another explanation, specific to the study by Gaillardet et al. (1999), shows more contrasted situations of chemical and physical erosion rates that were spread over several order of magnitudes and were often not affected by anthropogenic activities.
3.2 Discussion of the link between erosion and sediment export
It is commonly reported that the majority of in-stream sediments originate from the erosion of upstream areas (Gao and Pucket, 2011; Quilbe et al., 2008; Wilkinson et al., 2009). However, the relationship between upland erosion and sediment export is not straightforward because only a small fraction of the eroded particles generally contributes to river exports to the sea. In such erodible agricultural lowland as the Seine basin, most of the produced sediment is deposited locally on the hillslope (Delmas et al., 2012). For the finer particles, which have a longer travel distance, once the sediment reaches the stream, a substantial proportion is deposited in riverbeds, on floodplains, and in reservoirs (Wilkinson et al., 2009). Fig. 5 shows the specific sediment yield (t km−2 yr−1) of the main French rivers plotted against the mean soil surface erosion of the corresponding areas. On average, the SSY values are an order of magnitude lower than the erosion rates. The largest difference is shown for the Vilaine catchment, where only 4% of the eroded sediment is exported, and the minimum difference is shown for steeper catchments such as the Gaves or the Rhône, which have the highest SDR. Overall, the general scatter indicates the absence of good correlation between upland erosion and sediment export, and a given mean erosion rate can correspond to very different basin behaviour.
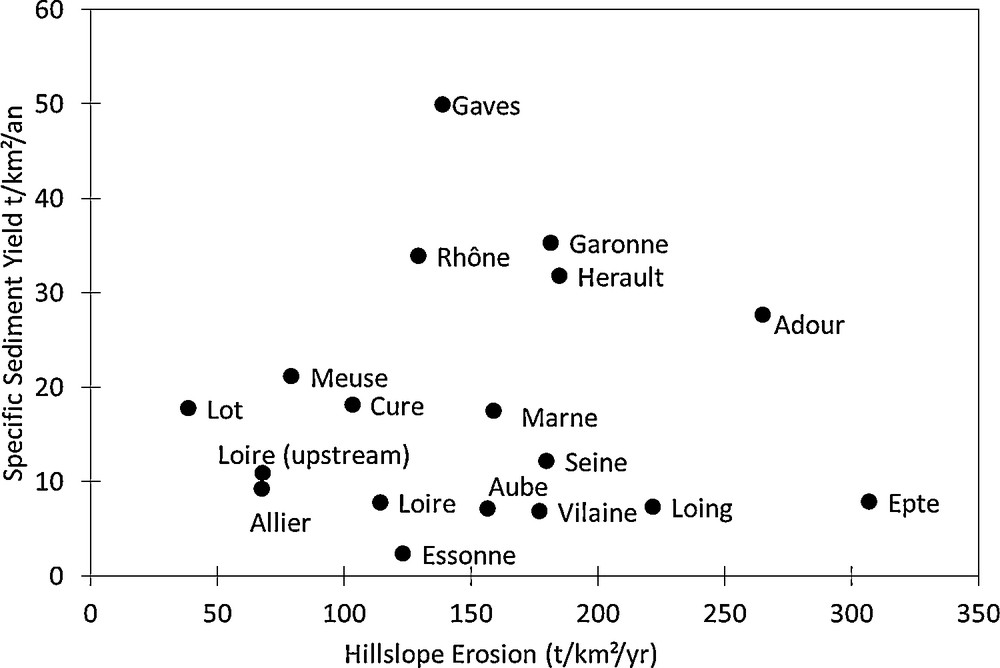
Specific sediment yield (t km−2 yr−1) of the main French rivers plotted against the mean soil surface erosion of the corresponding areas as calculated by Cerdan et al. (2010).
Débit spécifique de sédiment (t km−2 an−1) des principales rivières françaises, enregistré en regard de l’érosion moyenne de surface du sol des zones correspondantes, selon les calculs de Cerdan et al. (2010).
To explain this variability, the different compartments of the drained area that constitute sources, sinks and pathways must be considered. These compartments correspond to sediment redistribution processes on the hillslopes and in the river channel. The erosion processes that occur on slopes or in riverbeds constitute sources of sediments and sediment deposits on hillslopes or constitute sinks in the river channel. The deposition of sediments on a floodplain occurs when the river flows over its bank during flood events. This term of the sediment budget may represent an important component of the fluvial suspended sediment budget (Meade, 1994; Owens et al., 1999; Phillips, 1991). As functions of the river basin typology, landscape, and geomorphologic behaviour, these processes may be more or less influential on the sediment budget. In small hilly catchments, the erosion processes may dominate because the proportion of deposition areas (i.e., floodplains) is reduced. Referring to the sediment budget for the Lake Tahoe (California), Stubblefield et al. (2009) underlined the effect of vegetation cover and geological context, identifying the tributaries to the lake as the major sources. The sediment budgets described by Porto et al. (2010) for three Italian catchments show various expressions of the sediment sources and sinks as compartments in the budget and as a function of the catchment area: with increasing area, the proportion of deposition areas increases, and an increasing part of the detached sediments is deposited before reaching the catchment outlet. Variations in the sediment budget also depend on the climate and the meteorological event intensities, e.g., in Mediterranean contexts, the erosion processes due to extreme events may represent a major source of the sediment budget (Ollivier et al., 2010). In contrast, in low-land rivers under temperate conditions, a high proportion of sediments are deposited on floodplains, constituting important sediment storage depots (Delmas et al., 2011; Walling et al., 2006). Walling and Collins (2008) exposed various examples of sediment budget expressions due to the particular geographic, geomorphologic, and land management contexts. To investigate the importance of these processes for the French river basins, we have weighted the upland erosion rates with a simple connectivity index that combines information on slope, lithology and rainfall (Hillslope diffuse erosion × catchment slope + Mass Movement × Rainfall – Deposit; Mass movement and deposit are defined as in Delmas et al., 2009). Although a residual variability still exists, Fig. 6 shows the relevance of using these parameters to describe the sediment redistribution within the river basin and confirms the predominant role of surface connectivity, which is the principal explanatory factor used to characterise the fraction of sediment exported out of river drainage areas.
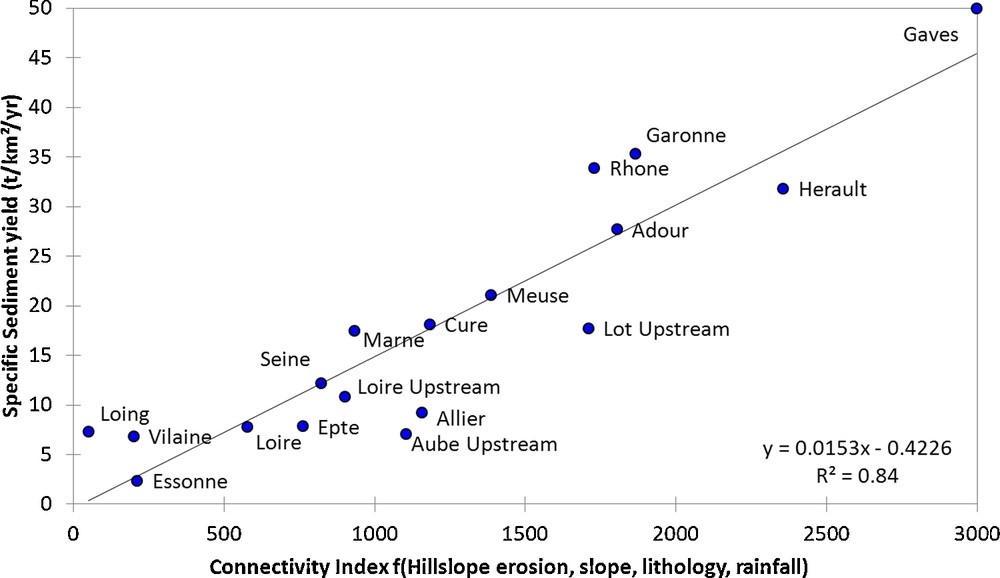
Specific sediment yield (t km2 yr−1) of the main French rivers plotted against the mean soil surface erosion of the corresponding areas weighted by a connectivity index that combines information on topography, lithology and rainfall.
Débit spécifique de sédiment (t km−2 an−1) des principales rivières françaises en fonction de l’érosion moyenne de surface du sol des zones correspondantes, pondérée par un index de connectivité qui combine les informations sur la topographie, la lithologie et la pluviosité.
The connectivity term is often used in surface hydrology to describe the internal linkages between the runoff in the upper parts of catchments and the corresponding sinks; the connectivity should also act as a valuable descriptor when studying sediment transfer. Hooke (2003) has shown that sediment production, transport, and delivery to downstream river channels depend not only on the catchment physiography, but also on the spatial organisation inside the catchment. Indeed, the spatial variability characterised by the relative location of each sub-area, the connectivity between areas that produce runoff, and the infiltrating areas are required to link the hydrological properties at the field and catchment scale; this relationship can be transposed for the connectivity between erosion and deposition areas (Bakker et al., 2008; Cerdan et al., 2004). Cammeraat (2002) and Cerdan et al. (2004) worked in different environments and found that scale effects on the erosion processes that occur between plots and catchments can be explained by the spatial configuration of the hydrological units and their connection to the flow network system. In the same line of reasoning, Rejman et al. (1999) argued that sediments collected from erosion plots are derived mainly from the zones closest to the outlet and outlined the role of the sediment travel distance from the sources to the outlet as well as their connection. These considerations would lead to a newly defined structure within the drained area that can describe the potential transfer of sediments downstream.
With respect to the export of dissolved sediments originating from weathering processes, the catchment physiography and connectivity no longer play the dominant roles. As shown in Fig. 7, there is a direct link between the soil production rates and the exported dissolved fluxes. In contrast to the suspended particles, which are transport-limited, the dissolved matter seems to be supply-limited.
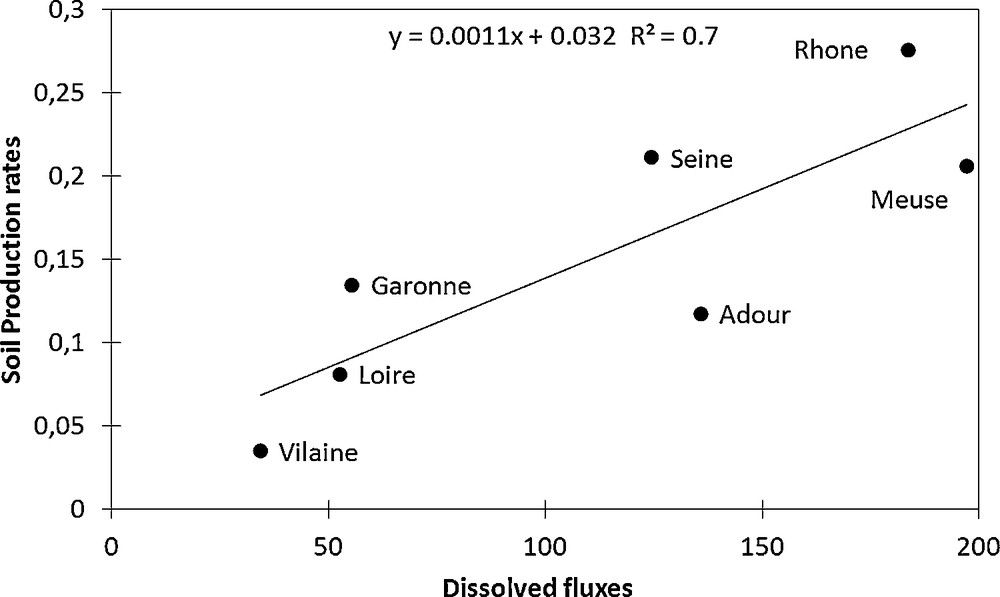
Total dissolved fluxes of the main French rivers plotted against the mean soil production rates calculated for the different catchments.
Flux totaux dissous des principales rivières de France en fonction des taux de production moyens de sol, calculés pour les différents bassins hydrographiques.
4 Conclusion
The compilation of an extensive and consistent database of the suspended and dissolved sediment loads for the main French rivers have permitted calculation of the sediment export fluxes from the continental areas to the seas. The resulting total flux of the suspended sediment export to the sea for the main French rivers amounts to ca. 14 Mt yr−1. The Rhône River contributes 69% of the total sediment export for France whereas its drainage area represents only 23% of the total considered area. In addition to the result that no relationship was found between the sediment exports and the drained area, this observation highlights the importance of the spatial variability within the drained areas. With respect to the mean annual total dissolved loads, we only considered the total DSL, including atmospheric inputs and anthropogenic activities. The percentage of the Rhône contributions to the total French DSL (ca. 40%) is less important than that of the SSL, and the total contribution from the Seine (22%), the Loire (16%) and the Garonne (11%) is more significant. The total export from French rivers is ca. 51 Mt yr−1, and the proportion of the total dissolved loads account for ca. 70%, ranging from 60% (Rhône) to 90% (Seine). We could also investigate the relative importance of the source terms in the sediment budgets of the different rivers. We have weighted the upland physical soil surface erosion rates with a simple connectivity index that combines information for slope, lithology and rainfall, demonstrated the relevance of using these parameters to describe the sediment redistribution within the river basin, and confirmed the predominant role of surface connectivity in characterising the fraction of sediment exported out of the river drainage areas. With respect to the export of dissolved sediment originating from weathering processes, the catchment physiography and connectivity no longer play the dominant roles. A direct link between soil production rates and the exported dissolved fluxes showed that, contrary to the transport-limited suspended particles; the dissolved matter seems to be supply-limited. The perspective offered by this study incorporates the proposed connectivity indices in a dynamic and distributed modelling approach. A distributed approach could provide a conceptual framework that includes all of the processes that play a role in sediment production and transfer that were not investigated in this study, such as gully and bank erosion. The interactions of these processes with the different forms of transport (including bedload) would facilitate the evaluation of the different temporal dynamics of the sediment exports.


