1 Introduction
Groundwater reserves are important exploitable water resources. Unfortunately, the intensive agriculture practised today requires the use of fertilizers and pesticides in large quantities and, sometimes, in an uncontrolled way, and significantly reduces the quality of groundwater (Ibnoussina et al., 2006; Laftouhi et al., 2003; Saâdi et al., 1999; Teijón et al., 2010; Worral and Kolpin, 2004).
To control the potential contamination of groundwater by pesticides, it is essential to understand the transport process involved (Kodešová et al., 2011). The approaches used include a field study conducted in natural agro-pedo-climatic conditions (Candela and Mariñô, 2004; Rekolainen et al., 2000), and a simulation using mathematical models (Beven, 2012).
Russo et al. (1994) studied the effects of variations of the soil water content on pesticides leaching in agricultural unsaturated zones. Kuntz and Grathwohl (2009) studied the simulation of pollutant flow and transport of two reactive compounds, i.e., lindane and phenanthrene, in a column of the unsaturated zone. They were interested in the validity of the hypothesis of a continuous stream percolation in the deterministic models, from local to larger scales.
Our study is focused on the modelling of transport of carbofuran, which is a broad-spectrum insecticide–nematicide that belongs to the carbamates chemical family. Carbofuran gives rise to harmful effects on human health and environment. Several previous studies showed that the mobility of carbofuran in a sandy soil was lower in organic matter, and presents an environmental problem, such as high potential leaching (Dahchour, 1995; Krishna and Philip, 2008). According to its mobility index (GUS = 3.75, Gustafson, 1989), this pesticide is leached easily after a heavy rainfall or a repetitive irrigation (Dahchour, 1995; El Mrabet, 2002). However, results of soil column suggest that there are real possibilities for carbofuran to reach relatively deep aquifers (Moreal and Van bladel, 1983).
To understand the mechanisms of this substance transport in sandy soils, and to study its impact on groundwater contamination, we carried out an experimental study of the water movement and the transport of both carbofuran and an anionic tracer flow (KBr) (Hmimou et al., 2011), on the bare soil of an experimental plot in the Mnasra region (Morocco). Particular attention was paid to the unsaturated soil, the location of the main flow and the transport process. On the other hand, to better evaluate the risk of groundwater contamination by carbofuran, we used a mechanistic mathematical model developed by the Interdisciplinary Laboratory Environment and Natural Resources (LIRNE) and validated on experimental data collected from the study site. It should be noted that the degradation products of carbofuran were not traced.
The developed model can reproduce the fate of carbofuran in the unsaturated zone, depending on the irrigation system used. Such simulations need an advanced hydrodynamic characterization of the soil. Hence, we carried out negative charge infiltration experiments at several locations in the experimental station (Perroux and White, 1988; Tamoh and Maslouhi, 2004).
2 Materials and methods
2.1 Study area
The study area is the experimental station (CDA 236) located in the Mnasra area, about 30 km north of the city of Kenitra, in northwestern Morocco (Fig. 1).
The Mnasra region showing the studied site location.
Mnasra region is a strip of land parallel to the Atlantic coast, of about 50,000 ha, located on the right bank of the Sebou River, 7 to 14 km wide and over about 50 km in length extending from the North of the Kenitra City. It is characterized by a diversity of crops, such as cereals, sugar beet, fodder and vegetables. The experimental site is equipped with a weather station that provided various data, such as rainfall and minimum and maximum temperatures (Fig. 1).
2.2 Description of experiments
The experiment was carried out on a 200-m2 field with flat topography, subdivided into ten basic 4 × 5m2 plots. This study is focused on uncultivated plots on which are applied a Br and carbofuran flow tracer, and on an uncultivated and untreated control plot.
The site sandy soil was classified as an Alfisol, according to U S Soil Taxonomy (Soil Survey and Staff, 1999) and a sandy loam according to the USDA (USDA-SCS, 1975). Its physicochemical characteristics are presented in Table 1.
Physicochemical characteristics of the soil.
| Depth (cm) |
pH | Organic matter (%) |
Clay (%) |
Loam (%) |
Sand (%) |
Bulk density (g·cm−3) |
| 0–20 | 7.04 | 1.41 | 10.00 | 7.45 | 82.75 | 1.55 |
| 20–40 | 6.97 | 0.62 | 9.65 | 7.95 | 82.36 | 1.76 |
| 40–60 | 7.59 | 0.58 | 9.20 | 8.60 | 82.40 | 1.69 |
The tracer used is an anionic tracer (Br–) form (KBr). It was applied with a dose of 61.77 g/m2. The carbofuran C12H15NO3 (2,3-dihydro-2,2-dimethylbenzofuran-7-yl-N-methyl carbamate) of the commercial product Furadan was applied with a dose of 4 g/m2 based on active ingredient. Carbofuran has a solubility of 700 mg/L and a low vapor pressure, i.e., 3.41 × 10−6 mmHg at 25 °C. The half-life of carbofuran reaches values ranging from 25.7 to 107 days in soils with pH values and temperatures close to those of our experiments (El Mrabet, 2002). An injection mode was used in a slot corresponding to the injection of a constant concentration for a certain time. Spatial variability was considered by many measurement reiterations on average three times. The solutes were injected using a pulverizer, advancing at a constant speed while keeping the same nozzle flow rates to ensure a homogeneous application. The application of solutes was followed by a first irrigation during the monitoring period. The cumulative amounts of precipitation and irrigation were 62 mm and 160 mm, respectively. Irrigation was carried out with a sprinkler. Evapotranspiration was calculated on a daily basis from observed in situ data.
The spatio-temporal monitoring of physical and chemical parameters, such as humidity, temperature, bromide and pesticide concentrations in the soil was conducted for 90 days.
Samples were collected using an auger from the following depths: 0–20 cm, 20–40 cm and 40–60 cm. No trace of carbofuran or bromide was detected at all levels before treatment.
Determination of bromide in soil samples was carried out by ion chromatography using a Metrohm 881 Compact IC Pro, with a detection limit of 0.1 mg/L (Tirumalesh, 2008).
It should be noted that another method of bromide analysis was carried out by XRF following the procedure of Margui et al. (2009). The comparison between the two methods was statistically evaluated, leading to similar results (Hmimou et al., 2011).
The carbofuran was analyzed by liquid chromatography using a HPLC device: LCQ Advantage Max, Brand Thermo Electron equipped with a type BDS Hypersil C18 (150 × 4, 6 mm × 5 μm) column.
2.3 Hydrodynamic characterization
The hydrodynamic characterization of the plot soil is performed in situ using a disc infiltrometer with the negative charge method. Several infiltration measurements are conducted. For the retention curve h(θ), we use the expression of Van Genuchten (1980):
| (1) |
| (2) |
2.4 Flow and transport model
Water movement in the unsaturated soil can be described by Richard's equation as follows:
| (3) |
The transport of an interactive and non-conservative solute in the vadose zone is described on the basis of the advection–dispersion equation assumed in the model. It also incorporates a homogeneous reaction, i.e., pesticide degradation described by first-order kinetics:
| (4) |
and , (5)
where R is the retardation factor, a dimensionless quantity, C is the solute concentration (M L−3), Da is the apparent hydrodynamic dispersion coefficient (L2 T−1), qz is the Darcian water flux (LT−1), μ is the degradation coefficient (T−1), ρ is the bulk density of the porous medium (M L−3), Kd is the distribution coefficient (L3 M−1). μw and μs are the degradation constants in the solid and the liquid phase, respectively.
Before the beginning of the experiment, we measured the water contents for each soil profile, since we are dealing with a homogeneous soil. Consequently, we can define an initial uniform water content profile with an average value of θ0 = 0.11 cm3/cm3. The solute is not present initially in the field. The initial conditions are expressed as:
| (6) |
| (7) |
At the upper boundary of the flow model, we applied a Neuman type flux boundary condition:
| (8) |
At the upper boundary of the transport model, the total advective and dispersive mass fluxes of solutes were prescribed as functions of time:
| (10) |
For the lower limit, we consider a gravity flow condition:
| (11) |
The solute convective flux is, in this limit, expressed by:
| (12) |
Richard equations and advection–dispersion equation (ADE) (Eqs. (3) and (4)) accompanied by their initial and boundary conditions were solved by a numerical finite difference scheme (Crank–Nicolson). Once all discretisations were established, a tridiagonal, and symmetric linear system of equations is obtained, which was resolved by the (SOR) algorithm. The non-linearity of equation (3) was resolved by initializing, at each time step ti, the c(h) term at time ti, and then doing as many iterations as necessary to reach an invariable solution.
At each time step, we resolved first equation (3), and then we used its solution in equation (4) to resolve it.
Parameters Hg, n, ks and η were calibrated by comparing the simulated and measured water contents. Parameter λ was calibrated by comparing the simulated and measured bromide concentrations, while kd, μs and μw were calibrated by comparing the simulated and measured concentrations of carbofuran.
The calibration was done by minimizing the RMSE error between measurement and simulation:
| (13) |
3 Results and discussion
3.1 Retention curve θ (h) and hydraulic conductivity K (h)
After several infiltrometer measurements at different pressures, we were able to reconstruct a part of the retention curve θ (h) (Fig. 2), the value θr was taken equal to zero, since the soil is very sandy and has a very low capacity to retain water in dry-state conditions. In Fig. 2, the experimental points are aligned with the fitted curve, hence justifying our choice of Van Genuchten's model (Van Genuchten, 1980). The results of this adjustment are presented in Table 2.
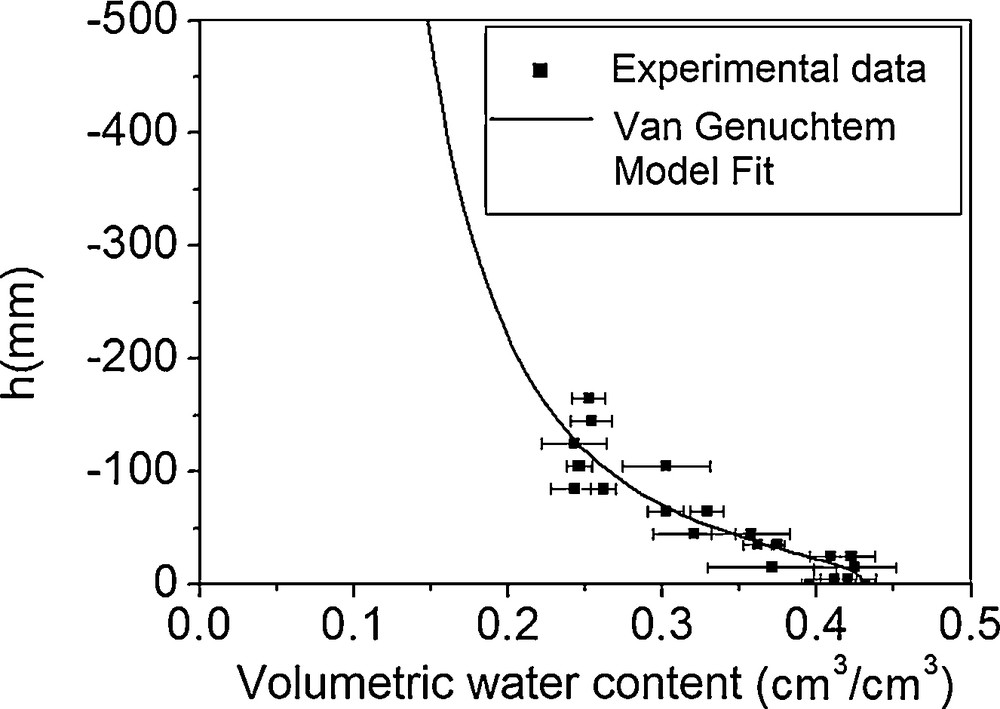
Suction curve for the studied soil.
Values and standard deviation of the parameters of the Van Genuchten model θ (h) and the Brooks–Correy model K (h) adjusted to fit the experimental values.
| Value | Standard deviation | |
| θs (cm3/cm3) | 0.431 | 0.007 |
| m | 0.156 | 0.032 |
| n | 2.36 | 0.09 |
| hg (cm) | –2.73 | 0.96 |
| Ks (cm/s) | 0.0089 | 0.0005 |
| η | 5.9 | 0.9 |
The measured K (h) during infiltration (Fig. 3) has a less dispersed curved shape. Table 2 shows the values of Ks and η obtained by fitting the Brooks and Corey model (Brooks and Corey, 1964) onto the measurement points; these values are close to the average values measured at Mnasra (Saâdi and Maslouhi, 2003).
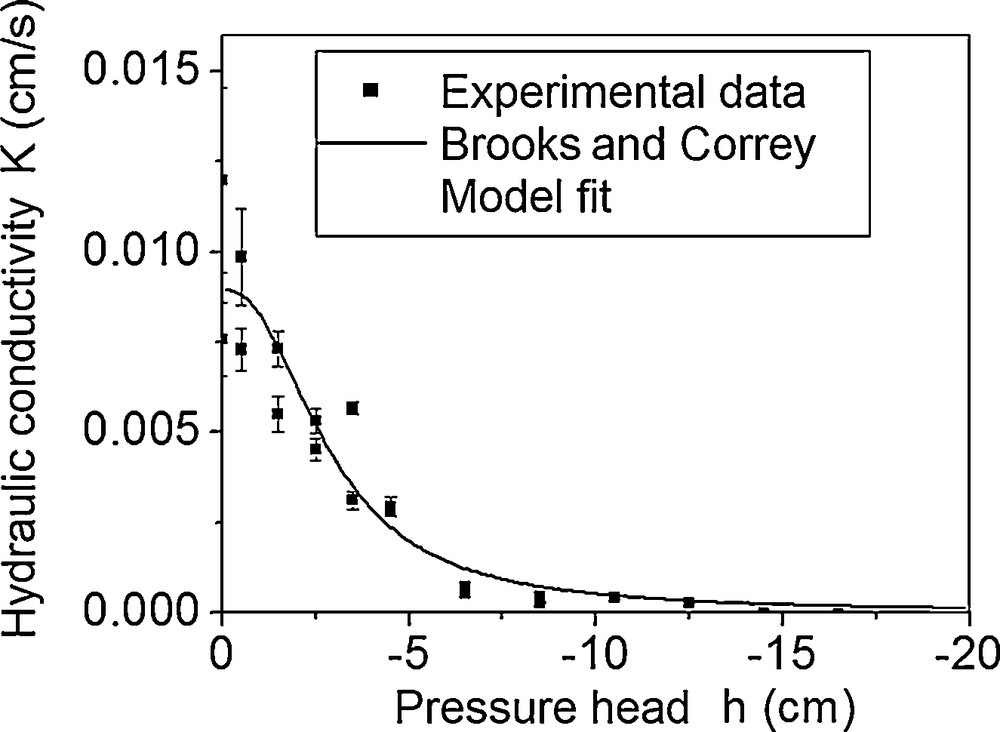
K (h) curve for the studied soil.
It should be noted that the adjustment of Figs. 2 and 3 was carried out following the Levenberg–Marquardt Algorithm (LMA). The shape parameter η is often estimated in the literature as (2 + 3L)/L, where 0.2 < L < 3 (Løvoll et al., 2011); in our case, the L value was 0.7. The η value estimated in this study, comprised between 5.8 and 7.4, is very close to the results of Saâdi et al. (1999) and Tamoh and Maslouhi (2004) in the coastal part of Mnasra.
3.2 The water movement
Solving Richard's equation yields solutions in h, which are converted into water content via relation θ (h). Simulations show that the water content of the soil could never mathematically go below its residual value θr, even if the internal evaporation phenomenon is taken into consideration. This confirms our consideration of an almost null residual water content (Bagarello and Iovino, 2012; Coppola et al., 2009; Mubarak et al., 2009; Saâdi and Maslouhi, 2003; Tamoh and Maslouhi, 2004). Moreover, considering the residual water content as null when it is very small allows us to cut down the number of parameters to be calibrated, and therefore to avoid over-parameterization. We performed a sensitivity analysis of the model results with respect to different values of the residual water content assigned to θr = 0.02, 0.04, 0.06. We found that the variation of the residual water content has only a very limited impact on the mass balance of carbofuran effect.
We measured and simulated water content profiles during three months at three soil depths, i.e., 0–20, 20–40, and 40–60 cm. The volumetric water content is characterized by small variations, especially in the lower depths. It is due to the soil sandy texture, characterized by low retention capacity, a potential drainage, and low initial volumetric water content (see Fig. 4). Fig. 4A shows that the model simulations are in good agreement with the experimental observations. In Fig. 4 B and C, the observed values are simulated with only a slight overestimation for the last sampling dates, probably due to the heterogeneity of the soil or error-related measurements.

Water content numerical simulations and experimental data at different soil depths.
The calibration error of hg, m and η parameters (RMSE) gives a satisfactory value of 0.09 (Table 3). The ks variation, within the limits of possible values for a soil like ours, does not affect the simulation results and, therefore, the value of RMSE. This allows us to consider that the hydrodynamic parameters are well represented. Furthermore, we find out that the model gives good predictions of the water content values, especially on the 0–20-cm profile.
Values of calibrated hydrodynamic parameters and parameters λ, Kd, μs, and μw, with calibration errors.
| Value | Calibration error (RMSE) | |
| hg (cm) | –2.9 | |
| n | 2.34 | 0.09 |
| η | 7.2 | |
| λ (cm) | 11.5 | 0.48 |
| Kd (cm3/g) | 0.21 | |
| μs (s−1) | 2·10−7 | 0.54 |
| μw (s−1) | 2·10−7 |
3.3 Bromide transport
Fig. 5 shows the temporal evolution of bromide concentrations for the three soil horizons studied. Therefore, the dispersivity value λ is 0.115 m (Table 3). The fact that the value of λ seems high may be due to physical phenomena neglected during modelling, including the three-dimensional nature of the flow across the field, the soil heterogeneity along the vertical profile, and the presence of preferential flows.
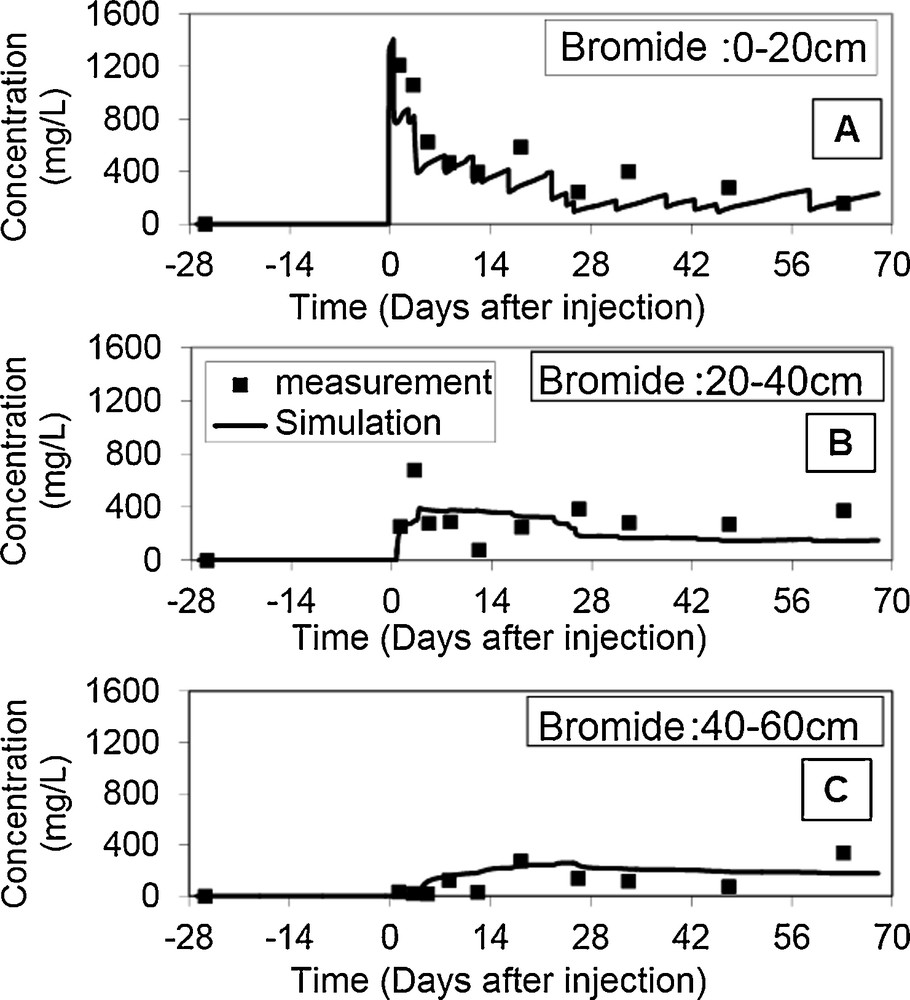
Bromide concentration numerical simulations and experimental data at different soil depths.
However, such a λ value is not surprising (Saâdi and Maslouhi, 2003), since according to the work of Nielsen et al. (1986), λ can take values ranging from 0.05 cm in a laboratory test, to 10 cm and higher for field conditions.
Table 3 shows an irrelevant λ = 0.48 value of the calibration error (RMSE), which is due to a slight fluctuation of the calculated values in the soil layers, especially in the lower ones. Nevertheless, the model yields results consistent with the observations. The calibration method seems therefore qualitatively acceptable, even for a heterogeneous soil.
3.4 Carbofuran transport
Simulated and observed concentrations of carbofuran, for levels 0–20 cm, 20–40 cm, and 40–60 cm are shown in Fig. 6. A few days after application, and after 25 days of leaching, carbofuran is practically distributed throughout the soil matrix, and the maximum rate of recovery is in the 0–20 cm layer. This observation suggests the existence of important phenomena of dispersion on the sandy substrate, which appear more pronounced on the topsoil horizon. The adsorption process is probably related to a slight increase in the organic matter content in this level (Table 1).
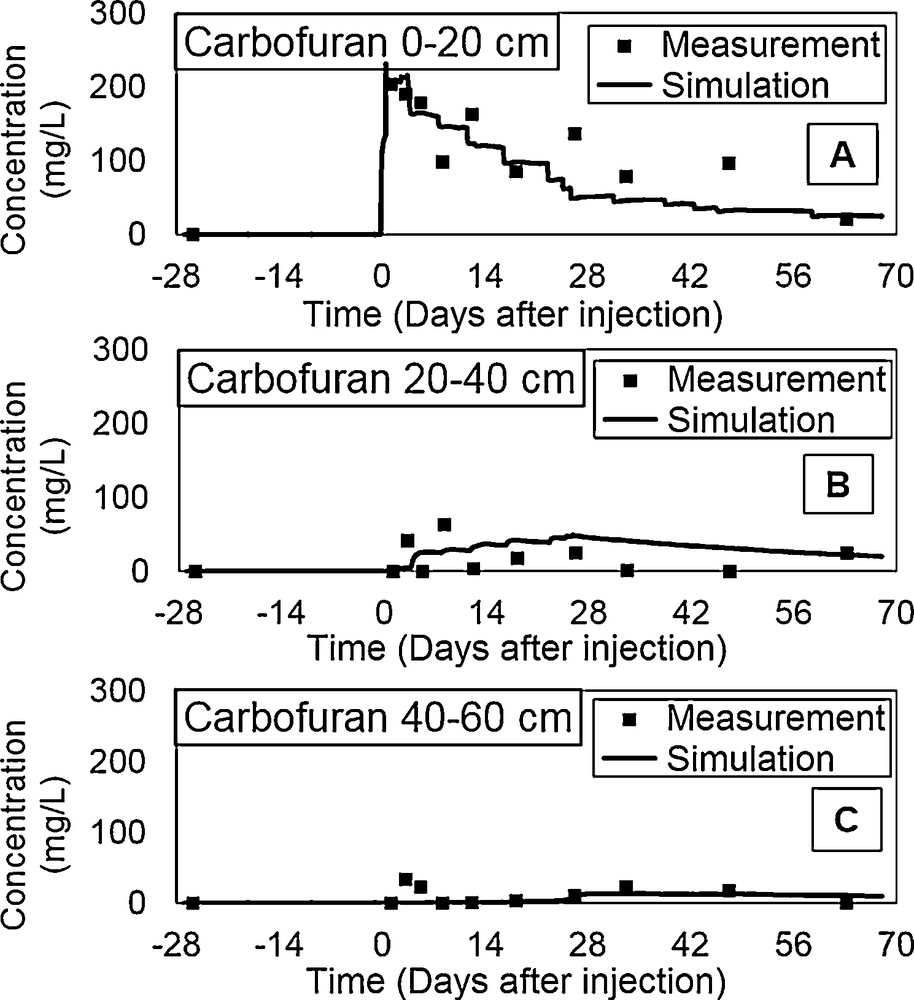
Carbofuran concentration numerical simulations and experimental data at different soil depths.
In addition, the model provides satisfactory results in terms of pesticide dynamics, except for the increase of the RMSE calibration error to 0.54 (Table 3). This increase is probably due to changes in distribution coefficients Kd and to μ degradation in each layer. Bearing in mind that we considered a homogeneous soil as the modelling approach, the physicochemical characteristics of the pesticide were the same in all soil profiles, whereas the soil is actually heterogeneous. The values of the rate of degradation (μs and μw) inferred by calibration, and those calculated by the equation (μs = μw = ln2/t1/2 = 0.693/t1/2) (Sparks, 1989) show some similarities, as the half-life (t1/2) of carbofuran derived from a previous study for a sandy soil similar to our soil gave a similar carbofuran half-life (El Mrabet, 2002).
Differences observed between simulated and measured concentrations are probably due to the following reasons:
- • errors in experimental measurements;
- • influence of other physical phenomena related to transport not considered in modeling;
- • we considered 1D model approach, whereas the real phenomena are in 3D.
It is appropriate to specify that the volatilization is not considered, since carbofuran has low volatility and is characterized by a low vapor pressure (3.41 × 10−6 mmHg at 25 °C). According to Lardier (Lardier, 1987), the volatilization of carbofuran is limited to 0.5% for sandy soils after two months of treatment.
A sensibility analysis shows little influence of θr on the water movement, and to a lesser degree, on carbofuran mass balance, especially on the carbofuran leaching flux.
Therefore, we used the model developed to simulate the transport of carbofuran for two different irrigation regimes, i.e., 222 mm and 350 mm. Fig. 7A and B present the simulation results of carbofuran transport in the unsaturated soil down to a 1-m depth in both irrigation schemes (222 mm and 350 mm) area. Fig. 7 shows the distribution of the pesticide 3, 26, 31, and 63 days after application.
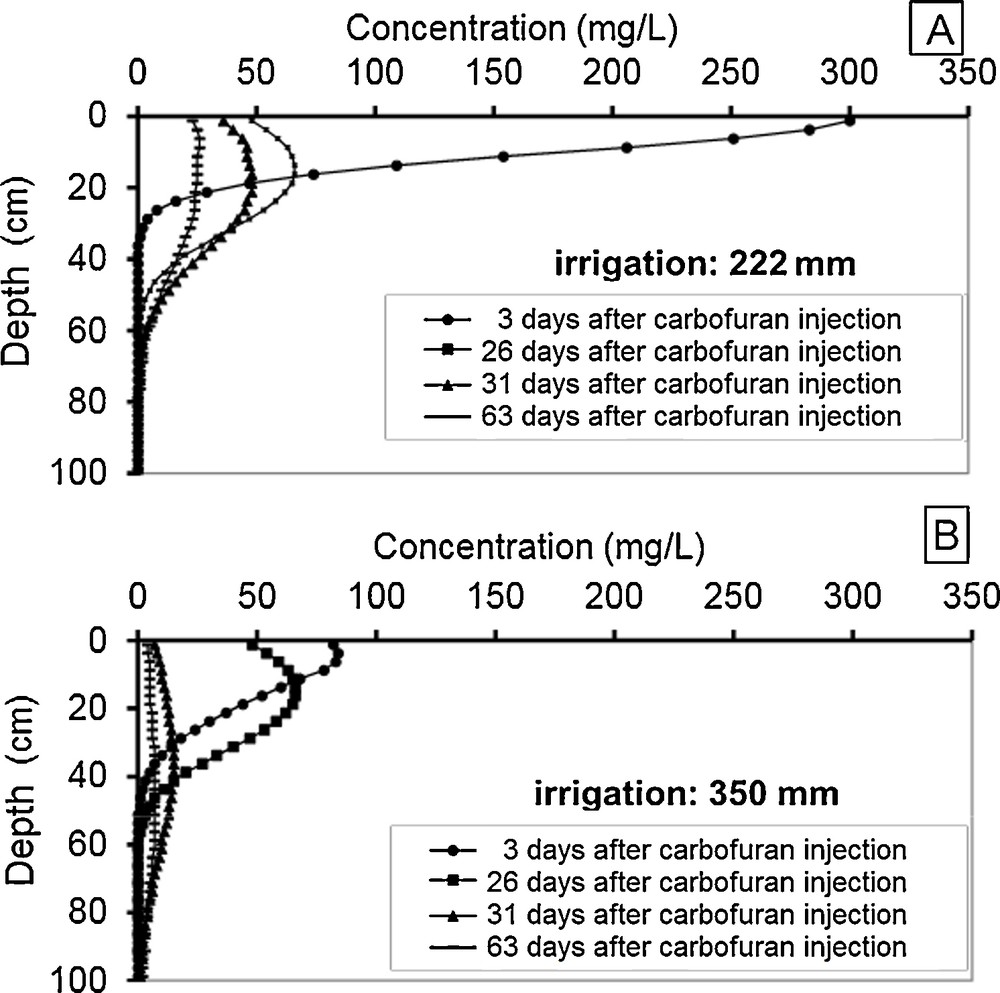
Simulations of carbofuran distribution in the soil following two irrigation regimes (A: 222 mm; B: 350 mm).
According to both irrigation regimes, the maximum carbofuran concentration in soil reaches 300 mg/L and 84 mg/L, respectively. These peaks appear three days after carbofuran surface application. We can observe a decrease in the maximum concentration and a slight advance of the concentration front according to the increase of irrigation amount. The same phenomenon is observed for these concentration profiles 26 days after treatment.
The two profile graphs of carbofuran concentrations appearing 31 and 63 days after application are flat and wide, including the largest irrigation system (Fig. 7B). The curves show that the dispersive transport is enhanced by irrigation. The analysis of the results shows some migration of carbofuran down into in soil. The downward movement of carbofuran is more pronounced in Fig. 7B, which coincides with the increase in irrigation, i.e., 350 mm in total. The carbofuran mobility is also facilitated by its high solubility in water, i.e., 700 mg/L, and the large amounts of water provided by the irrigation system.
4 Conclusion
We carried out an experimental and numerical study in order to improve our knowledge and understanding of the mobility of a pesticide in a soil, namely carbofuran, which has a broad application spectrum. The study is focused on the mobility of carbofuran in soils with strong hydraulic permeability and characterized by a weak organic matter content. The model developed for this study favorably reproduced the magnitude and the general trend of the spatio-temporal evolution of water content and carbofuran concentration in the soil. It was therefore used to simulate the transport of carbofuran in the same experimental conditions using higher irrigation level, i.e., 350 mm in total. The results of such simulations highlighted the importance of irrigation methods on the leaching of carbofuran especially to shallow groundwater: waters will be exposed to higher contamination for huge irrigation systems or during rainy periods. The migration of carbofuran residues and degradation products will be improved in the case of intensive crops treatment, which heavily depends on irrigation water such as gardening, banana plantation, etc., leading to faster and larger transports.
Overall, these data indicate that aquifers with an underlying unsaturated sandy zone characterized by a low clay content and soil organic matter are particularly vulnerable to carbofuran contamination. This is particularly true for drinking water after heavy rainfall or irrigation, and all the more after unsound repetitive pesticide applications. This problem requires in the future a more detailed study of carbofuran leaching on other soil types. It is also important to integrate the entire crop cycle, the effect of land-use change that may affect soil content in clay (Cornu et al., 2012) and, consequently, the leached quantity of carbofuran and the effect of pesticide dose. In addition, the contamination by the major metabolites caused by the carbofuran degradation, i.e., carbofuran phenol, 3-hydroxy-carbofuran, and 3-keto-carbofuran will have to be evaluated in details in the future. They are known to have similar toxicity to the original compound, and their solubility in water is greater than that of carbofuran (El Mrabet, 2002).


