1 Introduction
One of the issues that has always led to considerable concern in the meteorological community is the skilful prediction of seasonal summer monsoon rainfall over India (Gadgil et al., 2005). Though the practice of predicting rainfall over the Indian subcontinent started some hundred years back with the India Meteorological Department (IMD) (Blanford, 1884; Goswami and Srividya, 1996; Gowariker et al., 1991; Sahai et al., 2003; Shukla and Mooley, 1987; Thapliyal, 1981; Walker, 1923), but still after numerous years of consistent efforts (in terms of methodology and skill of forecast; Rajeevan et al., 2000, 2007), the forecast is generally not very accurate. Nowadays, weather forecasting relies more on computer-based weather prediction, and the major contributors that opt to provide better forecasts are the latest-generation global climate models (GCMs). These GCMs represent physical processes of the atmosphere, ocean, and the land surface, and simulate the global climate system (Randall, 2000). But, despite major efforts to enhance the quality of GCMs, weather forecasting using these GCMs still remains a subject of keen interest (Wang et al., 2008). Because of their coarse resolution, the performance of the GCMs usually degrades when they are downscaled to a finer scale. Some of the studies that put forth the performance of few GCMs in detail are Pattanaik and Kumar (2010), Acharya et al. (2011), Gadgil and Srinivasan (2011), Janakiraman et al. (2011), Kulkarni et al. (2011), Singh et al. (2012), wherein attempts have also been made to develop forecasts of ISMR using GCMs. However, these studies have generally reported poor forecast skill levels, and found that the GCMs are often not able to well simulate the mean seasonal cycle and interannual variability of precipitation over India. This may be due to serious systematic errors in terms of the mean, the annual cycle or statistics of the inter-annual variability and, in some cases, all three of these characteristics (Kirtman et al., 2003).
To overcome these problems inherent in GCMs, some kind of statistical post-processing is required. Nair et al. (2012, 2013) used principal component analysis to improve the quality of GCMs and found that the models vary in capturing different features of observation. Kar et al. (2011) used a multimodel ensemble technique (MME) based on a superensemble to evaluate the skills of six GCMs predictions for the month of July and they found some skill in predicting July rainfall over the eastern part of the country. In view of the above, this study was undertaken to improve the predictive skill of Indian summer monsoon rainfall (ISMR) using outputs of six different GCMs on seasonal as well as monthly scale. Though seasonal rainfall (average of rainfall in June–September) over the Indian subcontinent does not follow any persistence and interannual variation is large, yet the skill of predicting Indian monsoon has advanced. On the other hand, even after more than 100 years of statistical forecasting and 50 years of climate model development, there is not much success in forecasting the rainfall on a monthly scale. Also, India (as a whole) is a large country and due to high spatial variability of monsoon rainfall over India, the prediction of ISMR at a finer scale is a very promising task that still needs lot of hard work and research.
This gap in predicting monthly and seasonal summer rainfall at a smaller spatial scale motivated us to develop a mathematical technique using outputs of different GCMs. The GCMs are considered using initial conditions of previous months, i.e. for June – initial conditions of May are used –, for July – initial conditions of June are used, and so on. The mathematical model is developed by doing a double screening on an ensemble mean using two sophisticated methods – synthetic superensemble (Yun et al., 2005) and supervised principal component regression method (Nair et al., 2012). The synthetic superensemble algorithm generates synthetic datasets from a combination of the past observations and forecasts, whereas SPCR is a prediction technique utilized for providing forecast. The SPCR technique is found to have better skill over almost all the zones of country than direct models in almost all the months of monsoon. It is also able to capture the year-to-year observed rainfall variability in terms of sign as well as – magnitude (Nair et al., 2012).
Therefore, in this study, we have made an attempt to integrate these two methods. For this, firstly the synthetics of GCMs are computed and the new synthetic datasets are considered as an input for supervised principal component regression analysis. This can also be viewed as a two-step screening procedure, wherein prior to regression the model biases are corrected by evaluating the synthetics. This methodology has been adopted to improve the performance of six GCMs outputs over India at 1° × 1° resolution during the summer monsoon season from June to September. The novelties of the present study are:
- • predicting seasonal and monthly rainfall over India;
- • a prediction that is carried out over the Indian subcontinent at 1° × 1° resolution;
- • two sophisticated mathematical techniques that are used to develop the prediction model-synthetic superensemble and supervised principal component regression. The former is used to correct for biases in the GCMs, and the latter is used for the prediction of seasonal and monthly rainfall.
The paper is presented in following way: Section 2 deals with the data source for the study. The methodology is discussed in section 3. The results of this study are presented in section 4. Conclusions follow in section 5.
2 Datasets used in the study
To carry out the study, two types of datasets are considered: one is the observational dataset and the other contains the precipitation outputs from different GCMs. The brief descriptions of both datasets are given below.
2.1 Multi-model datasets
The Global Climate Models (GCMs) considered in the study are from different agencies like the National Centre for Environmental Prediction (NCEP) and the International Research Institutes (IRI), Columbia. The model from NCEP is the fully coupled Climate Forecast System version 2 (CFSv2) and those from IRI are uncoupled 2 tier models namely CCM3v6, ECHAM4p5CASST (CASST), and ECHAM4p5CFSSST (CFSSST). CASST and CFSSST is a version of the European Centre-Hamburg Model and these are atmosphere only GCMs developed at the Max Planck Institute for Meteorology. CASST has been run by forcing them with prescribed sea surface temperature (SST) anomalies prepared using the constructed analogue method while CFSSST is developed by forcing CFS predicted SST. The other GCMs namely COLA (Centre for Ocean Land Atmosphere) and GFDL (Geophysical Fluid Dynamics Laboratory) are obtained from Earth System Grid Federation, wherein the US National Mutimodel Ensemble experiments for multimodel seasonal forecasting are carried out. The experiments consists of various models from US modelling centres including the National Oceanic and Atmospheric Administration (NOAA)/NCEP, NOAA GFDL, IRI, the National Centre for Atmospheric Research, the National Aeronautics and Space Administration (NASA) and Canada's Climate Modelling Centre (Collins et al., 2006; Kirtman et al., 2013).
These GCMs have different ensemble members and are considered for the summer monsoon season (June-September) with 1 month lead for season as well as individual months of monsoon. Here, we consider the ensemble mean of the GCMs. The details of these GCMs are also briefed in Table 1.
Description of Global Climate Models.
| Model | Resolution | Model Type | Ensemble Members |
Reference |
| CCM3v6 | 2.7° × 2.8° | 2-tier | 24 | Roeckner et al. (1996) |
| CASST | 2.7° × 2.8° | 2-tier | 24 | Roeckner et al. (1996) |
| CFSSST | 2.7° × 2.8° | 2-tier | 24 | Roeckner et al. (1996) |
| CFSv2 | 1° × 1° | Coupled | 24 | Saha et al. (2014) |
| COLA | 1° × 1° | Coupled | 6 | Collins et al. (2006) |
| GFDL | 1° × 1° | Coupled | 10 | Delworth et al., 2006 |
2.2 Observed data
Indian rainfall data for the summer monsoon season (June, July, August, and September) have been used as observed data that were available for the period 1951–2013. These data are high-resolution (1° × 1°) daily gridded rainfall values prepared by the India Meteorological Department (IMD) over the Indian land mass (6.5°N–38.5°N and 66.5°E–100.5°E). This dataset prepared by IMD is based on measurements from 2140 stations with minimum 90% data availability for all the 12 months of the year. The conversion of station data into grid data is briefly explained in Rajeevan et al. (2006).
Since the GCMs data are available from 1982 onwards, the time frame of our study is from 1982 to 2013. It is to be noted that, as these GCMs have a very low resolution, a bi-linear interpolation technique is employed to bring them in the observed data's resolution (1.0° × 1.0°).
3 Methodology
Despite the advent of various improvements in statistical dynamical forecasts, weather prediction still remains a challenging task. The main demand is to reduce the inherent bias that always coexists with the models. So, the first thing that should be carried out before constructing any mathematical model is to correct for biases in the GCM outputs. Here, we made an effort to remove the bias from the GCM outputs and then develop a prediction model that can predict rainfall on an extended timescale. For this purpose, two sophisticated mathematical methods are used. Firstly, the GCM outputs are corrected for the bias and then a prediction model is generated, in which the method of supervised principal component regression (SPCR) by Nair et al. (2012) has been adopted. Bias correction is done on individual GCM outputs using the synthetic superensemble (SSE) method of Yun et al. (2005). These corrected model outputs are known as synthetic products that are generated from the original dataset by finding a consistent spatial pattern between the observed data and the forecasted dataset. This procedure is a linear regression problem in the Empirical Orthogonal Function (EOF) space. The mathematical formulation and details of the SSE can be found in Yun et al. (2005). These synthetics are taken as inputs for the development of the prediction model. The prediction model is based on the supervised principal component regression (SPCR) methodology described in Nair et al. (2012) wherein the theory of principal component regression is used.
The difference between the SPCR of Nair et al. (2012) and the principle applied in this study is that in theirs they have used the normalization technique to correct for biases in the model outputs and they have not adopted any other bias correction technique on outputs of models. But, in this study, the synthetic superensemble technique is used to correct for biases in the model outputs and the synthetics obtained from bias correction are thus taken as an input for the SPCR. That is, the developed system is a hybrid of synthetic superensemble and SPCR techniques and is applied to each one of the grid points of the Indian subcontinent for the summer monsoon season and its individual months (June, July, August, and September). The methods that are used to quantify the performance of the developed mathematical model are the correlation coefficient, the root mean square error (RMSE), and the Nash and Sutcliffe Efficiency index (NSE). All the calculations are performed on a leave-one-out cross-validation mode (as recommended by WMO's standardized verification system) between actual and predicted rainfall. The performance of the final model is also judged in some of the exceptional monsoon years. The schematic of the methodology is described in Fig. 1. The GCM outputs (in the rectangular box) are the GCM products used for evaluating synthetics and prediction. Each of the 6 (M1, M2, M3… M6) model outputs are firstly subjected to bias correction using synthetic superensemble technique and thereby six synthetic products (bias corrected) are found (S1, S2, S3… S6). These six synthetics are taken as input for SPCR. Thus, the final product is a bias-corrected prediction model for the summer monsoon season in India at a 1° × 1° resolution.
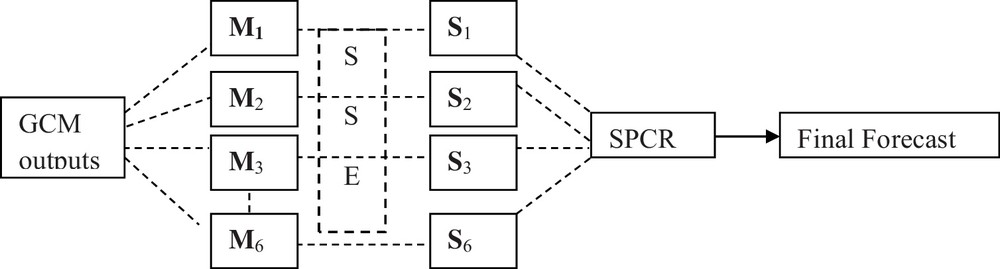
Scheme of the developed mathematical model.
4 Results and discussion
Before generating the mathematical model, the raw outputs of the GCMs have to be diagnosed. Firstly the skill of the raw GCMs is judged using correlation analysis. Then, the performance of bias-corrected model outputs is seen. Finally, the forecast from SPCR is analysed by correlation analysis, root-mean-square error (RMSE) and Nash and Sutcliffe efficiency (NSE) index and compared with the simple ensemble mean of the raw GCMs. The aforementioned procedure has been carried out on each of the gridpoints of the Indian subcontinent for the season as a whole and in individual months of monsoon. For the different subdivisions of the country encountered, please refer to Fig. 1 of Guhathakurta et al., 2011.
4.1 Performance of model outputs after bias correction/synthetic superensemble (SSE)
The performance of raw models before any bias correction is illustrated in Figs. S1 and S2 for the season as a whole and for the month of July, respectively, and discussed in Section S.1 of the supplementary material. Due to the brevity of the study, we only display the performance of raw models in the month of July (Fig. S2). From Figs. S1 and S2, it can be inferred that the skill of raw GCMs is not satisfactory when they are downscaled to finer levels, and more rigorous techniques have to be developed to improve the performance of GCMs at a smaller spatial scale. Hence, a bias correction technique known as SSE (Yun et al., 2005) is thus applied on the outputs of GCMs to remove the bias inherent in them. The performance of the bias-corrected GCMs is illustrated in Fig. 2. Subplots a to f are shown for each one of the GCMs for the JJAS season as a whole.
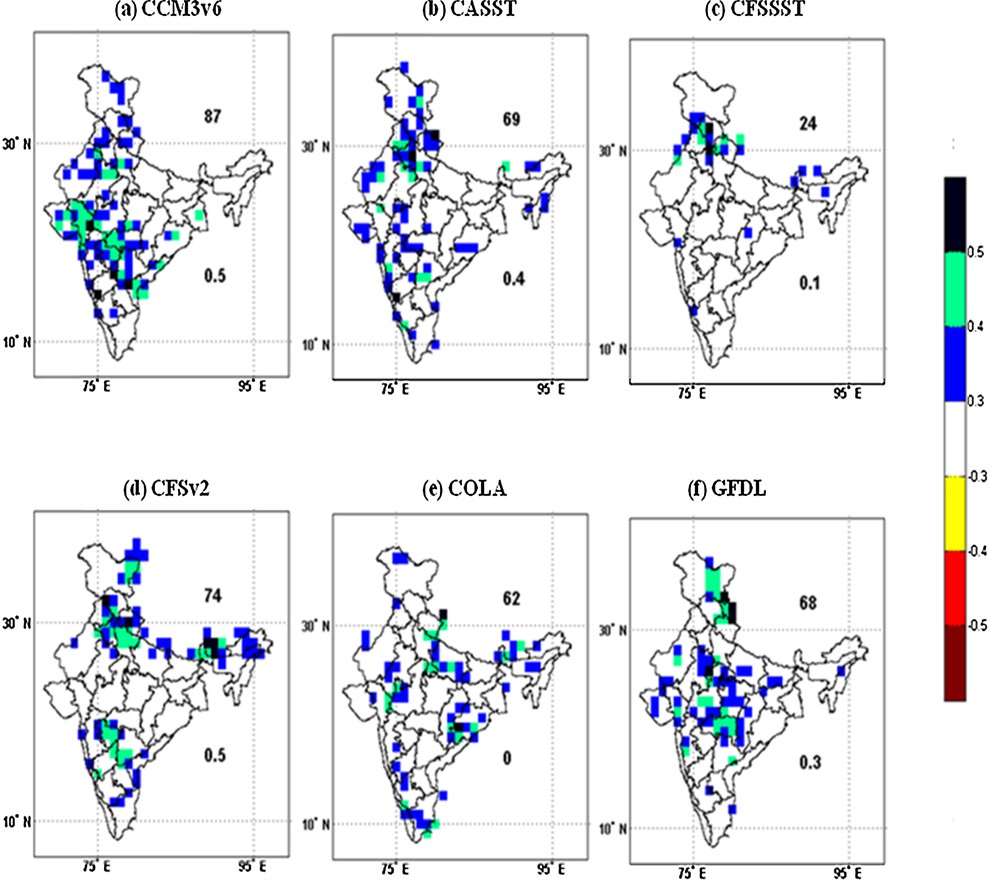
(Color online) The performance of bias-corrected GCMs shown at a 1° × 1° resolution for the JJAS season. The numbers on the upper right and bottom right corner indicate number of significant gridpoints and correlation, respectively.
The CCM3v6 model, which is displayed in subplot (a) of Fig. 2, shows much improvement in terms of skill over its biased counterpart. The number of gridpoints that are found to have significant correlation with the observed rainfall has increased to 87 from 47, i.e. there is an improvement by 11% of the total gridpoints. A significant correlation of 0.5 is also noticed for the country as a whole. The bias correction in CASST model also yielded significant improvement over its biased counterpart. The all-India average correlation is found to be 0.4, whereas it was 0.2 before bias correction. The total number of gridpoints that are found to be significant has increased to 69 from 35. In CFSSST model, the performance of the model shows little degradation in terms of the number of gridpoints, but correlation values at the all-India level before and after bias correction are almost identical. Positive correlations are found over Himachal Pradesh, Haryana, Uttarakhand, and Punjab. There are only 24 points that are found to be significant. In the CFSv2 model, which is a coupled model, 74 gridpoints are significantly correlated with observation. The correlation value at the all-India level is found to be 0.5, which is almost congruent to the biased counterpart. The next model (COLA) shows 62 gridpoints that are found significant and the correlation value at the all-India level is 0.1. The GFDL model, which is a coupled model, shows 68 gridpoints that are significantly correlated with observed rainfall. The all-India-level correlation is 0.3, which is similar to that in the raw model.
This discussion illustrates that the bias correction of GCMs yielded some improvement in most of the GCMs, except for CFSSST. For a more conclusive result, the above technique is also employed in each one of the individual months of monsoon. The results of the bias corrected GCMs in the month of July are presented in Figure S3 and discussed in supplement section S.2.
The results of the discussion yielded two important points:
- • it is important to correct the GCMs for biases and that the GCMs performance after bias correction is significantly improved in most of the cases;
- • it is also important to judge GCMs’ efficiency at a smaller scale adjacent to judging its capability at the all-India level in view of the fact that the averaging of points may not give a clear picture of GCM's potential to predict at a finer scale.
After the model outputs are bias-corrected, the next phase in developing the statistical model is to consider these bias-corrected GCM outputs for prediction. The prediction is employed using the SPCR technique introduced by Nair et al. (2012) wherein the principle of principal component regression is used.
4.2 Performance of supervised principal component regression (SPCR)
The SPCR technique by Nair et al. (2012) is used as a tool for predicting the seasonal and monthly rainfall over the Indian subcontinent. The performance of the predictive model is judged by correlation analysis, root mean square error (RMSE) and Nash and Sutcliffe Efficiency index (NSE). The ensemble mean (EM) (simple mean) of the members of the GCM outputs is taken as a benchmark to analyse the performance of the new predictive model.
4.2.1 Correlation coefficient: EM vs SPCR
The performances of EM of the GCMs for season and month are shown in Fig. S4. From the discussions therein (section S.3), it can be inferred that at the all-India level, the correlation values of EM of the models are significant at almost every individual month of monsoon and in the season as well but at a smaller spatial scale, the GCM outputs need improvement. Therefore, it is important to develop a model that can predict the monsoon rainfall at a smaller spatial scale. As suggested by Webster and Hoyos (2004), it would be difficult for even a skilful forecast of the all-India seasonal rainfall to provide regional community with information on regional features of seasonal rainfall as there are large inhomogeneities at finer scale. In addition to this, a recent study by Singh et al. (2014) revealed that the distribution of rainfall in each month is important as the contribution of monthly rainfall to the seasonal rainfall is considerably different in each month. So, for a good forecast, it is essential to build a model taking into account these two challenges of the present forecast system. Hence, we strive to develop a mathematical model, namely SPCR, which can yield better forecast at the grid level and in monthly and seasonal scales.
After the bias correction of the model outputs, they are regressed using the SPCR technique. The performances of the SPCR technique (in terms of correlation with observation) in different months of monsoon and season are shown in Fig. 3 (upper right: number of significant gridpoints; bottom right: all-India correlation). It can be seen that the skill of monsoon rain in each month and season has improved significantly from its EM (see Fig. S4 in the Supplementary Material). In the JJAS season, the number of gridpoints that are found significant is 97, which is higher than the EM of the models. The correlation value at the all-India level (0.4) also shows improvement over the EM of the models. Positive correlations are found for Jammu and Kashmir, Himachal Pradesh, Haryana, Uttarakhand, West Rajasthan and East Rajasthan. Most parts of northwestern and central India show positive correlation. Some positive correlations can be seen over South Peninsular India, Kerala and Tamilnadu regions. One of the interesting aspect that can be observed here is that after the SPCR, the performance of the model increased for central India, which is the monsoon core zone of the country (74.5°E to 86.5°E and 16.5°N to 26.5°N) (Goswami et al. (2006). Hence, for the JJAS season, the performance of SPCR has been significantly improved over that of EM. The skill of SPCR in other months is discussed in section S3.1 (in the Supplementary Material).
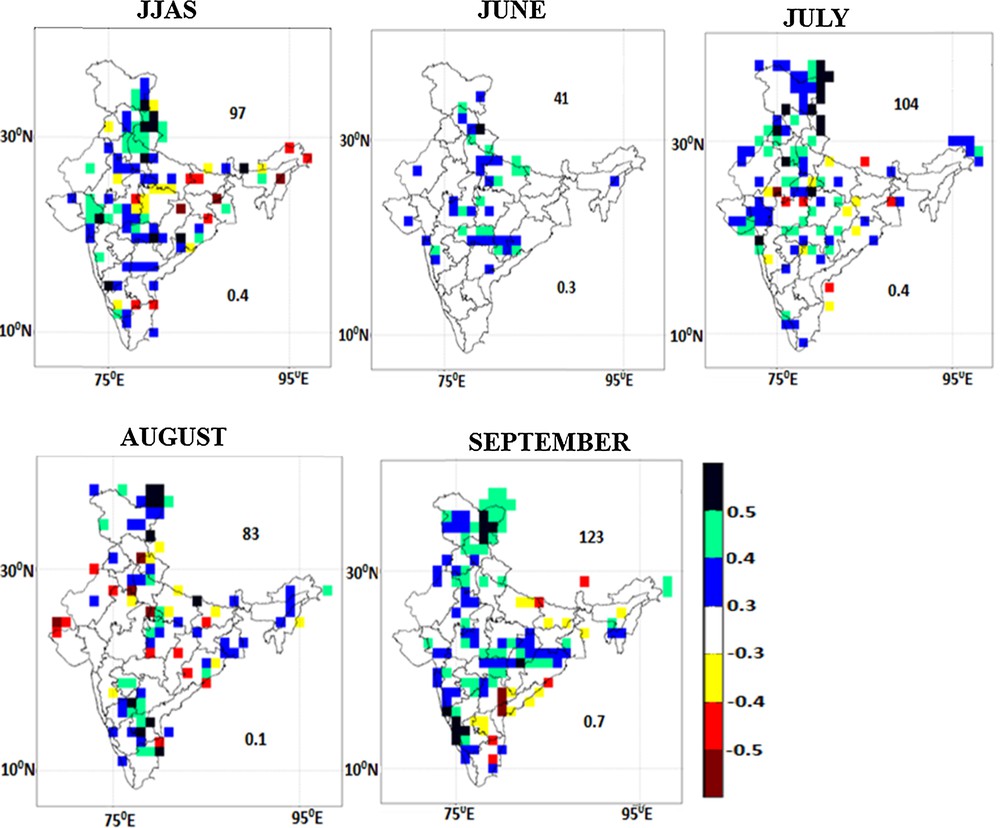
(Color online) The performance (in terms of correlation coefficient) of the SPCR technique for the season and the individual months of monsoon. The numbers on the upper right and bottom right corner indicate number of significant gridpoints and correlation, respectively.
In view of the above, we can conclude that the SPCR model is able to improve the performance of models in each of the individual months of monsoon and in season as well at a smaller spatial scale. At the all-India level also, the correlation values are higher than the EM of the models, except for the month of August.
4.2.2 Root Mean Square Error (RMSE)
To get more confidence in the SPCR model, RMSE is evaluated between observation and EM, and between observation and SPCR forecast. Rather than showing the RMSE of EM and SPCR separately, the difference of RMSE between SPCR and EM is evaluated and the same is shown for JJAS, June, July, August, and September in Fig. 4.
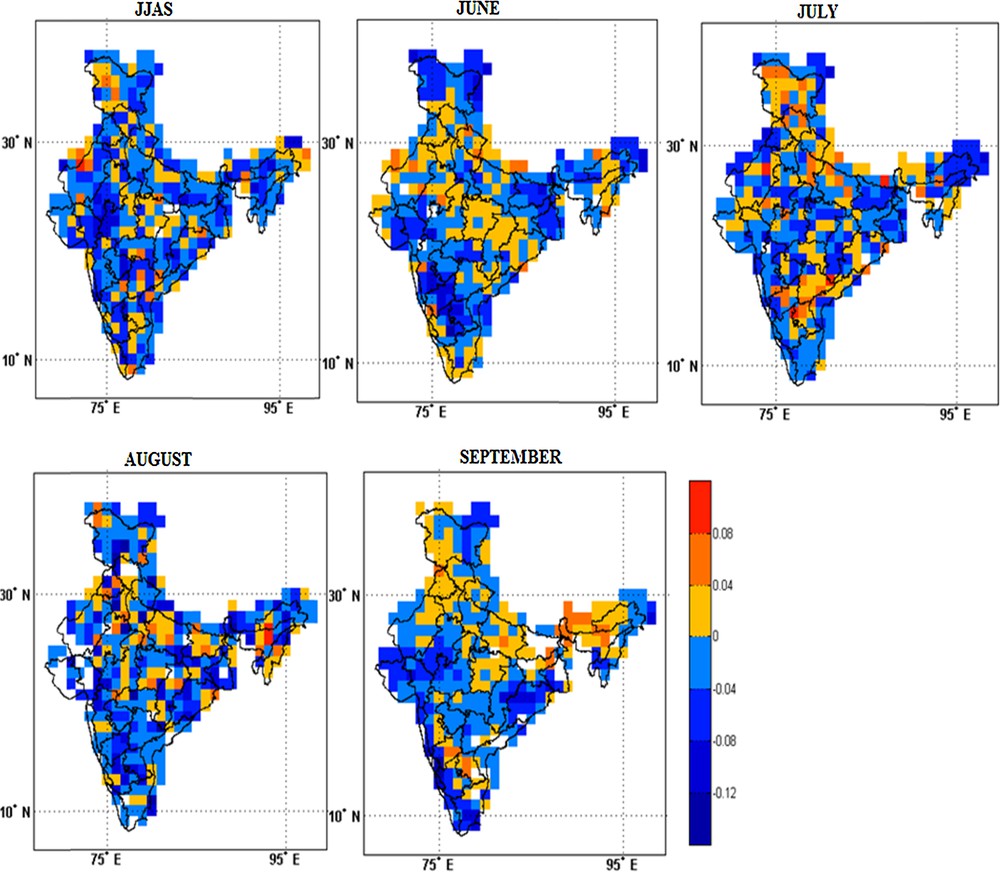
(Color online) The difference of RMSE between SPCR and EM technique for the season and for the individual months of monsoon.
For the JJAS season, the difference between the SPCR and EM is negative at almost every point of the Indian domain. The RMSE over central India is negative, evidencing the fact that the mathematically developed SPCR model is better than the EM of the models. Over the other gridpoints also, negative error values are found. In July, negative errors are seen over most parts of the country, which justifies that the SPCR model is better than the EM of the models during this month. Over some parts of Telangana and Rayalseema, positive errors are seen. In August, similar conclusion can be made with much of negative error over most parts of the country. Some positive error is seen over the northeastern parts of the country. In September, most parts of the country show negative errors, indicating again the betterment of the SPCR model over EM. But over the northeastern parts of the country, over Assam and Meghalaya, Andhra Pradesh, Bihar, East Madhya Pradesh, Punjab, positive errors are found.
4.2.3 Nash and Sutcliffe Efficiency index (NSE index)
We have also seen the efficiency of models using Nash and Sutcliffe efficiency index, which was defined by Nash and Sutcliffe (NSE) in 1970 (Nash and Sutcliffe, 1970). The basic application of NSE skill is found in the hydrological sector to judge the capability of mathematical models. It is defined as one minus the sum of the absolute squared differences between the predicted and observed values normalized by the variance of the observed values during the period under investigation. The same is mentioned below:

(Color online) The RNSE performance of the EM and SPCR techniques for the season and for the individual months of monsoon.
For the JJAS season, we can see that the majority of the area shows RNSE greater than 1. Almost every gridpoint of Northeast India has an RNSE value greater than one. In parts of Northwest India, like Gujarat, East Rajasthan, West Madhya Pradesh, the value of RNSE is found to be greater than 1. In the month of June, the northeastern regions show RNSE greater than one, indicating the efficiency of the SPCR technique over the EM, but it can be noted that over other parts of the country the skill of SPCR as indicated by RNSE is not good. Over parts of Saurashtra and Kutch, Konkan and Goa and Tamilnadu, the RNSE skill is greater than 1. In the month of July, the skill of RNSE is witnessed greater than 1 over western Ghats of the Indian subcontinent and over the northeastern parts of the country. The skill of RNSE is also noticed to be greater than 1 over the Gujarat, Saurashtra and Kutch regions. Central India is also found to have high RNSE values. Some pockets of high RNSE are found over Jammu and Kashmir and Uttarakhand region also. In August, RNSE values are found to be greater than 1 over parts of central India, over West Madhya Pradesh and East Madhya Pradesh and northeastern parts of the country. Positive RNSE values are also seen over Bihar, East Uttar Pradesh and Jammu and Kashmir. In the month of September, the entire belt of western Ghats shows high RNSE values, indicating that SPCR performed better than EM in these regions. The Jammu and Kashmir, Himachal Pradesh and Uttarakhand region also show values of RNSE greater than 1.
It can be noted that the skill of models quantified by RNSE is almost similar to that obtained by RMSE. The regions with negative RMSE are regions with positive RNSE, indicating that SPCR outperformed the EM of the models in those regions. It can be seen that the skill of SPCR is found satisfactory over western Ghats in the months of July and September, as this region is submitted to heavy rain that contributes much to the total rainfall (Kumar et al., 2013). This result ascertains that the SPCR model outperforms the EM of the models and can be experimented for prediction at a lower scale in the individual months of monsoon and the season as a whole. Therefore, in the next part of the study, we will see the performance of SPCR in predicting the anomalous years of monsoon. Therefore, in the upcoming section, we judge the efficiency of these models in predicting the peculiar years in ISMR.
4.2.4 Predictive skill of SPCR in anomalous years
After developing a model, it is important to judge its efficiency in predicting the abnormal years of monsoon. We are considering here two peculiar years (2009 and 2012) in the period 1982–2013, in which the rainfall values were found to be anomalous. The year 2009 is chosen because it was the third highest deficient all-India monsoon season rainfall. It was 78% of LPA for the season as a whole with June rainfall 53% of its LPA, July 96%, August 73% and September 80% of LPA. In the year 2012, the seasonal rainfall was normal (92% of LPA), but the monthly rainfall over the country as a whole showed large deviations. In June, the monthly rainfall over the country was 72% of LPA whereas in July it was 87% of LPA, and in August and September, it was 101 and 111%, respectively. This randomness in monthly rainfall makes the model incapable of correctly predicting the monthly rainfall. Hence, it is important for any developed model to project this non-stationary behaviour in the monthly rainfall.
The performance of SPCR model is presented in Fig. S5 for 2009 and Fig. S6 for 2012. In Fig. S5, anomalies of JJAS, June, July, August and September, rainfalls are shown for EM and SPCR, with the observed anomalies for each of the gridpoints of the Indian subcontinent. In 2009, the observed JJAS rainfall shows negative anomalies over most parts of the country with some positive anomalies over Northwest India, Tamilnadu, and North Interior Karnataka. Positive anomalies are also seen over small parts of Jammu and Kashmir. The EM of the models is able to predict the negative anomalies, but the positive anomalies are not well-captured. In the SPCR, the prediction shows negative anomalies over almost all parts of the country, which is similar to the observations. In SPCR, positive anomalies are seen over Tamilnadu and Odisha, which are similar to the observation. Over North Interior Karnataka also, the anomalies are reproduced well to some extent. In the month of June, the gridpoints show negative values over almost 90% of the Indian subcontinent, whereas over Saurashtra and Kutch and some parts of Rajasthan and Telangana regions, positive anomalies are observed. In the EM of the models, negative anomalies are seen over various gridpoints, which is similar to the observations, but the magnitude of rainfall is not well-captured. In the SPCR model, negative values are seen over most parts of the country, but the developed model is not able to predict the magnitude of the rainfall very well. Positive anomalies are seen over parts of Saurasthra and Kutch and parts of Rajasthan, which is akin to the observed counterpart. In July, the negative anomalies are replaced by positive anomalies over Telangana, South Interior Karnataka, coastal Andhra Pradesh, Uttarakhand, West and East Uttar Pradesh, Bihar, parts of Jammu and Kashmir and parts of Northeast. In Odisha also, positive anomalies are seen. The EM of the models shows positive anomalies over Odisha subdivision, over Chhatisgarh and over East Madhya Pradesh similar to the observation. The negative anomalies over different gridpoints are similar to the observation but the magnitude is not the same. In the SPCR, negative anomalies are seen over almost every gridpoint of the Indian subcontinent. Some positive anomalies are also seen over Odisha and Saurashtra and Kutch, Gujarat, in a similar fashion to the observations. The northeastern parts of the country also show positive anomalies that are also witnessed in the observed rainfall of July. The rainfall in the month of August shows positive anomalies over South Peninsular India and over parts of northeast India. Over rest of the gridpoints of the country, negative anomalies are seen. The positive anomalies over South Peninsular India are well-captured in SPCR, whereas anomalies over the northeastern region are not reproduced well. Over rest of the country, negative anomalies are seen similar to the observation. In the EM of the models, in the month of August, the positive anomalies over Tamilnadu are not captured, while the positive anomalies over the Northeast are well-captured. Over Odisha, Chhatisgarh, Bihar, Uttarakhand and Gangetic West Bengal, positive anomalies are seen, which are absent in the observations. In the month of September, positive anomalies are seen over parts of Peninsular India, Tamilnadu, South Interior Karnataka, Rayalseema, North Interior Karnataka, Jammu and Kashmir, Himachal Pradesh, and Uttarakhand. Over the rest of the country, negative anomalies are seen. The EM of the models shows negative anomalies over almost all parts of the Indian subcontinent, whereas some positive anomalies are seen over Jammu and Kashmir and Punjab region. After the SPCR technique, positive anomalies are seen over Tamilnadu, South Interior Karnataka, Telangana, in a similar fashion to what is observed. The negative anomalies over the rest of the gridpoints are also captured well after the SPCR technique. A similar type of discussion is carried out for the year 2012, which is summarised in section S4 of the supplementary material.
The above discussion yielded that after the SPCR technique, the observed anomalies in rainfall are precisely captured, but the magnitude of the rainfall anomalies are not simulated with 100% accuracy. Therefore, more rigorous work has to be done to improve the skill of these GCMs in the context of simulating the correct magnitude of the forecast at a smaller spatial scale.
5 Summary and conclusions
With the increasing use of Global Climate Models, the skill of predicting ISMR has significantly increased. The all-India summer monsoon rainfall is predicted with significant accuracy, but the skill of prediction decreases as the models are downscaled to higher resolution. In this paper, we are trying to improve the skill of six GCMs in predicting the summer monsoon rainfall of India over a 1° ×1° domain at the season and monthly scales. The aim is achieved by using two sophisticated statistical techniques: one is synthetic superensembling (SSE) and the other is the supervised principal component regression (SPCR) technique. The SSE technique is used to correct for biases in the models, whereas the SPCR technique is used as a predictive tool for forecasting monthly and seasonal rainfall. In other words, the SSE and SPCR methods are hybridised to form a tool that can be used for the prediction of summer monsoon rain of India at a smaller spatial scale.
It is seen that before any bias correction, the skill of the raw GCMs is not satisfactory at the grid level for the season and its months as well. It is also seen that, even though the models performance by averaging the gridpoints (all-India average) is satisfactory, it does not perform well at the grid level. On the other hand, if they are corrected for bias, there is significant improvement after the bias correction. The numbers of significantly correlated points are increased by 10–20% after bias correction. Also, the points that were negatively correlated with observed rainfall also showed improvement after the bias correction.
After the SPCR technique, the performance of GCMs increases at the grid level and at the all-India level also. There is an improvement in 15–20% gridpoints. For judging the SPCR model, the EM of the models is taken as a benchmark and it can be seen that the SPCR outperforms the EM in most of the cases. At the all-India level also, the value of the correlation is improved. The difference of RMSE between EM and SPCR shows the betterment of SPCR over the EM of the models. The difference is seen negative in almost every point of the Indian subcontinent for the individual months and for the season as well. We have also evaluated the Nash and Sutcliffe efficiency (NSE) index for the SPCR and the EM of the models for each one of the gridpoints of the Indian domain. It is found that the skill of SPCR is found better than the EM of the models in JJAS at almost all the gridpoints of the Indian domain. It is found that the skill of SPCR is found satisfactory over western Ghats in the months of July and September as this region is accounted by heavy rain that contributes much to the total rainfall. It can also be noted that the skill of the developed SPCR model is significantly better than the individual GCMs in each of the monsoon months and in the season as a whole. For example, in the JJAS season, the best model is CFSv2 with a total number of significant gridpoints equal to 56, but, after applying the SPCR, the total number of significant gridpoints increased to 97. Similarly, in the month of July, SPCR outperforms the CCM3v6 model, which is found to best among all the GCMs.
The prediction of the anomalous years of 2009 and 2012 is also judged here using this technique and it is found that the SPCR is able to predict the peculiarity in the rainfall anomalies over different points of the Indian domain to some extent in almost every month at a smaller spatial scale, but this technique is somewhat not able to correctly model the magnitude of the anomalies.
To conclude, we can infer from this study that, even though the developed mathematical model show satisfactory improvements in the skill of GCMs, yet this sophistication is not sufficient to predict anomalous behaviour of the summer monsoon rainfall of India. Moreover, the complexity of predicting the ISMR is limited as the potential limit on the predictability of the seasonal mean is governed by the relative contribution from a predictable “forced” component and an unpredictable “internal” component to the interannual variability(IAV) of the seasonal mean (Ajaya Mohan and Goswami, 2003). On the contrary, the study has brought an open challenge for the scientific community to fill the gap in forecasting the seasonal and monthly rain over grid points of the Indian subcontinent.
Acknowledgments
The study is conducted as part of a research project entitled “Development and Application of Extended Range Weather Forecasting System for Climate Risk Management in Agriculture”, sponsored by the Department of Agriculture and Cooperation, Government of India. Gridded rainfall data have been obtained from India Meteorological Department. We thank the IRI modelling and prediction group (USA) led by D. Dewitt for making their GCM-based seasonal forecasting systems available to us. The computing for GCM simulations made by IRI was partially sponsored by a grant from the NCAR Climate System Laboratory (CSL) program to the IRI. We also thank the NMME project and Climate Prediction Centre, IRI and NCAR in creating, updating, and maintaining the NMME archive.



Vous devez vous connecter pour continuer.
S'authentifier