1. Introduction
In the mid-sixties, considerable research efforts were devoted to the study of new materials with potential interest as solid electrolytes. At the time, focus was put on crystalline compounds. Very remarkable compounds were found such as sodium 𝛽-alumina, RbAg4I5, NASICON (Sodium Superionic Conductor). Not much interest was reserved for glasses since the conductivity of ion-conducting glasses, the only known ones being oxides, was rather poor. The situation changed in the late seventies with the publication of the “Weak Electrolyte Theory” (WET) [Ravaine and Souquet 1977].
In this model, the glass is treated as a weak electrolyte with the glass former compound, e.g. SiO2, being the solvent and the modifier compound, e.g. Na2O, being the solute, such assumption being supported by the fact that glasses have very low dielectric constants (𝜀r ∼ 5–10 in oxide glasses). The authors have established experimentally that the electrical conductivity of xNa2O–(1 − x)SiO2 glasses varied as the square root of their thermodynamic activity. And, with the assumption of a weak dissociation, so does the concentration of Na+ ions resulting from the dissociation of the modifier compound (Na2O ↔ Na+ + NaO−). Therefore, the conductivity varies as the concentration of these “free” ions. The authors proposed that the only charge carriers free to move throughout the glassy matrix in the presence of an electric field were those released as a result of the solute dissociation. A larger solute dissociation would then result in a larger number of free charge carriers, and subsequently in a larger conductivity.
According to the WET, the ionic conductivity in a glass is then closely related to the dielectric permittivity of the medium and will increase with increase in this parameter. Therefore, the replacement of oxygen by a more polarizable atom, such as S, or Se, was supposed to increase the conductivity. The first Na+-conducting thiogermanate glasses were then synthesized [Barrau et al. 1978]. In the following years, owing to the success of the WET, ion-conducting glasses based upon other sulfide networks such as thioborate [Levasseur et al. 1981], thiophosphate [Mercier et al. 1981], thioarseniate [Visco et al. 1985] and thiosilicate networks [Akridge 1984, Pradel and Ribes 1986, Sahami et al. 1985] were investigated.
It was the first time that these families, sulfide counterparts of the very well-known silicate, germanate, borate and phosphate glasses were elaborated. At the time, simple glasses comprising a network and a modifier were prepared. Later, more complex systems were elaborated in order to investigate famous effects, largely debated in the oxide family, such as the mixed alkali effect (MAE), the mixed glass former effect (MFE). The motivation of these investigations being the search for fast ion conductors, literature reports mainly on glass systems comprising Li+ and Na+ as mobile cations.
In this paper, we will only focus on thiosilicate and selenosilicate glasses, and report their preparation, structural, thermal and electrical characterization, showing their particularities compared to their oxide counterparts due to the larger polarizability of the chalcogen and the more covalent nature of the bonds but also, their similarities with the existence of both, bridging and non-bridging anions or the non-linear variation of properties when two mobile cations coexist in the glassy network.
2. Elaboration of thio and selenosilicate glasses
Like their oxide counterparts, thiosilicate and selenosilicate glasses can be prepared as bulk materials, powders or thin films. On the other hand, and in contrast to oxides, their preparation requires an oxygen-free atmosphere. After preparation, the glasses must be handled in moisture-free glove box since they are highly hygroscopic.
The usual way to prepare the glasses is the direct reaction of the constituting elements (for the former compounds, Si and S or Se) or the reaction of the constituting modifier compounds (e.g. Li2S), former compound (e.g. SiS2, GeS2…) and eventually “dopants” (e.g. LiI) mixed in stoichiometric quantities and placed in quartz tubes sealed under vacuum. The mixture is then melted at temperatures usually comprised between 1000 K and 1350 K, lower than the required temperatures for silicate glasses (Tf SiO2 = 1983 K; Tf SiS2 = 1373 K; Tf SiSe2 = 1243 K). Depending upon the ease of vitrification, the tube is quenched in air or in various liquids that increase the heat dissipation (water, salted water, liquid nitrogen). When preparing alkali-conducting chalcogenide glasses, vitreous carbon crucibles are often inserted in the tube in order to avoid contact of the reacting mixture with the quartz tube and thus contamination of the glass by silica [Levasseur et al. 1981, Pradel and Ribes 1986, Robinel et al. 1983]. The vitreous carbon crucible can be replaced by a layer of carbon obtained by pyrolysis of an organic compound such as acetone [Kennedy 1989, Zhang and Kennedy 1990]. Sulfur and to a lesser extend, selenium have high vapor pressures. A slow heating ramp of ∼6 K∕hour (in presence of S or Se) and ∼30 K∕hour (in presence of already prepared modifier, former compounds…) at the beginning of the reaction process is therefore required in order to avoid any risk of explosion of the quartz tube. The heat treatment can include steps with constant temperature for several hours to optimize the reaction.
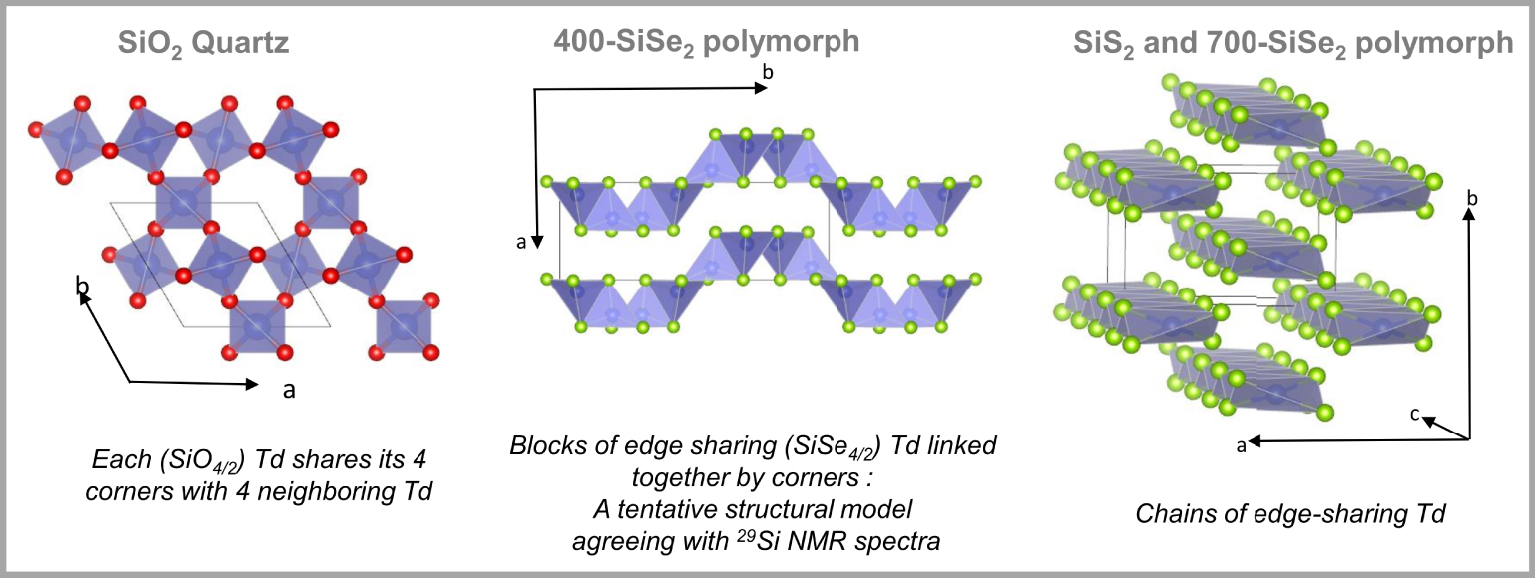
Basic building blocks of SiO2-quartz, crystalline SiS2 and 700-SiSe2. In the middle, tentative structural model for crystalline 400-SiSe2. O atoms are represented by red spheres, and S and Se atoms are represented by light green spheres.
Many glasses in the systems M2X–SiX2–YXn–MZ, M = Li, Na, Ag; X = S, Se; Y = Ge, Al, B, P; Z = Cl, Br, I; n = 2, 3/2, 5/2 were prepared in this manner [Kennedy and Zhang 1988, Kennedy 1989, Levasseur et al. 1981, Ribes et al. 1979].
However, thiosilicate glasses, even binary SiS2 and SiSe2 glasses, have a high tendency for crystallization. Therefore, faster quenching techniques were developed to produce glasses in larger (often, alkali-rich) composition domains. Several techniques can be considered from the simple crush of a droplet between two plates to more sophisticated techniques such as twin-roller quenching. In this technique, droplets of molten material are pushed between rotating twin rollers, giving 50–80 μm thick glassy flakes. The technique allows obtaining quenching rates of about 106 K∕s [Pradel et al. 1985]. Glasses of the system xLi2S–(1 − x)SiS2 were prepared in this manner up to large modifier content (x = 0.6) [Pradel and Ribes 1986]. Several series of thiosilicate and selenosilicate glasses were obtained in such a way [Aotani et al. 1994, Deshpande et al. 1988a, b, Michel-Lledos et al. 1992, Pradel et al. 1995, Pradel and Ribes 1986, Tatsumisago et al. 1996].
An alternative way to prepare thiosilicate glasses, i.e. the mechanical milling technique, has been proposed by Morimoto in 1999 [Morimoto et al. 1999]. Powders of the starting (former, modifier …) compounds are placed in a jar with a series of balls. Mechanical milling treatment is carried out on the mixture using a planetary ball mill. The mechanical energy transferred to the powder due to collision with the balls allows the reaction between the components of the mixture. Optimization of different parameters such as number and size of the balls, rotation speed, allowed the synthesis of 0.6Li2S–0.4SiS2 fine powders with similar properties than the melt-quenched samples. An advantage of this method is its ability to proceed at room temperature.
Finally, thin films of several thiosilicate glasses, i.e. Li2S–SiS2, Li2S–SiS2–LiI, Li2S–SiS2–P2S5–LiI, were obtained by thermal evaporation of the bulk glasses, which required the development of a specially designed device installed in a glove box under a controlled argon atmosphere [Creus et al. 1989]. Amorphous films were obtained and further used as solid electrolytes in exploratory research for microbattery development [Creus et al. 1992]. Owing to the difficulties to prepare and handle thin films in controlled atmosphere, very few experiments of this type were carried out but one can note a recent work on thiogermanate glasses by Seo and co-workers who prepared films by magnetron sputtering of a glassy target in an Ar atmosphere [Seo et al. 2016].
3. Network formers
Any thiosilicate/selenosilicate glass comprises SiS2∕SiSe2 as the network former compound.
In contrast to SiO2 whose structure comprises a 3D network of corner-sharing (CS) tetrahedra (Td), whatever the considered polymorph (quartz, trydimite, cristobalite), SiS2, in its unique known crystalline form, has a structure comprising infinitive chains of edge-sharing (ES) tetrahedra (Figure 1) [Zintl and Loosen 1935]. The situation is more complex in SiSe2 since, in addition to the usually reported polymorph, (named 700-SiSe2 hereafter) isotype of SiS2 [Hillel and Cueilleron 1971, Peters and Krebs 1982, Weiss and Weiss 1952], two other polymorphs, prepared by solid state reaction at 400 °C and 500 °C (named 400-SiSe2 and 500-SiSe2 respectively), have been identified [Pradel et al. 1993].
The vitreous counterparts of crystalline SiS2 and SiSe2 (named SiS(e)2 hereafter) can be prepared by conventional melt-quench technique even though they have a high tendency to crystallize. In the silicon sulfide and selenide families it is also possible to produce non-stoichiometric glasses, i.e. SixS1−x and SixSe1−x, which is not the case in the oxide family counterpart [Tenhover et al. 1983a, Griffiths et al. 1984, Johnson 1986]. This is based on the possibility of forming homopolar S(e)–S(e) and Si–Si bonds. Indeed, in these families, the difference in electronegativity between Si (1.8) and S (2.6)/Se (2.6) is not so large, in contrast with the difference in electronegativity between Si (1.8) and O (3.5) in the oxide family. Therefore, homopolar bonds are not as disadvantaged as they are in oxide glasses.
It has to be noted that these differences in electronegativity has a strong consequence on the nature of the chemical bonds in the oxide and sulfide/selenide glasses. In oxide glasses, the chemical bonds have a strong ionic character, and SiO2 can be considered as being built up with
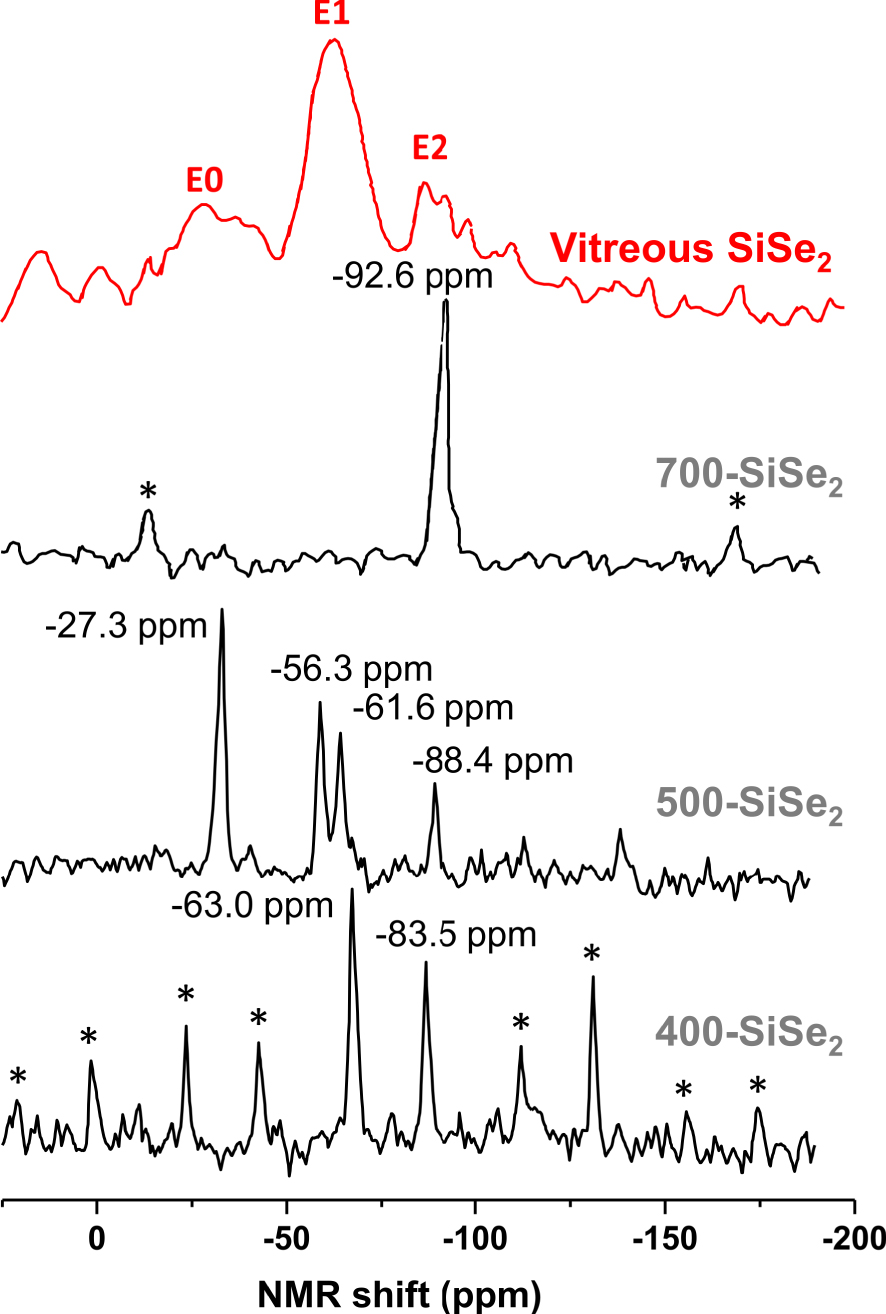
29Si MAS NMR spectra of SiSe2 polymorphs and SiSe2 glass. Spinning sidebands are indicated by asterisks.
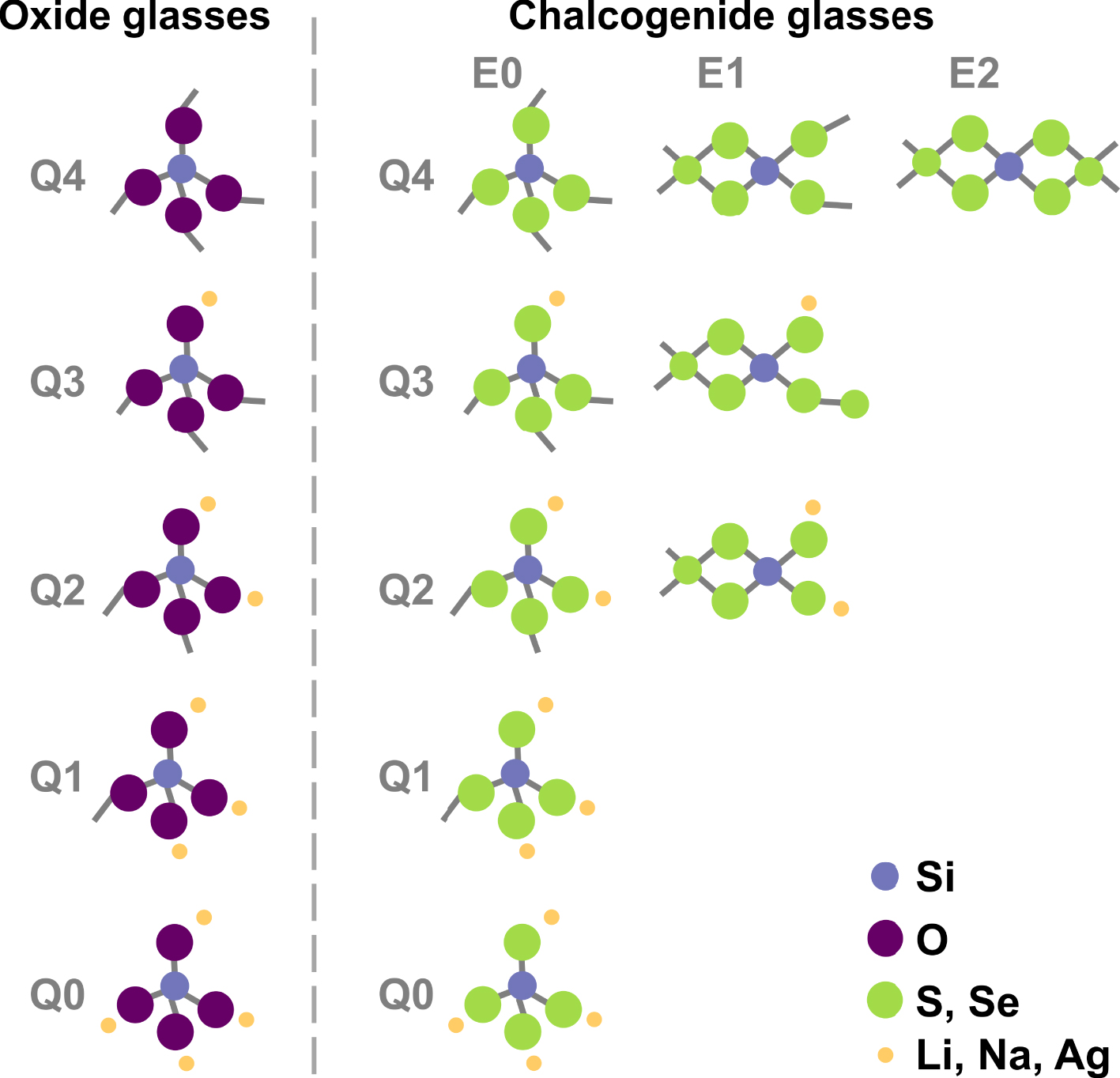
Possible Si environments in alkali silicate, thiosilicate and selenosilicate compounds.
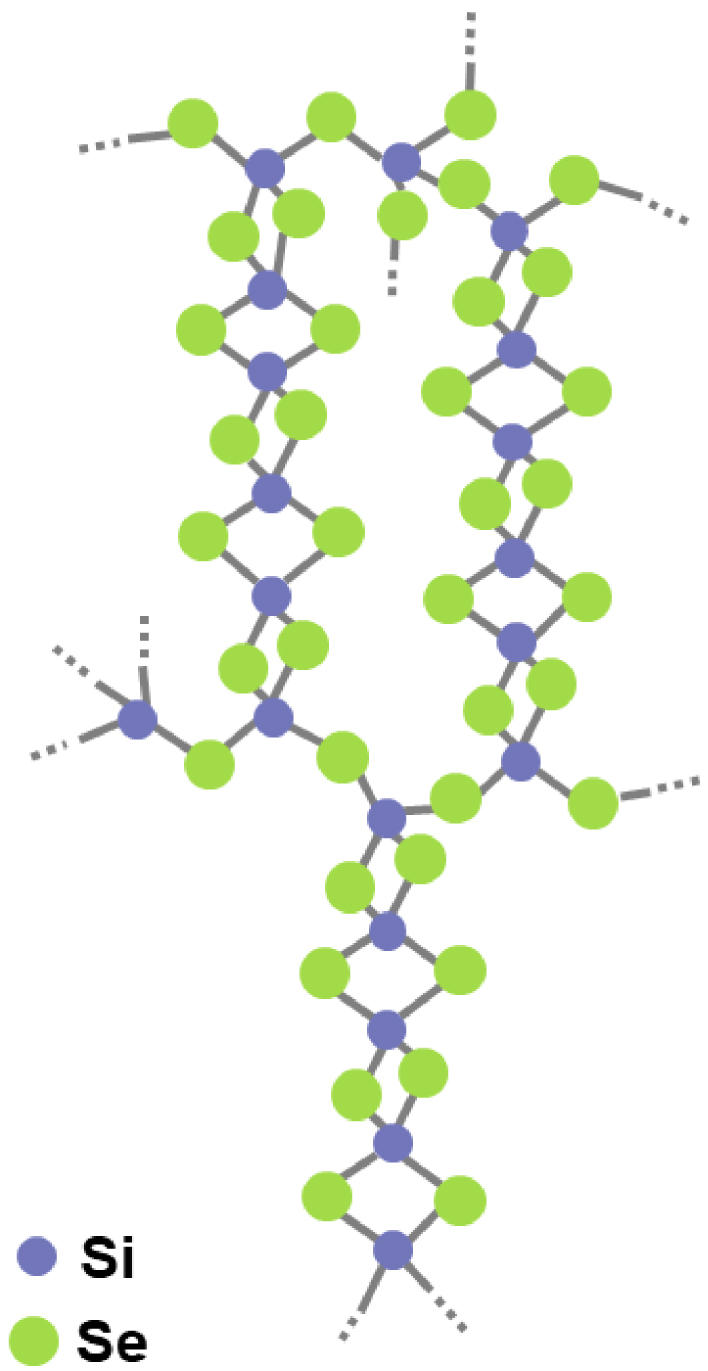
Schematic representation of a cross-linked chain cluster (CLCC) proposed by Griffiths and collaborators [Griffiths et al. 1984].
Raman [Griffiths et al. 1984, 1985, Pradel et al. 1993, Sugai 1987, Tenhover et al. 1983a, b, 1984, 1985] and 29Si NMR experiments [Moran et al. 1990, Pradel et al. 1993, Tenhover et al. 1988] as well as computer-modeling studies [Antonio et al. 1988, Gladden and Elliott 1987, 1989a, b, Gladden 1990] based on neutron-scattering data [Johnson et al. 1986a, b] were carried out in order to get an insight on the structure of the sulfide and selenide glasses and the unknown SiSe2 polymorphs. 29Si NMR spectra of the SiSe2 polymorphs and SiSe2 glass are shown in Figure 2 [Pradel et al. 1993]. The NMR spectrum of the 700-SiSe2 polymorph shows a single peak at −92.6 ppm which can be assigned to the unique Si site present in the structure and involved in ES tetrahedra. Similar findings were obtained for crystalline SiS2 with a single 29Si NMR peak at −19.5 ppm [Tenhover et al. 1988]. The spectra of 400-SiSe2 and 500-SiSe2 polymorphs are more complex. The first one shows two peaks at −83.5 ppm and −63.0 ppm and the second one four peaks at −88.4 ppm, −61.6 ppm, −56.3 ppm and −27.3 ppm. The spectrum of glassy SiSe2 shows three broad peaks at −86.0 ppm, −62.6 ppm, −28.7 ppm, similar to 29Si NMR spectrum of vitreous SiS2 where the peaks appear at −16.8 ppm, −7.6 ppm and +7.5 ppm [Tenhover et al. 1988]. The presence of several peaks in the 29Si NMR spectra of SiS(e)2 compounds suggests the existence of several Si environments. Three possible Si environments have been suggested: Si belonging to tetrahedra sharing two, one or zero edge(s), shown in Figure 3 and labeled E2, E1 and E0 respectively [Antonio et al. 1988, Gladden and Elliott 1987, 1989a, b, Gladden 1990, Griffiths et al. 1984, 1985, Moran et al. 1990, Pradel et al. 1993, Sugai 1987, Tenhover et al. 1983a, b, 1984, 1985, 1988]. For selenide (sulfide) compounds, peaks in the region −80∕−90 ppm (−10∕20 ppm) are attributed to E2 species, those in the region −60∕−70 ppm (−7∕8 ppm) to E1 species and E0 species have their signature in the region −20∕−30 ppm (+7∕+8 ppm). Therefore, 400-SiSe2 polymorph comprises E2 and E1 species in the ratio 1/1. A tentative structural model that fulfills this requirement is proposed in Figure 1 [Pradel et al. 1993]. Both, 500-SiSe2 and vitreous SiSe2 comprise the three species E2, E1 and E0, suggesting a close structural relationship between them. However, a minor discrepancy between E2:E1:E0 ratios (1:2:2 for the crystalline compound compared to 1:2:1 for the glass) exists, so it was suggested that an even better agreement could be achieved if one considered that the glass was comprised of a mixture of the units existing in 400-SiSe2 and 500-SiSe2. It was supported by the fact that the vitreous transition temperature, i.e. the temperature at which the vitreous structure is frozen in, lies around 450 °C. All Raman and computer-modeling studies based on neutron diffraction experiments (not described in detail here) are consistent with the above findings, i.e. they confirm the coexistence of E2, E1 and E0 species [Antonio et al. 1988, Gladden and Elliott 1987, 1989a, b, Gladden 1990, Griffiths et al. 1984, 1985, Moran et al. 1990, Pradel et al. 1993, Sugai 1987, Tenhover et al. 1983a, b, 1984, 1985, 1988]. On the other hand, they all failed in one way or another to give a complete description of the glass structure that agrees with all experimental data (relative amounts of species for example). Some models such as the random network model by Sugai [Sugai 1986, 1987], are too simplistic. In the cross-linked-chain-cluster (CLCC) model, Griffiths et al. proposed an intermediate range order built up with chain fragments containing E2 units interconnected by E1 and E0 tetrahedra, as shown in Figure 4 [Griffiths et al. 1984]. This model was refined by Gladden in an investigation based upon a computer-modeling study of neutron diffraction data [Gladden and Elliott 1987, 1989a]. In this work, several types of intermediate range order species were considered, including random chains and the Griffiths CLCC species. The best agreement led to a mixture of 85% random chains containing an average of seven E2 units and 15% of CCLC units, consisting of rings with two E0 and four E2 units each. This model still does not meet all the quantitative experimental constraints imposed by NMR since it underestimates the relative fractions of E1 and E0 units. Later on, Celino and Massobrio used extensive first-principle molecular dynamics simulations to describe the atomic structure of SiSe2 [Celino and Massobrio 2005]. In this case, it is the relative fraction of E2 that was underestimated. The dominant structural motifs were Si-triads comprising E0 and E1 species and chain fragments of E1 species. All these studies indicate that the glasses comprise a complex mixture of motifs including fragments of chains and CLCCs with various fractions of E2, E1 and E0 units. Compared to vitreous SiO2 whose structure comprises CS tetrahedron and intermediate range order comprises only tetrahedra rings, the structure of sulfide and selenide glasses is much more complex. It comprises ES tetrahedra and a very complex MRO including chains and rings.
The presence of ES tetrahedra constitutes a violation of the traditional Zachariasen network model, which explicitly excludes any connectivities different from corner sharing. It might explain their strong tendency toward crystallization.
4. Network former/network modifier
4.1. Single modifier
In oxide glasses, addition of a modifier oxide, e.g. Li2O, Na2O, in the former oxide SiO2, creates the well-known non-bridging oxygen (NBO) and the consequent Qn species of tetrahedrally coordinated silicon bound to a number, n, of bridging oxygen (BO) (n = 4, 3, 2, 1 or 0) as shown in Figure 3. Do similar non-bridging sulfur or selenium (NBS) exist when a modifier is added to SiS(e)2? In such a case, owing to the presence of ES tetrahedra, a larger number of entities, summarized in Figure 3, might be expected. For example, a E1Q3 entity would be a tetrahedron with three bridging sulfur or selenium (BS), one NBS and sharing an edge with its neighbor.
Structural investigation of glasses M2X–SiX2 (M = Li, Na, Ag to a less extent; X = S, Se) was carried out using many complementary characterization techniques including Raman, IR, 29Si, 23Na, 7Li NMR [Pradel et al. 1995], XPS [Foix et al. 2001, 2006] and neutron diffraction [Lee et al. 1997]. No technique alone could give a complete pattern of the structure at local and intermediate orders. However, their combination helped in getting a clear, even though still incomplete picture.

29Si MAS NMR spectra for xLi2S–(1 − x)SiS2 glasses.
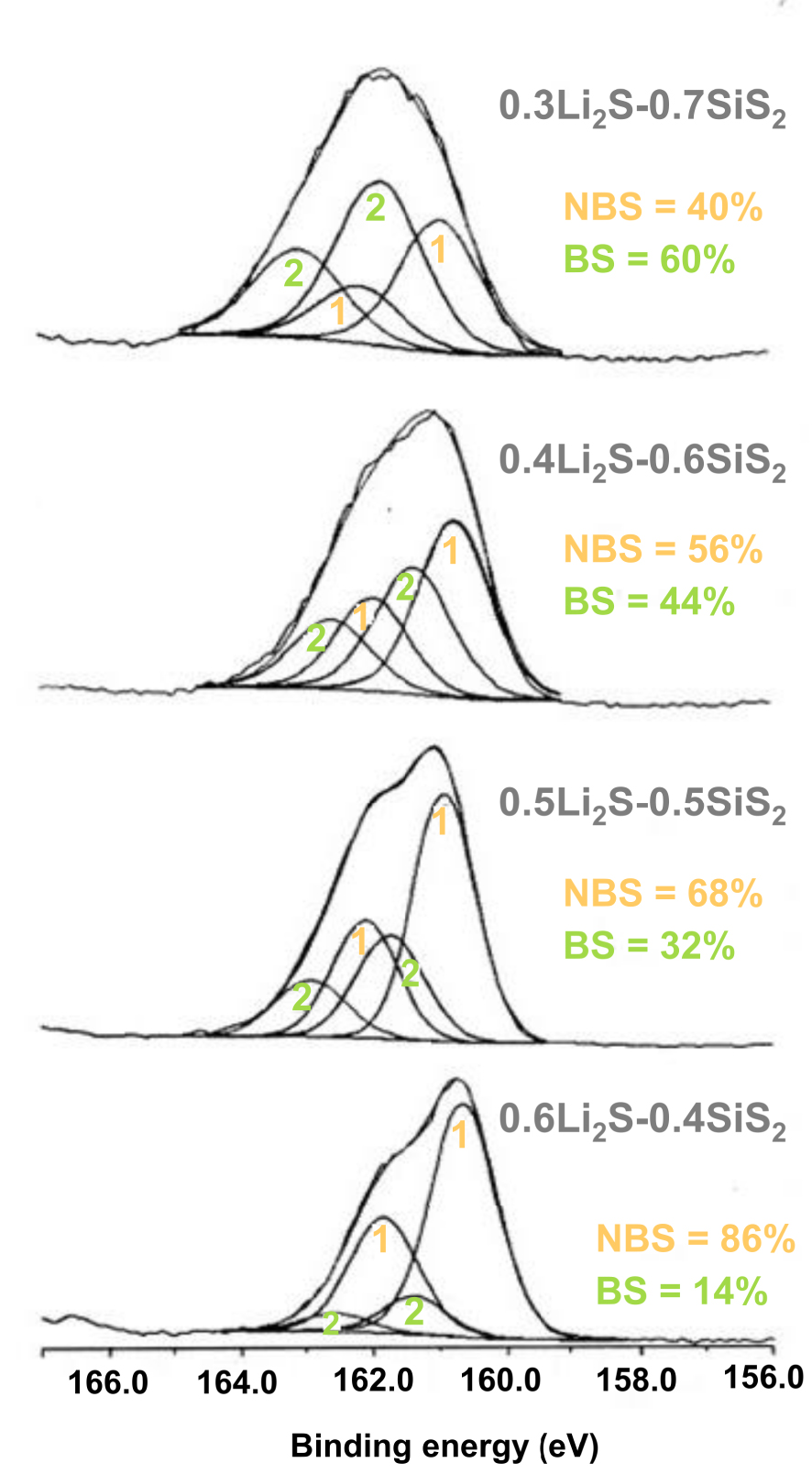
XPS S2p core peaks for xLi2S–(1 − x)SiS2 glasses. Doublet 1: NBS; doublet 2: BS.
Information on glass structure can be obtained by comparing data obtained for glasses with those for crystalline model compounds. On this basis, crystallized thiosilicate compounds in the system Na2S–SiS2, where crystallographic data are numerous [Cade et al. 1972, Olivier-Fourcade et al. 1972, 1978], have been used to understand 29Si NMR spectra of Na2S–SiS2, Li2S–SiS2 and Ag2S–SiS2 glasses [Eckert et al. 1989, Pradel et al. 1995]. The main information of this investigation can be summarized as follows. For all of the alkali-containing system, the spectra are dominated by two principal resonances in the chemical shift regions 1–7 ppm and −7 to −12 ppm, as shown in Figure 5 for the Li2S–SiS2 system. The first one is the signature of E0 entities, with no edge shared with neighbors; the second is the signature of E1 entities with a single edge shared with neighbor. At low modifier content (10% Li2S), still remains some E2 entities, whose signature occurs at ∼−20 ppm. Addition of modifier results in the preferential destruction of ES tetrahedra, this tendency being much stronger for Li2S than for Na2S, 23% E1 remaining in 0.5Li2S–0.5SiS2 against 50% E1 (48% according to Watson and Martin [2017]) in 0.5Na2S–0.5SiS2. Note that no ES tetrahedra exists in the related Ag2S–SiS2 glasses [Pradel et al. 1995]. Owing to the very small 29Si chemical shift variations for thiosilicates, 29Si NMR cannot give direct and straightforward information on BS and NBS presence and distribution. In a recent re-investigation of the structure of Na thiosilicate glasses, complementary deconvolution of both 29Si NMR and Raman spectra was used to extract this information [Watson and Martin 2017]. XPS experiments have also been carried out to study Li and Na thiosilicate glasses [Foix et al. 2001]. Data from XPS core peak analysis for lithium glasses are shown in Figure 6. For all glasses (the same applies for Na glasses), a decomposition of the large S2p peak into a minimum of two doublets was necessary in order to fit the experimental curve. These doublets are the signature of BS and NBS, similar to the BO and NBO in oxide glasses. The signal at lower energy was assigned to NBS that are more negative than BS associated with the doublet at higher energy. When the modifier increases, the proportion of NBS simultaneously increases in the glass. A thorough analysis of the XPS data including comparison with XPS spectra of model crystalline compounds has been carried out. Based on these data, Li2SiS3 and Na2SiS3 clusters were built and a Mulliken population analysis was carried out to investigate the charge distribution of the clusters. The main result of the whole study is the noticeable difference existing between the structures of lithium and sodium thiosilicate glasses, in agreement with NMR results. According to XPS data, this is due to different electronic redistribution over the network when one or the other alkali is added, the sodium addition resulting in a change in the electronic distribution over the entire network, which also affects BS. In oxide glasses, the splitting of 2 eV between NBO and BO is larger than the splitting of ∼0.9 eV between NBS and BS in sulfide glasses. It can be explained by the decreased ionic nature of the bonds in thiosilicate and smaller difference in the electronic density around NB and B atoms. XPS valence band spectra of Li2SiS3 and Na2SiS3 glasses combined with theoretical calculations have also been carried out [Foix et al. 2006]. The difference in spectra of Li and Na thiosilicate glasses points for the presence of a majority of CS tetrahedra in the Li glasses whereas a larger proportion of ES tetrahedra should be present in the Na glass, in agreement with 29Si NMR studies.
Structural investigation of lithium and sodium selenosilicate glasses and crystalline model compounds was also carried out using mainly Raman and 29Si NMR experiments [Pradel et al. 1992, 1995]. 29Si NMR proved to be very powerful in this case. Indeed, much larger 29Si chemical shifts were observed as compared to sulfide glasses and, therefore, species with different Qn could be discriminated as shown in Figure 7 for the Li2Se–SiSe2 family. It can be seen that the tendency to maintain ES species is lower in selenosilicate glasses than in thiosilicate ones. Indeed, none are left at x = 0.5 for selenosilicates. The combination of absence of ES species and possible discrimination between Qn species gave the opportunity to test different structural models that were much discussed in oxide glasses to identify the population distribution of Qn species, e.g. a completely random “statistical” [Schramm et al. 1984] or chemically ordered [Dupree et al. 1984, Grimmer et al. 1984] distribution. Figure 8 shows the experimental spectrum of 0.6Na2Se–0.4SiSe2 glass and the resulting simulated distribution based upon the experimental chemical shifts of Qn sites. The two extreme scenarios can be discarded: While the binary model predicts the presence of Q1 species only, the random model would predict less Q1 species than observed.

29Si MAS NMR spectra for xLi2Se–(1 − x)SiSe2 glasses. Spinning sidebands are indicated by asterisks.

Deconvolution of the 29Si MAS–NMR spectrum of 0.6Na2Se–0.4SiSe2 glass. Bottom: experimental spectrum; top: simulated spectrum assuming the chemical shifts and population distribution given in inset. Expected population distributions for statistical and chemically ordered models are also given.
On the whole, the structural investigation showed a more complex structure in thio and selenosilicate glasses than in oxide analogs. On the other hand, as it occurs in oxide glasses, the addition of modifier leads to the creation of non-bridging atoms (here S or Se ones), even though the Si–S(e) bonds are less ionic than the Si–O ones. The nature of both the modifier and chalcogen have consequences on different aspects of the structure such as the number of ES species and the charge on the atoms.
Physicochemical characterization of these glasses has been carried out in order to understand the influence of the structure on glass properties. Figure 9 shows the evolution of the glass transition temperature Tg with the addition of modifier in glasses xM2X–(1 − x)SiX2 with M = Li, Na, Ag and X = S, Se [Pradel and Ribes 1989a, Michel-Lledos et al. 1992, Tenhover et al. 1983a, b, 1984, Johnson 1986]. Tg decreases rapidly with the first addition of modifier, then at a slower pace, if any, to further addition. A rather large difference between Tg of the sulfide and selenide systems could partly be explained by their structural difference i.e. the larger presence of ES species in the sulfide glasses [Pradel and Ribes 1992]. The electrical characteristics (electrical conductivity and activation energy) of xM2X–(1 − x)SiX2 glasses with M = Li, Na, Ag and X = S, Se have been investigated. As an example, Figure 10 shows the composition dependence of room temperature conductivity and activation energy for lithium-conducting glasses including oxide ones [Pradel and Ribes 1992, Yoshiyagawa and Tomozawa 1982]. Sulfide and selenide glasses have comparable electrical characteristics. In contrast, the corresponding oxide glasses have much lower conductivities and much larger activation energies. This can be understood if the main factor that controls ion motion is the anion polarizability, which is comparable for S (7.3) and Se (7.5) and much lower for O (3.1). As described in the introduction section, this was predicted by the weak electrolyte theory, which is at the basis of the investigation of these glasses. At this point, another family of thiosilicate glasses, which will not be discussed further in the paper, can be mentioned, i.e. glasses with a “salt”, e.g. a lithium halide, dissolved in the matrix [Akridge 1984, Sahami et al. 1985, Kennedy et al. 1986, Pradel and Ribes 1989a]. These glasses show increased conductivity owing to the high polarizability of the anions and increase in numbers of mobile ions. Up to 40% of salt can be dissolved in a glass but it is at the expense of its thermal stability.

Glass transition temperatures in glasses xM2X–(1 − x)SiX2 with M = Li, Na, Ag and X = S, Se. The dashed lines are a guideline for experimental data.

Conductivity 𝜎 and activation energy of conductivity E𝜎 for xLi2X–(1 − x)SiX2 glasses (X = O, S and Se).
4.2. Multi-modifiers
In the previous section, it has been shown that addition of Li2S or Na2S to SiS2 has somewhat different consequences on the glass structure and properties with a stronger tendency for Li+ ions to destroy the ES tetrahedra and a charge redistribution over the entire network for Na+ ions leading to more negative BS and NBS. The question is: what would happen if both Li+ and Na+ were introduced in the glass network? Some answers were obtained with the investigation of the series of glasses 0.5(xNa2S–(1 − x)Li2S)–0.5SiS2 with 0⩽x⩽1. The structural investigation was only carried out by 29Si NMR [Pradel et al. 1995]. It was shown that, while the two main peaks observed in the binary glasses and related to E0 and E1 species (Figure 5) were still present in all mixed Na/Li glasses, their relative intensity was closer to that observed for the binary lithium glasses, even for the first addition of lithium in the sodium glass (Figure 11). The chemical shifts for the two peaks were intermediate between those measured for the binary glasses, which led to the conclusion of the absence of any preferential association of one type of cations for a specific site E1 or E2.

29Si MAS NMR spectra for 0.5(xNa2S–(1 − x)Li2S)–0.5SiS2 glasses.
While the replacement of lithium by sodium in the thiosilicate glasses does not seem to transform the structure drastically, it has drastic consequences on several properties. Dependence of glass transition temperature, Tg, electrical characteristics (conductivity 𝜎 and activation energy of conductivity E𝜎) and activation energy of the relaxation time T1, ET1, (measured by 7Li NMR spectroscopy) on composition are shown in Figure 12 [Pradel and Ribes 1994]. A strong non-linear variation of these characteristics is observed. Tg and 𝜎 show a high minimum at x ∼ 0.5, whereas the activation energies E𝜎 and ET1 display a maximum for the same values of x. These features are the signature of the mixed alkali effect (MAE), a very well-known phenomenon, reported many times in oxide glasses [Day 1976, Ingram 1987, 1992], in particular in silicate glasses, the oxide counterparts of the glasses described here [Elliott 1992]. MAE occurs when a modifier is substituted by another one, at a constant total modifier content. Therefore, it appears to be a common feature between oxide and chalcogenide glasses, even though reports on MAE in the second family are scarce and concern mainly two systems, the present one and the Ag2S–Rb2S–GeS2 system (here, we should rather call it “mixed cation effect”) [Rau et al. 2001].

(a) Conductivity 𝜎 and activation energy of conductivity E𝜎 and (b) glass transition temperature, Tg and activation energy of the relaxation time T1, ET1 for 0.5[xNa2S–(1 − x)Li2S]–0.5SiS2 glasses. The dashed lines are guidelines for experimental data.
The information reported above in Section 4 indicates that Li+ and Na+ ions do not favor the same sites in thiosilicate glasses; in particular, NBS are more negative around Na+ than in the neighborhood of Li+. In the Ag2S–Rb2S–GeS2 system, it has been clearly demonstrated by EXAFS experiments that the Ag+ and Rb+ cations maintained their own environment in the mixed glasses. A similar situation probably applies to the Li/Na thiosilicate glasses. So it can be anticipated that for an ion, to hop from one site to the next is more difficult in a mixed environment than in single alkali one where all the sites are similar and match the only mobile ion. The mobility would then be restricted, which would induce a lower conductivity and higher activation energy as observed.
5. Effect of a competitive network former on thiosilicate glasses
5.1. Thio-aluminosilicate
The glass forming ability of compositions belonging to the Li2S–Al2S3–SiS2 system, sulfide counterparts of lithium aluminosilicates, has been investigated [Deshpande et al. 1988b, Hayashi et al. 2004, Martin and Sills 1991, Pradel and Ribes 1992]. The explored region and vitreous domain extension, which depends upon the elaboration technique, i.e. conventional melt-quenching, twin-roller quenching and mechanical alloying, is shown in Figure 13. Compared to the oxide family, the glass forming ability is poor with a maximum ratio of Al/Li much below the 1.5 reported for oxide glasses.

Glass formation region in the Li2S–Al2S3–SiS2 system. Circles and triangles correspond to glasses, while stars refer to partially crystallized samples.
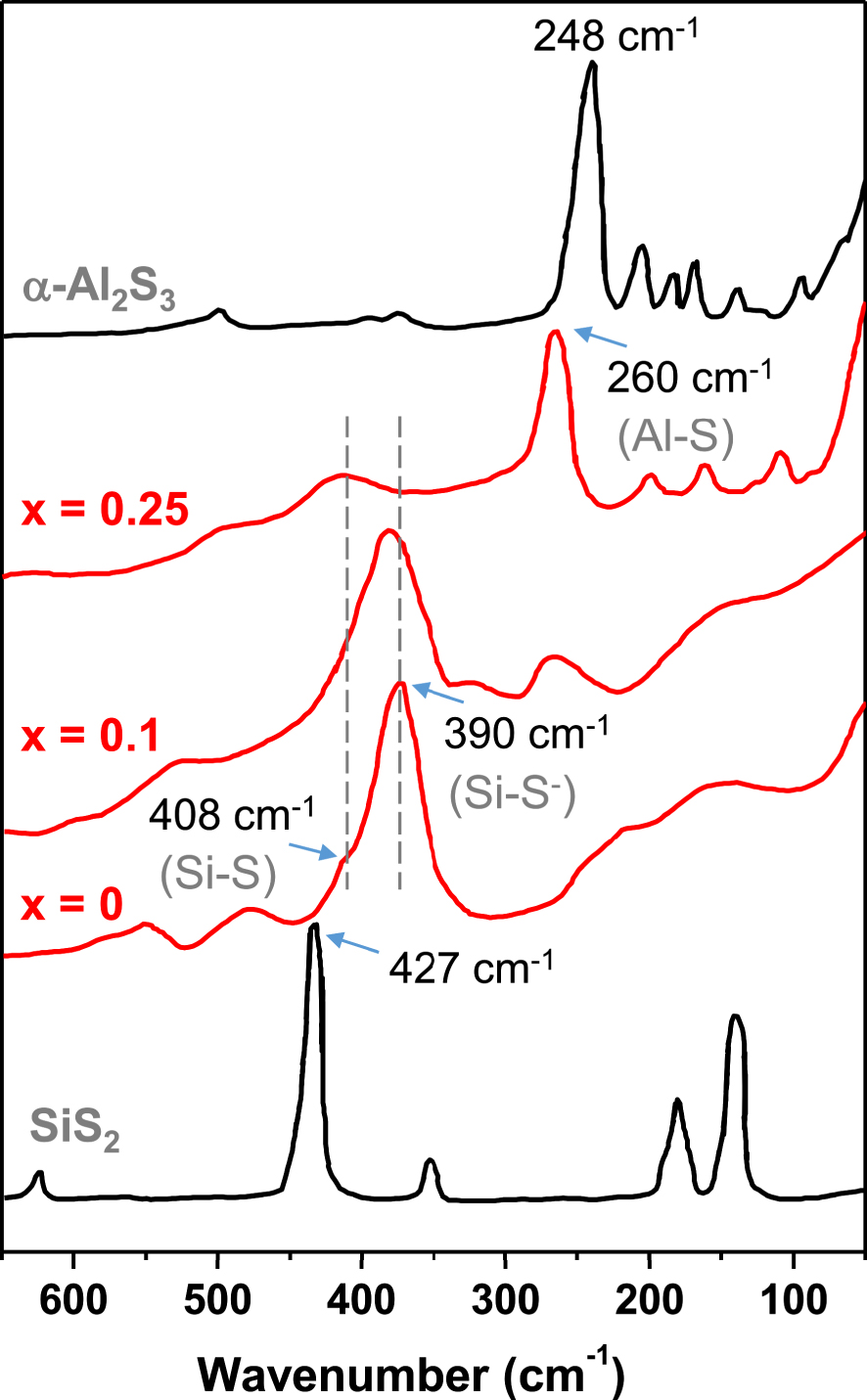
Raman spectra of 0.5 Li2S–xAl2S3–(0.5 − x)SiS2 glasses, (Si–S) and (Si–S−) stand for bridging Si–S bonds and non-bridging Si–S− bonds, respectively. Raman spectra of crystalline SiS2 and 𝛼–Al2S3 are reported for comparison.
Raman and 29Si, 27Al NMR investigations helped in getting some insights into the structure of these glasses. Raman spectra of glasses 0.5Li2S–xAl2S3–(0.5 − x)SiS2 with x = 0, 0.1, 0.25, along with the spectra of crystalline SiS2 and crystalline 𝛼–Al2S3 are shown in Figure 14 [Pradel and Ribes 1992]. The low temperature form of crystalline Al2S3, 𝛼-Al2S3, has a lacunar wurtzite structure with aluminum occupying tetrahedral sites, a difference with the high temperature form of crystalline Al2O3 where aluminum is in an octahedral environment. The main band in the Raman spectrum at 248 cm−1 is assigned to the symmetric valence vibrations of the AlS4∕2 tetrahedron. The main band in the Raman spectrum of crystalline SiS2 at 427 cm−1 can be assigned to the symmetric valence vibrations of ES SiS4∕2 tetrahedra [Tenhover et al. 1983a] while the two main bands in the Raman spectrum of glass 0.5Li2S–0.5SiS2 (x = 0) at 408 cm−1 and 390 cm−1, are attributed to the stretching vibrations of bridging Si–S bonds or non-bridging Si–S− bonds. The addition of Al2S3 in vitreous 0.5Li2S–0.5SiS2 leads to the relative decrease in intensity of the band at 390 cm−1 compared to that at 408 cm−1 and the simultaneous appearance and further increase of a band at 260 cm−1, which can be attributed to the stretching vibrations of Al–S bonds. Compared to the crystalline compound, the band attributed to Al–S bonds is displaced toward high frequencies, consistent with a shortening of the bonds and therefore, leading to discarding an octahedral coordination for the aluminum. It is in agreement with the results from 27Al NMR experiments [Martin and Sills 1991]. In this case, the NMR spectra of all prepared Li2S–Al2S3–SiS2 glasses show a single peak at 110 ppm, similar to the peak present in the NMR spectrum of crystalline 𝛼-Al2S3. In this case, one expects the lithium to act as a charge compensator and therefore, a decrease in the number of non-bridging sulfur, consistent with the decrease in the band at 390 cm−1 in the Raman spectra.

Conductivity 𝜎, activation energy of conductivity E𝜎 and glass transition temperature Tg of 0.5Li2S–xAl2S3–(0.5 − x)SiS2 glasses elaborated by twin-roller quenching. The dashed lines are guidelines for experimental data.
This assumption is supported by the increase of the glass transition temperature Tg with the Al2S3 content in the 0.5Li2S–xAl2S3–(0.5 − x)SiS2 glasses as shown in Figure 15. It is consistent with an increasing polymerization of the network due to the disappearance of non-bridging sulfur. Such an increase of Tg with increase in the Al2S3 content in the glasses has been reported for other series of compositions such as series where the ratio Li/Al was constant and equals to 2/1, 1/1, 1/2 [Martin and Sills 1991].
The electrical properties of Li2S–Al2S3–SiS2 glasses have been reported. The conductivity 𝜎 and activation energy of conductivity E𝜎 for the 0.5Li2S–xAl2S3–(0.5 − x)SiS2 glasses are shown in Figure 15. The slight decrease in 𝜎 and increase in E𝜎 with the addition of Al2S3 point for a lower mobility of the lithium acting as charge compensator as compared to lithium close to a non-bridging sulfur. Such assumption is supported by the fact that, in the series yLi2S–0.1Al2S3–(0.9 − y)SiS2, the conductivity increases from 3.3 × 10−6 S⋅cm−1 to 1.3 × 10−4 S⋅cm−1 when y changes from 0.3 to 0.6.

Investigated glass compositions in the system Li2S–SiS2–GeS2, i.e. 0.3Li2S–0.7[(1 − x)SiS2–xGeS2] and 0.5Li2S–0.5[(1 − x)SiS2–xGeS2].
5.2. Thiogermanosilicate
The structure of SixGe1−xS2 glasses has been investigated by analyzing Raman experiments [Tenhover et al. 1983b]. It was shown that, whatever be x, separate clusters of the two formers were obtained, which was attributed to the impossible mixing of SiS2 and GeS2 networks that adopt different medium-range order configurations: dominance of ES tetrahedra as shown in Section 3 for the first one and dominance of CS tetrahedra for the second one [Feltz et al. 1985].

Raman spectra of 0.3Li2S–0.7[(1 − x)SiS2–xGeS2] glasses. (Si(Ge)–S) and (Si(Ge)–S−) stand for bridging Si(Ge)–S bonds and non-bridging Si(Ge)–S− bonds, respectively. Blue dashed line corresponds to the main peak of 0.5Li2S–0.5SiS2 glass. Raman spectrum of crystalline GeS2 is reported for comparison. SAXS intensity for five glasses belonging to the three different regions is shown in the inset.
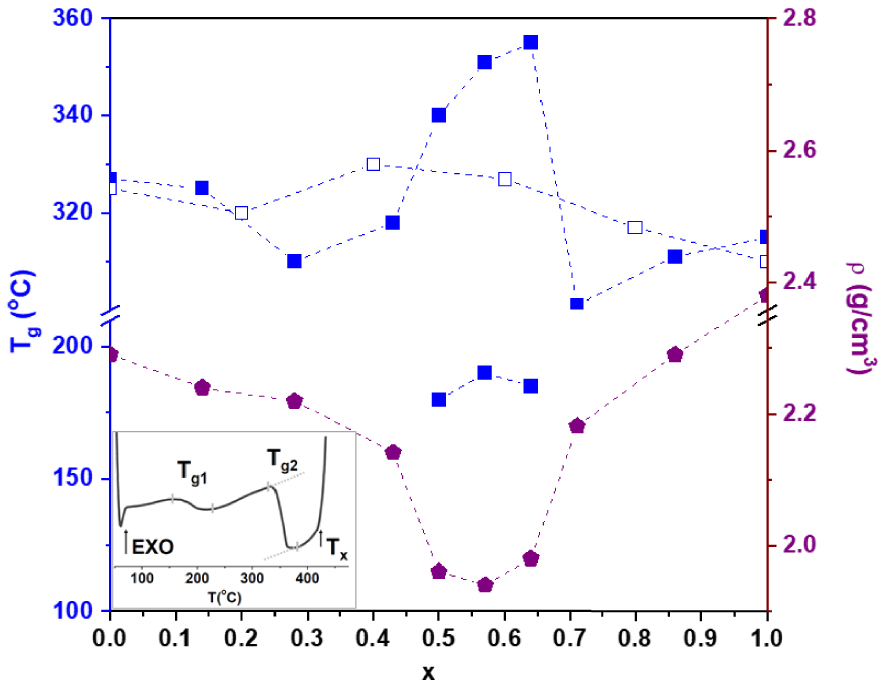
Glass transition temperature, Tg, density, 𝜌, for Li2S–SiS2–GeS2 glasses. Filled and empty symbols correspond to series 0.3Li2S–0.7[(1 − x)SiS2–xGeS2] and 0.5Li2S–0.5[(1 − x)SiS2–xGeS2], respectively. The inset displays the DSC curve of 0.3Li2S–0.25SiS2–0.45GeS2 glass. The dashed lines are guidelines for experimental data.
The glass forming ability and properties of glasses, whose composition lies along two lines of the system Li2S–SiS2–GeS2, i.e. 0.3Li2S–0.7[(1 − x)SiS2–xGeS2] and 0.5Li2S–0.5[(1 − x)SiS2–xGeS2] with 0⩽x⩽1, were also investigated (Figure 16) [Deshpande et al. 1988a, Pradel and Ribes 1989b, Pradel et al. 1998]. The glass elaboration required the use of the twin-roller quenching technique. Main structural information was obtained by a Raman experiment analysis. Raman spectra of 0.3Li2S–0.7[(1 − x)SiS2–xGeS2] glasses are shown in Figure 17. The spectra of the end-line compounds, 0.3Li2S–0.7SiS2 and 0.3Li2S–0.7GeS2 are dominated by the stretching vibrations of bridging Si–S (Ge–S) bonds and non-bridging Si–S− (Ge–S−) bonds at 412 cm−1 (338 cm−1) and 368 cm−1 (395 cm−1) respectively [Souquet et al. 1981]. When considering the general evolution of the spectra, three different domains can be identified: For the first substitutions of a glass former by the other one, i.e. for 0⩽x < 0.50 and 0.64 < x⩽1, a smooth change in the spectra is observed. A sudden change occurs when the Si/Ge ratio is close to 1, i.e. for 0.5⩽x⩽0.64. For x = 0.5 the spectrum narrows and the main peak suddenly shifts to higher frequency, close to the frequency of the stretching vibrations of non-bridging Si–S− bonds in 0.5Li2S–0.5SiS2 glass (377 cm−1). The two spectra look very much alike, but with a broadening for the mixed glass due to the presence of Ge–S bonds, which also explains the further broadening of the spectra upon further GeS2 addition. The situation is different in the second series of mixed glasses, i.e. 0.5Li2S–0.5[(1 − x)SiS2–xGeS2]. In this case, a smooth evolution of the Raman spectra (not shown here, Deshpande et al. [1988a]) is observed all along the line from x = 0 to x = 1. SAXS experiment on the first series 0.3Li2S–0.7[(1 − x)SiS2–xGeS2] were carried out in order to check the homogeneity of the glasses [Pradel et al. 1998]. Samples from the three regions were tested. Typical results are shown in the inset of Figure 17. Data obtained for samples belonging to the limiting regions (0⩽x < 0.50 and 0.64 < x⩽1) could be fitted in the framework of the Debye–Buëche model [Debye and Buëche 1949] and therefore, are homogeneous. In contrast, the higher scattering observed for glasses belonging to the central region (0.5⩽x⩽0.64) rather obeys Porod’s law [Porod 1982], which indicates the presence of aggregates (of about 50 Å) in the glass. Both Raman and SAXS experiments point toward homogeneous glasses in the limiting regions and the occurrence of a phase separation in the central one, leading probably to entities with a composition close to GeS2 embedded in a matrix whose composition is close to that of 0.5Li2S–0.5SiS2 glass, i.e. Li2SiS3.

Conductivity 𝜎 and activation energy of conductivity E𝜎 for Li2S–SiS2–GeS2 glasses. Filled and empty symbols correspond to series 0.3Li2S–0.7[(1 − x)SiS2–xGeS2] and 0.5Li2S–0.5[(1 − x)SiS2–xGeS2], respectively. The dashed lines are guidelines for experimental data.
Vitreous transition temperatures Tg and density 𝜌 were measured and are shown in Figure 18 while the electrical conductivity 𝜎 and corresponding activation energy E𝜎 are shown in Figure 19. A smooth evolution of Tg, 𝜎 and E𝜎 when SiS2 is substituted by GeS2 is observed for the 0.5Li2S–0.5[(1 − x)SiS2–xGeS2] glasses, which agrees with Raman data. In contrast, sudden changes in all parameters 𝜌, Tg, 𝜎 and E𝜎 occur in the central region for compositions pointed as phase-separated from SAXS and Raman experiments. Appearance of two Tg and lowering of 𝜌 strongly support the presence of a phase separation. Moreover, the larger conductivity of the glasses in the central region, close to the conductivity of the 0.5Li2S–0.5SiS2 glass, supports the structural scheme suggested by Raman data, i.e. GeS2 aggregates embedded in a Li2SiS3 matrix, provided that a percolation threshold is reached.
The differences between the two families of glasses, homogeneity versus phase separation, could be understood by the degree of modification of the matrix, which, upon increase, tends to lead to similar configurations for the two end-line compounds. GeS2 favors CS tetrahedra, hence few, if any, ES tetrahedra are expected in lithium thiogermanate glasses. For 0.3Li2S–0.7SiS2 glass, 34% of tetrahedra in the structure are ES ones; this number goes down to 23% for 0.5Li2S–0.5SiS2 glass [Eckert et al. 1989]. Therefore, mixing of the two end-line compounds is more favorable at high modifier content. It can also be pointed out that a crystalline metathiosilicate phase, Li2SiS3, exists [Weiss and Rocktäschel 1960], whereas crystalline thiodisilicate, Li2Si2S5 (0.33Li2S–067SiS2), does not. The phase separation occurs in the 0.3Li2S–0.7[(1 − x)SiS2–xGeS2] with the tendency to produce a glassy phase of composition Li2SiS3. On the other hand, homogeneous glasses are obtained for the family 0.5Li2S–0.5[(1 − x)SiS2–xGeS2] corresponding to the Li2SiS3 composition. This can be related to an investigation on lithium germanosilicate glasses, the oxide counterparts of the present glasses [Verweij et al. 1979]. Anomaly in the refractive index of several Li2O–SiO2–GeO2 glasses was indeed explained by the tendency of glasses to phase-separate with one of the resulting phase having the disilicate composition. In contrast, no anomaly was observed for 0.33Li2O–0.67[(1 − x)SiO2–xGeO2] glasses corresponding to the exact disilicate composition. A similar situation to ours since, in the oxide glasses, crystalline disilicate phase exists while the metasilicate one does not.
5.3. Thiophosphosilicate
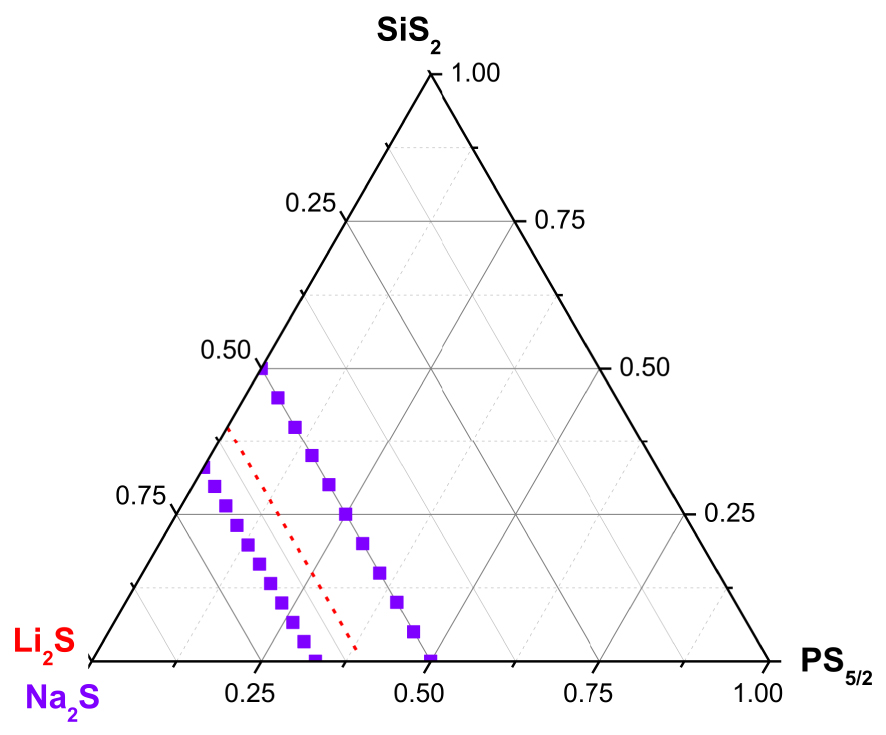
Investigated glass compositions in the system Na2S–SiS2–PS5∕2, i.e. 0.5Na2S–0.5[xSiS2–(1 − x)PS5∕2] and 0.67Na2S–0.33[xSiS2–(1 − x)PS5∕2] (purple symbols) and line of investigated compositions in the Li2S–SiS2–P2S5 system, i.e. glasses with 60 mol% Li2S.
Investigation of lithium thiophosphosilicate glasses of composition 0.6Li2S–0.4[(1 − x)SiS2–xP2S5] with 0⩽x⩽1 was carried out in the eighties (Figure 20) [Kennedy and Zhang 1989, Kennedy et al. 1990]. The main information is the anomalous evolution of some properties, e.g. glass transition temperature, when substituting a modifier by the other one, with a change at the particular composition corresponding to a ratio SiS2:P2S5 equals to 2:1, i.e. Si∕P = 1. Even though a paper, mainly focussed on electrochemical properties of this lithium family, was published very recently [Zhao et al. 2020], the renewal of interest for the thiophosphosilicate glasses concerns mainly the sodium family, and matches the increasing interest for the development of Na all-solid-state batteries. Two series of glasses with composition 0.5Na2S–0.5[xSiS2–(1 − x)PS5∕2] and 0.67Na2S–0.33[xSiS2–(1 − x)PS5∕2], 0⩽x⩽1, were recently investigated (Figure 20), based upon experiments carried out by complementary characterization techniques, i.e. IR, Raman, 29Si and 31P NMR, DSC, density measurements [Watson and Martin 2018a, b]. Thorough structural analysis with complete deconvolution of Raman and NMR spectra helped in proposing a picture of the glass structure on the basis of the distribution of the different species likely to exist in the glass, and resulting from disproportionation reactions [Watson and Martin 2018a]. The different species and their distribution are shown in Figure 21 for the 0.5Na2S–0.5[xSiS2–(1 − x)PS5∕2] glasses. The presence of both P Q0 and Si Q3 in glasses comprising 50 mol% Na2S indicates that there is unequal sharing of the Na+ ions between the two glass formers; P taking additional Na+ to form Q0 units and Si giving up Na+ to form Q3 structures. For the 0.67Na2S–0.33[xSiS2–(1 − x)PS5∕2] glasses, some complexity is added to the structure since a significant concentration of unreacted Na2S species are present in all glasses. Densities 𝜌 and glass transition temperatures Tg were measured for all glasses (Watson, 2018b). Their evolution with composition is consistent with the structural models proposed for the glasses. As an example, Figure 22 shows the evolution of Tg, molar volume (calculated from experimental 𝜌) and fraction of BS (BS/(BS + NBS) calculated from the distribution of all species) when P is substituted by Si for 0.5Na2S–0.5[xSiS2–(1 − x)PS5∕2] glasses. Tg remains fairly constant for the first additions of SiS2 when the structure is still dominated by P Q1 and Q0 species (Figure 21). When x⩾0.5, Si Q2 and Q3 species starts being dominant and hence, the fraction of BS. Then, Tg starts and keeps on increasing with further addition of SiS2. At the opposite, the molar volumes decrease with the increase in BS and therefore, with the networking increase through the increase in Si Q2 and Q3 species. Finally, a 23Na NMR investigation of these glasses has been reported recently [Shastri et al. 2019], which gives information on the dynamics and distribution of Na+ ions. The most relevant information, suggested by a Na NMR second moments study and related to the glass structure, is a homogeneous distribution of sodium in the glass network over most of the composition range, but for Na-richest ones where sodium tend to cluster.
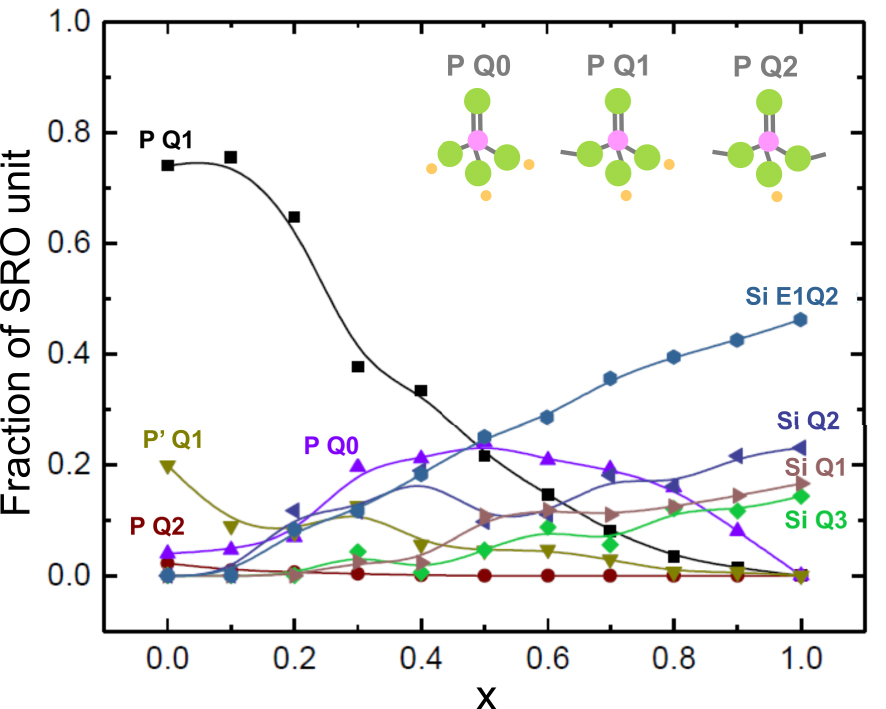
Composition dependence of the fractions of the P Qn and Si Qn species existing in the 0.5Na2S + 0.5[xSiS2 + (1 − x)PS5∕2] glass system. P Q0, P Q1 and P Q2 entities are shown at the top. P, S and Na atoms are represented by pink, green and light orange spheres, respectively. P′ Q1 stands for a P Q1 species with a P–P bond. Lines are only guidelines.

Glass transition temperature Tg, molar volume, and fraction of bridging sulfur (BS/(BS + NBS)) in the 0.5Na2S + 0.5[xSiS2 + (1 − x)PS5∕2] glass system. The dashed lines are guidelines for experimental data.
5.4. Thioborosilicate

Composition dependence of the fractions of the main B Qn and Si Qn units in 0.6Na2S + 0.4[xBS3∕2 + (1 − x)SiS2] glasses. In the inset is shown the line of studied compositions.
As far as we know, a single composition, i.e. the 0.30Li2S–0.21SiS2–0.09B2S3–0.40LiI glass, has been investigated in the late eighties [Kennedy 1989]. Nothing had been done in these systems ever since, until very recently a structural investigation of a series of glasses with composition 0.6Na2S–0.4[(1 − x)SiS2–xBS3/2], 0⩽x⩽1, has been reported (inset Figure 23) [Curtis et al. 2019]. IR, Raman, 29Si and 11B NMR experiments were carried out in order to study the changes occurring in the glass structure when a glass former was substituted by the other one. The structural analysis was similar to the analysis described in the previous section for thiophosphosilicate glasses. In the same way, deconvolution of Raman and NMR spectra helped in proposing a picture of the glass structure on the basis of the distribution of the different species likely to exist in the glass, and resulting from disproportionation reaction. The different species for these thioborosilicate glasses and their distribution are shown in Figure 23. In fact, owing to the difficulty to obtain pure B2S3 exempt of oxygen, several oxi-sulfide species were present in the glasses. These minority species are not shown in Figure 23. The main information can be summarized as follows. Tetrahedrally coordinated Si with a single BS (Si Q1) are the dominant species in the end-line member, 0.6Na2S–0.4SiS2 glass while B Q0 corresponding to 3-coordinated boron with no BS is the dominant one in 0.6Na2S–0.4BS3/2 glass. Upon substitution, there is a disproportionate sharing of the Na+ between the B and Si subnetworks with Si taking additional Na+ to form Si Q0 entities and B giving up Na+ to form B Q1 species. Once again, it is interesting to note that no crystalline phase with composition Na6Si2S7 has ever been reported, while Na4SiS4 exists [Cade et al. 1972, Eckert et al. 1989]. On the whole, it appears that, in multi-former thiosilicate glasses, the thiosilicate subnetwork tends to adopt a configuration close to that of a neighboring crystalline phase.
6. Conclusion
Thio- and selenosilicate glasses are the sulfide and selenide analogs of silicate glasses. Owing to the different characteristics of the chalcogen, e.g. size and polarizability, these glasses show markedly different structures and properties, in particular, a much higher electrical conductivity 𝜎, which attracted attention for the development of lithium and more recently sodium all-solid-state batteries. The structure of the glass formers, SiS(e)2, is comprised of both ES and CS tetrahedra, a major difference with silica. Upon addition of a modifier, a depolymerization of the network with appearance of NBS occurs, which is similar to the creation of NBO in silicate glasses. Preferential destruction of ES tetrahedra is generally observed with an increasing trend in the sequences: S to Se and Na to Li to Ag. Thiosilicate glasses comprising two modifiers show the very well-known mixed alkali effect with a strong decrease in both, Tg and 𝜎 for mixed glasses compared to single ones, a common characteristic with silicates. When added to lithium thiosilicate, aluminum sulfide, Al2S3, behaves as a former compound, which decreases the number of NBS and results in an increase in Tg and slight decrease in 𝜎. The mixed glass former effect, observed when a glass former is replaced by another one, the total amount of modifier being constant, has been investigated in thiosilicate glasses with the second former compound being GeS2, PS5∕2 or BS3/2. Depending upon the amount of modifier, lithium thiogermanosilicate glasses are either homogeneous or phase-separated, with a non-linear variation of properties, e.g. 𝜌, Tg and 𝜎, in the second case. A trend to phase-separate and produce a subnetwork with composition of an existing crystalline phase has also been reported in the oxide analogs, the germanosilicate glasses. In sodium thiophosphosilicate and thioborosilicate glasses, disproportionation reactions between the two formers occur with the transfer of Na+ from the Si subnetwork to the P subnetwork in the first family. In contrast, Na+ are transferred from the B subnetwork toward the Si subnetwork in thioborosilicate glasses. In both case, the resulting composition of the Si subnetwork tends to acquire the composition of an existing crystalline phase, i.e. Na4Si4S10 corresponding to Si Q3 species and Na4SiS4 corresponding to Si Q0 species.
One of the main interests of the investigation of these thio- and selenosilicate glasses is to shed light on the consequence of a change in the nature of the chemical bonds, from highly ionic in oxides to strongly ionocovalent in sulfides/selenides, on the structure and physicochemical properties of the obtained glasses. Apart from this academic interest, these glasses could get renewal of interest since they could be at the basis of the elaboration of new glass-ceramics to be used as solid electrolytes for the development of sodium all-solid-state batteries.
Conflicts of interest
Authors have no conflict of interest to declare.
Acknowledgments
The paper is a TRIBUTE TO MICHEL RIBES* who pioneered the research on ion-conducting chalcogenide glasses in the late seventies. He has inspired most of the work reported in the paper. *Professor (1974–2009) and Emeritus Professor (2009–2018) at the University of Montpellier (France).
The authors wish to thank Mickaël Bigot for his help in preparing all the figures of the manuscript.




 CC-BY 4.0
CC-BY 4.0