1 Introduction
Since its discovery in 1936 by Inge Lehman, the inner core of the Earth has raised a growing interest among the Earth scientists. This small rigid body at the centre of the liquid core has indeed a major importance in most of the physical and chemical processes that affect our planet, in particular its thermal evolution and its global dynamics. The inner core also plays an important role for stabilizing the magnetic field; a better knowledge of its structure and dynamics is thus important. It may also help to understand the Earth's differentiation process and to specify the chemical and mineralogical nature of the iron alloy that constitutes the centre of our planet. The recent advances concerning the structure of the inner core are mostly due to seismology, but they have also taken benefit of observational and computational results in mineral physics, geodynamics and geomagnetism.
With a radius of 1220 km, the inner core represents only 4.3% of the total volume of the core, and less than 1% of the volume of the Earth. It is generally accepted that it is the result of the solidification of the iron liquid core. The pressure rises from 330 GPa (3.3 Mbar) at the surface of the inner core to 360 GPa at the centre. The temperature inside the inner core is nearly constant [83], but it is poorly constrained (between 5000 and 6500 K, e.g., [1,43]), because it depends both on the melting temperature of core iron at core pressure and on the amount and nature of the light elements in the core [41]. On the other hand, the gravity is very low, decreasing from 4.4 m s−2 at the inner core surface to zero at the Earth's centre. These very extreme physical conditions are almost impossible to reproduce in the laboratory, although the physics of high pressures now allows to reach P–T conditions close to those present at the inner core surface [42]. Ab-initio computations allow us to predict the behaviour of iron alloys at core conditions. However, right now, our knowledge of the inner core mostly relies on indirect observations, in particular seismological data.
From the seismological point of view, the structure and properties of the inner core are mostly constrained by two body waves: PKIKP (also called PKP(DF)), a P-wave transmitted through the inner core, and PKiKP, a P-wave reflected at the inner core boundary (ICB) (Fig. 1a). In addition, the eigenmodes sensitive to the inner core give information on the mean values of S-velocity and density inside the inner core.
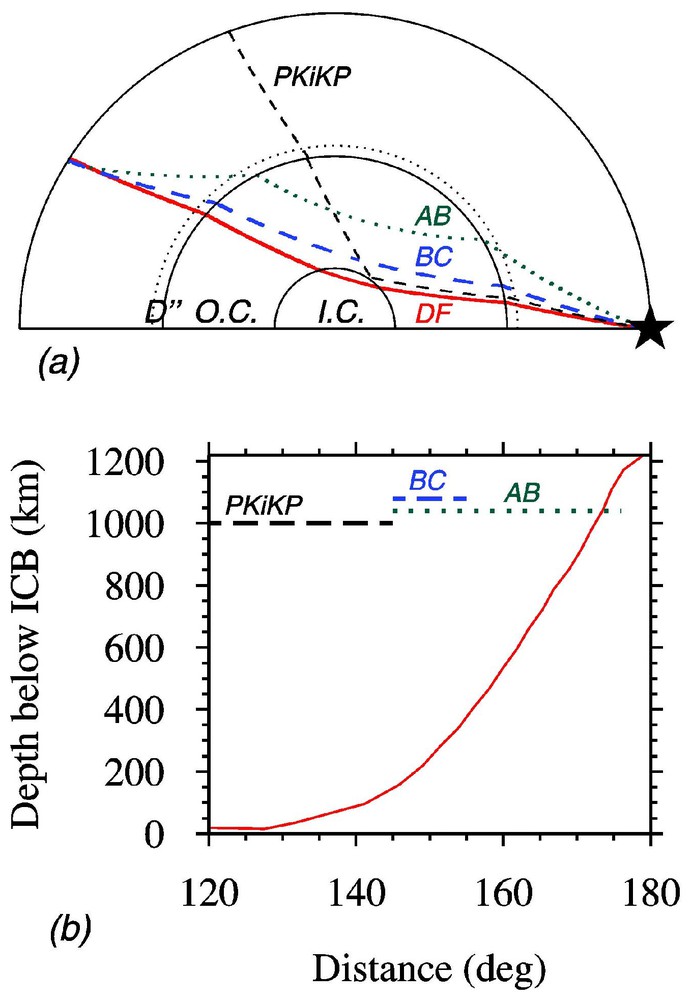
(a) Paths of the different core phases inside the Earth; (b) depths inside the inner core sampled by the PKP(DF) rays as a function of epicentral distance, for surface focus. Also indicated are the ranges where differential travel times with the other core phases are used.
(a) Trajet des différentes phases du noyau à l'intérieur de la Terre ; (b) profondeurs de la graine échantillonnées par les rais PKP(DF) en fonction de leur distance épicentrale, pour un foyer superficiel, et intervalles de distance où les temps différentiels avec les autres phases du noyau peuvent être utilisés.
The PKP(DF) phase is often compared to two other core phases that have their turning point in the liquid core (Fig. 1): PKP(BC), which turns at the base of the liquid core, with a path in the mantle very close to that of PKP(DF), and PKP(AB), which turns in the middle part of the liquid core. The liquid core is assumed to be homogeneous, thus it does not affect the BC and AB paths. The advantage to refer PKP(DF) to these nearby phases, by considering differential travel times, is to decrease the influence of focal mislocation, origin time errors and mantle heterogeneities. Unfortunately, PKP(AB) may be affected by the heterogeneities in the D″ layer at the base of the mantle. Fig. 1b indicates the domains where comparison with PKP(BC) and PKP(AB) is possible, as well as the depth of the turning point of the PKP(DF) ray inside the inner core as a function of epicentral distance. The top 50 km of the inner core are the most difficult to investigate, as the only possible reference phase is PKiKP, whose arrival is only a few seconds late compared to PKP(DF), so that the two phases generally interfere. The travel time anomalies of the different phases are quantified by their residuals, which represent the difference between the observed travel times and the travel times computed for a reference model, hereafter model ak135 [30], which is the best model for core phases. A negative PKP(DF) residual corresponds to propagation faster than normal.
The seismological investigation of the inner core concerns many different aspects of its internal and superficial structure: radius and topography of the inner core boundary, velocity and density jumps at ICB, radial dependence of the P- and S-velocities, presence or absence of internal discontinuities, of heterogeneities or anisotropy, attenuation. We will mostly focus on inner core anisotropy, which is one of the most intriguing features of the inner core, and on recent results concerning rigidity and attenuation. Finally, we will show how seismological observation may also give information about core dynamics, as they allow us to seek for a possible inner core rotation.
2 The anisotropy of the inner core
The PKP(DF) waves propagate faster in the north–south direction than in the equatorial plane. This surprising property has been detected two decades ago [44] thanks to the great amount of data recorded at the thousands of worldwide distributed seismological stations, which send their P-arrival times to the International Seismological Centre. Fig. 2 shows the mean PKP(DF) and PKP(BC) anomaly deduced from an improved catalogue of ISC residuals (EHB file [18]), plotted as a function of the angle θ between the ray at its turning point and the Earth's rotation axis. A procedure of data binning has been applied in order to avoid the predominance of the oversampled paths. No significant dependence in θ is observed for the paths inside the liquid core (PKP(BC)) and for the rays that turn inside the upper part of the inner core; by contrast, the residuals become strongly negative at small θ values for paths propagating deep inside the inner core, denoting fast propagation for polar paths. This PKP(DF) anomaly has been interpreted in terms of inner core anisotropy [35], an hypothesis which has been supported by many other body wave observations of absolute PKP(DF) travel times (e.g., [53,73]) and by differential BCDF or ABDF travel time residuals (e.g., [14,16,23,34,55,82]). The anomalous splitting of the core sensitive eigenmodes, i.e. the distortion of the resonance peaks observed after a large earthquake, are additional data in favour of inner core anisotropy (e.g., [48,50,77,78,84,85]), even though it has been difficult to reconcile body waves and eigenmode observations [78]. Proposed explanations are either preferred orientation of anisotropic iron crystals – the hexagonal closed-packed form Fe-ε being often invoked [8,72] – or orientation of non-spheroidal fluid inclusions [54].
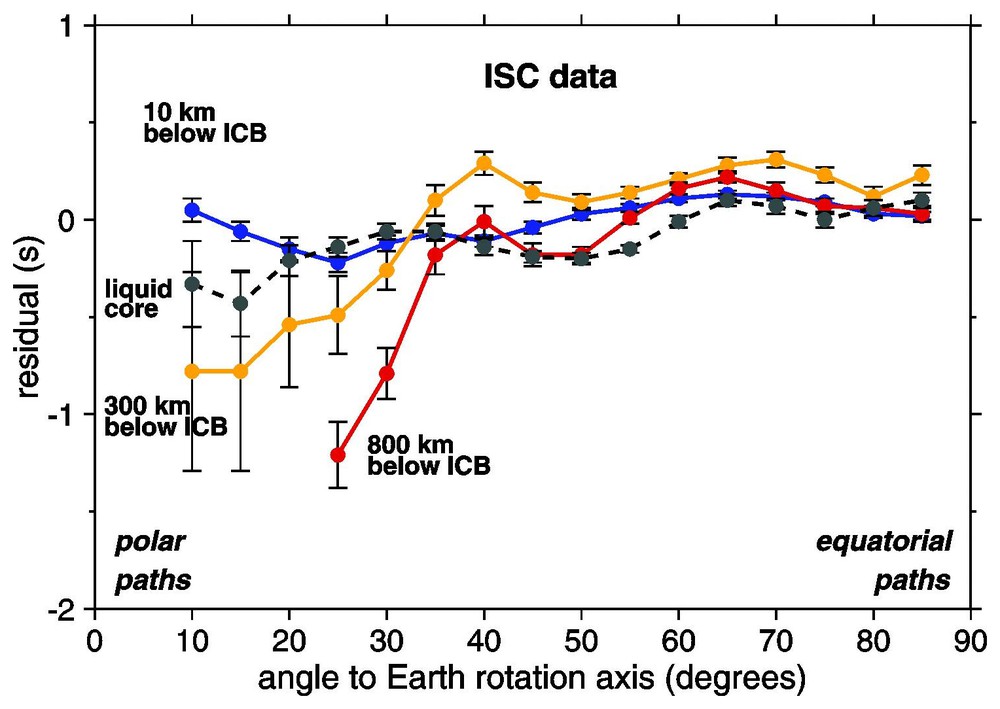
Evidence for anisotropy inside the inner core, revealed by the dependence of the travel time anomalies of PKP(DF) to ray orientation, for bulletin data (EHB file). The three coloured curves correspond to three mean depths below inner core boundary (ICB). Note the negative residuals (fast propagation) for polar paths for rays penetrating deep inside the inner core. For reference are plotted the residuals for PKP(BC), which stays inside the liquid core (dashed line). A binning procedure of the rays has been applied to avoid the overweighting of the most sampled paths compared to the poorly sampled paths. Errors bars are .
Mise en évidence de l'anisotropie de vitesse des ondes P dans la graine, à partir des anomalies de propagation des ondes PKP(DF) provenant de données de bulletins (fichier EHB), et reportées en fonction de l'orientation des rais. Les courbes en couleur correspondent à trois profondeurs différentes sous la surface de la graine. Les résidus sont plus faibles (propagation plus rapide) pour les rais parallèles à l'axe de rotation qui pénètrent profondément à l'intérieur de la graine. Pour comparaison sont reportés les résidus de la phase PKP(BC) qui ne pénètre pas dans la graine. Les rais ont été moyennés géographiquement pour éviter la prédominance d'un trajet particulier.
The exact geometry of the anisotropy, and/or the possibility of heterogeneities, in bulk or in anisotropy, constitute important information for understanding the physical nature and the origin of this anisotropy. The early observations led to propose a 3% to 3.5% anisotropy with cylindrical symmetry, and with a fast axis parallel to the Earth's rotation axis or possibly slightly tilted [14,73]. PKP(DF) travel times show that no strong anisotropy seems to be present in the uppermost 150 km [57]. This simple image has however been modified after the observation that the two hemispheres exhibit different anomalies [16,75]. Fig. 3a shows BCDF residuals for carefully hand-picked data collected by various authors (see [67] for more details about this dataset), plotted as a function of the longitude of the ray turning point inside the inner core. The data have been sorted into two classes: polar paths, for which θ<30°, and equatorial paths, for which θ>60°. This figure shows again that polar paths are faster than equatorial paths (smaller DF residuals, thus larger BCDF residuals), but also that the quasi-eastern hemisphere (longitude 40°E to 180°E) is less anisotropic than the western hemisphere. This hemispherical pattern is also well observed in the bulletin data of the EHB file. Fig. 3b, which concerns PKP(DF) paths turning about 300 km below ICB, clearly shows a difference between the two hemispheres at low θ-values. In this figure, epicentres and stations have been binned inside equal-area sectors at the surface of the Earth before computing mean residuals, in order to give the same weight to each path. As seen in Fig. 3c, the strong difference observed for PKP(DF) is not observed for PKP(BC) in the same distance range, indicating that the hemispherical pattern mostly originates in the inner core, rather than in the liquid core. Moreover, as shown in Fig. 3a, the residual variations are opposite for polar and equatorial paths, a result that suggests that a change in crystal alignment may be responsible for the hemispherical pattern of the anisotropy [22].
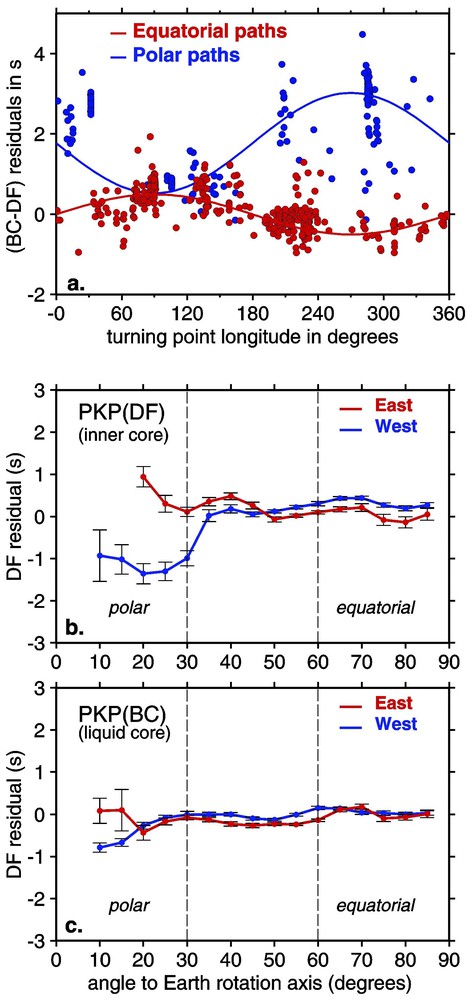
Hemispherical pattern of the residuals. (a) PKP(BC)–PKP(DF) travel time residuals for carefully selected data, plotted as a function of the ray turning point longitude, for polar paths and equatorial paths. Also shown is a fit of the residuals of the two data sets with two homothetic sine functions. (b) Mean PKP(DF) residuals from bulletin data, plotted as a function of the ray angle with respect to the Earth's rotation axis, for rays turning either in the quasi-eastern hemisphere (40°E to 180°E), or in the quasi-western hemisphere (−180°W to 40°E); epicentral distance range 149–155°. A ray binning has been applied to avoid the oversampling of some paths. Errors bars are . (c) Same as (b) for PKP(BC), which samples the liquid core.
Mise en évidence d'une structure hémisphérique dans la graine. (a) Résidus différentiels PKP(BC)–PKP(DF) pour des données dépouillées finement, tracés en fonction de la longitude du point le plus bas du rai, en distinguant les trajets polaires et équatoriaux. Les courbes correspondent à l'ajustement des résidus par deux fonctions sinusoı̈dales homothétiques. (b) Résidus moyens PKP(DF) déduits de données de bulletins, pour les distances 149 à 155°, tracés en fonction de l'angle du rai par rapport à l'axe de rotation de la Terre, en distinguant un hémisphère quasi-est (40°E à 180°E) et quasi-ouest (180°W à 400°E). Les rais ont été moyennés géographiquement pour éviter la prédominance d'un trajet particulier. Barres d'erreur de . (c) Comme (b), mais pour PKP(BC), qui échantillonne le noyau liquide.
A tomographic model of the inner core structure has been computed [23] in combining the PKP(DF) residuals of the bulletin data (EHB file, [18]) and the PKP(BC)–PKP(DF) hand picked residuals, which are less noisy and provide a better sampling of the uppermost 500 km of the inner core. The P-velocity variations inside the inner core are represented by:
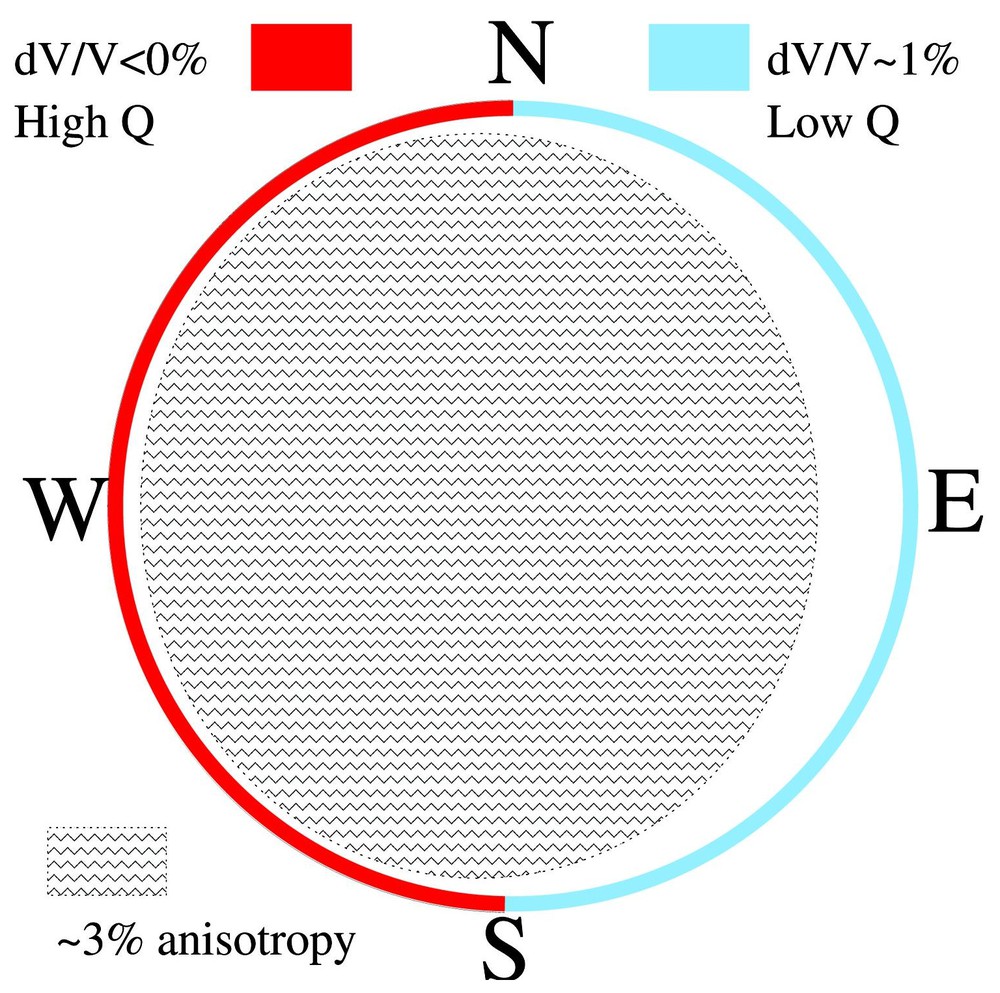
Scheme of a meridian cross-section of the inner core, showing the hemispherical pattern of the anisotropy inside the inner core (with fast axis parallel to the Earth's rotation axis), and the correlated heterogeneity pattern in the uppermost inner core.
Coupe méridienne schématique de la graine, montrant la partie centrale anisotrope (avec l'axe rapide parallèle à l'axe de rotation de la Terre) et la partie externe isotrope asymétrique, corrélée à une hétérogénéité de surface hémisphérique.
3 The heterogeneities inside the inner core
Although most of the propagation time anomalies are well explained by anisotropy, it is important to estimate whether heterogeneities also contribute to these anomalies. At the hemispherical scale, Voigt's isotropic average of P-velocity perturbations can be estimated from a combination of the α, ε, γ coefficients used to describe anisotropy by:
At intermediate wavelengths (50–200 km), many studies have reported the possible existence of heterogeneities (e.g., [5,11,15,63]). However, in none of these cases, it is possible to prove that the heterogeneity effectively takes place in the inner core, and not in the mantle.
Heterogeneities at very short wavelength have been detected in the uppermost 300 km of the inner core from the energy present in the coda of the PKiKP waves. They have been observed for Novaya Zemlya events recorded at the LASA array in Montana [80], but they could be a general property of the inner core. The observations are explained by the presence of scatterers of size ∼2 km, with velocity contrast of 1.2%. The modelling of the inner core attenuation by small-scale scattering also suggests the presence of kilometric-scale scatterers with a 5–12% velocity contrast [13]. Scatterers of scale length ∼10 km with velocity perturbations of 8.4%, due to the boundaries between single or ordered groups of crystals with various orientations, could explain the mean level of anisotropy and attenuation, as well as their apparent anisotropy [12].
4 Attenuation, rigidity and S-waves
The existence of a rather strong attenuation inside the inner core may give information on its thermal state and scattering properties, and on the presence of partial melting. The attenuation is estimated from the broadening of the peaks of the core sensitive eigenmodes ([20,33,84], see also [49] for a review), and from the amplitude variations of PKP(DF). Eigenmodes generally lead to much higher Q-values than body waves. This discrepancy is possibly due to the different contributions in bulk and shear dissipations, it is however not fully understood. For P-waves, the comparison of the amplitude of PKP(DF) with PKP(BC) leads to a Q-value of the order of 200 in the uppermost 100 km of the inner core, increasing to about 400 between 150 and 300 km [4,65,70]. Lateral heterogeneities in attenuation are possibly present [79]. Specific studies of the top 50 km from the modelling of PKP(DF) + PKiKP reveal a very low Q-value (Q⩽100) beneath ICB, and a hemispherical pattern in Q, correlated to the uppermost hemispherical heterogeneity (Fig. 4), with low Q (high attenuation) beneath the fast eastern hemisphere [21,37]. This correlation is opposite to that found in the mantle, where the dominant mechanism of attenuation is viscous relaxation. At greater depth inside the inner core, the possibility of an anisotropy in attenuation is suggested by the dependence of PKP(DF)/PKP(BC) ratio to the angle of the ray with respect to the Earth's rotation axis [66]. It is clearly apparent in Fig. 5, for rays whose turning point is beneath Africa. Some texturing models of the inner core [3] could explain these features by invoking scattering attenuation, as noted above [12]. This could be the predominant mechanism in the frequency band 0.02–2 Hz, and could explain the discrepancies between body waves and eigenmodes, modes being more sensitive to viscoelastic attenuation [12]. On the other hand, the presence of liquid inclusions in a mushy zone at ICB, proposed on the basis of thermodynamical arguments [32], could provide a possible explanation to the low Q-value observed at the top of the inner core; it is however hardly compatible with the positive correlation between attenuation and velocity previously mentioned.

(a) Examples of data (vertical components) showing the anisotropy in P-velocity and attenuation inside the inner core. All the paths have their turning point beneath Africa and correspond to nearly the same epicentral distance Δ, they differ by their orientation θ with respect to the Earth's rotation axis. The PKP(BC) phases, which sample the liquid core, are aligned. PKP(DF) samples the inner core. Note the decreasing delay between BC and DF when θ increases, due to the anisotropy in P-velocity, and the increasing DF/BC amplitude ratio, denoting a probable anisotropy in attenuation. (b) Variations of travel time anomalies and amplitude anomalies at 3-s period as a function of θ, for a set of data having their turning points beneath Africa (after [66]). The direction parallel to the Earth's rotation axis (small θ) corresponds to high velocities and strong attenuation.
(a) Enregistrements verticaux montrant l'anisotropie de vitesse et d'atténuation des ondes P dans la graine. Tous les trajets ont leur point le plus bas sous l'Afrique, ils correspondent tous à la même distance Δ, et ne diffèrent que par leur angle θ par rapport à l'axe de rotation de la Terre. Les phases PKP(BC), qui restent dans le noyau liquide, sont alignées. Noter la diminution du temps BCDF quand θ augmente, indiquant une anisotropie de vitesse, et l'augmentation du rapport DF/BC, indiquant une anisotropie d'atténuation. (b) Variation des anomalies de temps de propagation et d'amplitudes relatives avec θ, pour un ensemble de données sous l'Afrique (d'après [66]). La direction polaire correspond à des vitesses élevées et à une atténuation forte dans la graine.
The possibility of a strong proportion of partial melt, extending deep inside the inner core [19], raises the question of the inner core rigidity. There are several indirect evidences of the solid nature of the inner core. In particular, the eigenmodes frequencies constrain the S-velocity to be of the order of 3.6 km s−1 inside the inner core (e.g., [24]). The jump in P-velocity and density at the ICB (e.g., [36,64]) also suggests that the inner core is solid, and that it contains a much smaller amount of light elements than the liquid core. The direct observations of S-wave propagating through the inner core (a phase called PKJKP) would be a direct proof of its rigidity, and would allow to build an S-wave radial model, which would be very informative about the composition of the inner core. But this phase is very small and it arrives nearly at the same time and with the same slowness than another core phase (PKKP); it is thus very hard to observe.
A few attempts to detect PKJKP in the past have lead to contestable results. Recently, thanks to the use of stacking procedures that enhance the expected signal, two studies have reported possible observations of inner core shear waves. Okal and Cansi [38] report observations of PKJKP for a deep Flores Sea event recorded at short period French stations (frequency domain 0.1–0.5 Hz), whereas Deuss et al. [17] report observations of pPKJKP and SKJKP at low frequencies (0.01–0.1 Hz) for the same event, and for a Bolivian earthquake. The two studies lead to S-velocities of the order of 3.6 km s−1, on the basis of different phase identifications.
The major difficulty in searching for PKJKP is the lack of strong constraints concerning this phase. The distance at which it has its maximum amplitude, and this amplitude, depend drastically on the incidence angle and transmission coefficients at ICB, thus on the S-velocity immediately below ICB, which is poorly known. If it is close to zero, as suggested by the possible presence of a mushy zone at ICB [32], it would prevent the generation of a PKJKP phase, at least at short period. The low quality factor below ICB leads to believe that the PKJKP amplitude will be very small, and that its dominant period will be larger than the PKP(DF) one.
5 The differential rotation of the inner core
Some dynamo results [25,26] predict a differential rotation of the inner core with respect to the mantle, with a faster (eastward) inner core rotation. This property seems however not generally accepted [29]. On the other hand, the gravity anomalies due to the heterogeneities of the mantle deform the inner core and force it to rotate synchronously with the mantle [9]. The competition between these two effects depends on many parameters, among which the viscosity of the inner core is probably the most important [10], but it is unfortunately very poorly known.
Attempts to observe the inner core differential rotation from seismological methods relies on the detection of the drift with time of inner core heterogeneities in isotropic P-velocity or in anisotropic structure, either along a particular path, or at worldwide scale. A search for rotation using PKiKP from Tuamotu nuclear tests recorded at the Warramunga array in Australia, led to inconclusive results [62]. In 1996, Song and Richards [58] observed a variation of the PKP(DF) residuals of 0.3 s in 30 years along the path from South Sandwich Island (SSI) to station COL, in Alaska. Their interpretation, based on a tilt of the anisotropy symmetry axis, led to a fast rotation rate, of the order of 1.1° yr−1, compatible with dynamo results. Absolute PKP(DF) travel times processed at the worldwide scale led to a very large rotation rate, of the order of 3° yr−1 [74]. However, the tilt of the anisotropy symmetry axis as well as the large rotation rate may be artefacts due to uneven Earth sampling [69]. The SSI to COL data, reinterpreted in considering the drift of an heterogeneity beneath this path, led to rotation rates ranging from 0.05 to 0.3° yr−1, depending on how much of the signal is ascribed to mantle heterogeneities [15]. Polar paths as SSI to COL are a priori more suited than the other paths to detect inner core rotation, if a variation in the level of anisotropy is used to detect it. However, almost all the paths other than SSI to COL fail to detect large rotation rates, or lead to results that are poorly statistically significant. These paths mostly concern Antarctica records of events at high latitudes, in particular Novaya Zemlya nuclear tests (e.g., [28,40,60,63]; see [68] for a critical review). The main advantage of considering these nuclear tests is that no perturbing effect of a subduction zone is present. These results raise the question of possible causes other than inner core rotation for explaining the variations in time of the SSI to COL residuals, such as biases due to mantle heterogeneities or earthquake mislocations.
A doublet analysis [46] performed on core phases allows to discriminate between earthquake mislocations and inner core rotation. It has been applied to the same SSI to COL data as those used by Song and Richards [58], and to additional numerical data extracted from the IRIS data bank. The doublet method [45] is based on the comparison of the arrival times of the three core phases for a pair of events that are very close to each other, and which are recorded at the same station (Fig. 6). If the distance increases, a ‘time dilatation’ of the whole record is observed. By contrast, if inner core rotation occurs, only the DF phase, which samples the inner core heterogeneity, will be perturbed. This analysis, applied to the SSI to COL data, reveals that residual time variations may be ascribed in a large extent to mislocation of the SSI events [46]: the mislocation errors have decreased with time as new seismic stations were set-up in the southern hemisphere. The bias in latitude is evident when comparing PKP(DF) residuals at stations in northern azimuths with those in southern azimuths with respect to SSI, because the residual difference enhances the bias by a factor of two. Its variations with time (Fig. 7) exhibit a slope that corresponds to a mean shift in latitude of 22 km in 10 years with respect to the actual location.

Scheme explaining how to use doublets to discriminate between inner-core rotation and earthquake mislocation, for nearly similar paths. The reference event is noted by (0), at distance Δ0. Event (1), recorded at the same station, corresponds to an increase in epicentral distance: the differential times BCDF and ABBC both increase with respect to those of the reference event, proportionally to the distance increase. Trace (2) corresponds to an event with the same location as (0), but the arrival time of DF is affected by inner-core rotation. If these two effects are combined, i.e. if both a change in distance and a rotation occur, the ABBC time will vary proportionally to the distance change, but not the BCDF time, which will be in addition affected by rotation.
Principe d'utilisation des doublets pour discriminer entre une rotation de la graine et un biais de localisation du foyer, à partir de séismes voisins enregistrés dans une même station. Le séisme de référence est (0), à la distance Δ0. Le séisme (1) correspond à une augmentation de distance: les temps différentiels BCDF et ABBC augmentent tous deux proportionnellement à Δ1−Δ0. Le séisme (2) est localisé au même point que (0), mais la phase DF a été perturbée par la rotation de la graine. Si ces deux effets sont combinés, on observe qu'il n'y a plus proportionnalité entre les accroissements de temps de ABBC et de BCDF.
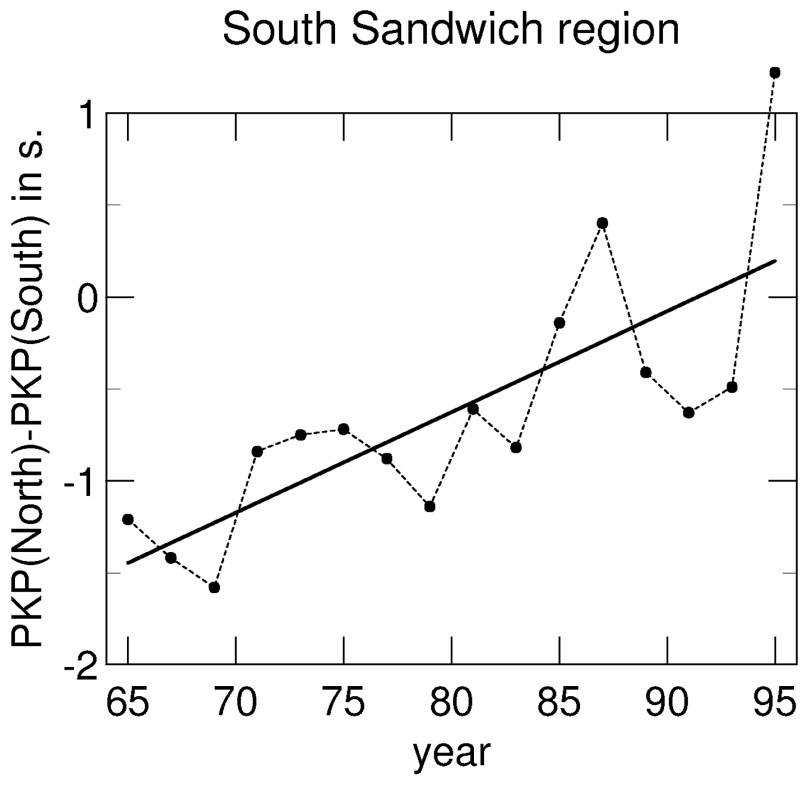
Difference between the residuals in the northern direction and those in the southern direction for South Sandwich Island events during the last three decades. They reveal that 30 years ago, the SSI events were located northward with respect to their actual position, and that this mislocation bias has decreased with time, as new stations where installed in the southern hemisphere.
Différence entre les résidus mesurés vers le nord et ceux mesurés vers le sud pour les séismes des ı̂les Sandwich sud au cours des trois dernières décennies. Ils montrent un biais de localisation vers le nord par rapport à la position réelle des foyers il y a 30 ans ; ce biais a ensuite diminué au fur et à mesure de l'installation de nouvelles stations dans l'hémisphère sud.
Another evidence of the absence of differential rotation, or of its very low rate (0±0.2° yr−1) is provided by the analysis of the splitting functions of the inner core sensitive modes, once corrected for the dominant effects of Earth ellipticity and rigid rotation, and for mantle heterogeneities: for the nine modes considered, the pattern of the splitting functions remains almost unchanged during 15 years [31].
A method based on the temporal changes of waves scattered in the uppermost inner core for Novaya Zemlya events recorded at LASA also leads to a low rotation rate, of the order of 0.15° yr−1 [81]. The great advantage of this method is that it does not require long temporal series of data; its main drawback is that it requires sources that are almost perfectly invariant, so that the two paths considered at two- or three-year intervals sample exactly the same scatterer.
To summarize, a steady rotation rate of 0±0.2° yr−1 seems compatible with most of the seismic observations for the last 30 years (Fig. 8). Some dynamo models have also predicted inner core oscillatory rotation rather than a monotonic rotation. A weak evidence of such oscillations with time scale 280 days is reported by Collier and Helffrich [11] from the analysis of PKP(DF) anomalies recorded at UK stations, but this result needs confirmation. A significant increase in the accuracy of inner core rotation rate measurements is still needed to better constrain the various processes acting on the inner core dynamics [2,10].
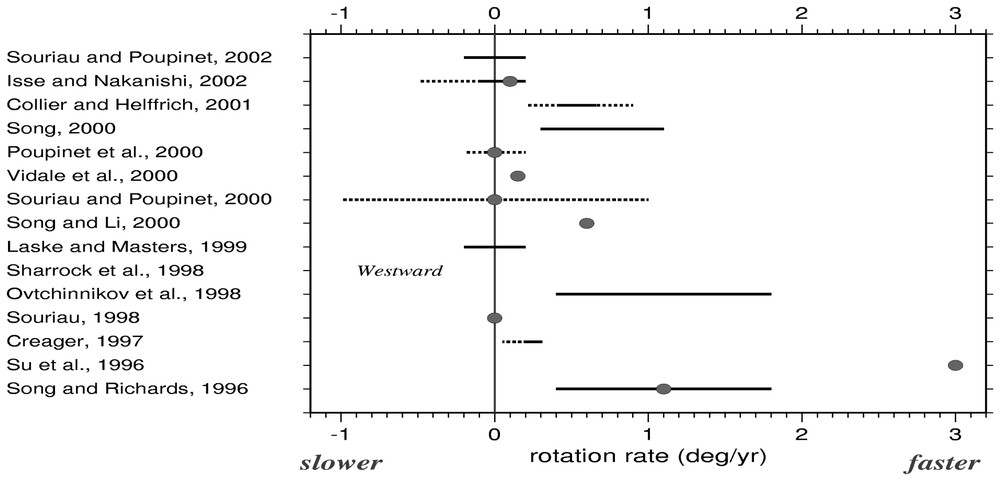
Summary of the main results about inner core rotation [11,15,28,31,40,46,52,56,58,60,63,67,68,74,80].
Résumé des principaux résultats concernant la rotation de la graine [11,15,28,31,40,46,52,56,58,60,63,67,68,74,80].
6 Discussion and conclusions
Our knowledge of the inner core structure and dynamics has been considerably improved during the last decade, thanks to the availability of more than 35 years of bulletin data, and an increasing number of digital seismological records with a worldwide distribution. The inversion of these data has led to a very simple inner core model in which a homogeneous inner part with a 3% uniform anisotropy is asymmetrically surrounded by a homogeneous isotropic layer with a thickness of 100–200 km on the western hemisphere, increasing to 400 km over the eastern hemisphere (Fig. 4). Heterogeneities in isotropic average velocity seem to be absent, except a hemispherical heterogeneity at the top 50 km, which is correlated to the anisotropy hemispherical pattern, and small structures at kilometric scale, which are responsible for wave scattering. How to generate this anisotropy and its hemispherical pattern is certainly right now one of the most difficult questions.
Some problems concerning this structure have however to be first clarified. First, the anisotropy model that has been obtained postulates a uniform behaviour of the anisotropy through the inner core, which is not necessarily exact [27]. On the other hand, it has been argued that the SSI to COL paths, which are dominant in the western hemisphere, are responsible for the hemispherical pattern. This is not the case, as this pattern is still observed when these paths are removed. However, heterogeneities in the D″ layer, in particular along the SSI to COL path, could by responsible for part of the observed BCDF travel time anomalies. If that were the case, this would allow a significant decrease of the amount of anisotropy inside the inner core from 3% to about 1.5% [7,76]. On the other hand, P′P′ waves that cross twice the inner core, do not detect a strong anisotropy for the polar path Alaska–Antarctica–Norway [6]. This raises the question of possible short wavelengths in the variation of anisotropy, thus in the crystal orientation inside the inner core [7]. Such short wavelengths could perhaps explain both the anisotropy variations and the attenuation through a scattering process [12].
Another interesting problem is raised by the structure inferred from normal mode splitting. Several authors have shown that a structure inside the liquid core is necessary to explain some of the modes [47,84]. In particular, the anomalous splitting could be explained by density anomalies located either in polar caps or inside the cylinder tangent to inner core, which is isolated from the rest of the core from a dynamical point of view [48]. This would be an alternative to anisotropy to explain the PKP(DF) anomalies [51]; however, sustaining such heterogeneities inside the liquid core seems impossible [71]. On the other hand, some body-wave observations predict a very high level of anisotropy (5% to 8%) beneath the isotropic layer at the top of the inner core [39,61], which seems difficult to reconcile with global models. The nature of the radial transition between isotropic and anisotropic structures, and the meridian transition between eastern and western hemispheres, is another point that has to be elucidated.
Inner core models have mostly focussed on P-wave velocity and anisotropy. An S-wave radial model would be very informative about the composition of the inner core, and the existence of partial melting, proposed on the basis of attenuation measurements. Although S-waves are very difficult to observe, as shown by the few attempts performed recently, the development of array seismology, and the combined interpretation of body waves and eigenmodes give some hope to obtain a radial S-model in a near future.
The most recent seismological studies of inner core differential rotation converge to rotation rates less than 0.2° yr−1, or possibly to the absence of rotation. Difficulties come from the fact that the observation of rotation relies on old data, which are often poorly controlled, and also on the existence of heterogeneities that, if they exist, are difficult to map. Another difficulty comes from the geodynamo models, which have to include poorly known parameters, like inner core viscosity. For seismologists, it is obvious that the patient accumulation of high-quality records at the seismological observatories, and the development of observatories at high latitudes and on the ocean floor, remain essential.
Acknowledgements
The authors thank J.-P. Poirier, B. Romanowicz and an anonymous reviewer for their critical reading of the manuscript.


