La version française de l’article est disponible à la suite de la version anglaise
1. Position of the problem
The exploitation of rock salt in layers or in domes by dissolution in situ is the subject of an ancient industry developed since the middle of the 19th century. This is the case of the Lorraine salt deposit, still widely in use today for the production of salt intended for chemicals, food or even snow removal. Among the current operators is the Salins group, which operates near the towns of Dombasle and Varangéville, to the east of Nancy. The layers of salt used are part of a powerful marl-salt ensemble of the Keuper. Two methods of exploitation are practiced, one, by extracting rock salt by mined cavities according to the method of abandoned rooms and pillars for snow removal (mine of Varangéville) and, the other, by pumping the brine obtained by leaching with fresh water of deep cavities, for industry (salines of the Haraucourt plateau).
In order to control the leaching, two questions arise among stakeholders; optimizing the recovery of salt, which is a valuable commodity, and preserving the environment from any pollution by brine and mechanical damage in surface. To this end, with regard to the Salins group, the leaching method currently aims to produce cavities isolated from each other, the long-term stability of which can be demonstrated on the hydraulic and mechanical levels. However, certain sectors of the deposit were utilised by means of communicating cavities, which compromised the control of spontaneous residual dissolutions at the end of their life and led, in certain cases, to collapses reaching the surface, creating craters filled with water.
In order to make the site safe, while optimizing salt production, the operator plans to resume the in situ dissolution of a panel on the Gellenoncourt site, on the Drouville concession. The so-called intensive mining method used will result in the enlargement, followed by a collapse, of the already existing cavities, ultimately resulting in a lake extending over approximately 36 ha. With the aim of obtaining authorization to implement the method, the operator submitted an impact file examining, on a scientific basis, the consequences of such a practice, in particular with regard to the risk of pollution of the surrounding aquifers with salt water.
This article discusses the potential mechanisms of salt release from collapsed cavities. It takes advantage of the research work of the French National Agency for Radioactive Waste (Andra), which is interested in understanding the interstitial overpressures observed in the Callovo-Oxfordian argillite layer of Bure in Meuse/Haute-Marne, subject of studies for the creation of a geological repository for high and intermediate long-lived radioactive waste. This work carried out in partnership with the Laboratory of Solid Mechanics of the Ecole Polytechnique and the UMR Sisyphe at the Pierre and Marie Curie University was the subject, in 2008, of a thesis defended in this university, under the presidency of Professor Ghislain de Marsily. We have structured the theoretical bases of our reasoning from this document, as well as from several resulting publications.
1.1. Elements of the geology of the Lorraine salt deposit
The numerous boreholes carried out on the salt concessions make it possible to propose the synthetic geological cross-section which shows from top to bottom the following sequence (Figure 1).
Synthetic geological log.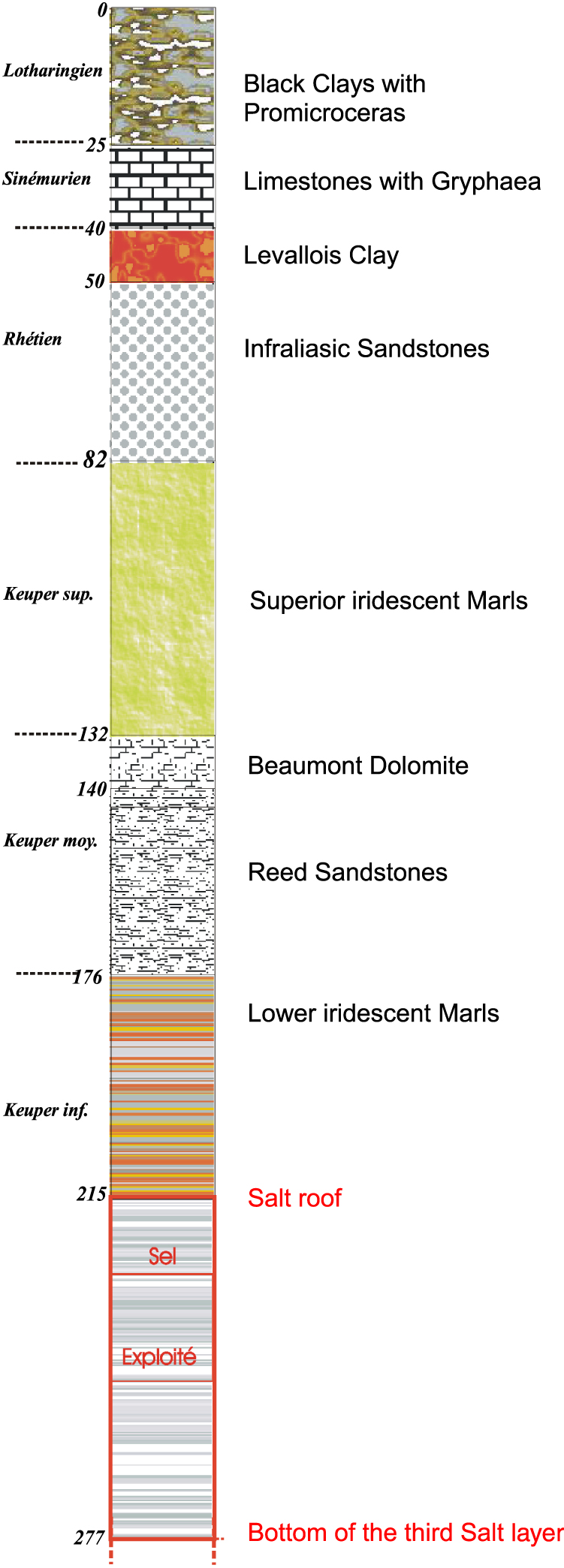
Black clays with Promicroceras (Lotharingian). Grey-blue plastic shales, sometimes schistose, with a maximum thickness of 25 m.
Limestones with Gryphea (Sinemurian). Decimetric alternation of blue to black marl and beds of rust-coloured clayey limestone, 15–17 m thick.
Levallois clays (Rhaetian). Salmon pink argillites which constitute a reference level throughout Lorraine. The average thickness is about ten meters.
Infraliasic sandstone (Rhaetian). Fine siliceous sandstone with centimetric to decimetric black or green clayey intercalations in the upper part. The average thickness is 32 m.
Superior iridescent marls (Upper Keuper). Green and purplish argillites which become brick red towards the base. Centimetric to decimetric dolomitic horizons are present as well as, at the base, decimetric levels of nodular white anhydrite. The thickness reaches 135 m at Gellenoncourt.
Beaumont dolomite—Reed sandstone (Middle Keuper). Beige or gray dolomite in decimetric beds surmounted by a massive anhydrite cap 3 m–4 m thick. The dolomite, 8 m thick, plays an important role in the stability of the land before the collapses. Below there are motley marls then very clayey fine micaceous sandstones containing numerous plant debris.
Lower iridescent marls (Lower Keuper). This powerful formation about 200 m thick is composed of argillites alternating with beds of gypsum and anhydrite on the first forty meters. Then comes the salt series 120 m thick but of which only the 3 upper beds, rich in salt and 65 m thick, are mined at Gellenoncourt and contain about 20% of insoluble materials. Thus, the cumulative thickness of leachable pure salt represents on average about forty meters.
The regularity of the layers appears in Figure 2 which shows the position of the reference levels, the Rhaetian and the salt roof, which are present respectively at an average of 50 m and 220 m below ground in the 44 boreholes available on the Gellenoncourt site.
Geological cross-section showing the position of Rhaetian sandstones and utilised salt.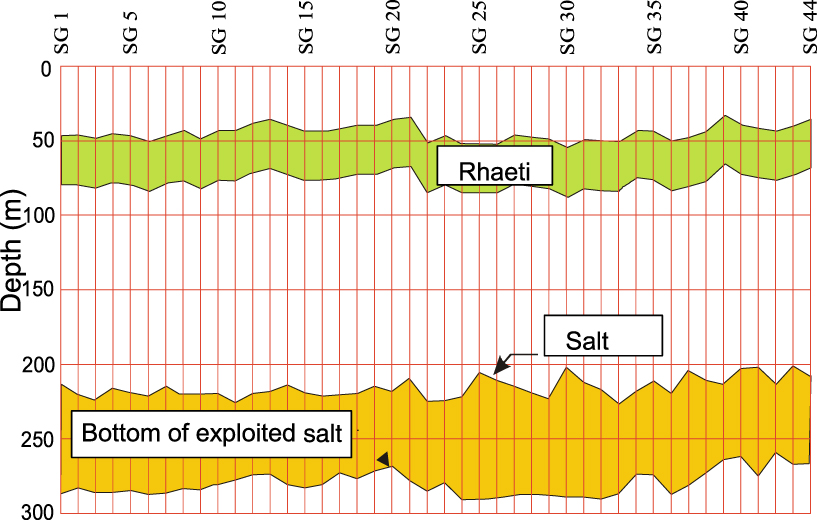
1.2. Elements of site hydrogeology
Among the geological formations present in the subsoil, only the Rhaetian sandstones constitute an aquifer likely to be impacted by salt mining.
This thirty meters thick aquifer contributed to the supply of drinking water to neighboring municipalities. It is still weakly utilised for irrigation. Protected by the low permeability and very continuous cover of the Levallois clays, this reservoir is fed on its outcrops at the southern and eastern edges of the plateau. The transmissivity is modest and varies between 10−4 m2/s and 10−5 m2/s, which leads to great sensitivity of the piezometric level to pumping.
The aquifer is most often captive under the Levallois clays and is artesian in the lower parts of the topography. The general piezometry indicates a flow towards the northwest to the Roanne river which drains this aquifer.
1.3. The consequences of salt mining
The exploitation of the Gellenoncourt panel was carried out for about twenty years from 1967. The method consisted in connecting by hydraulic fracturing at the bottom of several boreholes drilled to the basis of the third salt bed, then introducing fresh water in one or more wells and pumping the resulting brine in remote boreholes called “extractors”, thus causing the salt to dissolve and create cavities in the vicinity of the injectors. A good match between the flow rate and the arrangement of the device ensured the saturation of the brine. Periodic controls of the geometry of the voids were carried out by ultrasound in order to monitor the evolution of the cavities.
Thus, the extraction of salt has developed voids whose base is around 65 m deep under the roof of the salt and whose morphology evolves in time and space as the production of salt progresses. The precise geometry of the interconnection network of the cavities is poorly known; however, the ultrasonic measurements taken in the boreholes clearly indicate the extension of the cavities created at the level of the injectors.
In normal evolution, all of these voids remain confined within the saliferous formation. However, this evolution was disturbed in the past by the collapse of two central cavities of the Gellenoncourt device, SG4 and SG5 (Figure 3) according to the history described below.
Evolution of the SG4 and SG5 cavities up to the Beaumont Dolomite.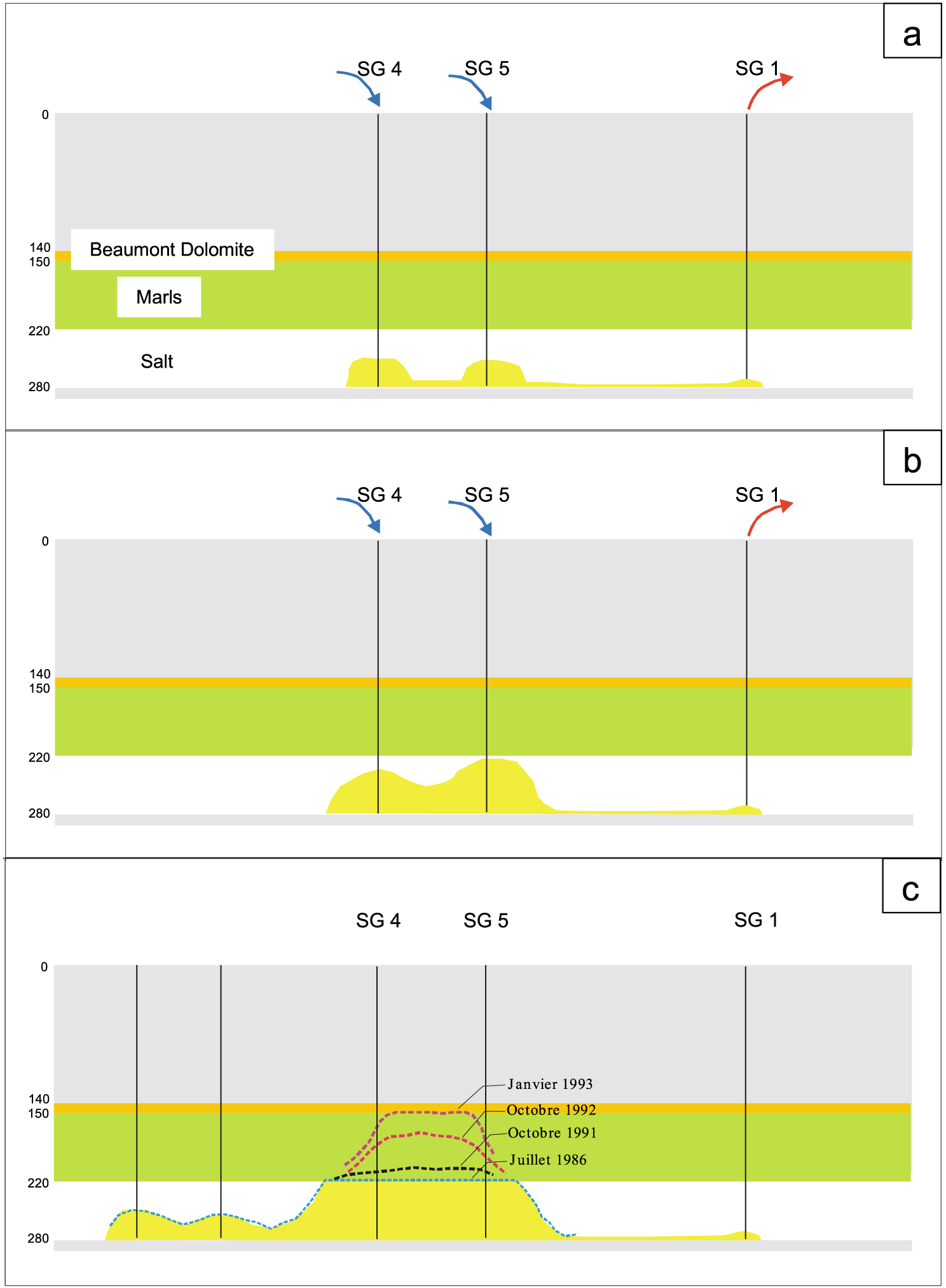
Wells SG4 and SG5 were used as freshwater injectors from the start of operations, SG1 being the brine extractor (Figure 3a). The device was maintained until the salt board at the top of SG5 was found to have reduced to 2 m, (Figure 3b) after which the injection of fresh water was moved to further points. A survey of the cavities subsequently showed that their volume continued to increase and the abandonment of the entire panel was decided. From 1982 to 1993, however, checks revealed a rise in the roof of SG5 in the argillites covering the salt, at first slowly, then rapidly until it came into contact with the Beaumont Dolomite (Figure 3c). The operator then took the decision to cause the collapse, by deliberately lowering the level of brine to maintain an air cushion at the top of the cavity. The event finally occurred in March 1998, leading to the formation of a surface crater about 50 m in diameter and 120 m deep [Buffet 1998]. The chimney was then partially filled due to sloping of the edges of the crater. The crater was initially dry after the collapse; it then filled with water and ended up as a lake whose level was about 30 m from the surface in June 1998.
This collapse locally disrupted the protective cover of the saline deposits and placed various hydraulic units in potential communication: the crater lake, the Rhaetian aquifer and the mining cavities filled with brine and dissolution residues. Given the lithological diversity of the overburden, the materials that fill the collapse chimney are heterogeneous with a dominant clay content. Their properties regulate the exchanges of fluid and dissolved salt between these units.
This experience motivated the Salins group to consider resuming the leaching of the entire panel until the still stable cavities collapsed, with the dual aim of increasing salt production but above all of securing the site in the long term.
Currently the lake has an area of about 1.7 ha; it should extend to 36 ha upon completion after resumption of operations. Once all the collapses have been attained, the system will evolve towards a deep saline aquifer and a lake on the surface hydraulically connected by the low permeability saturated rock materials filling a chimney. The saline aquifer will be confined within the saliferous formation, thanks to the high density of the brine which will prevent any convective circulation despite the presence of a thermal gradient, insofar as the lake will constitute a single body of water not generating hydraulic gradient in the system.
2. Long-term behavior review
2.1. Diffusion, a potential mechanism of salt emission
We consider here the case of the “post-mining” situation, in the long term, when the configuration of the site will be stabilized. The origin of the salt that can pollute the Rhaetian will be the saturated brine present in the cavities. This dense brine will not be able to circulate by convection but it could be a source of dissolved salt moving by diffusion through the materials of the collapsing chimney towards the fresher waters of the lake. Diffusion flux can be assessed using the following simple model (Figure 4).
Conceptual diagram of the diffusion of salt towards the Rhaetian.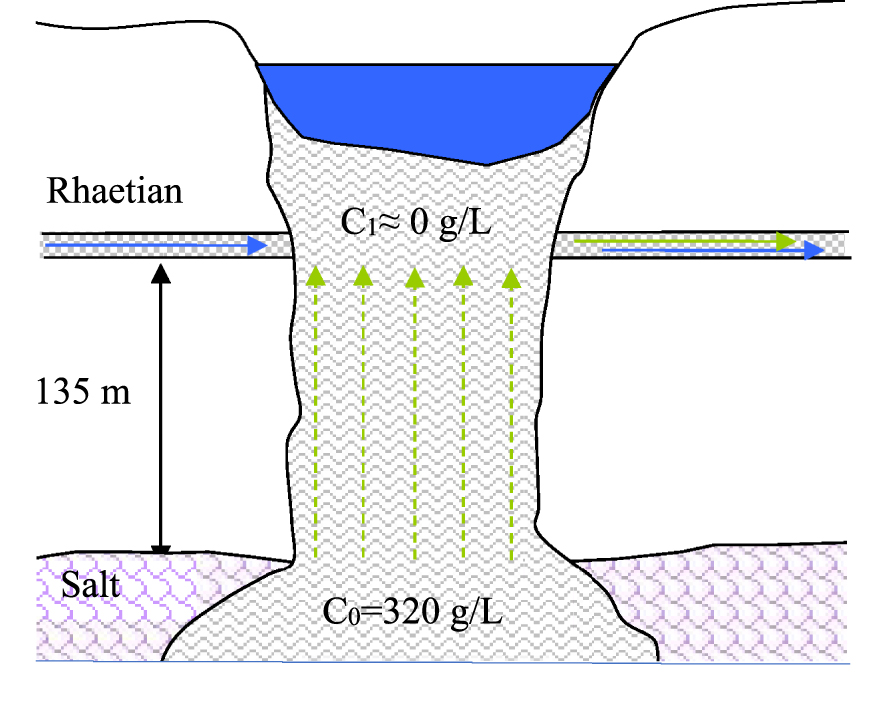
The chimney materials are assumed to be homogeneous with an average effective diffusion coefficient D for the different solutes. A concentration boundary condition at the C0 value of 320 g/L is imposed by the saturated brine at the base of the chimney where it penetrates the salt layer, while a low concentration of C1 value is maintained at the Rhaetian level under the effect of groundwater flow which dilutes the salt. Under these conditions the diffusive flux density in steady state is given by Fick’s law:
The effective diffusion coefficient in the materials filling the chimney is limited by the diffusion coefficient in the free water, the value of which is around 10−9–2 × 10−9 m2/s. We have considered a reduction of a factor of 10 due to the presence of solids which hinder diffusion and we have adopted the value of 2 × 10−10 m2/s for the calculation of the surface flux of salt:
For a collapsed chimney of 36 ha, an annual flow of 5–6 tons of salt is obtained. This diffusive flow is discharged into the Rhaetian aquifer under the effect of groundwater flow.
2.2. Chemical osmosis, another mechanism
The Regional Mission of the Environmental Authority which assessed the file presented by the Salins group gave an opinion in October 2018, at the request of the Prefect of Meurthe et Moselle and pointed out that osmotic phenomena were not considered and could cause a potential risk to long-term stability.
This article sets out some thoughts on the nature of this phenomenon and on the role it could possibly play in the configuration of the operation envisaged by the Salins.
It is made, initially, by applying the theoretical bases of chemical osmosis. We are then interested in the way in which the theory can be used in the particular context of salt mining, in order to identify orders of magnitude of the consequences that can be expected from the phenomenon. Finally, a confrontation with field observations will provide elements of validation of the approach adopted.
3. The theoretical bases of chemical osmosis
Chemical osmosis or chemo-osmosis designates the movement of water occurring through a semi-permeable membrane whose faces are bathed in ionic solutions of different concentrations. Such a membrane is said to be perfectly semi-permeable when it allows the passage of water molecules but totally opposes the transfer of ions. The water thus crosses the membrane from the zone where the concentration is low towards the zone of high concentration so as to cause a reduction in the concentration gradient by dilution effect.
In practice, membranes are only imperfectly semi-permeable and allow ions to pass at variable speeds depending on their properties; this type of transfer during which the ions of the solution pass from the zone of high concentration to the zone of low concentration is designated by diffusion. Thus, for the two types of mechanisms, osmosis and diffusion, the effect is to tend towards a homogenization of the concentrations on either side of the membrane.
The diagram of Figure 5 [Rousseau-Gueutin 2008], describes these phenomena in the cases of a perfect and imperfect membrane.
Illustration of diffusion and chemical osmosis in a U-tube [from Rousseau-Gueutin 2008].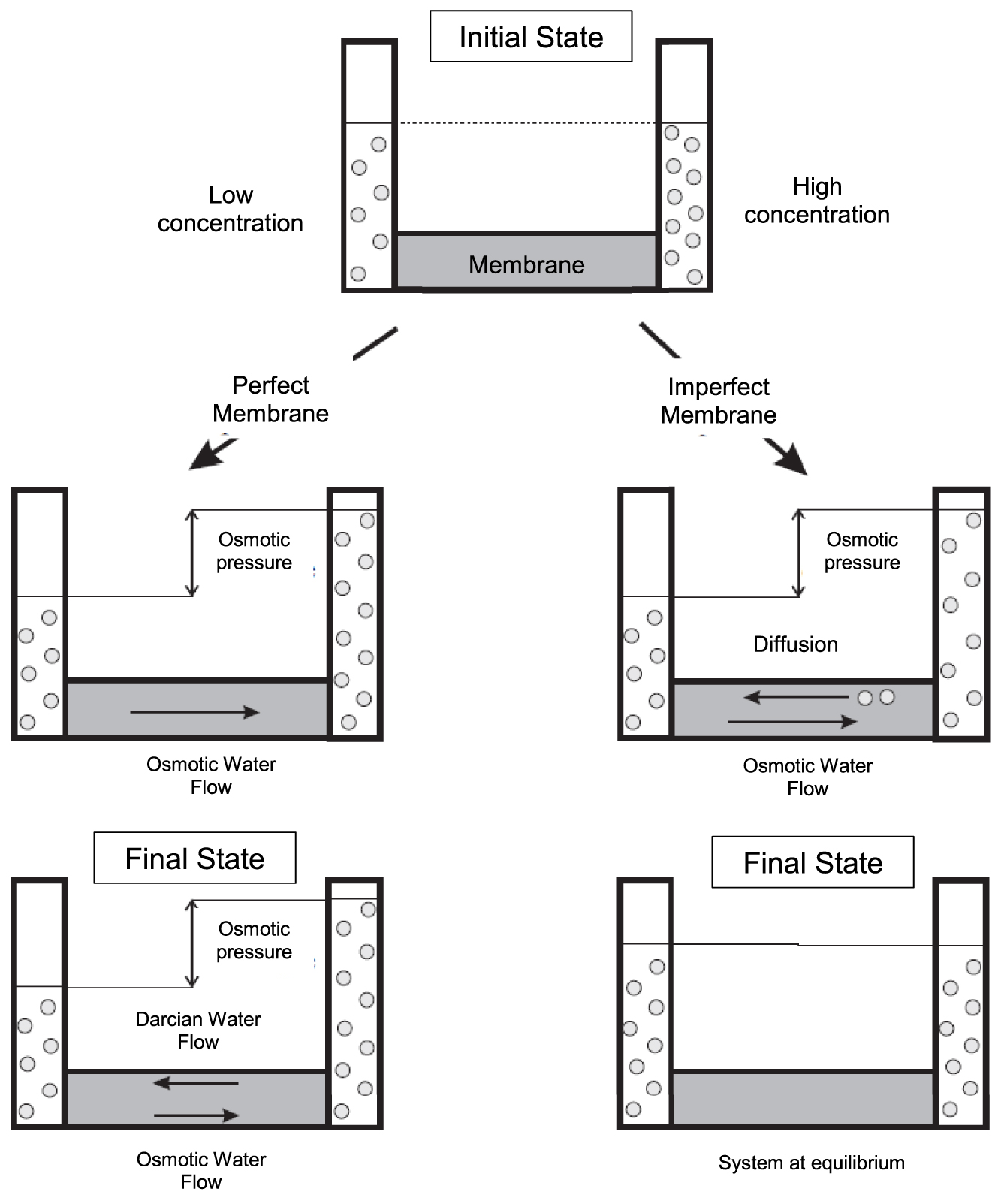
The diagram highlights a pressure difference between the two branches of the U-tube, called osmotic pressure. In the case of a perfect membrane, the pressure difference linked to the chemical activity generates a flow, in accordance with Darcy’s law, countercurrent to the osmotic flow and the system equilibrates when the flows of water osmotic and darcean are equal for the osmotic pressure corresponding to the difference in residual concentration between the two branches of the tube. In the case of an imperfect membrane, the presence of osmotic pressure is only transitory because the darcean flow and the diffusion tend to homogenize the concentration; the final state then translates into equal pressures and concentrations in the two branches. The duration of this transient phase depends on the permeability of the membrane.
It is therefore noted that the final state of the system is particularly dependent on the properties of the membrane. It also depends on the behavior of the ion source and will be demonstrated when applied to a salt deposit.
3.1. The thermodynamic model
The thermodynamics of irreversible phenomena provides a theoretical framework for modeling multi-physics coupling phenomena at the macroscopic scale. This theory postulates that, in general, the flux of a quantity is linked in a tensorial way to a driving force via a matrix of phenomenological coefficients. The different driving forces are expressed, themselves, in the form of the gradient of a scalar field corresponding to the different state variables of the system.
Table 1 brings together the different forces and fluxes taken into account in the problems of fluid mechanics concerned with chemical, thermal and electrical phenomena.
Coupled mechanisms linking driving forces and fluxes
| Driving forces | ||||
|---|---|---|---|---|
| Fluxes | Gradient of head or pressure | Gradient of electric potential | Gradient of concentration | Gradient of temperature |
| Flow velocity | Darcy’s law | Electro-osmosis | Chemical osmosis | Thermal osmosis |
| Electric current density | Filtration current | Ohm’s law | Diffusion current | Seebeck effect |
| Solute flux | Reverse osmosis | Electrophoresis | Fick’s law | Soret effect |
| Heat flux | Heat filtration | Peltier effect | Dufour effect | Fourier’s law |
The diagonal coupled mechanisms are said to be dominant and correspond to the phenomena classically taken into account in physics. The non-diagonal mechanisms refer to the non-dominant transfers which only play a significant role in particular configurations; chemical osmosis is one of them.
The phenomenological coefficients linking each flux to each force are not predicted by the macroscopic theory. They can be estimated by changing scale from other models considering the microscopic phenomena or, most often, empirically by means of experiments carried out at the right scale [Gonçalvès and Trémosa 2010].
3.2. The case of clay materials
According to Gonçalvès et al. [2015], as early as the 1960s, experimenters working on porous media had highlighted deviations from Darcy’s law in clay materials, one of the main reasons given was the existence of an osmotic effect in the presence of saline fluids. Knowledge on the subject has developed since the 1990s, in particular, thanks to studies on the storage of radioactive waste in low-permeability clay formations. It should be noted that these studies essentially concerned artificially prepared or reworked materials, on the scale of the laboratory sample; very few involved natural materials and even fewer in in situ conditions. On the scale of a geological layer 130 m thick at a depth of approximately 500 m, Andra revealed overpressures in the Callovo-Oxfordian argillites in Meuse/Haute-Marne. The role of chemical osmosis has been assessed and it appears, without being definitively demonstrated, that some of these overpressures could be due to osmotic phenomena [Rousseau-Gueutin 2008, Gonçalvès et al. 2015, Gueutin et al. 2007].
The origin of the osmotic effect in clays is explained by the fact that the surface of clay minerals, which is negatively charged, imposes electrical restrictions on the ions during their transport, resulting in a concentration of cations near the surface and an exclusion of anions towards the center of the pores. To respect electrical neutrality, the restriction on the transport of the anions affects the cations, which limits the total ionic transport like what an imperfect membrane would do. Surface charges are more easily compensated when the ionic strength of the solution is high and the effect is all the more important as the thickness of the electrostatic layers approaches the size of the pores. It is thus understood that the efficiency of the osmotic mechanism is linked to the nature of the clay minerals, to the size of the pores as well as to the concentration of the solutions. Clayey rocks with low permeability, such as Callovo-Oxfordian argillites, are characterized by pore dimensions of a few nanometers comparable to those of electrostatic layers, which explains the occurrence of osmotic phenomena in these systems.
In summary, the existence of the osmotic effect in clay materials is established; the question is to know what its intensity may be in the configuration that concerns us.
3.3. Laws and parameters
Gonçalvès et al. [2015] provided a very detailed synthesis of couplings in membranes and clay materials. It emerges from this synthesis that the phenomenological relations representing the coupling between the flow obeying Darcy’s law, the osmotic effect and the transport by convection–diffusion at the macroscopic scale are written as follows, in steady state:
| (1) |
The osmotic pressure π is given by Van’t Hoff’s formula where R (J/mol/K) is the ideal gas constant, T the Kelvin temperature and 𝜈 the number of separated ions (2 for NaCl).
We note the existence of two velocities for water, the classical Darcy velocity V , generated by the hydraulic head gradient and the osmotic velocity V′ generated by the osmotic pressure, therefore by the concentration gradient. Only the Darcy velocity intervenes on solute transport since the osmotic phenomenon only moves water molecules. The osmotic phenomenon is therefore not likely to cause the displacement of the ions.
An essential parameter is the osmotic efficiency coefficient 𝜀 (dimensionless) which varies between 0 and 1. In the case of a perfect membrane, this coefficient is equal to 1 and the diffusion coefficient is then zero, reflecting the absence of ionic transport. It is less than 1 for natural environments depending on their more or less semi-permeable character. In such media, the three fundamental parameters are the permeability, the effective diffusion coefficient and the osmotic efficiency coefficient. Their determination is experimental, using systems requiring particularly advanced metrology and their value is influenced by the scale of the problem dealt with.
Theoretical considerations [Bresler 1973] establish that the osmotic efficiency coefficient is a decreasing function of the product of the pore size of the medium times the square root of the concentration. Gonçalvès et al. [2015] have brought together in a single figure (Figure 6) the measurements available in the literature according to these parameters compared to the theoretical Bressler curve.
Osmotic efficiency coefficient as a function of . b is the average pore size in nm and C the concentration in mol/L. ⊞ represent the experimental values for the Bure argillite [from Gonçalvès et al. 2015].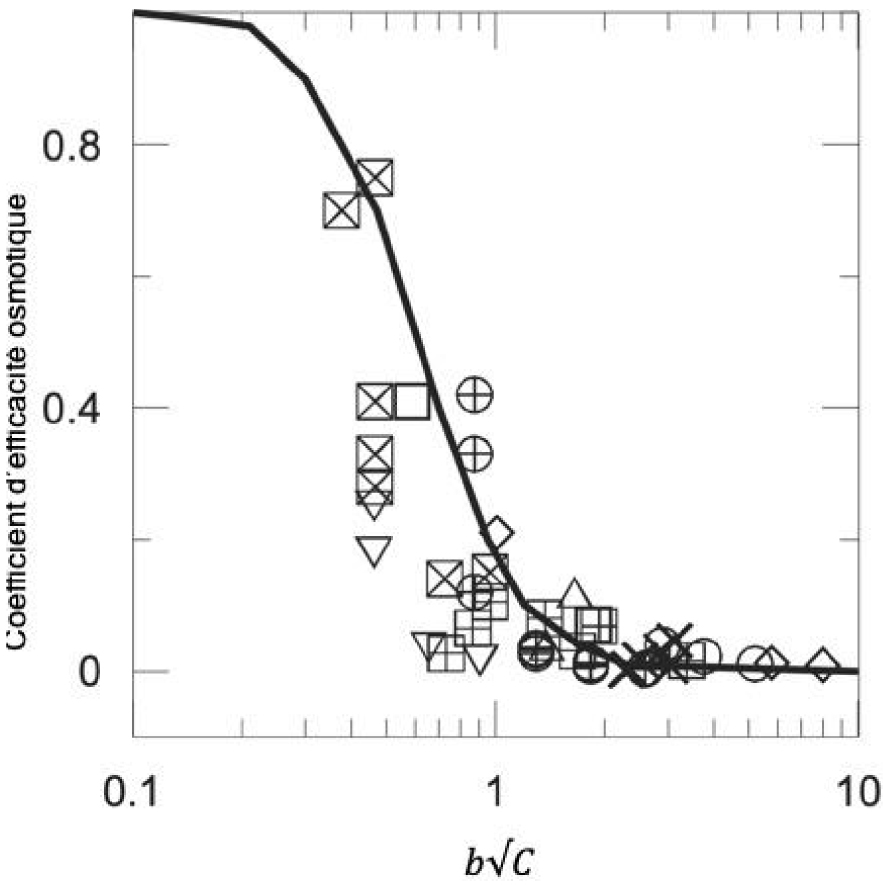
These data show that the measured osmotic efficiency coefficient is generally low with values in fairly good agreement with the theoretical curve. Note that the points relating to the very compact Bure argillites are at low values.
The theory also accounts for the dependence of the diffusion coefficient with the osmotic efficiency coefficient. Figure 7 taken from Rousseau-Gueutin [2008], based on the work of Revil et al. [2005] and Gonçalvès et al. [2007], indicates the shape of this dependence, established for a material composed of a smectite-type clay. We note that it is weak for low values of osmotic efficiency, which suggests that osmosis has little effect on the diffusive transport of ionic solute in media that behave like imperfect membranes.
Variation of the effective diffusion coefficient as a function of the osmotic efficiency coefficient for a smectite in the presence of an NaCl solution [Rousseau-Gueutin 2008].
3.4. Application to a saline cavity
In order to apply the above to the situation of a collapsed salt cavity, we will retain the following elements:
- it has been proven that chemical osmosis phenomena can occur in clay materials. This is linked to the surface electrical properties of clay minerals and to the small pore size which give to clay media the behavior of an imperfect semi-permeable membrane;
- at the macroscopic scale, the phenomenon is governed by an osmotic efficiency coefficient varying between 0 and 1 which weights the influence of osmotic pressure in the phenomenological relationship which describes the flow of water;
- the osmotic efficiency coefficient is highly variable, of complex and uncertain measurement, and has only rarely been assessed in natural environments;
- the efficiency coefficient depends on the size of the pores and on the concentration, which makes the non-linear phenomenon therefore difficult to quantify by a simple approach because the size of the pores is not a directly accessible parameter;
- the materials filling the collapse chimney of the saline cavities are essentially disturbed clayey materials whose porosity is increased compared to that of an argillite in place, which leads to a relative increase in the average size of the pores. Moreover, the salt concentrations are very high, at least in the lower part of the system. These elements are in favor of a very low value of the coefficient of osmotic efficiency if they are compared with the knowledge acquired on the argillites of the Callovo-Oxfordian of Bure which are considered as well characterized and having pores of very small dimensions. The hypothesis considering that the filling of the chimney is made up of homogeneous clay, leads to increasing the role of osmosis mechanisms, which goes in the direction of safety in the assessment of the danger;
- the osmotic phenomenon does not modify the transport of ionic solute within the medium, which remains dependent on the convection–diffusion mechanism.
4. Exploratory modeling of the behavior of a collapsed cavity
In order to quantify the potential effect of osmosis on the behavior of a collapsed salt cavity, we attempted a simple modeling based on the conceptual diagram in Figure 4.
4.1. Principles of the model
The assumptions are as follows:
- the transfers are considered to take place in a one-dimensional vertical fashion between the deep collapsed cavity and the Rhaetian aquifer system, through the chimney over a height of 135 m;
- the depth concentration is maintained by dissolving the salt at 320 g/L, i.e. 5480 mol/m3. It is imposed at 0 g/L at the Rhaetian level. This fixes the concentration gradient at the value 0.04 mol/L/m;
- the system is represented in steady state, in two distinct configurations of hydraulic boundary conditions illustrated in Figure 8;
- configuration 1: the cavity is in hydraulic relation with other cavities whose brine level is kept constant; this is currently the case at Gellenoncourt, where the collapse of the operated panel is only partial. We will consider a hydrostatic equilibrium between the Rhaetian and the cavity;
- configuration 2: the collapsed cavity is confined, with no possible hydraulic exchange with the external environment; this configuration is meant to represent the final state when the whole panel is collapsed on approximately 36 ha;
- in both configurations the concentration profile at equilibrium in the chimney is considered to be diffusive with a constant gradient between 320 and 0 g/L.
Simulation configurations, (on the left connected cavity, on the right isolated cavity).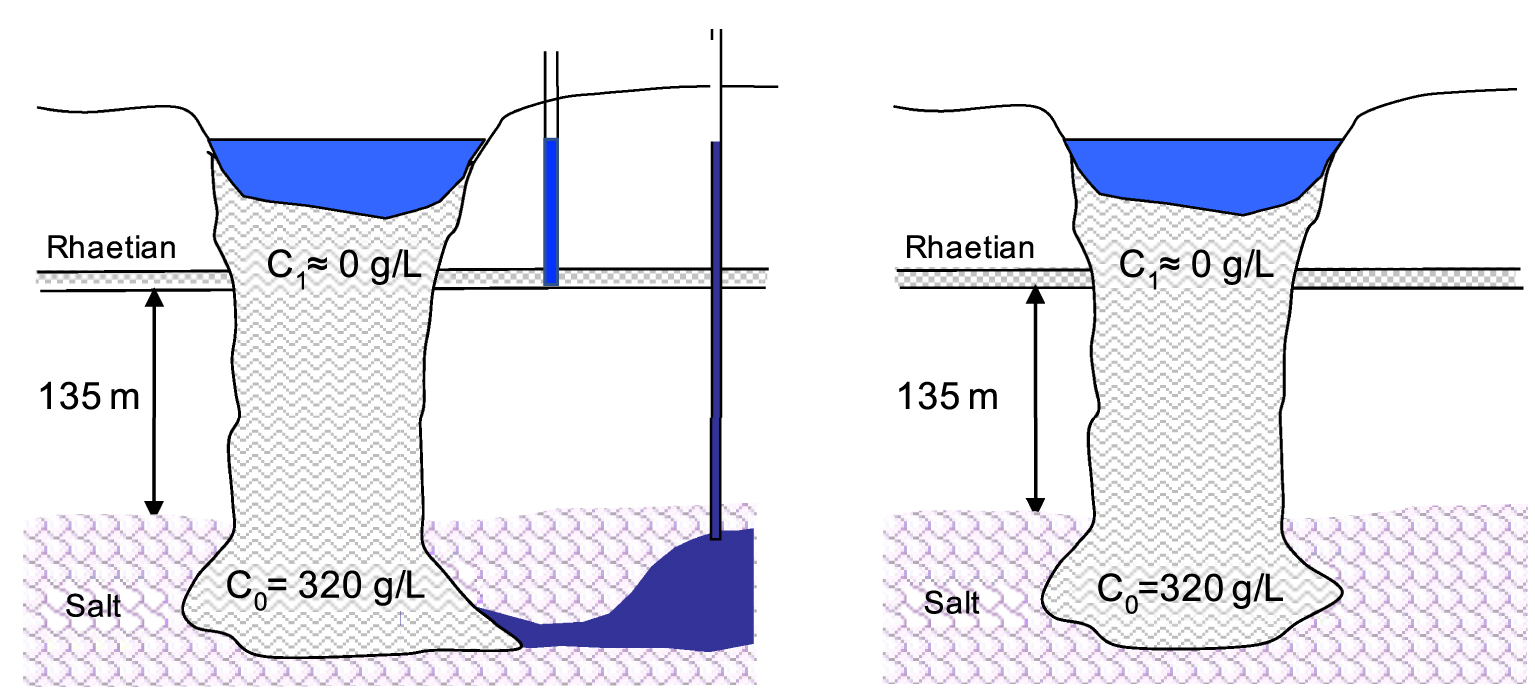
Under these assumptions the system of equations (1) simplifies to (2)
| (2) |
The system of equations (2) is non-linear because the coefficient of osmotic efficiency depends on the concentration. The numerical resolution by finite differences provides the profile of the head in the chimney and allows the calculation of the flow of water and salt flux exchanged between the cavity and the Rhaetian aquifer.
4.2. Choice of parameters
The Darcy permeability K and the effective diffusion coefficient D have been fixed at the values 10−10 m/s and 2 × 10−10 m2/s respectively. Note that if these parameters are constant on the vertical, they have no influence on the calculated profile. They intervene on the other hand in a linear way on the fluxes of water and salt. We consider that the values chosen are in the high range and that the fluxes will thus be assessed on an upward basis.
As indicated previously, the essential parameter of the osmotic phenomenon is the coefficient of osmotic efficiency 𝜀. We estimated it from the Bressler curve (cf. Figure 6) considering an average pore size of 10 nm and a linear concentration profile in the chimney between 320 and 0 g/L. This pore size was set arbitrarily by reference to the 4 nm value presented by Rousseau-Gueutin [2008], for the Callovo-Oxfordian argillites of Bure. It is very likely that it is largely underestimated, if one considers that the porosity of the unstructured clay materials of the chimney must be notably increased compared to that of compact argillites. By comparison, surface clays from the Albian in Aube show pore sizes between 50 and 80 nm.
With these hypotheses, deliberately chosen to increase the osmotic effects, the values of the osmotic efficiency coefficient range between 10% in the upper part where the concentration is low and 0.01% in the lower part where the brine reaches saturation (Figure 9). In order to obtain an appreciation of the sensitivity to this parameter, a simulation was also carried out by adopting a homogeneous value of 1% along the profile.
Profile of osmotic efficiency coefficient as a function of depth for a pore size of 10 nm.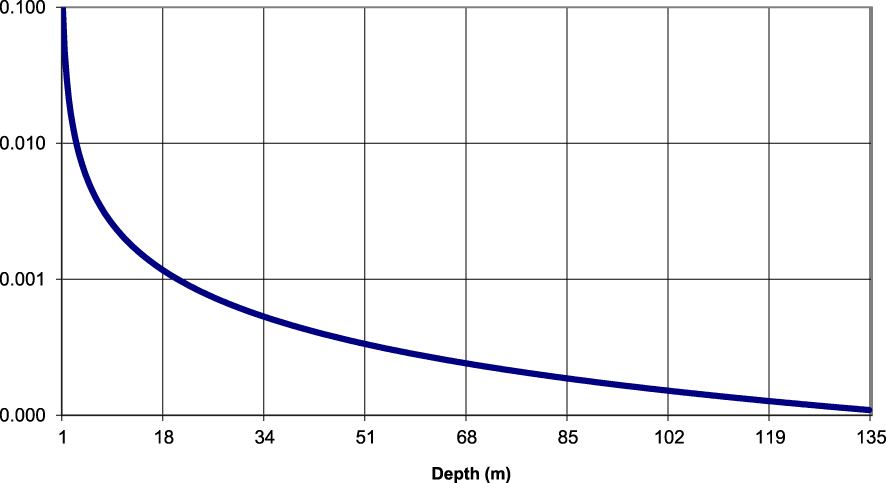
4.3. Simulation results
Figures 10 and 11 show the calculated hydraulic over-head profiles for the two model boundary condition configurations. The over-head represents the hydraulic head difference along the profile compared to the Rhaetian head considered as a reference.
Configuration 1, hydraulic over-head profiles as a function of depth calculated with a variable (in blue) and constant (in red) osmotic efficiency coefficient.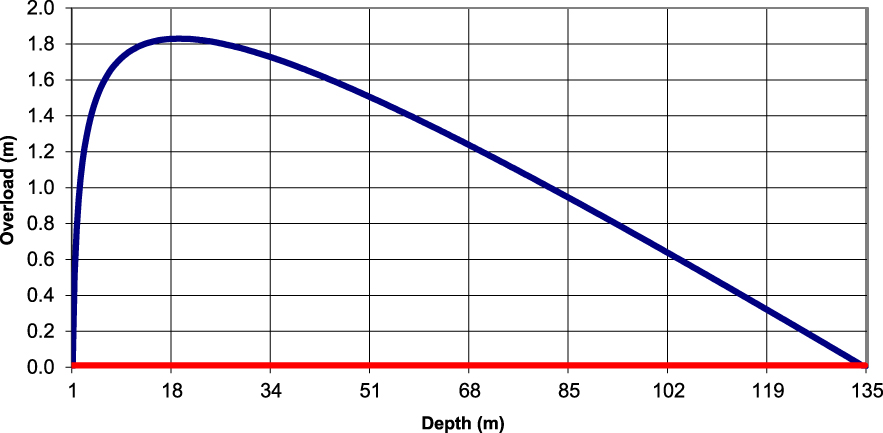
Configuration 2, hydraulic over-head profiles as a function of depth calculated with a variable (in blue) and constant (in red) osmotic efficiency coefficient.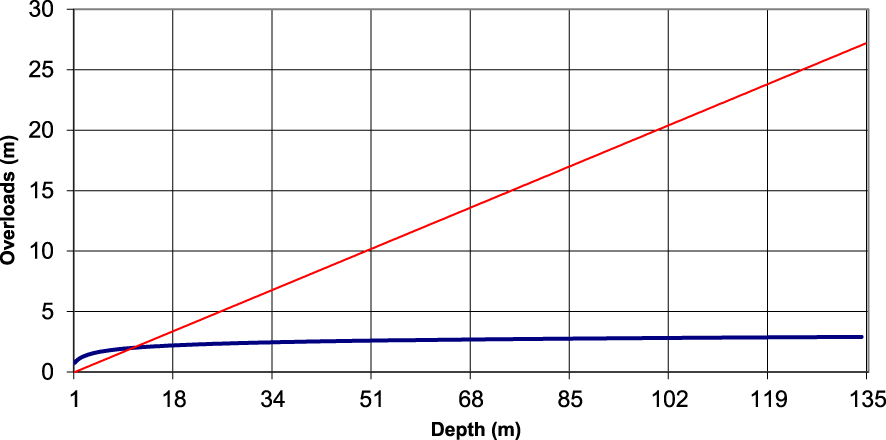
In the case of configuration 1 where the cavity is connected to the aquifer system, a hydraulic head of 0 m is arbitrarily imposed at the top and bottom of the chimney. The model therefore calculates an over-head compared to the hydrostatic head. It can be seen that the osmotic effect only deforms the head profile if the osmotic efficiency coefficient is variable as a function of depth. We thus find the results of Rousseau-Gueutin [2008], and Gonçalvès et al. [2007]. In both cases, the chimney is traversed by a downward flow of water, the speeds of which are respectively 2.2 × 10−12 m/s and 2.02 × 10−11 m/s. This flow is solely the consequence of the osmotic effect; it is evacuated to the outside by the boundary condition of constant level imposed at the base of the chimney. It should be noted that an interpretation in purely “Darcean” terms of the deformed profile would lead to an erroneous evaluation of the intensities and orientations of the fluxes.
In the case of configuration 2 where the cavity is totally confined, no water flow can travel through the chimney in steady state, so that the head rises with depth to compensate for the osmotic pressure. The over-head thus reaches 2.9 m or 27 m at the level of the cavity, depending on the osmotic efficiency coefficient profile adopted. Such over-heads would not endanger the mechanical stability of the cavity given the thickness of the covering. Let us recall that the values of osmotic efficiency coefficients are certainly chosen by excess.
4.4. Cavity salt balance
The preceding simulations make it possible to quantify the flux of salt evacuated from the cavity in the different configurations.
This flux has two components:
- a component by diffusion generating a flux towards the top of the chimney. This part is independent of the osmotic effect insofar as the diffusion coefficient is only slightly influenced by this effect for the low values of osmotic efficiency coefficient considered (cf. Figure 7);
- a so-called “convective” component linked to the downward flow of water which reaches the cavity under the effect of osmosis in the case of configuration 1 where the cavity is hydraulically connected to the external environment. Note that this flow is made up of fresh water but that it becomes saturated with salt when it reaches the salt formation. It will be considered that the mass of NaCl dissolved by 1 L of pure water is 355–360 g for a brine saturated at 320 g/L with a density of 1220 kg/m3.
Table 2 indicates these different fluxes for a 36 ha collapse chimney, as should be the case when the Gellenoncourt panel operation ends.
Annual salt balance at the end of a collapsed panel on 36 ha
| Setup 1 | Setup 2 | |||
|---|---|---|---|---|
| Variable 𝜀 profile 10% → 0.01% | Constant 𝜀 profile 1% | Variable 𝜀 profile 10% → 0.01% | Constant 𝜀 profile 1% | |
| Diffusive salt flux (tons/year) | 5.4 | 5.4 | 5.4 | 5.4 |
| “Convective” salt flux (tons/year) | 6.6 | 69 | 0 | 0 |
| Total salt flux (tons/year) | 12 | 74 | 5.4 | 5.4 |
| Volume increase of the cavity (m3/year) | 6.5 | 40 | 2.5 | 2.5 |
| Overflow volume of brine (m3/year) | 21 | 214 | 0 | 0 |
Let us recall the values adopted for the Darcy permeability and the diffusion coefficient, which are respectively 10−10 m/s and 2 × 10−10 m2/s. Salt fluxes are directly proportional to these values.
It will be noted that the diffusive flux of salt is independent of the osmotic effect but that the convective flux is directly linked to this effect with a high sensitivity to the profile of the osmotic efficiency coefficient. The line of the table entitled “volume increase of the cavity” corresponds to the volume of salt dissolved at depth under the effect of the various flows. The brine “overflow volume” represents the quantity of brine that must theoretically be evacuated to cancel the over-head generated in the cavity by the osmotic effect.
In addition to the diffusion and osmosis processes mentioned above, experience shows that deep saline cavities are subject to the creep of the surrounding saline mass which generates pressure rises or brine overflows depending on whether the cavity is kept closed or open [Brouard et al. 2017]. This mechanism does not appear to play an important role in the case that concerns us because the cavities are shallow and are self-filled by the materials from the collapse chimney. Ground movements are however likely to exist to compensate for the increase in volume generated by the dissolution at depth under the effect of the convective flow of fresh water caused by osmosis. However, these movements would be very slow given the low volumes involved and would primarily concern the depth of the lake.
5. On-site observations and conclusion
Figure 12 illustrates the current configuration of the Gellenoncourt panel where the collapse of two coalescing cavities (SG4 and SG5) in 1998 created a chimney opening on the surface into a crater, occupied by a lake whose initial diameter was 50 m, i.e. an area of 0.2 ha. This area then evolved over time to currently reach 1.7 ha under the effect of the natural sloping. The figure shows that the collapsed part of the cavities is in direct hydraulic relationship with other non-collapsed cavities whose brine level is controlled by operating boreholes. This diagram corresponds to configuration 1 of the model developed above. The simulation indicates that the annual volume of brine that would have to be evacuated to prevent overflow in the boreholes would amount to between 0.1 and 1 m3 according to the assumption on the osmotic efficiency coefficient, considering the value of 0.2 ha for the area of the collapse chimney. Such volumes would go unnoticed by comparison to the various pumping or purging operations carried out for mining purposes. It should be noted that the boreholes of the Gellenoncourt field remained open between 1998, the date of the collapse, and 2002, the date of the resumption of leaching operations, and that no variation in level was observed during this period.
Conceptual diagram of the current operation of Gellenoncourt.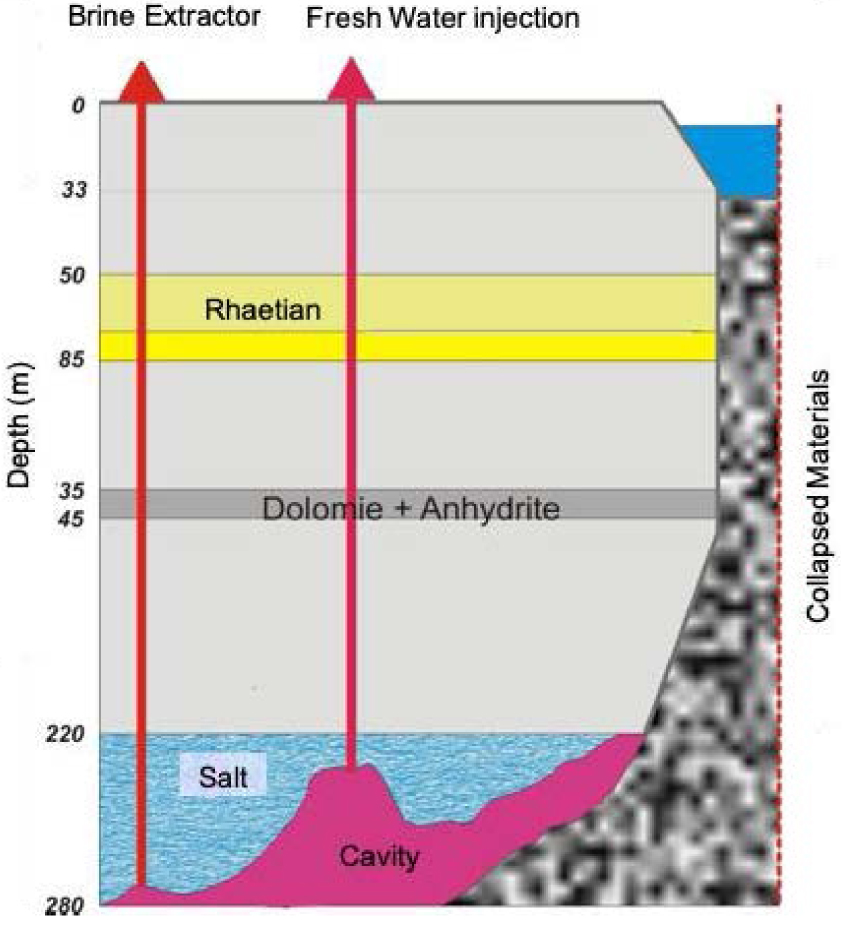
In conclusion, the preceding quantitative evaluations come from a theoretical approach to the problem. They highlight the sensitivity of chemo-osmosis to the macroscopic coefficient of osmotic efficiency, the value of which remains poorly understood for natural environments, at the relevant scales.
An application of the theory with values of this coefficient chosen on an upper bound basis with reference to a well-documented compact argillite such as that investigated by Andra on the site of the geological disposal project for radioactive waste, shows that the chemical osmotic effect is not likely to significantly modify the orders of magnitude of the salt fluxes evacuated into the environment by intensive exploitation of a salt layer, as envisaged by the Salins group in Gellenoncourt.
In general, field observations on the sites that exploit the layered salt deposit of the Lorraine plateau indicate that no unexplained overpressure has ever been observed in the salt aquifer created by dissolution within the salt formation while collapsing chimneys, filled with clayey materials, bring the deep saturated brine in contact with the fresh waters of the superficial aquifer system. This is consistent with the theoretical approach presented which shows that osmotic phenomena are not likely to generate disturbances of an exceptional nature compared to the various disturbances inherent in the practices of exploitation of the salt deposit by dissolution.
Conflicts of interest
Authors have no conflict of interest to declare.
Version française
1. Position du problème
L’exploitation du sel gemme en couches ou en dômes par dissolution in situ fait l’objet d’une industrie ancienne développée depuis le milieu du 19e siècle. C’est le cas du gisement salifère lorrain encore largement exploité de nos jours pour la production de sel destiné à la chimie, à l’alimentation ou encore au déneigement. Parmi les exploitants actuels, figure le groupe Salins qui opère à proximité des villes de Dombasle et Varangéville, dans l’est de Nancy. Les couches de sel sollicitées font partie d’un puissant ensemble marno-salifère du Keuper. Deux méthodes d’exploitation sont pratiquées, d’une part, en extrayant du sel gemme par cavités minées selon la méthode des chambres et piliers abandonnés pour le déneigement (mine de Varangéville) et, d’autre part, en prélevant la saumure obtenue par lixiviation à l’eau douce de cavités profondes, pour l’industrie (salines du plateau d’Haraucourt).
Dans le respect d’une exploitation par lixiviation bien contrôlée, deux questions se posent parmi d’autres, optimiser la récupération du sel qui est une denrée de valeur et préserver l’environnement de toute pollution par de la saumure et de mouvements de terrain en surface. A cette fin, s’agissant du groupe Salins, la méthode par lixiviation vise actuellement à réaliser des cavités isolées les unes des autres, dont on peut démontrer la stabilité à long terme sur les plans hydrauliques et mécaniques. Cependant, certains secteurs anciens du gisement ont été exploités au moyen de cavités communicantes, ce qui a compromis la maîtrise des dissolutions résiduelles spontanées en fin de vie et entrainé, dans certains cas, des effondrements parvenant en surface, créant des cratères remplis d’eaux.
Afin de mettre en sécurité les lieux, tout en optimisant la production de sel, l’exploitant envisage de reprendre la dissolution in situ d’un panneau du site de Gellenoncourt, sur la concession de Drouville. La méthode d’exploitation employée, dite intensive, aura pour conséquence l’élargissement, suivi d’un effondrement, des cavités déjà existantes, aboutissant au final à un lac s’étendant sur l’emprise du panneau sur environ 36 ha. Dans le but d’obtenir l’autorisation de mettre en œuvre la méthode, l’exploitant a constitué un dossier d’impact examinant, sur des bases scientifiques, les conséquences d’une telle pratique, notamment pour ce qui concerne le risque de pollution des aquifères environnants par des eaux salées.
Le présent article traite des mécanismes potentiels de relâchement de sel en provenance de cavités effondrées. Il met à profit des travaux de recherche de l’Agence nationale pour les déchets radioactifs (Andra) qui s’intéresse à la compréhension des surpressions interstitielles observées dans la couche d’argilite du Callovo-Oxfordien de Bure en Meuse/Haute-Marne, objet d’études pour la création d’un stockage géologique des déchets radioactifs de haute et moyenne activité à vie longue. Ces travaux réalisés en partenariat avec le Laboratoire de Mécanique des Solides de l’Ecole Polytechnique et l’UMR Sisyphe à l’Université Pierre et Marie Curie ont fait l’objet, en 2008, d’une thèse soutenue dans cette université, sous la présidence du Professeur Ghislain de Marsily. Nous avons emprunté les bases théoriques de notre raisonnement à cet ouvrage, ainsi qu’à plusieurs publications qui en ont résulté.
1.1. Éléments de géologie du gisement salifère de Lorraine
Les nombreux sondages réalisés sur les concessions salines permettent de proposer la coupe géologique synthétique qui montre du haut vers le bas la succession suivante (Figure 1).
Log géologique synthétique.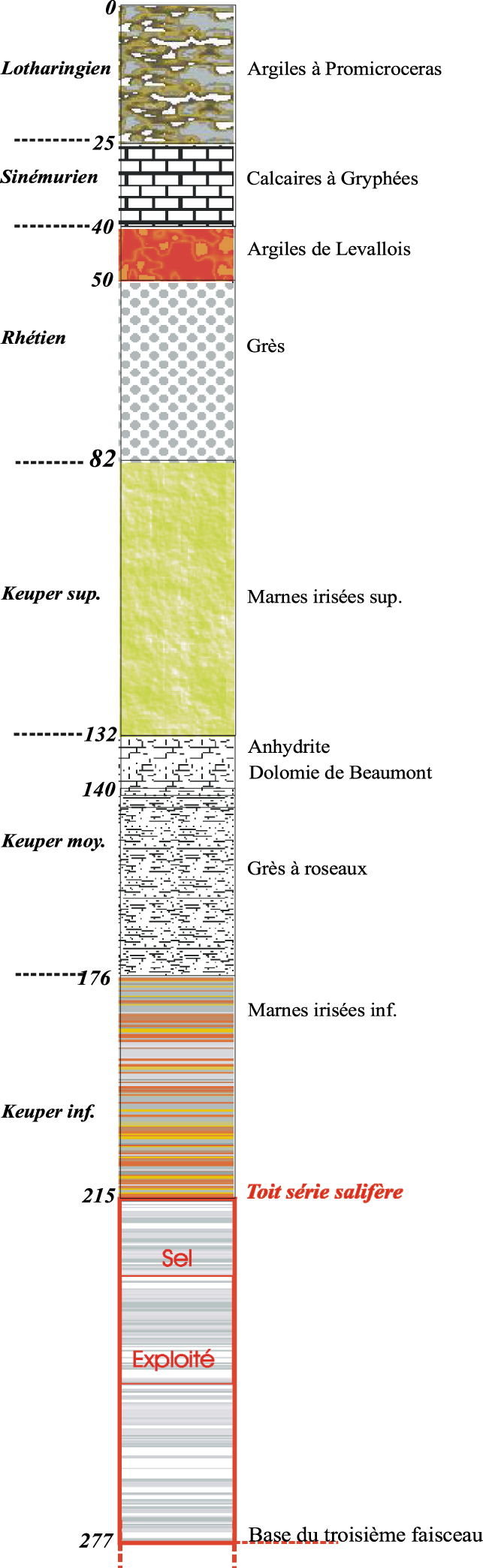
Argiles noires à Promicroceras (Lotharingien). Argilites gris-bleu plastiques, parfois schisteuses, d’épaisseur maximale 25 m.
Calcaires à Gryphées (Sinémurien). Alternance décimétrique de marnes bleues à noires et de bancs de calcaires argileux de couleur rouille, de 15 à 17 m d’épaisseur.
Argiles de Levallois (Rhétien). Argilites rose-saumon qui constituent un niveau repère dans toute la Lorraine. L’épaisseur moyenne est d’une dizaine de mètres.
Grès infraliasiques (Rhétien). Grès siliceux fins avec intercalations argileuses centimétriques à décimétriques noires ou vertes dans la partie sommitale. L’épaisseur moyenne est de 32 m.
Marnes irisées supérieures (Keuper supérieur). Argilites vertes et violacées qui deviennent rouge brique vers la base. Des horizons dolomitiques centimétriques à décimétriques sont présents ainsi que, à la base, des passées décimétriques d’anhydrite blanche nodulaire ou en filets anastomosés. L’épaisseur atteint 135 m à Gellenoncourt.
Dolomie de Beaumont — Grès à roseaux (Keuper moyen). Dolomie beige ou grise en bancs décimétriques surmontée d’un chapeau d’anhydrite massive de 3 m à 4 m d’épaisseur. La dolomie, épaisse de 8 m, joue un rôle important dans la stabilité des terrains avant les effondrements. Au-dessous on trouve des marnes bariolées puis des grès fins micacés très argileux contenant de nombreux débris végétaux.
Marnes irisées inférieures (Keuper inférieur). Cette puissante formation de l’ordre de 200 m d’épaisseur est composée d’argilites alternant avec des lits de gypse et d’anhydrite sur les quarante premiers mètres. On rencontre ensuite la série salifère épaisse de 120 m mais dont seuls les 3 faisceaux supérieurs, riches en sel et épais de 65 m, sont exploités à Gellenoncourt et renferment environ 20% d’insolubles. Ainsi, l’épaisseur cumulée de sel pur lixiviable représente en moyenne une quarantaine de mètres.
La régularité des couches apparait sur la Figure 2 qui montre la position des niveaux repères que sont le Rhétien et le toit du sel, qui se placent respectivement à une moyenne de 50 m et 220 m sous le sol dans les 44 sondages présents sur l’ensemble du site de Gellenoncourt.
Coupe géologique illustrant la position du sel exploité par rapport à l’aquifère rhétien.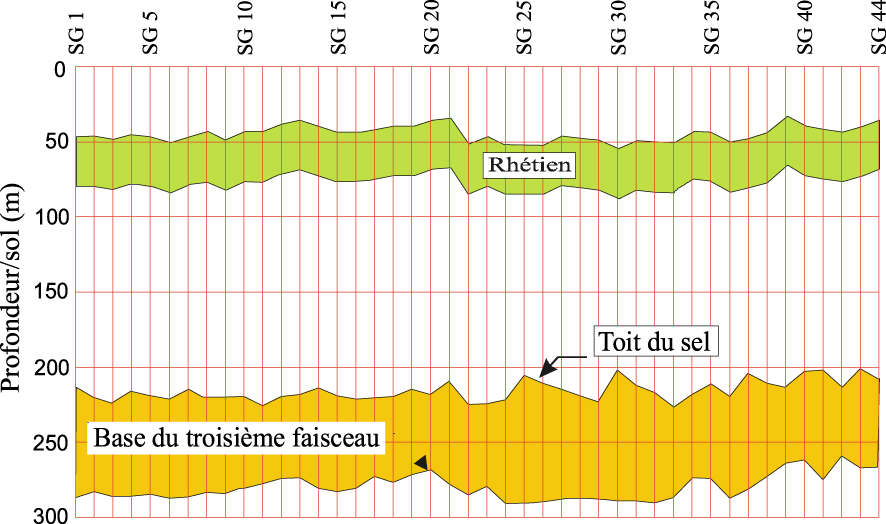
1.2. Éléments d’hydrogéologie du site
Parmi les formations géologiques présentes dans le sous-sol, seuls les grès du Rhétien constituent un aquifère susceptible d’être impacté par l’exploitation saline.
Épais d’une trentaine de mètres, cet aquifère a contribué à l’alimentation en eau potable des communes voisines. Il est encore faiblement exploité pour l’agriculture. Protégé par la couverture peu perméable et bien continue des argiles de Levallois, ce réservoir est alimenté par ses affleurements en bordure sud et est du plateau. La transmissivité est modeste et varie entre 10−4 m2/s et 10−5 m2/s, ce qui conduit à une grande sensibilité du niveau piézométrique aux prélèvements.
La nappe est le plus souvent captive sous les argiles de Levallois et est artésienne dans les parties basses de la topographie. La piézométrie générale indique un écoulement vers le nord-ouest vers la rivière Roanne qui draine cette nappe.
1.3. Les conséquences de l’exploitation du sel
L’exploitation du panneau de Gellenoncourt a été menée pendant une vingtaine d’années à partir de 1967. La méthode a consisté à relier par fracturation hydraulique la base de plusieurs sondages creusés jusqu’au mur du troisième faisceau salifère, puis à introduire de l’eau douce dans un ou plusieurs ouvrages et à pomper la saumure dans des sondages éloignés dits « extracteurs », entraînant ainsi par dissolution du sel la création de cavités au voisinage des injecteurs. Une bonne adéquation entre le débit et l’agencement du dispositif assurait la saturation de la saumure. Des contrôles périodiques de la géométrie des vides étaient réalisés par ultra-sons afin de surveiller l’évolution des cavités.
Ainsi l’exploitation du sel a développé des vides dont la base se trouve vers 65 m de profondeur sous le toit du sel et dont la morphologie évolue dans le temps et dans l’espace au fur et à mesure de la production de sel. La géométrie précise du réseau d’interconnexion des cavités est mal connue ; les mesures ultra-soniques réalisées dans les forages, indiquent par contre clairement l’extension des cavités créées au niveau des injecteurs.
En évolution normale l’ensemble de ces vides reste confiné au sein de la formation salifère. Cependant cette évolution a été perturbée dans le passé par l’effondrement de deux cavités centrales du dispositif de Gellenoncourt, SG4 et SG5 (Figure 3) selon l’historique décrit ci-dessous.
Evolution des cavités SG4–SG5 jusqu’à la Dolomie de Beaumont.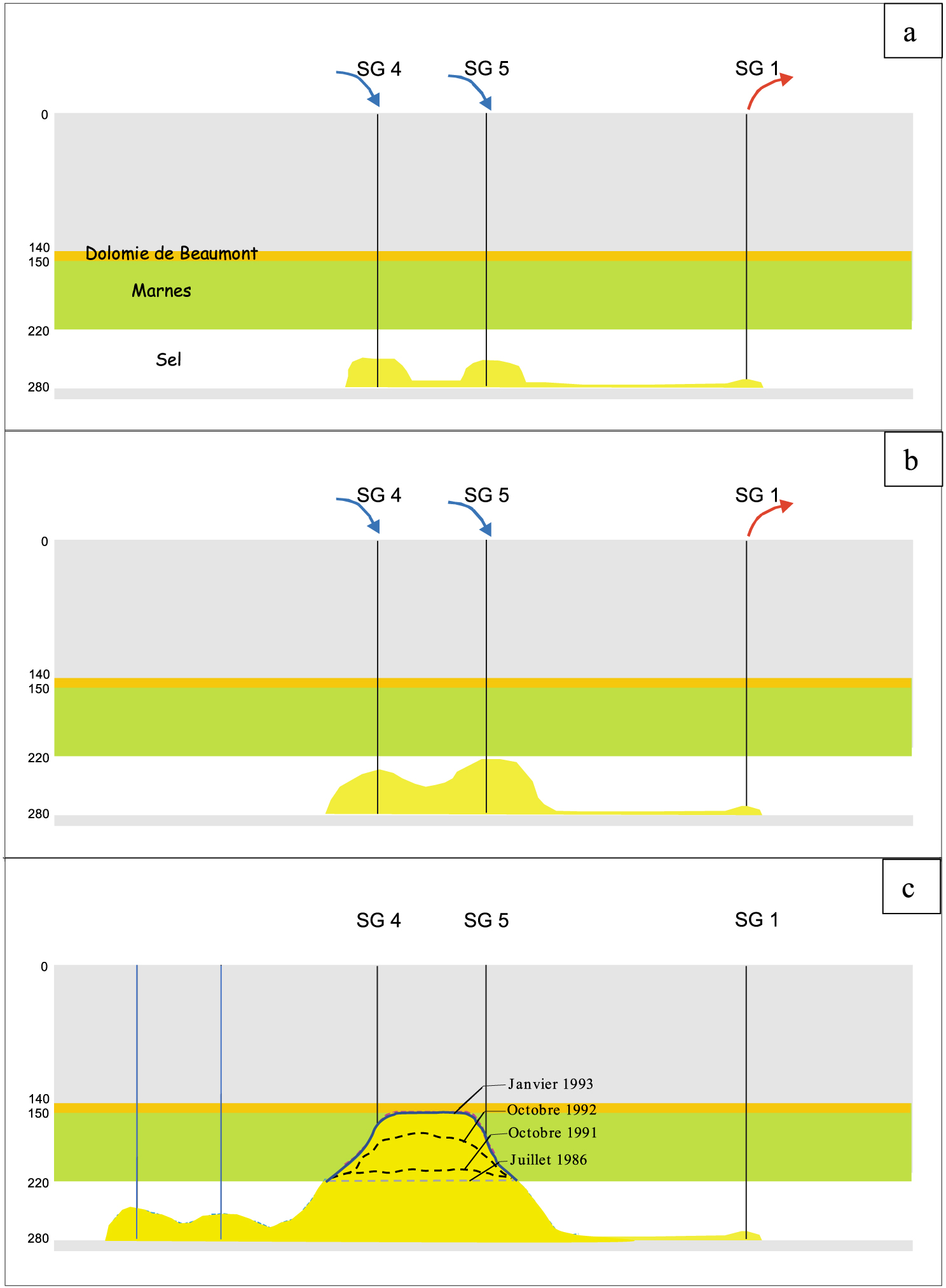
Les puits SG4 et SG5 ont été utilisés comme injecteurs d’eau douce dès le début de l’exploitation, SG1 étant l’extracteur de saumure (Figure 3a). Le dispositif a été maintenu jusqu’à ce qu’il ait été constaté que la planche de sel au sommet de SG5 était réduite à 2 m, (Figure 3b) après quoi l’injection d’eau douce a été reportée en d’autres points. Un suivi des cavités a par la suite montré que leur volume continuait à s’accroitre et l’arrêt d’exploitation de l’ensemble du panneau a été décidé. De 1982 à 1993 les contrôles ont cependant mis en évidence une remontée du toit de SG5 dans les argilites de couverture du sel, d’abord lente, puis rapide jusqu’à parvenir au contact de la Dolomie de Beaumont (Figure 3c). L’exploitant a alors pris la décision de provoquer l’effondrement en abaissant volontairement le niveau de saumure pour maintenir un matelas d’air au sommet de la cavité. L’événement s’est finalement produit en mars 1998, entrainant la formation d’un cratère en surface d’une cinquantaine de mètres de diamètre et d’une profondeur de 120 m [Buffet 1998]. La cheminée s’est ensuite partiellement comblée par talutage des bords du cratère. Le cratère était initialement sec après l’effondrement ; il s’est ensuite rempli d’eau et était occupé par un lac dont le niveau se situait à environ 30 m de la surface en juin 1998.
Cet effondrement a déstructuré localement la couverture protectrice du gisement salin et mis en communication potentielle diverses unités hydrauliques : le lac de cratère, l’aquifère du Rhétien et les cavités d’exploitation remplies de saumure et de résidus de dissolution. Compte tenu de la diversité lithologique des terrains de couverture, les matériaux qui remplissent la cheminée d’effondrement sont hétérogènes avec une dominante argileuse. Leurs propriétés règlent les échanges de fluide et de sel dissous entre ces unités.
Cette expérience vécue a motivé le groupe Salins à envisager de reprendre la lixiviation du panneau jusqu’à effondrement des cavités encore stables dans le double but d’accroitre la production de sel mais surtout de mettre le site en sécurité sur le long terme.
Actuellement le lac présente une superficie d’environ 1,7 ha ; il devrait s’étendre jusqu’à 36 ha à terminaison après reprise de l’exploitation. Une fois la totalité des effondrements obtenus, le système évoluera vers une nappe salée en profondeur et un lac en surface reliés hydrauliquement par les terrains saturés peu perméables remplissant une cheminée d’effondrement. La nappe salée sera confinée au sein de la formation salifère grâce à la forte densité de la saumure qui empêchera toute circulation convective malgré la présence d’un gradient thermique, dans la mesure où le lac constituera un plan d’eau unique n’engendrant pas de gradient hydraulique dans le système.
2. Examen du comportement à long terme
2.1. La diffusion, un mécanisme potentiel de l’émission de sel
On considère ici le cas de la situation « après-mine », à long terme, lorsque la configuration du site sera stabilisée. L’origine du sel pouvant polluer le Rhétien sera la saumure saturée présente dans les cavités. Cette saumure dense ne pourra pas circuler par convection mais elle pourrait être une source de sel dissous se déplaçant par diffusion à travers les matériaux de la cheminée d’effondrement vers les eaux plus douces du lac. On peut évaluer le flux de diffusion au moyen du modèle simple suivant (Figure 4).
Schéma conceptuel de la diffusion du sel dans la cheminée d’effondrement vers le Rhétien.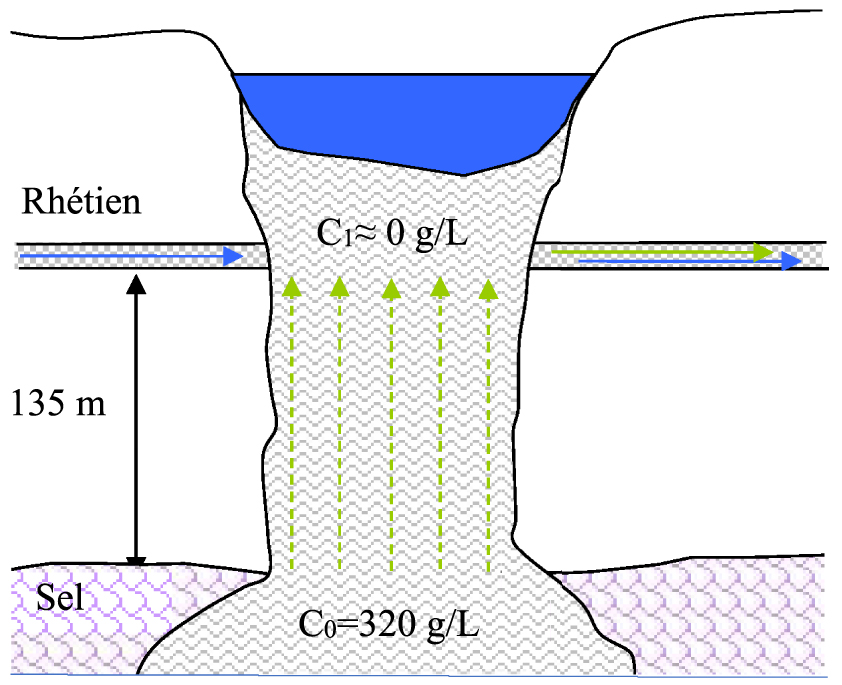
Les matériaux de la cheminée sont supposés homogènes avec un coefficient de diffusion effectif D moyen pour les différents solutés. Une condition à la limite de concentration à saturation à la valeur C0 de 320 g/L est imposée par la nappe salée à la base de la cheminée qui pénètre dans la couche de sel, tandis qu’une faible concentration de valeur C1 est maintenue au niveau du Rhétien sous l’effet de l’écoulement de la nappe qui dilue le sel. Dans ces conditions la densité de flux diffusif en régime stationnaire est donnée par la loi de Fick :
Le coefficient de diffusion effectif dans les matériaux remplissant la cheminée est majoré par le coefficient de diffusion dans l’eau libre dont la valeur est de l’ordre de 10−9 à 2 × 10−9 m2/s. Nous avons considéré une réduction d’un facteur 10 du fait de la présence de solides qui gênent la diffusion et avons adopté la valeur de 2 × 10−10 m2/s pour le calcul du flux surfacique de sel :
Pour une cheminée d’effondrement de 36 ha, on obtient un flux annuel de 5 à 6 tonnes de sel. Ce flux diffusif est évacué dans l’aquifère du Rhétien sous l’effet de l’écoulement de la nappe.
2.2. L’osmose chimique, un autre mécanisme
La Mission Régionale de l’Autorité environnementale qui a évalué le dossier présenté par le groupe Salins a remis un avis en octobre 2018, à la requête du Préfet de Meurthe-et-Moselle et a fait remarquer que les phénomènes osmotiques n’étaient pas considérés et pouvaient présenter un risque potentiel vis-à-vis de la stabilité à long terme.
La présente note expose quelques réflexions sur la nature de ce phénomène et sur le rôle qu’il pourrait éventuellement jouer dans la configuration de l’exploitation envisagée par les Salins.
Il est fait, dans un premier temps, appel aux bases théoriques de l’osmose chimique. On s’intéresse dans un second temps à la manière dont la théorie peut être utilisée dans le contexte particulier de l’exploitation saline, afin de dégager des ordres de grandeur des conséquences que l’on peut attendre du phénomène. Enfin, une confrontation avec des observations de terrain fournira des éléments de validation de l’approche retenue.
3. Les bases théoriques de l’osmose chimique
L’osmose chimique ou chemo-osmose désigne le mouvement de l’eau se produisant au travers d’une membrane semi-perméable dont les faces sont baignées par des solutions ioniques de concentrations différentes. Une telle membrane est dite parfaitement semi-perméable lorsqu’elle autorise le passage des molécules d’eau mais s’oppose totalement au transfert des ions. L’eau traverse ainsi la membrane depuis la zone où la concentration est faible vers la zone à forte concentration de façon à provoquer une diminution du gradient de concentration par effet de dilution.
En pratique, les membranes ne sont qu’imparfaitement semi-perméables et laissent passer les ions à des vitesses variables selon leurs propriétés ; on désigne par diffusion ce type de transfert au cours duquel les ions de la solution passent de la zone de concentration élevée à la zone de concentration faible. Ainsi, pour les deux types de mécanismes, osmose et diffusion, l’effet est de tendre vers une homogénéisation des concentrations de part et d’autre de la membrane.
Le schéma de la Figure 5 [Rousseau-Gueutin 2008], décrit ces phénomènes dans les cas d’une membrane parfaite et imparfaite.
Illustration de la diffusion et de l’osmose chimique dans un tube en U [d’après Rousseau-Gueutin 2008].
Le schéma met en évidence une différence de pression entre les deux branches du tube en U, dite pression osmotique. Dans le cas d’une membrane parfaite, la différence de pression liée à l’activité chimique engendre un écoulement, conforme à la loi de Darcy, à contre-courant de l’écoulement osmotique et le système s’équilibre lorsque les flux d’eau osmotique et darcéen sont égaux pour la pression osmotique correspondant à la différence de concentration résiduelle entre les deux branches du tube. Dans le cas d’une membrane imparfaite, la présence de la pression osmotique n’est que transitoire car l’écoulement darcéen et la diffusion tendent à homogénéiser la concentration ; l’état final se traduit alors par l’égalité des pressions et des concentrations dans les deux branches. La durée de cette phase transitoire dépend de la perméabilité de la membrane.
On note donc que l’état final du système est particulièrement dépendant des propriétés de la membrane. Il dépend également du comportement de la source d’ions comme cela sera mis en évidence lors de l’application à un gisement salifère.
3.1. Le modèle thermodynamique
La thermodynamique des phénomènes irréversibles fournit un cadre théorique pour modéliser les phénomènes de couplage multi-physiques à l’échelle macroscopique. Cette théorie postule que, de manière générale, le flux d’une grandeur est relié de façon tensorielle à une force motrice par l’intermédiaire d’une matrice de coefficients phénoménologiques. Les différentes forces motrices s’expriment, elles-mêmes, sous forme du gradient d’un champ scalaire correspondant aux différentes variables d’état du système.
Le tableau 1 suivant rassemble les différentes forces et flux entrant en ligne de compte dans les problèmes de mécanique des fluides concernés par les phénomènes chimiques, thermiques et électriques.
Mécanismes couplés reliant forces et flux
| Forces | ||||
|---|---|---|---|---|
| Flux | Gradient de charge ou de pression | Gradient de potentiel électrique | Gradient de concentration | Gradient de température |
| Vitesse d’écoulement | Loi de Darcy | Electro-osmose | Osmose chimique | Osmose thermique |
| Densité de courant électrique | Courant de filtration | Loi d’Ohm | Courant de diffusion | Effet Seebeck |
| Flux de soluté | Osmose inverse | Electrophorèse | Loi de Fick | Effet Soret |
| Flux de chaleur | Filtration de la chaleur | Effet Peltier | Effet Dufour | Loi de Fourier |
Les mécanismes couplés diagonaux sont dits dominants et correspondent aux phénomènes classiquement pris en compte en physique. Les mécanismes non-diagonaux traduisent les transferts non-dominants qui ne jouent un rôle notable que dans des configurations particulières ; l’osmose chimique en fait partie.
Les coefficients phénoménologiques reliant chaque flux à chaque force ne sont pas prédits par la théorie macroscopique. Ils peuvent être estimés par changement d’échelle à partir d’autres modèles considérant l’aspect microscopique des milieux ou, le plus souvent, empiriquement au moyen d’expériences réalisées à la bonne échelle [Gonçalvès and Trémosa 2010].
3.2. Le cas des matériaux argileux
Selon Gonçalvès et al. [2015], dès les années 60, les expérimentateurs travaillant sur les milieux poreux avaient mis en évidence des écarts à la loi de Darcy dans les matériaux argileux, une des raisons principales évoquées étant l’existence d’un effet osmotique en présence de fluides salins. Les connaissances sur le sujet se sont développées à partir des années 90, notamment à la faveur des études sur le stockage des déchets radioactifs dans les formations argileuses peu perméables. Notons que ces études concernaient essentiellement des matériaux préparés artificiellement ou remaniés, à l’échelle de l’échantillon de laboratoire ; très peu portaient sur des matériaux naturels et encore moins en conditions in situ. A l’échelle d’une couche géologique de 130 m d’épaisseur à 500 m environ de profondeur, l’Andra a mis en évidence des surpressions dans les argilites du Callovo-Oxfordien en Meuse/Haute-Marne. Le rôle de l’osmose chimique a été évalué et il apparaît, sans que cela soit démontré de manière définitive, qu’une part de ces surpressions pourraient être dues aux phénomènes osmotiques [Rousseau-Gueutin 2008, Gonçalvès et al. 2015, Gueutin et al. 2007].
L’origine de l’effet osmotique dans les argiles est expliquée par le fait que la surface des minéraux argileux qui est chargée négativement impose des restrictions électriques sur les ions lors de leur transport, entrainant une concentration des cations près de la surface et une exclusion des anions vers le centre des pores. Pour respecter la neutralité électrique la restriction sur le transport des anions se répercute sur les cations, ce qui limite le transport ionique total à l’instar de ce que ferait une membrane imparfaite. Les charges de surface sont plus facilement compensées lorsque la force ionique de la solution est élevée et l’effet est d’autant plus important que l’épaisseur des couches électrostatiques se rapproche de la taille des pores. On conçoit ainsi que l’efficacité du mécanisme osmotique soit liée à la nature des minéraux argileux, à la taille des pores ainsi qu’à la concentration des solutions. Les roches argileuses peu perméables, telles que les argilites du Callovo-Oxfordien, sont caractérisées par des dimensions porales de quelques nanomètres comparables à celles des couches électrostatiques, ce qui explique l’occurrence des phénomènes osmotiques dans ces systèmes.
En résumé, l’existence de l’effet osmotique dans les matériaux argileux est établie ; la question est de savoir quelle peut-être son intensité dans la configuration qui nous occupe.
3.3. Les lois et les paramètres
Gonçalvès et al. [2015] ont dressé une synthèse très détaillée des couplages dans les membranes et les matériaux argileux. Il ressort de cette synthèse que les relations phénoménologiques représentant le couplage entre l’écoulement obéissant à la loi de Darcy, l’effet osmotique et le transport par convection–diffusion à l’échelle macroscopique s’écrivent de la façon suivante, en régime stationnaire :
| (1) |
La pression osmotique π est donnée par la formule de Van’t Hoff où R (J/mol/K) est la constante des gaz parfaits, T la température Kelvin et 𝜈 le nombre d’ions séparés (2 pour NaCl).
On remarque l’existence de deux vitesses pour l’eau, la vitesse de Darcy V classique, engendrée par le gradient de charge hydraulique et la vitesse osmotique V′ engendrée par la pression osmotique, donc par le gradient de concentration. Seule la vitesse de Darcy intervient sur le transport de soluté puisque le phénomène osmotique ne déplace que les molécules d’eau. Le phénomène osmotique n’est donc pas susceptible de provoquer le déplacement des ions.
Un paramètre essentiel est le coefficient d’efficacité osmotique 𝜀 (sans dimension) qui varie entre 0 et 1. Dans le cas d’une membrane parfaite, ce coefficient vaut 1 et le coefficient de diffusion est alors nul, traduisant l’absence de transport ionique. Il est inférieur à 1 pour les milieux naturels en fonction de leur caractère plus ou moins semi-perméable. Dans de tels milieux les trois paramètres fondamentaux sont la perméabilité, le coefficient de diffusion effectif et le coefficient d’efficacité osmotique. Leur détermination est expérimentale, à l’aide de systèmes nécessitant une métrologie particulièrement pointue et, s’agissant de coefficients macroscopiques, leur valeur est influencée par l’échelle du problème traité.
Des considérations théoriques [Bresler 1973] établissent que le coefficient d’efficacité osmotique est une fonction décroissante du produit de la taille des pores du milieu par la racine carrée de la concentration. Gonçalvès et al. [2015] ont rassemblé sur une même figure (Figure 6) les mesures disponibles dans la littérature en fonction de ces paramètres en regard de la courbe théorique de Bressler.
Coefficient d’efficacité osmotique en fonction de . b est la taille moyenne des pores en nm et C la concentration en mol/L. ⊞ représentent les valeurs expérimentales pour l’argilite de Bure [d’après Gonçalvès et al. 2015].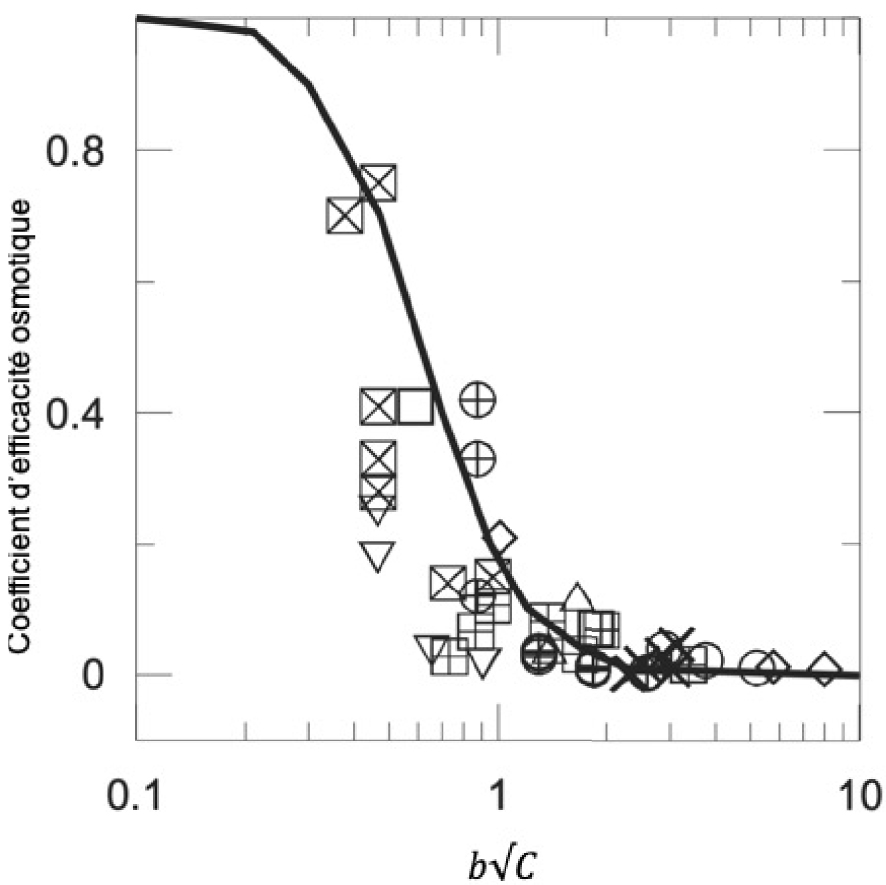
Ces données montrent que le coefficient d’efficacité osmotique mesuré est en général faible avec des valeurs en assez bon accord avec la courbe théorique. Notons que les points relatifs aux argilites de Bure, très compactes, se situent dans les faibles valeurs.
La théorie rend également compte de la dépendance du coefficient de diffusion avec le coefficient d’efficacité osmotique. La Figure 7 tirée de Rousseau-Gueutin [2008], d’après les travaux de Revil et al. [2005] et Gonçalvès et al. [2007], indique l’allure de cette dépendance, établie pour un matériau composé d’une argile de type smectite. On remarque qu’elle est peu marquée pour les faibles valeurs de l’efficacité osmotique, ce qui suggère que l’osmose a peu d’effet sur le transport diffusif de soluté ionique dans les milieux qui se comportent comme des membranes imparfaites.
Variation du coefficient de diffusion effectif en fonction du coefficient d’efficacité osmotique pour une smectite en présence d’une solution NaCl [Rousseau-Gueutin 2008].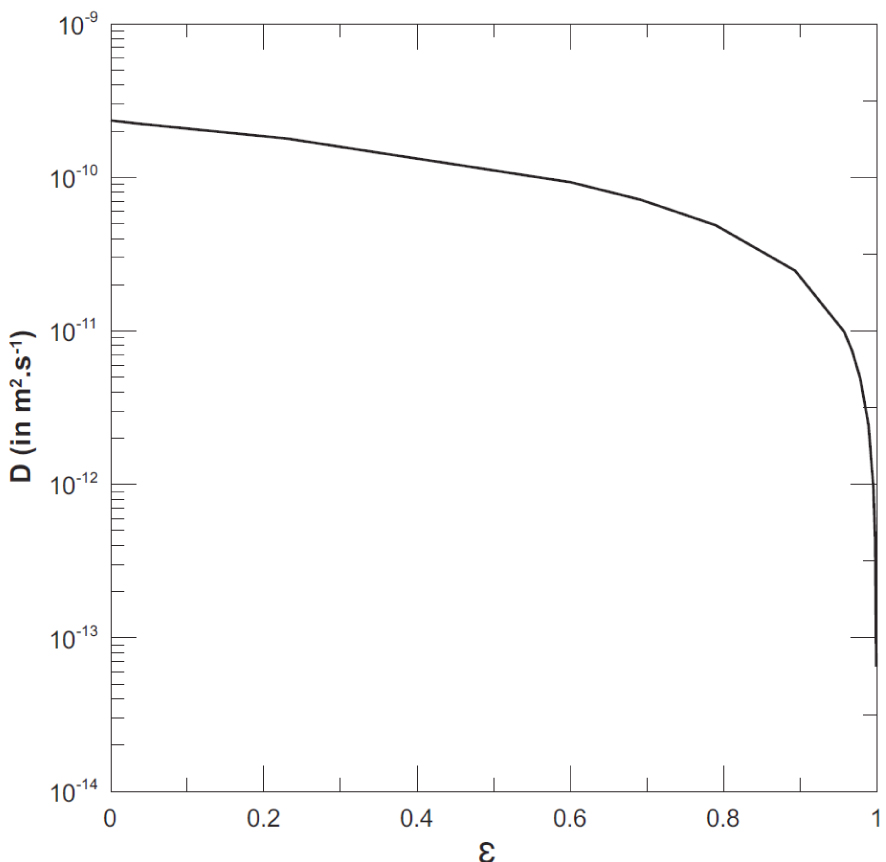
3.4. Application à une cavité saline
Dans le but d’appliquer ce qui précède à la situation d’une cavité saline effondrée, nous retiendrons les éléments suivants :
- il est prouvé que des phénomènes d’osmose chimique peuvent se manifester dans les matériaux argileux. Ceci est lié aux propriétés électriques de surface des minéraux argileux et à la faible dimension des pores qui confèrent aux milieux argileux un comportement de membrane semi-perméable imparfaite ;
- à l’échelle macroscopique, le phénomène est gouverné par un coefficient d’efficacité osmotique variant entre 0 et 1 qui pondère l’influence de la pression osmotique dans la relation phénoménologique qui décrit le flux d’eau ;
- le coefficient d’efficacité osmotique est très variable, de mesure complexe et incertaine, et n’a été que rarement évalué dans les milieux naturels ;
- le coefficient d’efficacité dépend de la taille des pores et de la concentration, ce qui rend le phénomène non-linéaire donc difficile à quantifier par une approche simple car la taille des pores n’est pas un paramètre directement accessible ;
- les matériaux remplissant la cheminée d’effondrement des cavités salines sont pour l’essentiel des matériaux argileux déstructurés dont la porosité est accrue par rapport à celle d’une argilite en place, ce qui conduit à une augmentation relative de la taille moyenne des pores. De plus les concentrations en sel sont très élevées, tout au moins en partie basse du système. Ces éléments sont en faveur d’une valeur très faible du coefficient d’efficacité osmotique si on les compare aux connaissances acquises sur les argilites du Callovo-Oxfordien de Bure qui sont considérées comme bien caractérisées et ayant des pores de très faibles dimensions. L’hypothèse qui consiste à considérer que le remplissage de la cheminée est constitué d’argile homogène conduit ainsi à majorer le rôle des mécanismes d’osmose, ce qui va dans le sens de la sécurité dans l’appréciation du danger ;
- le phénomène osmotique ne modifie pas le transport de soluté ionique au sein du milieu, qui reste dépendant du mécanisme de convection–diffusion.
4. Modélisation exploratoire du comportement d’une cavité effondrée
Dans le but de quantifier l’effet potentiel de l’osmose sur le comportement d’une cavité saline effondrée, nous avons tenté une modélisation simple sur la base du schéma conceptuel de la Figure 4.
4.1. Principes du modèle
Les hypothèses sont les suivantes :
- les transferts sont considérés s’effectuer de façon monodimensionnelle verticale entre la cavité effondrée profonde et le système aquifère du Rhétien, au travers de la cheminée sur 135 m de hauteur ;
- la concentration en profondeur est maintenue par la dissolution du sel à 320 g/L, soit 5480 mol/m3. Elle est imposée à 0 g/L au niveau du Rhétien. Ceci fixe le gradient de concentration à la valeur 0,04 mol/L/m ;
- le système est représenté en régime stationnaire, dans deux configurations distinctes de conditions aux limites hydrauliques illustrées sur la Figure 8
- configuration 1 : la cavité est en relation hydraulique avec d’autres cavités dont le niveau de saumure est maintenu constant ; c’est actuellement le cas à Gellenoncourt, où l’effondrement du panneau exploité n’est que partiel. On considèrera un équilibre hydrostatique entre le Rhétien et la cavité ;
- configuration 2 : la cavité effondrée est confinée, sans échange hydraulique possible avec le milieu extérieur ; cette configuration est censée représenter l’état final lorsque l’ensemble du panneau sera effondré sur environ 36 ha ;
- dans les deux configurations le profil de concentration à l’équilibre dans la cheminée est considéré comme diffusif avec un gradient constant entre 320 et 0 g/L.
Configurations de simulation (à gauche cavité connectée, à droite cavité isolée).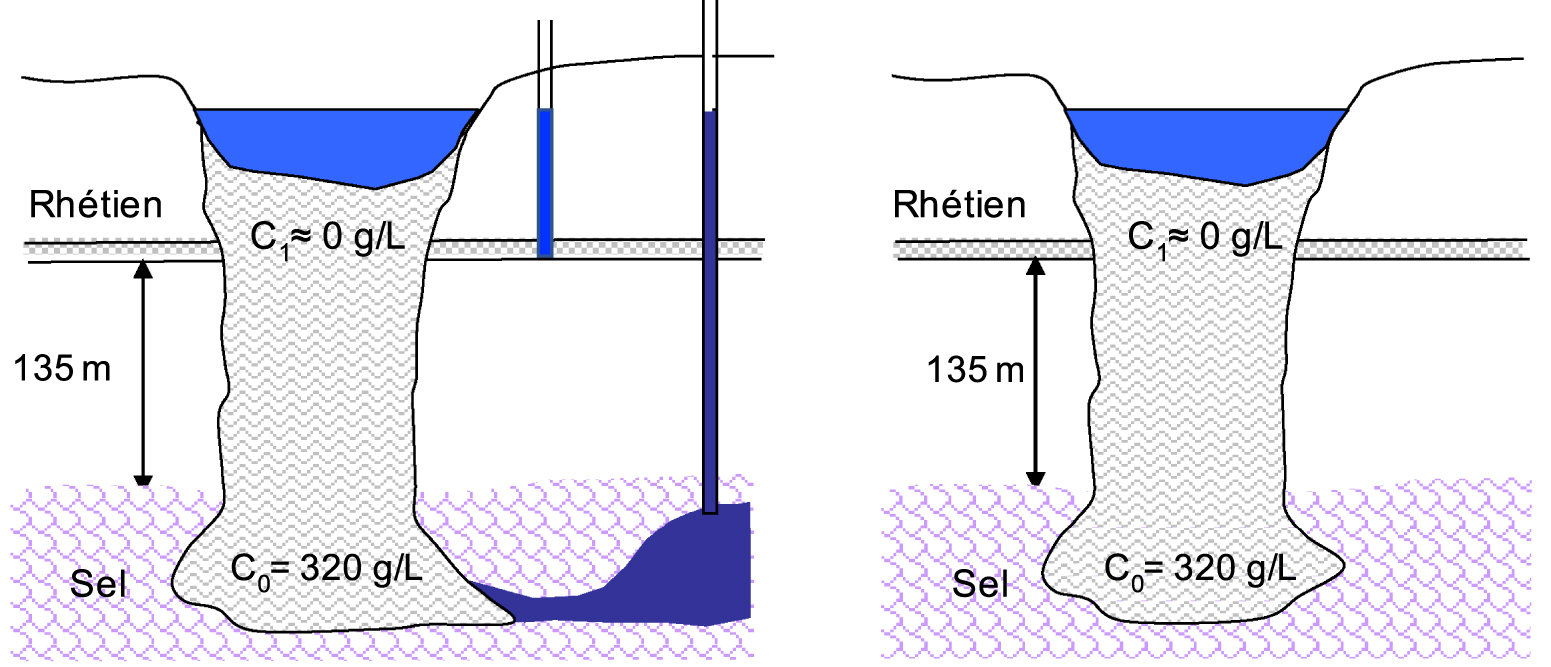
Sous ces hypothèses le système d’équations (1) se simplifie en (2)
| (2) |
Le système d’équations (2) est non linéaire car le coefficient d’efficacité osmotique dépend de la concentration. La résolution numérique par différences finies fournit le profil de charge dans la cheminée et permet le calcul des flux d’eau et de sel échangés entre la cavité et l’aquifère rhétien.
4.2. Choix des paramètres
La perméabilité de Darcy K et le coefficient de diffusion effectif D ont été fixés respectivement aux valeurs 10−10 m/s et 2 × 10−10 m2/s. Remarquons que dans le cas où ces paramètres sont constants sur la verticale, ils n’ont pas d’influence sur le profil de charge calculé. Ils interviennent par contre de manière linéaire sur les flux d’eau et de sel. Nous considérons que les valeurs choisies sont dans la gamme haute et que les flux seront ainsi évalués de façon majorante.
Comme indiqué précédemment, le paramètre essentiel du phénomène osmotique est le coefficient d’efficacité osmotique 𝜀. Nous l’avons estimé à partir de la courbe de Bressler (cf. Figure 6) en considérant une taille de pores moyenne de 10 nm et un profil de concentration linéaire dans la cheminée entre 320 et 0 g/L. Cette taille de pores a été fixée arbitrairement par référence à la valeur 4 nm présentée par Rousseau-Gueutin [2008], pour les argilites du Callovo-Oxfordien de Bure. Il est très probable qu’elle soit largement sous-estimée si l’on considère que la porosité des matériaux argileux déstructurés de la cheminée doit être notablement accrue par rapport à celle d’argilites compactes. Par comparaison, les argiles de surface de l’Albien dans l’Aube présentent des tailles de pores entre 50 et 80 nm.
Avec ces hypothèses, choisies délibérément pour majorer les effets osmotiques, les valeurs du coefficient d’efficacité osmotique s’échelonnent entre 10% en partie supérieure où la concentration est faible et 0,01% en partie inférieure où la saumure atteint la saturation (Figure 9). Afin d’obtenir une appréciation de la sensibilité à ce paramètre, une simulation a également été réalisée en adoptant une valeur homogène de 1% le long du profil.
Profil du coefficient d’efficacité osmotique en fonction de la profondeur pour une taille de pores de 10 nm.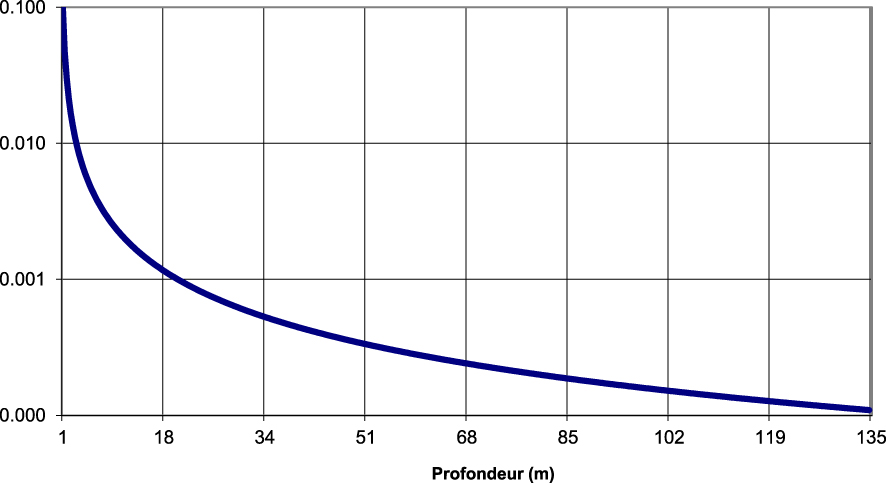
4.3. Résultats des simulations
Les Figures 10 et 11 montrent les profils de surcharge hydraulique calculés pour les deux configurations de conditions aux limites du modèle. La surcharge représente la différence de charge hydraulique le long du profil par rapport à la charge du Rhétien considérée comme référence.
Configuration 1, profils de surcharge hydraulique en fonction de la profondeur calculés avec un coefficient d’efficacité osmotique variable (en bleu) et constant (en rouge).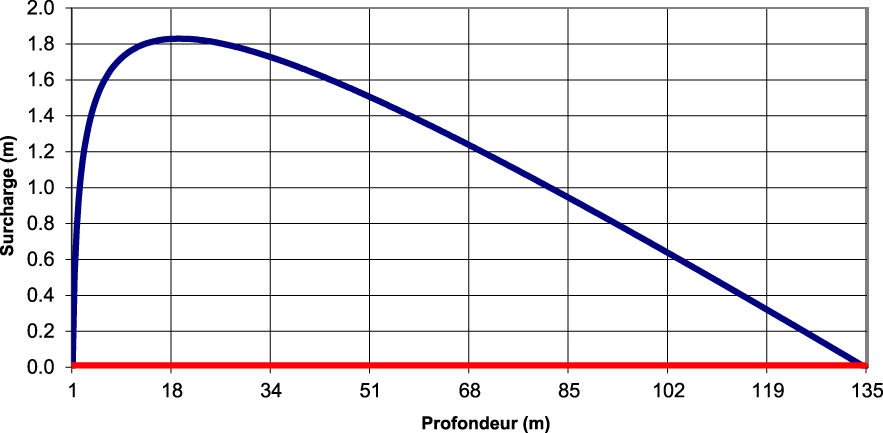
Configuration 2, profils de surcharge hydraulique en fonction de la profondeur calculés avec un coefficient d’efficacité osmotique variable (en bleu) et constant (en rouge).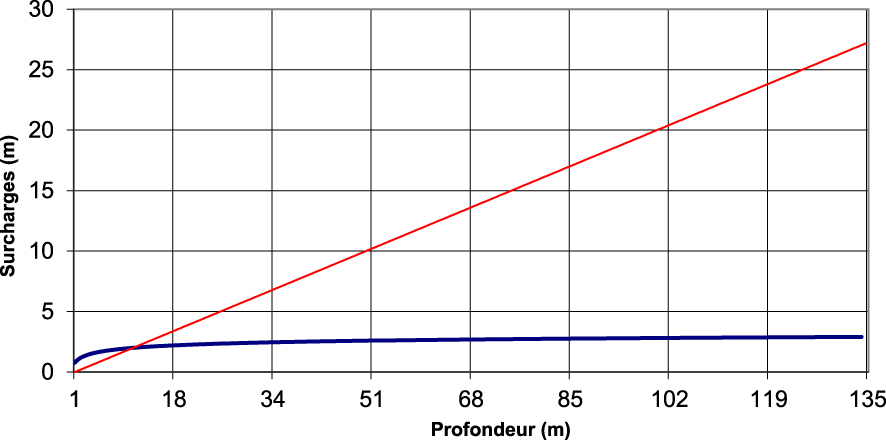
Dans le cas de la configuration 1 où la cavité est connectée au système aquifère, une charge hydraulique de 0 m est arbitrairement imposée en haut et en bas de la cheminée. Le modèle calcule donc une surcharge par rapport à la charge hydrostatique. On constate que l’effet osmotique ne déforme le profil de charge que si le coefficient d’efficacité osmotique est variable en fonction de la profondeur. On retrouve ainsi les résultats de Rousseau-Gueutin [2008], et Gonçalvès et al. [2007]. Dans les deux cas, la cheminée est parcourue par un flux d’eau descendant, dont les vitesses sont respectivement de 2,2 × 10−12 m/s et 2,02 × 10−11 m/s. Ce flux est uniquement la conséquence de l’effet osmotique ; il est évacué vers l’extérieur par la condition aux limites de niveau constant imposée à la base de la cheminée. Notons qu’une interprétation en termes purement « darcéens » du profil déformé conduirait à une évaluation erronée des intensités et des orientations des flux.
Dans le cas de la configuration 2 où la cavité est totalement confinée, aucun flux d’eau ne peut parcourir la cheminée en régime stationnaire, de telle sorte que la charge s’élève avec la profondeur pour compenser la pression osmotique. La surcharge atteint ainsi 2,9 m ou 27 m au niveau de la cavité, selon le profil de coefficient d’efficacité osmotique adopté. De telles surcharges ne mettraient pas en danger la stabilité mécanique de la cavité compte tenu de la profondeur du recouvrement. Rappelons que les valeurs de coefficients d’efficacité osmotique sont certainement choisies par excès.
4.4. Bilan en sel de la cavité
Les simulations précédentes permettent de quantifier le flux de sel évacué à partir de la cavité dans les différentes configurations.
Ce flux comporte deux composantes :
- une composante par diffusion engendrant un flux vers le haut de la cheminée. Cette part de flux est indépendante de l’effet osmotique dans la mesure où le coefficient de diffusion n’est que très peu influencé par cet effet pour les faibles valeurs de coefficient d’efficacité osmotique considérées (cf. Figure 7) ;
- une composante, dite « convective », liée au flux d’eau descendant qui atteint la cavité sous l’effet de l’osmose dans le cas de la configuration 1 où celle-ci est connectée hydrauliquement au milieu extérieur. Remarquons que ce flux est constitué d’eau douce mais qu’il se charge en sel à saturation lorsqu’il atteint la formation salifère. On considèrera que la masse de NaCl dissoute par 1 L d’eau pure est de 355 à 360 g pour une saumure saturée à 320 g/L de masse volumique 1220 kg/m3.
Le Tableau 2 indique ces différents flux pour une cheminée d’effondrement de 36 ha, telle que cela devrait être le cas à terminaison de l’exploitation du panneau de Gellenoncourt.
Rappelons les valeurs adoptées pour la perméabilité de Darcy et le coefficient de diffusion, qui sont respectivement de 10−10 m/s et 2 × 10−10 m2/s. Les flux de sel sont directement proportionnels à ces valeurs.
Bilan annuel en sel à terminaison d’un panneau d’exploitation effondré sur 36 ha
| Configuration 1 | Configuration 2 | |||
|---|---|---|---|---|
| Profil 𝜀 variable 10% → 0,01% | Profil 𝜀 constant 1% | Profil 𝜀 variable 10% → 0,01% | Profil 𝜀 constant 1% | |
| Flux sel diffusif (tonnes/an) | 5,4 | 5,4 | 5,4 | 5,4 |
| Flux sel « convectif » (tonnes/an) | 6,6 | 69 | 0 | 0 |
| Flux sel total (tonnes/an) | 12 | 74 | 5,4 | 5,4 |
| Augmentation de volume de la cavité (m3/an) | 6,5 | 40 | 2,5 | 2,5 |
| Volume de débordement de saumure (m3/an) | 21 | 214 | 0 | 0 |
On notera que le flux diffusif de sel est indépendant de l’effet osmotique mais que le flux convectif est directement lié à cet effet avec une forte sensibilité au profil du coefficient d’efficacité osmotique. La ligne du tableau intitulée « augmentation de volume de la cavité » correspond au volume de sel dissous en profondeur sous l’effet des différents flux. Le volume de débordement de saumure représente la quantité de saumure qu’il faut théoriquement évacuer pour annuler la surcharge engendrée dans la cavité par l’effet osmotique.
En complément des processus de diffusion et d’osmose invoqués ci-dessus, l’expérience montre que les cavités salines profondes sont soumises au fluage du massif salifère environnant qui engendre des remontées de pression ou des débordements de saumure selon que la cavité est maintenue fermée ou ouverte [Brouard et al. 2017]. Ce mécanisme n’apparait pas devoir jouer un rôle important dans le cas qui nous occupe car les cavités sont peu profondes et se trouvent auto-remblayées par les matériaux issus de la cheminée d’effondrement. Des mouvements de terrain sont cependant susceptibles d’exister pour compenser l’augmentation de volume engendrée par la dissolution en profondeur sous l’effet du flux convectif d’eau douce provoqué par l’osmose. Ces mouvements seraient toutefois très lents étant donné les faibles volumes en jeu et concerneraient en priorité la profondeur du lac.
5. Les observations sur site et conclusion
La Figure 12 illustre la configuration actuelle du panneau de Gellenoncourt où l’effondrement de deux cavités coalescentes (SG4 et SG5) en 1998 a créé une cheminée débouchant en surface sur un cratère, occupé par un lac dont le diamètre initial était de 50 m, soit une superficie de 0,2 ha. Cette superficie a ensuite évolué avec le temps pour atteindre actuellement 1,7 ha sous l’effet du talutage naturel des terrains. La figure montre que la partie effondrée des cavités se trouve en relation hydraulique directe avec d’autres cavités non effondrées dont le niveau de saumure est contrôlé par des forages d’exploitation. Ce schéma correspond à la configuration no 1 du modèle développé ci-dessus. La simulation indique que le volume annuel de saumure qu’il faudrait évacuer pour empêcher le débordement dans les forages s’élèverait entre 0,1 et 1 m3 selon l’hypothèse sur le coefficient d’efficacité osmotique, en considérant la valeur de 0,2 ha pour la superficie de la cheminée d’effondrement. De tels volumes passeraient inaperçus face aux différentes opérations de pompage ou de purge réalisées dans le gisement pour les besoins de l’exploitation. On peut noter que les forages du champ de Gellenoncourt sont restés ouverts entre 1998, date de l’effondrement et 2002, date de reprise de l’exploitation et qu’aucune variation de niveau n’y a été constatée.
Schéma conceptuel de l’exploitation actuelle de Gellenoncourt.
En conclusion, les évaluations quantitatives qui précèdent sont issues d’une approche théorique du problème. Elles mettent en évidence la sensibilité de la chemo-osmose au coefficient macroscopique d’efficacité osmotique dont la valeur reste mal appréhendée pour les milieux naturels, aux échelles pertinentes.
Une application de la théorie avec des valeurs de ce coefficient choisies de façon majorante par référence à une argilite compacte bien documentée telle que celle investiguée par l’Andra sur le site du projet de stockage géologique de déchets radioactifs, montre que l’effet osmotique chimique n’est pas susceptible de modifier notablement les ordres de grandeur des flux de sel évacués dans l’environnement par une exploitation intensive d’une couche salifère, telle qu’envisagé par le groupe Salins à Gellenoncourt.
D’une manière générale, les observations de terrain sur les sites qui exploitent le gisement de sel en couches du plateau lorrain indiquent qu’il n’a jamais été constaté de surpression inexpliquée dans la nappe salée créée par dissolution au sein de la formation salifère alors que des cheminées d’effondrement, comblées de matériaux argileux, mettent en contact la saumure saturée profonde avec les eaux douces du système aquifère superficiel. Ceci est cohérent avec l’approche théorique présentée qui montre que les phénomènes osmotiques ne sont pas susceptibles d’engendrer des perturbations de caractère exceptionnel par rapport aux différentes perturbations inhérentes aux pratiques d’exploitation du gisement de sel par dissolution.
Conflit d’intérêt
Les auteurs n’ont aucun conflit d’intérêt à déclarer.



 CC-BY 4.0
CC-BY 4.0