1 Introduction
L'étude des écoulements souterrains et du transport de matière repose sur une description des processus et du milieu à de nombreuses échelles liées aux appareils et méthodes de mesure, à la discrétisation spatiale nécessaire aux modèles numériques et aux hétérogénéités du réservoir [3,15]. Ainsi, les paramètres hydrodynamiques et de transport tels que la perméabilité et la dispersivité doivent pouvoir être évalués aux échelles pertinentes.
De nombreux travaux théoriques récents [15,17] traitent de l'estimation des paramètres équivalents à partir d'une description stochastique des conductivités hydrauliques du milieu naturel, dans un domaine suffisamment étendu pour y inclure plusieurs longueurs de corrélation ou échelles « intégrales » caractérisant la covariance de la distribution de la log-conductivité hydraulique. Cependant, dans de nombreux cas de contamination des aquifères alluviaux, la zone polluée n'est pas assez étendue pour intégrer un nombre suffisant d'échelles intégrales. Il est alors légitime de se demander si de tels outils peuvent être encore appliqués dans de telles situations.
Le travail de recherche présenté dans cette communication se place dans cette configuration. Son but est d'estimer la perméabilité et la dispersivité d'un milieu homogène équivalent (c'est-à-dire que, soumis aux mêmes conditions aux limites, le milieu « restitue », en moyenne, les variables observées) à partir d'essais de traçage menés en milieu hétérogène. Ces essais sont conduits au laboratoire, ce qui présente de nombreux avantages par rapport aux essais de terrain [8,19] : les mesures sont plus précises et moins coûteuses, les phénomènes non souhaités sont évités, plusieurs échelles d'observation sont possibles, l'hétérogénéité du milieu, les conditions aux limites et initiales sont bien connues et maîtrisées et les expériences peuvent être répétées assez facilement. L'approche expérimentale a été préférée à l'approche numérique, qui, elle aussi, comporte plusieurs difficultés (essentiellement de stabilité et/ou de diffusion artificielle) et qui repose souvent sur des approximations du même ordre que les théories stochastiques (développement à l'ordre 1).
Le support théorique aux expériences réalisées est présenté dans la première partie. La méthodologie expérimentale et les résultats expérimentaux sous différents types d'écoulements (uniforme et radial) font l'objet de la deuxième partie. Ces résultats sont ensuite comparés aux résultats théoriques présentés dans la première partie.
2 Quelques résultats théoriques
Le calcul de la perméabilité équivalente a fait l'objet de plusieurs travaux de synthèse [15,17,20]. Ils concernent surtout les régimes d'écoulement uniforme et, plus récemment, les écoulements radiaux [9,13,18].
Pour les écoulements uniformes, de nombreux auteurs ont vérifié que la perméabilité effective est toujours comprise entre les bornes de Wiener, c'est-à-dire la moyenne arithmétique et la moyenne harmonique des perméabilités locales :
| (1) |
La moyenne arithmétique caractérise la perméabilité équivalente des mailles en parallèle par rapport à la direction de l'écoulement moyen et privilégie les perméabilités locales élevées, tandis que la moyenne harmonique caractérise la perméabilité équivalente des mailles en série, par rapport à la direction de l'écoulement moyen et privilégie les faibles perméabilités.
Cette inégalité (1) est à l'origine de plusieurs études dont le but est de mieux borner la perméabilité équivalente et de proposer une formulation pour le calcul de celle-ci. Citons les bornes de Cardwell et Parsons [2] :
- • la moyenne arithmétique des moyennes harmoniques des perméabilités locales calculées sur l'axe parallèle à l'écoulement principal (selon x) pour la borne inférieure :
(2) - • la moyenne harmonique des moyennes arithmétiques des perméabilités locales calculées pour chaque plan perpendiculaire à l'écoulement principal pour la borne supérieure :
(3)
Matheron [12] propose une moyenne pondérée des bornes de Wiener comme approximation au premier ordre de la perméabilité effective dans la direction u :
| (4) |
Ababou [1] exprime α en fonction de la dimension de l'espace d (1, 2 ou 3), de la longueur de corrélation dans la direction u considérée et de la moyenne harmonique des échelles intégrales :
| (5) |
| (6) |
| (7) |
En écoulement radial, il est souvent impossible de caractériser un milieu hétérogène avec une seule valeur de perméabilité équivalente [7,10,13]. Indelman et al. [10] proposent une solution théorique pour le cas d'un écoulement radial dans un milieu tridimensionnel aléatoire présentant une anisotropie axisymétrique. Dans ce cas, la conductivité équivalente en écoulement radial, , est une combinaison linéaire de la conductivité équivalente en régime uniforme et de la moyenne arithmétique des conductivités locales :
| (8) |
Le coefficient de pondération ξ peut être approché par
| (9) |
Plus récemment, en régime permanent, Riva et al. [18] ont proposé une expression analytique de la transmissivité équivalente, à proximité d'un puits de pompage situé au centre d'un milieu aléatoire hétérogène cylindrique. Au niveau du puits, cette solution est égale à la moyenne harmonique des perméabilités locales. Pour des distances intermédiaires, elle croît vers la moyenne géométrique, à mesure que la taille du domaine croît devant la longueur de corrélation. Pour les grandes distances, elle continue de croître et décroît à proximité de la condition aux limites de Dirichlet, vers une valeur supérieure à la moyenne géométrique.
Enfin, dans le cas tridimensionnel d'un aquifère captif dont l'écoulement est dû à un pompage permanent, la perméabilité équivalente augmente avec l'anisotropie (milieu stratifié) [7]. Ainsi, la perméabilité équivalente ne dépend pas uniquement des perméabilités locales, mais aussi du régime d'écoulement et des conditions aux limites. Les études concernant l'écoulement radial restent peu nombreuses et se réduisent souvent à l'étude d'un cas spécifique, avec des hypothèses simplificatrices du fait de la complexité du problème.
Quant à la macrodispersivité, Dagan [4] distingue la macrodispersivité effective de la macrodispersivité apparente. En écoulement uniforme, pour les grands temps de séjour, les valeurs de macrodispersivité longitudinale et transversale horizontale et verticale tendent vers une même limite asymptotique :
| (10) |
Dans le cas d'un puits d'injection dans un milieu tridimensionnel, la macrodispersivité asymptotique serait trois fois plus petite pour un puits vertical, cinq fois pour une source ponctuelle, que le résultat (10) obtenu en écoulement uniforme [9].
3 Approche expérimentale
3.1 Le dispositif expérimental
MARCEAUS (Modèle d'analyse et de recherche sur la contamination des eaux souterraines – Fig. 1) est un modèle tridimensionnel de dimensions . Il contient un milieu poreux hétérogène, borné par deux limites amont et aval aux charges imposées par des déversoirs générant un gradient de charge. Les autres limites sont à flux nuls.
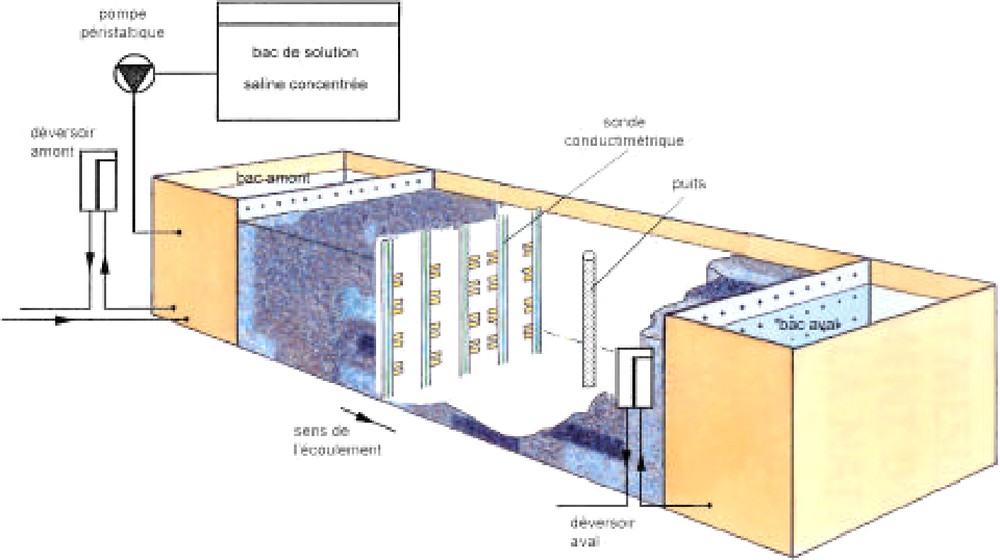
Vue schématique du MARCEAU'S.
Schematic presentation of MARCEAU'S.
Deux zones, à l'amont et à l'aval, remplies avec un sable grossier et homogène, assurent la répartition de l'écoulement dans tout le milieu hétérogène. Ce dernier est constitué d'une distribution aléatoire corrélée des perméabilités, i.e. la logconductivité suit une loi de covariance exponentielle, dans les directions horizontales, définie par :
| (11) |
Perméabilités des sables
Permeabilities of sands
| Milieu aléatoire | ||||||
| Sable | K60 | K40 | K30 | K20 | K10 | K150 |
| K (10−3 m s−1) | 0,20 | 0,70 | 1,20 | 1,40 | 10,0 | 77,0 |
3.2 Les essais de traçage
Trois types d'expérience ont été réalisés (Tableau 2) :
- – en écoulement uniforme (réf. TT1W0 – le chiffre 1 indique le numéro de l'expérience, le chiffre 0 le nombre de puits en fonction), un gradient de charge est imposé entre les bacs amont et aval ; le traceur est injecté dans le bac amont ;
- – en écoulement radial (réf. TT1W1 à TT4W1), un pompage à débit constant est ajouté à l'écoulement uniforme ; le traceur est injecté dans le bac amont ;
- – en injection–pompage (réf. TT1W2 et TT2W2), deux puits sont utilisés pour former un doublet d'injection–pompage à débit constant ; il n'y a pas d'autre écoulement ; le traceur est injecté dans le puits.
Conditions aux limites des expériences réalisées
Boundary conditions of the experiments
| Expérience | Distance de traçage | Puits | Débit dans le(s) puits | Débit à l'aval |
| TT1W0 | 560 cm | – | 0 cm3 min−1 | 1400 cm3 min−1 |
| TT1W1 | 285 cm | W2B | 400 cm3 min−1 | 1000 cm3 min−1 |
| TT2W1 | 285 cm | W2B | 850 cm3 min−1 | 1800 cm3 min−1 |
| TT3W1 | 405 cm | W3B | 770 cm3 min−1 | 1570 cm3 min−1 |
| TT4W1 | 405 cm | W3B | 400 cm3 min−1 | 1500 cm3 min−1 |
| TT1W2 | 240 cm | W1B/W3B | 500 cm3 min−1 | 0 cm3 min−1 |
| TT2W2 | 120 cm | W1B/W2B | 500 cm3 min−1 | 0 cm3 min−1 |
Le traceur choisi est le chlorure de sodium (NaCl). Trois cent cinquante cellules de mesures de conductivité électrique sont implémentées dans la cuve et réparties en 14 sections de cinq tiges supportant chacune cinq cellules (Fig. 2). La concentration est aussi mesurée, le cas échéant, à la sortie du puits de pompage.
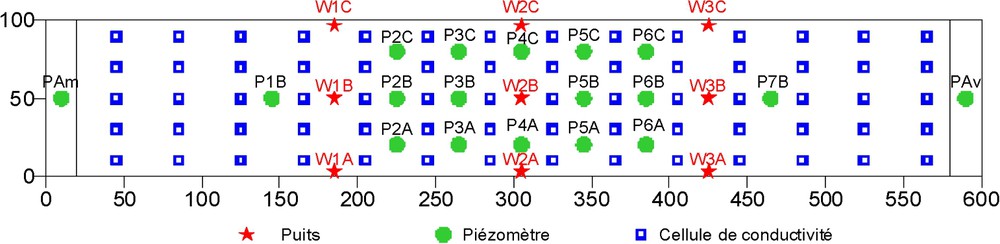
Localisation des puits, des piézomètres et des cellules de conductivité.
Wells, piezometer and conductivity cells location.
Le rabattement dans les puits est de 15 cm en injection pompage et, pour l'expérience TT1W1, de 40 cm pour les autres expériences avec pompage. La localisation des puits est précisée dans le Tableau 2 et la Fig. 2.
3.3 Méthode d'interprétation
En écoulement uniforme, la vitesse et la dispersivité sont déterminées en ajustant un modèle numérique 1D sur les phases transitoires du transport [11]. La méthodologie et les résultats sont détaillés dans [5,6].
Chaque expérience comportant un pompage est simulée à l'aide du logiciel MODFLOW–MT3DMS, en considérant un milieu homogène équivalent. Le milieu poreux est représenté par une seule couche homogène et la nappe est supposée libre. Les maillages sont réguliers avec mailles carrées de 4 cm de côté pour les expériences TT1W1 à TT4W1 et mailles de 2 cm de côté pour les expériences TT1W2 et TT2W2. Chaque maillage est validé en comparant les résultats de simulations avec ceux obtenus avec un maillage deux fois plus fin. La charge à l'amont et à l'aval, ainsi que les débits de pompage et d'injection constituent les conditions aux limites et termes puits/source pour le modèle hydrodynamique.
Pour le transport, la moyenne arithmétique des concentrations mesurées dans la première section de mesure (milieu homogène entre le bac et la section) est utilisée comme condition aux limites amont. On s'affranchit ainsi des incertitudes liées au mélange dans le bac amont.
L'estimation de la perméabilité et de la macrodispersivité est obtenue par calage du modèle numérique sur la concentration à la sortie du puits de pompage : c'est la seule mesure qui intègre un nombre significatif de lignes de courant pour évaluer des paramètres équivalents. Comme pour l'écoulement uniforme, seules les phases transitoires du transport sont utilisées pour ajuster les paramètres.
4 Résultats
En écoulement uniforme, la mesure conjointe des débits et des charges imposées aux extrémités du domaine permet une évaluation expérimentale de la perméabilité équivalente qui est de l'ordre de . Cette valeur est en accord avec l'estimation suggérée par Ababou [1]. L'ensemble des résultats théoriques est regroupé dans le Tableau 3. La valeur expérimentale de la perméabilité est supérieure à la moyenne géométrique des conductivités . Ce constat est en accord avec ceux de Neuman et Orr [14], qui montrent que la conductivité effective tend vers la moyenne arithmétique des perméabilités lorsque les dimensions du domaine tendent vers zéro. La valeur calculée est comprise entre les moyennes géométrique et arithmétique, le nombre d'échelles intégrales (23,1 cm) étant insuffisant dans la direction perpendiculaire à l'écoulement moyen (largeur du modèle égale à 100 cm) pour atteindre la moyenne géométrique.
La macrodispersivité expérimentale asymptotique est de l'ordre de 40 à 50 cm, bien supérieure à celle estimée par l'Éq. (10), qui vaut 23,8 cm. Au-delà de huit échelles intégrales, les valeurs expérimentales ne varient pas significativement avec la distance parcourue et le transport peut être considéré comme fickien [6]. La distance nécessaire à l'établissement d'un régime à dispersivité constante est de l'ordre de grandeur de celle prévue théoriquement. La valeur expérimentale plus élevée que celle prévue théoriquement est probablement due à l'extension transversale limitée de la cuve, qui atténue les fluctuations transversales du champ de vitesse et augmente les effets des fluctuations longitudinales.
En écoulement radial, un jeu de paramètres différent est obtenu pour chaque expérience (Tableau 4). Pour la conductivité hydraulique et la dispersivité, l'ordre de grandeur des paramètres calés (conductivité hydraulique et dispersivité) est le même qu'en écoulement uniforme. La Fig. 3 représente l'évolution de la concentration simulée (symboles) dans le puits pour chaque expérience et la concentration mesurée pour l'expérience TT3W1. Elle permet d'apprécier la très bonne reproduction des observations pour l'expérience TT3W1 par le modèle et les paramètres calés. Cette très bonne reproduction est également obtenue pour les autres expériences. Cette figure montre également que, même si ces paramètres sont du même ordre de grandeur, ils peuvent être considérés comme significativement différents d'une expérience à l'autre.
Paramètres équivalents ajustés numériquement
Numerically fitted equivalent parameters
| Expérience | TT1W0 | TT1W1 | TT2W1 | TT3W1 | TT4W1 | TT1W2 | TT2W2 |
| (10−3 m s−1) | 2,41 | 2,60 | 2,25 | 2,50 | 2,33 | – | – |
| (cm) | 40–50 | 60 | 50 | 30 | 40 | 23 | 20 |
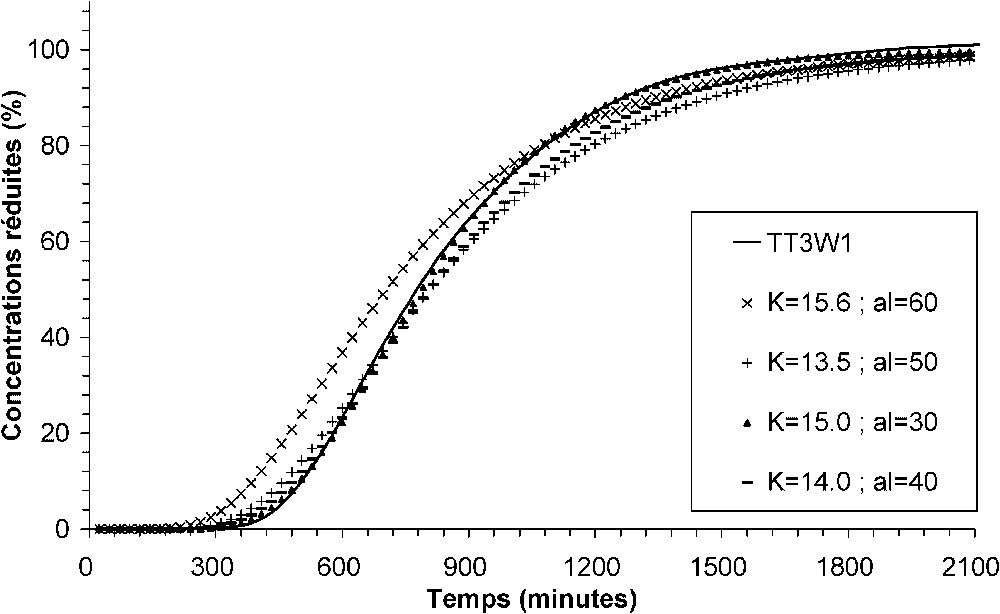
Simulation avec les paramètres ajustés dans les conditions de l'expérience TT3W1.
Simulation with the fitted parameters for boundary conditions of the TT3W1 experiment.
En configuration de doublet, la perméabilité ne peut être déterminée. Elle a été fixée arbitrairement à . Les valeurs de dispersivité obtenues sont 20 et 23 cm pour chacune des deux expériences. Elles sont jusqu'à trois fois plus petites que les autres valeurs expérimentales, conformément aux résultats de Indelman et Dagan [9].
5 Conclusion
Pour les conditions expérimentales étudiées, la modélisation du transport de masse dans un milieu tridimensionnel hétérogène à l'aide d'un milieu bidimensionnel homogène est possible, sous réserve d'utiliser les paramètres équivalents adaptés. Ce résultat n'était pas évident a priori, compte tenu de la faible dimension du domaine par rapport à la longueur de corrélation de la distribution des perméabilités et de la nature de l'écoulement moyen (uniforme, radial, doublet). L'intégration de la troisième dimension de l'écoulement avec des couches non corrélées entre elles au niveau de la distribution des perméabilités assure un effet de prise de moyenne, qui se traduit par un comportement identique à celui d'un milieu 2D, même si la distance parcourue est faible par rapport aux longueurs de corrélation.
L'ordre de grandeur de la conductivité équivalente obtenue est indépendant du type d'écoulement. La dispersivité est supérieure aux valeurs théoriques, probablement à cause des limites imperméables, qui limitent le déplacement transversal du polluant. Cependant, le rapport entre les valeurs obtenues avec un écoulement uniforme et celles obtenues dans la configuration du doublet est conforme aux développements d'Indelman et Dagan [9].
Les différences dans les jeux de paramètres montrent cependant un effet local significatif de la distance source–puits de pompage et du débit de pompage. Dans le cas du doublet, les variations du champ de vitesse sont essentiellement dues à l'hydrodynamique (lignes de courant et temps de parcours du champ moyen des vitesses). Les effets des hétérogénéités locales sont alors moins sensibles, ce qui se traduit par une macrodispersivité plus petite, comparée à celle obtenue en écoulement uniforme.
La généralisation de ces résultats à des milieux de taille limitée par rapport aux longueurs de corrélation est bien sûr prématurée. Les observations menées permettent de nourrir la réflexion sur ce type de configuration, qui, bien que fréquemment rencontré dans les cas de contamination d'aquifères alluviaux, ne bénéficie pas encore de tous les supports théoriques nécessaires.


