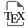Comptes Rendus
Article de recherche - Géométrie algébrique
Fano hypersurfaces in positive characteristic
Yi Zhu1
1 United States
Comptes Rendus. Mathématique, Volume 362 (2024), pp. 107-115.

We prove that a general Fano hypersurface in a projective space over an algebraically closed field is separably rationally connected.

Reçu le :
Accepté le :
Accepté après révision le :
Publié le :
DOI : 10.5802/crmath.438
Yi Zhu 1

1 United States
Licence : CC-BY 4.0
Droits d'auteur : Les auteurs conservent leurs droits 
@article{CRMATH_2024__362_G1_107_0,
     author = {Yi Zhu},
     title = {Fano hypersurfaces in positive characteristic},
     journal = {Comptes Rendus. Math\'ematique},
     pages = {107--115},
     publisher = {Acad\'emie des sciences, Paris},
     volume = {362},
     year = {2024},
     doi = {10.5802/crmath.438},
     language = {en},
}
TY  - JOUR
AU  - Yi Zhu
TI  - Fano hypersurfaces in positive characteristic
JO  - Comptes Rendus. Mathématique
PY  - 2024
SP  - 107
EP  - 115
VL  - 362
PB  - Académie des sciences, Paris
DO  - 10.5802/crmath.438
LA  - en
ID  - CRMATH_2024__362_G1_107_0
ER  - 
%0 Journal Article
%A Yi Zhu
%T Fano hypersurfaces in positive characteristic
%J Comptes Rendus. Mathématique
%D 2024
%P 107-115
%V 362
%I Académie des sciences, Paris
%R 10.5802/crmath.438
%G en
%F CRMATH_2024__362_G1_107_0
Yi Zhu. Fano hypersurfaces in positive characteristic. Comptes Rendus. Mathématique, Volume 362 (2024), pp. 107-115. doi : 10.5802/crmath.438. https://comptes-rendus.academie-sciences.fr/mathematique/articles/10.5802/crmath.438/

[1] Dawei Chen; Izzet Coskun Towards Mori’s program for the moduli space of stable maps, Am. J. Math., Volume 133 (2011) no. 5, pp. 1389-1419 | DOI | MR | Zbl

[2] Tom Graber; Joe Harris; Jason M. Starr Families of rationally connected varieties, J. Am. Math. Soc., Volume 16 (2003) no. 1, pp. 57-67 | DOI | MR | Zbl

[3] Robin Hartshorne Algebraic geometry, Graduate Texts in Mathematics, 52, Springer, 1977 | DOI

[4] Aise J. de Jong; Jason M. Starr Every rationally connected variety over the function field of a curve has a rational point, Am. J. Math., Volume 125 (2003) no. 3, pp. 567-580 | DOI | MR | Zbl

[5] János Kollár Rational curves on algebraic varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, 32, Springer, 1996 | DOI

[6] János Kollár; Yoichi Miyaoka; Shigefumi Mori Rationally connected varieties, J. Algebr. Geom., Volume 1 (1992) no. 3, pp. 429-448 | MR | Zbl

[7] Jason M. Starr Arithmetic over function fields, Arithmetic geometry (Clay Mathematics Proceedings), Volume 8, American Mathematical Society, 2009, pp. 375-418 | MR | Zbl

Cité par Sources :

Commentaires - Politique

Ces articles pourraient vous intéresser

The first cohomology of separably rationally connected varieties

Frank Gounelas

C. R. Math (2014)

Rational curves on Fermat hypersurfaces

Mingmin Shen

C. R. Math (2012)

Bigness of the tangent bundles of projective bundles over curves

Jeong-Seop Kim

C. R. Math (2023)