1 Introduction
Hematopoiesis is the term used to describe the production of blood cells. All blood cells come from a unique source, the hematopoietic stem cells (HSC), but mechanisms regulating this production are not completely understood. Particularly, the regulation of leucopoiesis (production of white blood cells) is not well understood and the local HSC regulation mechanisms are even less clear [1–8]. Because of their dynamical character, cyclical neutropenia and other periodic hematological disorders offer us opportunities to better comprehend the nature of these regulatory processes [9].
Cyclical neutropenia (CN) is a rare hematological disorder characterized by oscillations in the circulating white blood cell (WBC) count. Levels of neutrophils, a type of white blood cell, fall from normal to barely detectable levels with a period of 19 to 21 days in humans [4,10,11] and around 14 days in gray collies [4]. These oscillations in the WBC count about a subnormal level are generally accompanied by oscillations around normal levels in other blood cell lineages such as platelets, lymphocytes and reticulocytes [4,7].
The goal of this paper is to study a simple model of WBC production. We look for mechanisms leading to oscillations in the WBC count and relate these mechanisms to physiological features of the hematopoietic system. We use cyclical neutropenia data from a canine model, the gray collie, which is born with this hematological disorder [12].
The paper is organized as follow. In Section 2, we present the model, which is a simple two-compartment production system. In Section 3, we analyze the model using a combination of analytical and numerical continuation methods. It is shown that the positive steady state can be destabilized by a supercritical Hopf bifurcation and that saddle-node bifurcations of limit cycles exist. In Section 4, we discuss the implications for the physiological system of such instabilities.
2 Model
Fig. 1 illustrates the two cell types of this model represented in the two compartments outlined in bold: the hematopoietic stem cells (HSC) and the maturing WBCs. The HSCs are self-renewing and pluripotential (can differentiate into any blood cell type), and the rate at which they differentiate into the WBC line is assumed to be determined by the level of circulating WBCs. As these WBC precursors differentiate, their numbers are amplified by successive divisions. After a certain maturation time τM, they become mature WBCs and are released into the blood.
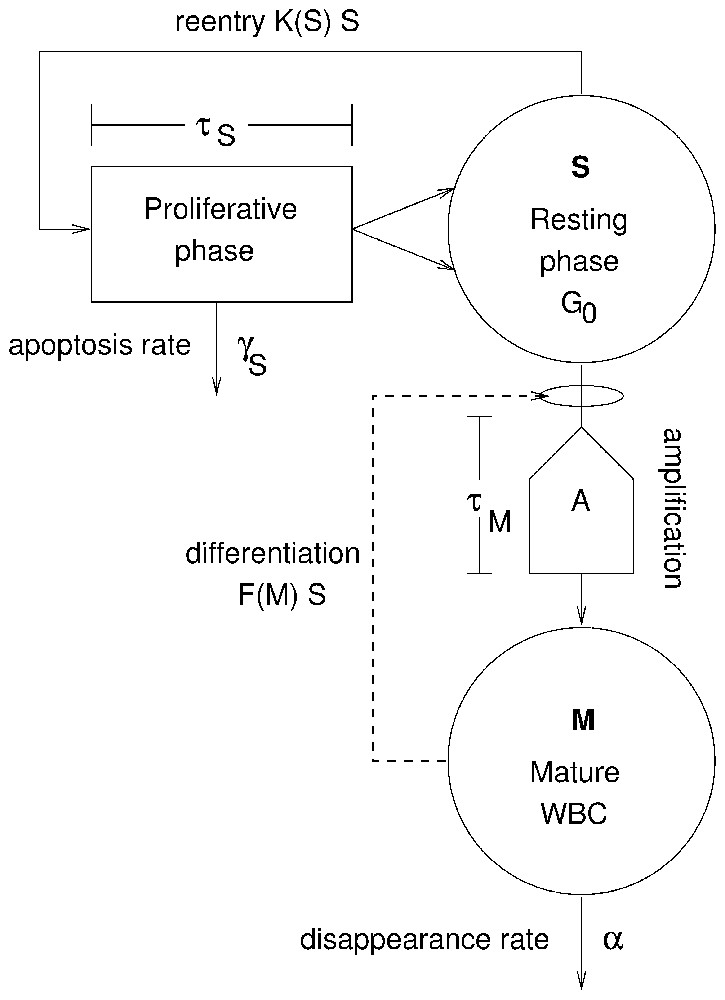
Model of WBC production. The variable S represents the number of hematopoietic stem cells in the resting (G0) phase. Cells in the resting phase can either enter the proliferative phase at a rate K(S) or differentiate at a rate F(M) to ultimately give rise to mature WBCs M, the second variable. Cells in the HSC proliferative phase undergo apoptosis at a rate γS and the cell cycle duration is τS. Cells in the differentiation pathway are amplified by successive divisions by a factor, A, which is also used to account for cell loss due to apoptosis. After a time τM, differentiated cells become mature WBCs M and are released into the blood. It is assumed that mature WBCs die at a fixed rate α. Two feedback loops control the entire process through the proliferation rate K(S) and the differentiation rate F(M). Masquer
Model of WBC production. The variable S represents the number of hematopoietic stem cells in the resting (G0) phase. Cells in the resting phase can either enter the proliferative phase at a rate K(S) or differentiate at ... Lire la suite
As shown in Fig. 1, there are two feedback loops. The first loop is between the mature WBC compartment and the rate F(M) of HSC differentiation into the WBC line. F(M) operates with a delay τM that accounts for the time required for WBC division and maturation, so the flux of cells from the resting phase of the HSC compartment is SτMF(MτM). Here, as elsewhere, the notation xτ means x(t−τ).
The second feedback loop regulates the rate K(S) at which HSCs re-enter the proliferative cycle from G0 state, and it operates with a delay τS that accounts for the length of time required to produce two daughter HSCs from one mother cell. K(S) is a monotone decreasing function of S and therefore acts as a negative feedback. The flux of cells out of the resting phase of the HSC compartment is given by SK(S). K(S) regulates the level of hematopoietic stem cells (S), while F(M) controls the number of WBCs.
The main agents controlling the peripheral WBC regulatory system through F(M) are the colony stimulating factors (CSFs) such as granulocyte CSF (G-CSF) or granulocyte–monocyte CSF (GM-CSF). The main effect of CSF is stimulating the production of WBCs. As WBCs are a factor in the clearance of CSF, the type of regulation meditated by these cytokines is a negative feedback. An increase of WBC count is followed by a decrease in CSF concentration, leading to a decrease in WBC count, which in turn leads to an increase in CSF concentration, stimulating WBC production.
From Fig. 1 we can write down by inspection the model equations:
| (1) |
| (2) |
The model parameters are the circulating WBC death rate α, the WBC pathway amplification A, the maturation delay of WBC precursors τM, the HSC proliferative phase duration τS and the apoptotic rate of proliferating HSC, γS. The feedback functions F and K are taken as Hill functions:
| (3) |
| (4) |
All parameters describe physiological quantities and are de facto assumed to be positive. Table 1 shows the parameter values used in this study. Some of them can be evaluated from experimental data found in the literature, and references are indicated in Table 1. However, the values of parameters such as
List of parameters used in the model
| Parameter | Unit | Value | References |
| A | 100 | 20 | [8,17] |
| f 0 | day−1 | 0.8 | [7] |
| θ 1 | 106 cell kg−1 | 0.36 | model |
| f 0 | day−1 | 8.0 | model |
| θ 2 | 106 cell kg−1 | 0.095 | model |
| s | 2∼3 | [18–20] | |
| τ M | day | 3.5 | [14,21,22] |
| τ S | day | 2.8 | [8,23] |
| γ S | day−1 | 0.07 | [8] |
| α | day−1 | 2.4 | [24] |
|
|
106 cell kg−1 | 1.1 | [8,25] |
|
|
106 cell kg−1 | 6.9 | [7,8] |
|
|
day−1 | 0.04 | [8] |
|
|
day−1 | 0.06 | [8] |
In normal condition, the duration of WBC transit time from the most primitive precursor cells to fully mature cells has been evaluated to approximately 12 days [14], the post-mitotic maturation phase to about 3.0 days in dogs [7]. Some authors even report a transit time of 42 days or more [15]. However, clinical data show that the transit time is shortened in CN patients or after granulocyte colony stimulating factor (G-CSF) administration. Considering that the hematopoietic regulatory system acts thorough the maturation cell line, we will take the feedback delay τM=3.5 days (in a recent study [16], primitive murine blood cells have been shown to divide up to 8 times in a 3-day in vitro culture). Numerical simulations show that large changes in τM (up to 42 days) do not affect significantly the behavior of the solution, although the solution may become apparently quasi-periodic in some ranges of τM values.
3 Analysis
In this section, we analyze the stability of steady states and their bifurcations. As the parameter space is vast, we have to choose the most relevant parameters to be examined. A key feature in the onset of hematopoietic disorders such as CN and PCML seems to be the apoptosis rate of blood cell precursors. In the present model, two parameters control this apoptotic rate, the HSC apoptosis rate γS and the precursor amplification A, which can be expressed as:
| (5) |
The parameter A is composed of an absolute amplification term 2q representing q successive divisions, and of a term representing the surviving fraction from apoptosis, exp(−γPT), where γP is the precursor apoptosis rate and T the time during which the apoptosis occurs. Therefore, our two main bifurcation parameters are γS and A. Other parameters are fixed as in Table 1 unless otherwise noted.
3.1 Linear stability. Quasi-steady-state assumption
In this section, we consider a simpler model by assuming the function F to be constant. This uncouples Eqs. (1) and (2) and allows a complete stability analysis of the stem cell compartment. In that case, it is easy to show that a single positive steady state exists for the system if F<k0r, where r=2exp(−γSτS)−1. The following relation defines the nonzero steady states,
| (6) |
When the apoptosis rate is increased to
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
Let us recall a well-known theorem [26,27] on linear-delay differential equations. The steady state leading to the characteristic equation (11) is locally stable if and only if:
| (12) |
| (13) |
When F=k0r, the only steady state is zero. If the apoptosis rate γS is decreased by a small amount, we can assume that, for small ε>0,
| (14) |
In that case, we can show that
| (15) |
Now, if we linearize around the trivial steady state, we find a linearized equation (with z=S)
| (16) |
| (17) |
| (18) |
| (19) |
We have thus shown that when γS takes the value given by Eq. (7), the unique positive steady state collapses with the trivial steady state, leading to a bifurcation point. In order to distinguish between the different possible bifurcations, we have to look at the value of the exponent s in the feedback function K. If s is even, then the s-root in Eq. (6) is not real when F>k0r, so only the trivial steady state exists. When γS decreases, leading to an increase of r, a pair of nonzero steady states appears around zero, giving a pitchfork bifurcation. If s is odd, then the s-root always exists. When γS decreases, the steady state
3.1.1 Oscillation around the positive steady state
There exists a range of γS for which the positive steady state


Left panel: bifurcation diagram with apoptosis rate γS as a parameter. The positive steady state is represented by the thin line and the envelope of the periodic solution by the thick line. The other parameter values are F=0.05, θ1=1.0, k0=1.77, τS=2.2 and s=3. In this case, a transcritical bifurcation occurs at point II. At point O, a supercritical Hopf bifurcation occurs and a stable limit cycle appears. This limit cycle eventually disappears through a reverse supercritical Hopf bifurcation at point I. Right panel: profiles of periodic solutions for values of γS between 0.24 and 0.28 (points O and I in the right panel). The periodic solutions have been rescaled on a time t′ so that each solution has a period T=1. For a given value of γS, the vertical axis is the HSC count as a function of t′ over one period. Masquer
Left panel: bifurcation diagram with apoptosis rate γS as a parameter. The positive steady state is represented by the thin line and the envelope of the periodic solution by the thick line. The other parameter values are F=0.05, ... Lire la suite
Many authors have speculated about the consequences of such oscillations. There might be a causal link between oscillation in the HSC compartment and oscillations seen in hematological disorders such as periodic chronic myelogenous leukemia or cyclical neutropenia.
3.2 Analysis of the full model
In this section, we focus on the behavior of the solution of the full model as the parameter A is varied. It is shown that a supercritical Hopf bifurcation destabilizes the positive fixed point and that for an interval of values of A, there is bistability. When A approaches 0, the steady state value
3.2.1 Existence and uniqueness of the positive steady state
The full model described by Eqs. (1) and (2) cannot be easily analyzed. However, by restricting the parameter space, we can give a condition for a single positive steady state to exist. In particular, we take:
| (20) |
| (21) |
| (22) |
Let the right-hand side of Eq. (22) be denoted
| (23) |
If we can prove that
| (24) |
| (25) |
| (26) |
3.2.2 Characteristic equation of the model
The linearization of Eqs. (1) and (2) around the unique positive steady state
| (27) |
| (28) |
The subscripts in the equalities denote the partial derivative with respect to the variable and the star subscript
| (30) |
The characteristic equation of Section 3.2.2 is defined as:
| (31) |
| (32) |
The locations of the roots of Eq. (32) will give information about the local stability of the steady state
3.2.3 Bifurcation analysis of the full model
The condition defined by Eq. (20) restricts the values taken by γS. Indeed, from Eq. (20), we find:
| (33) |
The right-hand side of this inequality is slightly smaller than the right-hand side of Eq. (7). Moreover, numerical simulations when γS approaches this value show that the behavior of the solution is highly irregular. Therefore, we concentrate our analysis on the behavior of solutions as the amplification parameter A is varied and keep γS well below the critical value defined by Eq. (33).
The fixed-point equations are defined by setting the left-hand sides of Eqs. (1), (2) equal to zero. Solving for the nonzero steady states leads to
| (34) |
| (35) |
| (36) |
| (37) |
This equation can be solved analytically using symbolic computation software such as Maple. At A=0, Eq. (37) simplifies and it is easy to show that there exists a double zero root and a double negative root. For A>0, as shown above, only one root is positive. With parameter values as in Table 1 and A=0, the system (1), (2) is unstable, since the characteristic equation (32) reduces to Eq. (11) and the values of the coefficients are A+=−0.056 and B+=1.41. As B+>|A+|, the condition for stability of the nonzero steady state when A=0 is then, from condition (13), τS<1.09. This condition is not satisfied, since τS takes larger values. When 0<A⪡1, by continuity, the stability of system (1), (2) does not change. At A=0, there is an unstable steady state
At this point, one must use numerical methods in order to understand the complexity of the system. To perform the numerical analysis, we used a Matlab package, DDE-BIFTOOLS [28], which is based on continuation methods that are in widespread use for ordinary differential equations through the software AUTO [29]. This package is well suited for analysis of delay differential equations.
In Fig. 3 we show bifurcation diagrams of M and S as well as their periodic solution profiles. If we follow the evolution of the steady state
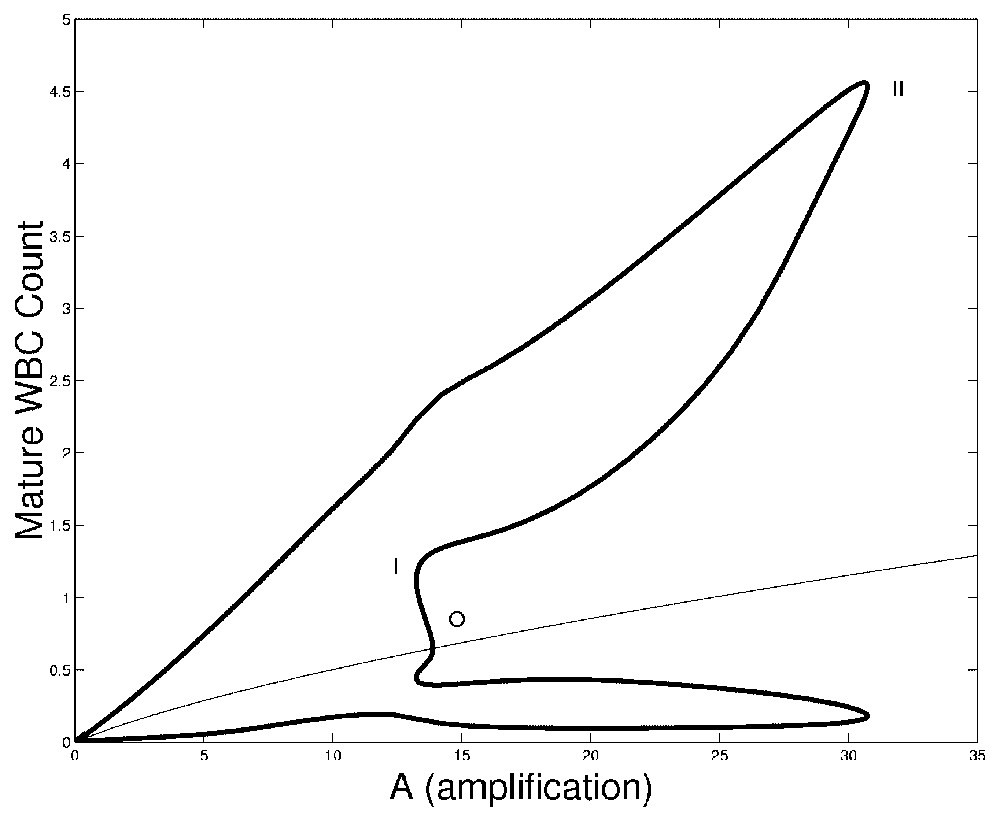
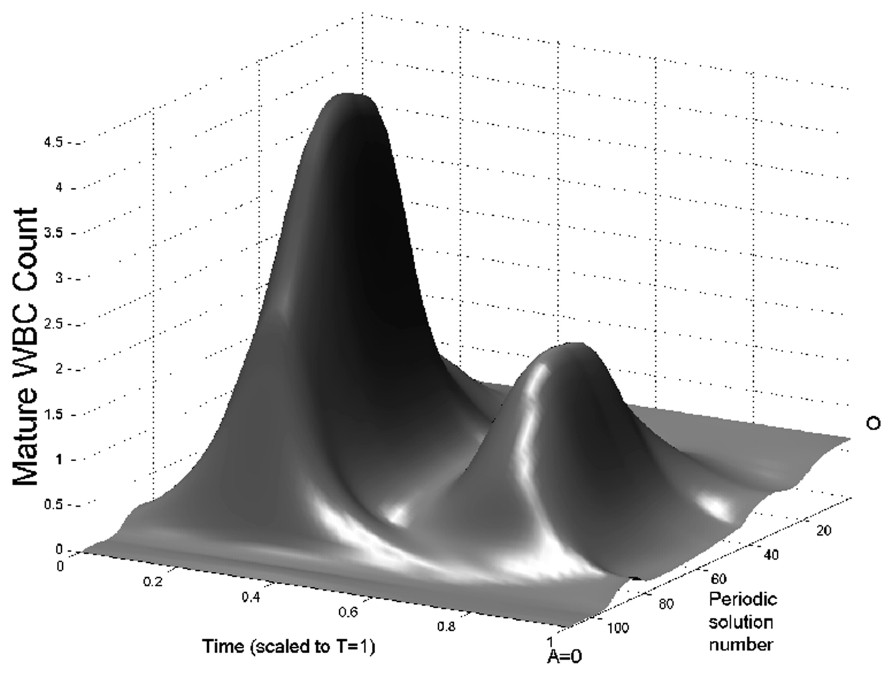

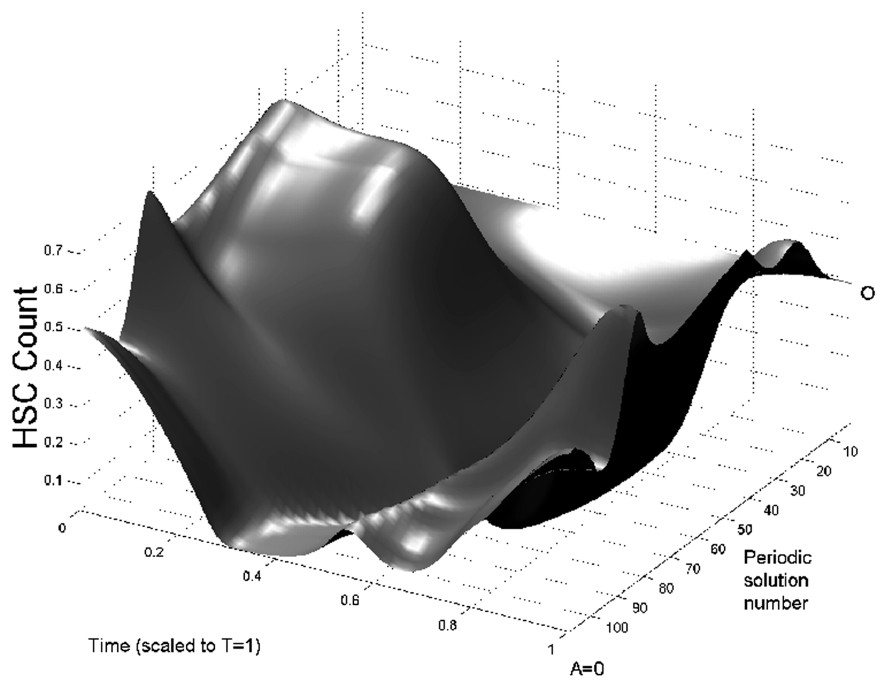
Bifurcation diagram of the full model (Eqs. (1) and (2)) as a function of A. On left panels, the bifurcation diagrams of mature WBC
Bifurcation diagram of the full model (Eqs. (1) and (2)) as a function of A. On left panels, the bifurcation diagrams of mature WBC
4 Discussion
We have analyzed a simple model of white-blood-cell production. Oscillations in blood-cell count have been observed in many hematological diseases such as cyclical neutropenia (CN) or periodic myelogenous leukemia (PCML) [30]. In both diseases, an alteration in the apoptotic rate of white-blood-cell precursors has been observed. The goal of the present paper was to establish, using a simple model, if these changes in apoptosis rates could explain the onset of oscillations. It has been shown in Section 3 that the elevation of the apoptosis rate is a sufficient condition for the onset of oscillations in the WBC count. This elevation has been observed in neutrophil precursors in CN patients. We make the hypothesis that this elevation in neutrophil precursor apoptosis rate is the cause of oscillation seen in CN.
The case of PCML is less clear. This form of leukemia is characterized by oscillations from normal to high levels of WBC with periods ranging from 35 to 80 days. A relationship exists between CN and certain forms of leukemia, since some CN patients eventually develop these leukemias [31–35]. However, experimental data show that leukemic cells have a decreased rate of apoptosis. The model presented here does not display any oscillatory behavior when apoptosis rate is decreased below normal. Further investigations will have to be carried out to establish a link between dynamics seen in CN and PCML.
Acknowledgements
MCM is supported by the Natural Sciences and Engineering Research Council (NSERC Grant No. OGP-0036920, Canada), MITACS (Canada), and the ‘Fonds pour la formation de chercheurs et l'aide à la recherche’ (FCAR Grant No. 98ER1057, Québec, Canada), and the Leverhulme Trust (UK). JB is supported by the Natural Sciences and Engineering Research Council (NSERC Grant No. OGP-0008806, Canada), MITACS (Canada), and the ‘Fonds pour la formation de chercheurs et l'aide à la recherche’ (FCAR Grant No. 98ER1057, Québec, Canada). SB is supported by MITACS (Canada) and the ‘Institut des sciences mathématiques’ (ISM, Québec, Canada).


