1 Introduction
The goal of this work is to construct a spatial individual-based model of a herbivore species and its interaction with the environment. The model is specifically designed for the prairie vole, Microtus Ochrogaster but can be easily adapted for other herbivore species.
The ultimate goal is to use this model as a ‘virtual laboratory’ that allows to test hypotheses involving spatial relationships, such as the effect of habitat size and the role of fragmentation on the population dynamics of a herbivore species.
This study is a part of a larger effort to evaluate the effect of oil development and site exploration activities on the population ecology of natural preserves. These activities lead to habitat fragmentation and habitat size reduction. A herbivore interacts with its spatial environment through the resource it utilizes, i.e. by reducing the density of vegetation, transforming it into energy, and meeting its energetic needs to survive. The reduction of habitat size leads to lower population sizes but may lead to increased population densities and over-utilization of the resource and possibly to extinction of the population. The effect of fragmentation of various types is not clear [1–4].
We strive to construct a ‘realistic’ model of the prairie vole dynamics. A ‘realistic’ model in our opinion is one that strives to incorporate the available well-established data and functional relationships which are meaningful for the goals of the model in a self-sufficient, logical scheme, while keeping the unknown or not well defined elements or relationships at a minimum.
The prairie vole is an extensively studied species. An enormous amount of literature contains data on virtually all aspects of its life history and describes its physiology and social activities. This is a prerequisite for constructing a ‘realistic vole model’.
The prairie vole is predated by virtually all middle-sized mammals, birds and snakes. Its population dynamics determines the abundance of its specific predators. Therefore, a reliable vole model would be useful in determining the effect of habitat size reduction and fragmentation of species at higher levels of the food-web.
Additionally, a ‘realistic’ vole model can be used as a foundation for many other applications, one of them being a study of the spread of diseases in animal populations and their relationship to human disease. For example, plague, tuberculosis, hanta virus and other bacterial and viral diseases are common for voles, humans and domestic animals.
The modelling of spatial movements and social behavior and the incorporation of a large amount of available quantitative information is possible only by using discrete simulations in the form of the so called individual-based model.
Individual-based models (IBM) represent discrete-time simulations. The basic elements of IBM are the ‘individuals’, and ‘environment’, which possess ‘attributes’ (constant data such as average size at birth or area size of a spatial cell or variable data such as age or vegetation cover) and ‘functional relationships’ that determine the values of the variable data at each discrete time moment (for example the size of an individual changes depending on the values of the other internal attributes of the individual and on the attributes of the environment).
Currently there is no standard for abstract representations of IBM. They are usually described with words and a few equations illustrating the functional relationships. We make an attempt to represent an individual-based model as a discrete map and define our model in this setting. Our representation may turn to be not the most suitable one but it is an attempt to propose a unified representation of an individual-based model. It differentiates IBM from cellular automata models which can be represented as discrete dynamical systems. The proposed representation is very convenient from the standpoint of coding the model. The standard representation we propose makes the model structure clear and the rules explicitly defined by formulae.
Our individual-based model has the following features. The spatial environment is represented as consisting of square cells with the size of the home range of M. ochrogaster. The simulated artificial spatial environments represent ‘enclosures’: voles neither leave or penetrate from outside the environments during a simulation. The population is subdivided into classes of wanderers and residents of spatial cells, which, together with the avoidance of same-sex competitors, models territorial behavior, a feature common to many species including the prairie vole. The female residents produce offspring if some additional conditions are met (energetic needs covered, enough generation time lap, presence of a male in the same cell). Individuals consume resource which replenishes itself due to vegetation growth dependent on precipitation and temperature. We have taken into consideration the climatic dependence of both vegetation growth and mammal breeding. We define the local rules of movement of each individual to be driven by the presence of resource and avoidance of competitors of the same gender.
The results from our simulations can be summarized as follows.
1) The model has been validated qualitatively and quantitatively by observing (see Section 5.2) that (a) the time series representing the density of population produced as an output of the simulations resemble qualitatively time series observed in various vole population studies; (b) the population densities are of the order reported in the literature for enclosed habitats. The meaning of validation we adopt is that a model is valid as long as it does not contradict to experimentally observed data.
2) The emergent spatial density distribution dynamics occurring as a result of the local interactions between herbivores and resource has a typical wave-like behavior, produced by diffusion-like colonization of new territories due to overgrazing and overpopulating of old one. Barriers produced by artificial structures simulating roads, pipelines or removal of habitat are surrounded by the moving population waves.
3) The effect of habitat area reduction studied via simulations showed that reducing habitat size reduces the time to extinction. A different set of simulations with removing patches of the habitat show that habitat fragmentation can have, in fact, a beneficial effect on the persistence of a population by reducing the amplitude of the fluctuations.
Typical simulations have been executed over 30 years of real time. The computational time depends on the size of the spatial area simulated and may be several hours long for simulations of 200 by 200 cells for example.
Finally, in this introductory part, we want to point that to the best of our knowledge, there exists no model of vole dynamics or even of herbivore dynamics with such detail and broadness of included factors. The model, being so complex, presents many challenges in regard to the interpretation of the results and manipulating of the data. It is absolutely impossible to deal with all these problems in a single paper. In addition, we note that this is a first version of the model that may undergo further improvements. The reported simulation results are also preliminary and serve to demonstrate some features of the output, to partially validate the model and to point to the existing problems that need to be resolved further.
The structure of the paper is as follows. In Section 2 we give an abstract formulation of an individual-based model as a nonlinear map. In Section 3 we summarize some of the population data we have gathered from the ecological literature. Section 4 is dedicated to a formal description of the model. We have made an attempt to write the mapping functions in a mathematical form and then briefly describe them in common language as is usually done in the ecological literature. In Section 5 we describe the results of some simulations.
2 Individual-based models as generalized discrete dynamical systems
Individual-based models (IBM) are discrete computational simulations which explicitly model large numbers of individual, heterogeneous entities interacting with each other and their environment.
IBM are the only available modelling approach that can meet the needs of a fast growing number of biological applications characterized by processes that incorporate entities with a large number of possible states changing in time or space due to a large number of possible mechanisms. The simulations make it possible for the scientist to carry out virtual experiments and test hypotheses based on available experimental and empirical data.
The IBM approach has certain advantages in comparison with continuous (differential equations) and discrete (discrete-time equations) dynamical systems models. They are summarized as follows.
- (a) IBM are by definition a natural tool for modelling systems made of systems. Each individual is represented as a system of interacting components such as age, energetic budgets, location, status, etc. and these individual systems interact with each other in ways depending on their own state and the state of the environment. Some of the components can be further represented as systems of components. The existing object oriented computer languages are specifically tailored to meet the needs of this type of modelling.
- (b) Straightforward model formulation. Models are based on rules observed in the real system to be simulated and are readily understandable by life scientists.
- (c) Versatility. IBM allow to incorporate both deterministic and stochastic components in the model.
- (d) The non-averaged behavior of the output allows for observing phenomena that would be impossible with PDEs but closer to reality. Shnerb et al., [5] find that in conditions in which the continuum approach would predict the extinction of all the population, the slightest microscopic granularity insures the emergence of macroscopic localized sub-populations with collective adaptive properties which allow their survival and development. This is observed in our simulations as well.
IBM are getting increasing popularity in the ecological community (see [6] and [7] for discussion and reviews up to 1999 and [8–16], just to mention a few specific models), but are readily extended to a finer scale (microbial communities [17,18]) or a slightly different setting (epidemic simulations [19]).
On the other hand, dynamical system models have the advantage to possess a certain theoretical framework that allows to predict the behavior of their solutions at least in some cases. This is not true for IBM in general.
In an attempt to present in a formal language the essence of IBM, we can describe them in mathematical terms as discrete-time highly-dimensional nonlinear maps. IBM are a more general type of maps than dynamical systems and therefore, the theoretical framework for the latter is not applicable to IBM in general.
A discrete dynamical system has the form:
An individual-based model is a nonlinear discrete time map which transforms a certain amount of matrices
The matrices are formed by the vector individuals. More specifically, at time t=n there are Ki(n) individuals, i=1,…,l of l different types. The individuals are vectors Aji whose components are the individuals' data:
The matrices' dimensions vary since the number of entities at each time step is variable (are born or die at various moments). This differentiates IBM from discrete dynamical systems, as they have a fixed number of equations across time. Additionally, the map Φ can contain random parameters or be entirely deterministic.
If no random parameters are present, and the nature of the problem is such that all matrices
3 The prairie vole: experimental and empirical data
Some of the vole data were collected through surveys with no experimental manipulation. We call it empirical data. Data collected through enclosure and removal experiments are actual ‘experimental’ data.
3.1 Demographic and physiological data
The data on life expectancy of the prairie vole is very inconsistent because the measurements depend on predation at the specific region as well as climatic factors. The prairie vole mean life expectancy was established by Getz et al. [21] to be between 50 and 80 days depending on the season. Animals born in summer and autumn had higher life expectancy (61–80 days) than ones born in winter and spring (41–50 days). However, some voles born in the summer or autumn season live up to 450 days, while these born in the winter or spring live up to 120–150 days [21].
Voles are considered adults if they have reached 30 days of age or approximately 30 g weight.
An adult prairie vole produces in average 3–5 offsprings per litter and 3–4 litters per year. The gestation period is 21 days and is approximately equal to the generation time (period between pregnancies) [22,23].
The daily food intake depends on the quality of the food but for green (undried) grass it can be estimated as follows. Sawicka-Kapusta et al. [24] estimates for the caloric value of biomass of various fodders, for grass being 0.85–0.98 kcal/g biomass. Bradley [25] calculates the daily food intake of M. ochrogaster to be approximately 600 cal/g body weight. For 30 g body weight then the daily caloric requirement is 18 kcal. Using the data from Sawicka-Kapusta et al. [24] we obtain that the dailly grass intake for an adult vole will be about 20 g.
3.2 Climatic dependence
Breeding shows seasonal dependence and is defined as between February and November. Rose and Gaines [23] report no breeding in December and January and even through April in one of the years, while Krebs et al. [26] report very low percentage of breeding females in November–January and peaks of breeding in August, September and October. Keeping in mind the bioenergetics of these small mammals, which spend most of the produced metabolic energy for maintaining their body temperature, these reports are reasonable.
3.3 The home range
Species that exhibit site fidelity have a mean amount of territory that they move around daily and defend, the home range (HR). HR size has been demonstrated to be related to the energetic needs of the mammal [27]. Thus, it is gender and season dependent. The HR size has been reported to be somewhere between 10 and 50 m [28–30].
3.4 Factors governing population density
It is known from observations [21,26] that highest vole population densities occur in the late autumn (October, November), that densities decrease drastically in January–March, the lowest densities usually occurring in March and then start steadily increasing until late autumn.
The population density of the prairie vole depends on the quality and quantity of vegetation as well as on the presence of sympatric herbivore species and/or predators. Food quality is very important for the population dynamics of the prairie vole. For example, alfalfa has a higher nutrition value than tall grass [31]. The maximum vole density in tallgrass prairie as recorded in [32] was 90 ha−1 while the mean density was 7 ha−1 showing high variability during a 25 year study. Cole and Batzli [31] report maximum density 38 ha−1 and 10 ha−1 respectively in a next year for the above mentioned types of vegetation.
Experiments on enclosed grids show that dispersal plays an important role in population density regulation. Density can become quite high in enclosed areas. Krebs et al. [26] compared fenced and unfenced grids and observed a rapid increase in population density in the fenced case, which led to overgrazing. A very interesting experiment of introducing 18 prairie voles in an empty fenced plot of 0.8 ha led to an extreme density of 494 vole/ha (395 voles in the plot) after 7 months. Consequently the vegetation was overgrazed and the population fell to 11 voles in early April when it started to increase steadily.
Absence or presence of a predator also plays an important role on population density regulation. Desy and Batzli [33] conducted experiments on enclosed plots with mixed vegetation including blue grass and observed maximum density of 550 ha−1 on enclosures with no predators and added food, while in enclosures with no supplemented food and with predators, the density was stable at about 90 ha−1.
Microtine species, one of which is the prairie vole species, exhibit seasonal and multi-annual population size fluctuations. The physiology of the vole, a very small mammal, which needs an enormous amount of energy (relative to its body mass) to maintain constant body temperature, is clearly seasonally dependent. At low temperatures, the vole has to diminish or abandon certain high-energy-consuming activities in order to survive. Breeding (as seen above), deaths due to predation and life expectancy are seasonally dependent phenomena. Several authors have reported multiannual fluctuations in population density with occurring peaks with frequency 2–4 years. Rose and Gaines [23] note that microtine cycles vary from 2 to 5 years in duration, with many having 3–4 year intervals between peaks. Getz and Hofmann [32] report high-peak densities appearing with periods of 4.3 years and secondary peaks at 2.1–2.4 years on three different habitats and that these fluctuations are synchronized for the three different habitats. The periodicity of the fluctuations does not depend on the external manipulations of the habitat (burning of tall grass, mowing of blue grass and alfalfa) but their amplitude does depend on the quality of food (alfalfa has the highest caloric quality, tall grass the lowest) and are positively correlated with it [34]. Cole and Batzli [31] also note that food availability may influence the amplitude of fluctuations but not the periodicity of the cycle. The multi-annual population size oscillations of the microtine species is a continuing puzzle to ecologists.
There are various hypotheses and studies related to them concerning vole population fluctuations. Some authors study the connection of population density and juvenile survival (Krebs et al. [26], Getz et al. [21]), while others put forward as a possible cause changes of food quality [31].
3.5 Social relations
Getz and McGuire [22] show that the majority of single males are wanderers while a considerably smaller proportion of single females wander. Wanderers frequently visit the nests of pairs but are kept away by the male [35]. Unrelated adults join communal groups only if they include already grown offspring male [35]. New pairs were formed after the winter period from surviving individuals mainly from different social groups [22]. Most of the new pairs formed in summer-autumn were made from two wandering individuals.
Prairie voles are monogamous animals. Paired males and females cohabit a nest and a home range [22]. McGuire and Getz [35] find that paired males exclude nonresident males from the areas around their nests. This was also confirmed in [22].
3.6 Territory specificity and defense
There is little overlap in use of space by social groups even at high population densities [35]. Spatial behavior limits interaction between members of adjacent social groups. Jacquot [36] found that vacant territories were fast occupied. Density of population was positively correlated with the time necessary to emigrate. Female prairie voles immigrated in response to vacant territories and not to potential mates. Males also immigrated in response to vacant territories. It is generally accepted that males show preference to territories with present females.
4 Description of the model
4.1 The variable matrices
At each time moment n the total amount of present animals is K1(n). The animal objects
Thus, at any time moment n the animal objects with their data represent a K1(n)×9 matrix, the matrix of animal objects.
| (4.1) |
K1(n) can take very big values depending on the amount of spatial cells (area size) we consider. In a typical simulation K1 reaches several hundred thousands up to a million. The lower bound is naturally 0, but in general, even if K1 does not become so small, it is highly variable, falling to several thousands in the winter months.
All animal objects share constant data characteristic of the species: average daily food intake DFI (in grams per day), life expectancy LE, maturation age MA, generation time GT (in days), litter size LS. The values of these quantities are taken to be in the ranges outlined in the previous section. Additionally, the following controlling parameters relevant for the energetic budget enbudget are introduced: MEB, maximum energetic budget, MeanEB, mean energetic budget, JEB, juvenile energetic budget. We explain the meaning of the controlling parameters in a following subsection. The values of the parameters are reported in Section 5.1.
Space is represented as a collection of a constant number K2 of square cells, C1,…,CK2, each one with an area roughly equal to the home range of the herbivore. The location of each cell is represented by two coordinates (row and column). The cells are individual objects possessing the following 5 variables: quantity of vegetation veg in the cell, total number pop of animals in the cell (juveniles, male and female), number of present male herbivores mpop, female herbivores fpop, and a variable p indicating whether the spatial cell has been polluted and therefore should be removed (i.e. it has been developed, polluted or otherwise rendered uninhabitable). Thus, at any time moment n the cells with their data represent a K2×5 matrix, the matrix of cell objects.
| (4.2) |
Note that we address the spatial cells in two different ways: we order the cells sequentially as C1,…,CK2, and we also address them by using their coordinates when defining an animal object. We need to have a way to link the coordinates with the cell.
Thus, given row and column coordinates, nrow, ncol, let #(nrow,ncol) be a function whose value is the sequential number of the cell with coordinates nrow, ncol. Otherwise said, C#(nrow,ncol) has coordinates (nrow,ncol). An animal object Aj will then be located in the cell C#(nrowj,ncolj).
The dimensions of the cell objects matrix do not change over time. The number of columns of the animal objects matrix may change at each time step because of births and deaths. The newborn objects are added as last columns of the matrix, while the dead objects (with remove=1) are deleted and the list of animals is updated. Thus, at time n an animal may have index j in the list, while at time n+1 this index may be different.
4.2 The mapping functions
The time unit used in the model is 1 day. We simplify the simulations by assuming that a month has 30 days and an year has 360 days.
The mapping functions describe the transition from matrices
In this model the only random map is the one that controls the animals' movements between cells.
(0) If at time n animal Aj has index j and removej=0, then we define img(j) as the function which calculates the new index, at time n+1, of animal j. Keeping in mind the way we do the rearrangement of the list, we find that img(j)=j− the number of animals that died and had index less than j=img(j)=j−∑k<jremovek.
(1) Cell population numbers
(2) Aging
This is the simplest mapping from time n to time n+1.
(3) The energetic budgets
To model the effect of food and starvation on survival, we use the variables enbudgetj(n), j=1,…,K1(n).
enbudgetimg(j)(n+1)=enbudgetj(n)−1, if veg#(nrowj(n),ncolj(n))<DFI×pop#(nrowj(n),ncolj(n))
Otherwise,
That is, if the animal feeds, it increases its energy store (unless it is at the maximum) and if it cannot feed because of lack of enough resource, its energy store drops. Additionally, there is a limit to the energy an animal can store, which is smaller for the juveniles.
(4) Survival or removal
removej(n+1)=0 if agej(n+1)<LE and if enbudgetj(n+1)>0. Otherwise, removej(n+1)=1. That is, an animal dies if its energy budget became 0 or if its age reached the life expectancy.
(5) Status change
The variable statj changes its value as follows.
statimg(j)(n+1)=resident, if ageimg(j)(n+1)<MA.
statimg(j)(n+1)=wanderer, if ageimg(j)(n+1)=MA.
If ageimg(j)(n+1)>MA and if statj(n)=wanderer, then
Otherwise, statimg(j)(n+1)=wanderer.
If ageimg(j)(n+1)>MA and if statj(n)=resident, then
statimg(j)(n+1)=wanderer if veg(#(nrowimg(j)(n),ncolimg(j)(n))=0.
Otherwise statimg(j)(n+1)=resident.
In plain words, all juveniles are residents until they reach adult age, when they become wanderers. Adults who were wanderers can become residents if they find themselves in a cell with no other individuals of the same gender, otherwise they continue to wander. Thus, each cell can contain only one pair of adult residents (plus their immediate offspring) and many wanderers. Adult residents become wanderers if the cell gets overgrazed and has no vegetation left.
Wanderers do not contribute to the population growth but use the resource, thus controlling the population in certain bounds.
(6) Births (4.3)
In other words, a female vole gives birth only in the months between February and October and if it is an adult resident, with energetic budget not less than MeanEB and if a male animal is present in the cell.
(7) The time between pregnancies τ (4.4)
(8) Location change
Wanderers change their location at each time moment until (if) they become residents.
If (nrowj(n),ncolj(n)) are the coordinates of the location of animal Aj at time n, then the 8 surrounding cells have pairs of coordinates (nrowj−1,ncolj−1),…,(nrowj+1,ncolj+1).
Let C#(nrowj−1,ncolj−1),…,C#(nrowj+1,ncolj+1) be the 8 neighboring cells. To ease notation, let us denote them by Cj(1),…,Cj(8).
If statj(n)= resident, then
(9) Vegetation growth and depletion
The variables vegi(n), i=1,…,K2, are transformed into vegi(n+1), i=1,…,K2, as follows

Plot of artificially generated green vegetation (in g m−2). Time is in days.
(10) Genders
Naturally,
(10) Finally, pj(n) is an externally defined function.
5 Simulations
We implemented the above described individual-based model in a C++ code. All calculations simulate a ‘fenced plot’, i.e. no animals are allowed to enter or leave the site. All simulations were calculated for a 30-year period, for which the input vegetation data was generated.
We use the term persistence in the sense of ‘time to extinction’. As our simulations were done for a 30-year period of time, we cannot say if the populations that persisted for 30 years would go extinct in a longer period of time or if they will persist for ever (see the discussion at the end).
5.1 Parameter values and initial distributions
In the simulations we use numeric values of the parameters close to the ones reported in the literature (compare with Section 3). The area of each cell is 900 square meters (30 m by 30 m cells), roughly corresponding to the prairie vole's HR size. The initial time is set as January 1, 1960. The life expectancy LE was varied across simulations between 90 and 140 days (which is close to the maximum observed life span of voles born in winter). Additionally, GT=21 days, MA=30 days as described by real data. The litter size LS is taken to be equal to 2, a twice lower value than the number of newborns, to account for a high mortality of offspring reported in many publications. DFI=10 is also taken at a lower value than the one known for adult voles, because it is an average value for both adults and juveniles. The controlling energetic budget values were taken as MEB=20; MeanEB=15; JEB=2. These are rather arbitrary because of lack of data. MEB=20 has the meaning that an adult vole would die after 20 days of starvation, while a juvenile would endure only 2 days of starvation (JEB=2).
Initially all cells were assumed to contain the same amount of vegetation (no spatial heterogeneity was assumed).
Two types of initial distributions of animals in the spatial cells were generated and used in the simulations.
The first type was a random (‘uniform’) distribution of animals on the whole region, created by using a random number generator. This was achievd by generating a random number between 0 and 3, 4 or 5 (in various experiments) of animals in each spatial cell.
The second type of initial distribution was ‘a single source’; i.e. generating a random number (as above) of animals only in a certain small number of aggregated cells usually in one corner of the region. This was considered as a simulation of an experiment where voles were let into an empty enclosed region to colonize it.
All initial distributions consisted of wandering adults.
5.2 Results
5.2.1 General observations
The simulation results share some important similarities as follows.
1) As expected, vole population densities (the total population divided by the area in hectares) fell drastically in the winter months due to overgrazing and to the lack of breeding. Populations reached maximum densities in the end of the autumn (usually in November) and minimum densities in February–March. This result matches the real-life experimental results reported in Section 3.
2) The time series of the vole densities showed annual peaks (probably due to the seasonality of the vegetation data) and multi-annual fluctuations with peaks separated by periods ranging between 2 to 5 years, similar to what is described in Section 3. Fig. 2 shows a typical time series of a 120×120 cells simulation with an initial ‘single source’ distribution of 348 animals. Similar time series patterns are seen in Figs. 5 and 7 (the non-extinct case). Fig. 7 shows an interesting observation: the peaks in density appear in the same years for the three plots. That is, the amplitude of fluctuations depends on the size of the plot, but the periodicity does not. This is comparable to the observations mentioned in Section 3 according to which the periodicity of fluctuations does not depend on the quality of the plot. Our simulations show that the peaks in population density do not coincide with the peaks in the resource density. One can hypothesize that the multi-annual fluctuations are due to the combined effect of the oscillatory vegetation forcing and the intrinsic population density oscillations due to the periodicity of breeding.

Annual and multi-annual population density fluctuations. See text for details.
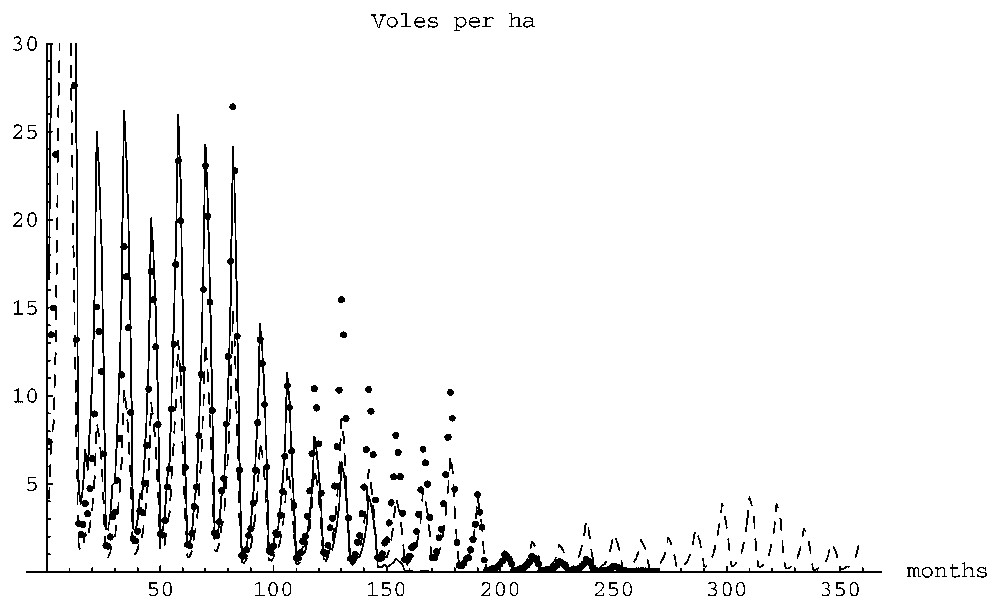
Comparison of the length of population persistence on three plots of 3600, 8100, and 14 400 ha. See text for details.
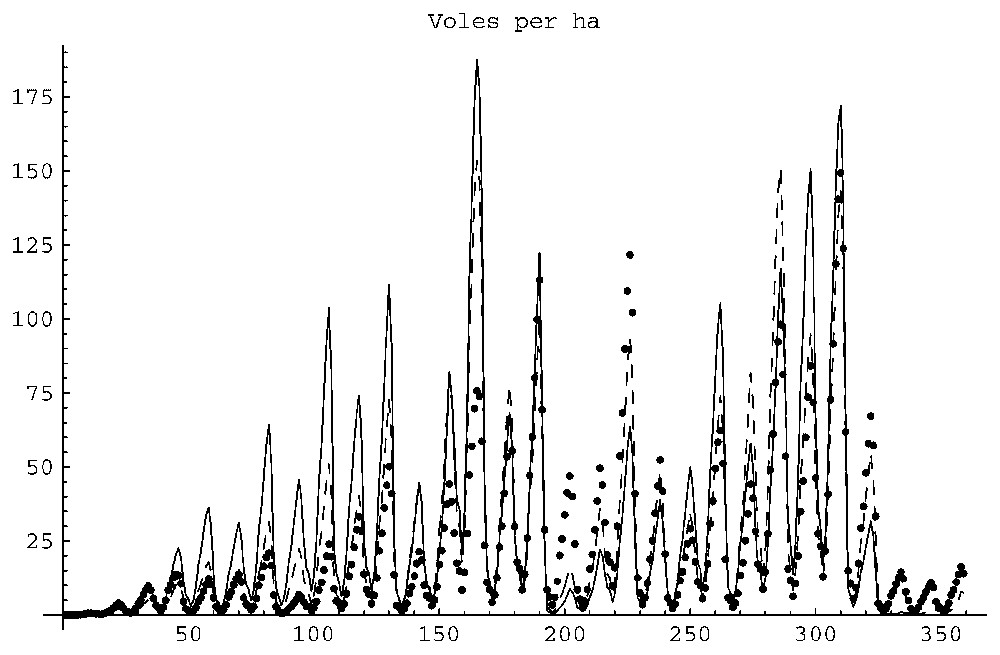
Comparison of the length of population persistence on three plots of 1866, 1872, and 3600 ha. See text for details.
3) Further, it is important to note that the maximum densities did not exceed 200 per ha, in the expected limits for this species in a closed area.
The above mentioned features support the validity of the model.
4) Specific spatial patterns similar to wave motion formed in all simulations. Simulations starting with uniform random distribution over the whole plot showed the formation of wave patterns after the first year when separate individuals survived and started reproducing and dispersing randomly. The random dispersal in all directions led to the formation of oval populated regions with highest density in the center of the ovals. The subsequent overgrazing led to the removal of animals from the central part of the ovals thus forming rings of nonzero density, which we refer to as ‘waves’. The waves further expanded and their central parts were removed as results of overgrazing and deaths. The waves hit one another subsequently forming various patterns of irregular structure. Fig. 3 shows typical patterns illustrating this observation.

Formation of wave-like patterns from a uniformly random distribution on a spatial plot with a removed central region. The top left graph corresponds to the initial distribution in January of year I, the second on top corresponds to December of year 1, the bottom left to November of the second year, and the bottom right to December of the second year.
5.2.2 Optimal conditions for survival
The survival of the population depended on the initial distribution and on the parameters we varied. If the initial distribution density was low (0–2 animal(s) per cell) and especially if the inhabited cells were sparse, the population died out because of a low number of mating pairs formed (Allee effect) and low amount of offspring throughout the breeding season. Additionally, if the initial density was high, the population amassed very high densities in the subsequent years, overgrazed the whole region and perished (compare with experimental results described in Section 3 [26]). At high and low initial densities the persistence of the population showed high sensitivity to initial conditions in the sense that different initial distributions with similar total population numbers developed different outcomes; the population sometimes perished after a few years, while in other cases it persisted for the 30-year test period. Overall, one can hypothesize the existence of an optimal range of initial population sizes that guarantee the persistence of the population.
5.2.3 The importance of the area size
In one simulation we compared three ‘fenced plots’ of 200×200, 300×300 and 400×400 cells respectively. We started the simulations with the same initial distribution of voles which was randomly generated in the smallest plot. The plots are contained into one another, with the bottom left corner being common for all plots. That is, the 300×300 plot was five ninths empty and the 400×400 plot was three quarters empty in the beginning. The parameters of the model were the same as described in the previous section with the life expectancy being 120 days. As an illustration, Fig. 4 shows the density distributions in the largest plot in December of the second, tenth and fifteenth year.

Spatial distribution of vole densities in a 400×400 plot in months 24, 36, 120, 180 (from left to right). See text.
The vole population on the smallest plot went extinct in about 180 months, on the second plot in 269 months, while on the third plot it persisted during the whole simulation period of 360 months. Fig. 5 demonstrates the time series of the total population densities per ha. The dashed line corresponds to population density on the largest plot, the dotted line to the middle-sized plot, and the continuous line to the smallest plot.
The smaller the plot, the higher the maximum and average density per ha and the larger the standard deviation. The latter measures the instability caused by oscillations. The maximum densities for the 200×200, 300×300 and 400×400 plots were 100, 82 and 46 correspondingly while the average densities were correspondingly 12, 6, 3 and the standard deviations were 17%, 11%, 10%, respectively.
On the smaller plots the population extinction is caused by severe overgrazing of most of the plot and subsequent starvation during the winter months. On the largest plot overgrazing does happen locally, while there are vast areas with sufficient vegetation remaining. Additionally, even in cases when the whole large area gets colonized, densely populated and overgrazed, the chances of locally surviving animals that restore the population in the following years are higher with larger plots than with smaller ones.
We did similar simulations with other sizes of ‘fenced plots’ and other initial distributions and we observed similar monotonous dependence of area size and length of population persistence.
5.2.4 The importance of dispersal and predation
Our simulations model a fenced habitat of a single population. The lack of dispersal outside the area causes the appearance of very high population densities and subsequent overgrazing. The insufficiency of vegetation combined with the lack of breeding in the winter months causes severe population crashes and may lead to rapid extinction. We already noted that extinction was dependent on area size, initial densities, life expectancy, etc. Any factor that contributes to lowering population density, such as dispersal through the boundaries of the habitat and predation should act in the direction of increasing the population's chance of survival.
5.2.5 Fragmentation is not necessarily a bad thing
We compared the results of simulations on plots of various sizes with identical initial distributions but with various types of ‘obstacles’. The obstacles are parts of the landscape unaccessible (or avoided) by the animals. Here we discuss the comparison between three simulations, two without obstacles and one in the form of a ‘checkerboard landscape’, see Fig. 6 for a visual representation.
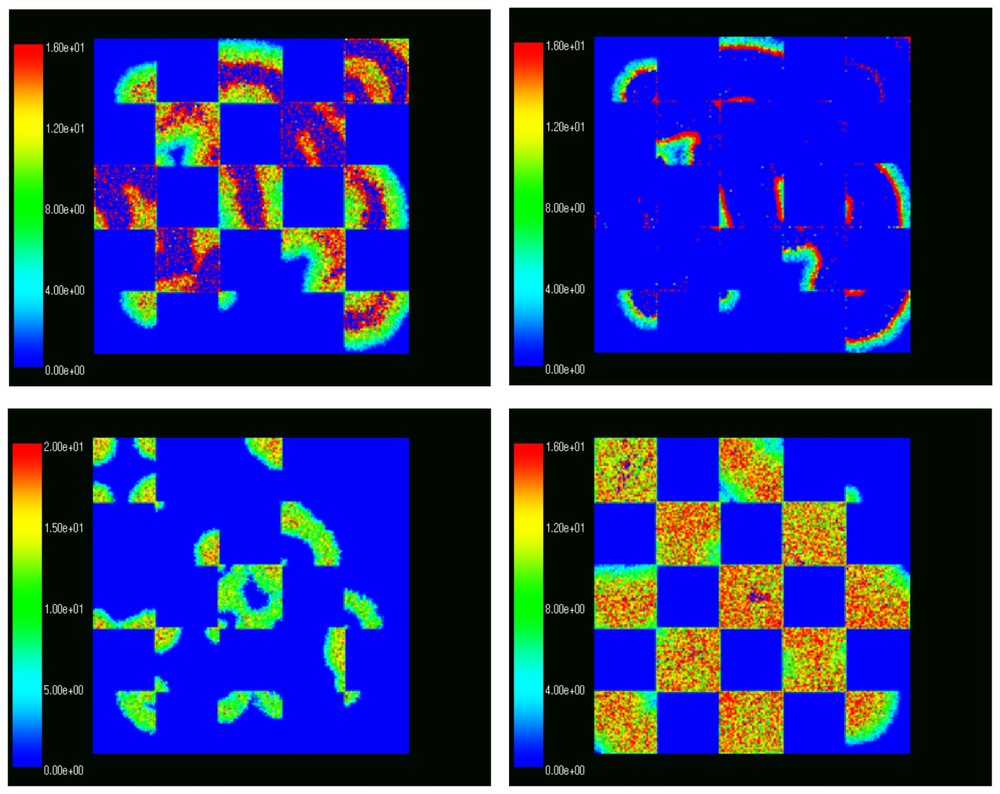
Density distributions of voles in different points of time in a checkerboard habitat.
The initial distribution simulated an experiment in which 42 adult voles were released into the plot in their bottom left corners. Interestingly, the overal spatial wave-like progression of density distribution was preserved as seen in Fig. 6. The patchiness of the landscape decreased the amplitude between the lowest and highest population per ha densities. We compare three simulations with same initial distributions: on a 200×200, 144×144 and 200×200 checkerboard plots. The 144×144 plot has almost the same area size as the total area of all accessible patches of the 200×200 checkerboard plot. We compare these two plots to study to the effect of patchiness on population persistence. The population densities in the three plots are represented in Fig. 7, with a solid, dotted and dashed line corresponding to the 144×144, checkerboard and 200×200 plots.
The population on the 144×144 plot went extinct near the end of the 30-year period, while the populations in the other two plots persisted till the end.
The maximum population densities per ha were 187, 149 and 153, while the average population densities per ha were 29, 21, 25 for the 144×144, checkerboard and 200×200 plot respectively. The standard deviation was 7%, 6% and 7%. This simulation shows that the checkerboard fragmentation has, in fact, a beneficial effect on the persistence of the population by reducing the maximum and average density and the amplitude of oscillations.
The results of various simulations with obstacles seem to confirm the conclusion that fragmentation does not have a clearly expressed negative effect on population persistence. Our results show that it is rather the decrease in the size of the inhabited population area that does have a clearly expressed effect on population persistence.
6 Discussion
This paper presents a spatial individual-based model of prairie vole dynamics and results of simulations with the model. The spatial feature of the model is crucial for the goals of the study which are to understand the effect of area size reduction and habitat fragmentation on the population size and persistence.
We define the model as a nonlinear discrete map which is more general than a discrete dynamical system. Although this representation does not bring new knowledge about the properties of the model, it represents a form of formalizing such models and may prove to be a suitable standard form we hope to be accepted by other modellers. Unifying the representation of IBM is an important task to be resolved by the IBM modellers. Accepting a common format will help define and solve problems and will facilitate communication between modellers. The possible disadvantages and restrictions of this format need to be adressed in subsequent work.
This paper is meant to be a first report on the model ideology, some simulation scenarios and results of simulations. A variety of problems arise which need to be addressed further. One important problem is to find methods to quantify the simulation results in suitable ways. For example, to quantify the dependence of population persistence on initial population size should include, among other methods, carrying out Monte Carlo simulations with a large number of randomly distributed inital populations. Quantifying and qualifying the dependence of population cycles on vegetation cycles is a challenge, especially since these are not periodic time series but rather chaotic ones. Is there any relation between them?
Our results allow to compare the persistence of the model populations over a 30 year period of time. Vole populations in the simulated artificial enclosures often went extinct in less than this period. The simulations with the model do not allow to state that a population will exist forever or that it will necessarily eventually die out. Whether a model population can persist forever is a very interesting question but unfortunately we do not have the theoretical framework that would allow us to find an answer. In the theory of dynamical systems it is often possible to predict the behavior of model solutions by examining the stability of steady states. Creating methods for prediction of the system's behavior is a serious challenge.
The energetic budget part of the model needs to be developed better further as well as the model should be put in a form that allows dispersion out of the region and the impact of predation on the vole dynamics.
The model will be further implemented with real vegetation data as well as real geographical information data on an existing landscape.
Acknowledgements
The authors would like to thank Nancy Comstock of the US Department of Energy, National Petroleum Technology Office, for providing financial support through the National Gas and Oil Technology Partnership Program. The authors also thank Yetta Jager and Rebecca Efroymson, Oakridge National Laboratory, for numerous useful discussions. We are indebted to Steve Smith from CASC, LLNL for help with improving the speed of computations and with the visualization of the spatial density distributions, done by using the visualization tool of the SAMRAI package, and to Jessie Coty, ERD, LLNL for help with ecological literature searches.
This work was performed under the auspices of the US Department of Energy by the University of California Lawrence Livermore National Laboratory under contract No. W-7405-Eng-48.


