1 Introduction
Assuming that the 2-[18F]fluoro-2-deoxy-d-glucose (18F-FDG) is trapped in cancer cells in an irreversible manner, PET-scan allows quantification of the metabolic rate of glucose in tumours, by several methods that aimed at quantifying the 18F-FDG uptake rate [1–5]. Is the irreversibility of the 18F-FDG uptake an oversimplification? Usually, most biological reactions do not occur in a completely irreversible manner, which has been clearly established in neuroreceptor quantification models [6]. Moreover, in the particular case of 18F-FDG PET imaging, the tracer metabolism by hepatic tumours challenges this notion of irreversibility [7]. A first quantification method of the 18F-FDG release rate constant has been proposed by Phelps et al. [8], as an extension of Sokoloff's model [1]. Then, Patlak has proposed a graphical method for reversible tracers [2], as an extension of his previous method for irreversible ones. These latter methods both require a dynamic acquisition, which is achieved during the first hour after the tracer injection, and an invasive blood tracer sampling.
The aim of this theoretical work is to propose a graphical method allowing for the assessment of the 18F-FDG release in tissues, on certain conditions, but without needing any blood tracer sampling. It is an extension of a recently published method that aimed at quantifying the rate constant for an irreversible tracer uptake [5]. It requires the acquisition of a dynamic PET scan at the later decreasing phase of the tissue tracer activity. Both a two-compartment and a three-compartment model are developed, and simulated data are provided.
2 Two-compartment model
Let us consider the 18F-FDG uptake from blood to an intracellular compartment (Fig. 1a). The 18F-FDG uptake rate constant is K, and the 18F-FDG release rate constant is . At the steady state, the rate of trapped tracer per tissue volume unit is:
| (1) |
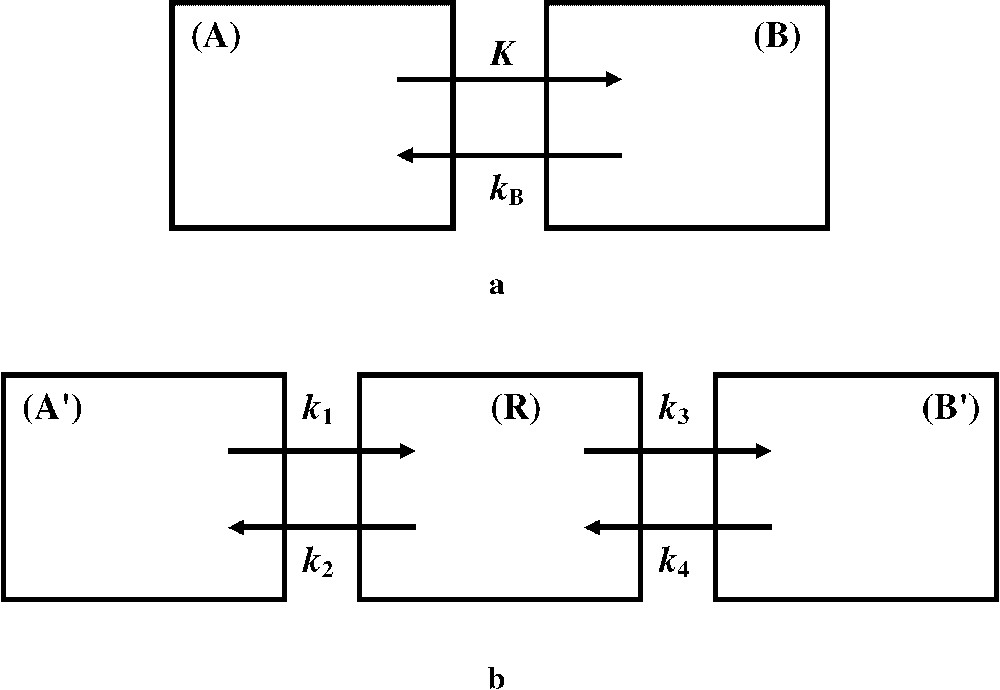
(a) The two-compartment model roughly considers compartments (A) and (B), which involve blood free 18F-FDG and 18F-FDG trapped in intracellular cytoplasm, respectively. The 18F-FDG uptake and release rate constants, K and , respectively, are the transport rate constants between the two compartments. (b) In comparison with the two-compartment model, the three-compartment model introduces an intermediate reversible compartment (R), which considers free 18F-FDG in interstitial fluid and intracellular cytoplasm. The rate constants and account for forward and reversed transport between compartments and (R), respectively. The rate constants and account for forward and reversed transport between compartments (R) and , i.e. for 18F-FDG phosphorylation by hexokinase and 18F-FDG-6-PO4 dephosphorylation by G-6-phosphatase, respectively.
In patients with a normal renal and hepatic function, the time duration required to reach the steady state is estimated to last about 5 min [3], and the amount of the tracer that accumulates in the tissue during this time duration is assumed to be negligible in comparison with that which accumulates during the whole examination. Moreover, for simplicity, let us assume that the 18F-FDG blood time-activity curve (TAC) exponentially decays with a mean constant α, after the peak (see simulated data for a multiexponential decay). In a nearly similar manner to that used in a previous work on 18F-FDG (irreversible) uptake [5], when is set at the blood tracer peak, the solution of Eq. (1) is:
| (2) |
Eq. (2) is very similar to that of a radioactive chain equation, but with a whole decay constant equal to . When is much greater than , i.e. when the clearance of 18F-FDG from plasma has occurred whereas 18F-FDG is still present in the tissue, the later phase of the trapped tracer TAC can be approximated by:
| (3) |
Eq. (3) shows that a single exponential fitting to the later phase of the 18F-FDG TAC can provide the release rate constant , since λ is known, without needing any arterial blood sampling. (If an arterial blood sampling is carried out, a graphical analysis can also provide the 18F-FDG uptake rate constant K [5].) Let us note that, at the later phase of the tracer activity in the tissue: (i) neglecting the part of the tracer amount accumulated in the tissue during the time duration to reach the steady state is justified, since both 18F physical decay and 18F-FDG release have occurred, and (ii) actually corresponds to the measured trapped 18F-FDG activity, since the blood 18F-FDG is negligible (see simulated data). Furthermore, Eq. (2) allows us to predict that the time corresponding to the maximal 18F-FDG activity in the tissue is lower than that estimated when no 18F-FDG release occurs [5]:
| (4) |
| (5) |
3 Three-compartment model
In a three-compartment model (Fig. 1b), the 18F-FDG transport rate constants between the compartments are different from those of a two-compartment model (Fig. 1a). However, relationships can be established [2]:
| (6) |
| (7) |
Following Patlak [2], let us suppose that is much lower than the other rate constants of the system. Furthermore, let us consider measurements are started up at the later phase of the 18F-FDG activity in the tissue, when the clearance of 18F-FDG from plasma has occurred whereas 18F-FDG is still present in the tissue, in other words, when the tracer uptake from the blood into the tissue is much lower than the tracer release from the tissue. Thereby, when the tracer uptake from the blood into the tissue can be ignored, the rate of change of trapped tracer per tissue volume unit is:
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
This result justifies that in Eq. (10) the second term of the right-hand side can be considered much lower than the first one. Furthermore, introducing Eq. (14) into Eq. (10) and rearranging yields the following expression for the trapped tracer activity:
| (15) |
| (16) |
Furthermore, Eq. (17) hereafter shows that the transport rate constants available from Eqs. (15) and (16), and in a three-compartment model, are in agreement with that available from Eq. (3), in a two-compartment model:
| (17) |
4 Simulated data
The proposed two-compartment model assumes, for simplicity, that the 18F-FDG blood TAC decays with a mean constant α. However, it has been shown that the 18F-FDG plasma clearance was multi-exponential, i.e. that the input function (IF) was three-exponential [9]. When such an IF is taken into account, Eq. (2) becomes:
| (18) |
Fig. 2 shows simulated data from Eq. (18) and references [9,10], for different values of and . At the later phase of the 18F-FDG TAC, when is much greater than , a single exponential fitting can provide the 18F-FDG release rate constant , since λ is known, without needing any arterial blood sampling. One hour after injection, in comparison with [10], the two first IF exponential constants satisfy this condition, and [9], but not [9].
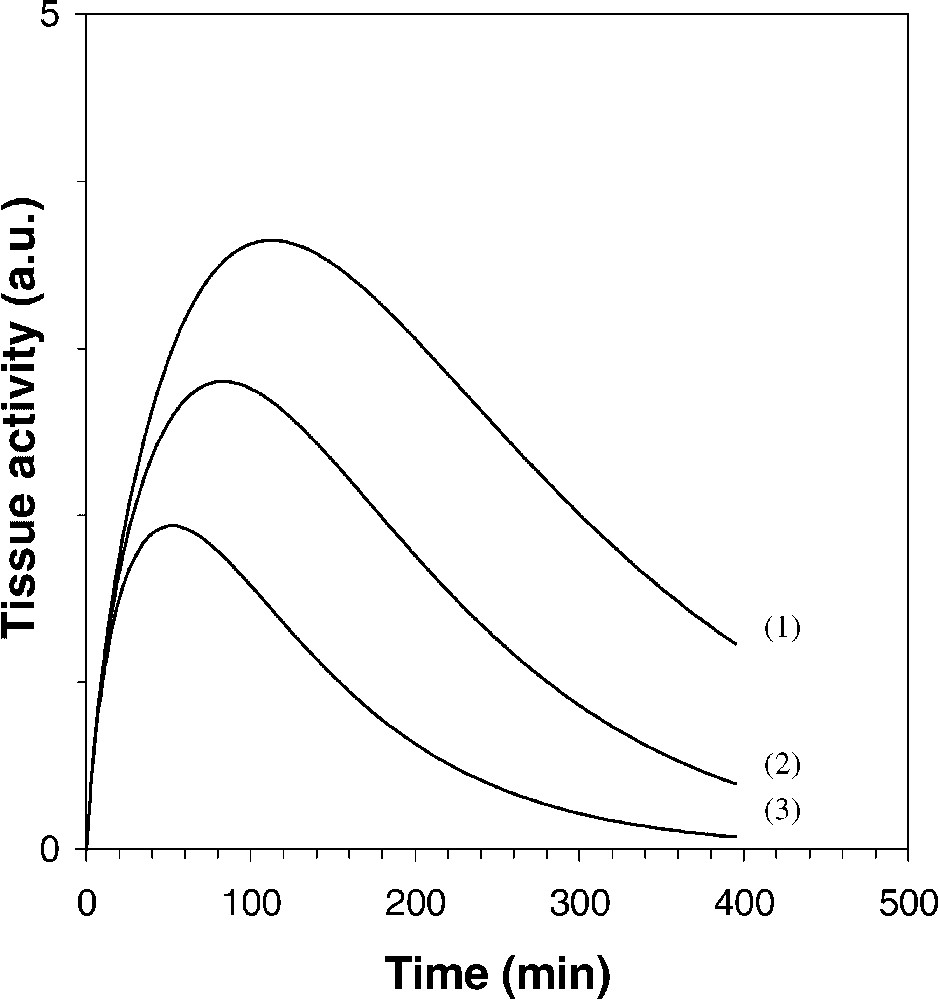
Simulation of the tissue 18F-FDG TAC in a two-compartment model (Eq. (18)), for different values of and [9–11]: (1) , ; (2) , ; (3) , . The axis origin is set at the blood tracer TAC peak (not shown).
The greater the constant , the faster the tracer plasma clearance 1 h after injection, the earlier the implementation of the method. This feature highlights the major part of hydration and/or phlorizin injection [11,12], which should be made in practice from the end of the routine static acquisition to the beginning of the dynamic acquisition, in order to increase . It has been shown indeed that phlorizin injection resulted in an increase by a factor of 2.25 in the plasma clearance rate of 18F-FDG in rats, and that urinary excretion of 18F-FDG in phlorizin-treated rats was very near that of hydrated rats [11]. Consequently, assuming that at least the condition:
| (19) |
From data involved in curve 3 of Fig. 2 ( and , i.e. with hydration and/or phlorizin injection), single exponential fittings to the 180–240, 240–300, 300–360, and 360–420-min time ranges lead to estimates of equal to 0.0042, 0.0046, 0.0048 and 0.0049 min−1, respectively, which should be compared with the value of 0.0050 min−1. Note that curve 2 in Fig. 2 ( and , i.e. without hydration and/or phlorizin injection), leads in the 360–420-min time range to an (under)estimate of 0.0023 min−1.
5 Discussion
Without needing any blood tracer sampling, when hydration and/or phlorizin injection are applied after the routine static PET acquisition, a two-compartment model analysis allows us to quantify the 18F-FDG release rate constant from a dynamic acquisition occurring at about 3 h after 18F-FDG injection. The later the dynamic acquisition, the more accurate the estimate, but, the greater the 18F-FDG release from the tissue, the more underestimated the value of . Moreover, this theoretical work presents a three-compartment model analysis, which supports the two-compartment one, and allows us to differentiate between the rate constants for 18F-FDG dephosphorylation and rephosphorylation, and , respectively. The principle of the present model analysis could be applied to other 18F-labelled tracers than the 18F-FDG, at the later decreasing phase of the tissue TAC, when the clearance of the tracer from plasma has occurred whereas it is still present in the tissue.
From Eq. (18) and literature data [9–11], Fig. 2 shows quite different 18F-FDG tissue TACs, related to different values of and of the late IF exponential constant . To the very best of our knowledge, the later decreasing phase of 18F-FDG tissue TACs and the significant parts of and have not been studied so far. It is suggested that, given the limited understanding of tumour metabolism, in addition to the quantification of the 18F-FDG uptake, the quantification of the 18F-FDG release could be investigated to characterize tumours, to differentiate malignant processes from infectious or inflammatory processes [13], and to assess the effects of treatment [7]. Furthermore, Patlak's graphical analysis for assessing 18F-FDG release rate constant requires an invasive arterial blood sampling and the acquisition of a dynamic PET scan that are performed during the first hour after the tracer injection [2–4]. In contrast, a similar assessment that can be obtained from the proposed graphical analysis appears to be easier to implement in a busy clinical environment, since it is non-invasive and requires a dynamic acquisition that occurs far from the static acquisition.
In conclusion, the principle of a graphical analysis that aimed at quantifying the rate constant for 18F-FDG release in tissues is presented, which is an extension of a recently published method for assessing the tracer uptake rate [5]. This whole method emphasizes the interest of the later decreasing phase of the 18F-FDG activity in tissues.
Acknowledgement
The authors wish to thank Schering-CISbiointernational for helpful discussion, and H. Dupouy and I. Hessling for technical assistance. They also thank an anonymous reviewer for his comments on the manuscript.


