Feasibility of an SUV normalization to 1 hour after the <sup>18</sup>F-FDG injection

Éric Laffon; Julie Vialard; Michèle Allard; Dominique Ducassou

doi:10.1016/j.crvi.2006.03.022

Medical sciences / Sciences médicales

Feasibility of an SUV normalization to 1 hour after the ¹⁸F-FDG injection
[Faisabilité d'une normalisation du SUV à 1 heure après injection du ¹⁸F-FDG]

Présenté par : Jean Rosa

Éric Laffon ^1,² ; Julie Vialard ^1,³ ; Michèle Allard ^1,³ ; Dominique Ducassou ¹

¹ Centre hospitalo-universitaire de Bordeaux, service de médecine nucléaire, hôpital du Haut-Lévêque, 33600 Pessac, France
² Laboratoire de physiologie cellulaire respiratoire, INSERM E356, université Victor-Ségalen–Bordeaux-2, 33076 Bordeaux, France
³ Laboratoire d'imagerie moléculaire et fonctionnelle, ERT–CNRS 5543, université Victor-Ségalen–Bordeaux-2, 33076 Bordeaux, France

Comptes Rendus. Biologies, Volume 329 (2006) no. 7, pp. 520-526.

Résumés

Anglais
Français

The aim of this work was to reduce the SUV variability related to the time delay between ¹⁸F-FDG injection and the static PET acquisition, by means of a normalization to a 1-h time delay. Two static PET acquisitions separated by approximately 1 h were performed on each of 14 cancer patients, with SUVs on 22 hypermetabolic lesions calculated for both scans. The pairs of SUVs were normalized to each other using the parameterized input function with one free parameter ( $α_{3}$ ). This optimized parameter was found by computing the value which yielded equal normalized SUV pairs, on average, over the whole series. Without normalization, SUVs measured at later scans were found to be significantly greater than the earlier ones: mean (± SD) ratio of 0.84 (±0.08; range 0.69–0.97). After normalization, with an $α_{3}$ value of 0.0257 min⁻¹, as expected, the mean (± SD) ratio was 1.00 (±0.07; range 0.88–1.10).

Une méthode de normalisation du SUV à 1 h après injection du ¹⁸F-FDG, afin de réduire sa dépendance par rapport au délai de temps entre injection et acquisition est présentée. Deux acquisitions statiques, séparées approximativement de 1 h, ont été acquises sur 14 patients atteints de cancers, et le SUV a été évalué pour 22 lésions apparaissant sur les deux acquisitions. Les paires de SUV ont été utilisées pour la normalisation, en introduisant une fonction d'entrée dont le paramètre $α_{3}$ a été optimisé en recherchant la valeur qui aboutissait en moyenne sur toute la série à des SUV normalisés égaux. Sans normalisation, le SUV tardif s'est révélé significativement plus élevé que le précoce : rapport moyen (± DS) de 0,84 ( $\pm 0, 08$ ; 0,69–0,97). Après normalisation ( $α_{3} = 0, 0257 {min}^{−1}$ ), le rapport moyen (± DS) des SUV normalisés est de 1,00 ( $\pm 0, 07$ ; 0,88 ; 1,10).

Métadonnées

Reçu le : 2005-10-14
Accepté le : 2006-03-04
Publié le : 2006-05-02

PMID

DOI : 10.1016/j.crvi.2006.03.022

Keywords: PET, Oncology, SUV correction, Kinetic modelling
Mot clés : TEP, Oncologie, Correction du SUV, Modèle cinétique

Affiliations des auteurs :

Éric Laffon ^{1, 2} ; Julie Vialard ^{1, 3} ; Michèle Allard ^{1, 3} ; Dominique Ducassou ¹

¹ Centre hospitalo-universitaire de Bordeaux, service de médecine nucléaire, hôpital du Haut-Lévêque, 33600 Pessac, France
² Laboratoire de physiologie cellulaire respiratoire, INSERM E356, université Victor-Ségalen–Bordeaux-2, 33076 Bordeaux, France
³ Laboratoire d'imagerie moléculaire et fonctionnelle, ERT–CNRS 5543, université Victor-Ségalen–Bordeaux-2, 33076 Bordeaux, France

@article{CRBIOL_2006__329_7_520_0,
     author = {\'Eric Laffon and Julie Vialard and Mich\`ele Allard and Dominique Ducassou},
     title = {Feasibility of an {SUV} normalization to 1 hour after the {\protect\textsuperscript{18}F-FDG} injection},
     journal = {Comptes Rendus. Biologies},
     pages = {520--526},
     publisher = {Elsevier},
     volume = {329},
     number = {7},
     year = {2006},
     doi = {10.1016/j.crvi.2006.03.022},
     language = {en},
}

TY  - JOUR
AU  - Éric Laffon
AU  - Julie Vialard
AU  - Michèle Allard
AU  - Dominique Ducassou
TI  - Feasibility of an SUV normalization to 1 hour after the 18F-FDG injection
JO  - Comptes Rendus. Biologies
PY  - 2006
SP  - 520
EP  - 526
VL  - 329
IS  - 7
PB  - Elsevier
DO  - 10.1016/j.crvi.2006.03.022
LA  - en
ID  - CRBIOL_2006__329_7_520_0
ER  -

%0 Journal Article
%A Éric Laffon
%A Julie Vialard
%A Michèle Allard
%A Dominique Ducassou
%T Feasibility of an SUV normalization to 1 hour after the 18F-FDG injection
%J Comptes Rendus. Biologies
%D 2006
%P 520-526
%V 329
%N 7
%I Elsevier
%R 10.1016/j.crvi.2006.03.022
%G en
%F CRBIOL_2006__329_7_520_0

Éric Laffon; Julie Vialard; Michèle Allard; Dominique Ducassou. Feasibility of an SUV normalization to 1 hour after the ¹⁸F-FDG injection. Comptes Rendus. Biologies, Volume 329 (2006) no. 7, pp. 520-526. doi : 10.1016/j.crvi.2006.03.022. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2006.03.022/

Version originale du texte intégral

1 Introduction

Patlak's analysis and compartmental analysis are considered as gold-standards for assessing the ¹⁸F-FDG uptake rate constant in tumours, hence tumour glucose metabolism [1–4]. However, these methods are invasive and cumbersome, as they require a serial arterial blood sampling, and a dynamic data acquisition for about one hour after tracer injection. Alternative simplified kinetic analyses have been proposed to reduce invasiveness of blood sampling by using a single venous sample or by using data from left ventricle or aorta blood appearing in images [5,6]. In comparison with these quantitative dynamic approaches, the semiquantitative SUV index is currently used in clinical practice, since it can be directly provided by static PET images [7]. Nevertheless, it has been shown that the SUV suffered from several shortcomings which are mainly [8,9]: (i) the injected dose/weight ratio is only a surrogate for the available tracer dose to the tumour; (ii) both the trapped and unmetabolized tracer are taken into account; (iii) the time duration between injection and data static acquisition affects the SUV. The aim of the present work was to reduce the SUV variability related to the injection-acquisition time delay. A recently published two-compartment model [10] has been further developed to compute the SUV at one hour after ¹⁸F-FDG injection, i.e. to normalize the SUV to 1 h, from the SUV obtained at an arbitrary PET static examination start.

2 Methods

2.1 SUV normalization

Assuming ¹⁸F-FDG is trapped in an irreversible manner, a two-compartment model has recently allowed us to derive the time–activity curve (TAC) of trapped tracer in a tumour [10]:

λ C_{T} (t) = K λ C_{p} (t = 0) (e^{- λ t} - e^{- α t}) / (α - λ)

(1)

where

C_{T} (t)

is the trapped ¹⁸F-FDG concentration in the tumour, λ (

= 0.693 / 110 {mn}^{−1}

) is the physical decrease constant of the tracer, (hence

λ C_{T} (t)

represents the trapped ¹⁸F-FDG activity per tumour volume unit which can be measured), K is the uptake rate constant, and

C_{p} (t = 0)

represents the tracer concentration in the plasma at the blood tracer peak. Eq. (1) assumes that the ¹⁸F-FDG blood TAC decays with a mean constant ‘α’, however, it has been shown that the ¹⁸F-FDG plasma clearance was multiexponential. Assuming a tri-exponential input function (IF), [5], Eq. (1) becomes:

λ C_{T} (t) = K λ f (t)

(2)

with

f (t) = \sum_{i = 1}^{3} H_{i} (e^{- λ t} - e^{- α_{i} t}) / (α_{i} - λ)

(3)

where

H_{i}

and

α_{i}

are the coefficients of the tri-exponential IF [5]. Consequently, at

t = 60

min the trapped tracer activity per tumour volume unit is:

λ C_{T} (60) = K λ f (60)

(4)

Substituting K by its value in Eq. (2) and rearranging, yields the following expression for the trapped tracer activity at 1 h after injection:

λ C_{T} (60) = λ C_{T} (t) f (60) / f (t)

(5)

where

λ C_{T} (t)

represents the trapped ¹⁸F-FDG activity per tumour volume unit at any time after tracer injection.

Let us now consider the SUV at time t, which is defined as:

SUV (t) = λ C_{Tot} (t) W / A_{inj}

(6)

where

λ C_{Tot} (t)

is the total tracer activity in the whole tumour volume (free ¹⁸F-FDG in blood and tissue, and trapped ¹⁸F-FDG),

A_{inj}

is the injected tracer activity, and W is the patient's weight. At

t = 60 min

, since

C_{Tot} (60)

is a surrogate for

C_{T} (60)

[8,9], introducing Eq. (4) in Eq. (6), and rearranging, yields:

SUV (60) = SUV (t) f (60) / f (t)

(7)

2.2 Patients and data acquisition

The investigation conforms with the principles outlined in the Declaration of Helsinki. An institutional ethics committee has approved the study and informed consent was obtained, after the procedure has been explained, from all of the subjects. A total of 14 patients (three females, eleven males) were included in this study. Table 1 presents patients' ages, weights, and heights. No patient suffered from known impaired renal or hepatic function. All patients presented primary or metastatic cancer: lung (6 primary, 5 metastatic), head and neck (2 primary), colon (1 primary). After a 6 hour fasting, preinjection blood glucose levels averaged 96 mg/dl (±16; range 61–129 mg/dl; 129 mg/dl for patient 1 with type II diabetes). Approximately 340 MBq of ¹⁸F-FDG was injected intravenously over less than 1 min (Table 1).

Patient and acquisition data	Results
Patient	No. of lesion	Age (year)	Weight (kg)	Height (cm)	Glycaemia (mg/dl)	$A_{inj}$ (MBq)	$t_{1}$ (min)	$t_{2}$ (min)	$t_{2} - t_{1}$ (min)	SUV₁/SUV₂	SUV_N1/SUV_N2	$α_{3}$ (min⁻¹)
1	1	69	67	169	129	320	105	172	67	0.87	0.95	0.0212
2	1	65	62	162	106	315	92	165	73	0.84	0.95	0.0218
	2						92	165	73	0.94	1.06	0.0334
3	1	40	56	160	90	298	94	150	56	0.97	1.08	0.0417
	2						94	150	56	0.91	1.01	0.0269
4	1	64	75	178	89	353	83	170	87	0.91	1.08	0.0328
5	1	75	77	175	96	344	73	158	85	0.87	1.07	0.0310
6	1	50	78	172	113	441	56	155	99	0.79	1.10	0.0312
7	1	67	92	167	109	448	62	140	78	0.69	0.90	0.0197
8	1	57	55	165	84	237	72	170	98	0.84	1.05	0.0292
	2						72	170	98	0.72	0.90	0.0205
9	1	68	54	164	97	280	72	150	78	0.72	0.88	0.0188
10	1	69	85	172	89	410	82	155	73	0.80	0.94	0.0212
	2						82	155	73	0.76	0.89	0.0184
	3						82	155	73	0.76	0.89	0.0183
11	1	61	60	178	61	312	125	175	50	0.91	0.96	0.0201
12	1	59	62	162	100	330	84	147	63	0.87	1.01	0.0263
13	1	73	70	182	84	365	70	128	58	0.86	1.03	0.0288
14	1	50	70	165	101	300	67	116	49	0.91	1.09	0.0362
	2						70	116	46	0.88	1.04	0.0296
	3						70	116	46	0.89	1.06	0.0320
	4						70	116	46	0.88	1.04	0.0299

Mean		62	69	169	96	340	80	150	69	0.84	1.00	0.0268
SD		10	12	7	16	60	16	20	17	0.08	0.07	0.0066

All ¹⁸F-FDG PET examinations were acquired on a PET-scan discovery ST (General Electric Medical System) in 3D mode, without septa, producing 47 slices over an approximately 150-mm axial field of view, and a 3-min time of acquisition per step. The imaging acquisition parameters were in-plane and axial resolution of 3.91 and 3.27 mm FWHM, respectively, in plane field of view of 600 mm, 128 ×128 pixel matrix. An image matrix of $256 \times 256$ pixel was used for iterative reconstruction (FORE + OSEM; subsets: 32; iterations: 5; Gaussian filter: 5.14 mm FWHM). CT transmission scans were acquired previously to the PET scanner for attenuation correction: pitch of 1.675, slice thickness of 2.5 mm, in plane field of view of 500 mm, $512 \times 512$ pixel matrix.

Patients underwent a first PET static acquisition for diagnostic purposes, involving several steps to cover a large part of the body. A second PET static acquisition was achieved at 69 min, on average, after the first (range 46–99 min), with identical acquisition parameters, but involving only one step over hypermetabolic lesions which appeared in the first one. Injection-acquisition time delays for the first (time $t_{1}$ ) and the second static acquisition (time $t_{2}$ ) are given in Table 1. For the first acquisition, the time $t_{1}$ corresponds to the acquisition of the particular step involving hypermetabolic lesions which were studied, and does not correspond to the start of the whole of the scan.

2.3 Evaluation of the SUV optimization

Maximal SUV normalized to patient's body weight was assessed over a total of 22 hypermetabolic lesions which appeared in the two static acquisitions (Xeleris station). For each hypermetabolic lesion, this SUV was assessed by investigating contiguous slices over the whole of the lesion, leading to SUV₁ and SUV₂ for the two acquisitions, respectively. Note that these former values were given by the manufacturer with a decay-correction. From each of these values (and taking into account the manufacturer decay-correction) 1-h-normalized SUV was also computed by using Eqs. (7) and (3) in order to get SUV_N1 and SUV_N2 for each lesion in each acquisition, respectively. The computation of these latter values was achieved on a Microsoft Excel sheet, and required to introduce a tri-exponential IF (Eq. (3)) [5]. The respective contribution of each IF monoexponential function (IF₁, IF₂, IF₃) to the whole blood ¹⁸F-FDG amount which is available for the tumour, should be compared. Each available amount is given by the area under the corresponding curve, and then is equal to $H_{i} \times [1 - \exp (- α_{i} t)] / α_{i}$ , at any time t after injection, respectively. From Hunter's results [5], after a bolus injection, for an injection-acquisition time delay of 55 min, the order of magnitude of the averaged relative contribution of IF₁, IF₂, and IF₃ are 2%, 9%, and 89%, respectively. In other words, the SUV mainly depends on the third exponential function ( $H_{3} - α_{3}$ ). Consequently, four coefficients of the tri-exponential IF, namely $H_{1} - α_{1}$ and $H_{2} - α_{2}$ , were set according to Hunter's results for a tracer bolus injection, i.e. $5943 - 9.33$ and $851 - 0.289$ , respectively. Then, the Excel solver program was used to target the SUV_N1/SUV_N2 ratio to a value of 1, by optimizing $H_{3} - α_{3}$ from Hunter's values of $725 - 0.0125$ , respectively [5]. First, in order to validate the method, this procedure was carried out over the first 7 patients (9 hypermetabolic lesions), and then the optimized values of $H_{3} - α_{3}$ were arbitrarily applied in each of the remaining 7 patients (13 hypermetabolic lesions). Second, further optimized values of $H_{3}$ and $α_{3}$ were computed by targeting the SUV_N1/SUV_N2 ratio to a value of 1 over the whole lesion series. Finally, the same procedure was also independently used for each hypermetabolic lesion, to obtain optimized values of $H_{3}$ and $α_{3}$ by targeting the SUV_N1/SUV_N2 ratio of each hypermetabolic lesion to a value of 1, respectively.

3 Results

The validation of the method, with two sub-series of patients, is presented in Table 2: the mean SUV_N1/SUV_N2 ratio (±95% reliability domain; Student's t distribution) for each group was $1.00 \pm 0.05$ (optimized $H_{3} - α_{3}$ over the first subseries was $725 - 0.0276$ ; $H_{3}$ did not change in comparison with Hunter's value) and $0.96 \pm 0.04$ ( $H_{3} - α_{3}$ arbitrarily taken equal to $725 - 0.0276$ for each lesion), respectively, showing no significant difference between the two groups.

Table 2

An optimized $α_{3}$ value of 0.0276 was found by using the Excel solver program to target the SUV_N1/SUV_N2 ratio to a value of 1 over the first 7 patients (9 hypermetabolic lesions). The optimization left $H_{3}$ unchanged (725). Then, the optimized value of $α_{3}$ was arbitrarily applied in each of the 13 hypermetabolic lesions of the remaining 7 patients. The mean SUV_N1/SUV_N2 ratio (±95% reliability domain; Student's t distribution) for each group was 1.00±0.05 and 0.96±0.04, showing no significant difference between the two subseries

First 7 patients	Last 7 patients
Patient	No. of lesion	SUV₁/SUV₂	SUV_N1/SUV_N3	Patient	No. of lesion	SUV₁/SUV₂	SUV_N1/SUV_N2
1	1	0.87	0.94	8	1	0.84	1.02
2	1	0.84	0.93		2	0.72	0.88
	2	0.94	1.04	9	1	0.72	0.86
3	1	0.97	1.07	10	1	0.80	0.92
	2	0.91	0.99		2	0.76	0.87
4	1	0.91	1.05		3	0.76	0.87
5	1	0.87	1.04	11	1	0.91	0.95
6	1	0.79	1.06	12	1	0.87	0.99
7	1	0.69	0.87	13	1	0.86	1.01
				14	1	0.91	1.07
					2	0.88	1.02
					3	0.89	1.04
					4	0.88	1.02

Mean		0.86	1.00			0.83	0.96
SD		0.08	0.07			0.07	0.07

The normalization procedure over the whole series provided further optimized values of $H_{3}$ and $α_{3}$ , which were found to be 725 ( $H_{3}$ did not change in comparison with Hunter's value) and 0.0257 min⁻¹, respectively (Table 1). As expected, the related mean SUV_N1/SUV_N2 ratio (±95% reliability domain; Student's t distribution) was $1.00 \pm 0.03$ (range 0.88–1.10; SD: 0.07), whereas, without normalization, the mean SUV₁/SUV₂ ratio (±95% reliability domain; Student's t distribution) was $0.84 \pm 0.03$ (range 0.69–0.97; SD: 0.08), indicating that the late (decay-corrected) SUV was significantly greater than the earlier one ( $p < 0.05$ ). After optimization over the whole lesion series, no significant correlation was found between the individual SUV_N1/SUV_N2 ratios and any of the following parameters: injected activity, patient's age, weight, height, pre-injection blood glucose level, time delay between injection and first PET acquisition, time delay between injection and second PET acquisition, time delay between the two acquisitions. It should be noted that we additionally checked that no optimization of $H_{1} - α_{1}$ and $H_{2} - α_{2}$ was possible (with $H_{3} - α_{3}$ fixed and the other 4 parameters left free and the system optimized again).

When the optimization procedure was independently performed for each hypermetabolic lesion, different optimized values of $α_{3}$ were found (Table 1). The mean value (±SD) over the $α_{3}$ series was 0.0268 min⁻¹ (±0.0066), which is slightly different from that found from the whole series. (The $H_{3}$ value for each lesion was again equal to 725.) A significant correlation was found between the SUV_N1/SUV_N2 ratio for each hypermetabolic lesion (penultimate column in Table 1), which was obtained with the optimized average $α_{3}$ value of 0.0257 min⁻¹, and the $α_{3}$ value independently optimized for each hypermetabolic lesion (last column in Table 1), respectively (Fig. 1; $r = 0.94$ ).

Fig. 1
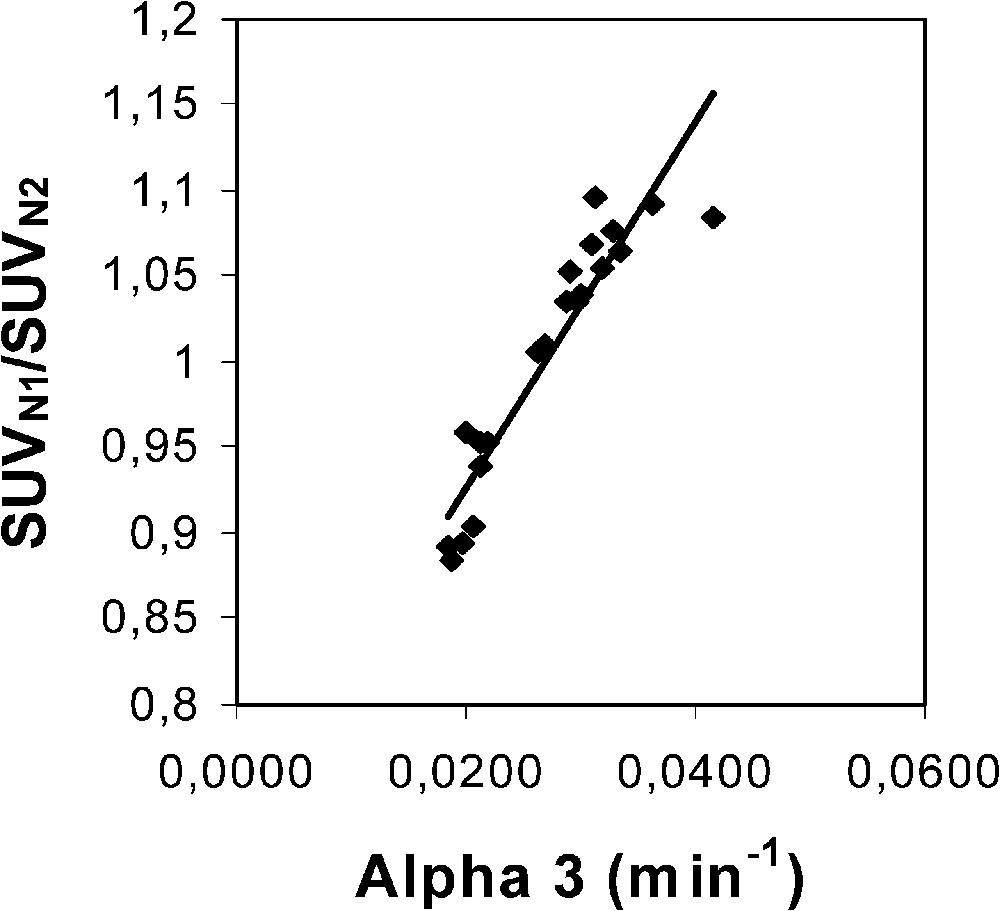
Plot of the SUV_N1/SUV_N2 ratio for each hypermetabolic lesion (penultimate column in Table 1), which was obtained with an optimized average $α_{3}$ value of 0.0257 min⁻¹ over the whole lesion series, versus the $α_{3}$ values independently optimized for each hypermetabolic lesion (last column in Table 1). The optimization did not change the $H_{3}$ value in comparison with Hunter's value (725). The optimized average $α_{3}$ value was found by using the Excel solver program to target the mean SUV_N1/SUV_N2 ratio over the whole lesion series to a value of 1, whereas the $α_{3}$ values of the x-axis were obtained by independently targeting the SUV_N1/SUV_N2 ratio of each hypermetabolic lesion to a value of 1, respectively. Equation of the linear fit is: y=10.57 x+0.72 (r=0.94).

The range of the SUV_N1/SUV_N2 ratio indicates that the normalization is efficient with a 7% SD and a 12% maximal relative measurement uncertainty (Table 1). Assuming that the measurement uncertainty of the time $t_{1}$ is 3 min, i.e. that of a step time duration, the change in the SUV_N1/SUV_N2 ratio related to a ±3-min change in $t_{1}$ has been assessed for each lesion (by computing on the Excel sheet), with an optimized average $α_{3}$ value of 0.0257 min⁻¹ (see above). This measurement uncertainty has been estimated to be 1.5% on average (range 0.5–3.0%). Moreover, Fig. 2 shows the plot of the SUV_N1/SUV_N2 ratio uncertainty related to a 3-min $t_{1}$ uncertainty, computed for each lesion, versus $t_{1}$ : the equation of the fit is $y = - 0.033 x + 4.182$ ( $r = 0.91$ ).

Fig. 2
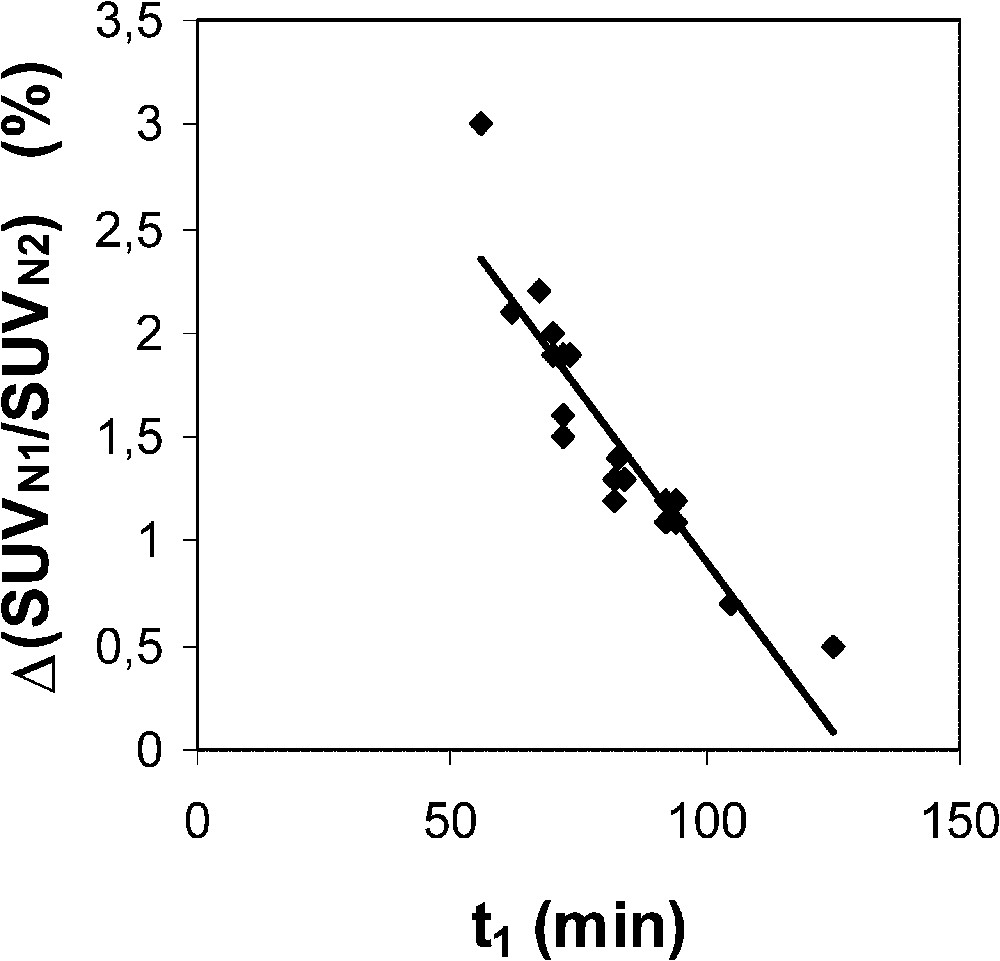
Plot of the SUV_N1/SUV_N2 ratio uncertainty related to a 3-min uncertainty of the time delay between injection and the first static acquisition ( $t_{1}$ ), computed for each lesion, versus $t_{1}$ . ( $α_{3}$ is set at 0.0257 min⁻¹.) Equation of the linear fit is y=−0.033 x+4.182 (r=0.91).

4 Discussion

This work shows that a non invasive SUV normalization to 1 h after ¹⁸F-FDG injection is feasible, in order to significantly reduce changes in the SUV related to the injection-acquisition time-delay. Although the principle of the method would allow us to normalize the SUV to any arbitrary time ( $t = 120 min$ , for example), the 1-h-normalization was chosen in order to keep usual landmarks of clinical practice. Before normalization, the late SUV was always found to be greater than the early one, up to 31%, i.e. the SUV₁/SUV₂ ratio was significantly lower than 1. As expected after normalization, with an optimized $α_{3}$ value of 0.0257 min⁻¹, the mean SUV_N1/SUV_N2 ratio was 1, with a standard deviation and a maximal relative measurement uncertainty equal to 7 and 12%, respectively.

The main part of the measurement uncertainty of the 1-h-normalized SUV is very likely related to known phenomena which influence the quantification of lesion activity [11]. Among these phenomena, in the present experiment design, it is suggested that scattered radiations, attenuation correction (in particular for lower lung lesions due to respiratory motion), and partial volume effect are responsible for the main part of the measurement uncertainty. However, the measurement uncertainty of the proposed normalization procedure is also partly related to the $t_{1}$ measurement uncertainty. A 3-min $t_{1}$ uncertainty leads to averaged and maximal changes in the ratio of 1.5 and 3%, respectively. Moreover, Fig. 2 clearly indicates that the earlier the first static acquisition, i.e. the shorter the time $t_{1}$ , the greater the measurement uncertainty in the 1-h-normalized SUV. Considering that the proposed normalization does allow us to assess the 1-h-normalized SUV from an acquisition achieved beyond 1 h after injection, it is then possible to partly lower the measurement uncertainty. In addition, it should be noted that the later the acquisition, the lower the part of the contribution of IF₁ and IF₂ to the whole blood ¹⁸F-FDG amount which is available for the tumour, and the more reliable is the only IF₃ optimization of the proposed normalization. A third origin of the measurement uncertainty of the 1-h-normalized SUV is likely related to the variability of the time constant $α_{3}$ for the decay of the slowest blood component of the input function. This constant plays a major role in ¹⁸F-FDG uptake, which is both supported by Hunter's results [5] and the present ones. However, there is a discrepancy between Hunter's average value of $α_{3}$ and that of the present results, 0.0125 and 0.0257 min⁻¹, respectively. Firstly, it should be noted that, to the very best of our knowledge, the ¹⁸F-FDG plasma clearance far beyond 1 h after injection has not been extensively studied. Secondly, Hunter's paper does not clearly state whether the ¹⁸F-FDG blood TACs have been corrected for the physical decay of the tracer before performing the tri-exponential fit: therefore, adding 0.0063 (= ln 2/110) to 0.0125 min⁻¹ would lead to a value of 0.0188 min⁻¹, which would get closer to that of the present results. Thirdly, Fig. 3 shows a comparison between two theoretical tumour TACs obtained with a tri-exponential IF involving the $α_{3}$ value by Hunter et al. and that of the present results (Eq. (3)), respectively. Simulation from Hunter's IF shows that the maximal activity in the tumour occurs at about 105 min after the tracer injection (70 min for that of the present results), that is not realistic. Finally, it should be noted that the proposed $α_{3}$ optimization affects the SUV, which involves all the tissue activity, from both trapped tracer and free tracer in blood and interstitial volumes [10] (Eq. (6)). This feature may also explain an overestimated $α_{3}$ value in comparison with that of Hunter et al., since the amount of free tracer in blood and interstitial volumes is greater at early imaging than at late imaging. Nevertheless, the major role of $α_{3}$ in ¹⁸F-FDG uptake is highlighted in the present experiments by the significant correlation (Fig. 1; $r = 0.94$ ) between the SUV_N1/SUV_N2 ratios for each hypermetabolic lesion, which were obtained with an optimized average $α_{3}$ value of 0.0257 min⁻¹ over the whole lesion series, and the $α_{3}$ values which were independently optimized for each hypermetabolic lesion. As a consequence, this correlation shows that the proposed non-invasive normalization procedure unavoidably involves a measurement uncertainty related to a $α_{3}$ variability.

Fig. 3
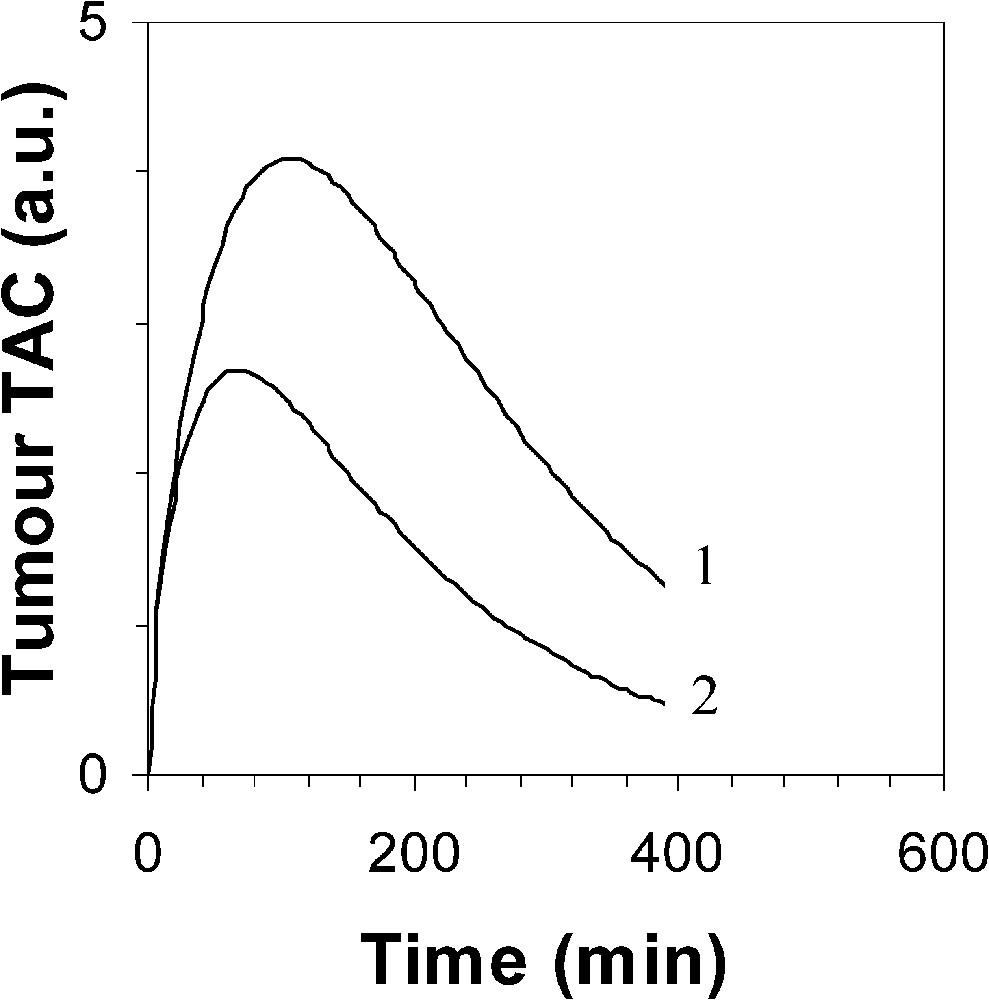
Simulated ¹⁸F-FDG tumour TAC using a tri-exponential IF (1) by Hunter et al. with $α_{3} = 0.0125 {min}^{−1}$ , and (2) with $α_{3} = 0.0257 {min}^{−1}$ ( $H_{3}$ value is 725 for both TAC).

In conclusion, a non invasive SUV normalization to 1 h after ¹⁸F-FDG injection is feasible, which could allow the physician to plan PET examinations with more flexibility about the injection-acquisition time delay. Although a larger number of cancer patients is required to assess more precisely the measurement uncertainty of the 1-h-normalized SUV, the presented preliminary results indicate that it is very likely reasonable (7% SD for the present series of 14 cancer patients), and that it could be partly lowered when the acquisition is achieved beyond one hour after injection.

Acknowledgements

The authors would like to thank the patients who participated in the study and their physicians. They gratefully acknowledge helpful discussions with GE Health Care engineers and with Schering CISbiointernational, the manuscript editing of Isabelle Hessling, and the technical assistance of Henri Dupouy.

Bibliographie

[1] L. Sokoloff; M. Reivich; C. Kennedy; M.H. Des Rosiers; C.S. Patlak; K.D. Pettigrew; O. Sakurada; M. Shinohara The [¹⁴C]deoxyglucose method for the measurement of local cerebral glucose utilization: theory, procedure, and normal values in the conscious and anesthetized albino rat, J. Neurochem., Volume 28 (1977), pp. 897-916

[2] C.S. Patlak; R.G. Blasberg; J.D. Fenstermacher Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data, J. Cereb. Blood Flow Metab., Volume 3 (1983), pp. 1-7

[3] C.S. Patlak; R.G. Blasberg Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data: generalizations, J. Cereb. Blood Flow Metab., Volume 5 (1985), pp. 584-590

[4] M.E. Phelps; S.C. Huang; E.J. Hoffman; C. Selin; L. Sokoloff; D.E. Kuhl Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18)2-Fluoro-2-Deoxy-d-Glucose: validation of method, Ann. Neurol., Volume 6 (1979), pp. 371-388

[5] G.J. Hunter; L.M. Hamberg; N.M. Alpert; N.C. Choi; A.J. Fischman Simplified measurement of deoxyglucose utilization rate, J. Nucl. Med., Volume 37 (1996), pp. 950-955

[6] S.K. Sundaram; N.M.T. Freedman; J.A. Carrasquillo; J.M. Carson; M. Whatley; S.K. Libutti; D. Sellers; S.L. Bacharach Simplified kinetic analysis of tumor ¹⁸F-FDG uptake: a dynamic approach, J. Nucl. Med., Volume 45 (2004), pp. 1328-1333

[7] H.S.C. Huang Anatomy of SUV, Nucl. Med. Biol., Volume 27 (2000), pp. 643-646

[8] L.M. Hamberg; G.J. Hunter; N.M. Alpert; N.C. Choi; J.W. Babich; A.J. Fischman The dose uptake ratio as an index of glucose metabolism: useful parameter or oversimplification?, J. Nucl. Med., Volume 35 (1994), pp. 1308-1312

[9] N.M. Freedman; S.K. Sundaram; K. Kurdziel; J.A. Carrasquillo; M. Whatley; J.M. Carson; D. Sellers; S.K. Libutti; J.C. Yang; S.L. Bacharach Comparison of SUV and Patlak slope for monitoring of cancer therapy using serial PET scans, Eur. J. Nucl. Med., Volume 30 (2003), pp. 46-53

[10] E. Laffon; M. Allard; R. Marthan; D. Ducassou A method to quantify the uptake rate of 2-[¹⁸F]fluoro-2-deoxy-d-glucose in tissues, Nucl. Med. Commun., Volume 25 (2004), pp. 851-854

[11] S.R. Meikle; R.D. Badawi Positron Emission Tomography: Basic Science and Clinical Practice (P.E. Valk; D.L. Bailey; D.W. Townsend; M.N. Maisey, eds.), Springer-Verlag London Limited, 2003, pp. 115-146

Commentaires - Politique