Dynamical and statistical models of vertebrate population dynamics

Jean-Dominique Lebreton

doi:10.1016/j.crvi.2006.06.007

Population biology / Biologie des populations

Dynamical and statistical models of vertebrate population dynamics
[Modèles dynamiques et statistiques et dynamique des populations de Vertébrés]

Présenté par : Pierre Buser

Jean-Dominique Lebreton ¹

¹ CEFE, UMR 5175, 1919, route de Mende, 34293 Montpellier cedex 5, France

Comptes Rendus. Biologies, Volume 329 (2006) no. 10, pp. 804-812.

Résumés

Anglais
Français

Population dynamics methodology now powerfully combines discrete time models (with constant parameters, density dependence, random environment, and/or demographic stochasticity) and capture–recapture models for estimating demographic parameters. Vertebrate population dynamics has strongly benefited from this progress: survival estimates have been revised upwards, trade-offs between life history traits have been demonstrated, analyses of population viability and management are more and more realistic. Promising developments concern random effects, multistate and integrated models. Some biological questions (density dependence, links between individual and population levels, and diversification of life histories) can now be efficiently attacked.

En dynamique des populations, une méthodologie puissante combine désormais modèles en temps discret (à paramètres constants, densité-dépendants, avec environnement aléatoire ou stochasticité démographique...) et modèles de capture–recapture d'estimation des paramètres démographiques. La biologie des populations de Vertébrés a fortement bénéficié de ces progrès : estimations de survie révisées à la hausse, mise en évidence de compensations entre traits démographiques, analyses de viabilité ou de gestion des populations de plus en plus réalistes. Des développements prometteurs (effets aléatoires, modèles intégrés et multi-états) permettent d'aborder diverses questions biologiques ouvertes (densité-dépendance, liens entre niveaux individuel et populationnel, diversification des histoires de vie).

Métadonnées

Reçu le : 2006-06-22
Accepté le : 2006-06-27
Publié le : 2006-08-04

PMID

DOI : 10.1016/j.crvi.2006.06.007

Keywords: Population dynamics, Models, Capture–recapture, Vertebrates
Mot clés : Dynamique des populations, Modèles, Capture–recapture, Vertébrés

Affiliations des auteurs :

Jean-Dominique Lebreton ¹

¹ CEFE, UMR 5175, 1919, route de Mende, 34293 Montpellier cedex 5, France

@article{CRBIOL_2006__329_10_804_0,
     author = {Jean-Dominique Lebreton},
     title = {Dynamical and statistical models of vertebrate population dynamics},
     journal = {Comptes Rendus. Biologies},
     pages = {804--812},
     publisher = {Elsevier},
     volume = {329},
     number = {10},
     year = {2006},
     doi = {10.1016/j.crvi.2006.06.007},
     language = {en},
}

TY  - JOUR
AU  - Jean-Dominique Lebreton
TI  - Dynamical and statistical models of vertebrate population dynamics
JO  - Comptes Rendus. Biologies
PY  - 2006
SP  - 804
EP  - 812
VL  - 329
IS  - 10
PB  - Elsevier
DO  - 10.1016/j.crvi.2006.06.007
LA  - en
ID  - CRBIOL_2006__329_10_804_0
ER  -

%0 Journal Article
%A Jean-Dominique Lebreton
%T Dynamical and statistical models of vertebrate population dynamics
%J Comptes Rendus. Biologies
%D 2006
%P 804-812
%V 329
%N 10
%I Elsevier
%R 10.1016/j.crvi.2006.06.007
%G en
%F CRBIOL_2006__329_10_804_0

Jean-Dominique Lebreton. Dynamical and statistical models of vertebrate population dynamics. Comptes Rendus. Biologies, Volume 329 (2006) no. 10, pp. 804-812. doi : 10.1016/j.crvi.2006.06.007. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2006.06.007/

Version originale du texte intégral

1 Introduction

Population dynamics studies aim at understanding variation in the size and structure of populations. This variation results from flows of individuals, which, together with flows of matter and energy and flows of genes are one of the three dominant dynamics of the living world. In population dynamics, the effects of births, deaths and dispersal, affected by various sources of variation [1], accumulate over time in a multiplicative process. As a consequence, population dynamics is often counter-intuitive [2] and mathematical models have been early and widely used [3,4].

With the development of computers, population dynamics modelling has developed explosively for the last 40 years. Vertebrate population studies have played a major role in this development, for at least three reasons: a wide diversity of life cycles (generation time ranges from a few weeks in small rodents to decades in whales or elephants), the fact that vertebrates can be counted, observed and marked relatively easily, and concerns on the impact of human activities on vertebrate populations [5,6]. Moreover, as discussed later, because of their sensitivity to demographic changes, vertebrates are good indicators of the impact of human activities on ecological systems.

I review here progress in population dynamics models, and how it has improved our understanding of vertebrate population ecology. I consider statistical and dynamical models, with an emphasis on empirical approaches. Mixing modelling and biological ideas, this text is intended for a wide audience, while keeping references to a minimum and not pretending to exhaustiveness in such a rapidly evolving field. In particular, little mention will be made of population dynamics studies of marine resources [7], despite strikingly parallel developments.

Studies of vertebrate populations have paid attention for a long time to survival [8], fecundity [9] and dispersal [10], broadly called ‘vital rates’, as life history traits of particular interest. In the 1950s and 1960s, density dependence in vital rates, acting as a negative feedback on population growth [11], was opposed to density-independent variation [11,12] in a long controversy [13]: the impossibility of long-term exponential growth requires density dependence, while density-independent environmental variation in vital rates is often prominent in empirical studies.

I will review progress since this period in dynamical models (Section 2) and in statistical ones (Section 3), which changed markedly our knowledge of vital rates and in turn our understanding of vertebrate population dynamics (Section 4), to conclude by a general discussion (Section 5).

2 The development of discrete time models

Dynamical population models consider changes in population size and structure over time. At one extreme, population size can be reduced to a scalar, neglecting any structure. At the other, population size can be viewed as a function of several real variables, such as age, body weight, or spatial coordinates. The time scale can be continuous or discrete. A wide and convenient type of models considers a discrete time scale and a discrete structure based on classes of individuals (age or size classes, sites or ‘patches’). Population at time t is then represented as a non-negative vector $N_{t}$ . Age-structured models with age class length equal to the time step are particularly straightforward [14], although developmental stages, sites or general states can be also considered and possibly combined with age [15–17].

A deterministic discrete time model consists then of a recurrence equation $N_{t + 1} = M (N_{t}) N_{t}$ , where $M (N_{t})$ is a square matrix. Matrix models sensu lato, excellently reviewed by Caswell [15], have several advantages:

– they are computationally practical [18], easily studied and communicated to biologists;
– they are easily generalized (Table 1), similar generalizations for other types of models [19] being generally more involved;
– they are biologically relevant for a seasonal environment, as common for vertebrates, and easily built from life cycle graphs, with vital rates as natural parameters (Figs. 1 and 2, about the White Stork C. ciconia [20]).

Feature	Recurrence equation	Type of model	Mathematical tools	Recent key reference
Constant parameters	$N_{t + 1} = M N_{t}$	Matrix models stricto sensu	Linear algebra	[15]
Density dependence	$N_{t + 1} = M (N_{t}) N_{t}$	Density-dependent matrix models, Discrete time logistic growth	Nonlinear dynamics	[15]
Random environment	$N_{t + 1} = M_{t} N_{t}$	Random environment models	Products of random matrices	[29]
Demographic stochasticity	$E (N_{t + 1} / N_{t}) = M N_{t}$	Branching processes	Applied probability	[31]

Fig. 1
Typical seasonal life-cycle graph for a vertebrate in a seasonal environment: the Alsace population of White Stork C. ciconia. The cycle goes from a pre-breeding season to the next. The females in the population are grouped in four age classes (1, 2, 3, and 4 or more years, respectively). First, one distinguishes the breeders, in proportion $U_{3}$ , among the individuals of age 3; all individuals aged 4 or more years breed. Reproduction takes place, producing f females aged 0 per breeding female. The survivors (in proportions $s_{1}$ and $s_{A}$ , depending on age) move in the next age class during the internuptial season; individuals aged 4 or more stay in that final age class.

Fig. 2
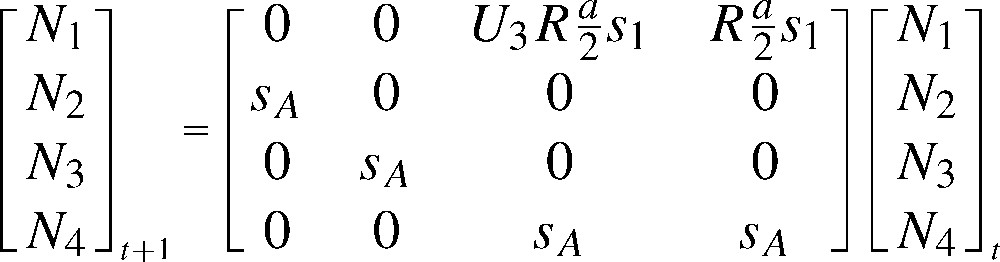
Matrix model for the Alsace population of the White Stork Ciconia ciconia (after [20]), deduced from the life cycle in Fig. 1. The matrix recurrence transforms the pre-breeding numbers of females at time t into those at time t+1. Newborn females enter the population at age 1 in $N_{1}$ , based on fecundity per female multiplied by first year survival, $s_{1}$ . Older individuals survive in proportion $s_{A}$ . The individuals aged 4 years or more are grouped into $N_{4}$ . The fecundity f is the product of a success probability R and a number of young raised per successful pair, a (divided by 2 to obtain a fecundity in female per female, assuming a balanced sex ratio at birth). A proportion $U_{3} < 1$ of females is supposed to reproduce at age 3, while all older individuals breed. Under $U_{3} = 0.475$ , R=0.800, a=3.000, $s_{1} = 0.482$ , $s_{A} = 0.750$ , the asymptotic population growth rate is λ=1.0195 and the generation time $\bar{T} = 6.2309 yr$ .

The asymptotic behaviour of constant parameter matrix models $N_{t + 1} = M N_{t}$ is well known [15]: under mild assumptions, the matrix M has a real positive dominant eigenvalue $ρ (M)$ associated to a positive right eigenvector, which give the asymptotic growth rate and structure of the population, respectively. The left eigenvector, also positive, consists of ‘reproductive values’, interpretable as relative age or stage specific contributions to growth. Constant parameter matrix models, albeit restrictive, are extremely useful for population ‘projections’, i.e., predictions valid under the current parameter values [15]. The asymptotic growth rate $ρ (M)$ is a nonlinear and non-explicit function of demographic parameters: sensitivity analysis helps understanding its variation with respect to the parameters. Generation time (the mean age of mothers at birth in the asymptotic population structure [21]) plays there a central role: for instance, the relative sensitivity (or ‘elasticity’) of $ρ (M)$ to a change in all fecundity parameters is the inverse of generation time [22,23]. In all long lived species, survival is thus the most sensitive parameter (White Stork: Table 2).

Parameter θ	Asymptotic growth rate λ	Elasticity, numerical $\frac{(Δ λ / λ)}{(Δ θ / θ)}$	Elasticity, formal $\frac{(Δ λ / λ)}{(Δ θ / θ)}$
		Based on a 2% change in parameter
Proportion of successful nests R	1.0228	0.1596	$\frac{1}{\bar{T}} = 0.1605$
Number of young per successful pair a	1.0228	0.1596	$\frac{1}{\bar{T}} = 0.1605$
First year survival $s_{1}$	1.0228	0.1596	$\frac{1}{\bar{T}} = 0.1605$
After first year survival $s_{A}$	1.0366	0.8386	$1 - \frac{1}{\bar{T}} = 0.8395$
Overall survival, $s_{1}$ and $s_{A}$	1.0399	1.0000	1.0000

One can distinguish between individuals just appeared in the population, by birth or immigration, as $F N_{t}$ , and other individuals, resulting from survival or dispersal within the population, as $T N_{t}$ [15]. The resulting model equation $N_{t + 1} = (F + T) N_{t}$ considers growth and turnover, closely linking matrix models with the stable population theory [3,24] and renewal theory [16]. One may easily show that the asymptotic proportion of new individuals, if counted in reproductive value, is the inverse of generation time. Reproductive value is also the relevant currency to compare flows of individuals in dispersal [25] or optimal harvesting [26] models. Generation time and reproductive value appear thus besides growth rate and population structure as key concepts and outputs of demographic models.

In density-dependent models $N_{t + 1} = M (N_{t}) N_{t}$ , the growth rate generally decreases when population increases (see, however, [27]). The behaviour of nonlinear dynamic systems has received a lot of mathematical attention. Discrete time models exhibit successive bifurcations in asymptotic behaviour when the maximum growth rate increases [28], often culminating in chaotic behaviour. However, most realistic applications to vertebrate populations lead to a stable equilibrium.

In random environment models, the demographic parameters, and hence the matrix $M_{t}$ change randomly over time t, as a stochastic process. The long-term growth rate of the population differs from the growth rate of expected population size (Fig. 3). It can be derived from ergodic theorems on products of random matrices, organised in a coherent theory of random environment models by Tuljapurkar [29]. Remarkably, there is little theory for the simultaneous presence and potentially complex interplay of density dependence and environmental stochasticity (see, however, [30]).

Fig. 3
A typical trajectory (logarithm of population size) of the model $N_{t + 1} = m_{t} N_{t}$ . The random variable $m_{t}$ takes values 2 and 0.3, with probabilities 0.5. Expected population size grows according to $E (N_{t}) = {1.15}^{t} N_{0}$ , while, asymptotically, all trajectories are decreasing with probability 1.

Another relevant generalisation concerns demographic stochasticity, which addresses the discrete and probabilistic nature of demographic processes. Mortality is then, for instance, a binomial process. Branching processes (BP) [31], in which integer population size varies according to a Markov chain, are a canonical tool. A particularly striking feature of BP is that, when population size is prevented to diverge to infinity by density dependence, extinction is certain: stabilization can then only occur conditional on non-extinction [31], as a ‘quasi-stationary’ distribution of population size. Time to extinction follows then a geometric distribution, as commonly observed in ad hoc extinction models used in ‘Population Viability Analysis’ [32].

Discrete time models can be studied numerically, with program ULM [18] standing out as a powerful and user-friendly tool. Their empirical use directly depends on demographic parameter estimation.

3 Statistical models: modern capture–recapture methodology

Among demographic parameters, fecundity is relatively easily estimated in vertebrates. Estimating survival probabilities is a challenge that has received considerable attention over the last 20 years. In animal populations, individuals are rarely, if ever, followed exhaustively long enough to efficiently estimate survival (e.g., radio-tagging [33]). Even in plants, dormancy can prevent from detecting individuals [34] and using models based on exhaustive follow-up. While early survival studies based on marked individuals [8] were derived from life table approaches, the entire topic of demographic parameter estimation in natural populations has been recast in the comprehensive framework of capture-mark-recapture (CMR) methodology. Marking individuals, at birth or later, and sampling them through time and space is indeed the closest counterpart that one may reach of the exhaustive registration of births and deaths in human populations.

CMR methods were first developed for closed populations, i.e., with no death or recruitment of individuals, recruitment in a generic sense being the entry in the part of the population amenable to capture. The assumption of closure often appeared untenable: mortality and recruitment were first viewed as nuisance parameters, needed to remain able to estimate population size. Early developments culminated in a fully stochastic model [35,36]. However, realizing that survival probabilities could be estimated based on successive sampling of marked individuals, without reference to their dilution among the unmarked ones [37], induced a move in emphasis from the estimation of population size to that of survival probabilities [38]. The resulting Cormack–Jolly–Seber (CJS) survival model generalises binomial chains for follow-up data to CMR data. In its original version, the survival and detection probabilities were time dependent, to be able to obtain explicit estimators. Soon, generalisations took into account variation in parameters with age [39]. Optimal goodness-of-fit contingency table tests partitioned into interpretable components were developed [40,41].

In parallel, the 1970s saw the development of generalized linear models (GLM), in which covariates or factors (as in Analysis of Variance) are considered to affect counts, proportions... [42]. GLM ideas spread progressively in CMR models, with constant parameter models, models with covariates, etc. [43–45]. These developments were gathered, with an emphasis on flexibility in answering biological questions, in a comprehensive framework [46] with powerful and flexible software [47,48]. As an example, Table 3 shows how survival of the Alsace White Stork was related to drought in the Sahel wintering grounds [49]. Flexibility was enhanced by the development of model selection ideas [50], parameter identifiability diagnostics [51], and models alleviating the deleterious effect of heterogeneity of capture [52,53].

Table 3

An example of relation between survival and an environmental covariate: Alsace White Stork adult survival and rain in Segou, in the Sahel wintering zone (after [49], simplified and completed). In the CMR survival models presented the probability of recapture is constant; ‘Experience’ corresponds to newly seen and already seen breeders; Rain corresponds to a logistic-linear relationship between survival and rain in Segou, by Experience class (2) or additively to Experience (3). The minimal Akaike Information Criterion [50] points to model (3) in which survival decreases with Sahel drought spells. Based on sensitivity analysis (Table 2), the induced variation in survival is sufficient to explain the strong decrease in the Alsace White Stork population

Survival model	Number of parameters	Relative deviance	Akaike information criterion
(1) Experience. Time	40	342.56	422.56
(2) Experience. Rain	5	375.50	385.50
(3) Experience + Rain	4	376.29	384.29
(4) Experience	3	385.75	391.75

Recent and promising developments concern random effects. For instance, survival probabilities over time can be modelled as $S_{t} = f (a + ε_{t})$ , with a single variance parameter $var (ε_{t}) = σ$ . Random effects are also useful to assess the effect of a covariate in the presence of unexplained environmental variability, as $S_{t} = f (a + b x_{t} + ε_{t})$ . Bayesian methods provide suitable algorithms such as Monte-Carlo Markov Chains to estimate parameters [54,55].

Multistate capture–recapture (MSCR) models are a recent and powerful generalization: individuals move among several sites or states, still with incomplete detection over discrete occasions [56–58]. MSCR models encompass survival models based on live recapture (CJS), dead recoveries of marked individuals [59], and mixtures of such pieces of information [60]. They cover also models to analyse and estimate recruitment [61,62], natal and breeding dispersal [63,64]. Multievent models, a most promising generalization of MSCR models, consider uncertainty in state determination [65]. MSCR and multievent models are CMR counterparts of longitudinal models used in human behaviour and health studies [66].

In empirical population assessment, demographic parameter estimates, denoted in a generic fashion $\hat{θ}$ , are often fed into a matrix model $N_{t + 1} = M_{t} (θ) N_{t}$ . For instance, under constant parameters, the resulting dominant eigenvalue $\hat{ρ} = ρ (M (\hat{θ}))$ is an estimate of the asymptotic population growth rate. Estimates of its sampling uncertainty can be derived from sensitivity analysis [67]. When parameters vary over time, the model trajectory and population counts can be graphically compared, in an ad hoc fashion. Recent promising work [55,68,69] has proposed to formally link dynamical and statistical models using state-space models. The information from population counts is then combined with that from CMR data to estimate demographic parameters and population numbers and structure over time, based on Kalman filtering of Bayesian techniques. Such integrated modelling also offers possibilities of forecasting, of special interest for population management [70].

4 Consequences on the understanding of vertebrate population dynamics

Progress in capture–recapture methodology, including software, has been rapidly transferred to biologists, in a fashion similar to the transfer of progress in survival models [71] in biomedical research. It induced a “revolution, [...] still ongoing, and literally induced hundreds of papers” [72]. Ad hoc and irrelevant techniques (return rates, life tables) were nearly abandoned, which resulted in less biased estimates, often validated by using dynamical models. Since most sources of bias tended to underestimate survival, progress thus often resulted in an upward trend in survival estimates for a same species over time [23,73].

The linear model philosophy in CMR induced a strong focus on biological questions, as in the White Stork example. Evidence was obtained of the effects of wide-scale climatic variables and climate change on animal demography [74]. Accession to reproduction in animal populations was proven to be progressive [63,75]. Unambiguous evidence for a cost of reproduction on survival or future reproduction was obtained in observational [76] and experimental studies [77], demonstrating some trade-offs predicted by evolutionary theory. Similarly, senescence in survival [78,79] and life-long differences in demographic performance between cohorts [80] were shown to be common in ungulates.

Dispersal studies greatly benefited from the development of multistate models, providing information complementary to molecular marker estimates of gene flow [81]. The greater site fidelity of adult birds compared to immatures was largely confirmed, and dispersal was shown to vary with the environment [64], disturbance [63], and social behaviour [82]. In parallel, reflections on subdivided populations, or ‘metapopulations’ sensu lato [83] and dispersal studies helped renewing the concept of density dependence, emphasizing local density dependence [84,85], according to which dispersal, fecundity and survival may vary with local density through access to resource. Strong results were obtained in mammals [78,86]. Surprisingly, density dependence has been the subject of few manipulative experiments since the 1950s [87], although bird species using nest boxes seem an ideal material.

Changes in numbers are now currently interpreted in terms of turnover of individuals and of influential parameters, in a striking shift from pattern to process, whether at the single species level [88] or in a comparative perspective [80]. The upward revisions of survival, and the downward revision of recruitment, breeding propensity and reproductive output resulted in larger estimates of generation time, a integrative index of the position of a species or population on the ‘slow–fast’ gradient [22]. This gradient ranks species from slow, low reproduction, low maximum growth rate (K) species to fast, high-reproduction, low-survival, high-growth rate (r) species [89]. Generation time being inversely related to maximum growth rate [90], maximum growth rates in Vertebrates are thus lower than previously thought, a conclusion critical for conservation biology. For instance seabirds, with, commonly, generation times >20 years, stand out as species with a low maximum growth rate ( $< 5 %$ per year). They are thus extremely sensitive to man-induced mortality, e.g., incidental fishery by-catch [90,91]. Longevity and body size, strongly correlated with longevity [92,93] are indeed good predictors of extinction risk. Whether one speaks of Albatross, Whales, California Condors, sea turtles or Sequoias, there is thus a genuine “malediction of long-lived species”. Progress in vertebrate population modelling has played a major role in drawing the attention to this problem. These concerns come close to those on the overexploitation of marine resources [7], for which progress in quantitative approaches has also been decisive.

5 Discussion

The joint development of matrix models and capture-mark-recapture methods has led to a comprehensive and powerful theory and methodology for vertebrate population dynamic studies [94]. These studies have both benefited from and been at the source of much of this methodological development, in a fascinating pluridisciplinary story. The data from many long-term programs are being efficiently used to address a variety of biological questions, from evolutionary theory [95] to conservation ecology [96]. This revolution has definitely moved the emphasis in population dynamics from pattern to process.

Based on foreseeable developments, one can clearly predict population modelling in the broad sense considered here will still develop and diversify, and go on intimately influencing population biology as a whole. Three most promising directions are mixed models (random effects), integrated modelling and multievent (‘uncertain-state’) models. Mixed models allow partitioning variation in demographic rates, and their spread will mostly depend on the availability of user-friendly software. Integrated modelling is a natural way of analyzing ‘integrated monitoring’ combining population counts with CMR data. Continuing progress in individual marks and electronic devices providing access to biological characteristics [97] will have several consequences. First, it will require further developments of multistate and multi-event models. Secondly, population modelling will emphasize process even more strongly by bridges with individual-based and behaviour-based models [98]. These models focus on optimal individual choice rules (for dispersal, reproduction...), at the expense of parameter estimation procedures, while the demographic methods reviewed here focus on estimation and population-level mechanisms.

On the biological side, experiments on density dependence are needed to progress on this still challenging question. Continuing progress in the reliability of demographic parameter estimates will also induce broad revaluations in comparative demography, with strong consequences on conservation biology and our understanding of the diversification of life histories. Population modelling has become an integral part of population biology.

Bibliographie

[1] P. Chesson Predator-prey theory and variability, Annu. Rev. Ecol. Syst., Volume 9 (1978), pp. 323-347

[2] M. Thellier Modélisation de systèmes complexes en agronomie et environnement, C. R. Biologies, Volume 329 (2006), pp. 1-2

[3] L. Euler Recherches générales sur la mortalité et la multiplication du genre humain, Hist. Acad. R. Sci. Belles Lettres Belg. (1760), pp. 144-164

[4] P.E. Verhulst Notice sur la loi que suit la population dans son accroissement, Corresp. Math. Phys., Volume 10 (1838), pp. 113-121

[5] N. Eldredge Life in the Balance: Humanity and the Biodiversity Crisis, Princeton University Press, Princeton, NJ, USA, 1998

[6] J.A. Thomas; M.G. Telfer; D.B. Roy; C.D. Preston; J.J.D. Greenwood; J. Asher; R. Fox; R.T. Clarke; J.H. Lawton Comparative losses of British butterflies, birds, and plants and the global extinction crisis, Science, Volume 303 (2004), pp. 1879-1881

[7] L. Laubier (coordinateur), Exploitation et surexploitation des ressources marines vivantes, Rapport sur la science et la technologie n° 17, Académie des sciences, Lavoisier, Paris, 2003

[8] D. Lack The age of the blackbird, Br. Birds, Volume 36 (1943), pp. 166-175

[9] J.C. Coulson; E. White An analysis of the factors influencing the clutch size of the Kittiwake, Proc. Zool. Soc. Lond., Volume 136 (1961), pp. 207-217

[10] P.J. Greenwood; P.H. Harvey The natal and breeding dispersal of birds, Annu. Rev. Ecol. Syst., Volume 13 (1982), pp. 1-21

[11] D. Lack The Natural Regulation of Animal Numbers, Oxford University Press, Oxford, UK, 1954

[12] H.G. Andrewartha; L.C. Birch The Distribution and Abundance of Animals, University of Chicago Press, Chicago, IL, USA, 1954

[13] M.A. Hixon; S.W. Pacala; S.A. Sandin Population regulation: Historical context and contemporary challenges of open vs. closed systems, Ecology, Volume 83 (2002), pp. 1490-1508

[14] P.H. Leslie On the use of matrices in population mathematics, Biometrika, Volume 33 (1945), pp. 183-212

[15] H. Caswell Matrix Population Models, Sinauer, Sunderland, MA, USA, 2001

[16] J.-D. Lebreton Demographic models for subdivided populations: the renewal equation approach, Theor. Popul. Biol., Volume 49 (1996), pp. 291-313

[17] J.-D. Lebreton Age, stages, and the role of generation time in matrix models, Ecol. Mod., Volume 188 (2005), pp. 22-29

[18] S. Legendre; J. Clobert ULM, a software for conservation and evolutionary biologists, J. Appl. Stat., Volume 22 (1995), pp. 817-834

[19] N. Keyfitz Reconciliation of population growth models: matrix, integral equation and partial fraction, J. R. Stat. Soc. A, Volume 130 (1967), pp. 61-83

[20] J.-D. Lebreton Un modèle probabiliste de la dynamique des populations de Cigogne blanche C. ciconia en Europe occidentale (J.M. Legay; R. Tomassone, eds.), Biométrie et écologie, Société française de biométrie, Paris, 1978, pp. 277-343

[21] P.H. Leslie The intrinsic rate of increase and the overlap of successive generations in a population of guillemots (Uria aalge Pont.), J. Anim. Ecol., Volume 35 (1966), pp. 291-301

[22] J.-M. Gaillard; N.G. Yoccoz; J.-D. Lebreton; C. Bonenfant; S. Devillard; A. Loison; D. Pontier; D. Allainé Generation time: a reliable metric to measure life history variation among mammalian populations, Am. Nat., Volume 166 (2005), pp. 119-123

[23] J.-D. Lebreton; J. Clobert Bird population dynamics, management and conservation: the role of mathematical modelling (C.M. Perrins; J.-D. Lebreton; G.J.M. Hirons, eds.), Bird Population Studies, Relevance to Conservation and Management, Oxford University Press, Oxford, UK, 1991, pp. 104-125

[24] F.R. Sharpe; A.J. Lotka A problem in age-distribution, Phil. Mag., Ser., Volume 6 21 (1911), pp. 435-438

[25] J.-D. Lebreton; M. Khaladi; V. Grosbois An explicit approach to evolutionarily stable dispersal strategies: no cost of dispersal, Math. Biosci., Volume 165 (2000), pp. 163-176

[26] E.N. Brooks; J.-D. Lebreton Optimizing removal to control a metapopulation: application to the yellow legged herring gull (Larus cachinnans), Ecol. Model., Volume 136 (2001), pp. 269-284

[27] F. Courchamp; T. Clutton-Brock; B. Grenfell Inverse density dependence and the Allee effect, Trends Ecol. Evol., Volume 14 (1999), pp. 405-410

[28] R.M. May; G.F. Oster Bifurcations and dynamic complexity in simple ecological models, Am. Nat., Volume 110 (1976), pp. 573-599

[29] S. Tuljapurkar Population Dynamics in Variable Environments, Springer-Verlag, New York, USA, 1990

[30] R. Lande; S. Engen; B.-E. Sæther Stochastic Population Dynamics in Ecology and Conservation, Oxford University Press, Oxford, UK, 2003

[31] F. Gosselin; J.-D. Lebreton The potential of branching processes as a modeling tool for conservation biology (S. Ferson; M. Burgman, eds.), Quantitative Methods in Conservation Biology, Springer, New York, USA, 2000, pp. 199-225

[32] M.S. Boyce Population viability analysis, Annu. Rev. Ecol. Syst., Volume 23 (1992), pp. 481-506

[33] K.H. Pollock; S.R. Winterstein; C.M. Bunck; P.D. Curtis Survival analysis in telemetry studies: the staggered entry design, J. Wildl. Manage., Volume 53 (1989), pp. 7-15

[34] M. Kéry Extinction rate estimates for plant populations in revisitation studies: importance of detectability, Conserv. Biol., Volume 18 (2004), pp. 570-574

[35] G.M. Jolly Explicit estimates from capture–recapture data with both death and immigration–stochastic model, Biometrika, Volume 52 (1965), pp. 225-247

[36] G.A.F. Seber A note on the multiple-recapture census, Biometrika, Volume 52 (1965), pp. 249-259

[37] R.M. Cormack Estimates of survival from the sighting of marked animals, Biometrika, Volume 51 (1964), pp. 429-438

[38] C. Brownie Recent models for mark-recapture and mark-resighting data, Biometrics, Volume 43 (1987), pp. 1017-1022

[39] K.H. Pollock A K-sample tag-recapture model allowing for age-dependent survival and catchability, Biometrika, Volume 62 (1975), pp. 577-583

[40] K.P. Burnham, D.R. Anderson, G.C. White, C. Brownie, K.H. Pollock, Design and analysis methods for fish survival experiments based on release–recapture, Am. Fish. Soc. Monogr. 5, Bethesda, MD, USA, 1987

[41] K.H. Pollock; J.E. Hines; J.D. Nichols Goodness-of-fit tests for open capture–recapture models, Biometrics, Volume 41 (1985), pp. 399-410

[42] P. McCullagh; J.A. Nelder Generalized Linear Models, Chapman and Hall, New York, USA, 1989

[43] J. Clobert; J.-D. Lebreton Dépendance de facteurs de milieu dans les estimations de taux de survie par capture–recapture, Biometrics, Volume 41 (1985), pp. 1031-1037

[44] G.M. Jolly Mark-recapture models with parameters constant in time, Biometrics, Volume 38 (1982), pp. 301-321

[45] P.M. North; B.J.T. Morgan Modelling heron survival using weather data, Biometrics, Volume 35 (1979), pp. 667-681

[46] J.-D. Lebreton; K.P. Burnham; J. Clobert; D.R. Anderson Modeling survival and testing biological hypotheses using marked animals: a unified approach with case studies, Ecol. Monogr., Volume 62 (1992), pp. 67-118

[47] R. Choquet; A.-M. Reboulet; R. Pradel; O. Gimenez; J.-D. Lebreton M-SURGE: New software specifically designed for multistate capture–recapture models, Anim. Biodivers. Conserv., Volume 27 (2004) no. 1, pp. 207-215

[48] G.C. White; K.P. Burnham Program MARK: survival estimation from populations of marked animals, Bird Study, Volume 46 (1999) no. suppl., pp. 120-139

[49] S. Kanyamibwa; A. Schierer; R. Pradel; J.-D. Lebreton Changes in adult annual survival rates in a western European population of the White Stork (Ciconia ciconia), Ibis, Volume 132 (1990), pp. 27-35

[50] K.P. Burnham; D.R. Anderson Model Selection and Inference, a Practical Information-Theoretic Approach, Springer-Verlag, New York, USA, 1998

[51] E.A. Catchpole; B.J.T. Morgan Detecting parameter redundancy, Biometrika, Volume 84 (1997), pp. 187-196

[52] W.L. Kendall; J.D. Nichols; J.E. Hines Estimating temporary emigration using capture–recapture data with Pollock's robust design, Ecology, Volume 78 (1997), pp. 563-578

[53] S. Pledger; K.H. Pollock; J.L. Norris Open capture–recapture models with heterogeneity. I. Cormack–Jolly–Seber model, Biometrics, Volume 59 (2003), pp. 786-794

[54] S.P. Brooks; E.A. Catchpole; B.J.T. Morgan Bayesian methods for analysing ringing data, J. Appl. Stat., Volume 29 (2002), pp. 187-206

[55] L. Thomas; S.T. Buckland; K.B. Newman; J. Harwood A unified framework for modelling wildlife population dynamics, Aust. N. Z. J. Stat., Volume 47 (2005), pp. 19-34

[56] A.N. Arnason The estimation of population size, migration rates and survival in a stratified population, Res. Popul. Ecol., Volume 15 (1973), pp. 1-8

[57] J.B. Hestbeck; J.D. Nichols; R. Malecki Estimates of movement and site fidelity using mark-resight data of wintering Canada geese, Ecology, Volume 72 (1991), pp. 523-533

[58] J.-D. Lebreton; R. Pradel Multistate recapture models: modeling incomplete individual histories, J. Appl. Stat., Volume 29 (2002), pp. 353-369

[59] C. Brownie, D.R. Anderson, K.P. Burnham, D.S. Robson, Statistical inference from band recovery data – a handbook, U.S. Fish Wildl. Serv. Resour. Publ. 156, 1985

[60] J.-D. Lebreton; T. Almeras; R. Pradel Competing events, mixtures of information and multistrata recapture models, Bird Study, Volume 46 (1999) no. suppl., pp. 39-46

[61] J. Clobert; J.-D. Lebreton; D. Allaine; J.-M. Gaillard The estimation of age-specific breeding probabilities from recaptures or resightings of marked animals. II Longitudinal models, Biometrics, Volume 50 (1994), pp. 375-387

[62] R. Pradel; J.-D. Lebreton Comparison of different approaches to study the local recruitment of breeders, Bird Study, Volume 46 (1999) no. suppl., pp. 74-81

[63] J.-D. Lebreton; J.E. Hines; R. Pradel; J.D. Nichols; J.A. Spendelow Estimation by capture–recapture of recruitment and dispersal over several sites, Oikos, Volume 101 (2003), pp. 253-264

[64] E.A. Schreiber; P.F.J. Doherty; G.A. Schenk Dispersal and survival rates of adult and juvenile red-tailed tropic birds (Phaethon rubricauda) exposed to potential contaminants, Anim. Biodivers. Conserv., Volume 27 (2004) no. 1, pp. 531-540

[65] R. Pradel Multievent: An extension of multistate capture–recapture models to uncertain states, Biometrics, Volume 61 (2005), pp. 442-447

[66] G.M. Fitzmaurice; N.M. Laird; S.R. Liptsitz Analyzing incomplete longitudinal binary responses: a likelihood-based approach, Biometrics, Volume 50 (1994), pp. 601-612

[67] E.R. Alvarez-Buylla; M. Slatkin Finding confidence limits on population growth rates, Trends Ecol. Evol., Volume 6 (1991), pp. 221-224

[68] P. Besbeas; J.-D. Lebreton; B.J.T. Morgan The efficient integration of abundance and demographic data, J. R. Stat. Soc. C (Appl. Stat.), Volume 52 (2002), pp. 95-102

[69] S.T. Buckland; K.B. Newman; L. Thomas; N.B. Koesters State-space models for the dynamics of wild animal populations, Ecol. Model., Volume 171 (2004), pp. 157-175

[70] G. Gauthier, P. Besbeas, J.-D. Lebreton, B.J.T. Morgan, Population growth in greater snow geese: a new modeling approach integrating demographic and census information (submitted for publication)

[71] D.R. Cox Regression models and life-tables, J. R. Stat. Soc. B, Volume 34 (1972), pp. 187-220

[72] G.A.F. Seber; C.J. Schwarz Capture–recapture: before and after EURING 2000, J. Appl. Stat., Volume 29 (2002), pp. 5-18

[73] B.R. Schmidt; M. Schaub; B.R. Anholt Why you should use capture–recapture methods when estimating survival and breeding probabilities: on bias, temporary emigration, overdispersion, and common toads, Amphibia-Reptilia, Volume 23 (2002), pp. 375-388

[74] I.L. Jones; F.M. Hunter; G.J. Robertson Annual adult survival of Least Auklets (Aves, Alcidae) varies with large-scale climatic conditions of the North Pacific Ocean, Oecologia, Volume 133 (2002), pp. 38-44

[75] P. Jouventin; H. Weimerskirch Changes in the population size and demography of southern seabirds: management implications (C.M. Perrins; J.-D. Lebreton; G.J.M. Hirons, eds.), Bird Population Studies, Relevance to Conservation and Management, Oxford University Press, Oxford, UK, 1991, pp. 297-314

[76] A. Viallefont; E.G. Cooch; F. Cooke Estimation of trade-offs with capture–recapture models: A case study on the lesser snow goose, J. Appl. Stat., Volume 22 (1995), pp. 847-861

[77] T. Boulinier; G. Sorci; J. Clobert; E. Danchin An experimental study of the costs of reproduction in the Kittiwake Rissa tridactyla: comment, Ecology, Volume 78 (1997), pp. 1284-1287

[78] M. Festa-Bianchet; J.-M. Gaillard; J.T. Jorgenson Mass- and density-dependent reproductive success and reproductive costs in a capital breeder, Am. Nat., Volume 152 (1998), pp. 367-379

[79] A. Loison; M. Festa-Bianchet; J.-M. Gaillard; J.T. Jorgenson; J.-M. Jullien Age-specific survival in five populations of ungulates: evidence of senescence, Ecology, Volume 80 (1999), pp. 2539-2554

[80] J.-M. Gaillard; M. Festa-Bianchet; N.G. Yoccoz; A. Loison; C. Toïgo Temporal variation in fitness components and population dynamics of large herbivores, Annu. Rev. Ecol. Syst., Volume 31 (2000), pp. 367-393

[81] P.M. Thompson; S. Goodman Direct and indirect estimates of dispersal distances, Trends Ecol. Evol., Volume 12 (1997), pp. 195-196

[82] E. Danchin; T. Boulinier; M. Massot Conspecific reproductive success and breeding habitat selection: implications for the study of coloniality, Ecology, Volume 79 (1998), pp. 2415-2428

[83] I. Hanski; M. Gilpin Metapopulation dynamics: brief history and conceptual domain, Biol. J. Linn. Soc. Lond., Volume 42 (1991), pp. 3-16

[84] W.W. Murdoch Population regulation in theory and practice, Ecology, Volume 75 (1994), pp. 271-287

[85] A. Stewart-Oaten; W.W. Murdoch Temporal consequences of spatial time-dependence, J. Anim. Ecol., Volume 59 (1990), pp. 1027-1045

[86] N.C. Stenseth; H. Viljugrein; T. Saitoh; T.F. Hansen; M.O. Kittilsen; E. Bølviken; F. Glöckner Seasonality, density dependence, and population cycles in Hokkaido voles, Proc. Natl Acad. Sci. USA, Volume 100 (2003), pp. 11478-11483

[87] M.M. Hensley; J.B. Cope Further data on removal and repopulation of the breeding birds in a spruce-fir forest community, Auk, Volume 68 (1951), pp. 483-493

[88] G. Loery; J.D. Nichols; J.E. Hines Capture–recapture analysis of a wintering Black-capped Chickadee population in Connecticut, 1958–1993, Auk, Volume 114 (1997), pp. 431-442

[89] D. Western; J. Ssemakula Life history patterns in birds and mammals and their evolutionary interpretation, Oecologia, Volume 54 (1982), pp. 281-290

[90] C. Niel; J.-D. Lebreton Using demographic invariants to detect overharvested bird populations from incomplete data, Conserv. Biol., Volume 19 (2005), pp. 826-835

[91] H. Weimerskirch; N. Brothers; P. Jouventin Population dynamics of Wandering Albatross Diomedea exulans and Amsterdam Albatross Diomedea amsterdamensis in the Indian Ocean and their relationships with long-line fisheries: conservation implications, Biol. Conserv., Volume 79 (1997), pp. 257-270

[92] M. Cardillo; G.M. Mace; K.E. Jones; J. Bielby; O.R.P. Bininda-Emonds; W. Sechrest; C.D.L. Orme; A. Purvis Multiple causes of high extinction risk in large mammal species, Science, Volume 309 (2005), pp. 1239-1241

[93] C.N. Johnson What can the data on late survival of Australian megafauna tell us about the cause of their extinction?, Quat. Sci. Rev., Volume 24 (2005), pp. 2167-2172

[94] B.K. Williams; J.D. Nichols; M.J. Conroy Analysis and Management of Animal Populations, Academic Press, San Diego, CA, USA, 2002

[95] J.D. Nichols; W.L. Kendall The use of multi-state capture–recapture models to address questions in evolutionary ecology, J. Appl. Stat., Volume 22 (1995), pp. 835-846

[96] Quantitative Methods for Conservation Biology (S. Ferson; M. Burgman, eds.), Springer, New York, USA, 2000

[97] J.-P. Gendner; M. Gauthier-Clerc; C. Le Bohec; S. Descamps; Y. Le Maho A new application for transponders in studying penguins, J. Field Ornithol., Volume 76 (2005), pp. 138-142

[98] P.A. Stephens; F. Frey-Roos; W. Arnold; W.J. Sutherland Model complexity and population predictions. The alpine marmot as a case study, J. Anim. Ecol., Volume 71 (2002), pp. 343-361

Commentaires - Politique